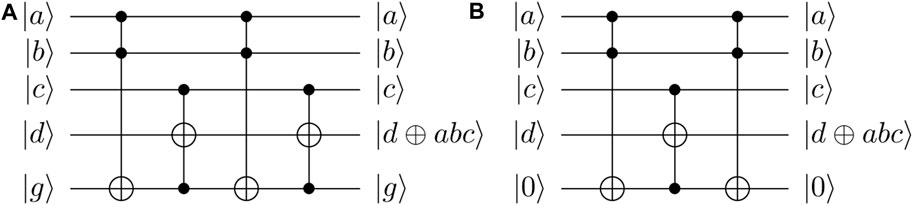- 1State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, China
- 2Henan Key Laboratory of Network Cryptography Technology, Zhengzhou, China
Optimizing the quantum circuit for implementing Advanced Encryption Standard (AES) is crucial for estimating the necessary resources in attacking AES by the Grover algorithm. Previous studies have reduced the number of qubits required for the quantum circuits of AES-128/-192/-256 from 984/1112/1336 to 270/334/398, which is close to the optimal value of 256/320/384. It becomes a challenging task to further optimize them. AimTaking aim at this task, we find a method for how the quantum circuit of AES S-box can be designed with the help of the automation tool LIGHTER-R. Particularly, the multiplicative inversion in
1 Introduction
The parallelism of quantum computing makes quantum computers have significant speed-up compared with classical computers in certain specific problems, such as solving linear systems [1–3], classification [4–8], dimensionality reduction [9–12], linear regression [13–15], association rule mining [16], anomaly detection [17,18] and so on. Quantum algorithms, such as Shor [19], Grover [20], and Simon [21], seriously threaten the security of modern cryptography. Although the scale of quantum computers is not enough to break through the cryptographic primitives so far, with the development of technology, these quantum algorithms will be realized in the future. Thus, accurately estimating the actual arrival time of quantum threats is the key to ensuring the steady renewal of the cryptosystem. With the steady development of quantum computing hardware, evaluating the minimum quantum resources required to realize Shor, Grover, Simon, and other cryptanalysis quantum algorithms has become one of the main factors affecting the actual arrival time of quantum threats. For example, because T-depth and number of qubits realized by current quantum computers are limited, they are regarded as the main optimization goal in most previous studies about the quantum circuit implementations of the above algorithms.
It is significant to estimate the cost of the Grover algorithm attacking Advanced Encryption Standard (AES) [22]. On the one hand, AES is one of the most studied and popular symmetric ciphers in the world. On the other hand, the cost was used as the benchmark to define different security levels of post-quantum public-key schemes when the National Institute of Standards and Technology (NIST) [23] called for proposals for the standardization of post-quantum cryptography. In the implementation, the quantum circuit of AES is the core of Grover oracle, which is the most complicated part of the whole algorithm. For this reason, optimizing the quantum circuit of AES becomes an important method of reducing the quantum resources required for Grover-algorithm-attacking AES. Among the tasks necessary to optimize the quantum circuit for AES, how to use fewer resources to realize the AES S-box, the only non-linear component, is one of the main influencing factors.
Some quantum circuits of AES were designed to reduce the T-depth. In 2020, Jaques et al. [24] constructed a quantum circuit of S-box for |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ (a, b and S(a) are 8-bit vectors) with T-depth 6, and then synthesized the quantum circuit of AES-128 with a T-depth of 120. In 2022, Li et al. [25] proposed the S-box circuits for |a⟩|0⟩ → |a⟩|S(a)⟩ and |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ with T-depth 4, and then reduced the T-depth required for the quantum circuit of AES-128 to 80. Huang et al. [26] gave the circuit for |a⟩|b⟩ → |a⟩|b ⊕ S(a)⟩ with a T-depth of 3, and then further reduced the T-depth required for the quantum circuit of AES-128 to 60. Jang et al. [27] synthesized the quantum circuit of AES-128 with a T-depth of 30 by introducing an improved pipeline method for round function iteration.
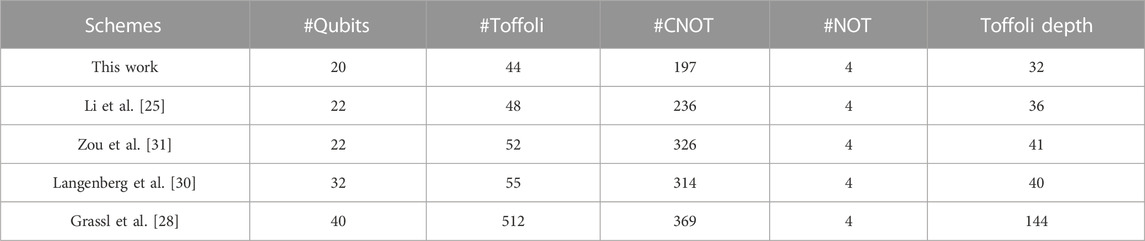
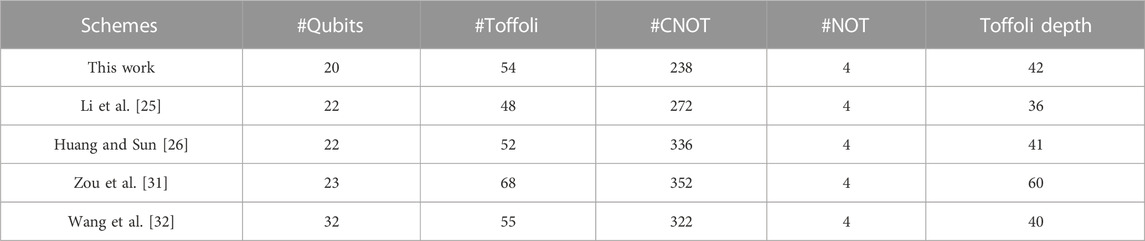
At the same time, quite a few quantum circuits of AES were designed to reduce the number of qubits (see Table 1). In 2016, Grassl et al. [28] implemented the quantum circuit of AES-128 with 984 qubits by presenting the 40 qubits quantum circuit of S-box for

TABLE 1. Summary of the number of qubits required for implementing AES-128. “RFIM” and “KSIM” represent the round function iteration method and key expansion iteration method respectively.
It can be seen that the number of qubits required for the quantum circuit of AES has been greatly improved through the efforts of scholars, approaching the optimal value of 256/320/384. It seems that further reducing them has become a challenging task. In this work, we study how the AES S-box can be constructed with fewer qubits, thereby reducing the number of qubits required for the quantum circuit of AES. Note that any mention of qubits in this work refers to logical qubits. Our contributions are as follows:
• We find a method to construct the quantum circuit of AES S-box with the help of automation tool LIGHTER-R, which can reduce the number of qubits required by
• We introduce a new technique to construct the quantum circuit of S-box for
• We find that uncomputation for removing ancilla qubits (i.e., reinstate the initial state |0⟩) in some cases can be completed with fewer Toffoli and CNOT gates (without adding additional qubits). Therefore, our S-box circuit for
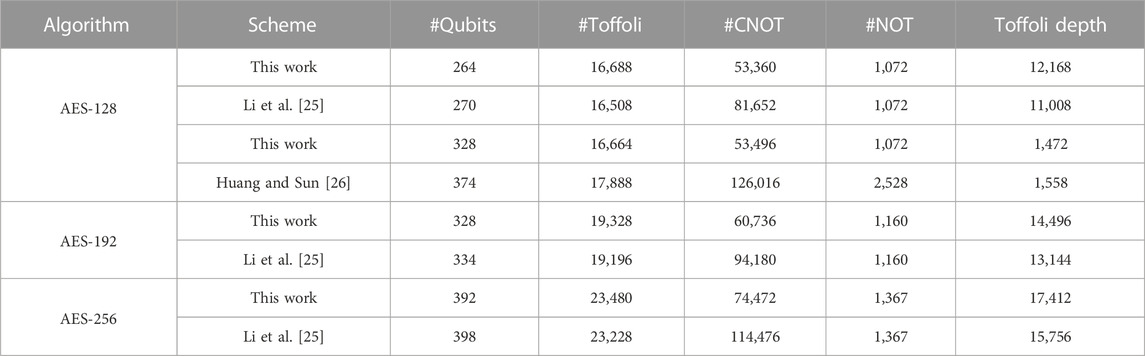
• By employing the above quantum circuits of S-box, we synthesize the quantum circuit of AES-128 with 264 qubits instead of 270 in a previous study [25], which implies a new record. Similarly, we also synthesize the quantum circuits of AES-192/-256 with 328/392 qubits instead of 334/398 in a previous study [25].
The rest of this paper is organized as follows. In Section 2, we briefly review the S-box of AES. In Section 3, we use the tool LIGHTER-R to obtain the quantum circuit of implementing the multiplicative inversion in
2 Preliminaries
2.1 The S-box of AES
2.1.1 Algebraic structure of S-box
The non-linear transformation S-box first takes a byte input
where
The computation of the S-box can be divided into two steps, i.e., computing the multiplicative inversion a−1 and performing the affine transformation. The affine transformation can be implemented with CNOT and NOT gates only. Thus, how to realize the quantum circuit of finding a−1 with low costs becomes one of the main factors optimizing the quantum circuit of the S-box.
2.1.2 A decomposition of S-box
In Ref. [34], Wolkerstorfer et al. constructed the following composite field
• The field polynomial of
• The field polynomial of
Due to isomorphism, the mapping matrix
Based on the composite field
The multiplication by invertible matrices M, AM−1 (merging of matrices A and M−1) and the addition of a constant vector c can be implemented with CNOT and NOT gates only. Thus, the key to optimizing the S-box circuit becomes how the quantum circuit of finding (Ma)−1
As pointed out in Ref. [34], any element
where
It can be seen that the implementation of the S-box can be divided into three modules, i.e., the multiplication in
3 Quantum circuit of implementing the multiplicative inversion in
Some quantum circuits of implementing the multiplicative inversion in
In Ref. [33], Dasu et al. presented an automation tool, namely, LIGHTER-R1, which can give the quantum circuit implementation of any 4-bit S-box based on a lookup table. The quantum circuit given by LIGHTER-R requires the optimal number of qubits. Recently, the tool has been widely applied in the quantum circuit implementation of other cryptography, such as Present and Gift [39], RECTANGLE and KNOT [40], DEFAULT [41] and so on.
We found that the multiplicative inversion in

FIGURE 1. Quantum circuit of implementing the multiplicative inversion in
The Tof4/C3(X)/CCCNOT gate2 in the dashed box of Figure 2 realizes the function of |a⟩|b⟩|c⟩|d⟩ → |a⟩|b⟩|c⟩|d ⊕ abc⟩ and can be decomposed by some Toffoli gates with an ancilla qubit (see Figure 2). Specifically, if the ancilla qubit is an unknown quantum state |g⟩, the CCCNOT gate can be decomposed by using the circuit in Figure 2A. If the state of |g⟩ is known to be |0⟩, the last Toffoli gate in Figure 2A is unnecessary which corresponds to Figure 2B. Thus, according to Figures 1, 2, we can obtain two quantum circuits of implementing the multiplicative inversion in
The resource estimates of these two quantum circuits for
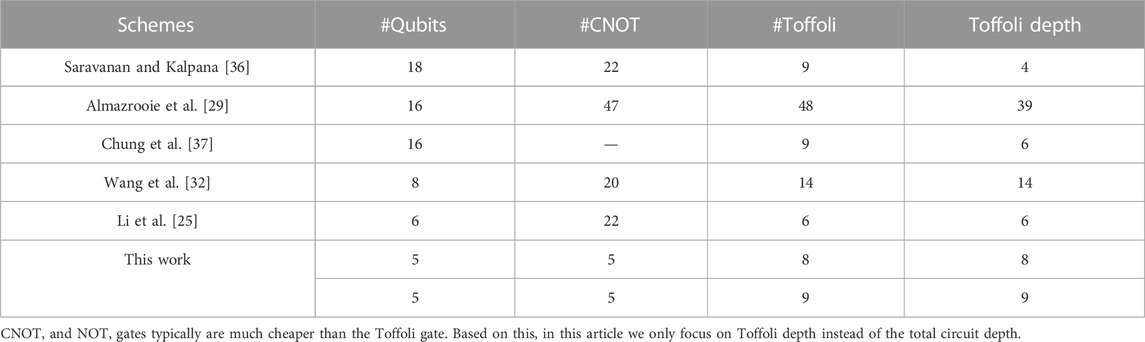
TABLE 3. Quantum resource estimates for the implementation of the multiplicative inversion in
4 Quantum circuits of S-box
In the section, we propose three quantum circuits of S-box for
• UM: |x⟩ → |Mx⟩ requires 8 qubits, 15 CNOT gates, and a total depth of 8;
• Mul: |f⟩|g⟩|04⟩ → |f⟩|g⟩|f ⋅ g⟩ requires 12 qubits, 9 Toffoli gates, 23 CNOT gates and a Toffoli depth of 6; B−Mul: |f⟩|g⟩|h⟩ → |f⟩|g⟩|h ⊕f ⋅ g⟩ requires 12 qubits, 9 Toffoli gates, 28 CNOT gates and Toffoli depth 6. Here,
•
4.1 Quantum circuit of S-box for
In order to implement the quantum circuit of S-box for
We divide into four steps, i.e., computing p17, calculating the multiplicative inversion

FIGURE 3. Quantum circuit for |p⟩|012⟩ → |p⟩|p−1⟩|04⟩. p = (p0, p1) and p−1 = (n0, n1) are 8-bit input and output vectors respectively. CNOT gates between four qubit-sized wires should be read as multiple parallel CNOT gates applied bitwise. Dashed lines indicate wires that are not used in the corresponding circuit of the square box. Using
By combining the quantum circuit in Figure 3 with UM and

FIGURE 4. Quantum circuit of the S-box for
The quantum resource estimates of
Remark 1. Compared with the circuit outlined by Li et al., our circuit is different in two aspects. First, we take an idle qubit from output qubits as ancilla qubits and then compute
Our results show that uncomputation for removing ancilla qubits (i.e., reinstate the initial state |0⟩) can be optimized when the algebraic relationship between the value in ancilla qubits and f(x) is simpler than that between x and the value in ancilla qubits. Here, assume that f(x) is an arbitrary invertible non-linear transformation, the goal circuit Uf: |x⟩|0⟩ → |x⟩|f(x)⟩ is implemented by introducing some ancilla qubits. For example, in Figure 4, x≔p, f(x)≔p−1, after getting the output information p−1, as analyzed above, the value
4.2 Quantum circuit of S-box for
In order to implement the quantum circuit of S-box for
Similar to Figure 3, we divide into four steps to implement |p⟩|h⟩ → |p⟩|h ⊕p−1⟩. First, |p17⟩ is obtained by performing
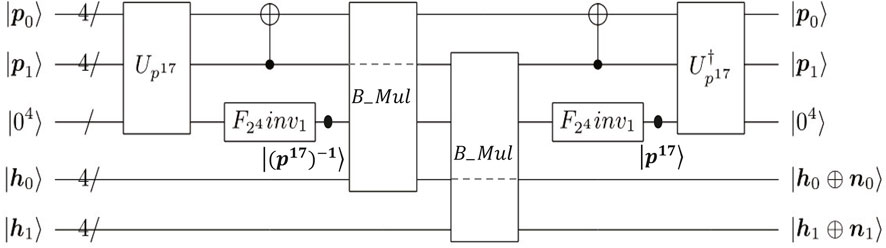
FIGURE 5. Quantum circuit for |p⟩|h⟩|04⟩ → |p⟩|h ⊕p−1⟩|04⟩. h = (h0, h1) is an arbitrary 8-bit vector.
By combining the quantum circuit in Figure 5 with UM and

FIGURE 6. Quantum circuit for
is implemented by the quantum circuit in
Figure 5 because MA−1b and Ma
are contained in
implemented by the inverse circuit of
Table 5 summarizes the quantum resources needed to realize
Remark 2. Compared with the circuit described by Li et al., we take an idle qubit from output qubits as ancilla qubits and then compute
4.3 Quantum circuit of S-box for
Based on the idea mentioned in Ref. [42], Li et al [25] and Huang et al. [26] realized the goal by connecting two quantum circuits for |a⟩|0⟩ → |a⟩|S(a)⟩ and |a⟩|S(a)⟩ → |0⟩|S(a)⟩. Here, different from the previous method, we realize the goal by proposing a quantum circuit for |p⟩ → |p−1⟩.
Similar to Figure 3, we first obtain |p17⟩ by performing
Observation 1. The quantum circuit for In−Mul: |f⟩|g⟩|0⟩ → |0⟩|g⟩|f ⋅ g⟩ can not only get f ⋅ g, but also release storage space to place other values if f is useless in subsequent operations. In−Mul can be implemented as follows
Due to (f ⋅ g) ⋅g−1 = f, the circuit Mul† (|f⟩|g⟩|f ⋅ g⟩ → |f⟩|g⟩|0⟩) is used to convert |f⟩|g−1⟩|f ⋅ g⟩ into |0⟩|g−1⟩|f ⋅ g⟩. At this moment, there exist an idle quantum state |0⟩, so |g−1⟩ is converted back into |g⟩ by
By combining the quantum circuit in Figure 7 with UM and

FIGURE 8. Quantum circuit for
Table 6 summarizes the quantum resources needed to implement the S-box circuit for
In order to reduce the number of qubits, we often would like to compute f(x) with an in-place circuit, i.e., |x⟩ → |f(x)⟩. For example, we directly obtain the in-place quantum circuit
Observation 2. |x⟩ → |f(x)⟩ can be constructed with at least 3n qubits. If f(x) can be expressed as f(x) = f0(x0)‖f1(x1) (f0(x0), f1(x1): {0,1}n → {0,1}n are invertible non-linear transformation) when x is divided into x0 and x1, i.e., x≔x0‖x1, |x⟩ → |f(x)⟩ is implemented as followed
|x0⟩ is removed to gain storage space to place f1 (x1) only when it is useless in subsequent operations. In our circuit for |p⟩ → |p−1⟩, x≔p = p0‖p1 and f(x)≔p−1 = f0 (x0)‖f1 (x1) (note
5 Quantum circuit implementations of AES
AES is a family of iterative block ciphers, which encrypts 16 bytes (i.e., 128 bits) of plaintexts and consists of a round function and key expansion. The subroutines of the round function include SubBytes, ShiftRows, MixColumns, and AddRoundKey (note the last round does not perform the MixColumns). The subroutines of key expansion include SubWord, RotWord, and Rcon. AES’s three instances AES-128 (10 iterations), AES-192 (12 iterations), and AES-256 (14 iterations) correspond to the key lengths of 128, 192, and 256 bits respectively. The full specification of AES can be found in Ref. [22].
In the present study, we implement the SubBytes (applying 16 S-box substitutions) and SubWord (applying 4 S-box substitutions) by the S-box circuits in Section 4. For other linear operations, the ShiftRows and Rotword can be implemented by appropriate rewiring. The MixColumns can be implemented with 368 CNOT gates [43]. The AddRoundKey is implemented with 128 CNOT gates. The Rcon is implemented by applying NOT gates.
In the following, we introduce the methods of round function iteration and key expansion iteration, then synthesize the quantum circuit of AES.
5.1 Method of round function iteration
As shown in Table 1, quite a few round function iteration methods were introduced. Grassl et al. [28] proposed the zig-zag method, which requires 512 + 24 = 536 qubits (24 is the number of ancilla qubits required by their S-box circuit for
We also apply Li et al.’s straight-line method to realize the round function iteration of AES-128. From Figure 8, we can see that our S-box circuit for
Remark 3. We can also make a trade-off between the number of qubits and Toffoli depth by adding the number of S-box circuits for
5.2 Method of key expansion iteration
Some key expansion iteration methods were proposed. Grassl et al. [28] proposed the pipeline method, which requires at least 448 + 24 = 472 qubits (24 is the number of ancilla qubits required by their S-box circuit for
Here, we apply the straight-line method to implement the key expansion iteration of AES-128. Because our S-box circuit for
Remark 4. In synthesizing the quantum circuit of the AES, if the SubBytes in Ri and SubWord in the key expansion are not constructed simultaneously, we can reuse idle qubits, which is applied to implement the round function iteration, to construct the SubWord. Thus, as the previous studies Grassl et al. [28]; Almazrooie et al. [29]; Langenberg et al. [30]; Wang et al. [32]; Li et al. [25]; Zou et al. [31], they implement the key expansion without adding additional ancilla (see Table 1). Otherwise, as a trade-off between the number of qubits and Toffoli depth, it is necessary to add new qubits as the previous studies [24,26].
5.3 Quantum circuits for implementing AES
Based on the straight-line method above, we synthesize the quantum circuit of AES-128 with 264 qubits, where 136 qubits and 128 qubits are used to complete the round function iteration and key expansion iteration. Note that 8 ancilla qubits in round function iteration are reused to implement the key expansion iteration.
First, as mentioned in the previous studies [25, 26, 28, 31], to save qubits, R0 which adds the key K0 on plaintext m (whitening step) is implemented by apply NOT gates on some specific qubits of |K0⟩ (at most 128 NOT gates). Then when |R0⟩ is used to compute the SubBytes in R1 later, |R0⟩ is reinstated |K0⟩ by applying NOT gates (at most 128 NOT gates). Particularly, the SubBytes in R1 are constructed by running our S-box circuit for
Then, we implement Ri (i > 1). Because
At last, by combining these quantum circuits above, we can obtain the quantum circuit for implementing AES-128. Similarly, the quantum circuit of AES-192/-256 can be implemented with 334/398 qubits, respectively. Table 7 gives the quantum resources required for implementing AES. Obviously, our improved quantum circuits of S-box result in a reduction of the number of qubits.
Remark 5. We can make a trade-off between the number of qubits and Toffoli-depth. From Figures 6, 8, it can be seen that the number of ancilla qubits required for two S-box circuits for
• When p = 1, circuit costs for implementing AES-128 is given in Table 7;
• When p > 1, the Toffoli-depth of constructing the SubBytes and SubWord in Ri (i > 1) becomes 78 × 18/p = 1,404/p.
• When p = 2, the depth of S-box circuit for
• When p = 3 or 6, the Toffoli-depth of SubBytes in constructing R1 is 32 × 2 = 64, and the Toffoli-depth of SubWord in constructing the round key K1 becomes 36. Thus, R1 is implemented with a Toffoli depth of 100. Here, the SubWord is constructed with the S-box circuit for
• When p = 9 or 18, the Toffoli-depth of SubBytes in constructing R1 is 32, and the Toffoli-depth of SubWord in constructing the round key K1 becomes 36. Thus, R1 is implemented with a Toffoli depth of 68. Table 7 also gives the quantum resources required for implementing AES-128 when p = 9.
6 Conclusion
In this study, we set a new record of the number of qubits required to synthesize the quantum circuit of AES. First, we find a method to realize the quantum circuit of the AES S-box with the help of the automation tool LIGHTER-R. Specifically, the main part of the S-box, i.e., the multiplicative inversion in
Some inspirations can be drawn from our results. On the one hand, automated tools, for example, the LIGHTER-R, should be fully utilized. On the other hand, similar to our circuit for |a⟩ → |S(a)⟩, we should design the goal circuit directly as far as possible instead of using the previous trivial method, i.e., connecting two circuits. Particularly, since other symmetric ciphers (such as SM4 and Camellia) also use a similar S-box, their quantum circuits might be optimized by our methods.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos 61972048, 62272056, and 61976024) and Henan Key Laboratory of Network Cryptography Technology (LNCT2021-A10).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1171753/full#supplementary-material
Footnotes
1The source code of LIGHTER-R is available at https://github.com/vdasu/lighter-r.
2They refer to the same quantum gate. Only CCCNOT is mentioned below.
3The code that verifies the correctness of these S-box circuits is available at https://github.com/lzq192921/quantum-circuit-implementation-of-AES.git.
References
1. Harrow AW, Hassidim A, Lloyd S. Quantum algorithm for linear systems of equations. Phys Rev Lett (2009) 103:150502. doi:10.1103/physrevlett.103.150502
2. Wan L, Yu C, Pan S, Gao F, Wen Q, Qin S. Asymptotic quantum algorithm for the toeplitz systems. Phys Rev A (2018) 97:062322. doi:10.1103/physreva.97.062322
3. Liu H, Wu Y, Wan L, Pan S, Qin S, Gao F, et al. Variational quantum algorithm for the Poisson equation. Phys Rev A (2021) 104:022418. doi:10.1103/physreva.104.022418
4. Lloyd S, Mohseni M, Rebentrost P. Quantum algorithms for supervised and unsupervised machine learning (2013). arXiv preprint arXiv:1307.0411.
5. Wiebe N, Braun D, Lloyd S. Quantum algorithm for data fitting. Phys Rev Lett (2012) 109:050505. doi:10.1103/physrevlett.109.050505
6. Rebentrost P, Mohseni M, Lloyd S. Quantum support vector machine for big data classification. Phys Rev Lett (2014) 113:130503. doi:10.1103/physrevlett.113.130503
7. Ye Z, Li L, Situ H, Wang Y. Quantum speedup for twin support vector machines (2019). arXiv preprint arXiv:1902.08907.
8. Li Q, Huang Y, Jin S, Hou X, Wang X. Quantum spectral clustering algorithm for unsupervised learning (2022). arXiv preprint arXiv:2203.03132.
9. Lloyd S, Mohseni M, Rebentrost P. Quantum principal component analysis. Nat Phys (2014) 10:631–3. doi:10.1038/nphys3029
10. Cong I, Duan L. Quantum discriminant analysis for dimensionality reduction and classification. New J Phys (2016) 18:073011. doi:10.1088/1367-2630/18/7/073011
11. Pan S, Wan L, Liu H, Wang Q, Qin S, Wen Q, et al. Improved quantum algorithm for a-optimal projection. Phys Rev A (2020) 102:052402. doi:10.1103/physreva.102.052402
12. Yu C, Gao F, Lin S, Wang J. Quantum data compression by principal component analysis. Quan Inf Process (2019) 18:249–20. doi:10.1007/s11128-019-2364-9
13. Wang G. Quantum algorithm for linear regression. Phys Rev A (2017) 96:012335. doi:10.1103/physreva.96.012335
14. Yu C, Gao F, Wen Q. An improved quantum algorithm for ridge regression. IEEE Trans Knowledge Data Eng (2019) 33:1–866. doi:10.1109/tkde.2019.2937491
15. Yu C, Gao F, Liu C, Huynh D, Reynolds M, Wang J. Quantum algorithm for visual tracking. Phys Rev A (2019) 99:022301. doi:10.1103/physreva.99.022301
16. Yu C, Gao F, Wang Q, Wen Q. Quantum algorithm for association rules mining. Phys Rev A (2016) 94:042311. doi:10.1103/physreva.94.042311
17. Liu N, Rebentrost P. Quantum machine learning for quantum anomaly detection. Phys Rev A (2018) 97:042315. doi:10.1103/physreva.97.042315
18. Guo M, Liu H, Li Y, Li W, Gao F, Qin S, et al. Quantum algorithms for anomaly detection using amplitude estimation. Physica A: Stat Mech its Appl (2022) 604:127936. doi:10.1016/j.physa.2022.127936
19. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Comput (1997) 26:1484–509. doi:10.1137/s0097539795293172
20. Grover LK. A fast quantum mechanical algorithm for database search. In: GL Miller, editor. Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. New York, NY, USA: ACM (1996). p. 212–9.
21. Simon DR. On the power of quantum computation. SIAM J Comput (1997) 26:1474–83. doi:10.1137/s0097539796298637
22. Joan D, Vincent R. Specification for the advanced encryption standard (aes). Springfield: FIPS 197 (2001).
23.NIST. Submission requirements and evaluation criteria for the post-quantum cryptography standardization process (2016).
24. Jaques S, Naehrig M, Roetteler M, Virdia F. Implementing grover oracles for quantum key search on aes and lowmc. In: A Canteaut,, and Y Ishai, editors. Advances in cryptology – eurocrypt 2020. Cham: Springer (2020). p. 280–310.
25. Li Z, Cai B, Sun H, Liu H, Wan L, Qin S, et al. Novel quantum circuit implementation of advanced encryption standard with low costs. Sci China Phys Mech Astron (2022) 65:290311. doi:10.1007/s11433-022-1921-y
26. Huang Z, Sun S. Synthesizing quantum circuits of aes with lower t-depth and less qubits (2022). Cryptology ePrint Archive, Paper 2022/620.
27. Jang K, Baksi A, Kim H, Song G, Seo H, Chattopadhyay A. Quantum analysis of aes (2022). Cryptology ePrint Archive, Paper 2022/683.
28. Grassl M, Langenberg B, Roetteler M, Steinwandt R. Applying grover’s algorithm to aes: Quantum resource estimates. In: T Takagi, editor. Post-quantum cryptography. Cham: Springer (2016). p. 29–43.
29. Almazrooie M, Samsudin A, Abdullah R, Mutter KN. Quantum reversible circuit of aes-128. Quan Inf Process (2018) 17:112–30. doi:10.1007/s11128-018-1864-3
30. Langenberg B, Pham H, Steinwandt R. Reducing the cost of implementing the advanced encryption standard as a quantum circuit. IEEE Trans Quan Eng (2020) 1:1–12. doi:10.1109/tqe.2020.2965697
31. Zou J, Wei Z, Sun S, Liu X, Wu W. Quantum circuit implementations of aes with fewer qubits. In: S Moriai,, and H Wang, editors. Advances in cryptology – asiacrypt 2020. Cham: Springer (2020). p. 697–726.
32. Wang Z, Wei S, Long G. A quantum circuit design of aes requiring fewer quantum qubits and gate operations. Front Phys (2022) 17:41501–7. doi:10.1007/s11467-021-1141-2
33. Dasu VA, Baksi A, Sarkar S, Chattopadhyay A. Lighter-r: Optimized reversible circuit implementation for sboxes. In: 2019 32nd IEEE International System-on-Chip Conference (SOCC). Singapore: IEEE (2019). p. 260–5. doi:10.1109/SOCC46988.2019.1570548320
34. Wolkerstorfer J, Oswald E, Lamberger M. An asic implementation of the aes sboxes. In: B Preneel, editor. Topics in cryptology - CT-RSA 2002. Berlin, Heidelberg: Springer (2002). p. 67–78.
35. Almazrooie M, Abdullah R, Samsudin A, Mutter KN. Quantum grover attack on the simplified-aes. In: Proceedings of the 2018 7th International Conference on Software and Computer Applications. New York, NY, USA: ACM (2018). p. 204–11. doi:10.1145/3185089.3185122
36. Saravanan P, Kalpana P. Novel reversible design of advanced encryption standard cryptographic algorithm for wireless sensor networks. Wireless Personal Commun (2018) 100:1427–58. doi:10.1007/s11277-018-5647-z
37. Chung D, Lee S, Choi D, Lee J. Alternative tower field construction for quantum implementation of the aes s-box. IEEE Trans Comput (2022) 71:2553–64. doi:10.1109/tc.2021.3135759
38. Boyar J, Peralta R. A new combinational logic minimization technique with applications to cryptology. In: P Festa, editor. Experimental algorithms. Berlin, Heidelberg: Springer (2010). p. 178–89.
39. Jang K, Song G, Kim H, Kwon H, Kim H, Seo H. Efficient implementation of present and gift on quantum computers. Appl Sci (2021) 11:4776. doi:10.3390/app11114776
40. Baksi A, Jang K, Song G, Seo H, Xiang Z. Quantum implementation and resource estimates for rectangle and knot. Quan Inf Process (2021) 20:395–24. doi:10.1007/s11128-021-03307-6
41. Jang K, Baksi A, Breier J, Seo H, Chattopadhyay A. Quantum implementation and analysis of default (2022). Cryptology ePrint Archive.
42. Amy M, Di Matteo O, Gheorghiu V, Mosca M, Parent A, Schanck J. Estimating the cost of generic quantum pre-image attacks on sha-2 and sha-3. In: R Avanzi,, and H Heys, editors. Selected areas in cryptography – SAC 2016. Cham: Springer (2017). p. 317–37.
Keywords: AES, S-box, quantum circuit, multiplication inversion, number of qubites
Citation: Li Z, Gao F, Qin S and Wen Q (2023) New record in the number of qubits for a quantum implementation of AES. Front. Phys. 11:1171753. doi: 10.3389/fphy.2023.1171753
Received: 22 February 2023; Accepted: 13 March 2023;
Published: 24 March 2023.
Edited by:
Nanrun Zhou, Shanghai University of Engineering Sciences, ChinaReviewed by:
Mingxing Luo, Southwest Jiaotong University, ChinaTan Xiaoqing, Jinan University, China
Copyright © 2023 Li, Gao, Qin and Wen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Gao, Z2FvZkBidXB0LmVkdS5jbg==
 Zhenqiang Li
Zhenqiang Li Fei Gao
Fei Gao Sujuan Qin
Sujuan Qin Qiaoyan Wen1
Qiaoyan Wen1