A percolation-based micromechanical model for elastic stiffness and conductivity of foam concrete

Void morphology effect on percolation and even physico-mechanical performance of foam concrete is of great interest in the evaluation of service-life of civil and hydraulic infrastructures. For experiments, it is a huge challenge to quantify the percolation threshold of voids affected by their morphologies, and the dependence of elastic modulus and conductivity of foam concrete on void configurations. In this work, we focus on the prolate spheroidal void morphologies with the aspect ratios of 2.5 and 2, following the microscopic measurements reported in the literature. A numerical framework is developed to capture the percolation threshold characterized by the critical porosity of voids with both morphological types. For the verification purpose, Measurement on the critical porosity of spherical voids using the present framework as a benchmark is compared against the percolation threshold of monodisperse overlapping spheres reported in literature. Furthermore, this work proposes a simple and powerful percolation-based micromechanical model for precisely predicting the effective elastic modulus and thermal conductivity of foam concrete. It can be convinced of a general micromechanical framework to elucidate the intrinsic relationship of void morphology and percolation to the physico-mechanical properties of concrete. The present framework is capable of tailoring physical and mechanical properties through void configuration and enable foam concrete design and multifunctional applications.

1 Introduction

Foam concrete contains a number of voids, in which the porosity is up to 80% [1]. Understanding the effect of connectivity (percolation) of void network with the high porosity on the elastic and conductive properties of foam concrete is very critical to tailor the performance of foam concrete, resulting in its extensive applications in thermal insulation screeds, masonry blocks, loading-bearing panels and tunnels in rocks [2, 3].

Recently, Youssef et al. [4] presented a numerical study on the effective elastic stiffness of foam concrete that was considered as a bi-phase microstructure consisting in rigid spherical voids (akin to aggregates) and homogeneous mortar [5]. But as reported where, the simulated results of elastic modulus were dramatically larger than the experiment measurements [6] (originated from the same authors in Ref. [4]). Accordingly, the authors [4] further considered mortar as a two-phase composite consisting in spherical sand particles and homogeneous cement paste, resulting to the three-phase composite of foam concrete, to match the experimental data. On the other hand, Li et al. [7] regarded an unsaturated cement-based composite as a two-phase structure with rigid spheroidal pores and bulk paste, and utilized an effective medium approximation, exactly to be the Maxwellʼs far-field scheme, to predict its effective thermal conductivity. Similar theoretical researches have also been gave in various composite fields like ceramic-based, and particulate-based composites [8–11], considering spheroidal pores. Plus, she et al. [12] applied the FEM to simulate the thermal conductivity of cellular concrete including two-dimensional elliptical pores. By extending the same numerical strategy to the three-dimensional (3D) case, Shen and Zhou [13] recently investigated the linear elasticity and conductivity of concrete with spherical and spheroidal inclusions. It is acknowledged that the previous theoretical and numerical contributions are certainly promising and interesting in understanding the effects of porosity and pore size distribution on the elastic stiffness and thermal conductivity of cementitious-based materials like foam concrete. However, there are several points that need further discussion that motivates us to carry out this work, involving that one is the percolation of anisotropic-shaped pore network, which is a critical physical configuration of foam concrete to determining the transport and mechanical properties of materials [14, 15]. Another is how to estimate accurately the elastic stiffness and conductivity of foam concrete interacted by the percolation of voids. In this article, we will address three main concerns in the following orders: a) the void geometrical morphology, b) the percolation of void networks and c) a simple and powerful percolation-based micromechanical model for accurately predicting the normalized effective thermal conductivity and elastic modulus of foam concrete with bi-phase microstructure.

2 Void geometrical morphology

Irrespective in foam concrete, the geometrical morphologies of pores or voids are normally not perfect spherical shape. As shown in Figure 1 published in Refs. [6–8], microscale measurements have visualized void shape is close to ellipsoidal shape rather than perfect spherical shape. Especially in cement-based materials, the probe of void shapes has been carried out using diverse experimental tools, and experiments found that void shape can be well portrayed by prolate spheroidal shape, such as κ = 2.5 in mortar [16] and κ = 2 in asphalt concrete [17], where κ is the aspect ratio of a prolate spheroidal pore. Accordingly, this work exploits the percolation threshold of prolate spheroidal voids and its effects on the elastic stiffness and conductivity of foam concrete.

FIGURE 1

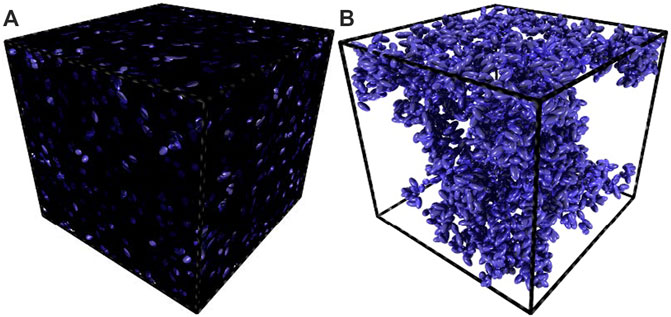
FIGURE 1. (A) Visualization of two-phase foam concrete as a finite-size cubic cell of L = 50 with periodic boundary conditions consisting in prolate spheroidal void networks (κ = 2) and homogeneous mortar; (B) Visualization of a percolating cluster of voids in foam concrete.

2.1 Percolation of voids

Under such the high porosity (up to 0.8), voids easily generate an interconnective path spanning the concrete sample, namely, the percolation of voids, which triggers the dramatic change of elastic modulus and thermal conductivity of foam concrete near the percolation threshold. Therefore, the percolation of anisotropic-shaped voids should be concerned in foam concrete. Following the experiment measurements [16, 17], we here focus on the percolation of prolate ellipsoidal voids with κ = 2.5, two and 1 (κ = 1 as spherical void that is a special case of ellipsoidal void). It is reported in Ref. [4] that the estimated moduli are nearly independent of void size distribution. Thus, we may use the continuum percolation of congruent prolate spheroidal voids to explore the dependence of percolation threshold on void geometrical shape. We adopt our previous studies [10, 18, 19] that developed a numerical framework to accurately estimate the critical porosity ϕ_c as the percolation threshold of prolate spheroidal voids, in which the Monte Carlo sampling method is applied to simulate the percolation probability versus porosity under a specific sample size, then the classical finite-size analysis is utilized to extrapolate from a local critical porosity to a global critical porosity for a specific void shape [10].

At a microscopic level, a microstructural representative volume element (RVE) of foam concrete is regarded that a number of penetrable spheroidal voids with random orientations and positions are embedded in homogeneous mortar matrix under periodic boundary conditions [19]. Without loss of generality, a cubic cell with the length of L is specified as the microstructural RVE, as shown in Figure 1A.

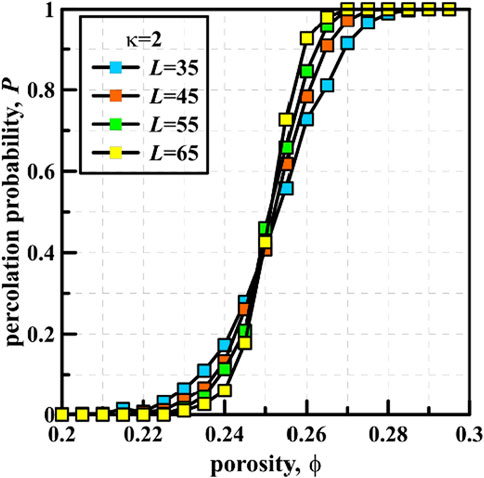
For continuum percolation models, the present coupled scheme contains two major components: 1) the identify of percolating clusters in numerical realizations under periodic boundary conditions (see Figure 1), of which the aim is the reliable derivation of curves of P (percolation probability)-ϕ (porosity) for various sample sizes L (see Figure 2), and 2) the determination of the global critical porosity of void network independent of sample size.

(1) A percolation probability P for a specific porosity is defined as the ratio of the number of RVEs with “wrapping” connective clusters to that of the total number of simulation samples [15]. For simulations, a large number of samples are required to ensure the reliability of the obtained P. In a sample, the number of spheroidal voids is calculated by N = L³ln (1- ϕ)⁻¹/V [19], where V and N is the volume and number of spheroidal void, and ϕ is porosity.

FIGURE 2

FIGURE 2. P-ϕ curves for κ = 2 with different sample sizes L.

In order to check the emergence of a “wrapping” connective cluster in each RVE, it is necessary to judge whether neighboring spheroidal voids overlap or not. With regard to spheroidal voids, a coupling strategy between the linear transformations of the coordinate system and a robust golden section search method reported by Xu and co-workers [20, 21] to realize this issue. Also, the search of a “wrapping” connective cluster in a RVE is accomplished by the famous “tree-burning” algorithm [18, 19]. Figure 1B shows a “wrapping” connective cluster in the RVE for spheroidal voids of κ = 2. Accordingly, we can obtain P corresponding to different porosities ϕ and RVE sizes L, as shown in Figure 2.

(2) As mentioned above, a local critical porosity ϕ_c(L) is defined as the porosity of the generation of a “wrapping” connective cluster in a RVE with the finite size L, which is measured by the following description. Similarly, a global critical porosity ϕ_c is defined as that of infinite-size system that is derived in a extrapolation manner, which is the objective of interest in this work. With accordance to the finite-size scaling theory [22], there is a scaling relation of the global critical porosity to the local critical porosity, namely, $\Delta \left(L\right)\propto \left|{\varphi }_c\left(L\right)-{\varphi }_c\right|$ [15, 22], where Δ(L) characterizes the percolation transition width of void network. In the following, we will illustrate how to simulate ϕ_c(L) and Δ(L), and even extrapolate ϕ_c in terms of this scaling relation.

From Figure 2, one can clearly see that each P‒ϕ curve has a typical sigmoidal shape and the simulated value at which the spanning probability go across 0.5, indicating that we can adopt a function to fit the curve with a similar shape, such as an error function, namely,

$P\left(\varphi ,L\right)=\frac{1}{2}\left[1+\mathit{erf}\left(\frac{\varphi -{\varphi }_c\left(L\right)}{\Delta \left(L\right)}\right)\right](1)$

Thus, for a fixed RVE size L, we can derive ϕ_c(L) and Δ(L). Furthermore, according to the scaling relation mentioned above, the global critical porosity ϕ_c can be extrapolated from the statistical values of ϕ_c(L) and Δ(L). It is worth stressing that the accuracy of simulated values strongly depends on the number and size of RVEs. Herein, we follow the previous contribution [10] that the RVE number is set to be 10,000 and L is specified to be at least 30 times larger than the void size, which have been confirmed to be a reasonable criterion for the balance between accuracy and efficiency in percolation simulations.

Through the above numerical framework, we can determine ϕ_c = 0.2896 ± 0.0007 for κ = 1, ϕ_c = 0.2492 ± 0.0003 for κ = 2, and ϕ_c = 0.2289 ± 0.0004 for κ = 2.5. The present ϕ_c = 0.2896 corresponds to spherical voids in foam concrete that well matches with the percolation threshold of congruent overlapping spheres simulated from Lorenz and Ziff for ϕ_c = 0.289,573 [23] and from Rintoul and Torquato ϕ_c = 0.2895 [24]. Both prominent contributions have been acknowledged as the most precise statistical values of ϕ_c for spheres so far. It strongly suggests the present numerical framework is an accurate tool to evaluate the percolation threshold of voids in foam concrete.

4 Percolation-based micromechanical model

As described above, we consider foam concrete as a two-phase composite composed of prolate spheroidal void network and homogeneous solid mortar. Here, we present a continuum percolation-based generalized effective medium theory (CP-GEMT) developed by Xu et al. [10, 15] to estimate the effective elastic and conductive properties of foam concrete affected by the percolation threshold of overlapping spheroidal voids. In the present microstructural RVE, voids possess a zero stiffness and insulation phase. In fact, McLachlan [25] has described a closed form of GEMT for two-phase media, namely,

$\frac{E_{eff}}{E_m}={\left[\mathrm{\Omega }+\sqrt{{\mathrm{\Omega }}^2+\frac{{\varphi }_c}{1-{\varphi }_c}{\left(\frac{E_p}{E_m}\right)}^{1/t}}\right]}^t,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{\Omega }=\frac{1}{2\left(1-{\varphi }_c\right)}\left[1-{\varphi }_c-\varphi +\left(\varphi -{\varphi }_c\right){\left(\frac{E_p}{E_m}\right)}^{1/t}\right](2)$

where E_eff is the effective elastic modulus of foam concrete, E_m and E_p are the elastic moduli of mortar and voids, namely, E_m = 24 GPa and E_p = 0 following the experiment from Youssef et al. [6]. T is a transport-percolation exponent that is a non-universal value greater/less than or equal to 2 [26, 27]. Figure 3 presents the theoretical values of normalized effective elastic modulus E_eff/E_m from the proposed homogeneous theory that are compared with the experimental data [6], numerical simulations [4] and the predicted values from differential effective scheme (Eq. 3) [28] and Mori-Tanaka model (Eq. 4) [29] for rigid spherical voids (inclusions).

$1-\varphi ={\left(\frac{E_m}{E_{eff}}\right)}^{\frac{1}{3}}\left(\frac{E_{eff}-E_p}{E_m-E_p}\right),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{e}(3)$

$\frac{E_{eff}}{E_m}=1+\varphi \left(E_p-E_m\right)\frac{3}{2E_m+E_p}{\left(1-\varphi +\frac{3E_m\varphi }{2E_m+E_p}\right)}^{-1},\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{M}\mathrm{o}\mathrm{r}\mathrm{i}-\mathrm{T}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{k}\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}(4)$

FIGURE 3

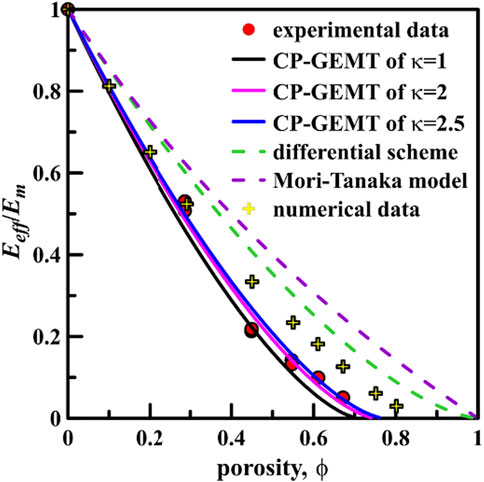
FIGURE 3. E_eff/E_m versus ϕ for the GEMT, differential effective scheme [28], Mori-Tanaka model [29], the experiment measurements [6], and numerical simulations [4]. T = 1.5 for an insulator-conductor material [26, 27].

From Figure 3, one can clearly see that, compared with the experimental data, the present theory can well predict the effective elastic modulus of foam concrete with various porosities including the global critical porosity, specifically for the theoretical values in κ = 2.5 with a wonderful accuracy. The predicted values from the differential effective scheme and Mori-Tanaka model and the numerical results are all larger than the experimental data. Actually, several theoretical researches for micromechanics-based homogeneous approximations have confirmed the applicability of the traditional differential effective scheme and Mori-Tanaka model in a diluted inclusion concentration level. The reason is the effective elastic properties of composites is approximately a linear function of ϕ under the low porosity, as shown in Figure 3 it elucidates that the necessity of considering the percolation threshold of spheroidal voids in the prediction of effective elastic moduli of foam concrete.

Moreover, it is worth stressing that the present CP-GEMT (Eq. 2) is also applicable to predicting the effective thermal conductivity of foam concrete using the classical Nernst-Einstein relation [10, 11], such as, E_p/E_m = T_p/T_m and E_eff/E_m = T_eff/T_m [15], where T_eff is the effective thermal conductivity, T_p and T_m are the thermal conductivities of voids and matrix, respectively. Plus, the present two-phase conductive issue suits for conductor-superconductor and insulator-conductor materials. For instance, in a conductor-superconductor material, voids are a high-conduction phase, whilst mortar is a low-conduction phase. Thus, T_eff/T_m of a conductor-superconductor material is expressed as

$\frac{T_{eff}}{T_m}={\left[\mathrm{\Omega }+\sqrt{{\mathrm{\Omega }}^2+\frac{{\varphi }_c}{1-{\varphi }_c}{\left(\frac{T_p}{T_m}\right)}^{1/t}}\right]}^t,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}-\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}(5)$

with

$\mathrm{\Omega }=\frac{1}{2\left(1-{\varphi }_c\right)}\left[1-{\varphi }_c-\varphi +\left(\varphi -{\varphi }_c\right){\left(\frac{T_p}{T_m}\right)}^{1/t}\right](6)$

In an insulator-conductor material, voids and mortar are the insulating and conductive phases, respectively. Accordingly, T_eff/T_m of an insulator-conductor material is written as

$\frac{T_{eff}}{T_m}={\left(\frac{1-\varphi -{\varphi }_c}{1-{\varphi }_c}\right)}^t,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{r}-\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}(7)$

Figure 4 shows that the predicted values for T_eff/T_m from the CP-GEMT (κ = 2.5) are compared against that from the differential effective scheme [28] and Mori-Tanaka model [29], and the experimental and numerical data [12]. In Ref. [12], voids are viewed as insulating inclusions so that foam concrete is an insulator-conductor material. For various porosities, the CP-GEMT for κ = 2.5 shows in good line with the experimental and numerical data, as shown in Figure 4.

FIGURE 4

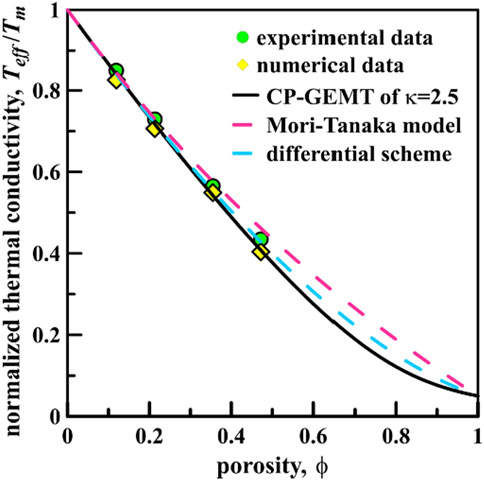
FIGURE 4. T_eff/T_m versus ϕ for the CP-GEMT, differential effective scheme [28], Mori-Tanaka model [29], and the experimental and numerical data [12].

5 Conclusion

This study has underlined the contribution of percolation of anisotropic-shaped void networks in foam concrete and the importance of using appropriate model to predict the elastic stiffness and thermal conductivity. The developed Monte Carlo finite-size scaling analysis gave the accurate percolate thresholds characterized by the global critical porosity of void networks with void aspect ratios of κ = 2.5, 2.0 and 1.0, namely, ϕ_c = 0.2289 ± 0.0004 for κ = 2.5, ϕ_c = 0.2492 ± 0.0003 for κ = 2, and ϕ_c = 0.2896 ± 0.0007 for κ = 1. Compared against the available experimental and numerical data, the traditional Mori-Tanaka model and the differential effective medium approximation, the proposed continuum percolation-based generalized effective medium theory (CP-GEMT) can accurately predict the effective elastic modulus and thermal conductivity of foam concrete with different porosities, specifically in the percolation threshold. The present microstructure-based framework has presented a powerful capacity that enables to shed light on the rigorous relation “constituent-structure-property” of foam concrete containing percolating clusters of voids.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FW: conceptualization, methodology, Writing—review and editing, writing—original draft, funding acquisition. ZX: methodology, validation, resources. JJ: conceptualization, methodology, supervision. SS: investigation, conceptualization, data curation, project administration. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52150067), the National Postdoctoral Program for Innovative Talents (No. BX2021065), the National Natural Science Foundation of China for Distinguished Young Scholars (No. 51925903), and the open research fund of Jiangsu Key Laboratory of Construction Materials, Southeast University (No. 202202).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Nguyen TT, Bui HH, Ngo TD, Nguyen GD, Kreher MU, Darve F. A micromechanical investigation for the effects of pore size and its distribution on geopolymer foam concrete under uniaxial compression. Eng Fract Mech (2019) 209:228–44. doi:10.1016/j.engfracmech.2019.01.033

CrossRef Full Text | Google Scholar

2. Amran YHM, Farzadnia N, Ali AAA. Properties and applications of foamed concrete; a review. Constr Build Mater (2015) 101:990–1005. doi:10.1016/j.conbuildmat.2015.10.112

CrossRef Full Text | Google Scholar

3. Raj A, Sathyan D, Mini KM. Physical and functional characteristics of foam concrete: A review. Constr Build Mater (2019) 221:787–99. doi:10.1016/j.conbuildmat.2019.06.052

CrossRef Full Text | Google Scholar

4. Youssef MB, Lavergne F, Sab K, Miled K, Neji J. Upscaling the elastic stiffness of foam concrete as a three-phase composite material. Cem Concr Res (2018) 110:13–23. doi:10.1016/j.cemconres.2018.04.021

CrossRef Full Text | Google Scholar

5. Xu W, Jia M, Guo W, Wang W, Zhang B, Liu Z, et al. GPU-based discrete element model of realistic non-convex aggregates: Mesoscopic insights into ITZ volume fraction and diffusivity of concrete. Cem Concr Res (2023) 164:107048. doi:10.1016/j.cemconres.2022.107048

CrossRef Full Text | Google Scholar

6. Youssef MB, Miled K, Neji J. Mechanical properties of non-autoclaved foam concrete: Analytical models vs. experimental data. Euro J Environ Civ Eng (2020) 24:472–80. doi:10.1080/19648189.2017.1398108

CrossRef Full Text | Google Scholar

7. Li HD, Zeng Q, Xu SL. Effect of pore shape on the thermal conductivity of partially saturated cement-based porous composites. Cem Concr Compos (2017) 81:87–96. doi:10.1016/j.cemconcomp.2017.05.002

CrossRef Full Text | Google Scholar

8. Pabst W, Gregorová E. Youngʼs modulus of isotropic porous materials with spheroidal pores. J Europ Ceram Soc (2014) 34:3195–207. doi:10.1016/j.jeurceramsoc.2014.04.009

CrossRef Full Text | Google Scholar

9. Suvorov AP, Selvadurai APS. Effective medium methods and a computational approach for estimating geometrical properties of porous materials with randomly oriented ellipsoidal pores. Comput Geotech (2011) 38:721–30. doi:10.1016/j.compgeo.2011.04.002

CrossRef Full Text | Google Scholar

10. Xu W, Jia M, Gong Z. Thermal conductivity and tortuosity of porous composites considering percolation of porous network: From spherical to polyhedral pores. Compos Sci Technol (2018) 167:134–40. doi:10.1016/j.compscitech.2018.07.038

CrossRef Full Text | Google Scholar

11. Xu W, Zhang D, Lan P, Jiao Y, Multiple-inclusion model for the transport properties of porous composites considering coupled effects of pores and interphase around spheroidal particles, Int J Mech Sci 150 (2019) 610–6. doi:10.1016/j.ijmecsci.2018.10.063

CrossRef Full Text | Google Scholar

12. She W, Zhao GT, Cai D, Jiang JY, Cao X. Numerical study on the effect of pore shapes on the thermal behaviors of cellular concrete. Constr Build Mater (2018) 163:113–21. doi:10.1016/j.conbuildmat.2017.12.108

CrossRef Full Text | Google Scholar

13. Shen ZL, Zhou HY. Predicting effective thermal and elastic properties of cementitious composites containing polydispersed hollow and core-shell microparticles. Cem Concr Compos (2020) 105:103439. doi:10.1016/j.cemconcomp.2019.103439

CrossRef Full Text | Google Scholar

14. Qi Y, Liu K, Peng Y, Wang J, Zhou CS, Yan DM, et al. Visualization of mercury percolation in porous hardened cement paste by means of X-ray computed tomography. Cem Concr Compos (2021) 122:104111. doi:10.1016/j.cemconcomp.2021.104111

CrossRef Full Text | Google Scholar

15. Xu W, Zhang Y, Jiang J, Liu Z, Jiao Y. Thermal conductivity and elastic modulus of 3D porous/fractured media considering percolation. Int J Eng Sci (2021) 161:103456. doi:10.1016/j.ijengsci.2021.103456

CrossRef Full Text | Google Scholar

16. Sun Z, Scherer GW. Pore size and shape in mortar by thermoporometry, Cem. Concr Res (2010) 40:740–51. doi:10.1016/j.cemconres.2009.11.011

CrossRef Full Text | Google Scholar

17. Chen SJ, Li WG, Ruan CK, Sagoe-Crentsil K, Duan WH. Pore shape analysis using centrifuge driven metal intrusion: Indication on porosimetry equations, hydration and packing. Constr Build Mater (2017) 154:95–104. doi:10.1016/j.conbuildmat.2017.07.190

CrossRef Full Text | Google Scholar

18. Xu W, Su X, Jiao Y. Continuum percolation of congruent overlapping spherocylinders. Phys Rev E (2016) 94:032122. doi:10.1103/physreve.94.032122

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Xu W, Zhu Z, Jiang Y, Jiao Y. Continuum percolation of congruent overlapping polyhedral particles: Finite-size-scaling analysis and renormalization-group method. Phys Rev E (2019) 99:032107. doi:10.1103/physreve.99.032107

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xu W, Chen HS. Mesostructural characterization of particulate composites via a contact detection algorithm of ellipsoidal particles. Powder Technol (2012) 221:296–305. doi:10.1016/j.powtec.2012.01.016

CrossRef Full Text | Google Scholar

21. Xu W, Zhang K, Zhang Y, Jiang J. Packing fraction, tortuosity and permeability of granular-porous media with densely packed spheroidal particles: Monodisperse and polydisperse systems. Water Resour Res (2022) 58:e2021WR031433. doi:10.1029/2021wr031433

CrossRef Full Text | Google Scholar

22. Stauffer D, Aharony A. Introduction to percolation theory. London: Taylor & Francis (2003).

Google Scholar

23. Lorenz CD, Ziff RM. Precise determination of the critical percolation threshold for the three-dimensional “Swiss cheese” model using a growth algorithm. J Chem Phys (2001) 114:3659–61. doi:10.1063/1.1338506

CrossRef Full Text | Google Scholar

24. Rintoul MD, Torquato S. Precise determination of the critical threshold and exponents in a three-dimensional continuum percolation model. J Phys A (1997) 30:L585–92. doi:10.1088/0305-4470/30/16/005

CrossRef Full Text | Google Scholar

25. McLachlan DS. An equation for the conductivity of binary mixtures with anisotropic structures. J Phys C Solid State Phys (1987) 20:865–77.

CrossRef Full Text | Google Scholar

26. Torquato S. Random heterogeneous materials: Microstructure and macroscopic properties. New York: Springer-Verlag (2002).

Google Scholar

27. Sahimi M. Heterogeneous materials I: Linear transport and optical properties. Berlin: Springer-Verlag (2003).

Google Scholar

28. Phan-Thien N, Pham DC. Differential multiphase models for polydispersed spheroidal inclusions: Thermal conductivity and effective viscosity. Int J Engrg Sci (2000) 38:73–88. doi:10.1016/s0020-7225(99)00016-6

CrossRef Full Text | Google Scholar

29. Xu W, Wu F, Jiao Y, Liu M. A general micromechanical framework of effective moduli for the design of nonspherical nano- and micro-particle reinforced composites with interface properties. Mater Des. (2017) 127:162–72. doi:10.1016/j.matdes.2017.04.075

CrossRef Full Text | Google Scholar