Enhancement of the physical adsorption of some insoluble lead compounds from drinking water onto polylactic acid and graphene oxide using molybdenum disulfide nanoparticles: Theoretical investigation

This study reports the enhancement of the physical adsorption of some insoluble lead compounds, from drinking water, onto polylactic acid (PLA) polymer and graphene oxide (GO) by filling with molybdenum disulfide (MoS₂) nanoparticles (NPs). Based on the Lifshitz theory, we demonstrate the attractive nature of the van der Waals (vdW) interactions that are responsible for the physical adsorption between the cerussite (PbCO₃), the pyromorphite (Pb₅(PO₄)₃Cl), and the lead dioxide (PbO₂) insoluble adsorbates and the GO/MoS₂ and PLA/MoS₂ adsorbent nanocomposites in water medium. Subsequently, we show an increase in the physical adsorption, at close and large separation distances (<100 nm) in the water medium, between the lead-insoluble adsorbate and the adsorbent GO/MoS₂ and PLA/MoS₂ nanocomposites by increasing the filling ratios (0%, 10%, 20%, and 30%) of MoS₂ NPs. Moreover, for each lead-insoluble adsorbate, we demonstrate that the vdW adsorption potential and force were more important for GO/MoS₂ than for PLA/MoS₂ adsorbent. However, for a fixed filling rate, the physical adsorption was more important in the order PbO₂ > Pb₅(PO₄)₃Cl > PbCO₃. Interestingly, we demonstrate that the physical adsorption strongly depended on the GO/MoS₂ and PLA/MoS₂ adsorbent type and weakly dependent to the lead compound adsorbates. For all “PbO₂, Pb₅(PO₄)₃Cl, and PbCO₃” adsorbates, we demonstrate that the vdW adsorption potential and force were higher ∼6, ∼3.1, ∼2.2, and ∼1.9 times for GO than for PLA adsorbent for, respectively, filling ratios 0%, 10%, 20%, and 30% of MoS₂ NPs.

1 Introduction

Despite the implementation of filtration and purification processes for drinking water, some lead-insoluble compounds remain persisting in domestic drinking water [1–3]. Recently, cerussite (PbCO₃), pyromorphite (Pb₅(PO₄)₃Cl), and lead dioxide (PbO₂) are among the most hazardous insoluble lead compounds that persist in drinking water distribution systems [2–4]. They are leached in drinking water primarily from corrosive water effects on the household plumbing systems containing lead in pipes, solder, or fittings or from the service connections to homes, galvanic corrosion [4–6]. According to the World Human Organization (WHO), the presence of lead and lead compounds in drinking water causes many hazardous human health diseases, such as neurotoxicity, mutagenicity, and carcinogenicity [7].

There are many physic-chemical purification processes for drinking water, such as photocatalysis, chemical adsorption, reverse osmosis, and chemical coagulation [8, 9]. However, these processes include some disadvantages, essentially high cost-effectiveness and energy consumption [10, 11], lack of solar sensitivity and lower efficiency [11], precipitation of insoluble substances during coagulation-flocculation [12], and removal of the essential multivalent and all monovalent minerals ions required for the human body [13]. In addition to their insolubility in the water medium, the PbO₂, PbCO₃, and Pb₅(PO₄)₃Cl compounds require higher decomposition temperatures of 588 K, 613 K, and 1,373 K, respectively [14, 15], which makes it very difficult to remove these compounds from drinking water by the previous processes. Moreover, these processes generally comprise the chemical procedure, which may allow the release of a secondary product and the rise in temperature and consequently affect the drinking water quality.

Adequately, physical adsorption is a suitable purification process for this case study. In fact, physical adsorption allows the removal of solid contaminants from water at room temperature and pressure and can operate simultaneously with other purification processes [16, 17]. In contrast to the previously cited process, physical adsorption is low-cost, simple, and easy to design, and no activation energy is necessary. It possesses high running speed compared to other purification processes, is of reversible nature, occurs on many solid surfaces, can remove multimolecular layers, and is performed under normal temperature and pressure conditions [16–18]. In addition, the physical adsorption process can be implemented essentially in a gravity microfilter, which allows the purification of the drinking water without any additional energy.

Nowadays, graphene oxide (GO), polylactic acid (PLA), and molybdenum disulfide (MoS₂) have received much attention in the research area of the water purification community. The purification efficiency of drinking water has been largely investigated by photocatalysis and membrane separation [19–21]. In fact, GO, PLA, and MoS₂ are promising materials for the application in the physical adsorption process because their natural abundantly, biocompatibility, wide variety of preparation procedures with different size and shape particles [22–24].

Currently, no previous research has investigated the examination of the physical adsorption of the insoluble lead compounds, “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂,” onto PLA and GO filled with MoS₂ NPs in the water medium.

In this work, we examine the physical adsorption of the lead compounds “PbCO₃, Pb₅(PO₄)₃Cl, PbO₂” onto GO, PLA matrixes filled with MoS₂ NPs in the water medium. First, using the Lifshitz theory, we evaluate the strength and type of van der Waals (vdW) interactions responsible for the physical adsorption by the calculation of the Hamaker constant at large and close separation distance between lead adsorbate and (GO/MoS₂, PLA/MoS₂) nanocomposites in water medium. Afterward, the investigation of the vdW adsorption potential and force as a function of the filling rates of the MoS₂ NPs of the GO and PLA matrix and the lead adsorbate type were made. Later, an enhancement of the adsorption by increasing the refractive index of the adsorbate and adsorbent in a water medium will be demonstrated. Eventually, a comparative study demonstrates that physical adsorption is highly sensitive to the adsorbent type and poorly depends on the adsorbate type.

2 Materials and methods

2.1 Materials

Adsorbent materials investigated in this study are the PLA polymer and GO filled with MoS₂ NPs. The thickness of the adsorbent nanocomposites is considered to be above 1 µm to ensure that the nanoparticle fillers, with an average size of a few nanometers (∼5 nm), were uniformly dispersed in the PLA and GO matrixes. The volume fraction Φ = (0%, 10%, 20%, and 30%) is defined as the percent volume fraction of the MoS₂ NPs of the total volume of the nanocomposite mixture. The adsorbates examined in this study are the water-insoluble lead compounds PbCO₃, PbO₂, and Pb₅(PO₄)₃Cl.

Hereafter, the proposed rates of volume fraction of MoS₂ NPs added to PLA and GO matrixes are designated and summarized in Table 1.

TABLE 1

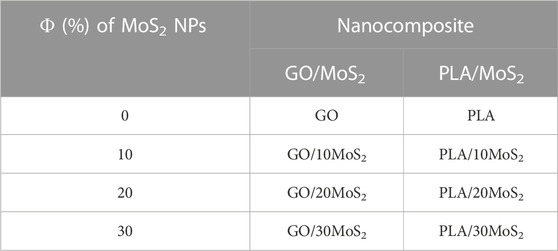
TABLE 1. Designation of GO/MoS₂ and PLA/MoS₂ nanocomposites as a function of volume fraction of MoS₂ filler rates.

2.2 Methods

2.2.1 vdW adsorption potential and force

In this work, physical adsorption designs the adhesion of the lead compound particles onto a nanocomposite surface in a water medium under the action of intermolecular surface forces. Essentially, physical adsorption is driven by hydrogen binding, hydrophobic interactions, and vdW intermolecular forces, which include Keesom, Debye, and London forces [16–18, 25].

However, in the aqueous medium, the water molecules are expected to occupy a large portion of the H-bonding sites [26]. Consequently, the hydrogen binding is reasonably ignored because the adsorbent and adsorbate were fully hydrated by extending their contact with water [27]. Additionally, for water-insoluble compounds, the hydrophobic interactions are much larger. Then, the higher the affinity, the greater the extent of the adsorption with other near materials [28]. Consequently, the insolubility of such lead compounds constitutes a favor factor for their physical adsorption onto PLA/MoS₂ and PLA/MoS₂ nanocomposite adsorbent from water medium.

Therefore, the physical adsorption of the insoluble lead compound onto the surface of PLA/MoS₂ and PLA/MoS₂ nanocomposites is driven solely by the vdW forces in a water medium. Hence, the physical adsorption was called vdW adsorption. Subsequently, the essential purpose of this study is to evaluate the type and strength of the vdW interaction potential and force between the insoluble lead compound and the GO/MoS₂ and PLA/MoS₂ nanocomposite adsorbate in the water medium.

As shown in Figure 1, the lead compound particle is assimilated to a spherical particle of a radius R_p (adsorbate) that reign in a water medium near a flat surface of the composites (adsorbent) at the distance x << R_p.

FIGURE 1

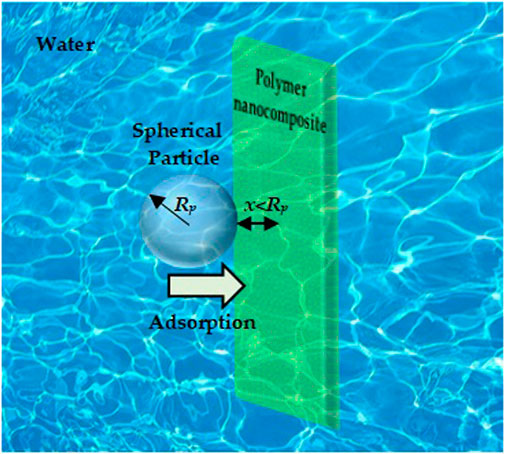
FIGURE 1. Schematic illustration of the physical adsorption: spherical particle adsorbate with radius R_p located near flat adsorbent nanocomposite surface in a water medium at separation distance (x << R_p).

For the evaluation of the vdW interactions, we used the computational methods that have demonstrated good accordance between theoretical and experimental results by many recent studies for evaluating the intermolecular vdW interactions either for accounting for the adhesion force and energy and the adsorption of a variety of materials liquids in aqueous media [25, 29–31].

According to Figure 1, the fully vdW potential involving the adsorption along the separation distance (x ≤ 100 nm) is given as follows [31]:

${\mathbf{U}}_{\mathbf{v}\mathbf{d}\mathbf{W}}\left(\mathbf{x}\right)=-\left[{\mathbf{A}}_{\mathbf{\nu }=\mathbf{0}}^{\mathbf{r}\mathbf{e}\mathbf{t}}+{\mathbf{A}}_{\mathbf{\nu }>\mathbf{0}}^{\mathbf{r}\mathbf{e}\mathbf{t}}\right]\frac{{\mathbf{R}}_{\mathbf{p}}}{\mathbf{6}\mathbf{x}}=-\left[{\mathbf{A}}_{\mathbf{\nu }=\mathbf{0}}{\mathbf{e}}^{-\mathbf{\kappa }\mathbf{x}}+\frac{{\mathbf{A}}_{\mathbf{\nu }>\mathbf{0}}}{\mathbf{1}+\mathbf{14}\mathbf{x}/\mathbf{100}}\right]\frac{{\mathbf{R}}_{\mathbf{p}}}{\mathbf{6}\mathbf{x}},(1)$

where ${\mathrm{A}}_{\mathrm{\nu }=0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ and ${\mathrm{A}}_{\mathrm{\nu }>0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ are, respectively, the retarded polar and dispersive parts of the Hamaker constants. ${\mathrm{A}}_{\mathrm{\nu }=0}$ is the zero-frequency, also called non-retarded Hamaker constant, which regroups the Keesom interactions arising from permanent molecular dipoles and Debye interactions arising from permanent and induced dipoles’ polar vdW interactions [32, 33]. For drinking water, the non-retarded Keesom and Debye interactions are reduced proportionally by e^−κx along the interacting distance x ≤ 100 nm under the action of the conduction effects [31, 34], where κ⁻¹, known as the Debye screening length, equals 960 nm for drinking water with pH 7 [31].

In contrast, ${\mathrm{A}}_{\mathrm{\nu }>0}$ is the non-zero-frequency, also called non-retarded, Hamaker constant, including the London dispersion interactions that result from the fluctuations in the charge densities of the electron clouds surrounding the nuclei of the atoms [35]. Along the separation distance (x ≤ 100 nm), Gregory stated that ${\mathrm{A}}_{\mathrm{\nu }>0}$ became retarded (${\mathrm{A}}_{\mathrm{\nu }>0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$) and it reduced approximately by 1/(1 + 14x/100) [36].

2.2.2 vdW adhesion energy and force

Once the spherical lead particle is submitted to the attractive vdW interactions from the nanocomposite surface in a water medium, it will be adsorbed onto the nanocomposite surface under the action of the vdW adhesion energy expressed analytically by [31]:

${\mathbf{U}}_{\mathbf{a}\mathbf{d}\mathbf{h}}=-\left({\mathbf{A}}_{\mathbf{\nu }=\mathbf{0}}+{\mathbf{A}}_{\mathbf{\nu }>\mathbf{0}}\right)\frac{{\mathbf{R}}_{\mathbf{P}}}{\mathbf{6}.{\mathbf{x}}_{\mathbf{0}}},(2)$

where x₀ is the closet separation distance between adsorbent and adsorbate molecules after adsorption. It is called the cut-off distance and typically equals 0.165 nm.

The correspondent adhesion force involved by the vdW interactions responsible for the physical adsorption is expressed as [31]:

${\mathbf{F}}_{\mathbf{a}\mathbf{d}\mathbf{h}}=-\left({\mathbf{A}}_{\mathbf{\nu }=\mathbf{0}}+{\mathbf{A}}_{\mathbf{\nu }>\mathbf{0}}\right)\frac{{\mathbf{R}}_{\mathbf{P}}}{\mathbf{6}.{\mathbf{x}}_{\mathbf{0}}^{\mathbf{2}}}.(3)$

2.2.3 Hamaker constant

The Hamaker constant was calculated using the Lifshitz theory, allowing for easy and rigorous analytical calculation of vdW interactions between any two macroscopic media 1 and 2 interacting across medium 3. In such a theory, the influence of neighboring atoms on the interaction between any pair of atoms is ignored, and the materials are treated as continuous media with the same absorption frequencies [31].

The polar Hamaker constant is expressed as a function of the static dielectric constant dominated by the Keesom and Debye interactions of the interacting media:

${\mathbf{A}}_{\mathbf{\nu }=\mathbf{0}}=\frac{\mathbf{3}}{\mathbf{4}}{\mathbf{k}}_{\mathbf{B}}\mathbf{T}\frac{{\mathbf{\epsilon }}_{\mathbf{1}}-{\mathbf{\epsilon }}_{\mathbf{3}}}{{\mathbf{\epsilon }}_{\mathbf{1}}+{\mathbf{\epsilon }}_{\mathbf{3}}}.\frac{{\mathbf{\epsilon }}_{\mathbf{2}}-{\mathbf{\epsilon }}_{\mathbf{3}}}{{\mathbf{\epsilon }}_{\mathbf{2}}+{\mathbf{\epsilon }}_{\mathbf{3}}},(4)$

where k_B is the Boltzmann constant, T is the temperature, ${\mathrm{\epsilon }}_1$, ${\mathrm{\epsilon }}_2$, and ${\mathrm{\epsilon }}_3$ are, respectively, the dielectric permittivity of the adsorbent, adsorbate, and water medium.

In contrast, the dispersive part of the Hamaker constant is expressed as a function of the refractive index of the three interacting media as follows [25]:

${\mathbf{A}}_{\mathbf{\nu }>\mathbf{0}}=\frac{\mathbf{3}\mathit{h}{\mathbf{\nu }}_{\mathbf{e}}}{\mathbf{8}\sqrt{\mathbf{2}}}\frac{\left.{\left(\mathit{n}\right.}_{\mathbf{1}}^{\mathbf{2}}-{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}){\left(\mathit{n}\right.}_{\mathbf{2}}^{\mathbf{2}}-{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}\right)}{{\left.{\left(\mathit{n}\right.}_{\mathbf{1}}^{\mathbf{2}}+{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}\right)}^{\mathbf{1}/\mathbf{2}}{\left.{\left(\mathit{n}\right.}_{\mathbf{2}}^{\mathbf{2}}+{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}\right)}^{\mathbf{1}/\mathbf{2}}\left[{\left.{\left(\mathit{n}\right.}_{\mathbf{1}}^{\mathbf{2}}+{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}\right)}^{\mathbf{1}/\mathbf{2}}+{\left.{\left(\mathit{n}\right.}_{\mathbf{2}}^{\mathbf{2}}+{\mathit{n}}_{\mathbf{3}}^{\mathbf{2}}\right)}^{\mathbf{1}/\mathbf{2}}\right]},(5)$

where ν_e is the main electronic absorption frequency in the UV, typically around 3 × 10¹⁵ s⁻¹ [25], h is the Planck constant, and $n_1$, $n_2$, and $n_3$ are, respectively, the refractive index of the adsorbent, adsorbate, and water.

In fact, the refractive index is the root square of the dielectric constant at optical frequencies (${ϵ}_{\mathrm{o}\mathrm{p}\mathrm{t}}$) as $n=\sqrt{{ϵ}_{opt}}$ dominated by the London dispersion interactions.

In Table 2, the dielectric constant and the refractive index for the calculation of the Hamaker constants are obtained from the bibliography.

TABLE 2

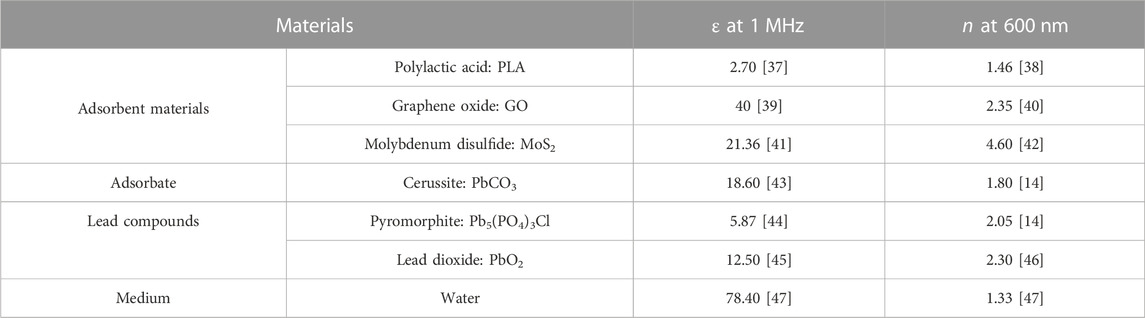
TABLE 2. Dielectric constants and refractive indexes of adsorbent (PLA, GO, and MoS₂) and lead-insoluble adsorbate “PbCO₃, Pb₅(PO₄)₃Cl, PbO₂” and water at room temperature (298 K).

2.2.4 Calculation of the dielectric constant and refractive index of nanocomposites

The dielectric constant of the nanocomposite materials is calculated using the Looyenga formula by considering that the nanoparticle filler has a spherical form and is uniformly dispersed in the continuous polymer matrix [48]:

${\mathbf{\epsilon }}^{\mathbf{1}/\mathbf{3}}={\mathbf{\Phi }\mathbf{\epsilon }}_{\mathbf{m}}^{\mathbf{1}/\mathbf{3}}+\left(\mathbf{1}-\mathbf{\Phi }\right){\mathbf{\epsilon }}_{\mathbf{f}}^{\mathbf{1}/\mathbf{3}},(6)$

where Φ is the volume fraction (%) of the filler and $\mathrm{\epsilon }$, ${\mathrm{\epsilon }}_{\mathrm{m}}$, and ${\mathrm{\epsilon }}_{\mathrm{f}}$ are the dielectric constant of the nanocomposites, polymer matrix, and filler, respectively.

The refractive index of the nanocomposites is calculated using the mixing theory of Maxwell Garnet as follows [49]:

${\mathit{n}}^{\mathbf{2}}={\mathit{n}}_{\mathit{m}}^{\mathbf{2}}\frac{{(\mathit{n}}_{\mathit{f}}^{\mathbf{2}}+\mathbf{2}{\mathit{n}}_{\mathit{m}}^{\mathbf{2}})+\mathbf{2}\mathbf{\Phi }\left({\mathit{n}}_{\mathit{f}}^{\mathbf{2}}-{\mathit{n}}_{\mathit{m}}^{\mathbf{2}}\right)}{{(\mathit{n}}_{\mathit{f}}^{\mathbf{2}}+\mathbf{2}{\mathit{n}}_{\mathit{m}}^{\mathbf{2}})-\mathbf{\Phi }\left({\mathit{n}}_{\mathit{f}}^{\mathbf{2}}-{\mathit{n}}_{\mathit{m}}^{\mathbf{2}}\right)},(7)$

where $n$, $n_{\mathrm{m}}$, and $n_{\mathrm{f}}$ are the refractive indexes of the nanocomposite, polymer matrix, and filler, respectively.

3 Results

All the theoretical calculations and discussions of the results were performed under normal conditions of temperature (298 K) and pressure (100 kPa). Hypothetically, the refractive index and the dielectric constant, which are intensive physical properties, are independent of the materials’ size and shape and are considered isotropic for all media.

3.1 Evaluation of the vdW interactions between the lead compounds and nanocomposites in water medium at close and large separation

To obtain the non-retarded Hamaker on the basis of the Lifshitz theory, we first calculated the dielectric constant (Eq. 6) and the refractive index (Eq. 7) of the GO and PLA matrices at volume fraction Φ = (0%, 10%, 20%, and 30%) of the MoS₂ NPs filler. As summarized in Table 2, the n of the GO/MoS₂ and PLA/MoS₂ increases notably with the volume fraction of the MoS₂ NPs filler. As it can interpret from equation 7, this is explained by the elevated value of the refractive index of MoS₂ NPs compared to GO and PLA matrices.

However, the ε decreases for GO/MoS₂ and increases for PLA/MoS₂ nanocomposites during filling with MoS₂ NPs. This fact is explained by the higher ε of the GO and the lower ε of PLA compared to that for MoS₂ NPs.

Therefore, referring to Tables 2, 3, the non-retarded Hamaker constants ${\mathrm{A}}_{\mathrm{\nu }=0}$ and ${\mathrm{A}}_{\mathrm{\nu }>0}$ are calculated using Eqs 4, 5. In Table 4, we compiled the Hamaker constant between the adsorbent nanocomposites (GO/MoS₂ and PLA/MoS₂) and the lead-insoluble adsorbates “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂” in the water medium.

TABLE 3

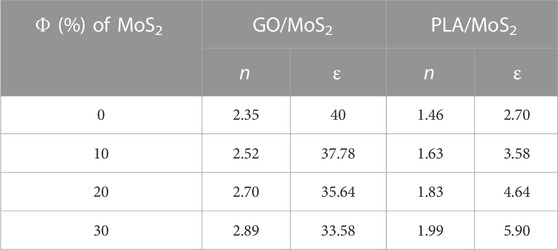
TABLE 3. Refractive index “n” and dielectric constant “ε” of nanocomposites GO/MoS₂ and PLA/MoS₂ as a function of the volume fraction (Φ) of MoS₂ NPs.

TABLE 4

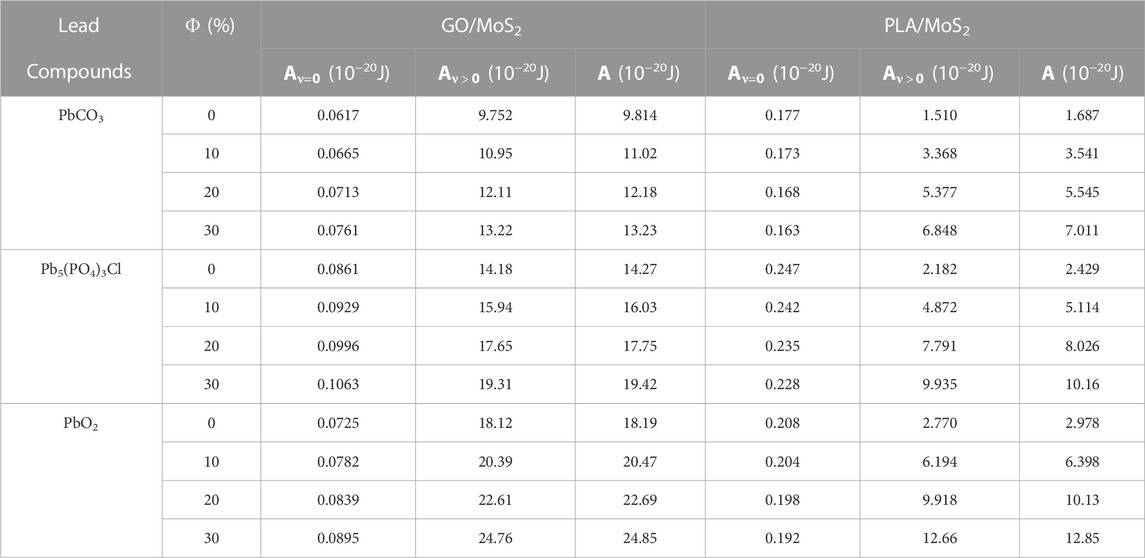
TABLE 4. Non-retarded Hamaker constants for the interactions between adsorbent nanocomposites (GO/MoS₂ and PLA/MoS₂) and the lead-insoluble adsorbates (PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂) in a water medium at 298 K.

As shown in Table 4, all the non-retarded Hamaker constants are in good accordance with the order of magnitude of the Hamaker constant, which ranges about ×10⁻²⁰ J [31]. Effectively, this demonstrates the preciseness of our used theoretical methods for the estimation of the vdW intermolecular interactions. Remarkably, the positive values of the non-retarded Hamaker constant demonstrate the attractive nature of the vdW intermolecular interaction between the nanocomposite adsorbents “GO/MoS₂ and PLA/MoS₂” and the “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂” adsorbates in the water medium. Interestingly, this demonstrates that the physical adsorption of the insoluble lead compounds onto the nanocomposite surface in the water medium is driven by the non-retarded vdW interactions. The findings are consistent with recent findings by Sato et al. [25] and Aoyama et al. [29], demonstrating that the vdW interactions are sufficiently strong to drive the adsorption of colloidal particle adsorption onto polymer gels in the water medium without any other special interaction.

Moreover, the non-retarded Hamaker constant (A) was dominated over >90% by the ${\mathrm{A}}_{\mathrm{\nu }>0}$ dispersive part. This suggests that the vdW adsorption forces were driven by the London dispersion interactions. Moreover, the strength of the A for the GO/MoS₂ was about ∼2 to ∼6 orders of magnitude higher than that of A for PLA/MoS₂ for all filler ratios and lead compounds. This is attributed to the high refractive index (i.e., London dispersion interactions) of GO/MoS₂ compared to those of PLA/MoS₂ nanocomposite.

Now let us discuss the evolution of the corresponding retarded Hamaker constant at a large separation distance (x ≤ 100 nm). For depicting the contribution of the London dispersion forces and the polar Keesom–Debye on the retarded Hamaker constant, we have drawn ${\mathrm{A}}_{\mathrm{\nu }=0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ and ${\mathrm{A}}_{\mathrm{\nu }>0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ along separation distance x ≤ 100 nm. As deduced from Figure 2, ${\mathrm{A}}_{\mathrm{\nu }>0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ (blue line) is reduced with increasing separation due to retardation effects, but it did not reach zero for all nanocomposites and lead compounds. Despite the poor contribution of the total Hamaker constant, the polar ${\mathrm{A}}_{\mathrm{\nu }=0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ vdW intermolecular interactions did not suffer retardation effects and remained constant at all separation distances and interacting systems.

FIGURE 2

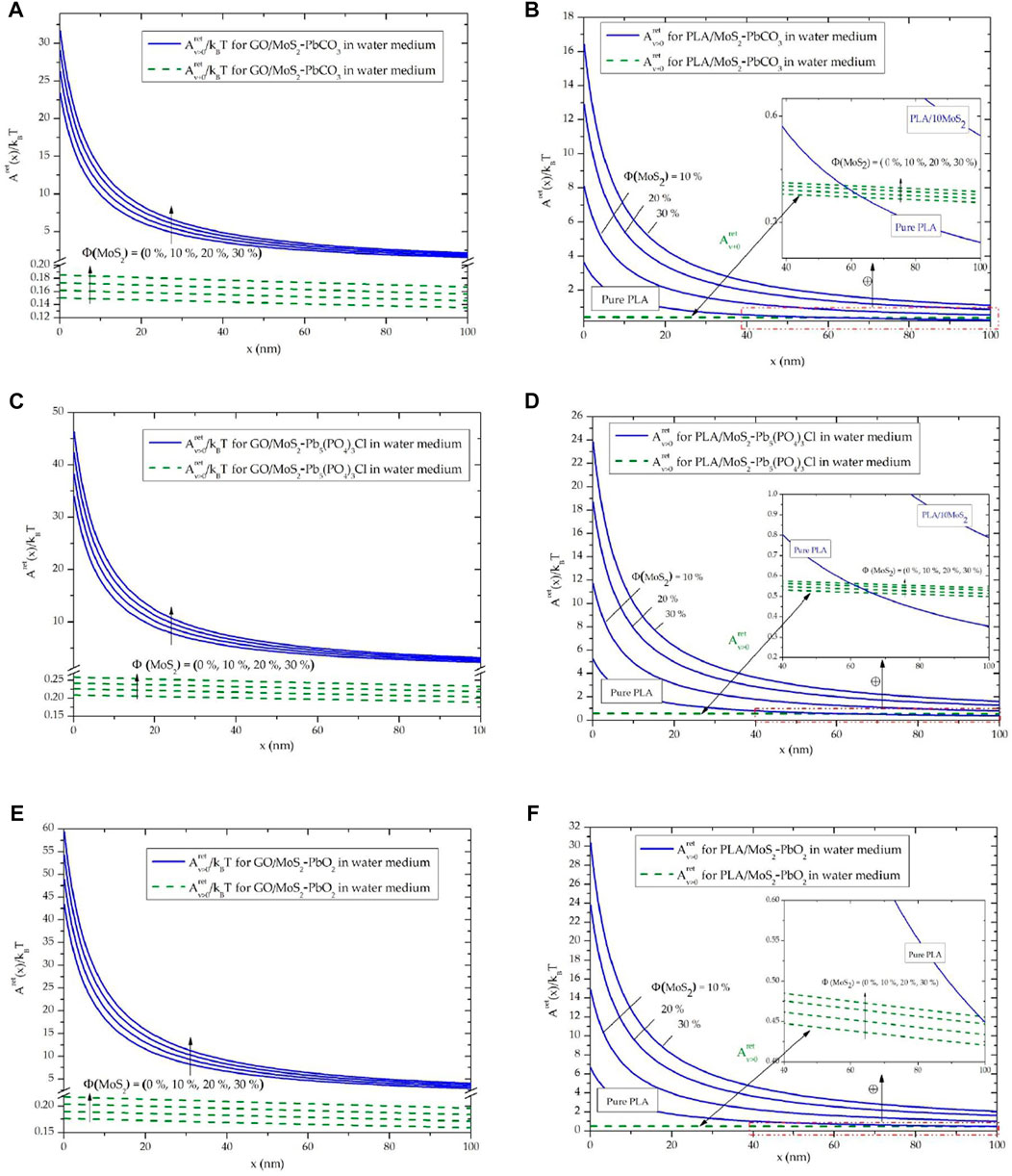
FIGURE 2. Evolution of the retarded Hamaker constant in a water medium between adsorbents and adsorbates: (A) GO/MoS₂-PbCO₃, (B) PLA/MoS₂-PbCO₃, (C) GO/MoS₂-Pb₅(PO₄)₃Cl, (D) PLA/MoS₂-Pb₅(PO₄)₃Cl, (E) GO/MoS₂-PbO₂, and (F) PLA/MoS₂-PbO₂.

Subsequently, Figure 2 shows an increase in the vdW interactions, for all adsorbents and adsorbates in the water medium, by increasing the filling with MoS₂ NPs. This fact was more important for the interactions between PLA/MoS₂ adsorbent, and it can be identified by the dispersion, as the separation becomes closer, of the curves of PLA/MoS₂ adsorbent for Φ = (0%, 10%, 20%, and 30%) (Figures 2B–F). From these results, it is important to depict the enhancement of the vdW interactions for PLA and GO adsorbent by increasing the filling rate of MoS₂ NPs.

Particularly, at large separation distances (40–100 nm), the dispersive ${\mathrm{A}}_{\mathrm{\nu }>0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ of pure PLA (Figures 2B–F) decay until overlapping the polar ${\mathrm{A}}_{\mathrm{\nu }=0}^{\mathrm{r}\mathrm{e}\mathrm{t}}$ of PLA/MoS₂ for Φ = (0%, 10%, 20%, and 30%). This particular result demonstrates that the Keesom–Debye vdW interactions, which do not suffer from retardation, remain approximately constant and become the dominant interactions compared to the London dispersion interactions at a sufficiently large separation distance.

3.2 Adsorption of lead compounds onto GO/MoS₂ and PLA/MoS₂ in water medium

Hereafter, the adsorption potential, adhesion energy, and force of lead particles onto GO/MoS₂ and PLA/MoS₂ adsorbent surfaces in the water medium are reported from the Hamaker constant. As presented in Figure 1, we consider the lead particles, with spherical shape with radius R_p = 200 nm, located near the flat adsorbent nanocomposite surface at separation distance (x = 100 nm) << R_p.

3.2.1 Effect of the filling rates of the MoS₂ NPs

The evolution of the vdW potential was calculated from the retarded Hamaker constant using Eq. 1. Figure 3 depicts the evolution of ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right)$ normalized to k_BT energy at Φ = (0%, 10%, 20%, and 30%) of MoS₂ NPs filler for the PbCO₃ adsorbate and the GO/MoS₂ and PLA/MoS₂ nanocomposite adsorbent in the water medium. For all adsorbents and PbCO₃ adsorbate, the vdW adsorption potential ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ is a typical attractive potential (negative interaction energy), which increases progressively as the separation distance becomes short [31].

FIGURE 3

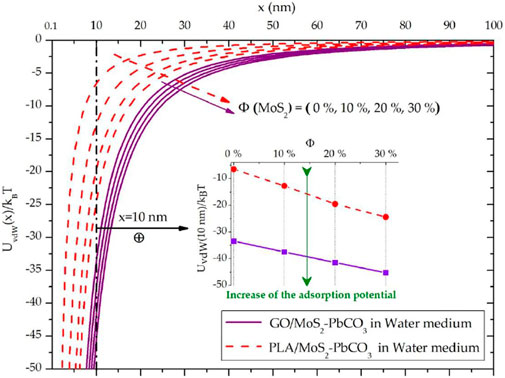
FIGURE 3. Effect of the filling rates with MoS₂ NPs on the evolution of the vdW adsorption potential between Cerussite “PbCO₃” adsorbate and GO/MoS₂ and PLA/MoS₂ nanocomposite adsorbents in water medium.

For both GO/MoS₂ and PLA/MoS₂ nanocomposites, an enhancement of the vdW potential (translating from left to right in Figure 3) with increasing the filling ratios of the MoS₂ NPs is remarked. Homogeneously, this result is attributed to the greater refractive index of the MoS₂ NPs (n = 4.6) compared with the refractive index of the GO (n = 2.35) and PLA (n = 1.46) (Table 1), which consequently involves an increase in the vdW dispersion forces that drive over 90% of the vdW interactions. As mentioned in Figure 3, for x = 10 nm, we demonstrate the enhancement of the adsorption potential ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(10\mathrm{n}\mathrm{m}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ with Φ = (0%, 10%, 20%, and 30%), which increases from ∼33.k_BT to ∼45.k_BT, respectively, for GO and GO/30MoS₂, and from ∼6.k_BT to ∼24.k_BT, respectively, for PLA and PLA/30MoS₂.

Analogically, the increase in the retarded Hamaker constant with Φ of the MoS₂ NPs, for the interacting systems “GO/MoS₂-Pb₅(PO₄)₃Cl,” “PLA/MoS₂-Pb₅(PO₄)₃Cl,” “GO/MoS₂-PbO₂,” and “PLA/MoS₂-PbO₂” in the water medium (cf. Section 3.1), involves an enhancement of the corresponding vdW adsorption potentials.

3.2.2 Effect of the lead compounds and nanocomposite types

3.2.2.1 Effect of nanocomposite adsorbent types

To examine the effect of the adsorbent type on the vdW adsorption potential, we have collected, in Figure 4, the evolution of ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ of the adsorbents, “GO/MoS₂ and PLA/MoS₂,” and the adsorbates, “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂,” in the water medium separately for fixed Φ of MoS₂ NPs. For Φ = 0%, 10%, and 20% (Figures 4A–C), ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ for the interacting media “GO/MoS₂-lead compounds” (bold violet curves) in the water medium is gradually more important than those for “PLA/MoS₂-lead compounds” (thin red curves) along the separation distance x.

FIGURE 4

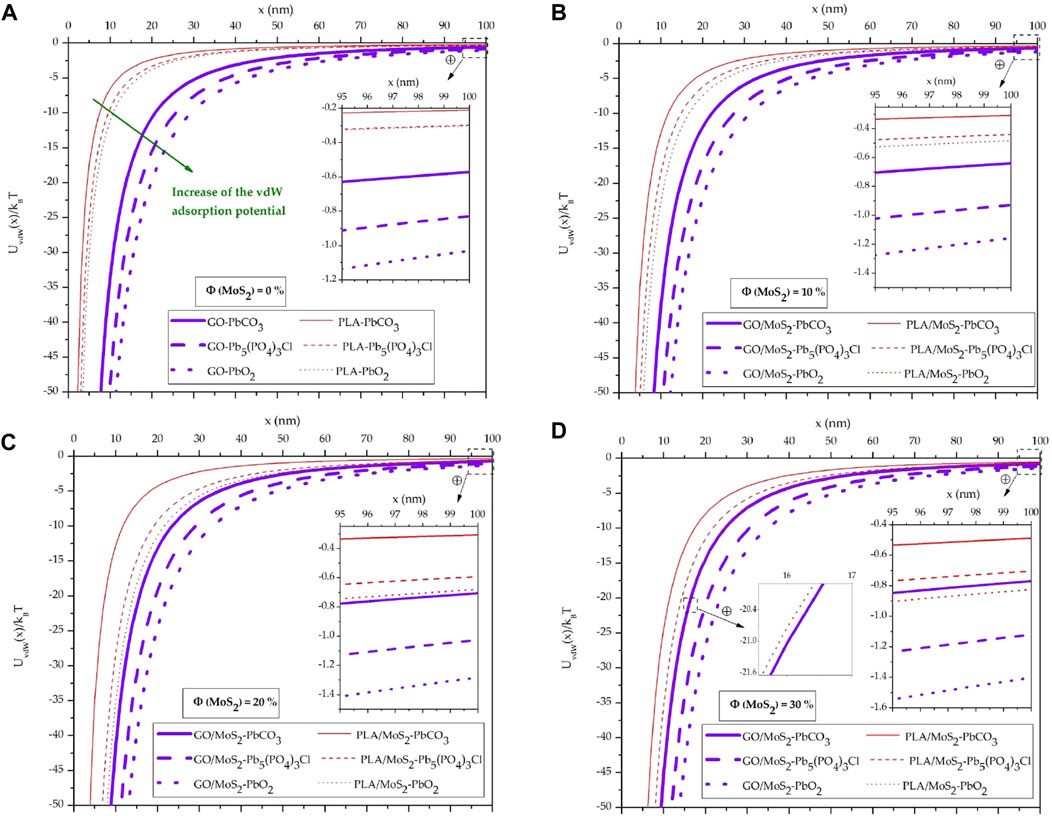
FIGURE 4. Evolution of the vdW adsorption potential between the GO/MoS₂ and PLA/MoS₂ nanocomposite adsorbents and the “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂” lead adsorbates in a water medium: (A) Φ = 0%, (B) Φ = 10%, (C) Φ = 20%, and (D) Φ = 30%.

Qualitatively, these findings indicate that the physical adsorption of the lead compounds is higher on the GO/MoS₂ nanocomposite surface than the PLA/MoS₂ one. However, for Φ = 30% and at x > 28.4 nm (Figure 4D), ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ for the interaction between PLA/MoS₂-PbO₂ becomes more important than the interaction between GO/MoS₂-PbCO₃ in the water medium. This can be explained by the fact that, on the one hand, the dispersion interactions for both PLA/MoS₂-PbO₂ and GO/MoS₂-PbCO₃ in the water medium are reduced at large separation (retardation effect) and, consequently, the polar vdW interactions that no suffer retardation effects become the driving interactions. On the other hand, by referring to Eq. 4 and Tables 2, 3, the elevated dielectric constant of the GO/30MoS₂ and PbCO₃ of 33.58 and 18.6, respectively, compared with PLA/30MoS₂ and PbO₂ of 5.90 and 12.5, respectively, yields the non-retarded Hamaker constant’s lower value for the interacting media GO/MoS₂-PbCO₃ (${\mathrm{A}}_{\mathrm{\nu }=0}$ = 0.76 10⁻²¹ J) compared to PLA/MoS₂ and PbO₂ (${\mathrm{A}}_{\mathrm{\nu }=0}$ = 1.92 10⁻²¹ J) in the water medium.

Particularly, this result highlights that despite the poor contribution of the polar Keesom–Debye interactions to the total vdW interactions at close separation, it becomes the driving force for the physical adsorption at large separation.

Thereafter, we examine the strength of the adhesion energy and force that corresponds to the vdW adsorption. The adhesion energy and force of the lead compounds with GO/MoS₂ and PLA/MoS₂ nanocomposites surface were calculated using Eqs 2, 3. As shown in Figure 5, the vdW adhesion energy and force are, respectively, in the order of ×1,000.k_BT and ×100 nN. This is in good agreement with the order of magnitude of the non-covalent interactions scales of the microscopic systems [31] and then demonstrates the accuracy of our used analytics methods.

FIGURE 5

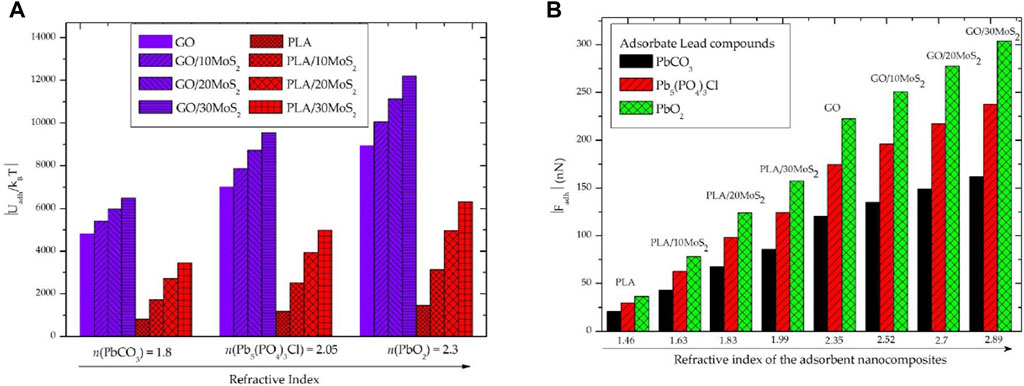
FIGURE 5. Evolution of the vdW adhesion energy and force corresponding to the physical adsorption of the “PbCO₃, Pb₅(PO₄)₃Cl, and PbO₂” lead compound adsorbates onto “GO/MoS₂ and PLA/MoS₂” nanocomposite adsorbents in a water medium as a function of the refractive index: (A) adhesion energy and (B) adhesion force.

However, for each adsorbate type of lead compounds, ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ and ${\mathrm{F}}_{\mathrm{a}\mathrm{d}\mathrm{h}}$ were more important for GO/MoS₂ compared to those for PLA/MoS₂ nanocomposite adsorbent. Consequently, this demonstrates the increased physical adsorption stability of the lead compounds onto GO/MoS₂ compared to the PLA/MoS₂ adsorbent.

3.2.2.2 Effect of lead compound type

As shown in Figure 4, for the same nanocomposite adsorbent (GO/MoS₂ or PLA/MoS₂), we found that ${\mathrm{U}}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(\mathrm{x}\right){/\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ was more important in the order of the adsorbate type “PbO₂” > “Pb₅(PO₄)₃Cl” > “PbCO₃”. Similarly, in Figure 5, this fact can be observed clearly in the vdW adhesion energy and force between lead compounds and the nanocomposite surface. As previously deduced from the Hamaker constant, this result demonstrates that the increase in the vdW adsorption is strongly associated with the increase in the London dispersion interactions that are proportional to an increase in the refractive index (“n(PbO₂) = 2.3” > “n(Pb₅(PO₄)₃Cl) = 2.05” > “n(PbCO₃) = 1.8”). These basic findings are consistent with recent previous research conducted by Sato et al. [25] and Aoyama et al. [29], showing that the quantity of adsorbed particles increased with increasing the refractive indices of the particles.

So far, it has been shown that vdW adsorption in the water medium is enhanced by increasing London dispersion interactions for either the adsorbent or the adsorbate or both.

Eventually, it is important to find which interacting medium (adsorbent or adsorbate) has the greatest contribution to the physical vdW adsorption in the water medium. To this purpose, it is efficient to scale the vdW adhesion energy and force of the GO/MOS₂ to the PLA/MoS₂ nanocomposites for each given lead compound (at R_p = cte) and filling rate of the MoS₂ NPs as follows:

${\mathbf{U}}_{\mathbf{a}\mathbf{d}\mathbf{h}}^{*}={\mathbf{F}}_{\mathbf{a}\mathbf{d}\mathbf{h}}^{*}={\left.\frac{{\mathbf{U}}_{\mathbf{a}\mathbf{d}\mathbf{h}}\left(\mathbf{G}\mathbf{O}/{\mathbf{M}\mathbf{o}\mathbf{S}}_{\mathbf{2}}\right)}{{\mathbf{U}}_{\mathbf{a}\mathbf{d}\mathbf{h}}\left(\mathbf{P}\mathbf{L}\mathbf{A}/{\mathbf{M}\mathbf{o}\mathbf{S}}_{\mathbf{2}}\right)}\right|}_{{\mathbf{P}\mathbf{b}\mathbf{O}}_{\mathbf{2},}{\mathbf{P}\mathbf{b}}_{\mathbf{5}}{\left({\mathbf{P}\mathbf{O}}_{\mathbf{4}}\right)}_{\mathbf{3}}\mathbf{C}\mathbf{l},{\mathbf{P}\mathbf{b}\mathbf{C}\mathbf{O}}_{\mathbf{3}},\mathbf{\Phi }}={\left.\frac{\mathbf{A}\left(\mathbf{G}\mathbf{O}/{\mathbf{M}\mathbf{o}\mathbf{S}}_{\mathbf{2}}\right)}{\mathbf{A}\left(\mathbf{P}\mathbf{L}\mathbf{A}/{\mathbf{M}\mathbf{o}\mathbf{S}}_{\mathbf{2}}\right)}\right|}_{{\mathbf{P}\mathbf{b}\mathbf{O}}_{\mathbf{2},}{\mathbf{P}\mathbf{b}}_{\mathbf{5}}{\left({\mathbf{P}\mathbf{O}}_{\mathbf{4}}\right)}_{\mathbf{3}}\mathbf{C}\mathbf{l},{\mathbf{P}\mathbf{b}\mathbf{C}\mathbf{O}}_{\mathbf{3}},\mathbf{\Phi }}.(8)$

As shown in Figure 6, there is little difference between ${\mathrm{U}}_{\mathrm{adh}}^{*}$ for PbO₂, Pb₅(PO₄)₃Cl and PbCO₃ adsorbate at fixed Φ. Consequently, this proves the poor contribution of the lead compound type on the adsorption energy and force.

FIGURE 6

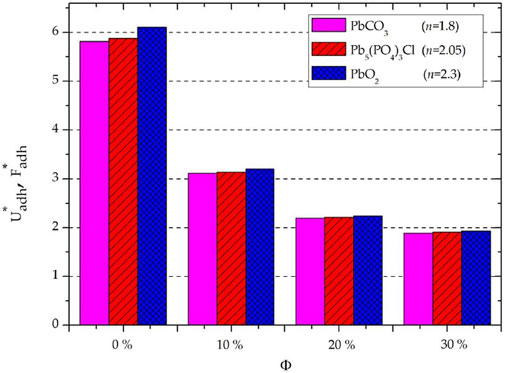
FIGURE 6. Scaled vdW energy and force using Eq. 8 with the same lead adsorbate radius Rp = cte.

Eventually, for all “PbO₂, Pb₅(PO4)₃Cl, and PbCO₃” adsorbates, ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}^{*}$ were ∼6, ∼3.1, ∼2.2, and ∼1.9, respectively, for Φ = 0%, 10%, 20%, and 30%. On the one hand, this result demonstrates the weak contribution of the adsorbate type to the vdW adhesion energy and force governing the physical adsorption. On the other hand, this reveals the higher dependency of the vdW adsorption energy and force on the adsorbent type, which is always higher for GO/MOS₂ than for PLA/MOS₂ nanocomposite.

Effectively, the decrease in the ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}^{*}$ ratio with increasing the filling ratios in Figure 6 is caused by the reduction in the gap between the refractive indexes of the GO/MoS₂ and PLA/MoS₂ nanocomposites during filling with MoS₂ NPs. In fact, the refractive index of the PLA/MoS₂ and GO/MoS₂ adsorbents increases during filling until it converges to the refractive index of the MoS₂ NPs.

Figure 7 compiles the evolution of ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}^{*}$ for the “PbO₂, Pb₅(PO₄)₃Cl, and PbCO₃” adsorbate as function of the refractive index ratio n* = n(GO/MoS₂)/n(PLA/MoS₂) for Φ = 0%, 10%, 20%, and 30%.

FIGURE 7

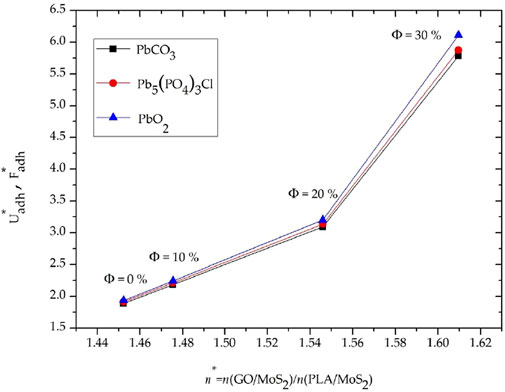
FIGURE 7. Evolution of the scaled energy and force as a function of the refractive index ratio n* considering the lead compounds have the same radius R_p = Cte.

Overall, it is observed in Figure 7 that ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}^{*}$ and n* curves provide the same profile behavior when increasing the filling rates of MoS₂. This result demonstrates that the London dispersion interactions on the PLA/MoS₂ and GO/MoS₂ adsorbent surface were the driving interactions for increasing the vdW adsorption (i.e., the physical adsorption).

Future studies could investigate the vdW adsorption for higher filling rates (Φ > 30%), in which ${\mathrm{U}}_{\mathrm{a}\mathrm{d}\mathrm{h}}^{*}$ continues to decrease to reach 1 for purely MoS₂ adsorbent (Φ = 100%). In this insight, a forthcoming experimental study may investigate the adsorbent nanocomposite stability and efficiency under real conditions, in which the vdW adsorption may be improved by decreasing temperature and varying the morphological properties, such as porosity and roughness.

Furthermore, it is important to note that the adhesion energy and force (Figure 6) constitute the threshold adhesion for the desorption of the lead compounds that may occur under the action of the water flow during nanofiltration or purification processes. Consequently, future theoretical and experimental research should be devoted to valorizing the findings of this study to examine the effect of the water velocity on the desorption of insoluble lead compounds during the nano/microfiltration process.

4 Conclusion

In summary, the physical adsorption of the PbCO₃, PbO₂, and Pb₅(PO₄)₃Cl compounds from water onto GO/MoS₂ and PLA/MoS₂ nanocomposite surface were theoretically investigated on the basis of the Lifshitz theory. The physical adsorption behavior was analyzed in terms of the Hamaker constant, vdW adsorption potential, vdW adhesion energy, and force.

From the analysis of the Hamaker constant at a large separating distance, it is shown that the vdW interactions, which are responsible for the physical adsorption of the insoluble compounds, are dominated over 90% by the London disperse interactions tuned by the refractive index of the adsorbent and adsorbate.

Collectively, for PLA and GO matrixes, it was demonstrated that the physical adsorption of the lead compounds from water was greater on the GO surface, which exhibits a higher refractive index. However, under the filling of the PLA and GO matrixes with MoS₂ nanoparticles, a significant enhancement of the Hamaker constant, vdW adsorption potential, vdW adhesion energy, and force was demonstrated.

Overall, the physical adsorption is essentially enhanced by increasing the refractive index of the PLA/MoS₂ and GO/MoS₂ adsorbents, which can be allowed using an MoS₂ nanoparticle.

These findings provide potential qualitative and quantitative recommendations for future experimental studies for the removal of lead compounds from water using GO/MoS₂ and PLA/MoS₂ nanocomposites.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization: NM, AA, and NA; methodology: NM and AA; software: NM; validation: NM and AA; formal analysis: NM, HO, and SH; investigation: NM and AA; resources: NM and NA; data curation: NM; writing—original draft preparation: NM, NA, and AA; writing—review and editing: NM, SH, AA, and HO; visualization: NM; supervision: NM, NA, SH, and AA; project administration: NM, NA, and AA; funding acquisition: NA and AA. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Deanship of Scientific Research at King Khalid University under Grant no. RGP.2/182/43. Additionally, this research was funded by Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R19), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups Project under Grant no. RGP.2/182/43. Also, the authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R19), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Darren L, Michael S, Casey F, Christina B-S, Stephen H, Mallikarjuna N, et al. Lead particle size fractionation and identification in newark, newersey’s drinking water. Environ Sci Tech (2020) 54(21):13672–9. doi:10.1021/acs.est.0c03797

CrossRef Full Text | Google Scholar

2. Shu C, Lu C, King C, Joseph L, John F, Kelvin K. Unraveling the causes of excess lead in drinking water supply systems of densely populated high-rise buildings in Hong Kong. Environ Sci Tech (2020) 54(22). doi:10.1021/acs.est.0c03232

CrossRef Full Text | Google Scholar

3. Yan Z, Yuanyuan Z, Yi-Pin L. Fast detection of lead Dioxide (PbO2) in chlorinated drinking water by a two-stage iodometric method. Environ Sci Tech (2010) 2 44(4):1347–52. doi:10.1021/es902299b

CrossRef Full Text | Google Scholar

4. Yu-Cheng P, Yi-Fang L, Yi-Pin L. Release of particulate lead from four lead corrosion products in drinking water: A laboratory study coupled with microscopic observations and computational fluid dynamics. Environ Sci Tech (2022) 56(17):12218–27. doi:10.1021/acs.est.2c02461

CrossRef Full Text | Google Scholar

5. Jing L, Jian-su M. Risk assessment of lead emissions from anthropogenic cycle. Trans Nonferrous Met Soc China (2016) 26:248–55. doi:10.1016/S1003-6326(16)64148-1

CrossRef Full Text | Google Scholar

6. Lu C, Joseph L, Fung Y. Prediction of lead leaching from galvanic corrosion of lead containing components in copper pipe drinking water supply systems. J Hazard Mater (2022) 436:129169. doi:10.1016/j.jhazmat.2022.129169

PubMed Abstract | CrossRef Full Text | Google Scholar

7.World Human Organization. Lead in drinking-water: Health risks, monitoring and corrective actions. WHO TEAM Environment, Clim Change Health Water Sanitation, Hyg Health (2022) 1–26. Available at: https://www.who.int/publications/i/item/9789240020863 [Accessed January 15, 2023]

Google Scholar

8. Alberto F, Mir D, Ali G. 4 - application of nanotechnology in drinking water purification” in Water Purification. Cambridge, USA: Elsevier Academic Press (2017). 119–67. doi:10.1016/B978-0-12-804300-4.00004-6

CrossRef Full Text | Google Scholar

9. Satinder A. Chapter 1 - overview of advances in water purification techniques. In: Advances in water purification techniques. Calabash, NC, United States: Elsevier (2019). 1–15. doi:10.1016/B978-0-12-814790-0.00001-6

CrossRef Full Text | Google Scholar

10. Antonio G, Luis G, Miguel V. Applications of advanced oxidation processes (AOPs) in drinking water treatment. In: The handbook of environmental chemistry. Cham, Switzerland: Springer Nature (2019). 66–149. doi:10.1007/978-3-319-76882-3

CrossRef Full Text | Google Scholar

11. Iervolino G, Zammit I, Vaiano V, Luigi R. Limitations and prospects for wastewater treatment by UV and visible-light-active heterogeneous photocatalysis: A critical review. Top Curr Chem (2020) 378:7. doi:10.1007/s41061-019-0272-1

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Muhammad H, Farwa N, Muhammad Z, Farkhanda K, Asma H, Muhammad A. Chapter 23 - applications of coagulation-flocculation and nanotechnology in water treatment. In: Micro and nano technologies, aquananotechnology. Elsevier (2021). 533–58. doi:10.1016/B978-0-12-821141-0.00012-4

CrossRef Full Text | Google Scholar

13. Yang Z, Zhou Y, Feng Z, Rui X, Zhang T, Zhang Z. A review on reverse osmosis and nanofiltration membranes for water purification. Polymers (2019) 11:1252. doi:10.3390/polym11081252

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lide DR. CRC handbook of chemistry and physics. 88Th ed. Boca Raton, FL: CRC Press, Taylor & Francis (2007). 4–64/65.

Google Scholar

15. Gu T, Qin S, Wu X. Thermal behavior of pyromorphite (Pb10(PO4)6Cl2): In situ high temperature powder X-ray diffraction study. Crystals (2020) 10:1070. doi:10.3390/cryst10121070

CrossRef Full Text | Google Scholar

16. Pouran P, Ali T, Mohsen T, Mehrorang G, Sepahdar H. Chapter 1 - fundamentals of adsorption technology” in interface science and technology. Elsevier (2021) 33:1–70. doi:10.1016/B978-0-12-818805-7.00001-1

CrossRef Full Text | Google Scholar

17. Tawfik S. Chapter 2 - adsorption technology and surface science” in interface science and technology. Elsevier (2022) 34:39–64. doi:10.1016/B978-0-12-849876-7.00006-3

CrossRef Full Text | Google Scholar

18. James C. Chapter 1 - an overview and some uninteresting history of physisorption. In: Surface area and porosity determinations by physisorption. 2nd ed. Elsevier (2020). 1–57. doi:10.1016/B978-0-12-818785-2.00001-5

CrossRef Full Text | Google Scholar

19. Arunima N, Brij B, Nupur K, Shreya K. Chapter 5 - graphene oxides and its composites as new generation adsorbents for remediation of toxic pollutants from water: An overview” in Sustainable Materials for Sensing and Remediation of Noxious Pollutants. Elsevier (2022). 65–85. doi:10.1016/B978-0-323-99425-5.00014-1

CrossRef Full Text | Google Scholar

20. Souravi B, Shubham R, Mousumi M, Sukhen D. 22 - metal oxide/graphene nanocomposites and their biomedical applications. In: Metal oxides, metal oxides for biomedical and biosensor applications. Elsevier (2022). 569–84. doi:10.1016/B978-0-12-823033-6.00020-X

CrossRef Full Text | Google Scholar

21. Luc A. 9—Synthesis, properties, environmental and biomedical applications of polylactic acid. In: Plastics design library, handbook of biopolymers and biodegradable plastics. New York: William Andrew Publishing (2013). 171–88. doi:10.1016/B978-1-4557-2834-3.00009-4

CrossRef Full Text | Google Scholar

22. Ashutosh P, Ranjna S, Sudha U, Mitali M, Virendra K, Lalit S, et al. Chapter 12 - production and applications of polylactic acid” in biomass, biofuels. Biochemicals, Elsevier (2021) 309–57. doi:10.1016/B978-0-12-821888-4.00013-7

CrossRef Full Text | Google Scholar

23. Levna C, Aswini P, Kumar. V, Aneesh P. Chapter 19 - MoS2, a new perspective beyond graphene. In: Micro and nano technologies, fundamentals and properties of multifunctional nanomaterials. Elsevier (2021). 499–541. doi:10.1016/B978-0-12-822352-9.00018-3

CrossRef Full Text | Google Scholar

24. Chang L, Qingmiao W, Feifei J, Shaoxian S. Adsorption of heavy metals on molybdenum disulfide in water: A critical review. J Mol Liquids (2019) 292:111390. doi:10.1016/j.molliq.2019.111390

CrossRef Full Text | Google Scholar

25. Sato N, Aoyama Y, Yamanaka J, Toyotama A, Okuzono T. Particle adsorption on hydrogel surfaces in aqueous media due to van der Waals attraction. Sci Rep (2017) 7:6099. doi:10.1038/s41598-017-06257-1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Antonius A, Meret A, Ronald J, Dominik R, Thérèse S, Tamar K, et al. Viruses at solid–water interfaces: A systematic assessment of interactions driving adsorption. A Syst Assess Interactions Driving Adsorption Environ Sci Tech (2016) 50:732–43. doi:10.1021/acs.est.5b04644

CrossRef Full Text | Google Scholar

27. Emily M, Kenneth R, Jacob I. Recent progress in understanding hydrophobic interactions. PNAS (2006) 103:15739–46. doi:10.1073/pnas.0606422103

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Christian W, Maria S. Effect of surface hydrophobicity on adsorption and relaxation kinetics of albumin and fibrinogen: Single-species and competitive behavior. Langmuir (2001) 17(10):3006–16. doi:10.1021/la0017781

CrossRef Full Text | Google Scholar

29. Yurina A, Naoko S, Akiko T, Tohru O, Junpei Y. Particle adsorption on polymer gel surface driven by van der Waals attraction. Chem Soc Jpn (2022) 95. 2. doi:10.1246/bcsj.20210356

CrossRef Full Text | Google Scholar

30. Mahdhi N, Alsaiari NS, Alzahrani M, Katubi M, Amari A, Hammami S. Theoretical investigation of the adsorption of cadmium iodide from water using polyaniline polymer filled with TiO2 and ZnO nanoparticles. Water MDPI (2021) 13:2591. doi:10.3390/w13182591

CrossRef Full Text | Google Scholar

31. Israelachvili J. Intermolecular and surface forces. 3rd ed. Burlington, NJ, USA: Academic Press (2011). p. 107–316.

CrossRef Full Text | Google Scholar

32. Keesom H. The cohesion forces in the theory of Van der Waals. Proc Ser B Phys Sci (1921) 23:943–8. Available at: https://ui.adsabs.harvard.edu/abs/1921KNAB.23.943K (Accessed January 15, 2023).

Google Scholar

33. Rimai D, Quesnel D. Chapter 3 - particle adhesion. In: Adhesion science and engineering. Elsevier Science B.V (2002). p. 139–91. doi:10.1016/B978-044451140-9/50003-2

CrossRef Full Text | Google Scholar

34. Russel W, Saville D, Schowalter W. Dispersion forces. In: Colloidal dispersions, cambridge monographs on mechanics. Cambridge: Cambridge University Press (1989). p. 129–61. doi:10.1017/CBO9780511608810.0081

CrossRef Full Text | Google Scholar

35. London F. The general theory of molecular forces. Trans Faraday Soc (1937) 33:8–26. doi:10.1039/TF937330008B

CrossRef Full Text | Google Scholar

36. John G. Approximate expressions for retarded van der waals interaction. J Colloid Interf Sci (1981) 83(1):138–45. doi:10.1016/0021-9797(81)90018-7

CrossRef Full Text | Google Scholar

37. Nicolás R, Francisco C, Valeria T, Claudio J, Ricardo F, Leonardo B. Complex dielectric permittivity of engineering and 3D-printing polymers at Q-band. J Infrared Milli Terahz Waves (2018) 39:1140–7. doi:10.1007/s10762-018-0528-9

CrossRef Full Text | Google Scholar

38. Si-Ting S, Hang W, Dong H, Ying-Li D, Yang Z, Dong-Po S, et al. Refractive index engineering as a novel strategy toward highly transparent and tough sustainable polymer blends. Chin J Polym Sci (2020) 38:1335–44. doi:10.1007/s10118-020-2439-1

CrossRef Full Text | Google Scholar

39. Prokhorov E, Barquera-Bibiano Z, Manzano-Ramírez A, Luna-Barcenas G, Kovalenko Y, Hernández-Landaverde A, et al. New insights in graphene oxide dielectric constant. Mater Res Express (2019) 6:085622. doi:10.1088/2053-1591/ab22f0

CrossRef Full Text | Google Scholar

40. Politano G, Versace C, Vena C, Castriota M, Ciuchi F, Fasanella A, et al. Physical investigation of electrophoretically deposited graphene oxide and reduced graphene oxide thin films. J Appl Phys (2016) 120:195307. doi:10.1063/1.4968000

CrossRef Full Text | Google Scholar

41. Beal R, Hughes H. Kramers-Kronig analysis of the reflectivity spectra of 2H-MoS2, 2H-MoSe2 and 2H-MoTe2. J Phys C: Solid State Phys (1979) 12:881–90. doi:10.1088/0022-3719/12/5/017

CrossRef Full Text | Google Scholar

42. Hui Z, Yaoguang M, Yi W, Xin R, Ziang X, Wei W, et al. Measuring the refractive index of highly crystalline monolayer MoS2 with high confidence. Sci Rep (2015) 5:8440. doi:10.1038/srep08440

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Young K, Frederikse H. Compilation of the static dielectric constant of inorganic solids. J Phys Chem Reference Data (1973) 2:313–410. doi:10.1063/1.3253121

CrossRef Full Text | Google Scholar

44. Joseph R, Dudley S. “The dielectric constant of mineral powders: Rensselaer polytechnic institute engineering and science series, No. 52,” in The American Mineralogist. Montana, United States: Literary Licensing, LLC (2013) 21 (2), 118.

Google Scholar

45. Raza A, Faizan M, Sultana I, Ghulam M, Shahid A, Aneeqa B, et al. Morphology and dielectric studies of natural fibers and PbO2 based flexible composite sheets for potential energy storage applications. J Electron Mater (2020) 49:1896–903. doi:10.1007/s11664-019-07877-1

CrossRef Full Text | Google Scholar

46. Weast RC. Handbook of chemistry and physics. 68th ed. Boca Raton, Florida: CRC Press Inc. (1987). B-100.

Google Scholar

47. Fernández P, Mulev Y, Goodwin H, Sengers L. A database for the static dielectric constant of water and steam. J Phys Chem Ref Data (1995) 24:33–70. doi:10.1063/1.555977

CrossRef Full Text | Google Scholar

48. Karkkainen K, Sihvola A, Nikoskinen K. Effective permittivity of mixtures: Numerical validation by the FDTD method. IEEE Trans Geosci Remote Sensing (2000) 38:1303–8. doi:10.1109/36.843023

CrossRef Full Text | Google Scholar

49. Vadim M. Introduction to the Maxwell garnett approximation: Tutorial, J Opt Soc Am (2016) 33. 1244, doi:10.1364/JOSAA.33.001244

CrossRef Full Text | Google Scholar