Forward-stimulated Brillouin scattering in silicon-core fibers

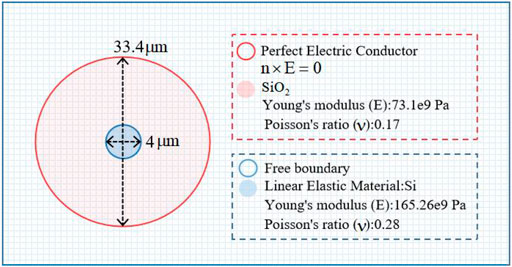
As a new type of semiconductor fiber, silicon-core fibers have a higher non-linear effect compared with silica fibers. Forward-stimulated Brillouin scattering as a typical optical non-linear effect holds strong promise for applications in, for example, fiber-optic sensing. The study of the FSBS effect in silicon-core fibers facilitates further theoretical exploitation of the potential of FSBS in fiber-optic sensing. In this paper, the FSBS in the silicon-core fiber is studied using the finite element method. The model is based on a silicon-core fiber, whose silicon-core diameter is 4 $\mathrm{\mu }\mathrm{m}$ and silica cladding diameter is 33.4 $\mathrm{\mu }\mathrm{m}$, and the optical field modes are classified by the vector method to obtain the acoustic field modes excited by FSBS—radial mode (R_0m) and torsional radial mode (TR_2m). The FSBS gain of the fiber shows that R_0m has the best coupling with TM and TE optical modes, and TR_2m has the best coupling with HE optical modes. It is concluded that the sound field frequency shift of R_0m is more sensitive to the change in the effective refractive index of the optical field than that of TR_2m. The factors affecting the gain are refined into photoelastic effects and moving boundary perturbations, and their contributions to the total gain are summarized. Finally, it was confirmed that a strong FSBS gain similar to 365.57 (1/mw) can be obtained with silicon-core fibers without the need to reduce the size to the usual dimensions of silicon waveguides, paving the way for further research studies in areas such as frequency-tunable laser emission, mode-locked pulsed lasers, low-noise oscillators, and optical gyroscopes.

1 Introduction

Silicon photonics, which emerged from the close combination of electrons and photons, is now the most active discipline in the field of integrated optics [1, 2]. The interaction of the optical field with electrons and phonons in silicon gives rise to a large number of non-linear effects and has a high third-order optical non-linearity [1, 3, 4]. Silicon-core fibers, which have been manufactured by Badding Group since 2008 [5], belong to a new type of semiconducting platform. The silicon-core fibers are robust, flexible, and cylindrically symmetric and are becoming a new platform for the development of non-linear optical devices [6]. The high refractive index contrast between the silicon core and the silica cladding can guarantee strong optical confinement for all signals near the near-infrared wavelength of 1,550 nm, resulting in strong optical guiding [1]. The high optical confinement generated by this large contrast (between Si and SiO₂) makes it possible to observe strong non-linear optical interactions as observed in chip-scale devices [7].

Forward-stimulated Brillouin scattering, as an optical non-linearity, is a third-order non-linear process in which the optical and acoustic fields are coupled [8]. Excitation of strong forward-stimulated Brillouin scattering (FSBS) in silicon has been realized in a new class of nanoscale opto-mechanical waveguides with record-high non-linearity (four times larger than that in silica fibers) [9]. Compared to nanoscale linear silica waveguides, both with micron-sized core diameters and silica cladding, these large-core fibers provide better power-handling capabilities [10]. However, its high core-cladding index contrast means that it does not support the weak waveguide approximation, and it will guide multiple vector modes [11]. The properties of FSBS in silica-core fibers in the presence of multiple vector modes have then not been studied in detail [12]. In this study, we model the forward Brillouin scattering in a multimode silicon-core fiber using the finite element method. The model is based on a silicon-core fiber with a core diameter of 4 $\mathrm{\mu }\mathrm{m}$ and a cladding diameter of 33.4 $\mathrm{\mu }\mathrm{m}$; it takes a vectorial approach to classify the optical field modes at high core-cladding index contrast to obtain the acoustic field modes excited by the FSBS—radial mode (R_0m) and torsional radial mode (TR_2m), and investigates the effects of these two types of acoustic modes on the FSBS gain and the frequency shift. Finally, it is confirmed that the silicon-core fiber does not need to be reduced to the usual size of a silicon waveguide to obtain similar strong gains.

2 Simulation and discussion

2.1 Simulation of optical wavefield modes in silicon-core fibers

In this study, we take silicon-core fiber as the prototype, where the core diameter is 4 $\mathrm{\mu }\mathrm{m}$, cladding diameter is 33.4 $\mathrm{\mu }\mathrm{m}$, core material is silicon, refractive index is 3.5, Young’s modulus is 165.26 GPa, Poisson’s ratio is 0.28, cladding material is silica, refractive index is 1.45, Young’s modulus is 73.1 GPa, Poisson’s ratio is 0.17, numerical aperture of fiber NA is 3.35, and incident light wavelength $\lambda$ is 1,550 nm [13]. The mechanical quality factor of the quartz fiber material is about 1,000 [14, 15]. Figure 1 shows the boundary conditions, selected materials, and parameters of the silicon-core fiber model. The red part is the fiber cladding, the blue part is the fiber core, the boundary between the cladding and the air layer is set as an ideal electrical conductor, the boundary between the core and the cladding is set as a free boundary to ensure that the sound field can be displaced on this boundary, and the silicon material of the fiber core is set as a linear elastic material. Since the difference between the relative refractive indices of the silicon-core silica-clad fiber simulated in this study does not satisfy the weak waveguide condition $n_2\approx n_1$, the longitudinal components $\left({\mathrm{E}}_z,{\mathrm{H}}_z\right)$ of the electric and magnetic fields are not much smaller than the transverse components $\left({\mathrm{E}}_r,{\mathrm{E}}_{\varphi },{\mathrm{H}}_r,{\mathrm{H}}_{\varphi }\right)$ in the electromagnetic field distribution in the silicon-core fiber [16]. When both electric and magnetic fields are present in the direction of electromagnetic wave propagation (z-direction), a hybrid mode ($\mathrm{E}{\mathrm{H}}_{mn}$ mode) (where the electric field component is more dominant in the direction of electromagnetic wave propagation, ${\mathrm{E}}_z>{\mathrm{H}}_z$) and a hybrid mode ($\mathrm{H}{\mathrm{E}}_{mn}$ mode) (where the magnetic field component is more dominant in the direction of electromagnetic wave propagation, ${\mathrm{H}}_z>{\mathrm{E}}_z$) are generated due to the different magnitudes of ${\mathrm{E}}_z$ or ${\mathrm{H}}_z$ relative effects [17, 18]. When only the electric field or only the magnetic field exists in the direction of electromagnetic wave propagation, the case of only the electric field produces the transverse magnetic mode (TM mode) (when the magnetic field direction is along the tangential direction of the fiber cross-section), and the case of only the magnetic field produces the transverse electric mode (TE mode) (when the electric field direction is along the tangential direction of the fiber cross-section) [19–21]. Figure 2 shows the field distribution of the HE mode, TM mode, and TE mode of the optical field present in the silicon-core fiber simulated by the finite element method, respectively, and the white and black arrows on the optical field image are the electric field vectors.

FIGURE 1

FIGURE 1. Simulation model of the silicon-core fiber.

FIGURE 2

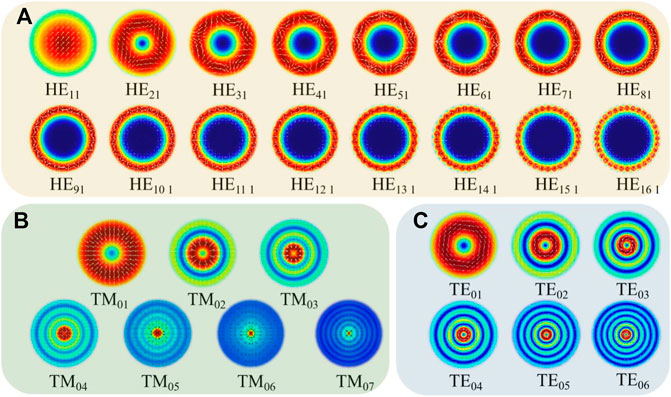
FIGURE 2. (A) Field intensity distribution of the HE mode in silicon-core fiber. (B) Field intensity distribution of the TM mode in silicon-core fiber. (C) Field intensity distribution of the TE mode in silicon-core fiber.

2.2 Phase matching of optical and acoustic fields

For FSBS, the optical and acoustic fields confined in the fiber can be coupled by inelastic light scattering, and electrostriction in the fiber causes a change in the dielectric constant, which affects the refractive index and forms a time-dependent refractive index grating [22]. In the process of interaction, both energy and momentum must be conserved, so the pump light, scattered light, and acoustic field must satisfy the phase-matching condition and the momentum conservation condition [23], specifically in the FSBS studied in this paper; the wave vectors of the pump light, scattered light, and acoustic field should follow [24]:

${\beta }_m\left(\mathrm{\Omega }\right)={\beta }_p\left({\omega }_p\right)-{\beta }_s\left({\omega }_p-\mathrm{\Omega }\right).(1)$

For multimode fibers, the pump light has multiple conduction modes, each with its own different effective refractive index ${\mathrm{n}}_{eff}$ and scattering angle ${\theta }_n$. The inelastic collision between the optical photons of the pump light and the acoustic phonons in the medium to produce scattered light also excites multiple conduction modes, each with a scattering angle of ${\theta }_m$. Any one of the conduction modes of the pump light and any one of the conduction modes of the scattered light will interact non-linearly by coupling with each other in the acoustic field. In forward intra-mode scattering, the pump light in mode $\left({\omega }_p,{\beta }_p\right)$ scatters the scattered light $\left({\omega }_s,{\beta }_s\right)$ of the same mode in the same direction, and they need to satisfy the phase matching condition as [25, 26]

${\beta }_m^{intra}={\beta }_p\left({\omega }_p\right)-{\beta }_s\left({\omega }_p-\mathrm{\Omega }\right)\approx 0.(2)$

As shown in Figure 3, the acoustic field mode at this point is at a position very close to the cutoff in the dispersion relation, but the wave vector of the acoustic mode is not exactly equal to 0. The wave vector of the acoustic mode can be estimated by [27, 28]:

${\beta }_m={\beta }_p-{\beta }_s\approx \left({\omega }_p-{\omega }_s\right)\frac{\partial \beta }{\partial \omega }=\frac{\mathrm{\Omega }}{v_g},(3)$

FIGURE 3

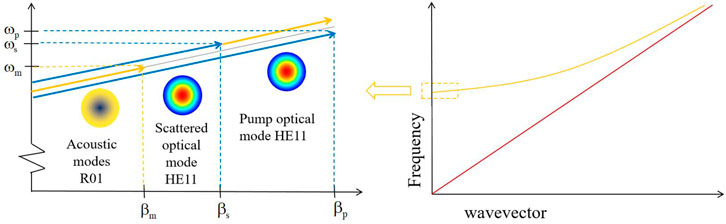
FIGURE 3. Phase-matching relationship of the pump light, scattered light, and acoustic field in silicon-core fiber.

where $v_g$ is the group velocity of the optical mode dispersion branch [29], the group velocity of the optical field fundamental mode within the forward Brillouin mode of the silicon-core fiber is $8.6142\times {10}^7$ m²/s, the optical frequency is $1.21526\times {10}^{15}$ Hz, and the frequency of the acoustic field mode R₀₁ is $1.9749\times {10}^{15}$ Hz, so the ratio of the wave vector of the acoustic mode R₀₁ to the pump optical fundamental mode should satisfy $\frac{{\beta }_m}{{\beta }_p}\approx \frac{\mathrm{\Omega }}{{\omega }_p}\approx 10^{-6}$. The absolute value of the wave vector of the acoustic mode R₀₁ is 22.9267 rad/m.

2.3 Excitation of guided acoustic modes in silicon-core fibers with multiple modes

The frequencies of the excitable elastic modes in FSBS are fixed by the structure and are independent of the incident light frequency. The acousto-optic matching condition for forward Brillouin scattering requires the acoustic field modes to be located at the approximate cutoff in the dispersion curve, when the phase velocity of these acoustic waves tends toward infinity and the group velocity tends toward zero, so the acoustic field modes in FSBS are called guided acoustic modes [30].The core of a silicon-core fiber is a linear elastic material, and the fluctuation equation of linear elastodynamics is established, and this equation describes various elastic waves in a uniform rod with a circular cross-section [31]:

$\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2}+2\mathrm{\Gamma }\frac{\partial \mathrm{U}}{\partial \mathrm{t}}-{\mathrm{V}}_{\mathrm{s}}^2\Delta \mathrm{U}-\left({\mathrm{V}}_{\mathrm{l}}^2-{\mathrm{V}}_{\mathrm{s}}^2\right){\nabla }^2\mathrm{U}=\mathrm{f},\hspace{0.17em}\Delta \equiv \mathrm{d}\mathrm{i}\mathrm{v}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}.(4)$

The f on the right-hand side of the equation is the density of the volume force that causes small-amplitude acoustic vibrations in the medium. For FSBS, ${\beta }_m$ tends toward 0, so when small-amplitude acoustic vibrations exist only in the radial and tangential directions, f is [31]:

${\mathit{f}}_r=-\frac{{\mathrm{E}}_0^2\left(t\right)\mathrm{V}\left(r\right)}{16\pi {\rho }_0}\frac{\partial \mathrm{V}\left(r\right)}{\partial r}\left(a_1+4a_2+a_1\mathit{cos}2\varphi \right).$(5.1)

${\mathit{f}}_{\varphi }=\frac{{\mathrm{E}}_0^2\left(t\right)\mathrm{V}\left(r\right)}{16\pi {\rho }_0}\frac{\partial \mathrm{V}\left(r\right)}{\partial r}{a}_1\mathit{sin}2\varphi .$(5.2)

In Eqs. 5.1, 5.2, ${\mathrm{E}}_r={\mathrm{E}}_0\left(t\right)\mathrm{V}\left(r\right)\mathit{cos}\varphi ,{\mathrm{E}}_{\varphi }=-{\mathrm{E}}_0\left(t\right)\mathrm{V}\left(r\right)\mathit{sin}\varphi ,a_1=-{\epsilon }_0^2\left({\mathrm{P}}_{11}-{\mathrm{P}}_{12}\right),a_2=-{\epsilon }_0^2{\mathrm{P}}_{12}\left[31\right]$; bringing Eqs. 5.1, 5.2into Eq. 4, the radial displacement ${\mathrm{U}}_r\left(t\right)$ and tangential displacement ${\mathrm{U}}_{\varphi }\left(t\right)$ can be solved for [32]:

${\mathrm{U}}_r\left(t\right)=\mathrm{W}\left(r\right)\left\{\begin{array}{c}\mathit{sin}n\varphi \\ \mathit{cos}n\varphi \end{array}\right\}{e}^{-j\left({\omega }_m^{\left(n\right)}t+\mathrm{\Gamma }t\right),}$(6.1)

${\mathrm{U}}_{\varphi }\left(t\right)=\mathrm{\Phi }\left(r\right)\left\{\begin{array}{c}\mathit{cos}n\varphi \\ -\mathit{sin}n\varphi \end{array}\right\}{e}^{-j\left({\omega }_m^{\left(n\right)}t+\mathrm{\Gamma }t\right)},$(6.2)

${\mathrm{U}}_z\left(t\right)=\mathrm{Z}\left(r\right)\left\{\begin{array}{c}\mathit{sin}n\varphi \\ \mathit{cos}n\varphi \end{array}\right\}{e}^{-j\left({\omega }_m^{\left(n\right)}t+\mathrm{\Gamma }t\right)}.$(6.3)

$\mathrm{\Gamma }$ is the spectral width, a parameter indicating the acoustic particle dissipation. $\mathrm{W}\left(r\right),\mathrm{\Phi }\left(r\right),\mathrm{Z}\left(r\right)$ is the radial dependence of the displacement expressed as a Bessel function with $\mathrm{Z}\left(r\right)$ = 0. n is related to the type of vibration, and m denotes the mth root of the characteristic equation that determines the frequency [33]. The upper and lower marks of ${\mathrm{\omega }}_m^{\left(n\right)}$ indicate that for the nth vibration type, m frequencies exist. The next section discusses what value of n is required to satisfy the phase-matching condition for forward Brillouin scattering. Equations 5.1, 5.2 contains the term associated with $2\mathrm{\varphi }$ and does not contain the term associated with $\varphi$. Therefore, n in Eqs. 6.1–6.3 is equal to 0 or equal to 2. When n = 0, only the term in Eq. 5.1 expressing ${\mathit{f}}_r$ that is independent of $\varphi$ plays a role. The case of ${\mathrm{U}}_r\left(t\right)\ne 0$ but not ${\mathrm{U}}_{\varphi }\left(t\right)=0$ in Eq. 6 occurs only if n = 0 is brought into the row below the flower brackets. This type of sound field vibration is named radial mode (${\mathrm{R}}_{nm}$, n = 0), so the displacement equation for ${\mathrm{R}}_{0m}$ is ${\mathrm{U}}_r\left(t\right)=\mathrm{W}\left(r\right)e^{-j\left({\omega }_m^{\left(0\right)}t+\mathrm{\Gamma }t\right)}$. The dispersion diagram of ${\mathrm{R}}_{0m}$ is shown on the right side of Figure 4A, and the left side shows the vibrations of the ${\mathrm{R}}_{0m}$ modes in the FSBS of the silicon-core fiber with markers m from one to six in order; they are located at the leftmost part of the dispersion diagram near the cutoff position. When n = 2, the terms ${\mathit{f}}_r$ and ${\mathit{f}}_{\varphi }$ related to $2\varphi$ in Eqs. 5.1, 5.2 come into play, and in Eqs. 6.1–6.3, n = 2 is brought into the upper row of the brackets with radial displacement ${\mathrm{U}}_r\left(t\right)\ne 0$ and tangential displacement ${\mathrm{U}}_{\varphi }\left(t\right)\ne 0$. This type of sound field vibration is named the torsional radial mode (${\mathrm{T}\mathrm{R}}_{nm},\mathrm{n}=0$), and thus, ${\mathrm{U}}_r\left(t\right)=\mathrm{W}\left(r\right)\mathit{sin}\left(2\varphi \right)e^{-j\left({\omega }_m^{\left(2\right)}t+\mathrm{\Gamma }t\right)}$, ${\mathrm{U}}_{\varphi }\left(t\right)=\mathrm{\Phi }\left(r\right)\mathit{cos}\left(2\varphi \right)e^{-j\left({\omega }_m^{\left(2\right)}t+\mathrm{\Gamma }t\right)}$ is the displacement equation. The right side of Figure 4B shows the dispersion diagram of $\mathrm{T}{\mathrm{R}}_{2m}$. On the left is the vibration of the $\mathrm{T}{\mathrm{R}}_{2m}$ mode in forward Brillouin scattering from the silicon-core fiber with marker m in order from 1 to 12, where marker n corresponds to the wave vector ${\beta }_m$ and marker m corresponds to the sound field frequency ${\omega }_m$.

FIGURE 4

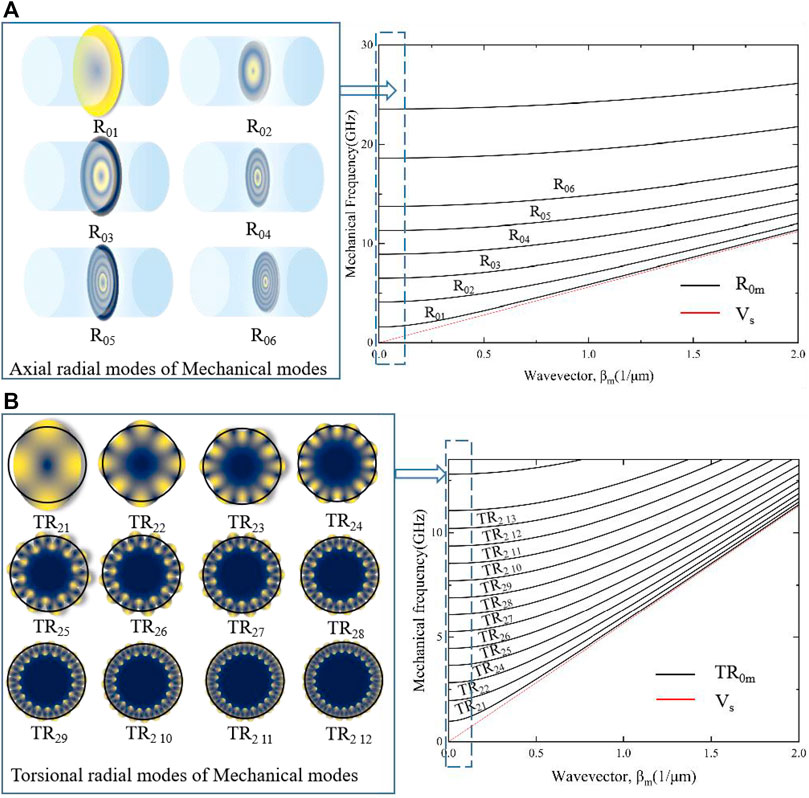
FIGURE 4. (A) Acoustic field modes ${\mathrm{R}}_{0m}$ present in forward Brillouin scattering from a silicon-core fiber. (B) Acoustic field modes $\mathrm{T}{\mathrm{R}}_{2m}$ present in forward Brillouin scattering from a silicon-core fiber.

The acoustic field modes excited by forward Brillouin scattering in the silicon-core fiber are the radial mode (${\mathrm{R}}_{0m}$) and torsional radial mode (TR_2m). The only force driving ${\mathrm{R}}_{0m}$ is the radial force ${\mathit{f}}_r$, and there is no ${\mathit{f}}_{\varphi }$ perpendicular to the radial force ${\mathit{f}}_r$. There is both ${\mathit{f}}_r$ and ${\mathit{f}}_{\varphi }$ driving $\mathrm{T}{\mathrm{R}}_{2m}$.

3 Gain of FSBS of the silicon-core fiber and the effects of ${\mathrm{R}}_{\mathrm{0}\mathit{m}}$ and $\mathrm{T}{\mathrm{R}}_{\mathrm{2}\mathit{m}}$ on the frequency shift

After the pump and scattered optical modes at a given $\mathrm{\omega }$ have been calculated, and when the acoustic field modes ${\mathrm{R}}_{0m}$ and $\mathrm{T}{\mathrm{R}}_{2m}$ meet the phase-matching condition q = k_p - k_s, the Brillouin gain values corresponding to each acoustic field mode can be calculated by computing the overlap integrals of the optical and acoustic fields. The acousto-optical overlap integral consists of two components: moving boundary perturbation (MB) and photoelastic effect (PE) [34]. The photoelastic effect refers to the disturbance of the dielectric constant by elastic strain, and moving boundary perturbation refers to the perturbation of the effective refractive index of the optical mode by the geometric deformation of the fiber caused by the acoustic field. The moving boundary perturbation and photoelastic effect describe the process of generating Brillouin gain in terms of the acoustic field perturbing the optical field, while the more classical radiation pressure and electrostriction describe the process in terms of the optical field electromagnetic force driving the acoustic field. The acousto-optical overlap integrals calculated from these two descriptive perspectives are consistent. Brillouin gain based on moving boundary perturbations and photoelastic effects is calculated as follows:

${\mathrm{G}}_{\mathrm{B}}\left(\mathrm{\Omega }\right)=\frac{2{\omega }_p{\mathrm{Q}}_m}{{\mathrm{\Omega }}_m^2}\frac{\mathit{max}\left(\sqrt{{\left|u\right|}^2+{\left|v\right|}^2+{\left|w\right|}^2}\right)}{\int \rho \left({\left|u\right|}^2+{\left|v\right|}^2+{\left|w\right|}^2\right)d\mathrm{A}}{\left|\int f_{mb}dl+\int f_{pe}d\mathrm{A}\right|}^2,(7)$

where ${\mathrm{Q}}_m$ is the mechanical quality factor, ${\mathrm{\omega }}_p$ is the pump light frequency, $\rho$ is the fiber core density, ${\mathrm{\Omega }}_m$ is the acoustic field frequency, $\int f_{mb}dl$ is the line integral representing the moving boundary effect, and $\int f_{pe}d\mathrm{A}$ refers to the area fraction representing the photoelastic perturbation [35].

$f_{mb}=\frac{u^{*}\cdot \widehat{n}\left[\left({\epsilon }_1-{\epsilon }_2\right){\epsilon }_0{\mathrm{E}}_{p,‖}^{*}\cdot {\mathrm{E}}_{s,‖}-\left(\frac{1}{{\epsilon }_1}-\frac{1}{{\epsilon }_2}\right)\frac{1}{{\epsilon }_0}{\mathrm{D}}_{p,\perp }^{*}\cdot {\mathrm{D}}_{s,\perp }\right]}{\mathit{max}\left(\left|u\right|\right){\mathrm{N}}_p{\mathrm{N}}_s}.(8)$

$f_{pe}=\frac{\delta {\epsilon }_{pe}{\mathrm{E}}_p^{*}{\mathrm{E}}_s}{\mathit{max}\left(\left|u\right|\right){\mathrm{N}}_p{\mathrm{N}}_s}.(9)$

$u\cdot \widehat{n}$ is the surface-normal component of the displacement vector, ${\epsilon }_1$ and ${\epsilon }_2$ refer to the relative dielectric constants of the core and cladding, the subscripts p or s refer to pump or scatter light, $\Vert$ refers to the tangential or normal direction, and E refers to the electric field ${\mathrm{D}}_{\perp }={\epsilon }_1{\mathrm{E}}_{1\perp }={\epsilon }_2{\mathrm{E}}_{2\perp }$. The denominators in $f_{mb}$ and $f_{pe}$ denote energy- or power-normalized integrals [36]. $p_{ij}$ is the photoelastic tensor, and $\delta {\epsilon }_{pe}{\mathrm{E}}_p^{*}{\mathrm{E}}_s$ is the time-harmonic electrostriction tensor [37, 38].

$\delta {\epsilon }_{pe}{\mathrm{E}}_p^{*}{\mathrm{E}}_s=-{\epsilon }_0{n}^4\left[\begin{array}{cccccc}{\mathrm{P}}_{11}& {\mathrm{P}}_{12}& {\mathrm{P}}_{13}& 0& 0& 0\\ {\mathrm{P}}_{12}& {\mathrm{P}}_{22}& {\mathrm{P}}_{23}& 0& 0& 0\\ {\mathrm{P}}_{13}& {\mathrm{P}}_{23}& {\mathrm{P}}_{33}& 0& 0& 0\\ 0& 0& 0& {\mathrm{P}}_{44}& 0& 0\\ 0& 0& 0& 0& {\mathrm{P}}_{55}& 0\\ 0& 0& 0& 0& 0& {\mathrm{P}}_{66}\end{array}\right]\left[\begin{array}{c}{\mathrm{E}}_{px}{\mathrm{E}}_{sx}^{*}\\ {\mathrm{E}}_{py}{\mathrm{E}}_{sy}^{*}\\ {\mathrm{E}}_{pz}{\mathrm{E}}_{sz}^{*}\\ {\mathrm{E}}_{py}{\mathrm{E}}_{sz}^{*}+{\mathrm{E}}_{pz}{\mathrm{E}}_{sy}^{*}\\ {\mathrm{E}}_{px}{\mathrm{E}}_{sz}^{*}+{\mathrm{E}}_{pz}{\mathrm{E}}_{sx}^{*}\\ {\mathrm{E}}_{px}{\mathrm{E}}_{sy}^{*}+{\mathrm{E}}_{py}{\mathrm{E}}_{sx}^{*}\end{array}\right].(10)$

The forward Brillouin gain of the silicon-core fiber can be obtained by bringing each physical parameter of silicon and silica in Table 1 into Eq. 7. Figure 5 shows the forward Brillouin gain of the acoustic field coupled with R_0m for the pump light-scattered light mode pairs TM₀₁–TM₀₁, TM₀₂–TM₀₂, TM₀₃–TM₀₃, TM₀₄–TM₀₄, and TM₀₅–TM₀₅, respectively. Figure 5A shows the FSBS gain when the sound field is coupled with R₀₁, Figure 5B shows the FSBS gain when the sound field is coupled with ${\mathrm{R}}_{0\mathrm{m}}$, and the yellow gain bars in Figure 5B represent the gains of R₀₂, R₀₃, R₀₄, R₀₅, and R₀₆ from left to right. The triangular squares, square squares, and yellow bars in Figure 5 represent the FSBS gain under three conditions: photoelastic perturbation only, moving boundary only, and combined effect.

TABLE 1

TABLE 1. Physical parameters of Si and SiO₂.

FIGURE 5

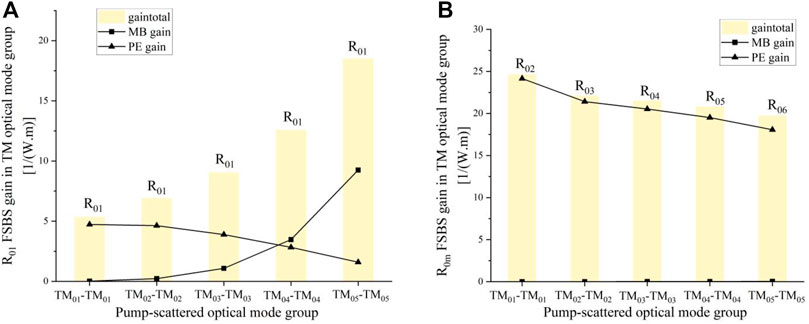
FIGURE 5. (A) Forward Brillouin gain of the acoustic field coupled with R₀₁ for the pump light-scattered light mode pair of transverse magnetic modes TM_0m–TM_0m. (B) Forward Brillouin gain of the acoustic field coupled to R_0m for the pump light-scattered light mode pair of transverse magnetic modes TM_0m–TM_0m.

In Figure 5A, the total gain increases with the higher order of the optical field mode pair and the contribution of the photoelastic perturbation to the total gain decreases, while the contribution of the moving boundary effect to the total gain increases all the time and exceeds the photoelastic perturbation at TM₀₄–TM₀₄ and reaches the maximum at TM₀₅–TM₀₅ in the case of both acoustic fields as R₀₁. As mentioned in Ref. 37, the FSBS gain is more dominated by the moving boundary effect as the size decreases, and the moving boundary effect decays sharply as the size increases. In the process of pumping light-scattering optical mode pairs from low to high order in silicon-core fibers, there is a gradual concentration of optical field energy in the core, and for coupling the same acoustic modes, the FSBS gain is also gradually dominated by the moving boundary effect, i.e., the higher-order optical modes of large-size silicon-core fibers have an effect similar to those of small-size fibers in the process of FSBS gain excitation.

In Figure 5B, R₀₂, R₀₃, R₀₄, R₀₅, and R₀₆ are all acoustic fields corresponding to the maximum value in the FSBS gain spectrum for each R_0m optical mode pair, with maximum gains of 24.65(1/mw), 22.14(1/mw), 21.54(1/mw), 20.8(1/mw), and 19.73(1/mw), respectively, and contributed almost exclusively by photoelastic perturbations. Figure 5B illustrates that the in-mode forward Brillouin scattering of TM optical modes can only obtain increased gain when coupling the axial radial mode R_0m and that the normal electrostriction force is the largest force driving the realization of this process. Figure 6 shows the complete FSBS gain spectra for the pump light-scattered light mode pairs TM₀₁–TM₀₁, TM₀₂–TM₀₂, TM₀₃–TM₀₃, TM₀₄–TM₀₄, and TM₀₅–TM₀₅, respectively. The line width of Brillouin scattering within the silicon-core fiber mode also gradually increases during the change in pump light and scattered light modes from lower to higher orders, and the spectral line width of Brillouin scattering gradually increases with the increase in the mode order. The main reason is that the smaller propagation constants of the higher-order modes in the multimode fiber make their effective refractive indices lower, as described in the paper [39].

FIGURE 6

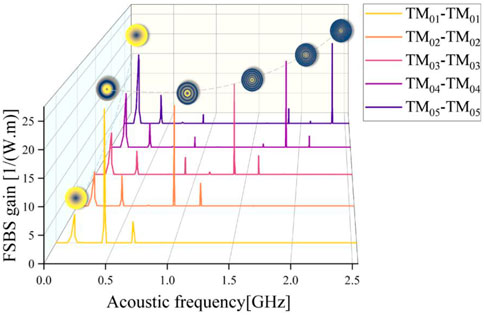
FIGURE 6. Complete FSBS gain spectrum for pump light-scattered light mode pairs for the transverse magnetic mode TM_0m–TM_0m, respectively.

The aforementioned results illustrate that each mode in the multimode silicon-core fiber independently excites its own Brillouin scattering spectrum, where the acoustic field mode R_0m always corresponds to the highest one in the gain spectrum of each optical mode pair, and its frequency shift varies greatly with the increasing order of the mode pair. The change in the mode pair can be equated to the change in the effective refractive index n_eff in the fiber, from which it can be concluded that the acoustic field mode R_0m has a non-linear change for the change in the effective refractive index of the core of the silicon-core fiber.

When the pump-scattered light mode pairs are mixed mode HE₁₁-HE₁₁, HE₂₁-HE₂₁, HE₃₁-HE₃₁, HE₄₁-HE₄₁, HE₅₁-HE₅₁, HE₆₁-HE₆₁, HE₇₁-HE₇₁, HE₈₁-HE₈₁, HE₉₁-HE₉₁, HE_{10 1}-HE_{10 1}, HE_{11 1}-HE_{11 1} HE_{12 1}-HE_{12 1}, HE_{13 1}-HE_{13 1}, HE_{14 1}-HE_{14 1}, HE_{15 1}-HE_{15 1}, HE_{16 1}-HE_{16 1} when the sound field is coupled to R₀₁ and TR_2m with the forward Brillouin gain shown in Figure 7A shows the FSBS gain when the sound field is coupled to R₀₁, and Figure 7B shows the FSBS gain when the sound field is coupled to TR_2m. The yellow gain bars in Figure 7B represent, from left to right, TR₂₁, TR₂₂, TR₂₃, TR₂₄, TR₂₅, TR₂₆, TR₂₇, TR₂₈, TR₂₉, TR_{2 10}, TR_{2 11}, TR_{2 12,} TR_{2 13}, TR_{2 14}, and the gain of TR_{2 15} and TR_{2 16}. In Figure 7A, the total gain decreases and then increases with the higher order of the optical field mode pair, and the contribution of the photoelastic effect to the total gain gradually decreases, while the contribution of the moving boundary perturbation to the total gain gradually increases, and the moving boundary perturbation and the photoelastic effect are equivalent at HE_{11 1}–HE_{11 1}, after which the moving boundary perturbation gradually exceeds the photoelastic effect and reaches the maximum at HE_{16 1}–HE_{16 1}. Unlike the transverse magnetic TM_0m mode pair, the total gain of the hybrid mode HE_n1–HE_n1 undergoes a process of decreasing and then increasing, with the FSBS gain of the lowest order HE₁₁–HE₁₁ controlled by the photoelastic effect and the FSBS gain of the highest order HE_{16 1}–HE_{16 1} controlled by the moving boundary perturbation.

FIGURE 7

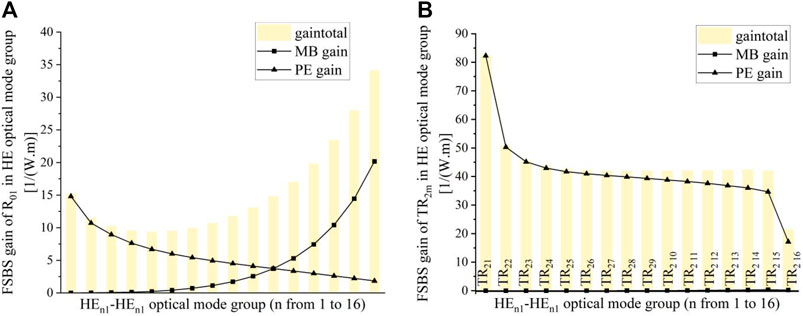
FIGURE 7. (A) Forward Brillouin gain of the acoustic field coupled to R₀₁ for pump light-scattered light mode pairs with mixed mode HE_n1–HE_n1, respectively. (B) Forward Brillouin gain of the acoustic field coupled to TR_2m for pump light-scattered light mode pairs with mixed mode HE_n1–HE_n1, respectively.

In Figure 7B, each order mode of R_0m is the acoustic field corresponding to the maximum value in the FSBS gain spectrum of each HE_n1–HE_n1 optical mode pair, with maximum gains of 82.49 (1/mw), and contributed almost exclusively by photoelastic perturbations. Figure 7B illustrates that unlike the TM optical mode, the in-mode forward Brillouin scattering of the HE optical mode can only obtain increased gain when coupling the tangential radial mode TR_2m, and the tangential electrostriction force is the largest force driving this process to be achieved.

Figure 5B and Figure 7B show that the electrostriction force is the largest driving force to achieve the maximum FSBS gain, both when coupling to R_0m and TR_2m. The moving boundary effect, however, is only better when coupling R₀₁ and is better when coupling R₀₁ in higher-order optical modes.

Figure 8 shows the complete FSBS gain spectrum for the pump light-scattered light mode pair of HE_n1–HE_n1 (n from 1 to 16), respectively. The line width of Brillouin scattering within the silicon-core fiber mode also gradually increases as the pump light and scattered light modes change from lower to higher orders, i.e., the spectral line width of Brillouin scattering gradually increases with the increase in the mode order.

FIGURE 8

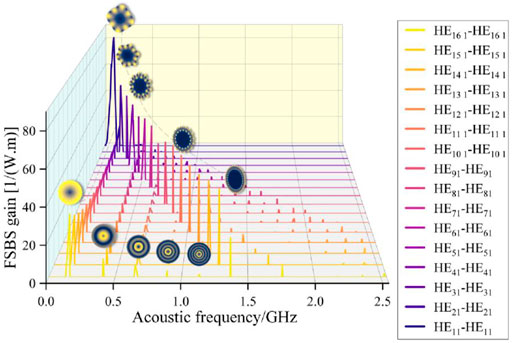
FIGURE 8. Complete FSBS gain spectrum for the pump light-scattered light mode pair with the mixed mode HE_n1–HE_n1, respectively.

The aforementioned results indicate that HE_n1–HE_n1 couples more torsional radial mode TR_2m, the frequency shift of the torsional radial mode also shifts to high frequencies as the mode pair changes, and its frequency shift varies greatly with the increase in the mode pair order. After the change in the mode pair is equated to the change in the effective refractive index n_eff in the fiber, it can be concluded that the acoustic field mode TR_2m has a non-linear change for the change in the effective refractive index of the core of the silicon-core fiber.

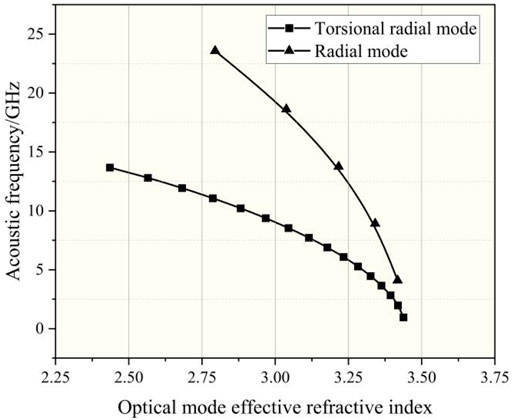
The horizontal coordinate of Figure 9 shows the effective refractive index change for the pumped light-scattered light mode pair, and the vertical coordinate shows the frequency shift of the sound field mode. The frequency shift of the acoustic field radial mode is larger than that of the torsional radial mode for the same effective refractive index change, implying that the radial mode R_0m is more sensitive to the effective refractive index change than the torsional radial mode TR_2m for the acoustic field frequency shift.

FIGURE 9

FIGURE 9. Comparison of frequency shifts of R_0m and TR_2m.

Figure 10 shows the FSBS gain when the acoustic field is coupled to R₀₁. In Figure 10, the total gain gradually increases with the higher order of the optical field mode pair, and the contribution of both the photoelastic effect and the moving boundary perturbation to the total gain gradually increases, and the moving boundary perturbation and the photoelastic effect are equivalent at TE₀₇–TE₀₇, after which the moving boundary perturbation increases more rapidly and reaches the maximum at TE₀₈–TE₀₈, but at this time, the photoelastic effect does not decrease to nearly 0. The moving boundary perturbation and photoelastic effect still work together.

FIGURE 10

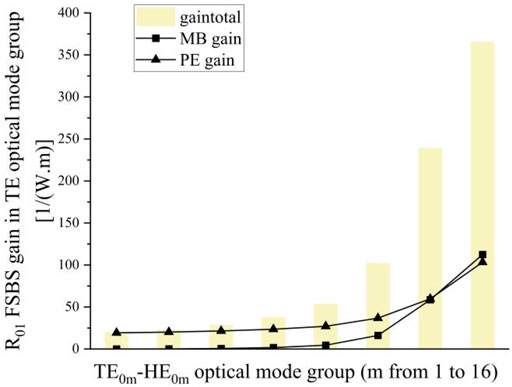
FIGURE 10. Forward Brillouin gain of the acoustic field coupled with R₀₁ when the pump light-scattered light mode pair is the mixed mode TE_0m–TE_0m, respectively.

Figure 11 shows the complete FSBS gain spectrum for the pump light-scattered light mode pair TE_0m–TE_0m (m from 1 to 8), respectively. Unlike the FSBS gain spectra of TM_0m–TM_0m and HE_1m–HE_1m, TE_0m–TE_0m has only one high peak, and its gain spectrum is not in the form of a double peak. This means that the TE_0m–TE_0m optical mode pair is only coupled to the fundamental mode R₀₁ of the axial radial mode, which is related to the fact that the electric field direction of the TE optical mode is only along the tangential direction of the fiber cross-section (without any axial direction).

FIGURE 11

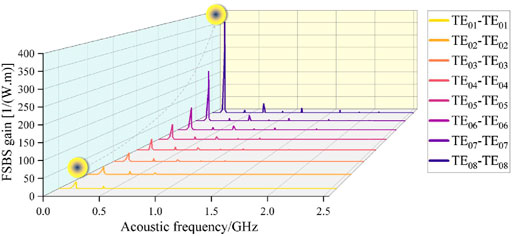
FIGURE 11. Complete FSBS gain spectrum for pump light-scattered light mode pairs for the mixed mode TE_0m–TE_0m, respectively.

The TE_0m–TE_0m optical mode pair and AR₀₁ coupling produced a maximum gain value of 365.57 (1/mw) for forward Brillouin scattering from a silicon-core fiber, resulting from TE₀₈–TE₀₈ coupling with R₀₁. Figure 12 shows the FSBS gain spectra of pumped and scattered light from different orders, that is, the gain spectra when scattered to higher orders, whose maximum value is also smaller than the FSBS gain of pumped and scattered light from the same order. It can be seen that the maximum FSBS gain in the silicon-core fiber should come from the intra-modal FSBS. Since the Brillouin gain is a combination of photoelastic perturbation and moving boundary effect, where the moving boundary effect decreases with the increase in the fiber volume, the forward Brillouin gain in the silicon waveguide decreases with the increase in the volume of the silicon waveguide [37, 40]. While a silicon fiber with a diameter of 4 $\mathrm{\mu }$ m is simulated in this study, its maximum Brillouin scattering gain can reach 365.57 (1/mw); the forward Brillouin gain of the silicon fiber is larger than the forward Brillouin gain of a silicon waveguide of the same size. The silicon-core fiber does not need to be reduced to the conventional size of a silicon waveguide to obtain a similar gain [9], and this advantage is derived from the cylindrically symmetric geometry of the silicon-core fiber, which allows better coupling of the acoustic and optical fields.

FIGURE 12

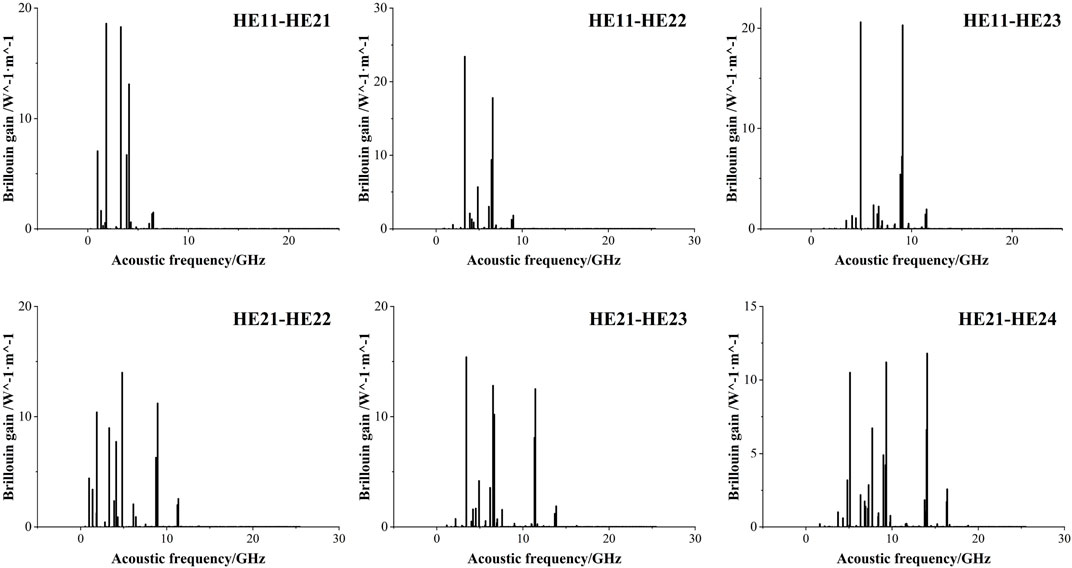
FIGURE 12. Forward Brillouin gain spectrum from lower-order light field scattering to the higher-order light field.

4 Conclusion

By studying the FSBS in the silicon-core fiber, it is shown that the sound field mode R_0m has the best coupling with the TM and TE optical mode, and the sound field mode TR_2m has the best coupling with the HE optical mode. In the case of the best coupling, the moving boundary perturbations and photoelastic effects each contribute. The contribution of the photoelastic effect is higher when R_0m and TM_0m are coupled, and the contribution of the photoelastic effect is also greater, when R_0m and HE_1m are coupled. Between R_0m and TE_0m, moving boundary perturbations and photoelastic effects contribute similarly. In the case of the same effective refractive index change, the frequency shift of the radial mode of the sound field is compared with that of the torsional radial mode. It is concluded that the radial mode R_0m is more sensitive to the change in the effective refractive index than the torsional radial mode TR_2m. This means that building on previous studies by Y Antman et al. [41] and Yanping Xu et al [42] for the study of FSBS-based opto-mechanical simultaneous sensors, this study offers a new possibility to design simultaneous sensors by exploiting the difference in sensitivity to n_eff between radial and torsional radial modes. Finally, it is confirmed that the silicon-core fiber can obtain a strong FSBS gain of 365.57 (1/mw) without reducing to the usual size of the silicon waveguide. In this case, the FSBS are coupled at R₀₁ and TE₀₈. This work opens up new possibilities in the field of CMOS and MEMS by mixing Brillouin device physics with silicon photonics. It paves the way for further research in the fields of frequency-tunable laser emission, mode-locked pulsed lasers, low-noise oscillators, and optical gyroscopes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YY: writing—original draft preparation, data curation, software, and validation. TW: writing—reviewing and editing and investigation. YL: investigation and reviewing. BW: reviewing and editing. MZ: reviewing and editing.

Funding

This work was supported by the National Natural Science Foundation of China (62075151, 62075153, 61527819, and 61875146), the Patent Promotion and Exploitation Program of Shanxi Province (20200734), the Transformation of Scientific and Technological Achievements Programs of Higher Education Institutions in Shanxi, Fund for Shanxi “1331 Project” Key Innovative Research Team, and Shanxi-Zheda Institute of Advanced Materials and Chemical Engineering.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jalali B, Fathpour S. Silicon photonics. J lightwave Technol (2006) 24(12):4600–15. doi:10.1109/JLT.2006.885782

CrossRef Full Text | Google Scholar

2. Hou C, Jia X, Wei L, Tan SC, Zhao X, Joannopoulos JD, et al. Crystalline silicon core fibres from aluminium core preforms. Nat Commun (2015) 6(1):6248–6. doi:10.1038/ncomms7248

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Leuthold J, Koos C, Freude W. Nonlinear silicon photonics. Nat Photon (2010) 4(8):535–44. doi:10.1038/nphoton.2010.185

CrossRef Full Text | Google Scholar

4. Gupta N, McMillen C, Singh R, Podila R, Rao AM, Hawkins T, et al. Annealing of silicon optical fibers. J Appl Phys (2011) 110(9):093107. doi:10.1063/1.3660270

CrossRef Full Text | Google Scholar

5. Healy N, Sparks JR, Petrovich MN, Sazio PJA, Badding JV, Peacock AC. Large mode area silicon microstructured fiber with robust dual mode guidance. Opt Express (2009) 17(20):18076–82. doi:10.1364/OE.17.018076

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mehta P, Healy N, Baril NF, Sazio PJA, Badding JV, Peacock AC. Nonlinear transmission properties of hydrogenated amorphous silicon core optical fibers. Opt express (2010) 18(16):16826–31. doi:10.1364/OE.18.016826

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ikeda K, Shen Y, Fainman Y. Enhanced optical nonlinearity in amorphous silicon and its application to waveguide devices. Opt express (2007) 15(26):17761–71. doi:10.1364/OE.15.017761

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Van Laer R, Kuyken B, Van Thourhout D, Baets R. Observation of 4.4 dB Brillouin gain in a silicon photonic wire[C]. In: 2014 IEEE Photonics Conference; 12-16 October 2014; San Diego, CA, USA (2014). p. 558–9. doi:10.1109/IPCon.2014.6995498

CrossRef Full Text | Google Scholar

9. Kittlaus EA, Otterstrom NT, Rakich PT. On-chip inter-modal Brillouin scattering. Nat Commun (2017) 8(1):15819–9. doi:10.1038/ncomms15819

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Peacock AC, Mehta P, Horak P, Healy N. Nonlinear pulse dynamics in multimode silicon core optical fibers. Opt Lett (2012) 37(16):3351–3. doi:10.1364/OL.37.003351

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Schulze C, Brüning R, Schröter S, Duparre M. Mode coupling in few-mode fibers induced by mechanical stress. J Lightwave Tech (2015) 33(21):4488–96. doi:10.1109/JLT.2015.2475603

CrossRef Full Text | Google Scholar

12. Wang N, Alvarado-Zacarias JC, Habib MS, Wen H, Antonio-Lopez JE, Sillard P, et al. Mode-selective few-mode Brillouin fiber lasers based on intramodal and intermodal SBS. Opt Lett (2020) 45(8):2323–6. doi:10.1364/OL.385444

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hounsome LS, Jones R, Shaw MJ, Briddon PR. Photoelastic constants in diamond and silicon. physica status solidi (2006) 203(12):3088–93. doi:10.1002/pssa.200671121

CrossRef Full Text | Google Scholar

14. Biegelsen DK. Photoelastic tensor of silicon and the volume dependence of the average gap. Phys Rev Lett (1974) 32(21):1196–9. doi:10.1103/PhysRevLett.32.1196

CrossRef Full Text | Google Scholar

15. Mashanovich GZ, Milosevic M, Matavulj P, Stankovic S, Timotijevic B, Yang PY, et al. Silicon photonic waveguides for different wavelength regions. Semiconductor Sci Technol (2008) 23(6):064002. doi:10.1088/0268-1242/23/6/064002

CrossRef Full Text | Google Scholar

16. Levine ZH, Zhong H, Wei S, Allan DC, Wilkins JW. Strained silicon: A dielectric-response calculation. Phys Rev B (1992) 45(8):4131–40. doi:10.1103/PhysRevB.45.4131

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Huang L, Leng J, Zhou P, Guo S, Lu H, Cheng X. Adaptive mode control of a few-mode fiber by real-time mode decomposition. Opt express (2015) 23(21):28082–90. doi:10.1364/OE.23.028082

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hong S, Choi K, Lee YS, Oh K, et al. Two-mode fiber with a reduced mode overlap for uncoupled mode-division multiplexing in C+ L band. Curr Opt Photon (2018) 2(3):233–40. doi:10.3807/COPP.2018.2.3.233

CrossRef Full Text | Google Scholar

19. Snitzer E, Osterberg H. Observed dielectric waveguide modes in the visible spectrum. JOSA (1961) 51(5):499–505. doi:10.1364/JOSA.51.000499

CrossRef Full Text | Google Scholar

20. Kawano K, Kitoh T. Introduction to optical waveguide analysis: Solving maxwell's equation and the schrödinger equation. United States: John Wiley and Sons (2004).

Google Scholar

21. Mahlein HF, Oberbacher R, Rauscher W. An integrated optical TE-TM mode splitter. Appl Phys (1975) 7:15–20. doi:10.1007/BF00900514

CrossRef Full Text | Google Scholar

22. Wagner D, Thumm M, Kasparek W, Muller GA, Braz O. Prediction of TE-TM-and hybridmode transmission losses in gaps of oversized waveguides using a scattering matrix code. Int J infrared millimeter waves (1996) 17(6):1071–81. doi:10.1007/BF02101439

CrossRef Full Text | Google Scholar

23. Bao X, Chen L. Recent progress in Brillouin scattering based fiber sensors. Sensors (2011) 11(4):4152–87. doi:10.3390/s110404152

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kobyakov A, Sauer M, Chowdhury D. Stimulated Brillouin scattering in optical fibers. Adv Opt Photon (2010) 2(1):1–59. doi:10.1364/AOP.2.000001

CrossRef Full Text | Google Scholar

25. Carmon T, Rokhsari H, Yang L, Kippenberg TJ, Vahala KJ. Temporal behavior of radiation-pressure-induced vibrations of an optical microcavity phonon mode. Phys Rev Lett (2005) 94(22):223902. doi:10.1103/PhysRevLett.94.223902

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Lin Q, Rosenberg J, Jiang X, Vahala KJ, Painter O. Mechanical oscillation and cooling actuated by the optical gradient force. Phys Rev Lett (2009) 103(10):103601. doi:10.1103/PhysRevLett.103.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Dainese P, Russell PSJ, Wiederhecker GS, Joly N, Fragnito HL, Laude V, et al. Raman-like light scattering from acoustic phonons in photonic crystal fiber. Opt express (2006) 14(9):4141–50. doi:10.1364/OE.14.004141

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys (2014) 86(4):1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

29. Wiederhecker GS, Dainese P, Mayer Alegre TP. Brillouin optomechanics in nanophotonic structures. APL Photon (2019) 4(7):071101. doi:10.1063/1.5088169

CrossRef Full Text | Google Scholar

30. Shelby RM, Levenson MD, Bayer PW. Guided acoustic-wave Brillouin scattering. Phys Rev B (1985) 31(8):5244–52. doi:10.1103/PhysRevB.31.5244

CrossRef Full Text | Google Scholar

31. Biryukov AS, Sukharev ME, Dianov EM. Excitation of sound waves upon propagation of laser pulses in optical fibres. Quan Elect (2002) 32(9):765–75. doi:10.1070/QE2002v032n09ABEH002289

CrossRef Full Text | Google Scholar

32. Lurie AI. Theory of elasticity. Germany: Springer Science and Business Media (2010).

Google Scholar

33. Thurston RN. Elastic waves in rods and clad rods. The J Acoust Soc America (1978) 64(1):1–37. doi:10.1121/1.381962

CrossRef Full Text | Google Scholar

34. Wolff C, Van Laer R, Steel MJ, Eggleton BJ, Poulton CG. Brillouin resonance broadening due to structural variations in nanoscale waveguides. New J Phys (2016) 18(2):025006. doi:10.1088/1367-2630/18/2/025006

CrossRef Full Text | Google Scholar

35. Wang Y, Li K, Yu Y, Wang W, Li S, Li Y, et al. Tailorable stimulated Brillouin scattering laser based on silicon ring waveguides. Front Phys (2021) 9:539. doi:10.3389/fphy.2021.749880

CrossRef Full Text | Google Scholar

36. Sturmberg BCP, Dossou KB, Smith MJA, Morrison B, Poulton CG, Steel MJ, et al. NumBAT: The integrated, open source numerical Brillouin analysis tool (2018). arXiv preprint arXiv:1811.10219, doi:10.48550/arXiv.1811.10219

CrossRef Full Text | Google Scholar

37. Qiu W, Rakich PT, Shin H, Dong H, Soljacic M, Wang Z. Stimulated Brillouin scattering in nanoscale silicon step-index waveguides: A general framework of selection rules and calculating SBS gain. Opt express (2013) 21(25):31402–19. doi:10.1364/OE.21.031402

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Schmidt MK, O’Brien MC, Steel MJ, Poulton CG. Arraw: Anti-resonant reflecting acoustic waveguides. New J Phys (2020) 22(5):053011. doi:10.1088/1367-2630/ab7d79

CrossRef Full Text | Google Scholar

39. Hansen TP, Broeng J, Libori SEB, Knudsen E, Bjarklev A, Jensen J, et al. Highly birefringent index-guiding photonic crystal fibers. IEEE Photon Tech Lett (2001) 13(6):588–90. doi:10.1109/68.924030

CrossRef Full Text | Google Scholar

40. Van Laer R, Kuyken B, Van Thourhout D, Baets R. Analysis of enhanced stimulated Brillouin scattering in silicon slot waveguides. Opt Lett (2014) 39(5):1242–5. doi:10.1364/OL.39.001242

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Antman Y, Clain A, London Y, Zadok A. Optomechanical sensing of liquids outside standard fibers using forward stimulated Brillouin scattering. Optica (2016) 3(5):510–6. doi:10.1364/OPTICA.3.000510

CrossRef Full Text | Google Scholar

42. Xu Y, Zhao X, Li Y, Qin Z, Pang Y, Liu Z. Simultaneous measurement of relative humidity and temperature based on forward Brillouin scattering in polyimide-overlaid fiber. Sensors Actuators B: Chem (2021) 348:130702. doi:10.1016/j.snb.2021.130702

CrossRef Full Text | Google Scholar