QE evolution of bialkali photocathode at cryogenic temperature

Photocathode plays an important role in generating high brightness and low emittance electron beam and K-Cs-Sb photocathode is preferred in SRF injectors for its high quantum efficiency, long lifetime, and low thermal emittance. To predict the QE change of K-Cs-Sb at cryogenic temperature more correctly, we have modified the QE formula of Spicer’s photoemission model considering the temperature dependence of work function and mean free path of photocathode material, which is obtained by fitting experimental data. The calculated QE drop of about 90.1% at 36.4 K fits well with the measured QE change in DC-SRF photoinjector at Peking University. This improved formula could provide a method to evaluate the QE performance of semiconductor photocathodes at cryogenic temperature.

1 Introduction

Accelerator-based large scientific devices, such as X-ray free electron lasers (XFEL) [1, 2] and electron cooling [3], require electron beams with high brightness, low emittance, and high average current. While most electron injectors adopt photocathodes to generate high-quality beams, the beam emittance at the injector exit still needs to be improved for practical applications [4–7]. With the development of the high-gradient accelerating technique and the optimization of beam dynamics, the emittance growth caused by the RF field and space charge force would have a minor contribution to the final beam emittance. Hence the thermal emittance of the photocathode has become the main limiting factor of the final beam emittance [8].

Thermal emittance represents the ratio of the normalized emittance at the cathode surface to the RMS size of the driving laser, and it can be evaluated using the mean transverse energy (MTE) of emitted electrons. According to [9], the MTE can be roughly estimated as E_excess/3, where E_excess=(ℏω-ϕ) is the excess energy defined as the difference between the photon energy, ℏω, and the work function, ϕ, of the photocathode material. Therefore, any method that reduces the excess energy of photoelectrons would lead to a smaller thermal emittance of the photocathode. For decreasing thermal emittance, three methods are mainly used: near-threshold emission [10], back-illumination [11], and photocathode cooling [12, 13]. Among these methods, cooling the photocathode down to cryogenic temperature is more promising for superconducting radio frequency (SRF) injectors because it is compatible with the photoinjectors’ operating environment. Thus, only minor changes in the structure of photoinjectors are needed. For semiconductor photocathodes with an initial QE of $\sim {10}^{-2}$ [14, 15], electron beams with lower emittance and relatively high average current could be generated at cryogenic temperature. For example, a MTE of 22 meV was reported for the Cs₃Sb photocathode cooled down to 90 K with a QE larger than 7 × 10⁻⁵ [12].

Among semiconductor photocathodes, K-Cs-Sb is an ideal candidate for electron sources [7, 16, 17] to obtain low-emittance beams at cryogenic temperature due to its high QE, low thermal emittance, and months-long lifetime in SRF injectors [15]. However, it is necessary to investigate the performance of the K-Cs-Sb photocathode at cryogenic temperature to establish a proper theoretical model for predicting the temperature-dependent behavior of QE. It was reported that the K-Cs-Sb photocathode suffered from QE degradation when the temperature drops to cryogenic temperature [13, 18–20], and different models for the observed behaviors were proposed.

BNL first established a QE formula based on the Maxwell-Boltzmann energy distribution of conduction band electrons and concluded that the increase in work function was the main reason for the QE drop at low temperatures [13]. However, the linear fit overestimated the work function at cryogenic temperature [21], limiting the temperature range where this model can be used. A photoemission model based on the Fermi-Dirac distribution of electrons was developed by the University of Wisconsin [22], and it was used to fit the experimental spectral response data of K-Cs-Sb by JLab. The basic assumption of this model is that the work function is independent of temperature, which is unsuitable for the K-Cs-Sb semiconductor photocathode [20].

Thus, it is necessary to establish the correct work function to predict the QE change of K-Cs-Sb at cryogenic temperature more precisely. The temperature dependence of transport property should also be included [23]. Cornell laboratory considered the influence of temperature change on the scattering rate of phonons in their photoemission models of Cs₃Sb [24] and GaAs [25]. In the photoemission model of Cs₃Sb proposed by Tsinghua University, the contribution from the acceptor level was included. While the absence of photoelectrons from the acceptor level was considered to cause QE drop at cryogenic temperature [26], the application to K-Cs-Sb should be careful due to its weak doping property [27, 28].

Therefore, to obtain a more accurate photoemission model of K-Cs-Sb at cryogenic temperature, the temperature dependence of work function and electron transport property should be considered. In this paper, we tried to modify the QE formula of Spicer’s three-step model for K-Cs-Sb, and compared the calculated results with experimental data of our DC-SRF photoinjector in which the temperature of the K-Cs-Sb photocathode is about 36.4 K.

2 Performance of a bialkali photocathode at cryogenic temperature

The performance of the K-Cs-Sb photocathode at cryogenic temperature was tested with the DC-SRF photoinjector proposed and developed at Peking University [29]. With the improvements in using K-Cs-Sb photocathode instead of Cs₂Te and drive laser of truncated Gaussian distribution in the transverse direction and a flat-topped distribution in the longitudinal direction, replacing the original 3.5-cell SRF cavity with a new 1.5-cell cavity, careful design of DC high voltage electrode structure and beam dynamics, the emittance of electron beams from DC-SRF photoinjector has been decreased obviously.

To improve the performance of the K-Cs-Sb photocathode, we developed an improved sequential deposition procedure [17], where a faster Cs evaporation rate was adopted, and the cesiation process took less than 10 min. The K-Cs-Sb samples fabricated according to this recipe exhibited a typical QE of 5%–8%, and could be stored without deterioration for more than 2 weeks.

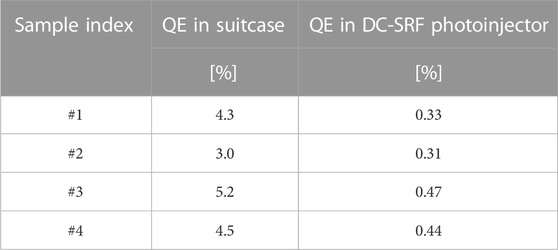
During the commissioning of the DC-SRF photoinjector, we observed a QE drop at the temperature of about 36.4 K. The temperature of the K-Cs-Sb photocathode was estimated using Comsol software [30] according to the heat distribution. The accuracy of temperature simulation has been verified by the measured values of upstream and downstream beam tubes using thermocouples, and the simulation results agreed well with the measured values. We compared different K-Cs-Sb samples, and the results are listed in Table 1. The typical QE drop is about 90%, and the QE could recover to its initial value when we transferred the K-Cs-Sb photocathodes to a room temperature environment after 2 weeks of operation [17].

TABLE 1

TABLE 1. Comparison of QE in the DC-SRF photoinjector and a suitcase for four K-Cs-Sb samples.

3 Analytical QE formula

For describing the QE-related behavior of K-Cs-Sb photocathode at cryogenic temperature, we modified the QE formula as a function of temperature based on Spicer’s three-step model, which is widely used to describe the photoemission process of semiconductors [31]. Band bending [32], initial photoelectrons generated from the doping energy level [26], and the built-in electric field [24] were discussed in the simulation process of GaAs and Cs₃Sb photocathodes. For K-Cs-Sb photocathode, less change was added, and the band gap was mostly focused on [13, 20]. This seems reasonable at room temperature because K-Cs-Sb is a weak p-type or even intrinsic semiconductor [27, 28], and suffers little influence from acceptor impurity. However, when we try to estimate the photoemission performance at cryogenic temperature, the changes of phonon scattering [23–25] and conductivity [33] should also be considered, because they affect the scattering rate [34], main scattering channel [35] and energy loss rate [36], changing the transport process compared to that at room temperature.

3.1 Basic QE formula

Generally, the initial electron energy distribution is related to the band gap, and the emission probability is influenced by the electron affinity [37]. For the convenience of analysis, we consider the contributions of band gap and electron affinity together as a threshold [38], and only photoelectrons with energy higher than work function could emit from the surface. Therefore the QE can be expressed as [38]:

$\mathrm{Q}\mathrm{E}\left(\hslash \omega \right)=\underset{0}{\overset{D}{\int }}\left(1-R\left(\hslash \omega \right)\right){\alpha }_p\left(\hslash \omega \right)G\left(\mathrm{z},\hslash \omega \right)e^{-{\alpha }_T\left(\hslash \omega \right)}dz,(1)$

where R (ℏω) and α_T (ℏω) are the reflectivity and absorption coefficient of K-Cs-Sb at the photon energy of ℏω, respectively, α_p (ℏω) is the part that contributes to photoemission, and G (z, ℏω) is the probability of an electron excited at depth z by a photon of energy ℏω escaping from the material.

By applying relations α_p (ℏω) = C (ℏω − ϕ)^3/2 [38] and G (z, ℏω) = Ae^Pℏωe^−z/λ [39], we obtain the final QE formula:

$QE\left(\hslash \omega \right)=\left(1-R\left(\hslash \omega \right)\right)C\frac{{\left(\hslash \omega -\varphi \right)}^{3/2}}{1/\lambda +{\alpha }_T\left(\hslash \omega \right)}{e}^{P\hslash \omega }\left[1-e^{-\left(1/\lambda +{\alpha }_T\left(\hslash \omega \right)\right)D}\right],(2)$

where C is a constant, λ is the mean free path of electrons, D is the thickness of the photocathode, and P is the photocathode parameter characterizing disorder degree and emission properties.

Eq. (2) represents the QE of the photocathode at a specific photon energy, with included photoemission parameters, like work function, mean free path and cathode’s thickness, enabling the calculation of the spectral responses of different photocathode materials using related experimental data. By changing the structure parameter P and the work function value, it can also be used to fit the spectral responses of degraded photocathodes.

While the calculated spectral responses fit well with experimental results for many alkali photocathodes [38], Eq. (2) is only suitable at room temperature since some photoemission parameters are temperature-dependent. To evaluate the cryogenic performance of a photocathode more precisely, the work function and mean free path should be considered as a function of temperature.

3.2 Temperature dependence of work function

Typically, the work function of semiconductors consists of the band gap, electron affinity, bulk potential and surface potential [40], which have different temperature coefficients. As K-Cs-Sb is almost an intrinsic semiconductor where band bending at the surface can be omitted [28], and the electron affinity, which is related to the surface state, can be considered constant, we assume that the temperature dependence of the work function originates only from the band gap [41]. As shown in many experimental results, the band gap of semiconductors increases as the temperature decreases [21, 41, 42]. Here, we choose a simplified phonon dispersion model [43], which includes the influence of electron-phonon interaction and lattice thermal expansion and thus is almost suitable for all semiconductor materials [42], to explain the pinch effect in band gap. The band gap and work function with respect to temperature can be expressed as follows [43]:

$E_g\left(T\right)=E_{\mathit{gcn}}-\mathrm{\Delta }{E}_{ZP}\left(1+\frac{2}{e^{\frac{\hslash {\omega }_{op}}{k_{B}T}}-1}\right)(3)$

$\varphi \left(T\right)={\varphi }_{\mathit{gcn}}-\mathrm{\Delta }{E}_{ZP}\left(1+\frac{2}{e^{\frac{\hslash {\omega }_{op}}{k_{B}T}}-1}\right),(4)$

where E_g and T are the band gap and temperature of the K-Cs-Sb photocathode, respectively, E_gcn and ϕ_gcn are constants, ΔE_ZP is the electron-phonon coupling strength parameter, ℏω_op is the energy of optical phonon, and k_B is the Boltzmann constant.

It is generally assumed that the K-Cs-Sb photocathode has a band gap of 1.2 eV and an electron affinity of 0.7 eV [33]. However, the work function values reported by different laboratories usually vary by about 0.1 eV around 1.9 eV [20, 44] due to different fabrication processes. Since the work function of the photocathode is a key parameter in the QE formula, it is necessary to use a suitable value to fit the QE behavior of the K-Cs-Sb photocathode fabricated using our fast-cesiation method [17].

Figure 1 shows the spectral response curves of the K-Cs-Sb photocathode measured using our cryogenic platform. The cathode was first slowly cooled down from 302 to 95.5 K, and then warmed up to 178 K and 302 K in turn using a pressured N₂ flow cooled by liquid nitrogen. The laser wavelength varied from 300 to 600 nm with a step of 20 nm. The measured QE at 520 nm decreased by more than 30% at the temperature of 95.5 K, but it gradually recovered during the cathode’s warming up, giving almost the same spectral response as before the cooling-warming circle at room temperature.

FIGURE 1

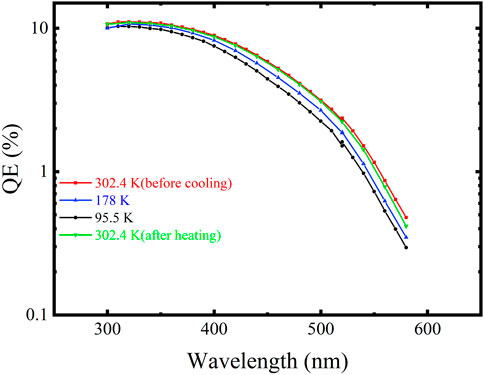
FIGURE 1. Spectral responses of the K-Cs-Sb photocathode at 302.4, 178, and 95.5 K during a cooling-warming cycle.

Near the photoemission threshold, QE approximately satisfies the following relationship with photon energy [37]:

$\sqrt{QE}\propto \left(\hslash \omega -\varphi \right).(5)$

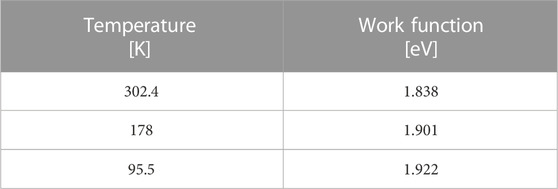
Then the values of the work function at different temperatures are derived by linear fitting of the data in Figure 1, and the results are shown in Table 2. The average work function of K-Cs-Sb samples is 1.838 eV at room temperature, which is slightly lower than the value of 1.9 eV. This is probably caused by our fabrication procedure, where the fast cesiation process generates excess Cs on the photocathode surface and, thus, decreases electron affinity [45]. Besides, the work function increases by 0.084 eV when the cathode is cooled to 95.5 K, which is consistent with the BNL result [13]. Using the data in Table 2, the parameters in Eq. (4) are determined to be ϕ_gcn = 2.015 [eV] and ΔE_ZP = 0.084 [eV].

TABLE 2

TABLE 2. The work function of the K-Cs-Sb photocathode at different temperatures.

3.3 Temperature dependence of mean free path

The change in electron transport property also needs to be considered when evaluating the QE of a photocathode at cryogenic temperature. Typically, the scattering rate and energy loss from lattice scattering decrease at low temperatures due to weakened lattice vibration [46]. Thus, the QE of alkali-antimonide photocathodes at high photon energies should increase as the temperature decreases [19]. However, the imperfection of the crystal structure and the micro-grained and porous nature of the photocathode [47] additionally complicate the situation, where the actual energy loss rate seems to be less temperature dependent [35], and the photoemission might be limited by the high resistivity of the photocathode [47]. As we focus more on the average scattering effect in the analytical model, this problem can be simplified by considering the temperature dependence of mean free path, which is proportional to free drift time. The movement of photoelectrons belongs to the transport process of non-equilibrium carriers, where the free drift time τ between two scattering events can be evaluated as follows [46]:

$\tau =\frac{\sigma }{n_{c}e},(6)$

where σ is the electric conductivity of the material, n_c is the density of carriers, and e is the electric charge.

For semiconductors, the electric conductivity decreases as the temperature decreases [33], indicating a shorter free drift time. Other researchers measured the temperature dependence of the conductivity of K-Cs-Sb and expressed it as follows [47]:

$\sigma \left(T\right)={\sigma }_0{e}^{-{\left(\frac{T_0}{T}\right)}^{1/4}},(7)$

where T₀ and σ₀ are calculated as 4.2 × 10⁶ K and 7 × 10³ (Ωm)⁻¹, respectively.

Therefore, the mean free path as a function of temperature can be evaluated as follows:

$\lambda \left(T\right)={\lambda }_0{e}^{-{\left(\frac{T_0}{T}\right)}^{1/4}},(8)$

where the constant λ₀ can be calculated as 2.601 × 10⁵ nm when the mean free path of K-Cs-Sb at room temperature is estimated to be 5 nm [31].

Combining Eqs 2, 4, and 8, we obtained the general QE formula as follows:

$QE\left(\hslash \omega ,T\right)=\left(1-R\left(\hslash \omega \right)\right)C\frac{{\left(\hslash \omega -{\varphi }_{\mathrm{g}\mathrm{c}\mathrm{n}}+{\mathrm{E}}_{ZP}\left(1+\frac{2}{e^{\frac{\hslash {\omega }_{op}}{k_{B}T}}-1}\right)\right)}^{3/2}}{e^{{\left(\frac{T_0}{T}\right)}^{1/4}}/{\lambda }_0+{\alpha }_T\left(\hslash \omega \right)}\times e^{P\hslash \omega }\left[1-e^{-\left(e^{{\left(\frac{T_0}{T}\right)}^{1/4}}/{\lambda }_0+{\alpha }_T\left(\hslash \omega \right)\right)D}\right].(9)$

The temperature dependence of QE originates from the changes in work function and mean free path.

4 Discussion

To verify the validity of the obtained analytical formula, we compared the calculated spectral responses and relative QE drop of the K-Cs-Sb photocathode with experimental results.

4.1 Validation of the QE formula

Figure 2 shows the spectral responses of K-Cs-Sb at different temperatures calculated using the parameters in Table 3. The experimental and analytical results generally agree, but some discrepancies exist at longer and shorter wavelengths. This might be due to the neglect of electron-electron scattering and trajectory change after scattering.

FIGURE 2

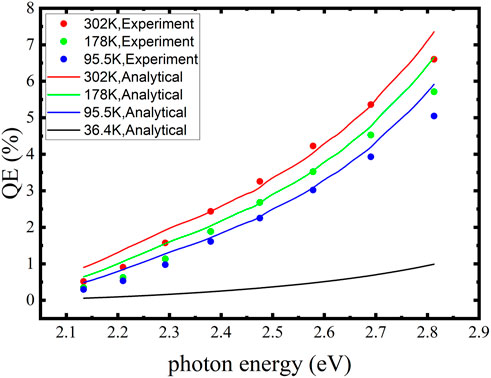
FIGURE 2. Comparison of the analytical and experimental results of spectral responses for the K-Cs-Sb photocathode at different temperatures. The black line represents the calculated spectral response at 36.4 K.

TABLE 3

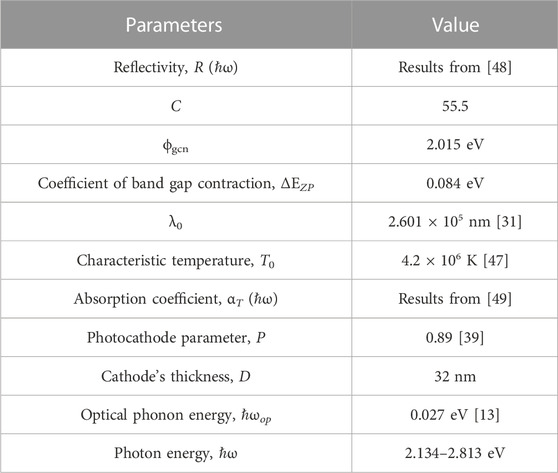
TABLE 3. Parameters used to calculate QE from Eq. 9.

When operating in SRF injectors, the Schottky effect of a strong surface field should also be considered to evaluate the QE of photocathodes, as the applied electric field would cause a decrease in electron affinity, which can be evaluated as follows [50]:

$\mathrm{\Delta }\varphi =\sqrt{\frac{e}{4\pi {\epsilon }_0}\frac{\epsilon -{\epsilon }_0}{\epsilon +{\epsilon }_0}{E}_{\mathit{cat}}},(10)$

where ɛ₀ and ɛ are the permittivity of vacuum and photocathode, respectively, and E_cat is the applied electric field strength. For DC-SRF photoinjector, a drive laser of 519 nm and a cathode surface field strength of 3.1 MV/m are adopted, causing a decrease of 0.059 eV in work function, where the permittivity of K-Cs-Sb is estimated as 7.87ɛ₀ [50]. Figure 3 shows the calculated relative QE drop compared to the value at room temperature with the photon energy of 2.38 eV. At a temperature higher than 100 K, the increase in work function is the main mechanism of the QE drop. The huge decrease in electric conductivity at lower temperatures, which causes a shorter mean free path, contributes to the rapid drop. The analytical curve predicts a QE drop of 90.1% at 36.4 K, which fits well with our experimental result of about 90% in DC-SRF photoinjector. The QE drops reported by other laboratories were also compared, showing some discrepancies that might originate from the differences in work function caused by fabrication procedures and the influence of the Schottky effect.

FIGURE 3

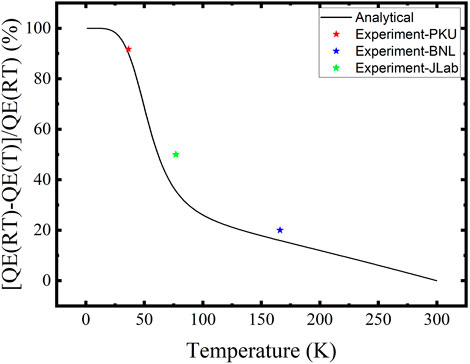
FIGURE 3. Calculated relative QE drop at 519 nm of K-Cs-Sb in DC-SRF photoinjector compared to room temperature; star dots represent the experimental results. The blue [13] and green [20] dots were reported by other laboratories with an extraction voltage of less than 300 V; therefore, the discrepancies might originate from the differences in work function and the lack of the Schottky effect.

4.2 QE variation during macro-pulse operation at different duty cycles

In our model, we assign the QE drop at cryogenic temperature to the changes in work function and mean free path. However, gas trapping at the emission surface in the cryogenic temperature environment may also cause a QE decrease. To verify whether gas trapping is the main reason, we measured the average beam current during macro-pulse operation at different duty cycles with DC-SRF photoinjector, where the extraction electric field strength was 3.1 MV/m, and the laser spot size and FWHM pulse width were set to 5 mm and 24 ps, respectively.

Figure 4 shows the extracted beam current from a degraded K-Cs-Sb sample during macro-pulse operation at different laser duty cycles, where the laser power remains constant during each operation. During the first CW operation, the beam current increased from 60 to 81 μA with a fixed laser power of 375 mW. At a duty cycle of 20%, the beam current increased slightly from 11.5 to 12.2 μA with the laser power of 75 mW. When the duty cycle increased to 50%, the beam current increased faster and gradually stabilized at 34.3 μA. Finally, during the second CW operation, the beam current showed the same behavior as the first CW operation. The intervals between operations at different duty cycles were long enough to reach the thermal equilibrium of the photocathode.

FIGURE 4

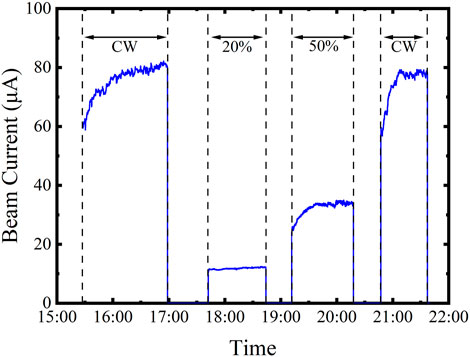
FIGURE 4. Macro-pulse operation results of a QE-degraded K-Cs-Sb sample with a fixed laser power during each operation. The applied laser power was 375 mW during the CW operation. For macro-pulse operation at the duty cycle of 20% and 50%, the laser power was 75 and 187.5 mW, respectively. The average beam current increased by more than 20 μA during the CW operation, but there was a minor increase at 20% duty cycle.

In the UHV environment of injectors, the average time to form a single molecular layer was in the range of several seconds, much longer than the macro pulse duration [51]; therefore, the effective number of absorbed gas molecules decreased continuously during operation, which resulted in the QE recovery before stabilization. If the QE degradation is mainly caused by gas trapping, after enough time, the QE should be able to recover to the same value for low and high duty cycles, as the single laser pulse energy is the same at different duty cycles. From the experimental data, we found that the QE recovered to different values at low and high duty cycles. Thus, we can conclude that gas trapping is not the main reason for the QE drop at cryogenic temperature. The different duty cycles of the drive laser only changed the temperature of the cooled photocathode by thermal effect, which was the real reason for the QE increase during macro-pulse operation.

The heating effect of the drive laser arises from the relaxation of photoelectrons during transport and the non-radiative recombination of non-emitted electrons [52]. For simplification, we used a conversion coefficient η_thermal to express the proportion of thermal energy in the absorbed laser energy, and the heat power can be expressed as follows:

$P_{\mathit{heat}}=\left(1-R\left(\hslash \omega \right)\right){\eta }_{\mathit{thermal}}{P}_{\mathit{laser}},(11)$

where P_laser is the laser power at a specific duty cycle.

We used Comsol software to simulate the temperature rise of the photocathode in DC-SRF photoinjector when illuminated by a 5-mm-diameter laser spot of different powers. The conversion coefficient η_thermal is fitted to 0.7, so the maximum heat power of 0.205 W was applied to the cathode surface during the CW operation. Figure 5A shows the simulation results of the temperature change during macro-pulse operation. Within 60 min, the photocathode temperature increased from 36.4 to 38.7 K at the duty cycle of 20%, while the increase during the CW operation was 10.3 K.

FIGURE 5

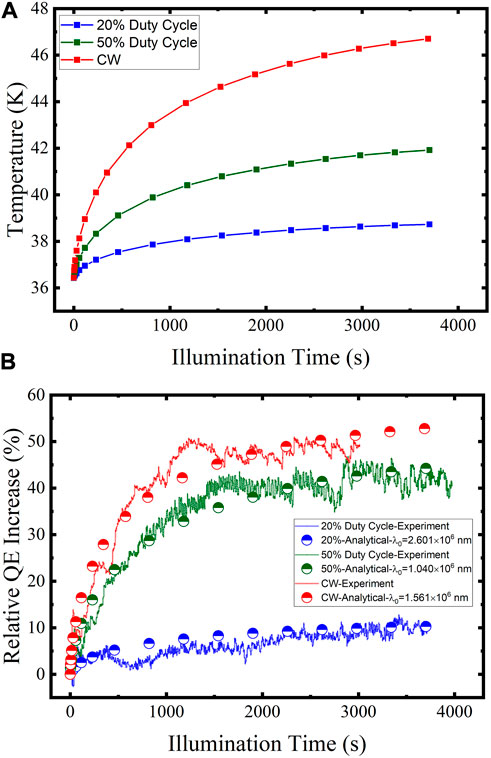
FIGURE 5. Simulation of QE changes in DC-SRF photoinjector during macro-pulse operation at different duty cycles. (A) Simulated temperature rise during laser illumination. (B) Comparison between the experimental data and the calculated relative QE increase using Eq. 9 with different λ₀ values.

The calculated results of QE changes during macro-pulse operation are shown in Figure 5B, which agree well with the experimental results and show the same trend as the temperature rise in Figure 5A. Due to the low initial value and rapid change rate at cryogenic temperature, the QE increases by nearly 50% during the CW operation, but less than 10% at 20% duty cycle, and the difference is obviously caused by the slow temperature increase at a lower duty cycle. This confirms that the laser-induced temperature rise of the cold photocathode is the main reason for the QE increase during macro-pulse operation.

5 Summary

Based on Spicer’s three-step model, we modified the analytical formula of QE for semiconductor photocathodes at cryogenic temperature. The temperature dependence of work function and mean free path of the photocathode material is included in the expression. The calculated QE drop of about 90.1% at 36.4 K fits well with the measured QE change in DC-SRF photoinjector at Peking University. This modified formula provides a method to evaluate the QE performance of semiconductor photocathodes at cryogenic temperature more precisely, and may help design photocathode SRF injectors to generate ultra-low emittance electron beams. The reliability of this analytical formula needs to be confirmed with more experimental results.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YZ: Methodology, Software, Investigation, Data curation, Writing—original draft. DO: Investigation, Data curation. HX: Conceptualization, Validation, Methodology, Funding acquisition, Writing—review and editing. KL: Conceptualization, Supervision, Project administration, Funding acquisition, Writing—review. SH: Funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key Research and Development Program of China under Grant No. 2017YFA0701001 and by the National Natural Science Foundation of China under Grant No. 12075012.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Musumeci P, Navarro JG, Rosenzweig JB, Cultrera L, Bazarov I, Maxson J, et al. Advances in bright electron sources. Nucl Instr Methods Phys Res (2018) 907:209–20. doi:10.1016/j.nima.2018.03.019

CrossRef Full Text | Google Scholar

2. Simone DM. On the importance of electron beam brightness in high gain free electron lasers. Photonics (2015) 2:317–41. doi:10.3390/photonics2020317

CrossRef Full Text | Google Scholar

3. Willeke F, Beebe-Wang J. Electron ion collider conceptual design report 2021 Report No.BNL-221006-2021-FORE TRN: US2215154 (2021). doi:10.2172/1765663

CrossRef Full Text | Google Scholar

4. Gulliford C, Bartnik A, Bazarov I, Cultrera L, Dobbins J, Dunham B, et al. Demonstration of low emittance in the cornell energy recovery linac injector prototype. Phys Rev Spec Topics-Accelerators Beams (2013) 16:073401. doi:10.1103/physrevstab.16.073401

CrossRef Full Text | Google Scholar

5. Sannibale F, Filippetto D, Qian H, Mitchell C, Zhou F, Vecchione T, et al. High-brightness beam tests of the very high frequency gun at the advanced photo-injector experiment test facility at the lawrence berkeley national laboratory. Rev Scientific Instr (2019) 90:033304. doi:10.1063/1.5088521

CrossRef Full Text | Google Scholar

6. Petrushina I, Litvinenko V, Jing Y, Ma J, Pinayev I, Shih K, et al. High-brightness continuous-wave electron beams from superconducting radio-frequency photoemission gun. Phys Rev Lett (2020) 124:244801. doi:10.1103/physrevlett.124.244801

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Dunham B, Barley J, Bartnik A, Bazarov I, Cultrera L, Dobbins J, et al. Record high-average current from a high-brightness photoinjector. Appl Phys Lett (2013) 102:034105. doi:10.1063/1.4789395

CrossRef Full Text | Google Scholar

8. Pierce CM, Andorf MB, Lu E, Gulliford C, Bazarov IV, Maxson JM, et al. Low intrinsic emittance in modern photoinjector brightness. Phys Rev Acc Beams (2020) 23:070101. doi:10.1103/physrevaccelbeams.23.070101

CrossRef Full Text | Google Scholar

9. Bazarov I, Cultrera L, Bartnik A, Dunham B, Karkare S, Li Y, et al. Thermal emittance measurements of a cesium potassium antimonide photocathode. Appl Phys Lett (2011) 98:224101. doi:10.1063/1.3596450

CrossRef Full Text | Google Scholar

10. Maxson J, Cultrera L, Gulliford C, Bazarov I. Measurement of the tradeoff between intrinsic emittance and quantum efficiency from a naksb photocathode near threshold. Appl Phys Lett (2015) 106:234102. doi:10.1063/1.4922146

CrossRef Full Text | Google Scholar

11. Lee H, Cultrera L, Bazarov I. Intrinsic emittance reduction in transmission mode photocathodes. Appl Phys Lett (2016) 108:124105. doi:10.1063/1.4944790

CrossRef Full Text | Google Scholar

12. Cultrera L, Karkare S, Lee H, Liu X, Bazarov I, Dunham B. Cold electron beams from cryocooled, alkali antimonide photocathodes. Phys Rev Spec Topics-Accelerators Beams (2015) 18:113401. doi:10.1103/physrevstab.18.113401

CrossRef Full Text | Google Scholar

13. Xie H, Ben-Zvi I, Rao T, Xin T, Wang E. Experimental measurements and theoretical model of the cryogenic performance of bialkali photocathode and characterization with Monte Carlo simulation. Phys Rev Acc Beams (2016) 19:103401. doi:10.1103/physrevaccelbeams.19.103401

CrossRef Full Text | Google Scholar

14. Xiang R, Teichert J. Photocathodes for high brightness photo injectors. Phys Proced (2015) 77:58–65. doi:10.1016/j.phpro.2015.11.010

CrossRef Full Text | Google Scholar

15. Wang E, Litvinenko V, Pinayev I, Gaowei M, Skaritka J, Belomestnykh S, et al. Long lifetime of bialkali photocathodes operating in high gradient superconducting radio frequency gun. Scientific Rep (2021) 11:4477. doi:10.1038/s41598-021-83997-1

CrossRef Full Text | Google Scholar

16. Pinayev I, Altinbas Z, Belomestnykh S, Ben-Zvi I, Brown K, Brutus JC, et al. Record performance of srf gun with csk2sb photocathode. Upton, NY (United States): Tech. rep., Brookhaven National Lab.BNL (2016).

Google Scholar

17. Ouyang D, Zhao Y, Xie H, Zhang X, Zhao S, Feng L, et al. Performance of bialkali photocathode in dc-srf photoinjector. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2022) 1026:166204. doi:10.1016/j.nima.2021.166204

CrossRef Full Text | Google Scholar

18. Konomi T, Honda Y, Kako E, Kobayashi Y, Michizono S, Miyajma T, et al. Development of srf gun applying new cathode idea using a transparent superconducting layer. In: Proceedings of the 59th ICFA Advanced Beam Dynamics Workshop on Energy Recovery Linacs; June 18-23, 2017; Geneva, Switzerland (2017). p. 18–23.

Google Scholar

19. Nathan R, Mee C. Photoelectric and related properties of the potassium—Antimony—Caesium photocathode. Int J Elect (1967) 23:349–54. doi:10.1080/00207216708961542

CrossRef Full Text | Google Scholar

20. Mamun M, Hernandez-Flores M, Morales E, Hernandez-Garcia C, Poelker M. Temperature dependence of alkali-antimonide photocathodes: Evaluation at cryogenic temperatures. Phys Rev Acc Beams (2017) 20:103403. doi:10.1103/physrevaccelbeams.20.103403

CrossRef Full Text | Google Scholar

21. Panish M, Casey H. Temperature dependence of the energy gap in gaas and gap. J Appl Phys (1969) 40:163–7. doi:10.1063/1.1657024

CrossRef Full Text | Google Scholar

22. Fowler RH. The analysis of photoelectric sensitivity curves for clean metals at various temperatures. Phys Rev (1931) 38:45–56. doi:10.1103/physrev.38.45

CrossRef Full Text | Google Scholar

23. Ghorai A, Bhattacharya D. Effect of non-parabolic band on the scattering rates of free electrons in high purity semiconductors at low lattice temperatures. physica status solidi (b) (1991) 163:247–58. doi:10.1002/pssb.2221630125

CrossRef Full Text | Google Scholar

24. Gupta P, Cultrera L, Bazarov I. Monte Carlo simulations of electron photoemission from cesium antimonide. J Appl Phys (2017) 121:215702. doi:10.1063/1.4984263

CrossRef Full Text | Google Scholar

25. Karkare S, Bazarov I. Effect of nanoscale surface roughness on transverse energy spread from gaas photocathodes. Appl Phys Lett (2011) 98:094104. doi:10.1063/1.3559895

CrossRef Full Text | Google Scholar

26. Huang PW, Qian H, Du Y, Huang W, Zhang Z, Tang C. Photoemission and degradation of semiconductor photocathode. Phys Rev Acc Beams (2019) 22:123403. doi:10.1103/physrevaccelbeams.22.123403

CrossRef Full Text | Google Scholar

27. Ghosh C. Photoemissive materials. Phys Thin Films (1982) 12:53–166.

CrossRef Full Text | Google Scholar

28. Fisher D, McDonie A, Sommer A. Band-bending effects in na2ksb and k2cssb photocathodes. J Appl Phys (1974) 45:487–8. doi:10.1063/1.1663009

CrossRef Full Text | Google Scholar

29. Quan S, Hao J, Lin L, Zhu F, Wang F, Feng L, et al. Stable operation of the dc-srf photoinjector. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2015) 798:117–20. doi:10.1016/j.nima.2015.07.025

CrossRef Full Text | Google Scholar

30. Multiphysics C. Introduction to comsol multiphysics®. Burlington, MA: COMSOL Multiphysics (1998).

Google Scholar

31. Spicer WE, Herrera-Gomez A. Modern theory and applications of photocathodes. Photodetectors and Power Meters (SPIE) (1993) 2022:18–35.

CrossRef Full Text | Google Scholar

32. Karkare S, Dimitrov D, Schaff W, Cultrera L, Bartnik A, Liu X, et al. Monte Carlo charge transport and photoemission from negative electron affinity gaas photocathodes. J Appl Phys (2013) 113:104904. doi:10.1063/1.4794822

CrossRef Full Text | Google Scholar

33. Ghosh C, Varma B. Preparation and study of properties of a few alkali antimonide photocathodes. J Appl Phys (1978) 49:4549–53. doi:10.1063/1.325465

CrossRef Full Text | Google Scholar

34. Ridley BK. Quantum processes in semiconductors. Oxford, United Kingdom: Oxford University Press (2013).

Google Scholar

35. Sen R, Vast N, Sjakste J. Hot electron relaxation and energy loss rate in silicon: Temperature dependence and main scattering channels. Appl Phys Lett (2022) 120:082101. doi:10.1063/5.0082727

CrossRef Full Text | Google Scholar

36. Shah J, Pinczuk A, Gossard A, Wiegmann W. Energy-loss rates for hot electrons and holes in gaas quantum wells. Phys Rev Lett (1985) 54:2045–8. doi:10.1103/physrevlett.54.2045

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Rao T, Dowell DH. An engineering guide to photoinjectors. arXiv preprint arXiv:1403.7539 (2014).

Google Scholar

38. Spicer WE. Photoemission and related properties of the alkali-antimonides. J Appl Phys (1960) 31:2077–84. doi:10.1063/1.1735505

CrossRef Full Text | Google Scholar

39. Zhao M, Sun J, Qian Y, Si S, Jin M, Jian L, et al. Theoretical investigation of spectral response characteristics of k2sbcs photoelectric cathode. Infrared Tech (2018) 40:289–93.

Google Scholar

40. Mönch W, Koenders L. On the temperature coefficient of the ionization energy in iii-v compound semiconductors. In: Proceedings of the 17th International Conference on the Physics of Semiconductors; August 6–10, 1984; San Francisco, California, USA (1985). p. 85–8.

Google Scholar

41. Chen B, Zhuang C, Wang X. Work function change of hydrogen chemisorped si(100) surface. Chin J Semiconductors (1983) 4:403.

Google Scholar

42. Zhang A, Chen P, Zhou J, Li Y, Yang Y, Mao X, et al. Study on temperature dependence of semiconductor bandgap. Optoelectronic Tech (2019) 39:160.

Google Scholar

43. Giustino F. Electron-phonon interactions from first principles. Rev Mod Phys (2017) 89:015003. doi:10.1103/RevModPhys.89.015003

CrossRef Full Text | Google Scholar

44. Mohanty S, Rocco GG, Hillert W, Krasilnikov M, Michelato P, Monaco L, et al. Development of multialkaliantimonides photocathodesfor high brightness photoinjectors. In: Proc. IPAC’21; 24 - 28 May 2021; Geneva, Switzerland (2021). p. 1416–9.

Google Scholar

45. Yang Z, Zou JJ, Niu J, Zhang YJ, Chang BK. Research on high temperature cs activated gaas photocathode. Guang Pu Xue Yu Guang Pu Fen Xi (2010) 30:2038.

PubMed Abstract | Google Scholar

46. Zohuri B. Physics of cryogenics an ultralow temperature phenomenon. Amsterdam, Netherlands: Elsevier (2013).

Google Scholar

47. Hirohata T, Mizushima Y. Conductivity mechanism of cs-sb-type photoemissive cathode film. Jpn J Appl Phys (1990) 29:1795. doi:10.1143/JJAP.29.1795

CrossRef Full Text | Google Scholar

48.JARVIS. Jvasp-22672 (2018). Available from: https://www.ctcms.nist.gov/∼knc6/jsmol/JVASP-22672.html.

Google Scholar

49. Kalarasse L, Bennecer B, Kalarasse F. Optical properties of the alkali antimonide semiconductors, and. J Phys Chem Sol (2010) 71:314–22. doi:10.1016/j.jpcs.2009.12.083

CrossRef Full Text | Google Scholar

50. Xie HM, Wang ED, Liu KX. Analytical model and simulation of the Schottky effect on a cryo-cooled bialkali photocathode. Nucl Sci Tech (2018) 29:71. doi:10.1007/s41365-018-0400-6

CrossRef Full Text | Google Scholar

51. Gao B, Cui S. Vacuum Physics. Beijing, China: Science Press (1983).

Google Scholar

52. Meyer JR, Bartoli FJ, Kruer MR. Optical heating in semiconductors. Phys Rev B (1980) 21:1559–68. doi:10.1103/PhysRevB.21.1559

CrossRef Full Text | Google Scholar