Abstract
The amalgamation of microorganisms in the nanofluid is significant in beautifying the thermal conductivity of several systems, such as microfluid devices, chip-shaped microdevices, and enzyme biosensors. The current investigation studies mixed convective flow of the entropy minimization of unsteady MHD tangent hyperbolic nanoliquid because a stretching surface has motile density via convective and slip conditions. For the novelty of this work, the variable transport characteristics caused by dynamic viscosity, thermal conductivity, nanoparticle mass permeability, and microbial organism diffusivity are considered. It is considered that the vertical sheet studying the flow. By using the appropriate alteration, the governing equations for the most recent flow analysis were altered into a non-dimension relation. Through MATLAB Software bvp4c, the PDE model equations have been made for these transformed equations. Engineering-relevant quantities against various physical variables include force friction, Nusselt number, Sherwood number, and microorganism profiles. The results showed good consistency compared to the current literature. Moreover, these outcomes revealed that augmentation in the magnitude of the magnetic field and velocity slip parameter declines the velocity profile. The reverse impact is studied in . In addition, heat transfer is typically improved by the influence of thermal radiation parameters, Brownian movement, and thermophoretic force. The physical interpretation has existed through graphical and tabular explanations.
1 Introduction
A passion sparked by the study of non-Newtonian fluids in recent decades. Several researchers have various features in the technological, chemical, and mechanical industries. The most convenient applications to encounter non-Newtonian fluids like polymeric relation, atomic rector, solvent, biomedical in tumor, and many more. Because of the complexity of their design and subsequent management according to the model of power kind, non-Newtonian fluids can produce a connection between shear stress and shear rate that is non-linear. Because of the complexity of these fluids, it is not possible to understand the rheological properties of fluids of this type using a straightforward relation, in contrast to the Newtonian fluid. In order to determine the nature of these occurrences, the researchers offered a number of mathematical studies to investigate the material associated with non-Newtonian fluids. The tangent hyperbolic fluid model illustrates a model in which an increase in the shear effect reduces the effective viscosity of the fluid. References [1, 2] first described the flow of tangent hyperbolic fluid in a boundary layer caused by a stretched sheet. Hayat et al. [3] described the boundary-layer flow of tangent hyperbolic fluid under mass flux conditions. The double solution of tangent hyperbolic was probed by Nagendramma et al. [4]. The effect of convective conditions on tangent hyperbolic fluid induced by the homogenous–heterogeneous reaction was completed by Kumar et al. [5]. The bioconvection flow of tangent hyperbolic due to a movable surface using numerical methods was completed by Kamel et al. [6]. The effect of numerical analysis of the bioconvection flow on the tangent hyperbolic fluid past Riga plate was scrutinized by Waqas et al. [7]. The impact of the zero mass flux condition for the tangent hyperbolic nanoparticles past an exponential surface due to statistical analysis was found by Shafiq et al. [8]. The unsteady flow on the tangent hyperbolic fluid past a wedge surface was conducted by Ali et al. [9]. Hussain et al. [10] scrutinized the unsteady flow of permeable surfaces for the tangent hyperbolic fluid under slip conditions. Shafiq et al. proposed the influence of Newtonian heating having microorganisms on tangent hyperbolic nanofluid [11]. Ramzan et al. presented the 3D tangent hyperbolic nanofluid of the heat flux theory with activation energy [12].
According to experts, nanoliquid is the most innovative and compelling technology currently used in engineering and technological products, including cooling agents, vehicles, catalyst reactions, and computer chips. The thermophysical characteristics of a nanoliquid are more important than those of a regular liquid. The presence of the nanoparticle in the regular fluid is investigated for potential effects on the fluid’s thermophysical characteristics. Choi [13] created the main invention in this field. The Williamson nanofluid due to the permeable surface was done by Bhatti and Rashidi [14]. Hayat et al. [15] described the melting heat transfer with thermal radiation induced by the variable thickness of the carbon nanotubes (CNT). Kumar et al. studied the effect of semiconductors on the thermal properties of CuO-H2O with the base fluid of nanoparticles [16]. The influence of thermal radiation using Sisko nanofluid with activation energy was evaluated by Ijaz et al. [17]. Khan and Shehzad [18] investigated the joule heating effect for the flow of third-grade nanomaterials due to the periodic motion sheet. The induction of nanoparticles in solar energy was discussed by Fayaz et al. [19]. Faizan et al. [20] examined how fluids move thermally and generate entropy during the tangent hyperbolic flow with the Darcy–Forchheimer flow across a stretching surface. Olanrewaju et al. [21] exploited Maxwell nanofluid due to the permeable surface by second law analysis. The heat transfer in the porous surface for the second law analysis of Maxwell nanofluid was reported by Alagumalai et al. [22], elaborating on applying nanofluid with thermal energy and technological applications. Tayebi et al. [23] discovered the natural convection flow of nanofluids with entropy generation due to annular enclosure. Chamka et al. [24] constituted an MHD natural convection flow and thermal radiation in the cavity enclosure using the finite element method. Seyyedi et al. [25] examined the MHD natural convection flow of nanofluids on entropy minimization in a wavy porous enclosure. Dogonchi et al. [26] explained the combined effect of thermal radiation and joule heat on the natural convection of nanoliquid between two disks. Eshaghi et al. [27] discussed the Baffle length H-shaped cavity with the addition of nanoparticles. Afshar et al. [28] probed the free convection flow of nanofluids inside the porous wavy enclosure. A titanium dioxide nanofluid based on 10 W40 subjected to electroosmotic forces and peristaltic propulsion in a curved microchannel is the subject of the current study, which focuses on the fluid flow analysis and heat transfer properties of the material explored by Akram et al. [29]. Maraj et al. [30] analyzed the oscillatory pressure-driven MHD flow of a hybrid nanofluid in a vertical rotating channel with velocity slip, thermal periodic limitations, and the effect of hall current, which are the main topics of the current mathematical investigation. Akram et al. [31] investigated the fluid flow properties and heat transmission by the drilling muds augmented with nanoparticles flowing through the drilling pipes under different physical conditions. Shah et al. [32] investigated how energy is transferred as engine oil-based Prandtl–Eyring nanofluid flows across a heated stretching surface. The influence of slip velocity across a vertically declining sheet, heat generation and absorption, and convection in a two-dimensional magnetic nanofluid are all statistically investigated by Asghar et al. [33]. Some other important studies can be found [34–39].
Researchers have used the oxytactic and erratic motion of microorganisms as a model to examine the processes of bioconvection. Slanting swimming cells are related to bioconvection, which focuses on different types of microorganisms. Ecological systems, biofuels, biosensors, and many more technologies successfully use the physical meaning of bioconvection. Due to the interaction of microorganisms, the bioconvection of nanoparticles is correlated with density. It has been noted that gyrotactic bacteria successfully increased the stability of nanoparticles. In recent years, several researchers have examined significant events. The effect of bioconvection employing nanoparticles past a permeable sheet was studied by Saini and Sharma [40]. Dhanai et al. [41] investigated the MHD flow gyrotactic microorganism on the nanoparticles past an inclined sheet. The force connection with bioconvection resulting from a vertical wedge plate was performed by Mahdy [42]. Avinash et al. [43] found the magnetic field of natural convective and microorganisms together with nanoliquid. Makinde and Animasaun [44] analyzed the impact of non-linear thermal radiation induced by the microorganism with a magnetic field and nanofluid. The impact of the slip effect with MHD flow on gyrotactic microorganisms was conducted by Khan et al. [45]. The mixed convective flow of bioconvection past a spongy plate was designed by Mutuku and Makinde [46]. The impact of convective conditions on the magnetic field flow of bioconvection was worked on by Khan et al. [47].
It has been brought to our attention that the second law analysis of bioconvection phenomena in the flow of tangent hyperbolic nanofluids with a slip effect under thermal radiation has not yet been considered. The motive is to fill the gap. This was discovered after careful observation of the review highlighted previously. In contrast to the standard approach, the flow, in this case, is caused by a vertical surface. It has been thoroughly reviewed and determined that such characteristics are not researched. Fluid flow past vertical stretching sheets has been proven to have numerous applications in current times due to physical and technological applications, such as the processing of polymers, the petrochemical sector, various production processes, glass production, and rolling hot. Because of these motivating factors, we decided to direct our attention to this substantial research gap. The present investigation was performed by simulating the features of thermal radiation, which has studied a large variety of features in thermal extrusion processing, solar energy, defense system, heavy automatic equipment, atomic chain reactions, and many other processes. The answer to the inserted problem is approached by methodically computing it using the BVP4c approach. The graphical results of various emerging variables besides the flow field are studied and evaluated.
2 Problem formulation
We presume a two-dimensional, laminar, unsteady, velocity effect of an MHD incompressible tangent hyperbolic nanofluid comprising bioconvection with entropy analysis. The fluid system is surrounded by a stretched sheet that is saturated with motile microorganisms and has a velocity of along the direction. Magnetic fields and stretched sheets are perpendicular to one another, whereby the induced magnetic field is ignored by the truly low magnetic Reynolds number (Figure 1). The Roseland approximation can be used to anticipate the radiation effect because the fluid is considered optically thick. Furthermore, it is assumed that the temperature of the fluid on the sheet is higher than the temperature in the free stream. The mathematical formulation in this study employs the Cartesian coordinate. The impacts of Brownian motion, thermophoresis, and convective effects are used to examine the heat, concentration, and motile density of the transit rates of microorganisms. The flow phenomena are described using the following equations.
FIGURE 1
Geometry of the problem.
The constitutive equation for the flow of the model (continuity, momentum, energy, concentration, and microorganism) is represented as follows [48–53]:
The corresponding boundary conditions are
Here, the component of velocity is in the direction of , volume expansion of the fluid is , stretching velocity is , gravity of the fluid is , heat transfer coefficient is , thermophoretic diffusion is , Brownian movement is , microorganism diffusivity is , specific heat is , kinematic viscosity is , electric conductivity of the nanofluid is , temperature of the fluid is , density of the nanofluid id , swimming speed cell is , density of the nanomaterial is , the density of microorganism particles is , ambient temperature is , ambient concentration is and ambient microorganism concentration is .
By considering the appropriate transformation [20],
The application of the suitable alteration in Eqs 2–5, subject to the boundary conditions in Eq. 6, is rendered into a system of ODEs [48]:
The boundary conditions are as follows [20], [42], [48]:
The dimensionless variables in the aforementioned equations are the unsteady parameter denoted by , Weissenberg number denoted by , magnetic number denoted by , Brownian motion denoted by , thermophoretic parameter denoted by , Schmidt number denoted by , Peclet number denoted by , bioconvection Lewis number denoted by , Biot number denoted by , heat capacity ratio of the nanofluid denoted by , Prandtl number denoted by , microorganism concentration difference denoted by , mixed convection parameter denoted by , bouncy force denoted by , and bioconvection Rayleigh number denoted by :
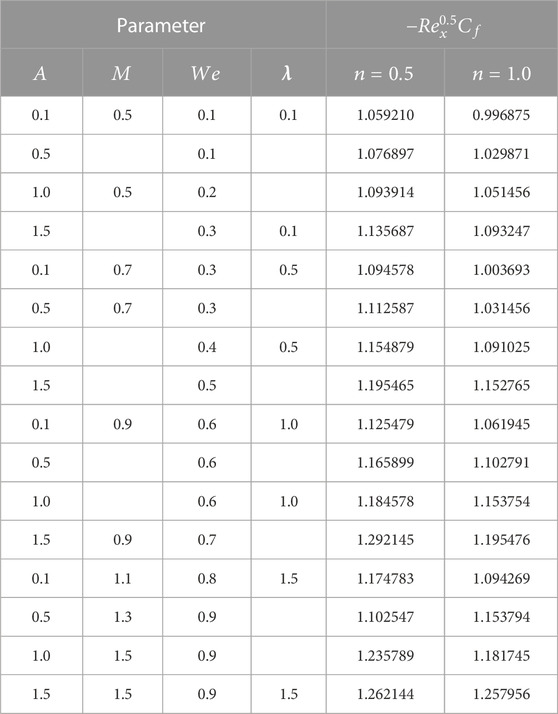
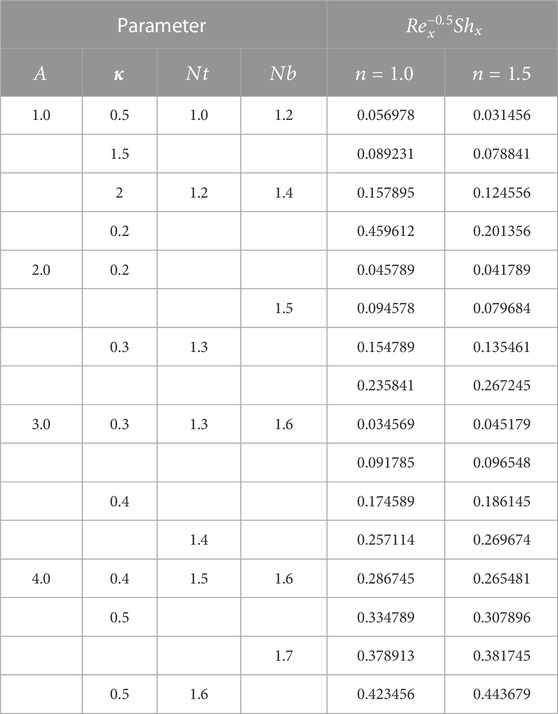
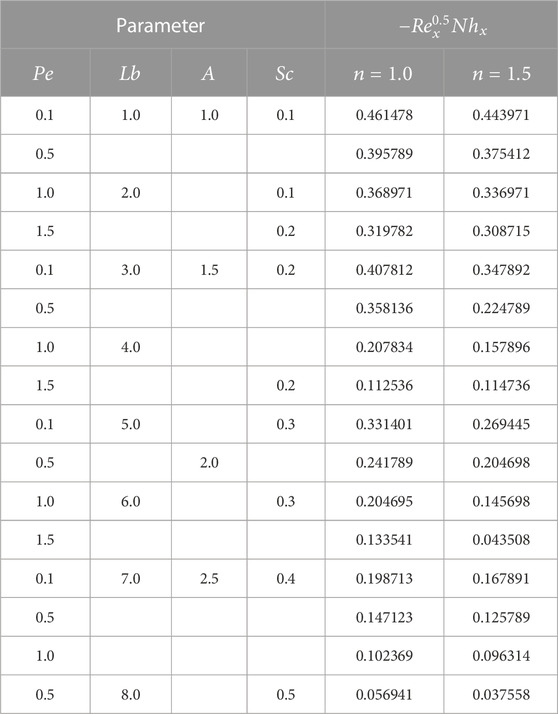
Skin friction, Nusselt number, Sherwood number, and motile microorganism are as follows:
The values for the aforementioned quantities are as follows:
3 Implemented strategy
It is obvious that the presented problem Eqs. (8–11) with boundary assumptions Eq. 12 cannot be handled analytically due to the problem’s extreme non-linearity. Hence, we employ the well-known BVP4c technique to simulate the numerical solution. Actually, BVP4c is used as a powerful method to achieve accurate results. The ordinary differential boundary value problem is resolved using this method. Each method, such as bvp4c MATLAB, has advantages and disadvantages. The main advantage is that it accepts multipoint BVPs natively, in contrast to many other solvers. As the source code is public, we can easily and gratis modify it to function with already-existing equations. MATLAB is an interpreted language; thus, making corrections is easy. Moreover, there are several issues concerning its ability to resolve first-order differential equations. You must first reduce your system to the first order before utilizing the bvp4c MATLAB method to solve higher orders. MATLAB executes more slowly than C and C++ because, as was already mentioned, it is an interpreted language. The technique turns the initial BVP into an IVP by applying the following presumptions: we will assign a few extra variables to accomplish this goal:
The criteria for new variable boundaries include
The far boundary is ; we put it by (for different distributions). The method produces consistent and quick convergence throughout the extensive deviation of calculating parameters. We utilized the step size of and continued to perform this method until the parameters for the tolerance level were reached .
4 Entropy generation
The influence of the magnetic field, thermal radiation and diffusion, and entropy generation for the tangent hyperbolic nanofluid is given by [54]
Eq. 20 shows the formation of entropy through the first phrase, which represents heat transfer, the second term, fluid friction, and the third term through the sixth term, diffusive irreversibility. The importance of entropy production can be expressed mathematically as
Using Eq. 6, it is possible to modify the rate of entropy minimization using tangent hyperbolic [54]:
5 Result and discussion
The numerous variables over are elaborated in Figures 2–10. It has been noted that each flow variable has remained constant throughout the procedure, such as This section describes the behavior of each of the physical parameters. Figures 2A–F show the variation of on velocity profile , temperature field , concentration , motile density profiles, entropy production , and Bejan number .
FIGURE 2
(A–F), and profiles for dissimilar values.
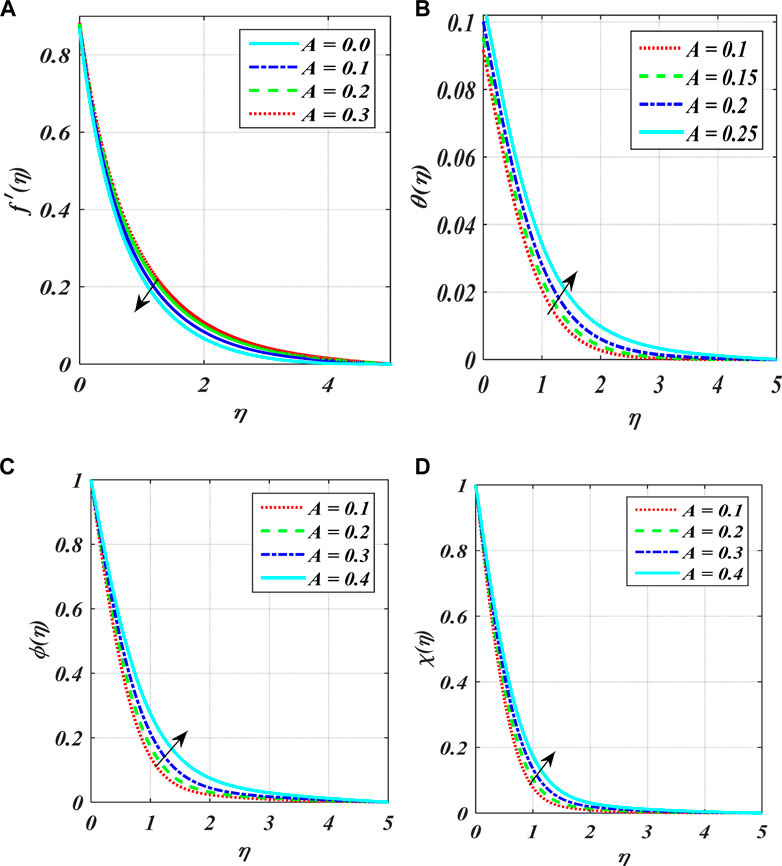
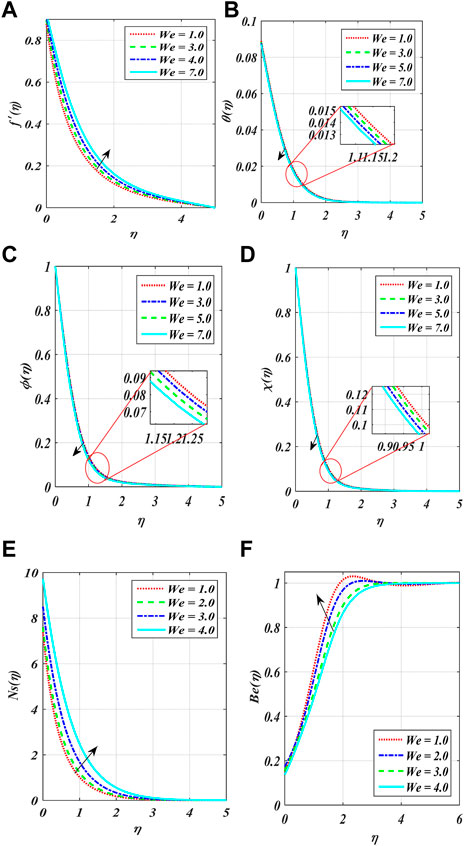
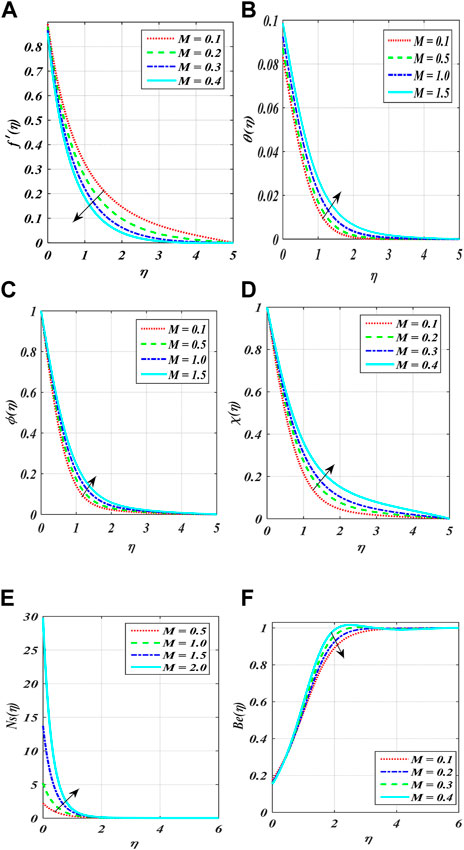
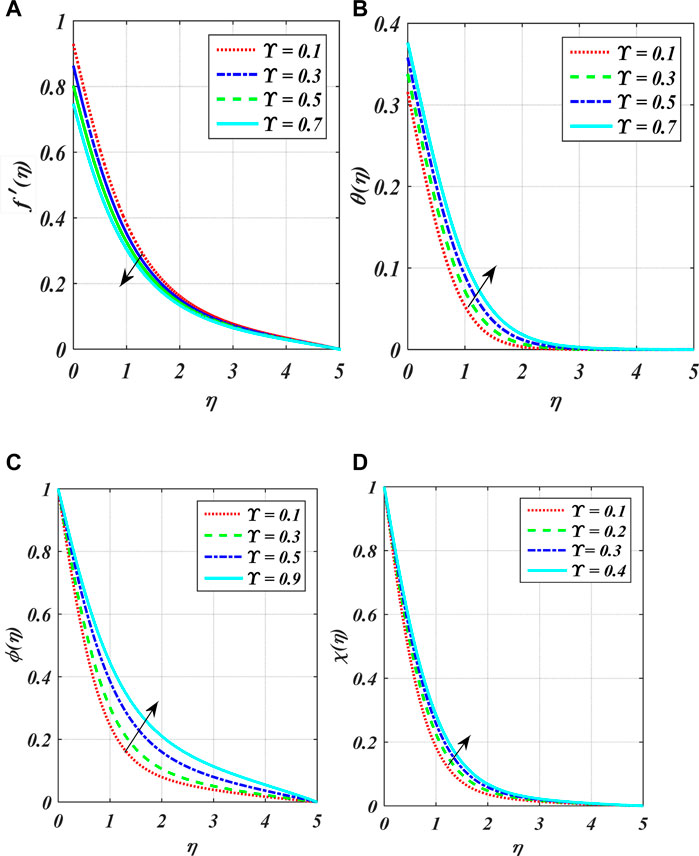
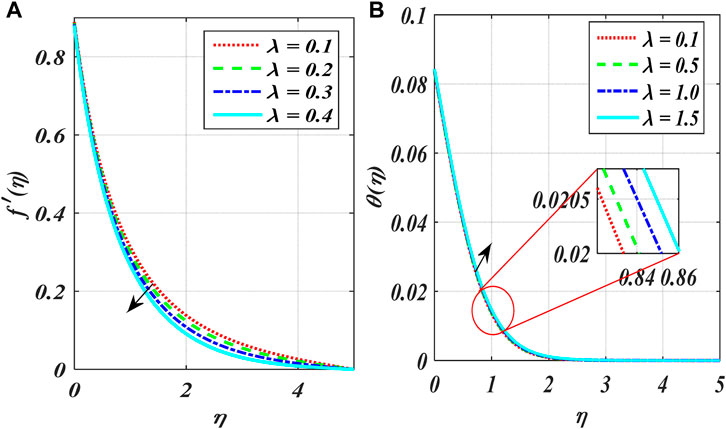
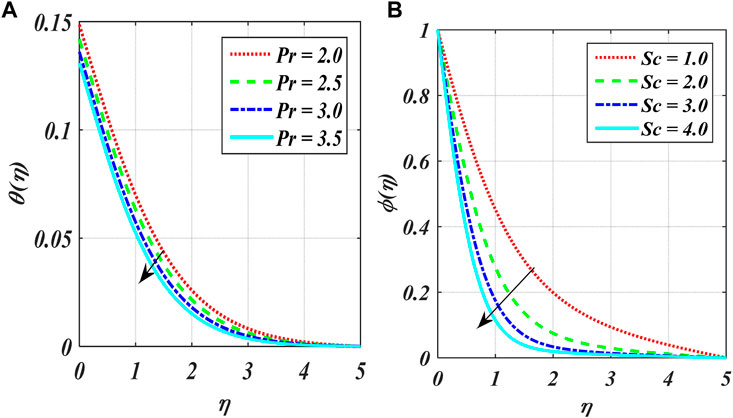
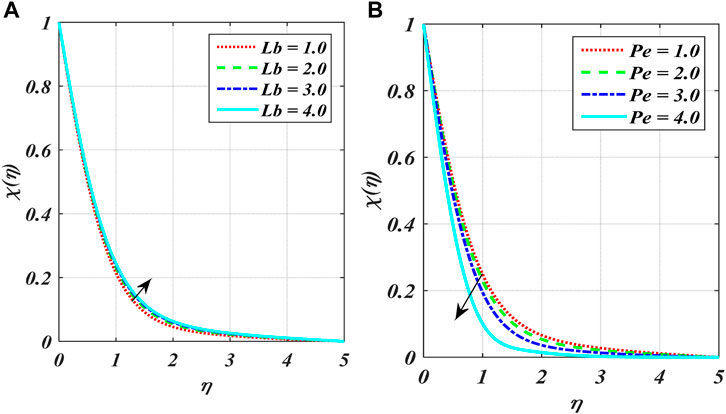
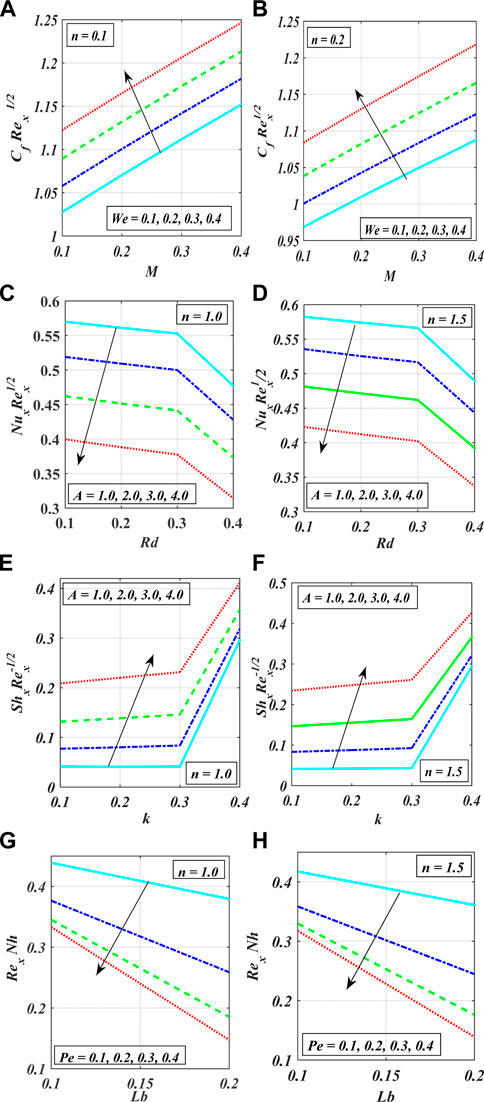
Figures 2A–F show the variation in power index number over , , , , , and . It is clear from depreciating in with the larger value of . Physically, the fluid’s viscosity, or its thickness, is determined by this characteristic. For small values of , the fluid exhibits shear thinning characteristics; for larger values of , shear thickening; and for , Newtonian characteristics. When is larger than one, the fluid’s velocity slows down, producing a weaker velocity field. The thermal layer field , concentration of nanoparticles , and motile density profiles are shown in Figures 2B–D. The thermal field and corresponding layer thickness have been improved for the bigger magnitude of . In essence, the described model becomes more sophisticated as the power-law index rises. With the development of this component, the fluid’s non-Newtonian properties steadily get worse. As a result, the velocity’s diminishing tendency can be explained. Figures 2C, D show concentration and motile density profiles and exhibit observable similarities in their behavior. With an increase in the power-law coefficient , the fluid becomes more viscous. As a result, the concentration and motile density profile improve gradually. Figures 2E, F present the influence of on and profile. It is reported that with the increase in values, the entropy generation increased significantly, whereas the Bejan number fell considerably. Figures 3A–D show the over velocity curve , temperature field , concentration , and motile density profiles . Figure 3A shows that the velocity distribution has been minimized to achieve a more accurate assessment of . Actually, the slower pace of the stretched sheet allows the fluid to cool down. As a result, the fluid’s particles settle down, and the system’s heat is released. The effect is that fluid viscosity also gradually increases. As a result, as can be seen in the image, the profile gradually decreases as the unsteadiness parameter’s values rise. The increase in the value of induces an acceleration in all three profiles—thermal , concentration , and motile density —as shown in Figures 3B–D. An increase in the unsteady parameter results in an increase in the kinetic energy of the fluid, which increases the motion of the liquid film. Figures 4A–F show fluctuation of on velocity profile , temperature field , concentration , motile density profiles , entropy production , and Bejan number . When applied to the flow field, reflects the fraction of the time scale corresponding to the actual time. Accordingly, the increase in improves the velocity profile shown in Figure 4A. Actually, the movement of fluid slowly decreases with the Weissenberg number. Moreover, is the proportion of relaxation time and other process time due to this relaxation time depreciating the fluid velocity increase with . Figures 4B–D show the temperature field , concentration , and motile density profiles diminished with a larger value of . The Weissenberg number influence on entropy generation and Bejan number are revealed in Figures 4E, F. For larger, We the and enhances. Physically, for higher We, more heat is lost because of relaxation time and more resistance between fluid particles, which is the reason and increase. Figures 5A–F show the performance of for velocity profiles , temperature fields , concentrations , motile density profiles , entropy production , and the Bejan number . For larger magnitudes of the magnetic field , it is obvious that the velocity profile will decrease due to an increase in the magnetic field’s strength. When , the flow is hydrodynamic, and when , the flow is magnetic. Actually, the decrease in velocities is caused by the resistive force of the magnetic field, which is always normal to an electrically conducting fluid flow. The Lorentz force is the name of this opposite force. There is a consequent consequence of fluid flow retardation. There is a deceleration in the velocity as a result. Moreover, a thickening of its boundary layer is observed. Figures 5B–D illustrate how temperature, concentration profile, and motile density tend to grow dramatically along with an increase in . Figures 5E, F depict the independent effects of magnetic field on the formation of entropy and the Bejan number. In contrast to Bejan number’s effect, entropy creation has risen. The entropy generation becomes better due to a rise in hostility to big . Actually, as the Lorentz magnetohydrodynamic body forces grow strong, the rate of heat transmission (temperature gradient) at the wall increases. The fact that is a function of temperature gradient causes stronger magnetic field effects to increase levels. The Bejan number decreases because viscous effects dominate the heating and mass transfer effect in our situation. Generally, in this plot, in the free stream, far from the stretching sheet, the Bejan number plummets to zero, whereas the maximum Bejan number arises closer to the wall. Based on these data, the profile increases and the profile decreases. Figure 6A displays the performance of the slip parameter over the dimensionless velocity. Here, when the slip parameter is estimated to be larger, the dimensionless velocity curves fall. Figures 6B–Dshow that , , and are mounting behavior leading to the slip parameter . Figures A, B manifest the impact of the mixed convection parameter on momentum boundary layer and temperature , showing that the improve value of let the velocity gradient profile fall. In fact, magnifying produces a less bouncy force due to this diversity in the velocity of the fluid. In contrast, reducing performance is noted for the temperature profile in Figure 7B. Figure 8A depicts the impact of on temperature. The Prandtl number governs the thermal pattern in the illustration . The arcs in this diagram demonstrate how the energy profile decreases as increases because the heat conductivity diminishes as increases. A high value indicates poor thermal conductivity, which lowers the thermal boundary layer and, consequently, conduction, resulting in a drop in fluid temperature. Figure 8B illustrates how the Schmidt number affects the concentration profile . The results of this figure show that when increases, the thickness of the layers and the associated also increase. Momentum diffusivity divided by thermal diffusivity gives the Schmidt number. In fact, when increases, momentum diffusivity improves. This is why declines.Figures 9A, B show the effect of density on the Lewis number and Peclet number . Restoration in motile density is correlated with increasing levels of the bioconvection Lewis number . As the Lewis number increases, the microorganism’s diffusivity increases, leading to a progressive rise in the fluid’s motile density. The thickness of actively moving microorganisms decreases as the Peclet number increases. The Peclet number quantifies the physical relationship between the prolixity of a microbe and its top swimming speed of individual cells. As the Peclet number rises, the rate at which the cell can swim increases. As the Peclet number of bioconvection increases, the density of motile bacteria decreases. The dispersion of motile microorganisms in the nanofluid is reduced in both scenarios with increasing diffusivity.
FIGURE 3
(A–D), and profiles for dissimilar values.
FIGURE 4
(A–F), and profiles for dissimilar values.
FIGURE 5
(A–F), and profiles for dissimilar values.
FIGURE 6
(A–D), and profiles for dissimilar values.
FIGURE 7
(A,B) and profiles for dissimilar values.
FIGURE 8
(A,B) and profiles for dissimilar and values.
FIGURE 9
(A,B) profiles for dissimilar and values.
The impact of versus magnetic parameter and Peclet number has been shown in Figures 10A–H for different values . Figures 10A–H show skin friction and Nusselt enhancement, whereas Sherwood and motile density decline as the Weissenberg number parameter and the Bioconvection Lewis number rise .
FIGURE 10
(A–H) Fluctuation of , , , and for and versus and .
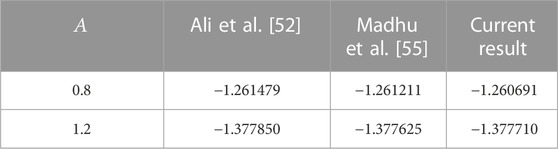
Table 1 compares the current problem with the published results of Ali et al. [52] and Madhu et al. [55]. In this comparison, the current outcomes present excellent achievement with the existing published results. Table 2 shows the variation with different values for the two cases when and . The skin friction is enhanced by enhancing values of and . The escalating performance is bigger for the two cases and . The numerical simulation for is seen in Table 3 for and . is lessened for the larger values of , , and . The Nusselt number is declined for the case of and . The influence of flow variables on for two values of and is presented in Table 4, showing that is enhanced for the larger values of and . Table 5 discovers that the bigger magnitude of and leads to depreciation with numerous values of and .
TABLE 1
| Ali et al. [52] | Madhu et al. [55] | Current result | |||||
|---|---|---|---|---|---|---|---|
| 0.8 | −1.261479 | −1.261211 | −1.260691 | ||||
| 1.2 | −1.377850 | −1.377625 | −1.377710 | ||||
Comparison of for .
TABLE 2
| Parameter | |||||
|---|---|---|---|---|---|
| 0.1 | 0.5 | 0.1 | 0.1 | 1.059210 | 0.996875 |
| 0.5 | 0.1 | 1.076897 | 1.029871 | ||
| 1.0 | 0.5 | 0.2 | 1.093914 | 1.051456 | |
| 1.5 | 0.3 | 0.1 | 1.135687 | 1.093247 | |
| 0.1 | 0.7 | 0.3 | 0.5 | 1.094578 | 1.003693 |
| 0.5 | 0.7 | 0.3 | 1.112587 | 1.031456 | |
| 1.0 | 0.4 | 0.5 | 1.154879 | 1.091025 | |
| 1.5 | 0.5 | 1.195465 | 1.152765 | ||
| 0.1 | 0.9 | 0.6 | 1.0 | 1.125479 | 1.061945 |
| 0.5 | 0.6 | 1.165899 | 1.102791 | ||
| 1.0 | 0.6 | 1.0 | 1.184578 | 1.153754 | |
| 1.5 | 0.9 | 0.7 | 1.292145 | 1.195476 | |
| 0.1 | 1.1 | 0.8 | 1.5 | 1.174783 | 1.094269 |
| 0.5 | 1.3 | 0.9 | 1.102547 | 1.153794 | |
| 1.0 | 1.5 | 0.9 | 1.235789 | 1.181745 | |
| 1.5 | 1.5 | 0.9 | 1.5 | 1.262144 | 1.257956 |
Numerical simulation of the skin friction coefficient .
TABLE 3
| Parameter | ||||||
|---|---|---|---|---|---|---|
| 1.0 | 0.5 | 1.0 | 1.3 | 0.1 | 0.615793 | 0.594833 |
| 1.0 | 0.516896 | 0.537169 | ||||
| 1.5 | 0.456345 | 0.479256 | ||||
| 2.0 | 0.396453 | 0.496371 | ||||
| 2.0 | 0.5 | 1.1 | 1.4 | 0.2 | 0.535465 | 0.573915 |
| 1.0 | 0.596486 | 0.523975 | ||||
| 1.5 | 0.414568 | 0.469145 | ||||
| 2.0 | 0.356822 | 0.409762 | ||||
| 3.0 | 0.5 | 1.2 | 1.5 | 0.4 | 0.591176 | 0.535978 |
| 1.0 | 0.4 | 0.551978 | 0.493671 | |||
| 1.5 | 0.439165 | 0.427196 | ||||
| 2.0 | 0.398121 | 0.393971 | ||||
| 4.0 | 0.5 | 1.3 | 1.6 | 0.493145 | 0.497345 | |
| 1.0 | 0.437128 | 0.456914 | ||||
| 1.5 | 0.371930 | 0.409725 | ||||
| 2.0 | 0.5 | 0.309153 | 0.346571 | |||
Numerical simulation of the local Nusselt number . .
TABLE 4
| Parameter | |||||
|---|---|---|---|---|---|
| 1.0 | 0.5 | 1.0 | 1.2 | 0.056978 | 0.031456 |
| 1.5 | 0.089231 | 0.078841 | |||
| 2 | 1.2 | 1.4 | 0.157895 | 0.124556 | |
| 0.2 | 0.459612 | 0.201356 | |||
| 2.0 | 0.2 | 0.045789 | 0.041789 | ||
| 1.5 | 0.094578 | 0.079684 | |||
| 0.3 | 1.3 | 0.154789 | 0.135461 | ||
| 0.235841 | 0.267245 | ||||
| 3.0 | 0.3 | 1.3 | 1.6 | 0.034569 | 0.045179 |
| 0.091785 | 0.096548 | ||||
| 0.4 | 0.174589 | 0.186145 | |||
| 1.4 | 0.257114 | 0.269674 | |||
| 4.0 | 0.4 | 1.5 | 1.6 | 0.286745 | 0.265481 |
| 0.5 | 0.334789 | 0.307896 | |||
| 1.7 | 0.378913 | 0.381745 | |||
| 0.5 | 1.6 | 0.423456 | 0.443679 | ||
Numerical simulation of the local Sherwood number .
TABLE 5
| Parameter | |||||
|---|---|---|---|---|---|
| 0.1 | 1.0 | 1.0 | 0.1 | 0.461478 | 0.443971 |
| 0.5 | 0.395789 | 0.375412 | |||
| 1.0 | 2.0 | 0.1 | 0.368971 | 0.336971 | |
| 1.5 | 0.2 | 0.319782 | 0.308715 | ||
| 0.1 | 3.0 | 1.5 | 0.2 | 0.407812 | 0.347892 |
| 0.5 | 0.358136 | 0.224789 | |||
| 1.0 | 4.0 | 0.207834 | 0.157896 | ||
| 1.5 | 0.2 | 0.112536 | 0.114736 | ||
| 0.1 | 5.0 | 0.3 | 0.331401 | 0.269445 | |
| 0.5 | 2.0 | 0.241789 | 0.204698 | ||
| 1.0 | 6.0 | 0.3 | 0.204695 | 0.145698 | |
| 1.5 | 0.133541 | 0.043508 | |||
| 0.1 | 7.0 | 2.5 | 0.4 | 0.198713 | 0.167891 |
| 0.5 | 0.147123 | 0.125789 | |||
| 1.0 | 0.102369 | 0.096314 | |||
| 0.5 | 8.0 | 0.5 | 0.056941 | 0.037558 | |
Numerical simulation of the motile density microorganisms.
6 Final remarks
This study measured the impact of velocity slip on the erratic flow of a mixed convection MHD tangent hyperbolic nanofluid containing moving microorganisms. The articulated ordinary differential equation and specified boundary conditions generated from the similarity solutions are resolved using the bvp4c solver in MATLAB. MATLAB bvp4c is time-saving, efficient, durable, fast-converging, and consistent with earlier studies. The effects of a few associated control parameters are highlighted. The physical variables over
, and
have been discussed in detail, and the cogency of the numerical results gained in this study is confirmed by relating them with those obtained earlier. The main result is given as follows:
• Boundary-layer thickness augments for temperature, concentration, and density distributions, although the velocity profile decays as an enhancement in due to resistive Lorentz force.
• The velocity profile declines in contrast to the increasing value of the power law index. Since the dimensionless parameter controls how the fluid behaves under shear, as the power index law magnitude rises, more resistance is put up to the fluid velocity, which decreases the flow.
• When the unsteady variable values increase, the temperature profile increases; however, when the Weissenberg number increases, it decreases.
• The microorganism field has diminished due to the change in and .
• Rising the values of reduces the concentration of the nanoparticles because when grows, the particles prefer to cluster closer together. Conversely, an opposite effect is examined in . Actually, thermophoresis is the movement of tiny particles from a hot to a cool area. When the nanoparticles migrate in the presence of a thermal radiation parameter, more particles are introduced to the process.
• At higher quantities of and , temperature and concentration decrease. Actually, the Prandtl number is determined by the thermal diffusivity to momentum diffusivity ratio. Also, the mass diffusivity decreases with increasing , causing the temperature and concentration contour to be smaller.
• and have revealed accelerating and decreasing behavior through dissimilar values of parameters , and .
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study was funded by Prince Sattam Bin Abdulaziz University (Project no. PSAU/2023/R/1444).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
unsteady parameter (dimensionless)
magnetic field strength
nanoparticle volume fraction (dimensionless)
skin-friction coefficient (dimensionless)
specific heat
mixed convective parameter (dimensionless)
coefficient of Brownian diffusion
coefficient of thermophoresis diffusion
microorganism diffusion coefficient
magnetic field parameter (dimensionless)
power-law index (dimensionless)
motion of Brownian parameter (dimensionless)
parameter of thermophoresis (dimensionless)
local Nusselt number (dimensionless)
Prandtl number (dimensionless)
local Reynolds number (dimensionless)
Schmidt number (dimensionless)
local Sherwood number (dimensionless)
temperature
temperature at the wall
ambient fluid temperature
microorganism profile (dimensionless)
surface concentration of microorganisms
ambient concentration of microorganisms
maximum cell swimming speed
Peclet number (dimensionless)
bioconvection Lewis number (dimensionless)
local volumetric entropy generation rate
time
bioconvection Rayleigh number (dimensionless)
nanoparticle concentration (dimensionless)
stretching sheet velocity
velocity components
Weissenberg number (dimensionless)
direction along the sheet
direction normal to the sheet
slip parameter (dimensionless)
Biot number (dimensionless)
coefficient of heat transfer
entropy generation (dimensionless)
Bejan number (dimensionless)
stretching parameter
radiation parameter (dimensionless)
- Greeks
time constant
stream function (dimensionless)
dimensionless concentration (dimensionless)
density of fluid
density of particles
time material constant
dimensionless temperature (dimensionless)
similarity variable
thermal diffusivity
heat capacity of fluid
effective heat capacity of the nanoparticle material
volume expansion coefficient
wall shearing stress
electrical conductivity
kinematic viscosity
References
1.
NadeemSHussainST. Changhoon lee, “flow of a williamson fluid over astretching sheet. Brazillian J Chemeng (2013) 30(03):619–25. July - September.
2.
ZakirUllahGZ. Lie group analysis of magnetohydrodynamic tangent hyperbolic fluid flow towards a stretching sheet with slip conditions. Cite as: Heliyon (2017) 3:e00443. 10.1016/j.heliyon.2017.e00443
3.
HayatTUllahIAlsaediAAhmadB. Modeling tangent hyperbolic nanoliquid flow with heat and mass flux conditions. Eur Phys J Plus (2017) 132:112. 10.1140/epjp/i2017-11369-0
4.
NagendrammaVLeelarathnamARajuCSKShehzadSAHussainT. Doubly stratified MHD tangent hyperbolic nanofluid flow due to permeable stretched cylinder. Res Phys (2018) 9:23–32. 10.1016/j.rinp.2018.02.019
5.
Geethan KumarSVarmaSVKKiran KumarRVMSSRajuCSKShehzadSABashirMN. Three-dimensional hydromagnetic convective flflow of chemically reactive Williamson fluid with non-uniform heat absorption and generation. Int J Chem Reactor Eng (2019).
6.
Al-KhaledKhanKhanKSUI. Chemically reactive bioconvection flow of tangent hyperbolic nanoliquid with gyrotactic microorganisms and nonlinear thermal radiation. Heliyon (2020) 6:e03117. 10.1016/j.heliyon.2019.e03117
7.
WaqasHKafaitAMuhammadTFarooqU. Numerical study for bio-convection flow of tangent hyperbolic nanofluid over a Riga plate with activation energy. Alexandria Eng J (2022) 61:1803–14. 10.1016/j.aej.2021.06.068
8.
ShafqALoneSASindhuTNAl-MdallalQMRasoolG. Statistical modeling for bioconvective tangent hyperbolic nanofluid towards stretching surface with zero mass flux condition. Sci Rep () 11:13869. 10.1038/s41598-021-93329-y
9.
AliBsHussainNaqviSIRHabibDAbdalS. Aligned magnetic and bioconvection effects on tangent hyperbolic nanofluid flow across faster/slower stretching wedge with activation energy: Finite element simulation. Int J Appl Comput Math (2021) 7:149. 10.1007/s40819-021-01097-0
10.
HussainSAhmadFAyedHMalikMYWaqasHAl-SawalhaMMet alCombined magnetic and porosity effects on flow of time-dependent tangent hyperbolic fluid with nanoparticles and motile gyrotactic microorganism past a wedge with second-order slip. Case Stud Therm Eng (2021) 26:100962. 10.1016/j.csite.2021.100962
11.
ShafiqAHammouchZSindhuTN, “Bioconvective MHD flow of tangent hyperbolic nanofluidwithnewtonian heating,” International Journal of Mechanical SciencesVolume133, November2017, Pages 759–66. 10.1016/j.ijmecsci.2017.07.048
12.
RamzanMChuYMGulHKadrySYu-MingC. Role of bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with Cattaneo-Christov heat flux and activation energy. Int Commun Heat Mass TransferVolume (2021) 120:104994. bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with Cattaneo-Christov heat flux and activation energy 10.1016/j.icheatmasstransfer.2020.104994
13.
ChoiSUS. Enhancing thermal conductivity of fluids with nanoparticles. Int Mech Eng Cong Exp Asme, FED (1995) 66:99–105.
14.
BhattiMMRashidiMM. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J Mol Liq September (2016) 21:567–73. 10.1016/j.molliq.2016.05.049
15.
HayatTMuhammadKFarooqM. AlsaediA.Melting heat transfer in stagnation point flow of carbon nanotubes towards variable thickness surface. AIP Adv (2019) 6015214.
16.
KumarPCMKumaCMA. Numerical evaluation of cooling performances of semiconductor using CuO/water nanofluids. Heliyon (2019) 5:5e02227. 10.1016/j.heliyon.2019.e02227
17.
IjazMAyubMKhanH. Entropy generation and activation energy mechanism in non-linear radiative flow ofSiskonanofluid: Rotating disk. Heliyon (2019) 5:5e01863. 10.1016/j.heliyon.2019.e01863
18.
KhanSUShehzadSA. Brownian movement and thermophoretic aspects in third grade nanofluid over oscillatory moving sheet. Phys Scr (2019) 94:94095202. 10.1088/1402-4896/ab0661
19.
FayazHNasrinRRahimNAHasanuzzamanM. Energy and exergy analysis of the PVT system: Effect of nanofluid flow rate. Solar Energy (2018) 169:217–30. 10.1016/j.solener.2018.05.004
20.
AhmedMFKhalidMAliFAlduaisFSAl-BosslyASaeedA. Second law analysis in Darcy- Forchheimer flow of tangent hyperbolic nanofluid in the presence of gyrotacticisroorganisms. Z Angew Math Mech (2023) e202200466.
21.
OlanrewajuAMSalawuSOOlanrewajuPOAmooSA. Unsteady radiativemagnetohydromagnetic flow and entropy generation ofmaxwellnanofluidin a porous medium with arrhenius chemical kinetic. Cogent Eng (2021) 8(1):1942639. 10.1080/23311916.2021.1942639
22.
AlagumalaiAQinCVimalKEKEvgenySLiu .YZhangPet alConceptual analysis framework development to understand barriers of nanofluid commercialization. Nano Energy (2022) 92:106736. 10.1016/j.nanoen.2021.106736
23.
TayebiTSattarDogonchiAKarimiNGe-JiLeHChamkhaAJElmasryY. “2021, Thermo-economic and entropy generation analyses of magnetic natural convective flow in a nanofluid-filled annular enclosure fitted with fins.” Sustainable Energ Tech Assessments46 (2021): 101274. 10.1016/j.seta.2021.101274
24.
ChamkhaAJDogonchiASGanjiDD. MagnetohydrodynamicNanofluid natural convection in a cavity under thermal radiation and shape factor of nanoparticles impacts: A numerical study using cvfem. Appl Sci (2018) 8:2396–12. 10.3390/app8122396
25.
SeyyediSMDogonchiASHashemi-TilehnoeeMGanjiDDChamkhaAJ. Second law analysis of magneto-natural convection in a nanofluid filled wavy-hexagonal porous enclosure. Int J Numer Methods Heat Fluid Flow (2020) 30:4811–36. 11 (January 1, 2020): 4811–36. 10.1108/HFF-11-2019-0845
26.
DogonchiASWaqasMAfsharSRSeyyediSMHashemi-TilehnoeeMChamkhaAJet alInvestigation of magneto-hydrodynamic fluid squeezed between two parallel disks by considering joule heating, thermal radiation, and adding different nanoparticles. Int J Numer Methods Heat Fluid Flow (2019) 30(2):659–80. 10.1108/HFF-05-2019-0390
27.
EshaghiSFarhadISattar DogonchiAChamkhaAJMohamedBBenHet al2021. “The optimum double diffusive natural convection heat transfer in H-shaped cavity with a baffle inside and a corrugated wall.” Case Stud Therm Eng28 (2021): 101541. 10.1016/j.csite.2021.101541
28.
AfsharSRMishraSRSattarDogonchiAKarimiNChamkhaAJAbulkhairH. Dissection of entropy production for the free convection of NEPCMs-filled porous wavy enclosure subject to volumetric heat source/sink. J Taiwan Inst Chem Eng (2021) 128:98–113. 10.1016/j.jtice.2021.09.006
29.
AkramJAkbarNSMonairahATripathiD, “Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel” Intternational Commun Heat Mass Transfer, Vol. 136, 106208, 10.1016/j.icheatmasstransfer.2022.1062082022, 1062.
30.
MarajENZehraIAkbarNS, “Rotatory flow of MHD (MoS2-SiO2)/H2O hybrid nanofluid in a vertical channel owing to velocity slip and thermal periodic conditions(MoS2-SiO2)/H2Ohybrid nanofluid in a vertical channel owing to velocity slip and thermal periodic conditions,” Colloids Surf A: Physicochemical Eng Aspects, Vol. 639, 2022, 128383, 10.1016/j.colsurfa.2022.128383
31.
AkramJAkbarNS. Mathematical modeling of Aphron drilling nanofluid driven by electroosmotically modulated peristalsis through a pipe. Math Model Nat Phenom (2022) 17:19. 10.1051/mmnp/2022012
32.
ShahZRoomanMShutaywiM. Computational analysis of radiative engine oil-based Prandtl–Eyring hybrid nanofluid flow with variable heat transfer using the Cattaneo–Christov heat flux model. RSC Adv Issue (2023) 13:3552–60. 10.1039/d2ra08197k
33.
AsgharAChandioAFShahZVrinceanuNDeebaniWShutaywiMet alMagnetized mixed convection hybrid nanofluid with effect of heat generation/absorption and velocity slip condition. Heliyon (2023) 9(issue 2):e13189. 10.1016/j.heliyon.2023.e13189
34.
AkbarNSMarajENNoorNFMHabibMB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature – dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. 10.1016/j.csite.2022.102124
35.
HabibMBAkbarNS. New trends of nanofluids to combat Staphylococcus aureus in clinical isolates. J Therm Anal Calorim (2021) 143:1893–9. 10.1007/s10973-020-09502-4
36.
AkramJAkbarNSTripathiD, “ Electroosmosis augmented MHD peristaltic transport of SWCNTs suspension in aqueous media,” J Therm Anal Calorim, 2022, Vol. 147 Issue 3, p2509-26. 10.1007/s10973-021-10562-3
37.
ShahZUllahA. Ferrofluid treatment with insertion of electric field inside a porous cavity considering forced convection. Waves in Random and Complex Media (2023) 1–19. 10.1080/17455030.2023.2169386
38.
TangT-QRoomanMShahZMAVrinceanuNRacheriuM, “2023, Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries,” J Magnetism Magn Mater, Vol. 569, 2023, 170448, 10.1016/j.jmmm.2023.170448
39.
KhanIRajaMAZKhanMARShoaibMIslamSShahZ. Design of backpropagated intelligent networks for nonlinear second-order lane–emden pantograph delay differential systems. Arabian J Sci Eng (2022) 47:1197–210. 10.1007/s13369-021-05814-1
40.
SainiSSharmaYD. Double-diffusive bioconvection in a suspension of gyrotactic microorganisms saturated by nanofluid. Int J Appl Fluid Mech (2019) 12:271–80. 10.29252/jafm.75.253.29097
41.
DhanaiRRanaPKumarL. Lie group analysis for bioconvection MHD slip flow and heat transfer of nano fluid over an inclined sheet: Multiple solutions. J Taiwan Instchem Eng (2016) 66:283–91. 10.1016/j.jtice.2016.07.001
42.
MahdyA. Gyrotactic microorganisms mixed convection nanofluid flow along an isothermal vertical wedge in porous media. Int J Mech Aero Indus Mechatronmanuf Eng (2017) 11(4):840–50.
43.
AvinashKSandeepNMakindeODAnimasaunIL. Aligned magnetic field effect on radiativebioconvection flow past a vertical plate with thermophoresis and Brownian motion. Defect Diffus Forum (2017) 377:127–40. 10.4028/www.scientific.net/ddf.377.127
44.
MakindeODAnimasaunIL. Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with non-linear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. J Mol Liq (2016) 21:733–43. 10.1016/j.molliq.2016.06.047
45.
KhanWAMakindeODKhaNZH. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int J Heat Mass Transf (2014) 74:285–91. 10.1016/j.ijheatmasstransfer.2014.03.026
46.
MutukuWNMakindeOD. Hydromagnetic bioconvection of nanofluid over a permeable vertical plate due to gyrotactic microorganisms. Comput Fluids (2014) 95:88–97. 10.1016/j.compfluid.2014.02.0262014
47.
KhanWAMakindeOD. MHD nanofluidbioconvection due to gyrotactic microorganisms over a convectively heat stretching sheet. Int J Therm Sci (2014) 81:118–24. 10.1016/j.ijthermalsci.2014.03.009
48.
ShafiqASindhuTMasood KhaliqueC. Numerical investigation and sensitivity analysis on bioconvective tangent hyperbolic nanofluid flow towards stretching surface by response surface methodology. Alexandria Eng J (2020) 59(6):4533–48. 10.1016/j.aej.2020.08.007
49.
AtifSMKhanWAAbbasMRashidU. BioconvectionMangnetohydrodynamic tangent hyperbolic nanofluid flow with quartic chemical reaction past a paraboloid surface. Comput Model Eng Sci (2022) 130(1):205–20. 10.32604/cmes.2022.017304
50.
AshrafMZRehmanSUFaridSHusseinAKAliBShahNAet alInsight into significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics (2022) 10:2592. 10.3390/math10152592
51.
ReddyCSAliFAl-FarhanyKSridharW. Numerical analysis of gyrotactic microorganisms in MHDradiative Eyring–Powell nanofluid across a static/movingwedge with Soret and Dufour effects. Z Angew Math Mech (2022) 102:e202100459. 10.1002/zamm.202100459
52.
AliFPadmavathiTHemalathaB. Entropy minimization in Darcy Forchheimer on Sutterbynanofluid past a stretching surface with swimming of gyrotactic microorganisms. Waves in Random and Complex Media (2022) 1–24. 10.1080/17455030.2022.2112635
53.
AliFReddyCSSummayyaNAhmedMF. Effect of nonlinear thermal radiation on unsteady MHD flow of Maxwell nanoliquid over a porous vertical sheet with chemical reaction. Heat Transfer (2021) 50:8259–79. 10.1002/htj.22276
54.
ZhaoTKhanMRChuYIssakhovAAliRKhanS. Entropy generation approach with heat and mass transfer in magnetohydrodynamic stagnation point flow of a tangent hyperbolic nanofluid. Appl Maths Mech (2021) 42:1205–18. 10.1007/s10483-021-2759-5
55
MadhuMKishanNChamkhaAJ. Unsteady flow of a Maxwell nanofluid over a stretching surface in thepresence of magnetohydrodynamic and thermal radiation effects. Purpul Power Res (2015) 6:31–40. 10.1016/j.jppr.2017.01.002
Summary
Keywords
nanofluids, entropy minimization, gyrotactic microorganism, MHD, thermal radiation
Citation
Faizan Ahmed M, Khalid M, Ali F, Al-Bossly A, Alduais FS, Eldin SM and Saeed A (2023) Importance of bioconvection flow on tangent hyperbolic nanofluid with entropy minimization. Front. Phys. 11:1154478. doi: 10.3389/fphy.2023.1154478
Received
30 January 2023
Accepted
20 March 2023
Published
07 April 2023
Volume
11 - 2023
Edited by
Felix Sharipov, Federal University of Paraná, Brazil
Reviewed by
Noreen Sher Akbar, National University of Sciences and Technology (NUST), Pakistan
Ebenezer Bonyah, University of Education, Winneba, Ghana
Updates
Copyright
© 2023 Faizan Ahmed, Khalid, Ali, Al-Bossly, Alduais, Eldin and Saeed.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sayed M. Eldin, sayed.eldin22@fue.edu.eg; Anwar Saeed, anwarsaeed769@gmail.com
This article was submitted to Fluid Dynamics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.