- 1College of Electronic Science, National University of Defense Technology, Changsha, China
- 2Scholol of Electronic Information Engineering, Beihang University, Beijing, China
The Chinese BeiDou navigation satellite system (BDS) has already completed its three phases and developed into a global navigation satellite system for open positioning, navigation, and timing services. The BDS-3 satellites feature the inter-satellite link (ISL). The ISL observation-related error model and ambiguity resolution for L-band observation are the crucial factors in precise data processing. In this study, we present for the first time the impact of ambiguity resolution on phase center offsets (PCOs) and hardware delay estimation of BDS-3 inter-satellite links. Two weeks’ L-band observations from 99 globally distributed ground stations and Ka-band ISL observations are collected for experimental validation and analysis. First, network solutions with and without ISL observations are conducted to investigate the role of ISL observation in ambiguity resolution. Afterward, ISL observation-related errors, mainly PCOs and hardware delays, are estimated by processing L-band with ISL observations with and without ambiguity resolution to analyze the impact of ambiguity resolution on these two factors. Finally, orbit accuracy in the network solution is assessed to further validate the effectiveness of the estimated PCOs and hardware delays in our experiment. The result indicates that introducing the ISL can slightly improve the fixing rate compared to only L-band observations from 83.7% to 84.3%. Furthermore, ambiguity resolution has a positive influence on the stability of estimated PCOs and hardware delays in turn, although the root mean square (RMS) values basically remain unchanged. The standard deviation (STD) of the x-offset is reduced from 0.021 m to 0.012 m, a significant improvement of about 43%, and 0.022 m–0.016 m, with an improvement of about 27%, for the y-offset. There is a slight improvement of about 8% for z-offset. Similarly, around 10% improvement in the STD for hardware delays can be achieved while the RMS values almost stay the same except for C40. Orbit determination from network solutions shows high accuracy compared to the public products for the satellite with good geometry configuration, which further validates our estimates for ISL PCOs and hardware delays.
1 Introduction
The Chinese BeiDou navigation satellite system (BDS) has already completed its three phases and developed into a global navigation satellite system for open positioning, navigation, and timing services. The third phase, i.e., BDS-3, constellation consists of three geostationary Earth orbit (GEO) satellites, three inclined geosynchronous Earth orbit (IGSO) satellites, and 24 medium Earth orbit (MEO) satellites. The 24 BDS-3 MEO satellites are of the Walker 24/3/1 configuration with an altitude of 21528 km and an orbital inclination of 55°, placed in three orbital planes named A, B, and C with eight MEO satellites in each plane.
The BDS-3 satellites feature the inter-satellite link. It is a wireless link for communication and ranges between satellites or any other spacecraft. According to Wang et al. [1], the Ka-band-phased array antenna can scan the large space range of up to 70° with the antenna element and enable dynamic links between satellites. The ISL measurement is described by a dual one-way ranging model that follows a time division multiple access (TDMA) scheme. One satellite is linked with a different satellite according to a pre-designed timeslot scheduling; thus, the ISLs in the entire satellite network are set up. The timeslot scheduling defines how one satellite connects with the other satellite of the constellation through a polling mechanism. After transforming the dual one-way observations to the same epoch, clock-free and geometry-free observables can be obtained by the addition and subtraction of dual one-way observations, which is of great significance for a modern global navigation satellite system.
Until now, many studies on ISLs have been carried out, from the validation of the experimental satellite to those in-orbit operations. All the existing research can be divided into three categories, namely, observation quality analysis, autonomous navigation [2, 3], and the contribution to orbit determination and clock estimation through the joint use of L-band observations. As aspects of ISL observation quality, Tang et al. [4] and Zhou et al. [5] analyzed the characteristics of ISL measurement in detail using the geometry-free observables, whose noise is confirmed to be less than 10 cm. Xie and Wang [6–8] showed the visibility between the ISL and antennas of some BDS-3 satellites according to the dynamic satellite network topology. Many researchers have studied the autonomous navigation only with ISL observations, which is one of the original intentions of the ISLs. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with ISL measurements were shown in the study by Tang et al. [4]. Afterward, Guo et al. [9] proposed an on-board extended Kalman filter (EKF) method and conducted the orbit determination for BDS-3 satellites with a distributed mode. Ren et al. [10] compared the ISL orbit determination by batch processing and the EKF, and the orbit precision in the radial component for batch processing and the EKF is about 0.1 m and 0.3 m, respectively. In addition, the additional ISL ranging measurements can also improve the accuracy of orbit determination compared with only using the observations from ground stations, especially for GNSS whose ground stations are limited in regions such as the BDS. Wang et al. [8] and Ren et al. [10] presented model refinement and comparisons for the contribution of inter-satellite links to BDS-3 orbit determination. It showed that about a 40% improvement can be achieved for regional cases and 20% for global cases, after ISL data were used for precise orbit determination. Yang et al. [11, 12] and Xie et al. [6] analyzed the orbit and clock of BDS-3 using inter-satellite link observations, which showed its superiority to that of the L-band. Pan et al. [13] preliminarily evaluated the performance of ISL time synchronization by the relative clock offsets between two visible satellites computed by the BDS-3 ISLs.
Thanks to the detailed validation and analysis performed by these scholars, ISL data are currently used in daily data processing of the BDS-3 operational control system. Stable and reliable high-precision satellite orbit products are the prerequisites for the positioning services with high performances [14–16]. It should be noted that similar to L-band pseudo-range and carrier phase observations, the ISLs are also affected by the phase center offsets of the Ka-band-phased array antenna and hardware delay. As the a priori values of PCOs are gross estimates, it is necessary to calibrate them when the ISLs are combined with the L-band data. Meanwhile, in L-band satellite–ground precise orbit determination, the hardware biases are often absorbed in the estimated clock offsets, while for precise orbit determination, including the ISL clock-free observables, the hardware delay must be precisely calibrated. In precise data processing, strategies for dealing with these possible factors or errors caused by complex external observation environments will fall into two categories. One is the steady signal processing method on the front end [17–19], and the other is optimized observation processing strategies on the back end. Furthermore, ambiguity resolution for L-band observation [20–24] is the crucial factor in precise data processing, and various ambiguity resolution methods have been developed. However, current studies only involve PCOs or hardware delays for part of the satellites, and there is no exploration of the impact of ambiguity resolution on the estimation of two aspects for BDS-3 ISLs in network solutions using Ka-band and L-band observations. Thus, we present the calibration of PCOs and hardware delays for ISLs simultaneously and analyze the influence of ambiguity resolution on these two calibration values.
This paper is organized as follows: In Section 2, the basic models and methods are introduced. Section 3 describes the collected data and processing strategies. In Section 4, experiments are conducted. The performance of estimates of PCOs and hardware delays of ISL observations are analyzed, and the influence of ambiguity resolution on the estimates is discussed. Finally, the conclusions and discussion are provided.
2 Models and methods
This section describes the basic models and methods involved in our study. Starting from the original observations’ equation of L-band and Ka-band ISL observables, along with the presented ambiguity resolution method used in our study, we derive the mathematical model for estimating ISL’s PCOs and hardware delays simultaneously.
2.1 Basic observation equation
The L-band, i.e., pseudo-range and carrier phase observations, and Ka-band ISL observations follow different structures. Herein, we express the L-band and Ka-band observation equations, respectively. Usually, to remove or weaken the influence of ionosphere delay, ionospheric-free combinations of the dual-frequency undifferenced code and carrier phase observations are used in precise orbit determination and positioning. The ionosphere-free (IF) combinations can be derived from the raw observations as
where
It can be noticed that the hardware delay of code for the receiver and satellite is linearly dependent on the clock parameters, and the same is true for the hardware delay of phase with ambiguity parameters. Hence, in L-band-based observations, the hardware delay of code and phase for the receiver and satellite can be absorbed into the corresponding clock and ambiguity parameters.
The ISL ranging data are dual one-way range measurements following a time division multiple access structure. The forward and backward observations are at times whose difference is shorter than 3 s. Hence, it is necessary to transform the dual one-way measurements at the different times to a common epoch
where
The sum of
where
2.2 Virtual observation equation from ambiguity resolution
Carrier phase observation is widely applied in precise orbit determination and positioning thanks to the high precision of measurement at the level of centimeter to millimeter, provided that cycle slips and ambiguity are well dealt with. As is known, the ambiguity parameters are easy to lose their integer characteristic and are, thus, estimated as float because of the linear dependence on some other parameters, such as hardware delay and initial phase bias [20–24]. Recovering their integer characteristic can effectively improve the accuracy of parameter solutions, and many ambiguity resolution methods and methods have been developed [25–30]. In our study, the double-differenced ambiguity resolution methods described by Ge et al. [21] are adopted. It can be expressed as
where
2.3 Mathematical model for estimation
The previous equations, the basic observation equation for L-band and Ka-band measurements, and the virtual observation equation from ambiguity resolution are processed together in our study to calibrate the ISL’s PCOs and hardware delays simultaneously in network solutions. To be consistent with the orbit dynamics, we express the linearized observation equations in the earth-centered inertial (ECI) frame. By combining the code phase with ISL observation equations, we can get the mathematical model for the network solution; that is,
where
where
3 Data collection and strategy
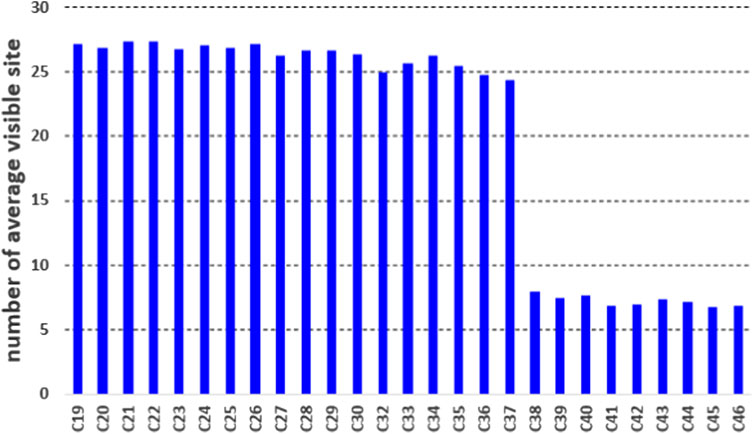
The BDS-3 satellites have been put into operation for more than 2 years. As equipment continues to upgrade, more and more receivers provided by the International GNSS Service (IGS) can support BDS-3 observations. To validate the proposed algorithm and get stable results for all BDS-3 satellites, we collect ISL data from all BDS-3 satellites and select L-band data from 99 globally distributed stations. The detailed descriptions of BDS-3 ISL can be referred to in existing articles; here, we will not go into detail. All selected stations have the capacity to track the B1I and B3I signals of BDS-3 satellites for network solutions. The distribution of these stations is shown in Figure 1.
FIGURE 1. Distribution of 99 stations selected for calibration of PCOs and hardware delays for ISLs.
Specifically, 2 week data from DOY 289 to DOY 302, 2020, are used to generate the network solutions, including orbit-related parameters, the coordinate of receivers, the clock of satellite and receiver, zenith tropospheric delays, and ambiguities. Furthermore, the PCOs and hardware delays of Ka-band ISL observations are estimated. Table 1 summarizes the detailed models and estimated parameters.
All parameters are estimated using the batch processing method. Cycle slips are detected, and gross errors are removed before parameter estimation. The orbit-related status parameters, receiver coordinates, and ambiguities are estimated as constant parameters, while the clocks of the receivers and satellites and the zenith tropospheric wet delay are estimated as random parameters. Ambiguities estimated as float and integer ones are done, respectively.
4 Experiments and analysis
We first investigate the effectiveness of ambiguity resolution in network solutions with and without ISLs in terms of fixing rates. Then, the performance of estimated ISL’s PCOs and hardware delays and the impact of ambiguity resolution on them are analyzed in detail. Finally, the orbit accuracy of satellites produced in the network solution is evaluated.
4.1 Fixing rate
As is known, ambiguity resolution can improve the accuracy of orbit determination and positioning for L-band observations. Furthermore, in this section, the contribution of introducing ISL observations processed together with L-band observations to ambiguity resolution is explored for the first time.
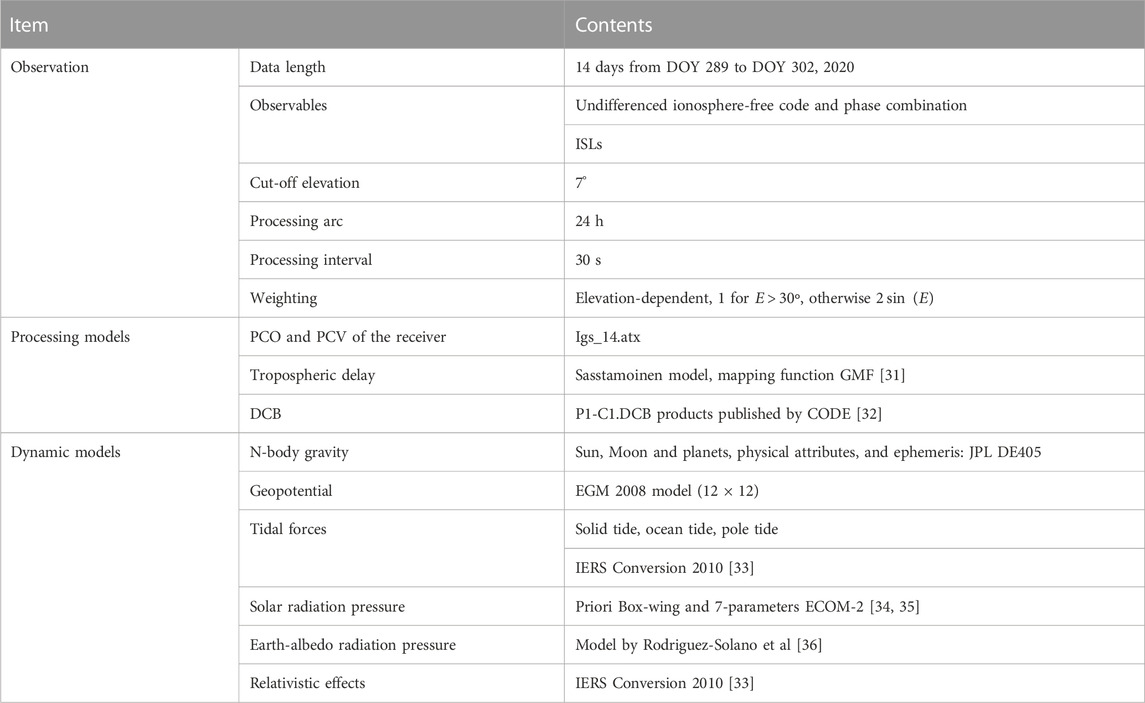
Two experimental schemes are designed, namely, L-band ambiguity resolution and L-band + Ka-band ambiguity resolution. Fixing rate is chosen as the indicator, which is the proportion of fixed double-differenced ambiguity to all double-differenced ambiguity. The statistical results are shown in Figure 2; Table.2.
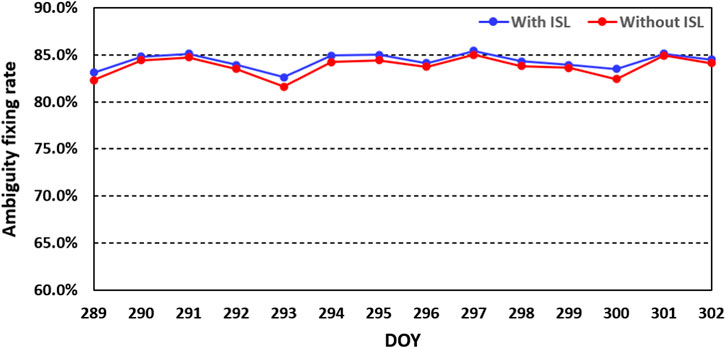
FIGURE 2. Daily fixing rate of ambiguity resolution with ISL observation (blue line) and without ISL observations (red line) during DOY 289-302, 2020.
We can see that, under the condition of a cautious empirical threshold for wide-lane deviation, narrow-lane deviation, and ratio as 0.25 cm, 0.2 cm, and 3, the statistical daily fixing rate keeps stable among different days at the level of about 83.5%. What is more notable is that there is a slight improvement in the fixing rate when ISL observations are introduced. The fixing rate increases up to about 84.5%. That is, ISL observations perform a positive influence on the ambiguity resolution for L-band observation in the network solutions. It can make contributions to the fixing rate with a proportion of about 1%. This may be due to the accuracy improvement of estimated parameters thanks to the stronger geometry characteristic. Therefore, this, in turn, inspires us to further investigate the impact of ambiguity resolution on the estimation of ISL-related errors, such as PCOs and hardware delays.
4.2 ISL PCOs
Usually, the GNSS orbit is computed with respect to the mass center of the satellite. However, the observation refers to the antenna’s phase center. The offset between these two centers must be known. In fact, the offset is difficult to measure since the phase center is not a mechanical point but an electronic one. So, the calibration before injection will strictly not be an exact value, and calibration after in-orbit is necessary.
In our study, the ISL PCOs are regarded as constant over a 24 h arc. Through processing L-band and ISL observations together in network solutions, we obtain ISL PCOs for all BDS-3 satellites. Taking C46 as an example, the daily estimated values in the x-component, y-component, and z-component are presented in Figure 3 as follows.
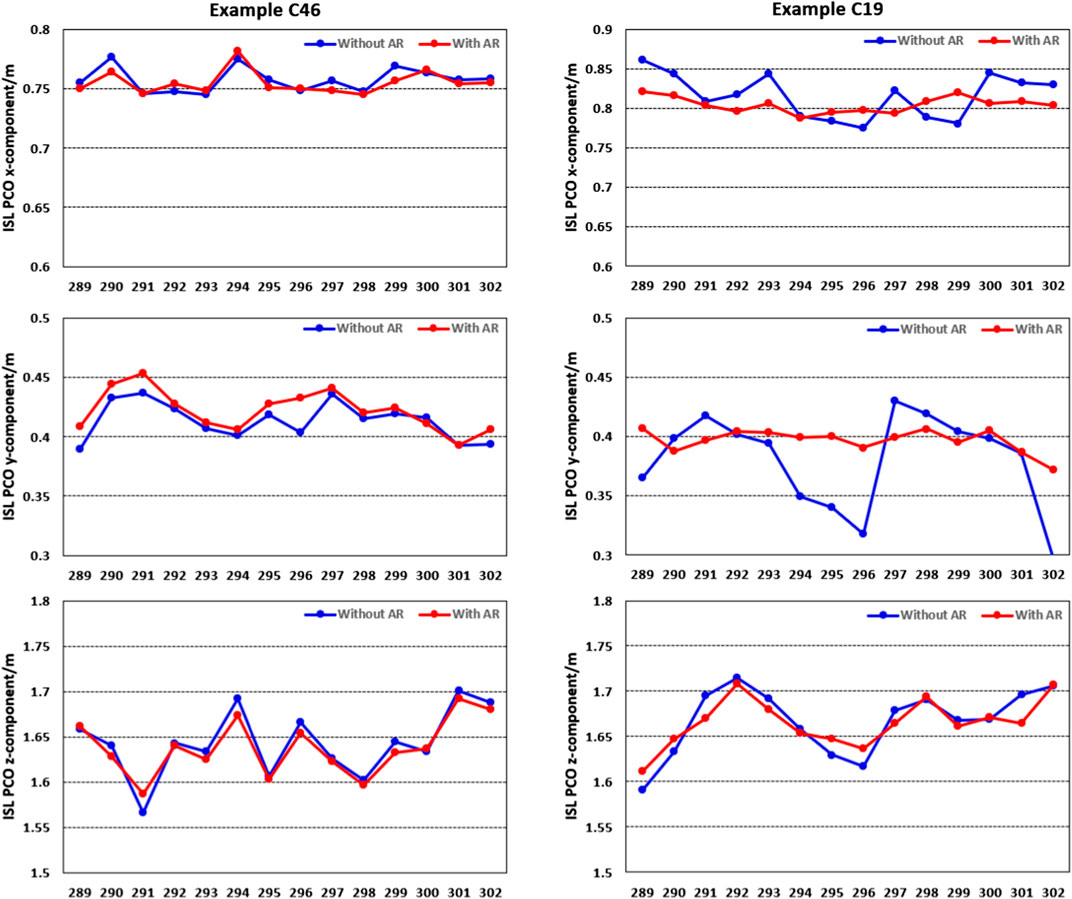
FIGURE 3. Daily estimated ISL PCOs in the x-component, y-component, and z-component with and without ambiguity resolution, respectively, for C46 and C19 during 14 days.
As can be seen from the abovementioned figure, there is very good consistency in each component between different days. Considering the stability of daily estimates, we calculate the RMS and STD values of all results over 14 days for each satellite. The details are shown in Figures 4, 5, respectively.
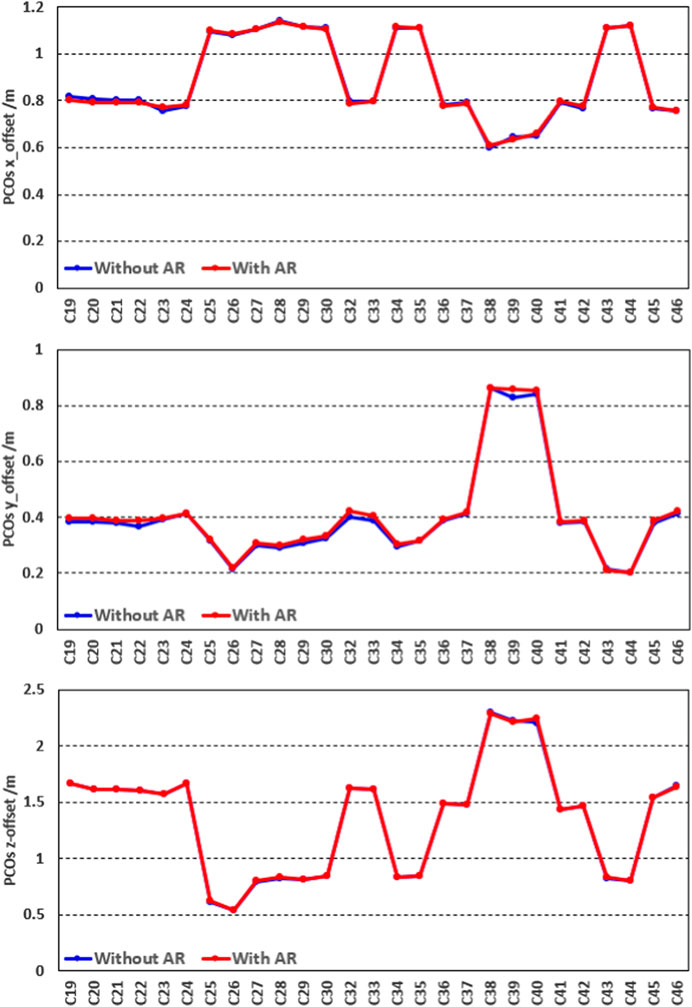
FIGURE 4. Statistical RMS values of PCOs in the x-component (upper panel), y-component (middle panel), and z-component (bottom panel) with ambiguity resolution (the red line) and without ambiguity resolution (the blue line), respectively, for all BDS-3 satellites during 14 days.
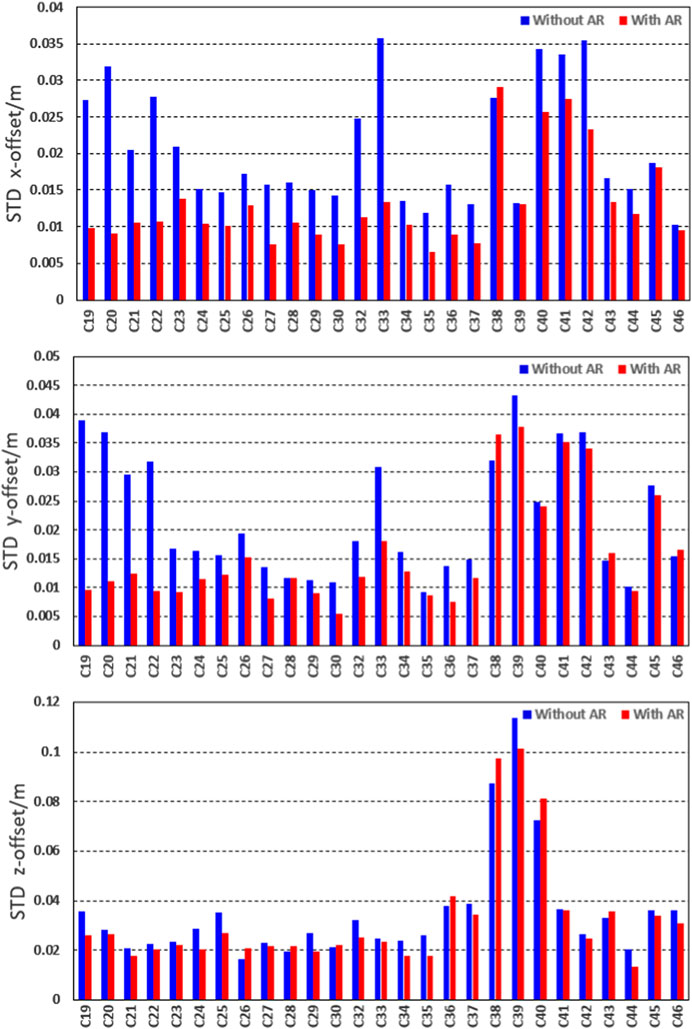
FIGURE 5. Statistical STD values of calibrated PCOs in the x-component (the upper panel), y-component (the middle panel), and z-component (the bottom panel) for all BDS-3 satellites without ambiguity resolution (the blue bars) and with ambiguity resolution (the red bars) during 14 days.
As shown in Figure 4, the RMS of estimated ISL PCOs presents a slight difference in all three components between results with and without ambiguity resolution for almost satellites. The z-offsets show the best consistency for all satellites; x-offsets are the second, while a slight difference can be found in the y-offsets for some satellites. In addition, it is obvious that ISL PCOs of some satellites almost stay at the same level. By collecting the information on satellite and inter-satellite link payload manufacturers, shown in Table 3, we find the correlation. ISL PCOs of the satellites from the same manufacturer perform similar characteristics, except for the three IGSO satellites, i.e., C38–C40.
Then, we calculate the standard deviation for all satellites using daily estimations. The results are as follows in Figure 5.
From Figure 5, we can see that the STD of the estimated ISL PCOs with ambiguity resolution decreases obviously overall compared to the ones without ambiguity resolution. In other words, the stability of estimated ISL PCOs improves. To be more specific, different satellites show various improvements, and different components perform differently. Despite the ambiguity resolution, the z-offset stays almost the same for most satellites. Only a slight improvement can be found for C19, C24, C25, C29, C34, C35, and C39. Moreover, it is noteworthy that the STD of PCOs in z-offset estimation keeps around 0.02 m for almost all satellites except for three satellites in the IGSO, i.e., C38, C39, and C40, whose STD values reach up to around 0.08 m. For the x-offset and y-offset, obvious improvements can be seen for most satellites. We discover that the largest improvement occurs on C19, C20, C21, C22, and C33. After ambiguity resolution, the STD of PCOs estimation is about 0.012 m and 0.016 m for the x-offset and y-offset, respectively. The statistical average value and maximum and minimum STD values are shown in Table 4.
Based on the previous results, we can draw a preliminary conclusion that ambiguity resolution plays a positive role in the stability of the ISL PCO estimation. There is an obvious improvement for STD values by 43%, 27%, and 8% for the x-offset, y-offset and z-offset, respectively.
4.3 ISL hardware delay
Hardware delays always exist in navigation measurements. The most recognized hardware delay is the L-band pseudo-range bias associated with both the GNSS satellite and receiver. This hardware delay is often determined as the differential code bias (DCB), which is the differential hardware delay between two or more frequencies [30]. The DCB parameters are typically incorporated into the definition of the clock for the dual- or triple-frequency L-band code measurement. ISL measurement also suffers from the hardware delay. However, unlike the DCBs of the pseudo-range measurement, which are estimated in a relative sense, the ISL hardware delay is the absolute delay between the ISL measurement and the geometric distance.
We estimate the ISL hardware delay together with the previous ISL PCOs in the network solution. All strategies are the same as the ISL PCO calibration. Like the evaluation of PCOs, the RMS and STD of the estimated hardware delay with and without ambiguity resolution are also counted and analyzed. Figure 6 shows the absolute value of the hardware delay and its time series for C19, C37, and C46. It can be seen that the estimated hardware delays are stable for 2 weeks, and ambiguity resolution plays a positive role in the stability.
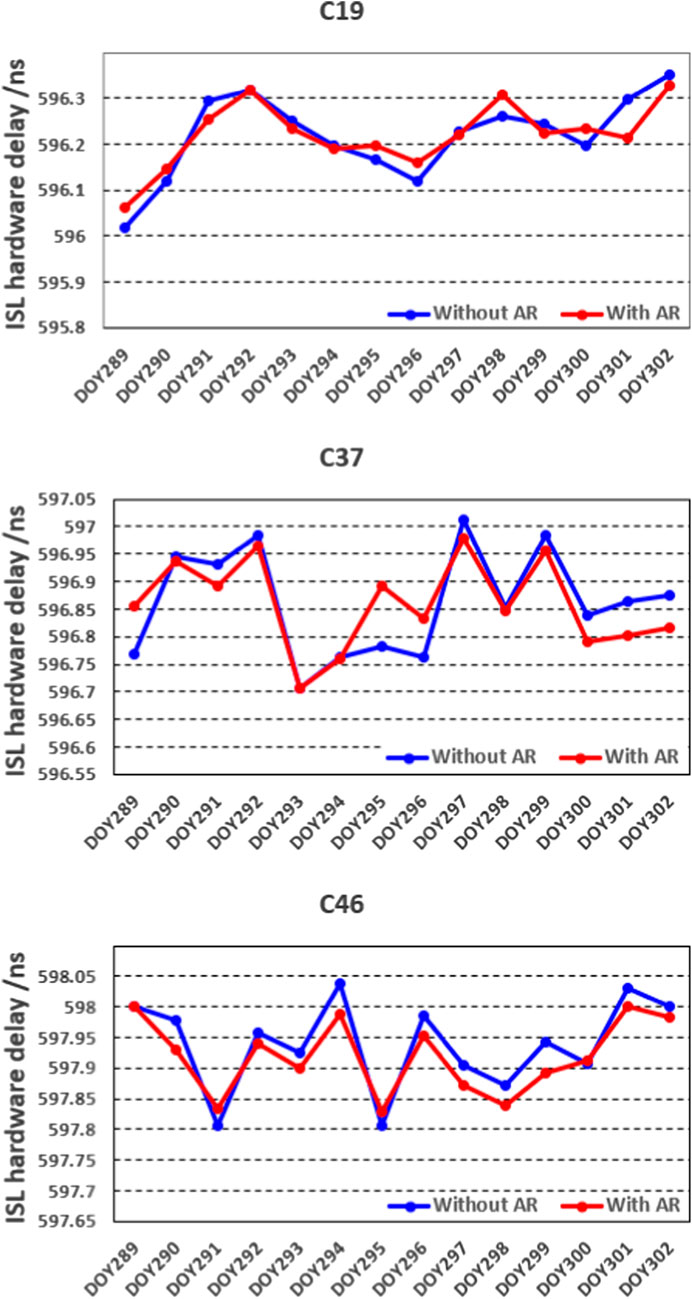
FIGURE 6. Estimated hardware delay in time series during 2 weeks for satellites C19, C37, and C46 as examples.
Considering the various ISL hardware delay magnitudes of different satellites, the difference in the RMS between the results with and without ambiguity resolution is shown. The details are presented in Figure 7.
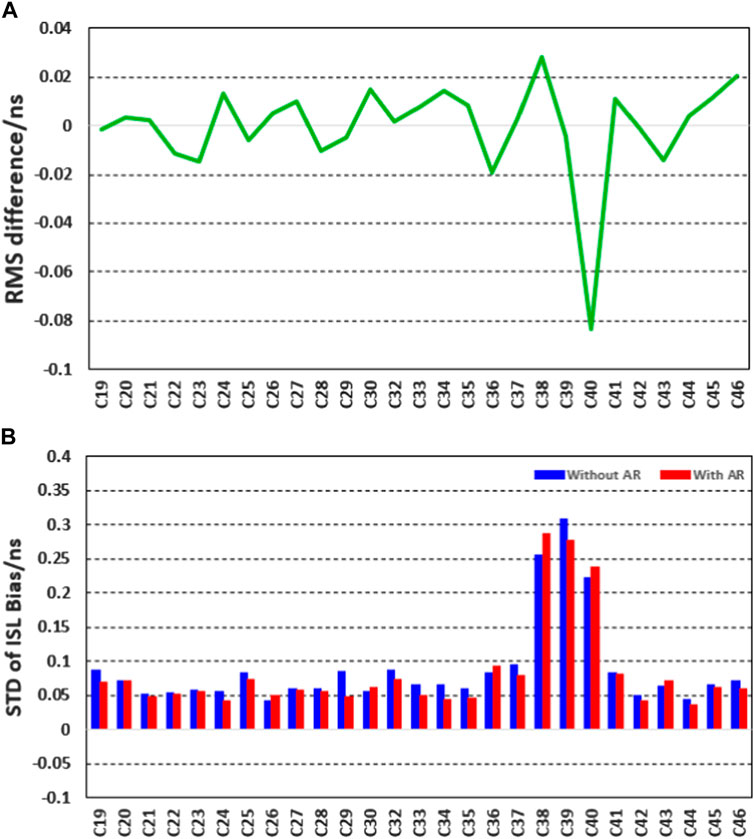
FIGURE 7. Statistical RMS (the upper panel) and STD values (the bottom panel) of ISL hardware delay without ambiguity resolution for all BDS-3 satellites. In (A), the green curve denotes the RMS without ambiguity resolution minus the one with ambiguity resolution; in (B), the blue bars represent the STD without ambiguity while red bars for the one with ambiguity resolution.
In Figure 7, the blue and red bars denote the STD of the estimated ISL hardware delay with and without ambiguity resolution, respectively. The green line is the differenced RMS value between the estimated hardware delay with and without ambiguity resolution. We can see that the STD decreases for all satellites except for C38, C40, and C43. The stability of the estimated hardware delay improves by about 10% after ambiguity resolution. In addition to the three IGSO satellites, the STD of the estimated ISL hardware delay is better than 0.05 ns after ambiguity resolution. The RMS of the estimated hardware delay with and without ambiguity resolution performs well in terms of consistency, except for C40, whose difference can reach up to about 0.1 ns. The cause of its formation needs further research.
4.4 Orbit validation
In this section, we assess the quality of orbit determined together with the ISL PCOs and hardware delay estimation from the network solutions. Only satellites in the medium Earth orbit (MEO) for BDS-3 are validated. Considering the public orbit products from IGS are results with ambiguity resolution, we compare our orbit products with ambiguity resolution to the current final orbit products from Wuhan University. The daily difference between two orbit products is counted, and RMS values are obtained. Then, the final RMS values for each MEO satellite can be obtained by averaging the daily RMS values over 14 days of our experiment. The RMS results in along-track, cross-track, radial, and 3D are shown in Figure 8.
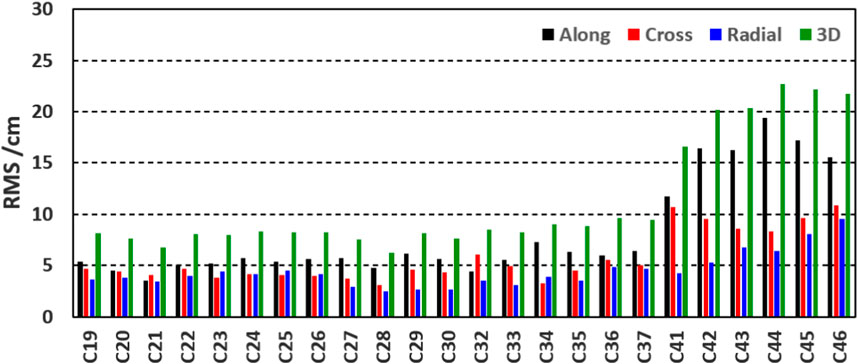
FIGURE 8. Average RMS of each BDS-3 MEO satellite orbit in along-track (the black bars), cross-track (the red bars), radial (the blue bars), and 3D (the green bars) compared to the wum products.
We can see that the satellites from C19 to C37 have better accuracy than the satellites from C41 to C46. The RMS values of the former group are about 5.5 cm, 4.0 cm, 3.5 cm, and 8.0 cm in along, cross, radial, and 3D components, respectively. This indicates that accurate orbits are obtained. Obviously there is an increase in the RMS values of satellites from C41 to C46. It almost reaches up to 16.0 cm, 10 cm, 7 cm, and 21 cm in along, cross, radial, and 3D components, respectively. This means that the orbit accuracy of this group of satellites decreases. The detailed statistical RMS values can be seen in Table. 5.
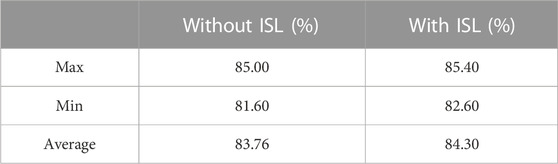
We conjecture that the different performance of orbit accuracy results from two factors. One is that the product of WHU has not used the ISL observation, but this may not be the major factor because the satellites C19–C37 show good consistency. Another is the number of tracking stations for each satellite. To better understand this phenomenon, the number of stations with tracking ability for every satellite is counted and presented in Figure 9.
According to the previously shown Figure and statistical results, there is an obvious difference in the visible station numbers between the C19–C37 and C41–C46. The average number of the former group is about 25, while it is around 6 for the latter group. In experience, the more the tracking stations and periods are, the better geometrical configuration can be obtained, which contributes to the accuracy of orbit determination. Thus, it is understandable that there is different orbit accuracy for these two groups of satellites. Overall, orbit products produced with the ISL PCOs and hardware delay estimation from network solutions shows good consistency compared with the public final orbit product for the satellites with good configuration. It further validates the effectiveness of the estimated ISL PCOs and hardware delays with ambiguity resolution.
5 Conclusion and discussion
A rapid and successful buildup of the BDS-3 constellation and the realization of ISL technology provide an opportunity for the analysis of orbit and clock, geodesy parameters, and so on. PCOs and hardware delays are two essential factors when using ISL observations. In addition, ambiguity resolution is an essential method for precise data processing. The interrelation of ambiguity resolution and estimation of ISL-related errors has not been explored so far. This contribution focuses on the impact of ambiguity resolution on PCOs and hardware delay estimation of BDS-3 inter-satellite links for the first time.
Also, two weeks of L-band observations from 99 globally distributed ground stations and ISL observations are collected for experimental validation and analysis. First, the effect of introducing ISL observations on ambiguity resolution is investigated. Then, the ISL PCOs and hardware delays estimated using the proposed algorithm with and without ambiguity resolution are obtained and analyzed, respectively. Finally, the estimated orbits in network solutions are assessed to validate the ISL’s PCOs and hardware delay estimation. Based on the experimental results, the following conclusions can be summarized:
Introducing ISL observations plays a positive role in ambiguity resolution. The ambiguity fixing rate increases from about 83.5% to 84.5% after introducing ISL observations into L-band observations. Analysis of estimated daily ISL PCOs and hardware delay values shows that there is good consistency for 14 days. Furthermore, the stability of the estimated values improves overall after ambiguity resolution. There is an obvious improvement with proportions of 43%, 27%, and 8% for x-offset, y-offset, and z-offset, respectively. To be specific, different satellites and different components show various improvements. For PCOs, the x-offset and y-offset benefit more from the ambiguity resolution compared to the z-offset for most of the satellites. The average standard deviations of PCO values with ambiguity resolution are 0.012 m, 0.016 m, and 0.032 cm for x-offset, y-offset, and z-offset, respectively. For hardware delays, compared to the ones without ambiguity resolution, STD decreases for all satellites except for C38, C40, and C43. The stability of the estimated hardware delay improves by about 10% after ambiguity resolution. In addition to the three IGSO satellites, the STD of the estimated ISL hardware delay is better than 0.05 ns The RMS with and without ambiguity resolution performs well in terms of consistency, except for C40. Once the ISL PCOs and hardware delays are well-calibrated with ambiguity resolution, the orbit accuracy is assessed compared to the WUM final products to further validate the estimated ISL PCOs and hardware delays. The daily stability helps ensure stable and accurate orbit products.
The ISL provides a promising way for GNSS orbit determination and clock estimation. The ambiguity resolution when processing L-band and ISL observations in network solutions can have a positive influence on each other. The mechanism needs further investigation.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ZL performed the theoretical study, conducted the experiment and analysis, and wrote the manuscript; WX revised the manuscript; LF provided conceptualizations and research suggestions; and ZL helped with programming and revised the manuscript. All authors read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Foundation (U20A0193) and National Natural Science Foundation of China (Grant Nos. 41931075 and 42274041).
Acknowledgments
The authors would like to thank the editors and reviewers for their efforts in supporting the publication of this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wang H, Xie J, Zhuang J, Wang Z. Performance analysis and progress of inter-satellite-link of Beidou system. In: Proceedings of the 30th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2017); September 2017; Portland, OR (2017). p. 1178–85.
2. Rajan JA. Highlights of GPS II-R autonomous navigation. In: Proc. the 58th annual meeting of the Institute of Navigation and CIGTF 21st guidance test symposium; June 24–26; Albuquerque, NM, USA. Institute of Navigation (2002). p. 354–36.
3. Rajan JA, Brodie P, Rawicz H. Modernizing GPS autonomous Navigation with anchor capability. In: Proc. ION GPS/GNSS 2003; September 9–12; Portland, Oregon, USA. Institute of Navigation (2003). p. 1534–42.
4. Tang C, Hu X, Zhou S, Liu L, Pan J, Chen L, et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements. J Geodesy (2018) 92:1155–69. doi:10.1007/s00190-018-1113-7
5. Zhou Y, Wang Y, Huang W, Yang J, Sun L. In-orbit performance assessment of BeiDou intersatellite link ranging. GPS Solutions (2018) 22(4):119. doi:10.1007/s10291-018-0784-0
6. Xin X, Tao G, Qile Z, Cai H, Zhang F, Wang X, et al. Precise orbit determination for BDS-3 satellites using satellite-ground and inter-satellite link observations. GPS Solutions (2019) 23:40. doi:10.1007/s10291-019-0823-5
7. Xin X, Tao G, Qile Z, Lv Y, Cai H, Liu J. Orbit and clock analysis of BDS-3 satellites using inter-satellite link observations. J Geodesy (2020) 94:64. doi:10.1007/s00190-020-01394-4
8. Wang C, Zhao Q, Guo J, Liu J, Chen G. The contribution of intersatellite links to BDS-3 orbit determination: Model refinement and comparisons. Navigation (2019) 66:71–82. doi:10.1002/navi.295
9. Lei G, Fuhong W, Gong X, Sang J, Liu W, Zhang W. Initial results of distributed autonomous orbit determination for Beidou BDS-3 satellites based on inter-satellite link measurements. GPS Solutions (2020) 24:72. doi:10.1007/s10291-020-00985-0
10. Ren X, Yang Y, Zhu J, Xu T. Comparing satellite orbit determination by batch processing and extended Kalman filtering using inter-satellite link measurements of the next-generation BeiDou satellites. GPS Solutions (2019) 23:25. doi:10.1007/s10291-018-0816-9
11. Ren X, Yang Y, Zhu J, Xu T. Orbit determination of the next generation Beidou satellites with intersatellite link measurements and a priori orbit constraints. Adv Space Res (2017) 60(10):2155–65. doi:10.1016/j.asr.2017.08.024
12. Yang D, Yang J, Li G, Zhou Y, Tang C. Globalization highlight: Orbit determination using BeiDou inter-satellite ranging measurements. GPS Solutions (2017) 21(3):1395–404. doi:10.1007/s10291-017-0626-5
13. Pan J, Hu X, Zhou S, Tang C, Guo R, Zhu L, et al. Time synchronization of new-generation BDS satellites using inter-satellite link measurements. Adv Space Res (2018) 61(1):145–53. doi:10.1016/j.asr.2017.10.004
14. Lou Y, Dai X, Gong X, Li C, Qing Y, Liu Y, et al. A review of real-time multi-GNSS precise orbit determination based on the filter method. Satellite Navigation (2022) 3:15. doi:10.1186/s43020-022-00075-1
15. Zhao Q, Guo J, Wang C, Lyu Y, Xu X, Yang C, et al. Precise orbit determination for BDS satellites. Satellite Navigation (2022) 3:2. doi:10.1186/s43020-021-00062-y
16. Zuo X, Jiang X, Li P, Wang J, Ge M, Schuh H. A square root information filter for multi-GNSS real-time precise clock estimation. Satellite Navigation (2021) 2:28. doi:10.1186/s43020-021-00060-0
17. Li B, Qiao J, Lu Z. Influence of swept-frequency interference on satellite navigation time-domain anti-jamming. Front Phys (2022) 10. doi:10.3389/fphy1063474
18. Wu R, Dong J, Wang M. Wearable polarization conversion metasurface MIMO antenna for biomedical applications in 5 GHz WBAN. Biosensors (2023) 13(1):73. doi:10.3390/bios13010073
19. Pan Y, Dong J. Design and optimization of an ultrathin and broadband polarization-insensitive fractal FSS using the improved bacteria foraging optimization algorithm and curve fitting. Nanomaterials (2023) 13(1):191. doi:10.3390/nano13010191
20. Blewitt G. An automatic editing algorithm for GPS data. Geophys Res Lett (1990) 17(3):199–202. Nagivation. Nashville, TN.
21. Ge M, Gendt G, Rothacher M, Shi C, Liu J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J Geodesy (2008) 82:389–99. doi:10.1007/s00190-007-0187-4
22. Laurichesse D, Mercier F. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP. In: Proceedings of the 20th International Technical Meeting of the Satellite Division (2007).
23. Laurichesse D, Mercier F, Berthias JP, Bijac J. Real time zero-difference ambiguities fixing and absolute RTK. In: Proceedings of the 2008 National Technical Meeting of The Institute of Navigation; San Diego, CA (2008).
24. Laurichesse D, Mercier F, Berthias J-P, Broca P, Cerri L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navig J Inst Navig (2009) 56(2):135–49. doi:10.1002/j.2161-4296.2009.tb01750.x
25. Geng J, Bock Y. Triple-frequency gps precise point positioning with rapid ambiguity resolution. J Geodesy (2013) 87(5):449–60. doi:10.1007/s00190-013-0619-2
26. Geng J, Meng X, Dodson AH, Ge M, Teferle FN. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J Geodesy (2010) 84:705–14. doi:10.1007/s00190-010-0404-4
27. Geng J, Shi C, Ge M, Dodson AH, Lou Y, Zhao Q, et al. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J Geodesy (2012) 86:579–89. doi:10.1007/s00190-011-0537-0
28. Geng J, Teferle FN, Meng X, Dodson AH. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv Space Res (2011) 47:1664–73. doi:10.1016/j.asr.2010.03.030
29. Gu S, Lou Y, Shi C, Liu J. BeiDou phase bias estimation and its application in precise point positioning with triple-frequency observable. J Geodesy (2015) 89:979–92. doi:10.1007/s00190-015-0827-z
30. Wilson BD, Mannucci AJ. Instrumental biases in ionospheric measurement derived from GPS data. In: Proceedings of ION GPS93; September, 1993; Salt Like City (1993). p. 1343–13.
31. Boehm J, Niell A, Tregoning P, Schuh H. Global mapping function (gmf): A new empirical mapping function based on numerical weather model data. Geophys Res Lett (2006) 33(7):L07304. doi:10.1029/2005gl025546
32. Schaer S, Steigenberger P. Determination and use of GPS differential code bias values. IGS Workshop, https://specialsci.cn/detail/25284480-036c-4588-8a7f-4f05b992f3e7?resourceType=0 (2006).
33. Petit G, Luzum B. IERS conventions 2010. No. 36 in IERS technical note. Frankfurt am Main, Germany: Verlag des Bundesamts fürKartographie und Geodäsie (2010).
34. Springer TA, Beutler G, Rothacher M. A new solar radiation pressure model for GPS. GPS Solutions (1999) 2(3):673–6. doi:10.1016/s0273-1177(99)00158-1
35. Springer TA, Beutler G, Rothacher M. Improving the orbit estimates of GPS satellites. J Geodesy (1999) 73(3):147–57. doi:10.1007/s001900050230
Keywords: BDS-3, ambiguity resolution, PCO calibration, hardware delay, inter-satellite links, L-band
Citation: Li Z, Xiao W, Fan L, Lu Z and Wang F (2023) Impact of ambiguity resolution on phase center offsets and hardware delay estimation for BDS-3 inter-satellite links. Front. Phys. 11:1154159. doi: 10.3389/fphy.2023.1154159
Received: 30 January 2023; Accepted: 28 March 2023;
Published: 17 April 2023.
Edited by:
Jian Dong, Central South University, ChinaReviewed by:
Nickolay Ivchenko, Royal Institute of Technology, SwedenNingbo Wang, Aerospace Information Research Institute (CAS), China
Wenwen Li, Wuhan University, China
Copyright © 2023 Li, Xiao, Fan, Lu and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Feixue Wang, Znh3YW5nQG51ZHQuZWR1LmNu
 Zongnan Li
Zongnan Li Wei Xiao1
Wei Xiao1 Zukun Lu
Zukun Lu