Analytical analysis of fractional nonlinear Jaulent-Miodek system with energy-dependent Schrödinger potential

In this work, a novel technique is considered for analyzing the fractional-order Jaulent-Miodek system. The suggested approach is based on the use of the residual power series technique in conjunction with the Laplace transform and Caputo operator to solve the system of equations. The Caputo derivative is applied to express the fractional operator, which is more suitable for modeling real-world phenomena with memory effects. As a real example, the proposed technique is implemented for analyzing the Jaulent-Miodek equation under suitable initial conditions. Additionally, the proposed technique’s validity (accuracy and effectiveness) is examined by studying some numerical examples. The obtained solutions show that the suggested technique can provide a reliable solution for the fractional-order Jaulent-Miodek system, making it a helpful tool for researchers in different areas, including engineering, physics, and mathematics. We also analyze the absolute error between the derived approximations and the analytical solutions to check the validation and accuracy of the obtained approximations. Many researchers can benefit from both the obtained approximations and the suggested method in analyzing many complicated nonlinear systems in plasma physics and nonlinear optics, and many others.

1 Introduction

Fractional differential equations (DEs) are types of DEs that involve fractional derivatives (FDs). Unlike ordinary DEs, where the order of the derivative is a positive integer, fractional DEs (FDEs) involve operators of non-integer orders. These equations are applied to model various physical and biological phenomena, such as anomalous diffusion, viscoelasticity, and fractal growth [1–3]. FDEs have several unique properties that differentiate them from ordinary DEs, such as non-locality and memory effects. Solving the FDEs requires specialized techniques, such as fractional calculus and numerical methods [4–8]. These equations have become an active area of research in recent decades due to their potential application in various fields of science [9–12].

Fractional nonlinear systems of partial DEs (PDEs) are mathematics model that describes the behavior of complex models in different areas, such as chemistry, biology, physics, engineering, and finance [13–15]. These systems are characterized by the presence of FDs, which are generalizations of the classical integer-order derivatives. FDs describe the system’s memory and long-range interactions and allow for modeling anomalous diffusion, power-law behavior, and other non-local effects that classical models cannot capture. Nonlinearities are another essential feature of fractional systems, as they can lead to the emergence of rich and diverse phenomena, such as chaos, bifurcations, solitons, and patterns. Nonlinear systems are ubiquitous in nature and technology, and understanding their dynamics is crucial for predicting and controlling their behavior [16–23].

Fractional nonlinear systems of PDEs are challenging to study due to their non-locality, nonlinearity, and complexity. They require developing new analytical and numerical tools, such as fractional calculus (FC), dynamical systems theory, and computer simulations [24–26]. Despite the difficulties, fractional nonlinear systems of PDEs have attracted increasing attention in recent years due to their relevance in many applications. They provide a powerful framework for modeling and understanding complex phenomena and offer new opportunities for scientific and technological advances [27, 28].

It has been found that FDEs describe real-world problems more precisely than integral order DEs. The study of coupled systems of FDEs is also quite interesting. Because mathematical models of many phenomena in bio-mathematics, physics, psychology, and other fields are coupled systems of DEs [29, 30]. Among such coupled systems of fractional PDEs (FPDEs), we have the coupled Jaulent-Miodek models with Schrodinger energy-dependent potential. This type of equation system is widely applied as a model for the solution of several real worlds problems in the areas of applied sciences [31, 32]. Extensive analysis of nonlinear coupled fractional-order Jaulent-Miodek models a key role in many areas fields of science, such as plasma physics [33], condensed matter physics [34, 35]. There are a variety of techniques applied in achieving analytic and numeric results to linear and nonlinear FPDE, such as the homotopy perturbation technique (HPT) [36–39], the variational iteration technique [40], the q-homotopy analysis transformation technique [41], the fractional natural decomposition technique [42], the fractional multi-step differential transform technique [43], the new iterative technique [44, 45] and the homotopy analysis technique [46, 47], Residual power series technique [48].

The suggested method is called Laplace residual power series method (LRPSM) which was introduced recently to address nonlinear DEs (NLDEs) with fractional orders [49, 50]. This method is a combination between Laplace transform (LT) and RPSM which provides a more accurate solution, requiring less time and simpler calculations than other analytical methods. Unlike other methods, LRPSM does not involve differentiation or linearization and only utilizes the LT, followed by taking the limit at infinity. Thus, the current work aims to apply an innovative analytical technique (LRPSM) to obtain highly accurate estimated fractional solutions to the Jaulent-Miodek equation in the Caputo sense subject to suitable initial conditions. Also, the outcomes of the LRPSM will be compared with the precise answer by creating graphs and tables for the numerical problem. The suggested technique has been used to make exact results for emerging realistic models of physical phenomena by using fast convergent power series. This method succeeded because it is straightforward and handles different kinds of initial conditions directly. Also, it doesn’t need linearization or restrictive assumptions, doesn’t need a lot of computing power, takes less time, and is more accurate.

The framework of this study is detailed as follows: Section 2 reviews certain essential concepts, properties, and theorems related to FC, LT, and Laplace fractional expansion. The general methodology of LRPSM for the proposed model is presented in Section 3. Fractional solution Jaulent-Miodek equations are provided applying the LRPSM in Section 4. Section 5 contains the result and discussion. Finally, the conclusion is given in Section 6.

2 Basic definitions

Definition 1. For at least n time differentiable function, the fractional Caputo derivative of order ρ reads [51]

${}^{C}D_{\tau }^{\rho }\psi \left(\gamma ,\tau \right)=\left\{\begin{array}{cc}{\int }_0^{\tau }\frac{{\left(\tau -w\right)}^{n-\rho -1}\psi \left(\eta ,w\right)}{\mathrm{\Gamma }\left(n-\rho \right)}dw,\hfill & n-1<\rho \le n,\hfill \\ \frac{{\partial }^n\psi \left(\eta ,\tau \right)}{\partial {\tau }^n},\hfill & n=\rho ,\hfill \end{array}\right.(1)$

where n ∈ N and the fractional Riemann–Liouville (RL) of Ω(γ, τ) of order κ becomes

$J_{\tau }^{\rho }\psi \left(\eta ,\tau \right)=\frac{1}{\mathrm{\Gamma }\left(\rho \right)}{\int }_0^{\tau }{\left(\tau -w\right)}^{\rho -1}\psi \left(\eta ,w\right)dw,(2)$

assuming that the given integral exists.

Lemma 1. For n − 1 < ρ ≤ n, q > − 1, τ ≥ 0 and λ ∈ R, we have [52]:

1. $D_{\tau }^{\rho }{\tau }^q=\frac{\mathrm{\Gamma }(q+1)}{\mathrm{\Gamma }(q-\rho +1)}{\tau }^{q-\rho }$,

2. $D_{\tau }^{\rho }\lambda =0$,

3. $D_{\tau }^{\rho }{I}_{\tau }^{\rho }\psi (\eta ,\tau )=\psi (\eta ,\tau )$,

4. $I_{\tau }^{\rho }{D}_{\tau }^{\rho }\psi (\eta ,t)=\psi (\eta ,\tau )-{\sum }_{j=0}^{n-1}{\partial }^j\psi (\eta ,0)\frac{{\tau }^j}{j!}$.

Definition 2. The function of LT ψ(η, τ) is given as [52]

$\psi \left(\eta ,s\right)={\mathcal{L}}_{\tau }\left[\psi \left(\eta ,\tau \right)\right]={\int }_0^{\infty }{e}^{-s\tau }\psi \left(\eta ,\tau \right)d\tau ,s>\mu .(3)$

The expression for the inverse of LT reads

$\psi \left(\eta ,\tau \right)={\mathcal{L}}_{\tau }^{-1}\left[\psi \left(\eta ,s\right)\right]={\int }_{l-i\infty }^{l+i\infty }{e}^{s\tau }\psi \left(\eta ,s\right)ds,l=\mathit{\text{Re}}\left(s\right)>l_0,(4)$

where l₀ is in the right half-plane of absolute convergence the Laplace integral’s.

Lemma 2. Assuming that ψ(η, τ) is a piecewise continuous function with exponential-order δ, we can obtain $\psi (\eta ,s)={\mathcal{L}}_{\tau }[\psi (\eta ,\tau )]$ by taking the LT of ψ(η, τ).

1. ${\mathcal{L}}_{\tau }[J_{\tau }^{\rho }\psi (\eta ,\tau )]=\frac{\psi (\eta ,s)}{s^{\rho }},\kappa >0$.

2. ${\mathcal{L}}_{\tau }[D_{\tau }^{\rho }\psi (\eta ,\tau )]=s^{\rho }\psi (\eta ,s)-{\sum }_{k=0}^{m-1}{s}^{\rho -k-1}{\psi }^k(\eta ,0),m-1<\rho \le m$.

3. ${\mathcal{L}}_{\tau }[D_{\tau }^{n\rho }\psi (\eta ,\tau )]=s^{n\rho }\psi (\eta ,s)-{\sum }_{k=0}^{n-1}{s}^{(n-k)\rho -1}{D}_{\tau }^{k\rho }\psi (\eta ,0),0<\rho \le 1$.

Theorem 1. Consider a function Ω(γ, τ) that is continuous and piecewise-defined over the interval I × [0, ∞) and has an exponential order of ζ. Let us define the term Ω(γ, s) as the Laplace transform of Ω(γ, τ) with respect to τ. It is worth noting that Ω(γ, s) has a fractional expansion.

$\mathrm{\Omega }\left(\gamma ,s\right)={\displaystyle \sum _{n=0}^{\infty }}\frac{f_n\left(\gamma \right)}{s^{1+n\mu }},0<\mu \le 1,\gamma \in I,s>\zeta .(5)$

Then, $f_n(\gamma )=D_{\tau }^{n\mu }\mathrm{\Omega }(\gamma ,0)$.

3 General implementation laplace residual power series method

Consider the general FPDE

$\begin{array}{cc}\hfill & D_{\tau }^{\rho }\psi \left(\eta ,\tau \right)+N\left[\psi \left(\eta ,\tau \right)\right]+A\left[\psi \left(\eta ,\tau \right)\right]=0,\text{\hspace{0.17em}where\hspace{0.17em}}0<\rho \le 1,\hfill \end{array}(6)$

subject to initial condition:

$\begin{array}{c}\hfill \psi \left(\eta ,\tau \right)=f_0\left(\eta \right).\end{array}(7)$

The function dψ(η, τ) is unknown and depends on the independent variables η and τ, where the operator A is linear and N is nonlinear.Applying LT to Eq. 6 and making use of Eq. 7 we get

$\begin{array}{c}\hfill \psi \left(\eta ,s\right)-\frac{f_0\left(\eta ,s\right)}{s}+\frac{1}{s^{\rho }}{\mathcal{L}}_{\tau }\left[N\left[{\mathcal{L}}_{\tau }^{-1}\left[\psi \left(\eta ,s\right)\right]\right]+A\left[\psi \left(\eta ,\tau \right)\right]\right]=0.\end{array}(8)$

The result of Eq. 8 is given as

$\begin{array}{c}\hfill \psi \left(\xi ,s\right)={\displaystyle \sum _{n=0}^{\infty }}\frac{f_n\left(\xi ,s\right)}{s^{n\rho +1}},\end{array}(9)$

the kth-truncate terms series are

$\begin{array}{c}\hfill \psi \left(\eta ,s\right)=\frac{f_0\left(x,s\right)}{s}+{\displaystyle \sum _{n=1}^k}\frac{f_n\left(\eta ,s\right)}{s^{n\rho +1}},\\ \hfill n=\mathrm{1,2,3,4}\cdots \end{array}(10)$

The residual Laplace function reads [53].

$\begin{array}{c}\hfill {\mathcal{L}}_{\tau }Res\left(\eta ,s\right)=\psi \left(\eta ,s\right)-\frac{f_0\left(\eta ,s\right)}{s}+\frac{1}{s^{\rho }}{\mathcal{L}}_{\tau }\left[N\left[{\mathcal{L}}_{\tau }^{-1}\left[\psi \left(\eta ,s\right)\right]\right]+A\left[\psi \left(\eta ,\tau \right)\right]\right].\end{array}(11)$

And the kth-LRFs as:

$\begin{array}{c}\hfill {\mathcal{L}}_{\tau }Re{s}_k\left(\eta ,s\right)={\psi }_k\left(\eta ,s\right)-\frac{f_0\left(\eta ,s\right)}{s}+\frac{1}{s^{\rho }}{\mathcal{L}}_{\tau }\left[N\left[{\mathcal{L}}_{\tau }^{-1}\left[{\psi }_k\left(\eta ,s\right)\right]\right]+A\left[{\psi }_k\left(\eta ,\tau \right)\right]\right].\end{array}(12)$

The few properties of the LRPSM [53], is expressed as.

• ${\mathcal{L}}_{\tau }Res(\eta ,s)=0$ and ${\lim }_{j\to \infty }{\mathcal{L}}_{\tau }Re{s}_k(\eta ,s)={\mathcal{L}}_{\tau }Re{s}_{\psi }(\eta ,s)$ for each s > 0,

• ${\lim }_{s\to \infty }s{\mathcal{L}}_{\tau }Re{s}_{\psi }(\eta ,s)=0\Rightarrow {\lim }_{s\to \infty }s{\mathcal{L}}_{\tau }Re{s}_{\psi ,k}(\eta ,s)=0$,

• ${\lim }_{s\to \infty }{s}^{k\rho +1}{\mathcal{L}}_{\tau }Re{s}_{\psi ,k}(\eta ,s)={\lim }_{s\to \infty }{s}^{k\rho +1}{\mathcal{L}}_{\tau }Re{s}_{\psi ,k}(\eta ,s)=0,0<\rho \le 1,k=\mathrm{1,2,3},\cdots$.

To investigate the coefficient f_n(η, s) and g_n(η, s), we find the solution of the following system

$\begin{array}{c}\hfill \underset{s\to \infty }{\lim }{s}^{k\rho +1}{\mathcal{L}}_{\tau }Re{s}_{\psi ,k}\left(\eta ,s\right)=0,\underset{s\to \infty }{\lim }{s}^{k\rho +1}{\mathcal{L}}_{\tau }Re{s}_{\varphi ,k}\left(\eta ,s\right)=0,k=\mathrm{1,2},\cdots .\end{array}(13)$

Finally, we apply the inverse of the LT to Eq. 9, to get the k^th analytical solution of ψ_k(η, τ) and ϕ_k(η, τ).

4 Numerical problem

Consider the coupled fractional-order Jaulent-Miodek equations:

$\begin{array}{cc}\hfill & D_{\tau }^{\rho }\varphi \left(\eta ,\tau \right)+\frac{{\partial }^3\varphi \left(\eta ,\tau \right)}{\partial {\eta }^3}+\frac{3}{2}\psi \left(\eta ,\tau \right)\frac{{\partial }^3\psi \left(\eta ,\tau \right)}{\partial {\eta }^3}+\frac{9}{2}\frac{\partial \psi \left(\eta ,\tau \right)}{\partial \eta }\frac{{\partial }^2\psi \left(\eta ,\tau \right)}{\partial {\eta }^2}-6\varphi \left(\eta ,\tau \right)\frac{\partial \varphi \left(\eta ,\tau \right)}{\partial \eta }\hfill \\ \hfill -& 6\varphi \left(\eta ,\tau \right)\psi \left(\eta ,\tau \right)\frac{\partial \psi \left(\eta ,\tau \right)}{\partial \eta }-\frac{3}{2}{\psi }^2\left(\eta ,\tau \right)\frac{\partial \varphi \left(\eta ,\tau \right)}{\partial \eta }=0,\hfill \\ \hfill & D_{\tau }^{\rho }\psi \left(\eta ,\tau \right)+\frac{{\partial }^3\psi \left(\eta ,\tau \right)}{\partial {\eta }^3}-6\frac{\partial \varphi \left(\eta ,\tau \right)}{\partial \eta }\psi \left(\eta ,\tau \right)-6\varphi \left(\eta ,\tau \right)\frac{\partial \psi \left(\eta ,\tau \right)}{\partial \eta }-\frac{15}{2}\frac{\partial \psi \left(\eta ,\tau \right)}{\partial \eta }{\psi }^2\left(\eta ,\tau \right)=0,\hfill \\ \hfill & \text{\hspace{0.17em}where\hspace{0.17em}}0<\rho \le 1,\hfill \end{array}(14)$

with the initial conditions (ICs)

$\left\{\begin{array}{cc}\hfill & \varphi \left(\eta ,0\right)=\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right),\hfill \\ \hfill & \psi \left(\eta ,0\right)=\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right).\hfill \end{array}\right.(15)$

By utilizing Eq. 14 and taking advantage of Eq. 15, we get

$\begin{array}{cc}\hfill & \varphi \left(\eta ,s\right)-\frac{\varphi \left(\eta ,0\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\varphi \left(\eta ,s\right)}{\partial {\eta }^3}+\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}\right]\hfill \\ \hfill & +\frac{9}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^2\psi \left(\eta ,s\right)}{\partial {\eta }^2}\right]-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right]=0,\hfill \\ \hfill & \psi \left(\eta ,s\right)-\frac{\varphi \left(\eta ,0\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{15}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2\right]=0.\hfill \end{array}(16)$

By applying the ICs, we get

$\begin{array}{cc}\hfill & \varphi \left(\eta ,s\right)-\frac{\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\varphi \left(\eta ,s\right)}{\partial {\eta }^3}+\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}\right]\hfill \\ \hfill & +\frac{9}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^2\psi \left(\eta ,s\right)}{\partial {\eta }^2}\right]-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right]=0,\hfill \\ \hfill & \psi \left(\eta ,s\right)-\frac{\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{15}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2\right]=0.\hfill \end{array}(17)$

The kth-truncated term series reads

$\begin{array}{cc}\hfill & \varphi \left(\eta ,s\right)=\frac{\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+{\displaystyle \sum _{n=1}^k}\frac{f_n\left(\eta ,s\right)}{s^{n\rho +1}},\hfill \\ \hfill & \psi \left(\eta ,s\right)=\frac{\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+{\displaystyle \sum _{n=1}^k}\frac{f_n\left(\eta ,s\right)}{s^{n\rho +1}},\hfill \\ \hfill & n=\mathrm{1,2,3,4}\cdots .\hfill \end{array}(18)$

The Laplace residual functions (LRFs) reads

$\begin{array}{cc}\hfill & {\mathcal{L}}_{\tau }Res\left(\eta ,s\right)=\varphi \left(\eta ,s\right)-\frac{\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\varphi \left(\eta ,s\right)}{\partial {\eta }^3}+\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}\right]\hfill \\ \hfill & +\frac{9}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^2\psi \left(\eta ,s\right)}{\partial {\eta }^2}\right]-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }\right],\hfill \\ \hfill & {\mathcal{L}}_{\tau }Res\left(\eta ,s\right)=\psi \left(\eta ,s\right)-\frac{\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3\psi \left(\eta ,s\right)}{\partial {\eta }^3}-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \varphi \left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\varphi \left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }\right]-\frac{15}{2s^{\rho }}{\mathcal{L}}_{\ell }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial \psi \left(\eta ,s\right)}{\partial \eta }{\left({\mathcal{L}}_{\tau }^{-1}\psi \left(\eta ,s\right)\right)}^2\right].\hfill \end{array}(19)$

The kth-LRFs are given by

$\begin{array}{cc}\hfill & {\mathcal{L}}_{\tau }Re{s}_k\left(\eta ,s\right)={\varphi }_k\left(\eta ,s\right)-\frac{\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3{\varphi }_k\left(\eta ,s\right)}{\partial {\eta }^3}+\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}{\psi }_k\left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^3{\psi }_k\left(\eta ,s\right)}{\partial {\eta }^3}\right]\hfill \\ \hfill & +\frac{9}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial {\psi }_k\left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}\frac{{\partial }^2{\psi }_k\left(\eta ,s\right)}{\partial {\eta }^2}\right]-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}{\varphi }_k\left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial {\varphi }_k\left(\eta ,s\right)}{\partial \eta }\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}{\varphi }_k\left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}{\psi }_k\left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial {\psi }_k\left(\eta ,s\right)}{\partial \eta }\right]-\frac{3}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\left({\mathcal{L}}_{\tau }^{-1}{\psi }_k\left(\eta ,s\right)\right)}^2{\mathcal{L}}_{\tau }^{-1}\frac{\partial {\varphi }_k\left(\eta ,s\right)}{\partial \eta }\right],\hfill \\ \hfill & {\mathcal{L}}_{\tau }Re{s}_k\left(\eta ,s\right)={\psi }_k\left(\eta ,s\right)-\frac{\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}+\frac{1}{s^{\rho }}\frac{{\partial }^3{\psi }_k\left(\eta ,s\right)}{\partial {\eta }^3}-\frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial {\varphi }_k\left(\eta ,s\right)}{\partial \eta }{\mathcal{L}}_{\tau }^{-1}{\psi }_k\left(\eta ,s\right)\right]-\hfill \\ \hfill & \frac{6}{s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}{\varphi }_k\left(\eta ,s\right){\mathcal{L}}_{\tau }^{-1}\frac{\partial {\psi }_k\left(\eta ,s\right)}{\partial \eta }\right]-\frac{15}{2s^{\rho }}{\mathcal{L}}_{\tau }\left[{\mathcal{L}}_{\tau }^{-1}\frac{\partial {\psi }_k\left(\eta ,s\right)}{\partial \eta }{\left({\mathcal{L}}_{\tau }^{-1}{\psi }_k\left(\eta ,s\right)\right)}^2\right].\hfill \end{array}(20)$

To compute f_k (η, s) and g_k (η, s) for k = 1, 2, 3, … , we can use Eq. 18 which gives the nth-truncated series, and substitute it into Eq. 20, which gives the nth-Laplace residual term. Then, we can multiply the solution of the equation by s^nρ+1 and solve the relation recursively for ${\lim }_{s\to \infty }(s^{n\rho +1}\mathcal{L}\tau Res\varphi ,n(\eta ,s))=0$ and ${\lim }_{s\to \infty }(s^{n\rho +1}\mathcal{L}\tau Res\psi ,n(\eta ,s))=0$ for n = 1, 2, 3, ⋯. The following are the first few terms:

$\begin{array}{cc}\hfill & f_0=\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right),\hfill \\ \hfill & g_0=\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right),\hfill \\ \hfill & f_1=-\frac{1}{128}{\lambda }^{5}Sec{h}^7\left(\frac{\lambda \eta }{2}\right)\left(794Sinh\left(\frac{\lambda \eta }{2}\right)-165Sinh\left(\frac{3\lambda \eta }{2}\right)+\sinh \left(\frac{5\lambda \eta }{2}\right)\right)\hfill \\ \hfill & g_1=-\frac{1}{32}{\lambda }^4\left(-189+52Cosh\left(\lambda \eta \right)+Cosh\left(2\lambda \eta \right)\right)Sec{h}^6\left(\frac{\lambda \eta }{2}\right)Tanh\left(\frac{\lambda \eta }{2}\right),\hfill \\ \hfill & f_2=\frac{{\lambda }^8}{16384}\left(10003020-11000862Cosh\left(\lambda \eta \right)+1410960Cosh\left(2\eta \lambda \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)+\hfill \\ \hfill & \frac{{\lambda }^8}{16384}\left(61341Cosh\left(3\lambda \eta \right)-4700Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right),\hfill \\ \hfill & g_2=\frac{{\lambda }^7}{8192}\left(-1713684+1217538Cosh\left(\lambda \eta \right)315984Cosh\left(2\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)\hfill \\ \hfill +& \frac{{\lambda }^7}{8192}\left(-79491Cosh\left(3\lambda \eta \right)+1348Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right),\hfill \end{array}(21)$

Now, by using the values of f_k(η), k = 1, 2, 3, … , we get

$\begin{array}{cc}\hfill & \varphi \left(\eta ,s\right)=\frac{\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}-\frac{\frac{1}{128}{\lambda }^{5}Sec{h}^7\left(\frac{\lambda \eta }{2}\right)\left(794Sinh\left(\frac{\lambda \eta }{2}\right)-165Sinh\left(\frac{3\lambda \eta }{2}\right)+\mathit{sinh}\left(\frac{5\lambda \eta }{2}\right)\right.}{s^{\kappa +1}}\hfill \\ \hfill +& \frac{\frac{{\lambda }^8}{16384}\left(10003020-11000862Cosh\left(\lambda \eta \right)+1410960Cosh\left(2\eta \lambda \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{s^{2\kappa +1}}\hfill \\ \hfill +& \frac{\frac{{\lambda }^8}{16384}\left(61341Cosh\left(3\lambda \eta \right)-4700Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{s^{2\kappa +1}}+\cdots ,\hfill \end{array}(22)$

$\begin{array}{cc}\hfill & \psi \left(\eta ,s\right)=\frac{\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)}{s}-\frac{\frac{1}{32}{\lambda }^4\left(-189+52Cosh\left(\lambda \eta \right)+Cosh\left(2\lambda \eta \right)\right)Sec{h}^6\left(\frac{\lambda \eta }{2}\right)Tanh\left(\frac{\lambda \eta }{2}\right)}{s^{\kappa +1}}\hfill \\ \hfill +& \frac{\frac{{\lambda }^7}{8192}\left(-1713684+1217538Cosh\left(\lambda \eta \right)315984Cosh\left(2\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{s^{2\kappa +1}}\hfill \\ \hfill +& \frac{\frac{{\lambda }^7}{8192}\left(-79491Cosh\left(3\lambda \eta \right)+1348Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{s^{2\kappa +1}}+\cdots .\hfill \end{array}(23)$

Applying the inverse of LT, we get

$\begin{array}{cc}\hfill & \varphi \left(\eta ,\rho \right)=\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)-\frac{\frac{1}{128}{\lambda }^{5}Sec{h}^7\left(\frac{\lambda \eta }{2}\right)\left(794Sinh\left(\frac{\lambda \eta }{2}\right)-165Sinh\left(\frac{3\lambda \eta }{2}\right)+\mathit{sinh}\left(\frac{5\lambda \eta }{2}\right)\right.}{\mathrm{\Gamma }\left(\rho +1\right)}{\tau }^{\rho }\hfill \\ \hfill +& \frac{\frac{{\lambda }^8}{16384}\left(10003020-11000862Cosh\left(\lambda \eta \right)+1410960Cosh\left(2\eta \lambda \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{\mathrm{\Gamma }\left(2\rho +1\right)}{\tau }^{2\rho }\hfill \\ \hfill +& \frac{\frac{{\lambda }^8}{16384}\left(61341Cosh\left(3\lambda \eta \right)-4700Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{\mathrm{\Gamma }\left(2\rho +1\right)}{\tau }^{2\rho }+\cdots ,\hfill \end{array}(24)$

$\begin{array}{cc}\hfill & \psi \left(\eta ,\rho \right)=\left.\lambda Sec{h}^2\left(\frac{\lambda \eta }{2}\right)\right)-\frac{\frac{1}{32}{\lambda }^4\left(-189+52Cosh\left(\lambda \eta \right)+Cosh\left(2\lambda \eta \right)\right)Sec{h}^6\left(\frac{\lambda \eta }{2}\right)Tanh\left(\frac{\lambda \eta }{2}\right)}{\mathrm{\Gamma }\left(\rho +1\right)}{\tau }^{\rho }\hfill \\ \hfill +& \frac{\frac{{\lambda }^7}{8192}\left(-1713684+1217538Cosh\left(\lambda \eta \right)315984Cosh\left(2\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{\mathrm{\Gamma }\left(2\rho +1\right)}{\tau }^{2\rho }\hfill \\ \hfill +& \frac{\frac{{\lambda }^7}{8192}\left(-79491Cosh\left(3\lambda \eta \right)+1348Cosh\left(4\lambda \eta \right)+Cosh\left(5\lambda \eta \right)\right)Sec{h}^{12}\left(\frac{\lambda \eta }{2}\right)}{\mathrm{\Gamma }\left(2\rho +1\right)}{\tau }^{2\rho }+\cdots .\hfill \end{array}(25)$

The exact solutions of ϕ(η, τ) and ψ(η, τ) are, respectively, given by

$\begin{array}{c}\hfill \varphi \left(\eta ,\tau \right)=\frac{{\lambda }^2}{8}\left(1-Sec{h}^2\left(\frac{\lambda }{2}\left(\eta +\frac{{\lambda }^2\tau }{2}\right)\right)\right),\end{array}(26)$

$\begin{array}{c}\hfill \psi \left(\eta ,\tau \right)=\lambda Sech\left(\frac{\lambda }{2}\left(\eta +\frac{{\lambda }^2\tau }{2}\right)\right).\end{array}(27)$

In the results section, we will discuss the profile of the obtained solutions as well as will make a comparison with the exact solutions and the other literature approximations.

5 Results and discussion

Figures 1, 2 represent both two- and three-dimensional graphs for the approximations (24) and (25), respectively, using the LRPSM at different values of fractional order derivative ρ. It is clear that the absolute amplitude of the approximation ϕ(η, τ) decreases with the enhancement of ρ while the amplitude of the approximation ψ(η, τ) has an opposite behavior, i.e., its amplitude increases with increasing ρ. Moreover, the two approximations are presented in Tables 1, 2 at different values of ρ and discrete values for η and τ. Furthermore, the absolute error for the approximations ϕ(η, τ) and ϕ(η, τ) at ρ = 1 as compared to the exact solutions is estimated in Tables 1, 2, respectively. After analyzing the obtained results, we can conclude that the obtained approximations using the proposed technique are closely aligned with the exact solutions, indicating a strong level of agreement. We have applied the proposed method to the fractional-order Jaulent-Miodek system to analyze it, and this is not the only example, and it can be applied to a wide range of complicated systems related to nonlinear mediums such as plasma physics and optical fibers.

FIGURE 1

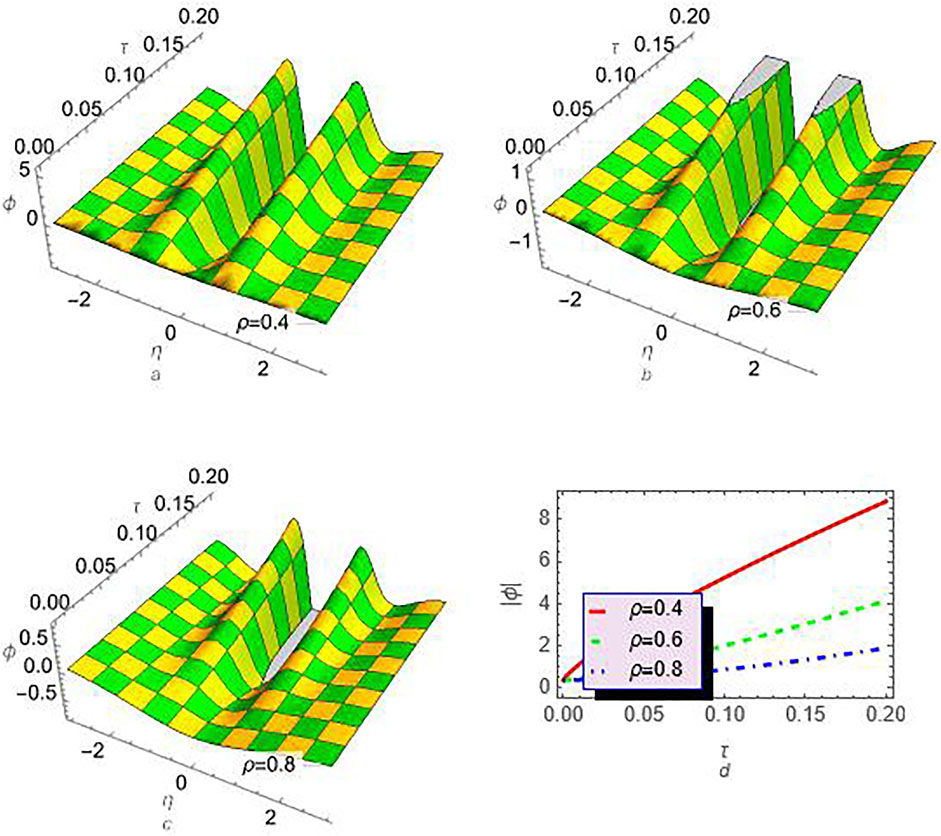
FIGURE 1. The profile of the approximation ϕ(η, τ) (24) is plotted at different values of ρ and with λ = 1: (A) ρ = 0.4, (B) ρ = 0.6, (C) ρ = 0.8., and (D) the comparison between different values of ρ at x = 0.

FIGURE 2

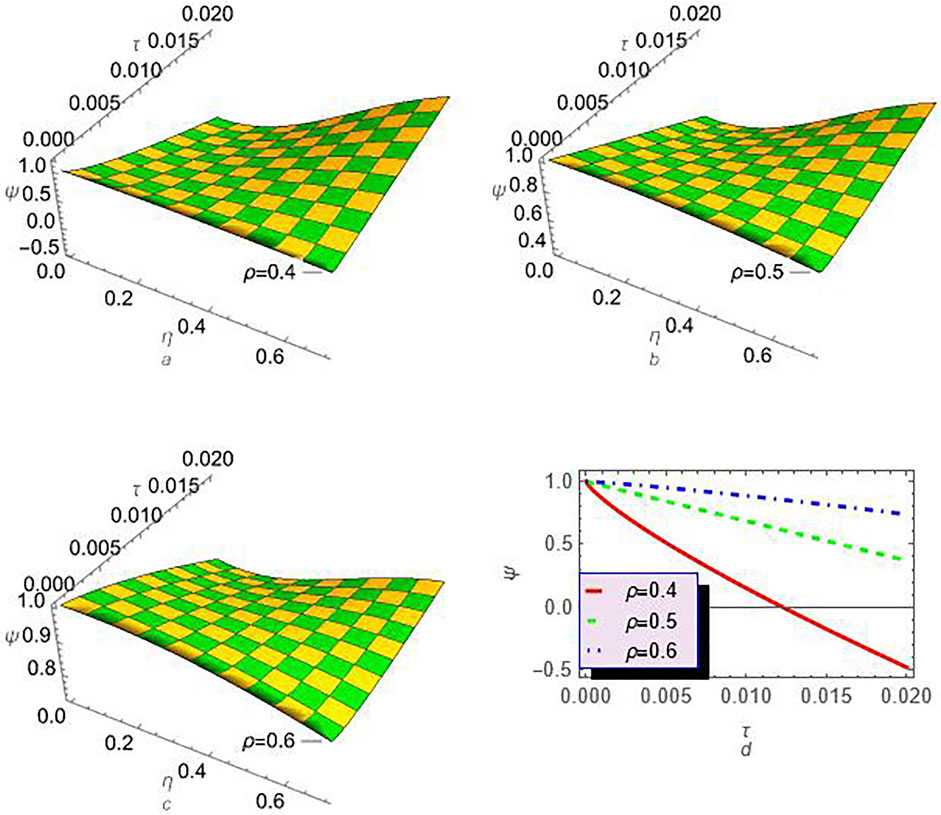
FIGURE 2. The profile of the approximation ψ(η, τ) (25) is plotted at different values of ρ and with λ = 1: (A) ρ = 0.4, (B) ρ = 0.5, (C) ρ = 0.6., and (D) the comparison between different values of ρ at x = 0.

TABLE 1

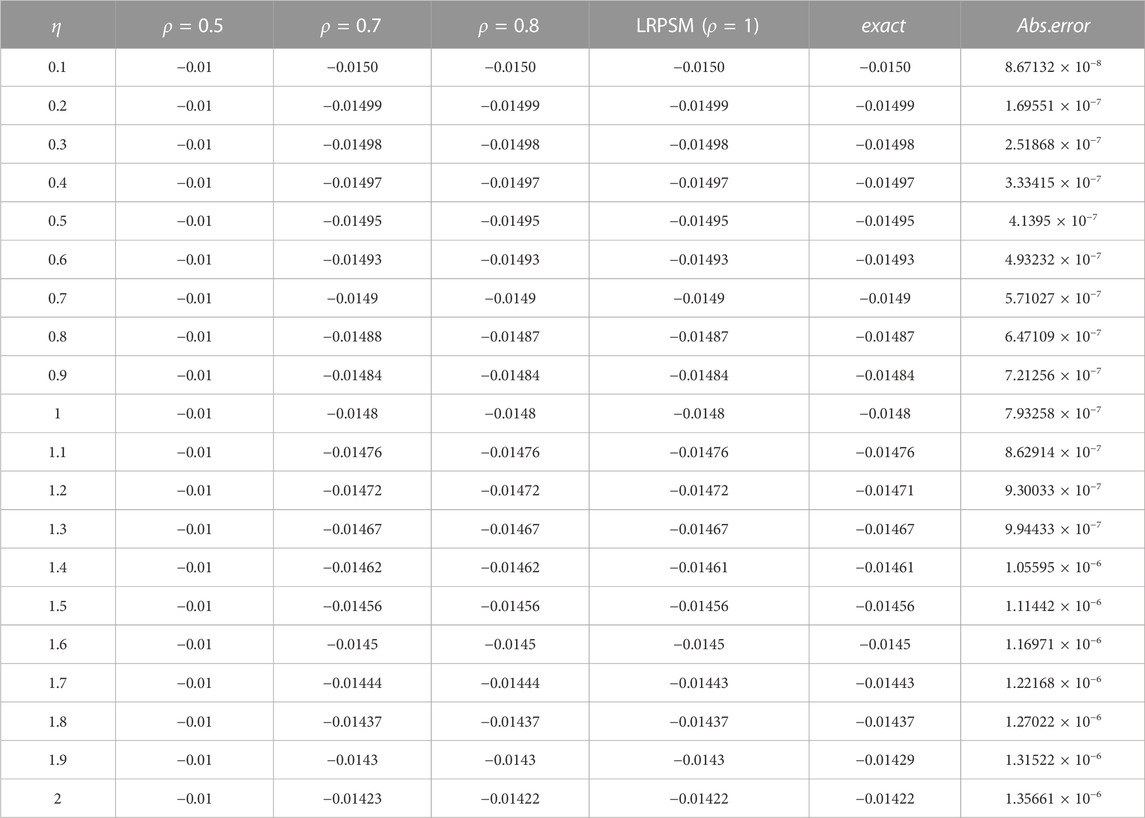
TABLE 1. The approximate solution ϕ(η, τ) (24) is considered at different values ρ and with (τ = 0.0099, λ = 0.2). Also, the absolute error of ϕ(η, τ) (24) at ρ = 1 as compared to the exact solution (26) is estimated.

TABLE 2

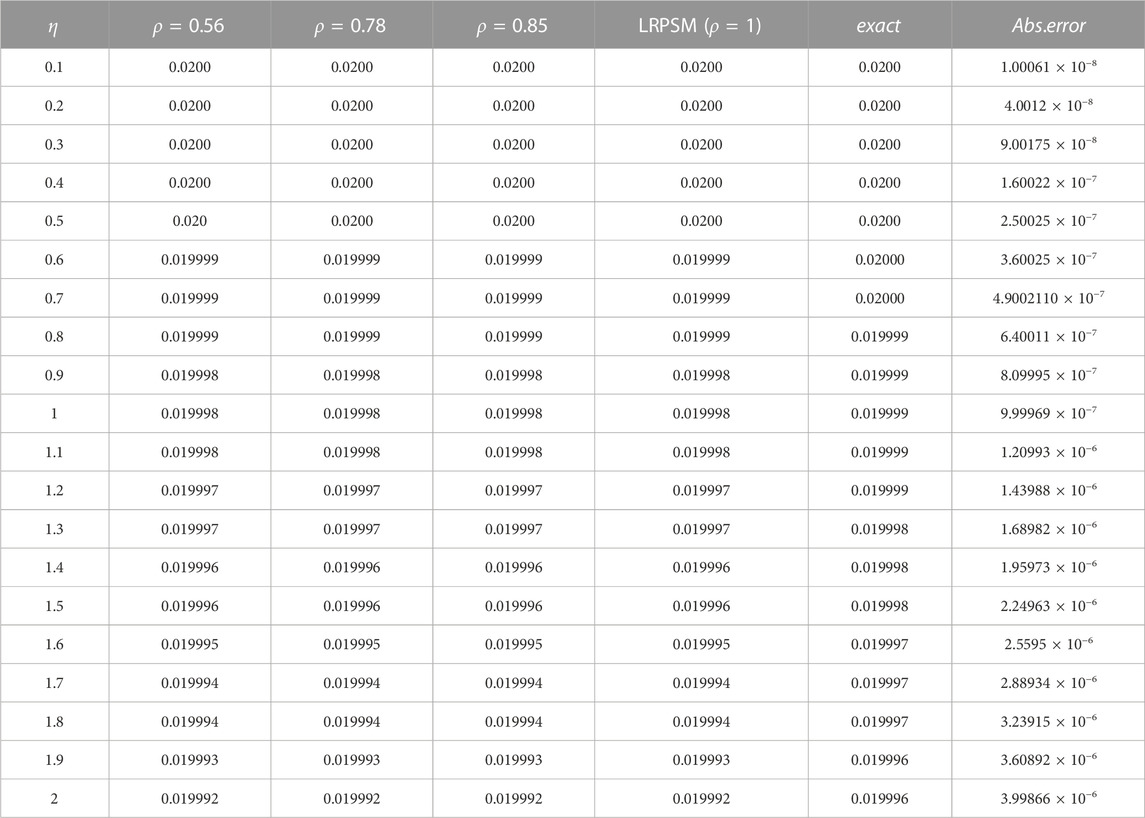
TABLE 2. The approximate solution ψ(η, τ) (25) is considered at different values ρ and with (τ = 0.0095, λ = 0.02). Also, the absolute error of ψ(η, τ) (25) at ρ = 1 as compared to the exact solution (276) is estimated.

6 Conclusion

In conclusion, the fractional-order Jaulent-Miodek system has been solved using a novel technique, called the residual power series method with the help of the Laplace transform (LT) in the sense of the Caputo operator. The LT, in conjunction with the Caputo operator, has been used to transform the fractional differential equation into an algebraic equation, which can then be solved using the residual power series method. The suggested method (Laplace residual power series method (LRPSM)) involves using a truncated power series to approximate the solution, and the residual error is minimized by adjusting the power series coefficients. The study of fractional-order systems has gained significant attention in recent years due to their ability to model complex phenomena in various fields of science and engineering. For instance, the Jaulent-Miodek system is a well-known example of such a fractional system, and its solution has been a topic of interest for many researchers. Accordingly, the LRPSM has been applied for derived high accurate approximations for the fractional-order Jaulent-Miodek system. The derived approximations have been compared with the analytical solutions. It was found great harmony and agreement with a very small absolute error between both the approximate solutions and the analytical solutions. This method has proven to be an effective tool for solving fractional-order systems, as it can provide accurate and efficient solutions. The findings of this study may be helpful in different areas of applied sciences where fractional-order systems are commonly encountered.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MH: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal). AA: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal). RS: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal). SI: validation (equal), formal analysis (equal), investigation (equal), data curation (equal). SA-T: methodology (equal), writing—review and editing (equal), visualization (equal), supervision (equal). All authors contributed to the article and approved the submitted version.

Funding

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Acknowledgments

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R378), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Oldham K, Spanier J. The fractional calculus theory and applications of differentiation and integration to arbitrary order. Elsevier (1974).

Google Scholar

2. Kumar S. A numerical study for the solution of time fractional nonlinear shallow water equation in oceans. Z Naturforsch A (2013) 68:547–53. doi:10.5560/zna.2013-0036

CrossRef Full Text | Google Scholar

3. Yao JJ, Kumar A, Kumar S. A fractional model to describe the Brownian motion of particles and its analytical solution. Adv Mech Eng (2015) 7:168781401561887. doi:10.1177/1687814015618874

CrossRef Full Text | Google Scholar

4. Dahmani Z, Anber A, Gouari Y, Kaid M, Jebril I. Extension of a method for solving nonlinear evolution equations via conformable fractional approach. In: 2021 International Conference on Information Technology, ICIT 2021 - Proceedings, 2021. p. 38–42. doi:10.1109/ICIT52682.2021.9491735

CrossRef Full Text | Google Scholar

5. Hammad MA. Conformable fractional martingales and some convergence theorems. Mathematics (2021) 6:6. doi:10.3390/math10010006

CrossRef Full Text | Google Scholar

6. Hammad MA, Alsharif S, Shmasnah A, Khalil R. Fractional Bessel differential equation and fractional Bessel functions. Ital J Pure Appl Math 47(2022):521–31.

Google Scholar

7. Hammad MA, Horani MA, Shmasenh A, Khalil R. Ruduction of order of fractional differential equations. J Math Comput Sci (2018) 8(6):683–8.

Google Scholar

8. Yasmin H, Hammad MA, Shah R, M Alotaibi B, Ismaeel SME, El-Tantawy SA. On the solutions of the fractional-order sawada–kotera–ito equation and modeling nonlinear structures in fluid mediums. Symmetry (2023) 15(3):605. doi:10.3390/sym15030605

CrossRef Full Text | Google Scholar

9. Ain QT, Anjum N, Din A, Zeb A, Djilali S, Khan ZA. On the analysis of Caputo fractional order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model. Alexandria Eng J (2022) 61(7):5123–31. doi:10.1016/j.aej.2021.10.016

CrossRef Full Text | Google Scholar

10. Anjum N, He CH, He JH. Two-scale fractal theory for the population dynamics. Fractals (2021) 29(07):2150182. doi:10.1142/s0218348x21501826

CrossRef Full Text | Google Scholar

11. Atangana A, Gomez-Aguilar J. Numerical approximation of riemann-liouville definition of fractional derivative: From riemann-liouville to atangana-baleanu. Numer Methods Partial Differ Equations (2018) 34:1502–23. doi:10.1002/num.22195

CrossRef Full Text | Google Scholar

12. Anjum N, Ain QT, Li XX. Two-scale mathematical model for tsunami wave. GEM-Int J Geomathematics (2021) 12(1):10. doi:10.1007/s13137-021-00177-z

CrossRef Full Text | Google Scholar

13. Chen H, Xiong Y, Li S, Song Z, Hu Z, Liu F. Multi-sensor data driven with PARAFAC-IPSO-PNN for identification of mechanical nonstationary multi-fault mode. Machines (2022) 10:155. doi:10.3390/machines10020155

CrossRef Full Text | Google Scholar

14. Chen H, Li S. Multi-sensor fusion by CWT-PARAFAC-IPSO-SVM for intelligent mechanical fault diagnosis. Sensors (2022) 22:3647. doi:10.3390/s22103647

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sun L, Hou J, Xing C, Fang Z. A robust hammerstein-wiener model identification method for highly nonlinear systems. Processes (2022) 10:2664. doi:10.3390/pr10122664

CrossRef Full Text | Google Scholar

16. Alharbey RA, Alrefae WR, Malaikah H, Tag-Eldin E, El-Tantawy SA. Novel approximate analytical solutions to the nonplanar modified kawahara equation and modeling nonlinear structures in electronegative plasmas. Symmetry (2023) 15:97. doi:10.3390/sym15010097

CrossRef Full Text | Google Scholar

17. Ismaeel SM, Wazwaz AM, Tag-Eldin E, El-Tantawy SA. Simulation studies on the dissipative modified kawahara solitons in a complex plasma. Symmetry (2023) 15:57. doi:10.3390/sym15010057

CrossRef Full Text | Google Scholar

18. Khattak MY, Masood W, Jahangir R, Siddiq M, Alyousef HA, El-Tantawy S. Interaction of ion-acoustic solitons for multi-dimensional Zakharov Kuznetsov equation in Van Allen radiation belts. Chaos, Solitons & Fractals (2022) 161:112265. doi:10.1016/j.chaos.2022.112265

CrossRef Full Text | Google Scholar

19. Ain QT, Anjum N, He CH. An analysis of time-fractional heat transfer problem using two-scale approach. GEM-Int J Geomathematics (2021) 12:18–0. doi:10.1007/s13137-021-00187-x

CrossRef Full Text | Google Scholar

20. Shohaib M, Masood W, Siddiq M, Alyousef HA, El-Tantawy SA. Formation of electrostatic solitary and periodic waves in dusty plasmas in the light of Voyager 1 and 2 spacecraft and Freja satellite observations. J Low Frequency Noise, Vib Active Control (2022) 41:896–909. doi:10.1177/14613484221091340

CrossRef Full Text | Google Scholar

21. Wazwaz AM, Alatawi NS, Albalawi W, El-Tantawy S. Painleve analysis for a new (3+ 1)-dimensional KP equation: Multiple-soliton and lump solutions. Europhys Lett (2022) 140:52002. doi:10.1209/0295-5075/aca49f

CrossRef Full Text | Google Scholar

22. El-Tantawy S, Bakry A, Alhejaili W, Wazwaz AM. On the analytical approximations to the nonplanar damped Kawahara equation: Cnoidal and solitary waves and their energy. Phys Fluids (2022) 34:113103. doi:10.1063/5.0119630

CrossRef Full Text | Google Scholar

23. El-Tantawy S, Salas AH, Alharthi M. On the analytical and numerical solutions of the linear damped NLSE for modeling dissipative freak waves and breathers in nonlinear and dispersive mediums: An application to a pair-ion plasma. Front Phys (2021) 9:580224. doi:10.3389/fphy.2021.580224

CrossRef Full Text | Google Scholar

24. Liu L, Li Z, Fu X, Liu X, Li Z, Zheng W. Impact of power on uneven development: Evaluating built-up area changes in chengdu based on NPP-VIIRS images (2015-2019). Land (2022) 11:489. doi:10.3390/land11040489

CrossRef Full Text | Google Scholar

25. Liu X, Tong D, Huang J, Zheng W, Kong M, Zhou G. What matters in the e-commerce era? Modelling and mapping shop rents in guangzhou, China. Land Use Policy (2022) 123:106430. doi:10.1016/j.landusepol.2022.106430

CrossRef Full Text | Google Scholar

26. Qin X, Liu Z, Liu Y, Liu S, Yang B, Yin L, et al. User OCEAN personality model construction method using a BP neural network. Electronics (2022) 11:3022. doi:10.3390/electronics11193022

CrossRef Full Text | Google Scholar

27. Guechi S, Dhayal R, Debbouche A, Malik M. Analysis and optimal control of φ-Hilfer fractional semilinear equations involving nonlocal impulsive conditions. Symmetry (2021) 13:2084. doi:10.3390/sym13112084

CrossRef Full Text | Google Scholar

28. Sultana M, Arshad U, Ali AH, Bazighifan O, Al-Moneef AA, Nonlaopon K. New efficient computations with symmetrical and dynamic analysis for solving higher-order fractional partial differential equations. Symmetry (2022) 14:1653. doi:10.3390/sym14081653

CrossRef Full Text | Google Scholar

29. Alyousef HA, Shah R, Shah NA, Chung JD, Ismaeel SM, El-Tantawy SA. The fractional analysis of a nonlinear mKdV equation with Caputo operator. Fractal Fractional (2023) 7(3):259. doi:10.3390/fractalfract7030259

CrossRef Full Text | Google Scholar

30. Albalawi W, Shah R, Shah NA, Chung JD, Ismaeel SM, El-Tantawy SA. Analyzing both fractional porous media and heat transfer equations via some novel techniques. Mathematics (2023) 11(6):1350. doi:10.3390/math11061350

CrossRef Full Text | Google Scholar

31. Atangana A, Alabaraoye E. Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv Differ Equations (2013) 2013:94–14. doi:10.1186/1687-1847-2013-94

CrossRef Full Text | Google Scholar

32. Atangana A, Kilicman A. Analytical solutions of the space-time fractional derivative of advection dispersion equation. Math Probl Eng (2013) 2013:1–9. doi:10.1155/2013/853127

CrossRef Full Text | Google Scholar

33. Naeem M, Yasmin H, Shah NA, Nonlaopon K. Investigation of fractional nonlinear regularized long-wave models via novel techniques. Symmetry (2023) 15(1):220. doi:10.3390/sym15010220

CrossRef Full Text | Google Scholar

34. Tao H, Yu-Zhu W, Yun-Sheng H. Bogoliubov quasiparticles carried by dark solitonic excitations in nonuniform Bose-Einstein condensates. Chin Phys Lett (1998) 15:550–2. doi:10.1088/0256-307x/15/8/002

CrossRef Full Text | Google Scholar

35. Ma WX, Li CX, He J. A second Wronskian formulation of the Boussinesq equation. Nonlinear Anal Theor Methods Appl (2009) 70:4245–58. doi:10.1016/j.na.2008.09.010

CrossRef Full Text | Google Scholar

36. El-Tantawy S, Shan SA, Mustafa N, Alshehri MH, Duraihem FZ, Turki NB. Homotopy perturbation and Adomian decomposition methods for modeling the nonplanar structures in a bi-ion ionospheric superthermal plasma. The Eur Phys J Plus (2021) 136:561–16. doi:10.1140/epjp/s13360-021-01494-w

CrossRef Full Text | Google Scholar

37. Kashkari BS, El-Tantawy S. Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. Eur Phys J Plus (2021) 136:121–3. doi:10.1140/epjp/s13360-021-01120-9

CrossRef Full Text | Google Scholar

38. Kashkari BS, El-Tantawy S, Salas AH, El-Sherif L. Homotopy perturbation method for studying dissipative nonplanar solitons in an electronegative complex plasma. Chaos, Solitons Fractals (2020) 130:109457. doi:10.1016/j.chaos.2019.109457

CrossRef Full Text | Google Scholar

39. Abdulaziz O, Hashim I, Momani S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys Lett A (2008) 372:451–9. doi:10.1016/j.physleta.2007.07.059

CrossRef Full Text | Google Scholar

40. Neamaty A, Agheli B, Darzi R. Variational iteration method and He’s polynomials for time-fractional partial differential equations. Prog Fractional Differ Appl (2015) 1:47–55.

Google Scholar

41. Naeem M, Yasmin H, Shah R, Shah NA, Chung JD. A comparative study of fractional partial differential equations with the help of yang transform. Symmetry (2023) 15(1):146. doi:10.3390/sym15010146

CrossRef Full Text | Google Scholar

42. Prakasha DG, Veeresha P, Rawashdeh MS. Numerical solution for (2+ 1)-dimensional time-fractional coupled Burger equations using fractional natural decomposition method. Math Methods Appl Sci (2019) 42:3409–27. doi:10.1002/mma.5533

CrossRef Full Text | Google Scholar

43. Alshehry AS, Ullah R, Shah NA, Nonlaopon K. Implementation of Yang residual power series method to solve fractional non-linear systems. AIMS Math (2023) 8:8294–309. doi:10.3934/math.2023418

CrossRef Full Text | Google Scholar

44. Daftardar-Gejji V, Bhalekar S. Solving fractional boundary value problems with Dirichlet boundary conditions using a new iterative method. Comput Math Appl (2010) 59:1801–9. doi:10.1016/j.camwa.2009.08.018

CrossRef Full Text | Google Scholar

45. Akinyemi L, Iyiola OS, Akpan U. Iterative methods for solving fourth-and sixth-order time-fractional Cahn-Hillard equation. Math Methods Appl Sci (2020) 43:mma.6173–4074. doi:10.1002/mma.6173

CrossRef Full Text | Google Scholar

46. Abdulaziz O, Hashim I, Saif A. Series solutions of time-fractional PDEs by homotopy analysis method. Differ Equations Nonlinear Mech (2009) 2008:1–16. doi:10.1155/2008/686512

CrossRef Full Text | Google Scholar

47. Rashidi M, Domairry G, Dinarvand S. The homotopy analysis method for explicit analytical solutions of Jaulent-Miodek equations. Numer Methods Partial Differ Equations: Int J (2009) 25:430–9. doi:10.1002/num.20358

CrossRef Full Text | Google Scholar

48. El-Ajou A, Al-Smadi M, Moa’ath NO, Momani S, Hadid S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng J (2020) 11:1243–54. doi:10.1016/j.asej.2020.03.016

CrossRef Full Text | Google Scholar

49. Burqan A, El-Ajou A, Saadeh R, Al-Smadi M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alexandria Eng J (2022) 61:1069–77. doi:10.1016/j.aej.2021.07.020

CrossRef Full Text | Google Scholar

50. Alderremy AA, Shah R, Iqbal N, Aly S, Nonlaopon K. Fractional series solution construction for nonlinear fractional reaction-diffusion brusselator model utilizing Laplace residual power series. Symmetry (2022) 14:1944. doi:10.3390/sym14091944

CrossRef Full Text | Google Scholar

51. Caputo M. Elasticita e Dissipazione. Bologna: Zani-Chelli (1969).

Google Scholar

52. El-Ajou A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. Eur Phys J Plus (2021) 136:229–2. doi:10.1140/epjp/s13360-020-01061-9

CrossRef Full Text | Google Scholar

53. Areshi M, Khan A, Shah R, Nonlaopon K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math (2022) 7:6936–58. doi:10.3934/math.2022385

CrossRef Full Text | Google Scholar