The new stochastic solutions for three models of non-linear Schrödinger’s equations in optical fiber communications via Itô sense

In this paper, we consider three models of non-linear Schrödinger’s equations (NLSEs) via It\^{o} sense. Specifically, we study these equations forced by multiplicative noise via the Brownian motion process. There are numerous approaches for converting non-linear partial differential equations (NPDEs) into ordinary differential equations (ODEs) to extract wave solutions. The majority of these methods are a type of symmetry reduction known as non-classical symmetry. We apply the unified technique based on symmetry reduction to produce some new optical soliton solutions for the proposed equations. The obtained stochastic solutions depict the propagation of waves in optical fiber communications. The theoretical analysis and proposed results clarify that the presented technique is sturdy, appropriate, and efficacious. Some graphs of selected solutions are also depicted with the help of the MATLAB packet program. Indeed, the structure, bandwidth, amplitude, and phase shift are controlled by the influences of physical parameters in the presence of noise term via It\^{o} sense. Our results show that the proposed technique is better suited for solving many other complex models arising in real-life problems.

1 Introduction

The subject of non-linear waves has become increasingly important in layers of the Earth’s magnetotail plasma [1], liquid crystals [2], fluid dynamics [3], gas–liquid [4], plasma [5], birefringent fibers [6], and non-linear optics [7]. These waves describe so many complex phenomena and are reflected in the form of deterministic or stochastic non-linear partial differential equations (NPDEs), such as the resonant non-linear Schrödinger equation [8], the Phi-4 equation and foam drainage equation [9], the system of ISALWs [10], and the (1 + 1)-dimensional Benjamin–Bona–Mahony and (2 + 1)-dimensional asymmetric Nizhnik–Novikov–Veselov equations [11]. The study of the nature of these equations and their applications has attracted the attention of many scientists [12–16].

A stochastic process is a mathematical representation of how a random phenomenon might appear at any given time after it first occurs [17]. The Brownian motion (Wiener process) is a physical process. It is a widely used stochastic process in a dispersive environment. This process has been used in quantum mechanics, biophysics, modeling stock markets, and chemistry [18]. The Brownian motion is the basic example of both a martingale and a Markov process [17]. The Brownian process gave rise to the study of continuous time martingales. An Itô process is a stochastic process that has been modified for Brownian motion [17]. There are numerous processes that depend on particles moving stochastically in random potentials. In particular, Brownian motion is a crucial method for stochastic non-linear partial differential equations (SNPDEs). These equations have a significant impact on a variety of natural science application domains [16, 19]. There has been recent progress in the study of stochastic stabilization and destabilization of deterministic systems [20, 21].

The dynamics of optical soliton propagation in nanofibers, quantum mechanics, magnetohydrodynamics, plasma physics, and superfluids are primarily described by the non-linear Schrödinger equation (NLSE). [22] investigated the perturbed NLSE with Kerr law non-linearity in the existence of random dispersion effect. [23] studied the stochastic higher-order dispersive NLSE and the stochastic unstable NLSE. The generalized Schrödinger-Boussinesq model, which depicts the interaction of complex short-wave and real long-wave envelopes, has been solved in new ways by [24]. This equation includes a dynamical balance between the non-linear self-interaction and linear dispersive spreading of the wave. In picosecond models, the NLSE is considered a primary model to investigate pulse propagation. This equation emerges in different physical settings in hydrodynamics and fluid mechanics, depicting the evolution of surface gravity water waves. In spite of the fact that the symmetries of the Schrödinger model are of great importance in solving several problems of quantum mechanics, it remains indubitable that they are most beneficial in constructing their exact solutions [25]. Due to the potential applications of the NLSEs, the study of soliton solutions has been performed from different perspectives [26–31]. The investigation of chiral non-linear NLSEs in two dimensions are of great importance [32]. Indeed, the NLSE has also been taken into account as a model to study the oceanic rogue waves brought on by a non-linear energy transfer in the open ocean, deterministically and stochastically [33, 34].

The stochastic effect of the NPDEs plays a key role in illustrating many vital phenomena in various fields of applied sciences, such as magneto-static spin waves, solid state physics, electromagnetic wave propagation, biology, and fluid mechanics [10, 23, 35]. In this paper, we consider three models of NLSEs forced by multiplicative noise in the Itô sense. We first consider the NLSE forced by multiplicative noise in the Itô sense, labeled as NLS⁺, and given by [36]:

$i{u}_t+u_{xx}+2\gamma \mid u{\mid }^{2}u+\sigma u{\beta }_t=0.$(1.1)

$\gamma \in \mathbb{R}-\{0\}$ is the non-linear coefficient, and u (x, t) is a complex-valued function, whereas σ is the noise strength. The term u_xx denotes the effect of dissipation, and the term ∣u∣² u denotes the non-linearity effect. The noise β_t is the time derivative of the Brownian motion β(t).

We second consider the NLSE forced by multiplicative noise in the Itô sense, labeled as NLS⁻, and given by [36]:

$i{u}_t+u_{xx}-2\gamma \mid u{\mid }^{2}u+\sigma u{\beta }_t=0.$(1.2)

We third consider the NLSE forced by multiplicative noise in Itô sense labeled as the complex cubic NLSE with δ-potential and given by [37]:

$i{u}_t+\frac{1}{2}{u}_{xx}-\alpha \delta u-\rho \mid u{\mid }^{2}u+\sigma u{\beta }_t=0.$(1.3)

$\alpha ,\delta ,\rho \in \mathbb{R}-\{0\}$; δ is the Dirac measure at the origin. The delta potential is “attractive” for α < 0 whereas “repulsive” for α > 0 [38]. [39] studied the stability of solutions for Eq. 1.3. [40] investigated the behavior of the flow through Eq. 1.3. [41] solved this model utilizing the variational method. These authors considered this equation in the absence of the noise term.

In the ongoing work, we produce some new stochastic solutions for the aforementioned three models of NLSEs forced by multiplicative noise in the Itô sense. Specifically, we apply the durable technique [42] to produce these new solutions. The proposed essential technique has various advantages, including avoiding difficult and time-consuming computations and providing precise solutions. This technique is simple, reliable, and potent. Moreover, this solver can be utilized as a box solver for a variety of other models. To the best of our knowledge, no previous study has been conducted utilizing this technique for solving these models via Brownian motion process in the Itô sense. Specifically, in a deterministic sense, most standard publications considered the same models. In contrast to these publications, we approached it in a stochastic manner. The acquired results are very beneficial in optical fiber communications, neuroscience, plasma physics, and applications of energy. Finally, the presented technique can be applied to solve many other physical systems inherently non-linear in applied science.

The rest of the article is arranged as follows: Section 2 presents the definition of the Brownian motion process; Section 3 introduces some new stochastic solutions for the types of NLSEs forced by multiplicative noise in the Itô sense. It also presents an investigation of the acquired solutions for the considered models. Indeed, we show the influence of the non-linear parameter on the behavior of solutions. Finally, Section 4 gives a conclusion remark about the acquired results.

2 Preliminaries

Here, we recall the definition of the Brownian motion process. The noise β_t is the time derivative of the Brownian motion β(t) [43]. We only consider instances of spatially continuous noise. A Brownian motion is a stochastic process that is continuous in time. The main properties of Brownian motion {β(t)}_t≥0 are

(i) β(p), where p ≥ 0 is a continuous function of p.

(ii) For q < p, β(q) − β(p) is independent of increases,

(iii) β(p) − β(q) has a normal distribution with a mean of 0 and variance p − q.

The white noise in time is the distributional derivative of the Brownian motion $\dot{\beta }={\beta }_t=\frac{d\beta }{dt}$. In the formal sense, it is delta-correlated.

$\mathbb{E}\left(\dot{\beta }\left(p\right)\dot{\beta }\left(q\right)\right)={\delta }_{p-q}.$

δ is the Dirac mass. It is common to view white noise as a mathematical idealization of events like sudden and enormous fluctuations. Furthermore, there are many research works for NPDEs via the Brownian motion process [44].

Theorem 2.1. [45] Assume that $g:\mathbb{R}\to \mathbb{R}$ is twice continuously differentiable and β_t is the Brownian motion. Then, for every t ≥ 0, a.s.,

$g\left({\beta }_t\right)=g\left({\beta }_0\right)+{\int }_0^t{g}^{\prime }\left({\beta }_s\right)d{\beta }_s+\frac{1}{2}{\int }_0^t{g}^{″}\left({\beta }_s\right)ds.$

Definition 2.1. [45] An n-dimensional process, ${\beta }_t=({\beta }_t^1,\dots ,{\beta }_t^n)$, is a standard n-dimensional Brownian motion if each ${\beta }_t^i$ is a standard Brownian motion and ${\beta }_t^i$’s are independent of each other.

The Itô differential is defined as

$dg=g\left({\beta }_{t+dt},t+dt\right)-g\left({\beta }_t,t\right).$

This is the change in g over a small period of time dt.

3 Main results and discussions

Here, we consider three types of NLSEs forced by multiplicative noise in the Itô sense. Specifically, we introduce some new stochastic solutions for these models using the unified technique [42]. We also provide the investigation of the acquired solutions for the considered models.

3.1 NLS⁺

Using the transformation [36],

$u\left(x,t\right)=q\left(\xi \right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)},\xi =x+vt,$(3.1)

where k, c, and v are constants, and we obtain

$q^{″}+2\gamma q^3-\left(k^2+c\right)q=0,v=-2k.$(3.2)

In view of the box solver [42], the solutions for Eq. 3.2 are

Family I is expressed as

$q_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{k^2+c}{\gamma }}\text{sech}\left(\pm \sqrt{k^2+c}\left(x+vt\right)\right).$(3.3)

Consequently, the solutions of Eq. 1.1 are

$u_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{k^2+c}{\gamma }}\text{sech}\left(\pm \sqrt{k^2+c}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.4)

Family II is expressed as

$q_{\mathrm{3,4}}\left(x,t\right)=\pm \sqrt{\frac{35\left(k^2+c\right)}{36\gamma }}{\text{sech}}^2\left(\pm \sqrt{\frac{5\left(k^2+c\right)}{12}}\left(x+vt\right)\right).$(3.5)

Consequently, the solutions of Eq. 1.1 are

$u_{\mathrm{3,4}}\left(x,t\right)=\pm \sqrt{\frac{35\left(k^2+c\right)}{36\gamma }}{\text{sech}}^2\left(\pm \sqrt{\frac{5\left(k^2+c\right)}{12}}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.6)

Family III is expressed as

$q_{\mathrm{5,6}}\left(x,t\right)=\pm \sqrt{\frac{k^2+c}{2\gamma }}\tanh \left(\pm \sqrt{\frac{-\left(k^2+c\right)}{2}}\left(x+vt\right)\right).$(3.7)

Consequently, the solutions of Eq. 1.1 are

$u_{\mathrm{5,6}}\left(x,t\right)=\pm \sqrt{\frac{k^2+c}{2\gamma }}\tanh \left(\pm \sqrt{\frac{-\left(k^2+c\right)}{2}}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.8)

3.2 NLS⁻

Using the transformation [36],

$u\left(x,t\right)=q\left(\xi \right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)},\xi =x+vt,$(3.9)

where k, r, and v are constants, and σ is the noise strength; we obtain

$q^{″}-2\gamma q^3-\left(k^2+c\right)q=0,v=-2k.$(3.10)

In view of the box solver [42], the solutions for Eq. 3.10 are

Family I is expressed as

${\tilde{q}}_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+c\right)}{\gamma }}\text{sech}\left(\pm \sqrt{k^2+c}\left(x+vt\right)\right).$(3.11)

Consequently, the solutions of Eq. 1.2 are

${\tilde{u}}_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+c\right)}{\gamma }}\text{sech}\left(\pm \sqrt{k^2+c}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.12)

Family II is expressed as

${\tilde{q}}_{\mathrm{3,4}}\left(x,t\right)=\pm \sqrt{\frac{-35\left(k^2+c\right)}{36\gamma }}{\text{sech}}^2\left(\pm \sqrt{\frac{5\left(k^2+c\right)}{12}}\left(x+vt\right)\right).$(3.13)

Consequently, the solutions of Eq. 1.2 are

${\tilde{u}}_{\mathrm{3,4}}\left(x,t\right)\left(x,t\right)=\pm \sqrt{\frac{-35\left(k^2+c\right)}{36\gamma }}{\text{sech}}^2\left(\pm \sqrt{\frac{5\left(k^2+c\right)}{12}}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.14)

Family III is expressed as

${\tilde{q}}_{\mathrm{5,6}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+c\right)}{2\gamma }}\tanh \left(\pm \sqrt{\frac{-\left(k^2+c\right)}{2}}\left(x+vt\right)\right).$(3.15)

Consequently, the solutions of Eq. 1.2 are

${\tilde{u}}_{\mathrm{5,6}}\left(x,t\right)\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+c\right)}{2\gamma }}\tanh \left(\pm \sqrt{\frac{-\left(k^2+c\right)}{2}}\left(x+vt\right)\right)e^{i\left(kx+ct+\sigma \beta \left(t\right)\right)}.$(3.16)

3.3 The complex cubic NLSE with δ-potential

Utilizing wave transformation [37],

$u\left(x,t\right)=q\left(\xi \right)e^{i\left(kx+ct+\kappa +\sigma \beta \left(t\right)\right)};\xi =\mu \left(x-wt\right),$(3.17)

yields w = k from the imaginary part, while the real part yields

${\mu }^2{q}^{″}-2\rho q^3-\left(k^2+2\left(c+\alpha \delta \right)\right)q=0.$(3.18)

In view of the box solver [42], the solutions for Eq. 3.18 are

Family I is expressed as

${\widehat{q}}_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+2\left(c+\alpha \delta \right)\right)}{\rho }}\text{sech}\left(\pm \sqrt{k^2+2\left(c+\alpha \delta \right)}\left(x-wt\right)\right).$(3.19)

Consequently, the solutions of Eq. 1.3 are

${\widehat{u}}_{\mathrm{1,2}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+2\left(c+\alpha \delta \right)\right)}{\rho }}\text{sech}\left(\pm \sqrt{k^2+2\left(c+\alpha \delta \right)}\times \left(x-wt\right)\right)e^{i\left(kx+ct+\kappa +\sigma \beta \left(t\right)\right)}.$(3.20)

Family II is expressed as

${\widehat{q}}_{\mathrm{3,4}}\left(x,t\right)=\pm \sqrt{\frac{-35\left(k^2+2\left(c+\alpha \delta \right)\right)}{36\rho }}{\text{sech}}^2\left(\pm \frac{\sqrt{5\left(k^2+2\left(c+\alpha \delta \right)\right)}}{2\sqrt{3}}\left(x-wt\right)\right).$(3.21)

Consequently, the solutions of Eq. 1.3

${\widehat{u}}_{\mathrm{3,4}}\left(x,t\right)\left(x,t\right)=\pm \sqrt{\frac{-35\left(k^2+2\left(c+\alpha \delta \right)\right)}{36\rho }}{\text{sech}}^2\left(\pm \frac{\sqrt{5\left(k^2+2\left(c+\alpha \delta \right)\right)}}{2\sqrt{3}}\times \left(x-wt\right)\right)e^{i\left(kx+ct+\kappa +\sigma \beta \left(t\right)\right)}.$(3.22)

Family III is expressed as

$q_{\mathrm{5,6}}\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+2\left(c+\alpha \delta \right)\right)}{2\rho }}\tanh \left(\pm \frac{\sqrt{-\left(k^2+2\left(c+\alpha \delta \right)\right)}}{2}\left(x-wt\right)\right).$(3.23)

Consequently, the solutions of Eq. 1.3 are

${\widehat{u}}_{\mathrm{5,6}}\left(x,t\right)\left(x,t\right)=\pm \sqrt{\frac{-\left(k^2+2\left(c+\alpha \delta \right)\right)}{2\rho }}\tanh \left(\pm \frac{\sqrt{-\left(k^2+2\left(c+\alpha \delta \right)\right)}}{2}\left(x-wt\right)\right)e^{i\left(kx+ct+\kappa +\sigma \beta \left(t\right)\right)}.$(3.24)

3.4 Physical interpretation

The optical solitary waves for the NLSEs through the Brownian motion process explain many interesting complex phenomena in nanofibers, condensed matter physics, Bose–Einstein condensation (BEC), liquid crystal fiber material, and plasma physics. The Brownian process is a very effective method for a variety of real random phenomena. This process is a fundamental object in martingale theory. One of the main building blocks of stochastic calculus and the key to modeling stochastic systems is Brownian motion. It can be utilized to create processes with a variety of characteristics and behaviors. This process has been applied to the study of perpetual inflation in physical cosmology and the motion of particles in a fluid.

Most standard papers considered the proposed three models of NLSEs in the deterministic case. In contrast to our approach, we consider these models in the stochastic case, namely, forced by multiplicative noise in the Itô sense. We have applied the robust approach to these models and provided some vital stochastic solutions. The main advantages of this approach over others are that it avoids laborious and complicated computations and offers a wider applicability for solving other equations of applied science. Indeed, this approach can be utilized as a box solver for scientists. To the best of our knowledge, the proposed technique for solving the stochastic NLSEs has never been used previously.

The influence of a noise parameter on the spread of soliton solutions has recently drawn increasing attention in the last decade due to its vital applications. In this regard, the results are significant in explaining the wave propagation of NLSEs emerging in various areas of physical perspective. For example, hyperbolic secant solutions arise in the profile of a laminar jet [46], whereas hyperbolic tangent solutions arise in the magnetic moment and special relativity. Moreover, the acquired solutions’ behavior, which might be soliton, explosive, rough, periodic, or dissipative, based on the physical parameters of the NLSEs, for example, at specific values of the wave number known as critical values, the behavior of a wave changes from compressive to rarefactive, and stability regions change to unstable regions [47, 48]. The instability regions have changed in the presence of wave increase extremely like huge waves [49].

It was anticipated that the presented results could be interpreted using the basics of spatiotemporal patterns, hot plasma, femtosecond pulse, and modeling of deep water [50, 51]. Figure 1 shows the behavior of solution (3.4) in the deterministic case (σ = 0) and stochastic case (σ = 2). In stochastic case, the Brownian motion function β(t) is given in more detail in [52]. This figure illustrates that with the increasing noise term σ, the effectiveness of randomization increases, as does the ability of quick wave collapse. Figures 2–5 demonstrate the influence of the intensive randomness coefficient on structure, bandwidth, amplitude, and phase shift. Figure 6 depicts enveloped waves for solution (3.4). Figures 7, 8 depict dark waves for solution (3.16). Figures 9, 10 depict bright envelope waves for solution (3.22).

FIGURE 1

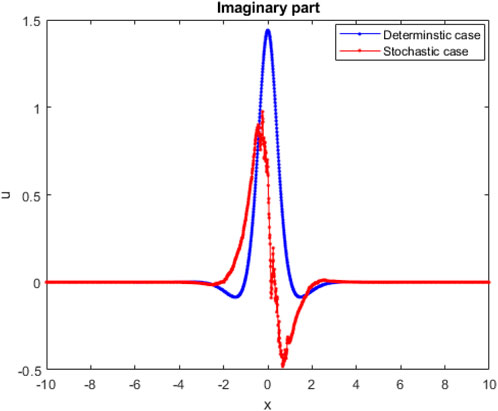
FIGURE 1. Influence of stochastic refinement on soliton solution (3.4) for k = 1.5, c = 1.9, and γ = 3.

FIGURE 2

FIGURE 2. Trajectory of solution (3.4) with t for k = 1.5, c = 1.9, and γ = 3.

FIGURE 3

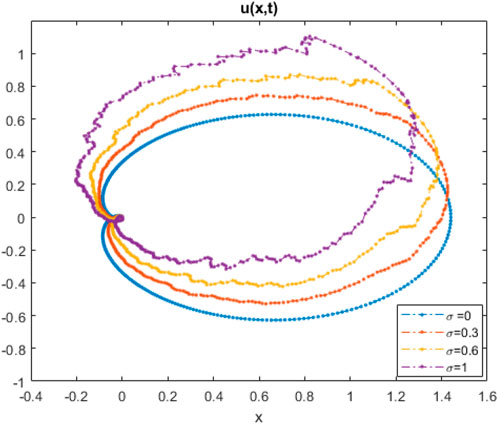
FIGURE 3. Trajectory of solution (3.4) with σ for k = 1.5, c = 1.9, and γ = 3.

FIGURE 4

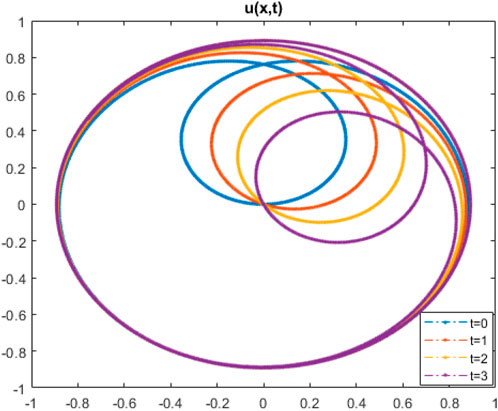
FIGURE 4. Trajectory of solution (3.16) with t for k = 1.1, c = −2.8, and γ = 1.

FIGURE 5

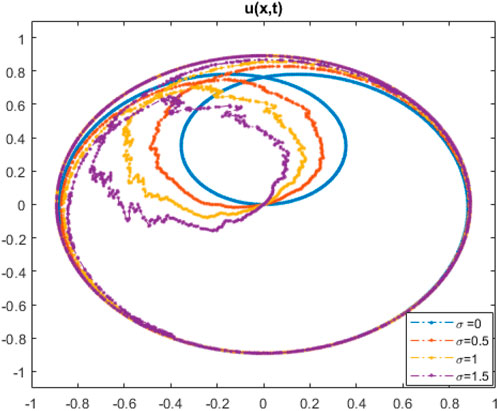
FIGURE 5. Trajectory of solution (3.16) with σ for k = 1.1, c = −2.8, and γ = 1.

FIGURE 6

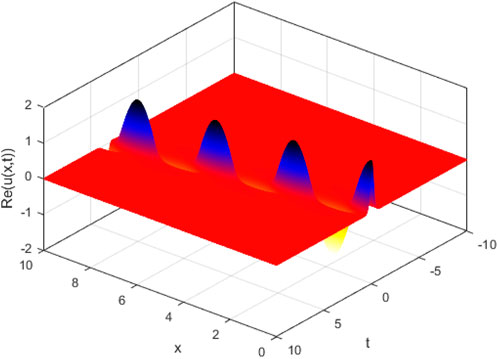
FIGURE 6. 3D plot for solution (3.4) with k = 1.5, c = 1.9, and γ = 2.

FIGURE 7

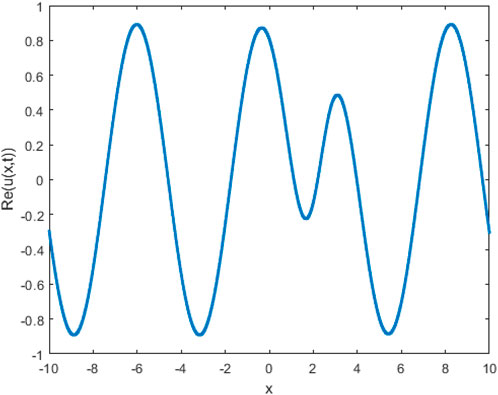
FIGURE 7. 2D plot for solution (3.16) with k = 1.1, c = −2.8, and γ = 1.

FIGURE 8

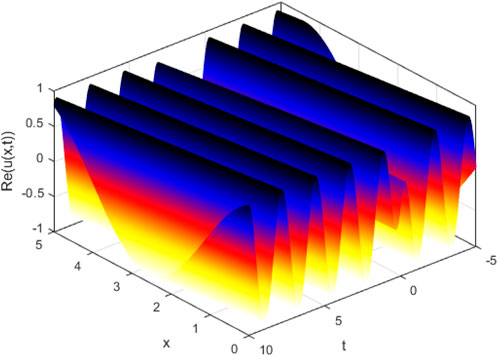
FIGURE 8. 3D plot for solution (3.16) with k = 1.1, c = −2.8, and γ = 1.

FIGURE 9

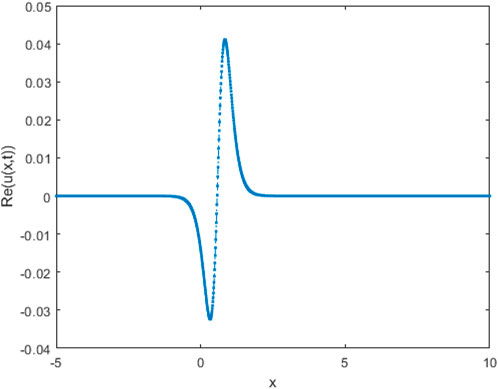
FIGURE 9. 2D plot for solution (3.22) with k = 0.6, α = 0.3, δ = 0.5, c = 2.8, and ρ = 1.

FIGURE 10

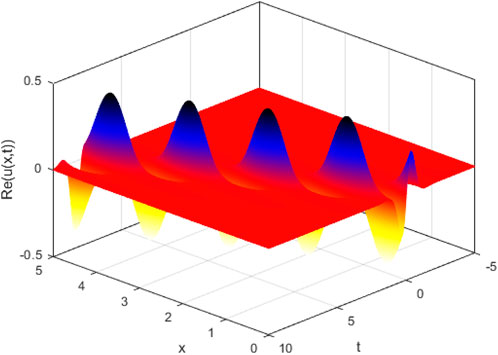
FIGURE 10. 3D plot for solution (3.22) with k = 0.6, α = 0.3, δ = 0.5, c = 2.8, and ρ = 1.

3.5 The influence of γ

Clarifying the influence of γ on the characteristics of the wave modes is one of the main goals of this work. Figure 11 shows the wave pictures of solution (3.16) for various values of γ. It is observed that an increase in beta reduces the optical periodic amplitude of solution (3.16) without any change in space or direction. Additionally, this amplitude does not change or reverse in any way.

FIGURE 11

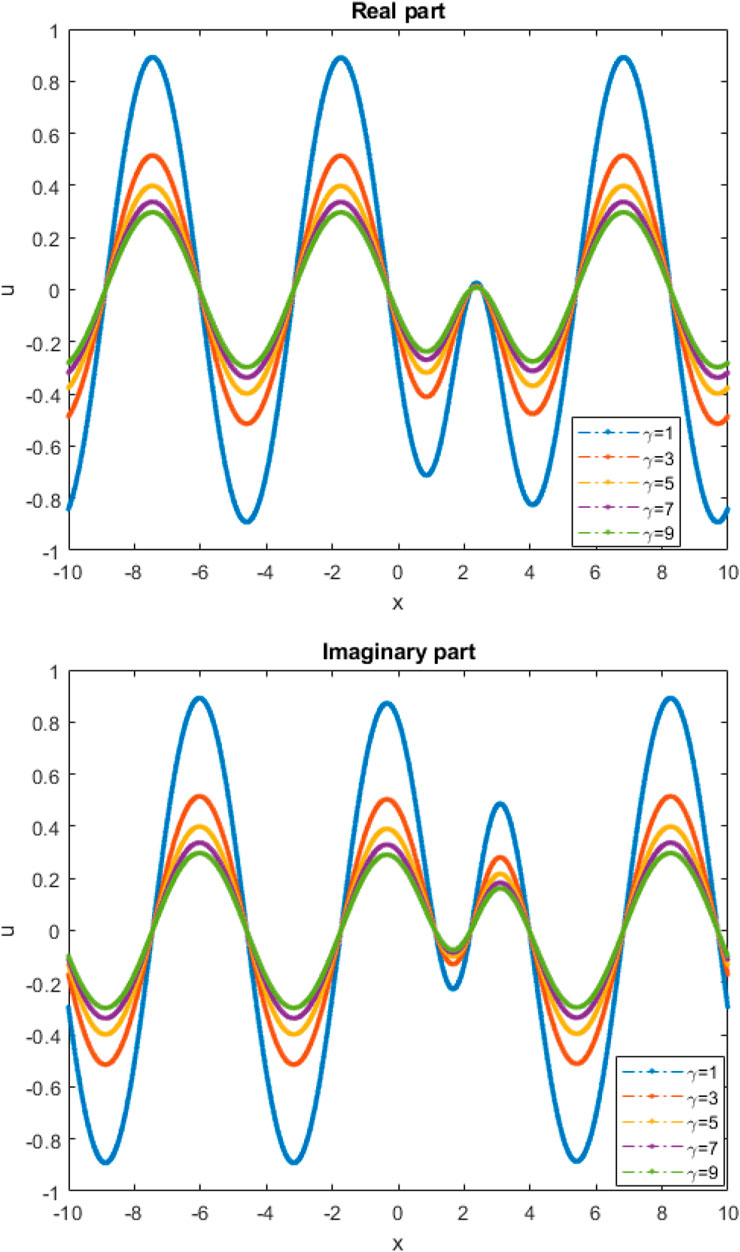
FIGURE 11. Variations of solution (3.16) with k = 1.1, c = −2.8 and γ = 1, 3, 5, 7, and 9.

4 Conclusion

The three models of stochastic NLSEs forced by multiplicative noise in the Itô sense were the subject of the current research. We have applied the consolidated and efficient technique to produce some new vital stochastic solutions for the presented three models. The suggested approach is not only simple and direct but also succinct and suitable for producing vital new results. This approach can be used as a box solver for mathematicians, physicists, and engineers. Some 2D, 3D, and trajectory graphs are plotted to show the behavior of stochastic solutions via the Brownian motion process. The proposed technique can potentially be used to implement further models that develop in the fields of natural science.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

Researchers would like to thank the Deanship of Scientific Research, Qassim University for funding publication of this project.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Abdelwahed HG, Abdelrahman MAE, Inc M, Sabry R. New soliton applications in earth’s magnetotail plasma at critical densities. Front Phys (2020) 8:181. doi:10.3389/fphy.2020.00181

CrossRef Full Text | Google Scholar

2. Ekici M, Mirzazadeh M, Sonmezoglu A, Ullah MZ, Zhou Q, Moshokoa SP, et al. Nematicons in liquid crystals by extended trial equation method. J Nonlinear Opt Phys Mater (2017) 26(1):1750005. doi:10.1142/s0218863517500059

CrossRef Full Text | Google Scholar

3. Mohamed K, Sahmim S, Abdelrahman MAE. A Predictor–corrector scheme for simulation of two-phase granular flows over a moved bed with a variable topography. Eur J Mech B/fluids (2022) 96:39–50. doi:10.1016/j.euromechflu.2022.07.001

CrossRef Full Text | Google Scholar

4. Rehman HU, Ullah N, Imran MA. Exact solutions of Kudryashov-Sinelshchikov equation using two analytical techniques. Eur Phys J Plus (2021) 136:647. doi:10.1140/epjp/s13360-021-01589-4

CrossRef Full Text | Google Scholar

5. Rehman HU, Inc M, Asjad MI, Habib A, Munir Q. New soliton solutions for the space-time fractional modified third order Korteweg-de Vries equation. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.05.032

CrossRef Full Text | Google Scholar

6. Ullah N, Asjad MI, Rehman HU, Akgül A. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers. Nonlinear Eng (2022) 11(1):80–91. doi:10.1515/nleng-2022-0010

CrossRef Full Text | Google Scholar

7. Chai HP, Tian B, Du Z. The nth-order darboux transformation, vector dark solitons and breathers for the coupled defocusing hirota system in a birefringent nonlinear fiber. Chin J Phys (2018) 56(5):2241–53. doi:10.1016/j.cjph.2018.07.013

CrossRef Full Text | Google Scholar

8. Alharbi YF, Abdelrahman MAE, Sohaly MA, Inc M. Stochastic treatment of the solutions for the resonant nonlinear Schrödinger equation with spatio-temporal dispersions and inter-modal using beta distribution. Eur Phys J Plus (2020) 135:368. doi:10.1140/epjp/s13360-020-00371-2

CrossRef Full Text | Google Scholar

9. Abdelrahman MAE, Sohaly MA. The development of the deterministic nonlinear PDEs in particle physics to stochastic case. Results Phys (2018) 9:344–50. doi:10.1016/j.rinp.2018.02.032

CrossRef Full Text | Google Scholar

10. Abdelrahman MAE, Alkhidhr HA, Amin AH, El-Shewy EK. A new structure of solutions to the system of ISALWs via stochastic sense. Results Phys (2022) 37:105473. doi:10.1016/j.rinp.2022.105473

CrossRef Full Text | Google Scholar

11. Ghanbari B, Kuo C. New exact wave solutions of the variable-coefficient (1 + 1)-dimensional Benjamin-Bona-Mahony and (2 + 1)-dimensional asymmetric Nizhnik-Novikov-Veselov equations via the generalized exponential rational function method. Eur Phys J Plus (2019) 134:334. doi:10.1140/epjp/i2019-12632-0

CrossRef Full Text | Google Scholar

12. Akram G, Rehman HU. Numerical solution of eighth order boundary value problems in reproducing Kernel space. Numer Algor (2013) 62:527–40. doi:10.1007/s11075-012-9608-4

CrossRef Full Text | Google Scholar

13. Li Z, Han T, Huang C. Bifurcation and new exact traveling wave solutions for time-space fractional Phi-4 equation. AIP Adv (2020) 10:115113. doi:10.1063/5.0029159

CrossRef Full Text | Google Scholar

14. Khodadad FS, Nazari F, Eslami M, Rezazadeh H. Soliton solutions of the conformable fractional Zakharov–Kuznetsov equation with dual-power law nonlinearity. Opt Quant Electron (2017) 49(11):384. doi:10.1007/s11082-017-1225-y

CrossRef Full Text | Google Scholar

15. Triki H, Bensalem C, Biswas A, Khan S, Zhou Q, Adesanya S, et al. Self-similar optical solitons with continuous-wave background in a quadratic-cubic non-centrosymmetric waveguide. Opt Commun (2019) 437:392–8. doi:10.1016/j.optcom.2018.12.074

CrossRef Full Text | Google Scholar

16. Mirzaee F, Rezaei S, Samadyar N. Numerical solution of two-dimensional stochastic time-fractional sine-Gordon equation on non-rectangular domains using finite difference and meshfree methods. Eng Anal Bound Elem (2021) 127:53–63. doi:10.1016/j.enganabound.2021.03.009

CrossRef Full Text | Google Scholar

17. Karatzas I, Shreve SE. Brownian motion and stochastic calculus. Berlin: Springer-Verlag (1991).

Google Scholar

18. Pishro-Nik H. Introduction to probability, statistics and random processes. Greece: Kappa Research, LLC (2014).

Google Scholar

19. Mirzaee F, Rezaei S, Samadyar N. Solving one-dimensional nonlinear stochastic sine-Gordon equation with a new meshfree technique. Int J Numer Model Electron Netw Devices Fields (2021) 34(4):e2856. doi:10.1002/jnm.2856

CrossRef Full Text | Google Scholar

20. Zhao Y, Zhu Q. Stabilization of stochastic highly nonlinear delay systems with neutral-term. IEEE Trans Automat Contr (2022) 1–8. doi:10.1109/TAC.2022.3186827

CrossRef Full Text | Google Scholar

21. Zhu Q, Huang T. Stability analysis for a class of stochastic delay nonlinear systems driven by G-Brownian motion. Syst Control Lett (2020) 140:104699. doi:10.1016/j.sysconle.2020.104699

CrossRef Full Text | Google Scholar

22. Alharbi YF, Sohaly MA, Abdelrahman MAE. Fundamental solutions to the stochastic perturbed nonlinear Schrödinger’s equation via gamma distribution. Results Phys (2021) 25:104249. doi:10.1016/j.rinp.2021.104249

CrossRef Full Text | Google Scholar

23. Alkhidhr HA, Abdelwahed HG, Abdelrahmand MAE, Alghanim S. Some solutions for a stochastic NLSE in the unstable and higher order dispersive environments. Results Phys (2022) 34:105242. doi:10.1016/j.rinp.2022.105242

CrossRef Full Text | Google Scholar

24. Kumar D, Hosseini K, Kaabar MKA, Kaplan M, Salahshour S. On some novel solution solutions to the generalized Schrödinger-Boussinesq equations for the interaction between complex short wave and real long wave envelope. J Ocean Eng Sci (2022) 7(4):353–62. doi:10.1016/j.joes.2021.09.008

CrossRef Full Text | Google Scholar

25. Magazev AA, Boldyreva MN. Schrödinger equations in electromagnetic fields: Symmetries and noncommutative integration. Symmetry (2021) 13(8):1527. doi:10.3390/sym13081527

CrossRef Full Text | Google Scholar

26. Rehman HU, Imran MA, Ullah N, Akgül A. Exact solutions of (2+1)-dimensional Schrödinger’s hyperbolic equation using different techniques. Numer Methods Partial Differential Eq (2020) 1–20. doi:10.1002/num.22644

CrossRef Full Text | Google Scholar

27. Sultan AM, Lu D, Arshad M, Rehman HU, Saleem MS. Soliton solutions of higher order dispersive cubic-quintic nonlinear Schrödinger equation and its applications, Chin. J Phys (2020) 67:405–13.

CrossRef Full Text | Google Scholar

28. Rehman HU, Seadawy AR, Younis M, Yasin S, Raza STR, Althobaiti S. Monochromatic optical beam propagation of paraxial dynamical model in Kerr media. Results Phys (2021) 31:105015. doi:10.1016/j.rinp.2021.105015

CrossRef Full Text | Google Scholar

29. Alquran M. New interesting optical solutions to the quadratic–cubic Schrodinger equation by using the Kudryashov-expansion method and the updated rational sine–cosine functions. Opt Quant Electron (2022) 54:666. doi:10.1007/s11082-022-04070-3

CrossRef Full Text | Google Scholar

30. Ali M, Alquran M, Salman OB. A variety of new periodic solutions to the damped (2+1)-dimensional Schrodinger equation via the novel modified rational sine–cosine functions and the extended tanh–coth expansion methods. Results Phys (2022) 37:105462. doi:10.1016/j.rinp.2022.105462

CrossRef Full Text | Google Scholar

31. Alquran M, Jaradat I. Multiplicative of dual-waves generated upon increasing the phase velocity parameter embedded in dual-mode Schrödinger with nonlinearity Kerr laws. Nonlinear Dyn (2019) 96:115–21. doi:10.1007/s11071-019-04778-0

CrossRef Full Text | Google Scholar

32. Rehman HU, Imran MA, Bibi M, Riaz M, Akgül A. New soliton solutions of the 2D-chiral nonlinear Schrodinger equation using two integration schemes. Math Methods Appl Sci (2021) 44(7):5663–82. doi:10.1002/mma.7140

CrossRef Full Text | Google Scholar

33. Onorato M, Osborne AR, Serio M, Bertone S. Freak waves in random oceanic sea states. Phys Rev Lett (2001) 86(25):5831–4. doi:10.1103/physrevlett.86.5831

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Osborne AR. The random and deterministic dynamics of ’rogue waves’ in unidirectional, deep-water wave trains. Mar Struct (2001) 14(3):275–93. doi:10.1016/s0951-8339(00)00064-2

CrossRef Full Text | Google Scholar

35. Abdelwahed HG, El-Shewy EK, Sabry R, Abdelrahman MAE. Characteristics of stochastic Langmuir wave structures in presence of Itô sense. Results Phys (2022) 37:105435. doi:10.1016/j.rinp.2022.105435

CrossRef Full Text | Google Scholar

36. Bhrawy AH, Abdelkawy MA, Biswas A. Optical solitons in (1+1) and (2+1) dimensions. Optik (2014) 125:1537–49. doi:10.1016/j.ijleo.2013.08.036

CrossRef Full Text | Google Scholar

37. Baskonus HM, Sulaiman TA, Bulut H, Akturk T. Investigations of dark, bright, combined dark-bright optical and other soliton solutions in the complex cubic nonlinear Schrödinger equation with δ-potential. Superlattices Microstruct (2018) 115:19–29. doi:10.1016/j.spmi.2018.01.008

CrossRef Full Text | Google Scholar

38. Segata J-I. Final state problem for the cubic nonlinear Schrödinger equation with repulsive delta potential. Commun Partial Differ (2015) 40(2):309–28. doi:10.1080/03605302.2014.930753

CrossRef Full Text | Google Scholar

39. Goodman RH, Holmes PJ, Weinstein MI. Strong NLS soliton defect interactions. Phys D (2004) 192:215–48. doi:10.1016/j.physd.2004.01.021

CrossRef Full Text | Google Scholar

40. Holmer J, Zworski M. Slow soliton interaction with delta impurities. J Mod Dyn (2007) 1:689–718. doi:10.3934/jmd.2007.1.689

CrossRef Full Text | Google Scholar

41. Fukuizumi R, Ohta M, Ozawa T. Nonlinear Shrödinger’s equation with a point defect. Ann Inst H Poincar’e Anal Non Linaire (2008) 25:837–45.

CrossRef Full Text | Google Scholar

42. Alomair RA, Hassan SZ, Abdelrahman MAE. A new structure of solutions to the coupled nonlinear Maccari’s systems in plasma physics. AIMS Math (2022) 7(5):8588–606. doi:10.3934/math.2022479

CrossRef Full Text | Google Scholar

43. Mirzaee F, Sayevand K, Rezaei S, Samadyar N. Finite difference and spline approximation for solving fractional stochastic advection-diffusion equation, Iran. J Sci Technol Trans A: Sci (2021) 45(2):607–17.

CrossRef Full Text | Google Scholar

44. Samadyar N, Ordokhani Y, Mirzaee F. The couple of Hermite-based approach and Crank-Nicolson scheme to approximate the solution of two dimensional stochastic diffusion-wave equation of fractional order. Eng Anal Bound Elem (2020) 118:285–94. doi:10.1016/j.enganabound.2020.05.010

CrossRef Full Text | Google Scholar

45. Burdzy K. Brownian motion and its applications to mathematical analysis. Cham, Switzerland: Springer (2014).

Google Scholar

46. Weisstein EW. Concise encyclopedia of mathematics. New York: CRC Press (2002).

Google Scholar

47. Ikezi H, Schwarzenegger K, Simsons AL, Ohsawa Y, Kamimura T. Nonlinear self-modulation of ion-acoustic waves. Phys Fluids (1978) 21:239. doi:10.1063/1.862198

CrossRef Full Text | Google Scholar

48. Zakharov VE, Ostrovsky LA. Modulation instability: The beginning. Phys D: Nonlinear Phenom (2009) 238(5):540–8. doi:10.1016/j.physd.2008.12.002

CrossRef Full Text | Google Scholar

49. Elwakil SA, El-hanbaly AM, Elgarayh A, El-Shewy EK, Kassem AI. Nonlinear electron-acoustic rogue waves in electron-beam plasma system with non-thermal hot electrons. Adv Space Res (2014) 54(9):1786–92. doi:10.1016/j.asr.2014.07.020

CrossRef Full Text | Google Scholar

50. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Deng Y, Yang J, Tian X, Li X, Xiao L. An experimental study on deterministic freak waves: Generation, propagation and local energy. Ocean Eng (2016) 118:83–92. doi:10.1016/j.oceaneng.2016.02.025

CrossRef Full Text | Google Scholar

52. Higham DJ. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM REVIEW (2001) 43(3):525–46. doi:10.1137/s0036144500378302

CrossRef Full Text | Google Scholar