Oblique propagation of arbitrary amplitude ion acoustic solitary waves in anisotropic electron positron ion plasma

The oblique propagation of arbitrary ion acoustic solitary waves (IASWs) in magnetized electron-positron-ion plasmas is investigated by employing Sagdeev pseudopotential approach. Ions are assumed to be adiabatic having anisotropic thermal pressure. Electrons and positrons are considered to be isothermal, following Maxwellian distribution. In terms of electrostatic potential, Sagdeev potential function is obtained and analyzed numerically in the context of relevant plasma configuration parameters. The existence region of solitary pulses is defined accurately. It is investigated how several plasma configuration parameters, such as the positron concentration, parallel, and perpendicular ion pressure affect soliton characteristics.

1 Introduction

To understand the fundamental processes in the Universe, most of the researchers have taken keen interest in the study of electron-positron-ion (e − p − i) plasma. Such plasmas are thought to have most probable appearance in the early Universe [1]. Other regions of space where such plasma is assumed to be found are atmospheres of Sun, neutron stars, active galactic nuclei and pulsar magnetosphere [2–4]. The existence of ions in astrophysical plasmas has some interior source, i.e., the processes of accretion, evaporation or seismic processes on the surface of stars might be a source of ions [5]. Moreover in matter, intense short laser pulse propagation can generate e − p − i plasma [6]. In laboratory experiments, the production of such three component plasma is possible when positron were made to probe particle transport in tokamaks, in which case the two-component electron-ion (e − i) plasma becomes a three-component e − p − i plasma [7, 8]. Clearly the wave motion behavior should be totally different in e − p − i plasma compared to the two component electron-positron (e − p) and e − i plasmas. The existence of ions is necessary for various low-frequency wave propagation which is other wise not possible in e − p plasma [9].

The ion-acoustic (IA) waves are the low frequency waves which have been investigated in both linear and non-linear limits in e − i plasma [10–13]. Several researchers have theoretically studied the linear as well as the non-linear wave phenomena in both magnetized and unmagnetized e − p − i plasmas [14–18]. The IA solitary waves (IASWs) were first investigated in unmagnetized e − p − i plasmas by Popel et al. [14] by considering one dimensional perturbations. The solution of non-linear equations was obtained in the form of a solitary pulse or soliton. It was shown that positron concentration reduces the maximum amplitude of the solitons. The study of IASWs in magnetized e − p − i plasmas was made by Mushtaq et al. [18]. In their research work, they found that the increase values of positron concentration leads to an increase in the amplitude of the solitary structure which is the opposite behavior to the previous study of these waves in an unmagnetized plasma [14].

Various techniques, such as the reductive perturbation and the Sagdeev pseudopotential are used to examine non-linear waves in plasma. Reductive perturbation technique (RPT) is applied to study small amplitude non-linear waves in unmagnetized/magnetized plasmas in the form of Korteweg-de Vries (KdV) equation, modified KdV equation and Zakharov-Kuznetsov (ZK) equation etc. For the very first time SWs in plasmas were studied by Washimi and Taniuti [19] through RPT and derived the KdV equation for IASWs [20]. However with this technique large amplitude excitations can not be studied. To overcome the limitation of small amplitude approximations, Sagdeev pseudo-potential method [21], usually called the mechanical-motion analog, provides an exact approach to the problem of finding arbitrary amplitude SWs. This method provides non-linear solutions for a plasma model which can be considered as candidates for SWs. The method basically modifies the Poisson’s equation which results into general energy equation of the form

${\left(d\varphi /dx\right)}^2+2G\left(\varphi \right)=0$

The first term of the energy equation corresponds to kinetic energy, while the second term corresponds to potential energy. The equation basically represents a moving classical particle of unit mass in one dimensional potential $G\left(\varphi \right)$ at time x. This method has been adopted for studying wave phenomena in various plasma environments like dusty plasmas, e − p − i plasmas and magnetospheric plasmas [22, 23].

The presence of an external magnetic field causes the collisionless plasma to behave in an anisotropic manner. As a result, according to the Chew-Goldberger-Low (CGL) theory, pressure differs in directions that are parallel and perpendicular to the magnetic field [24]. Therefore two equations of states are necessary to evaluate ion pressure i.e., the parallel ion pressure p_‖ and perpendicular ion pressure p_⊥ relative to the external magnetic field. Magnetic compression and expansion generated by plasma convection in some space regions might be one of the reason of this anisotropic behavior of plasma [25]. The CGL theory can be applied to such anisotropic plasma in the case when, the coupling between degree of freedom is ignorable [26]. While in the isotropic plasma the strong coupling between the degree of freedom gives rise to a simplified description due to wave-particle interaction, and hence ionic pressure can be evaluated using single equation of state [25].

IASWs in magnetized e − i plasma using Sagdeev pseudopotential method have been investigated by Chatterjee et al. [27]. They used quasi neutrality condition to discuss the existence conditions, shape and speed of SWs. The same approach was used by Sultana et al. [28] to analyze the oblique propagation of IASWs in a magnetized plasma in the presence of excess superthermal electrons. Oblique IA excitations in a magnetoplasma having κ-deformed Kaniadakis distributed electrons have also been discussed using Sagdeev’s potential approach [29]. The same technique has also been used by various researchers to discuss the SWs in e − p − i magnetoplasma [15, 30, 31].

The role of ion pressure anisotropy on the propagation characteristics of IA solitary structures in magnetized plasmas can not be ignored. Choi et al. used the Sagdeev potential approach and investigated the effect of anisotropy of ions on dust ion acoustic solitary waves (DIASWs) and double layer structures [32]. Adnan et al. [33] have examined the influence of pressure anisotropy on IASWs in superthermal magnetized e − p − i plasma by applying RPT. It has been shown that the solitary structures are affected by superthermality of electrons and positrons, pressure anisotropy of ions as well as the positron concentration. Similarly pressure anisotropy effect on DIASWs in a nonthermal plasma in Ref. [34] have also been investigated. The oblique propagation of electrostatic SWs in non-Maxwellian e − i plasma in the presences of ion pressure anisotropy with Sagdeev approach are studied in Ref. [35]. Khalid et al. [36] used Maxwellian electrons to investigate the modulation of multidimensional waves in anisotropic e − i plasma. Similarly, Alyousef et al. have also used Sagdeev approach to study the IASWs in magnetoplasma [37]. In [38] Sagdeev approach is utilized and IASWs in magnetized e-i plasma in the presences of pressure anisotropy is discussed. The results have revealed that the model supports only positive potential non-linear structures. Furthermore, the effect of relevant plasma parameters on the characteristics of IA solitary structures is evaluated. However, to the best of authors knowledge, the non-linear IASWs in the presence of pressure anisotropy in magnetized e − p − i plasma has not been explored, so for. We aim to considered anisotropic e − p − i plasma with Maxwellian electrons and positrons to study these waves.

The following is a breakdown of how this paper is structured. The model equations are presented in Section 2. The linear wave analysis is covered in Section 3. The Sagdeev pseudopotential technique is used to analyze large-amplitude electrostatic excitations in Section 4. The soliton existence domain for propagation of IASWs is discussed in Section 5. In Section 6, a parametric investigation is carried out to examine the effect of various relevant parameters on the solitary wave characteristics. The summary of the present study is given in Section 7.

2 Basic equations

The goal of the present study is to propose a model for the propagation of IASWs in a magnetized plasma made up of Maxwellian electrons (n_e) and positrons (n_p) as well as adiabatically heated ions (n_i). The ions are considered to be inertial exhibiting pressure anisotropy relative to the external magnetic field. The external magnetic field is assumed to be uniform and is taken along x-axis, i.e., B $=B_0\widehat{x}$. In the presence of ion pressure anisotropy, the ion fluid equations are,

${\partial }_t{n}_i+\nabla .\left(n_i{\mathbf{u}}_i\right)=0,(1)$

${\partial }_t{\mathbf{u}}_i+\left({\mathbf{u}}_i.\nabla \right){\mathbf{u}}_i=-\frac{Ze}{m_i}\nabla \varphi +\frac{Ze}{m_{i}c}\left({\mathbf{u}}_i\times B_0\widehat{x}\right)-\frac{1}{m_i{n}_i}\nabla .{\tilde{\mathbf{P}}}_i\text{,}(2)$

where u_i, ϕ, m_i, e and Z stand for ion fluid velocity, electrostatic potential, ion mass, magnitude of electron charge and ionic charge state (for simplicity Z = 1 is chosen), respectively. Owing to the plasma anisotropy because of a strong external magnetic field B₀, the plasma behaves differently in the parallel and perpendicular direction (s). Thereby the pressure tensor ${\widetilde{\left(\mathbf{P}\right.}}_i$) is divided into two components, i.e., the parallel $\left(p_{\Vert i}\right)$ and perpendicular $\left(p_{\perp i}\right)$ pressure components [24, 25], thus

${\tilde{\mathbf{P}}}_i=p_{\perp i}\widehat{I}+\left(p_{\Vert i}-p_{\perp i}\right)\widehat{\mathbf{x}}\widehat{\mathbf{x}}\text{,}(3)$

where $\widehat{I}$ represents unit tensor and $\widehat{x}$ shows the unit vector along B₀. The expressions for p_‖i and p_⊥i are

$p_{\Vert i}=p_{\Vert i0}{\left(\frac{n_i}{n_{i_0}}\right)}^3\text{and\hspace{0.17em}\hspace{0.17em}}{p}_{\perp i}=p_{\perp i0}\left(\frac{n_i}{n_{i0}}\right)\text{.\hspace{0.17em}}(4)$

In Eq. 4 p_‖i0 = n_i0k_BT_i‖ and p_⊥i0 = n_i0k_BT_i⊥ which are, respectively, the equilibrium values of parallel and perpendicular pressure functions, where n_i0 is the unperturbed ion density. In case of ion pressure isotropy, we have p_‖i = p_⊥i and $\nabla .{\tilde{\mathbf{P}}}_i=\nabla p_i$.

The electrons and positrons are assumed to follow the Boltzmann distributions under the electrostatic potential perturbation, and their number densities are given as

$n_e=n_{e0}\exp \left(\frac{e\varphi }{T_e}\right),(5)$

and

$n_p=n_{p0}\exp \left(\frac{-e\varphi }{T_p}\right)\text{.}(6)$

The system of evolution equations is closed via Poisson’s equation

${\nabla }^2\varphi =4\pi e\left(n_e-n_p-n_i\right)\text{,}(7)$

where T_e and T_p are, respectively, the electron and positron temperatures, while n_e0 (n_p0) is the unperturbed electron (positron) number density. We consider n_e0 = n_i0 + n_p0 at equilibrium i.e., the quasineutrality condition does hold.

2.1 Evolution equations

We have considered two dimensional perturbation in the xy-plane, by setting $\partial z=0$. Thus, the above system of equations can be written as follows;

${\partial }_t{n}_i+{\partial }_x\left(n_i{u}_{ix}\right)+{\partial }_y\left(n_i{u}_{iy}\right)=0,(8)$

${\partial }_t{u}_{ix}+\left(u_{ix}{\partial }_x+u_{iy}{\partial }_y\right)u_{ix}=-\frac{e}{m_i}{\partial }_x\varphi -\frac{3p_{\Vert i0}}{m_i{n}_{io}^3}{n}_i{\partial }_x{n}_i,(9)$

${\partial }_t{u}_{iy}+\left(u_{ix}\partial +u_{iy}{\partial }_y\right)u_{iy}=-\frac{e}{m_i}{\partial }_y\varphi +{\mathbf{\Omega }}_i{u}_{iz}-\frac{p_{\perp i0}}{m_i{n}_0{n}_i}{\partial }_y{n}_i,(10)$

${\partial }_t{u}_{iz}+\left(u_{ix}{\partial }_x+u_{iy}{\partial }_y\right)u_{iz}=-{\mathbf{\Omega }}_i{u}_{iy},(11)$

${\partial }_x^2\varphi +{\partial }_y^2\varphi =4\pi e\left(n_e-n_p-n_i\right)\text{.}(12)$

Here ${\mathbf{\Omega }}_i=\frac{e{B}_0}{m_{i}c}$ is ion gyro-frequency, while u_ix, u_iy, and u_iz denote the fluid velocity components.

2.2 Scaled evolution equations

To normalize the above system of equations, we normalize the number density variables n_s (s = e, i, p) by the unperturbed ion density n_i0, the electrostatic potential ϕ by T_eφ/e, the ion fluid velocity components by the ion acoustic speed ${(T_e/m_i)}^{\frac{1}{2}}$. The time and space variables are scaled by the inverse ion plasma frequency ${\omega }_{pi}^{-1}={\left(4\pi n_{i0}{e}^2/m_i\right)}^{\frac{1}{2}}$ and electron Debye radius ${\lambda }_{De}={\left(T_e/4\pi n_{e0}{e}^2\right)}^{\frac{1}{2}}$, respectively. The normalized equations obtained by applying the mentioned normalization to Eqs 5, 6 and to Eqs 8–12 are:

${\partial }_t{n}_i+{\partial }_x\left(n_i{u}_{ix}\right)+{\partial }_y\left(n_i{u}_{iy}\right)=0\text{,}(13)$

${\partial }_t{u}_{ix}+\left(u_{ix}{\partial }_x+u_{iy}{\partial }_y\right)u_{ix}=-{\partial }_x\phi -p_{\Vert }{n}_i{\partial }_x{n}_i\text{,}(14)$

${\partial }_t{u}_{iy}+\left(u_{ix}{\partial }_x+u_{iy}{\partial }_y\right)u_{iy}=-{\partial }_y\phi +\mathrm{\Omega }{u}_{iz}-\frac{p_{\perp }}{n_i}{\partial }_y{n}_i\text{,}(15)$

${\partial }_t{u}_{iz}+\left(u_{ix}{\partial }_x+u_{iy}{\partial }_y\right)u_{iz}=-\mathrm{\Omega }{u}_{iy}\text{,}(16)$

$n_e=\exp \left(\phi \right)\text{,}(17)$

$n_p=\exp \left(-\sigma \phi \right)\text{,}(18)$

${\partial }_x^2\phi +{\partial }_y^2\phi =\eta n_e-\gamma n_p-n_i\text{.}(19)$

Here $p_{\Vert }=\frac{3p_{\Vert i0}}{n_{io}{T}_e}$ and $p_{\perp }=\frac{p_{\perp i0}}{n_{io}{T}_e}$ represent the normalized parallel and perpendicular pressures, respectively, and are normalized by the thermal pressure in the relevant directions, with $\frac{{\mathbf{\Omega }}_i}{{\omega }_{pi}}=\mathrm{\Omega }$ being the dimensionless parameter. Furthermore, $\sigma =\frac{T_e}{T_p}$, $\eta =\frac{n_{e0}}{n_{i0}}$, and $\gamma =\frac{n_{p0}}{n_{i0}}$ signify the electron to positron temperature ratio, unperturbed electron-to-ion density ratio and positron-to-ion density ratio, respectively. The over all charge neutrality in normalized form is η − γ = 1.

3 Linear wave analysis

To derive the dispersion relation (DR), we employ Poisson’s Eq. 19 instead of plasma approximation, although plasma approximation will be used in Section 5 for non-linear analysis. The DR while using Eqs 13–19 is obtained as

${\omega }^4-\left(\frac{k^2}{\left(k^2+\eta +\gamma \sigma \right)}+k_x^2{p}_{\Vert }+k_y^2{p}_{\perp }+{\mathrm{\Omega }}^2\right){\omega }^2+\left(p_{\Vert }+\frac{1}{\left(k^2+\eta +\gamma \sigma \right)}\right){\mathrm{\Omega }}^2{k}_x^2=0\text{,}(20)$

where k_x = k cos θ and k_y = k sin θ are the wave numbers in the parallel and perpendicular directions to the magnetic field, re spectively, and $k_x^2+k_y^2=k^2$. It can be noticed from Eq. 20 that DR depends on the ion pressure anisotropy. Also, the magnetic field dependence is visible through the frequency ratio Ω. By solving Eq. 20, we get

$\begin{array}{ll}\hfill {\omega }_{\pm }^2& =\frac{1}{2}\left[\left(\frac{k^2}{\left(k^2+\eta +\gamma \sigma \right)}+k_x^2{p}_{\Vert }+k_y^2{p}_{\perp }+{\mathrm{\Omega }}^2\right)\right.\hfill \\ \hfill & \pm \left.\sqrt{{\left(\frac{k^2}{\left(k^2+\eta +\gamma \sigma \right)}+k_x^2{p}_{\Vert }+k_y^2{p}_{\perp }+{\mathrm{\Omega }}^2\right)}^2-4\left(p_{\Vert }+\frac{1}{\left(k^2+\eta +\gamma \sigma \right)}\right){\mathrm{\Omega }}^2{k}_x^2}\right]\text{.}\hfill \end{array}(21)$

Equation 21 gives two modes i.e., ω₋ and ω₊, representing slow and fast electrostatic modes, respectively. An acoustic mode is obtained by setting, k_y → 0 and k_x = k and considering k ≪ 1. Thus, the phase speed parallel to the magnetic field is calculated as

$\frac{{\omega }_{-}}{k}=\cos \theta \sqrt{\frac{1}{\left(\eta +\gamma \sigma \right)}+p_{\Vert }}\text{.}(22)$

This is called phase speed of acoustic mode which is independent of the magnetic field Ω and perpendicular pressure p_⊥. By inserting γ = 0 (i.e., in the absence of positron) and taking p_‖ = 0, Eq. 22 reduces to the result of Ref. [29]. In Figure 1 Eq. 22 has been plotted for various values of obliqueness of the propagation direction, manifested via α (= cos θ). Increasing obliqueness (lowering α) results in a decrease in wave frequency and, consequently, in the phase speed of the magnetized IAW.

FIGURE 1

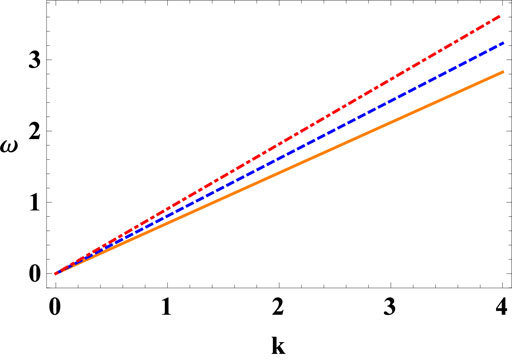
FIGURE 1. Plot of ω vs. k defined in Eq. 22 for different values of α i.e., α = 0.70 (solid curve), 0.80 (dashed curve) and 0.90 (dot-dashed curve) with p_‖ = 0.2, γ = 0.2 and σ = 0.1.

4 Arbitrary amplitude solitary wave analysis

We are now interested to investigate the existence of large amplitude solitary waves in Maxwellian plasmas with the inclusion of ion pressure anisotropy. The fluid variables in the evolution equations are considered to be transformed into a single variable via the transformation

$\xi =\alpha x+\beta y-Mt\text{,}(23)$

to a moving frame (here M is the Mach number indicating the normalized pulse propagation velocity) where the solitary pulses are stationary. The parameters $\alpha =\frac{k_x}{k}=\cos \theta$ and $\beta =\frac{k_y}{k}=$ sin θ, respectively, imply the direction cosines along x − axis and y-axis subject to the condition that α² + β² = 1. By utilizing Eq. 23 in Eqs 13–18 we obtain a set of dimensionless non-linear differential equations in the co-moving co-ordinate (ξ). The transformed equations can be expressed as,

$-M{d}_{\xi }{n}_i+\alpha d_{\xi }\left(n_i{u}_{ix}\right)+\beta d_{\xi }\left(n_i{u}_{iy}\right)=0,(24)$

$\left(-M+\alpha u_{ix}+\beta u_{iy}\right)d_{\xi }{u}_{ix}+\alpha d_{\xi }\phi +\alpha p_{\Vert }{n}_i{d}_{\xi }{n}_i=0,(25)$

$\left(-M+\alpha u_{ix}+\beta u_{iy}\right)d_{\xi }{u}_{iy}+\beta d_{\xi }\phi -\mathrm{\Omega }{u}_{iz}+\beta p_{\perp }\frac{1}{n_i}{d}_{\xi }{n}_i=0,(26)$

$\left(-M+\alpha u_{ix}+\beta u_{iy}\right)d_{\xi }{u}_{iz}+\mathrm{\Omega }{u}_{iy}=0.(27)$

By integrating Eqs 24–27 and implementing the appropriate boundary conditions, i.e., n_i → η − γ = 1, u_ix,iy → 0 and φ → 0 at ξ → ±∞, we obtain

$\alpha u_{ix}+\beta u_{iy}=\frac{M\left(n_i-1\right)}{n_i},(28)$

$u_{ix}=\frac{\alpha }{M}\left\{-\left(\eta +\frac{\gamma }{\sigma }\right)+\int n_{i}d\phi +\frac{1}{3}{p}_{\Vert }\left(n_i^3-1\right)\right\},(29)$

$u_{iy}=\frac{M}{\beta }\frac{\left(n_i-1\right)}{n_i}-\frac{{\alpha }^2}{M\beta }\left\{-\left(\eta +\frac{\gamma }{\sigma }\right)+\int n_{i}d\phi +\frac{1}{3}{p}_{\Vert }\left(n_i^3-1\right)\right\}.(30)$

The combination of Eq. 28 with Eqs 26, 27 results in

$-\frac{M}{n_i}{d}_{\xi }{u}_{iy}+\beta d_{\xi }\phi -\mathrm{\Omega }{u}_{iz}+\beta p_{\perp }\frac{1}{n_i}{d}_{\xi }{n}_i=0,(31)$

$-\frac{M}{n_i}{d}_{\xi }{u}_{iz}+\mathrm{\Omega }{u}_{iy}=0.(32)$

Substituting the value of u_iy from Eq. 30 into Eq. 32 one obtains

$d_{\xi }{u}_{iz}=\frac{n_i\mathrm{\Omega }}{\beta }\left(1-\frac{1}{n_i}\right)-\frac{{\alpha }^2\mathrm{\Omega }}{M^2\beta }\left\{-n_i\left(\eta +\frac{\gamma }{\sigma }\right)+n_i\int n_{i}d\phi +\frac{1}{3}{p}_{\Vert }{n}_i\left(n_i^3-1\right)\right\}\text{,}(33)$

Differentiating Eq. 31 with respect to ξ and using Eqs 30 and 33 and after simplification, we have

$\begin{array}{l}{d}_{\xi }\left[d_{\xi }\left(\frac{M^2}{2}{n}_i^{-2}+\frac{{\alpha }^2{p}_{\Vert }}{2}{n}_i^2+{\beta }^2{p}_{\perp }\log \left[n_i\right]+\phi \right)\right]\hfill \\ ={\mathrm{\Omega }}^2\left[n_i\left(1+\frac{{\alpha }^2}{M^2}\left(\eta +\frac{\gamma }{\sigma }\right)\right)\right.-1-\frac{{\alpha }^2}{M^2}{n}_i\int n_{i}d\phi \left.-\frac{{\alpha }^2}{3M^2}{p}_{\Vert }{n}_i\left(n_i^3-1\right)\right]\hfill \end{array}(34)$

Multiplying Eq. 34 by $d_{\xi }\left(\frac{M^2}{2}{n}_i^{-2}+\frac{{\alpha }^2{p}_{\Vert }}{2}{n}_i^2+{\beta }^2{p}_{\perp }\log [n_i]+\phi \right)$ and integrating once under the boundary conditions φ → 0 and d_ξφ → 0 at ξ → ±∞, we obtain the energy integral equation for the electrostatic potential φ, in the form

$\frac{1}{2}{\left(d_{\xi }\phi \right)}^2+\psi \left(\phi \right)=0\text{,}(35)$

where $\psi \left(\phi \right)$ is the Sagdeev pseudopotential, which is written as

$\begin{array}{ll}\hfill \psi \left(\phi \right)& ={\mathrm{\Omega }}^2\left[\phi -\left\{1+\frac{{\alpha }^2}{M^2}\left(\eta +\frac{\gamma }{\sigma }\right)+\frac{{\alpha }^2{p}_{\Vert }}{3M^2}\right\}{\delta }_1\left(\phi \right)\right.+\frac{{\alpha }^2}{2M^2}{\delta }_2\left(\phi \right)-\left\{\frac{{\alpha }^4{p}_{\Vert }}{3M^2}-\frac{{\alpha }^2{p}_{\Vert }}{3M^2}\right\}{\delta }_3\left(\phi \right)\hfill \\ \hfill & -\left\{M^2+{\alpha }^2\left(\eta +\frac{\gamma }{\sigma }\right)+\frac{{\alpha }^2{p}_{\Vert }}{3}\right\}{\delta }_4\left(\phi \right)+\frac{M^2}{2}{\delta }_5\left(\phi \right)-{\alpha }^2\phi +{\alpha }^2{\delta }_6\left(\phi \right)\hfill \\ \hfill & +\frac{{\alpha }^2{p}_{\Vert }}{3}{\delta }_7\left(\phi \right)-\left\{\frac{{\alpha }^2{p}_{\Vert }}{3}+\frac{{\alpha }^4{p}_{\Vert }}{3M^2}\left(\eta +\frac{\gamma }{\sigma }\right)+\frac{{\alpha }^4{p}_{\Vert }^2}{9M^2}\right\}{\delta }_8\left(\phi \right)+\frac{{\alpha }^4{p}_{\Vert }}{3M^2}{\delta }_9\left(\phi \right)\hfill \\ \hfill & +\frac{{\alpha }^4{p}_{\Vert }^2}{18M^2}{\delta }_{10}\left(\phi \right)-\left\{{\beta }^2{p}_{\perp }+\frac{{\alpha }^2{\beta }^2{p}_{\perp }}{M^2}\left(\eta +\frac{\gamma }{\sigma }\right)+\frac{{\alpha }^2{\beta }^2{p}_{\perp }{p}_{\Vert }}{3M^2}\right\}{\delta }_{11}\left(\phi \right)\hfill \\ \hfill & +{\beta }^2{p}_{\perp }{\delta }_{12}\left(\phi \right)+\frac{{\alpha }^2{\beta }^2{p}_{\perp }}{M^2}{\delta }_{13}\left(\phi \right)-\frac{{\alpha }^2{\beta }^2{p}_{\perp }}{M^2}{\delta }_{14}\left(\phi \right)\left.+\frac{{\alpha }^2{\beta }^2{p}_{\perp }{p}_{\Vert }}{12M^2}{\delta }_{15}\left(\phi \right)\right]\hfill \\ \hfill & \times \left[1-M^2{\delta }_{16}\left(\phi \right)\right.+{\alpha }^2{p}_{\Vert }{\delta }_{17}\left(\phi \right){\left.+{\beta }^2{p}_{\perp }{\delta }_{18}\left(\phi \right)\right]}^{-2}\text{.}\hfill \end{array}(36)$

Equation 35 is a well known pseudoenergy conservation equation of an oscillating particle of unit mass, with velocity d_ξφ and position φ in a potential well $\psi \left(\phi \right)$. In Eq. 36 the potential functions ${\delta }_1\left(\phi \right)$, ${\delta }_2\left(\phi \right)\cdot \cdot \cdot {\delta }_{18}\left(\phi \right)$ are given in the Appendix.

5 Soliton existence conditions

Solitary wave solutions are allowed by Eq. 35, if the following constraints are fulfilled [21]:

1. $\psi {\mid }_{\phi =0}=d_{\phi }\psi {\mid }_{\phi =0}=d_{\phi }\psi {\mid }_{\phi ={\phi }_m}=0$,

2. ψ(φ) < 0 at 0 < φ < φ_m,

3. $d_{\phi }^2\psi {\mid }_{\phi =0}<0$

where φ_m represents the maximum amplitude of SWs. The origin at φ = 0 defines the equilibrium state, which should represent a local maximum of the Sagdeev pseudopotential ψ(φ). From Eq. 36, it is clear that both ψ∣_φ=0 = 0 and d_φψ∣_φ=0 = 0 holds at equilibrium. We have to investigate $d_{\phi }^2\psi {\mid }_{\phi =0}<0$, from which one can specify a range of velocity values in which SWs may occur. Using the procedure explained in Refs. [28, 39], the third condition takes the form

$d_{\phi }^2\psi {\mid }_{\phi =0}={\mathrm{\Omega }}^2\frac{M^2-M_1^2}{M^2\left(M^2-M_2^2\right)}<0\text{,}(37)$

with

$M_1=\mid \alpha \mid \sqrt{\frac{1}{\eta +\gamma \sigma }+p_{\Vert }}\le 1\text{,}(38)$

and

$M_2=\sqrt{\frac{1}{\eta +\gamma \sigma }+{\alpha }^2{p}_{\Vert }+\left(1-{\alpha }^2\right)p_{\perp }}\text{,}(39)$

where M₁ and M₂ are the lower (threshold M_c) and the upper (maximum M_max) limits of the Mach number. It is clear from Eq. 38 that the lower Mach number does not depends on p_⊥, while upper Mach number does depend on both p_‖ and p_⊥. While keeping α = 1, both the equations reduce to the true acoustic phase speed of IAWs given in Eq. 22. Eq. 37 is satisfied for Mach number values in the range

$M_1<M<M_2\text{,}(40)$

i.e.,

$\alpha <\frac{M}{M_2}<1\text{.}(41)$

In other words, the inequality in Eq. 37 is valid if α = cos θ ≤ 1. Because we employed the neutrality hypothesis rather than Poisson’s equation, our results are valid in the long wavelength limit. To examine the polarity of the non-linear structures, we have to check third derivative of Sagdeev potential ψ(φ) at φ = 0 and M = M_c. If $d_{\phi }^3\psi >0$, then only positive structures (solitons or shocks) can exist otherwise, the plasma system can then support negative structures as well. It is found that,

$d_{\phi }^3\psi {|}_{\phi =0,M=M_c}=\frac{{\mathrm{\Omega }}^2\left(2\right.+\gamma \left(1+\sigma \right)\left(5+\sigma +3\gamma \left(1+\sigma \right)\right)+4{\left(\eta +\gamma \sigma \right)}^3{p}_{\Vert }}{\left(1-{\alpha }^2\right)\left(1+\left(\eta +\gamma \sigma \right)p_{\Vert }\right)\left(1+\left(\eta +\gamma \sigma \right)p_{\perp }\right)}\text{,}(42)$

which indicates that the current model can only support compressive (positive potential) solitary pulses. By keeping γ = 0 and neglecting p_‖ and p_⊥ we can retrieve the result of Ref. [29].

In order to emphasize the soliton existence region, we have plotted M₁ and M₂ in Figure 2 for different values of p_‖ = 0.20 (solid curve), 0.30 (dashed curve) and 0.40 (dot-dashed curve). Considering, p_⊥ = 0.1, α = 0.8 and σ = 0.1, it can be seen that M decreases with the increasing values of γ while both limits of Mach numbers increase with increasing values of p_‖.

FIGURE 2

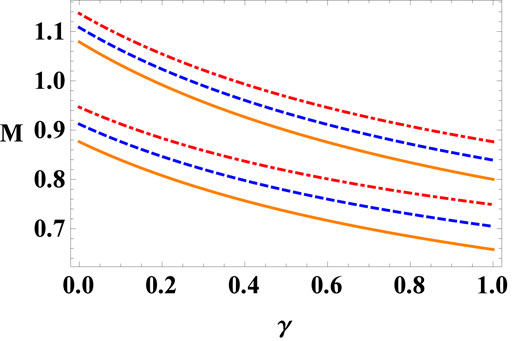
FIGURE 2. Variation of Mach number M vs. positron concentration γ for different values of p_‖ = 0.20 (solid curve), 0.30 (dashed curve) and 0.40 (dot-dashed curve) with α = 0.80, p_⊥ = 0.1 and σ = 0.1.

6 Parametric study

The Sagdeev potential $\psi \left(\phi \right)$ depends on a number of important physical parameters in addition to the electric potential φ, including the excitation speed M, positron concentration γ, electron to positron temperature ratio σ, the obliqueness of propagation (via α = cos θ), parallel ion pressure p_‖ and perpendicular ion pressure p_⊥. In this study, we specifically focus to assess the effect of γ, p_‖ and p_⊥. Therefore, the effect of these three parameters is studied on propagation characteristics of solitary structures.

In Figure 3, the variation of Sagdeev potential ψ(φ), the resulting electrostatic potential φ and the associated electric field profile E have been shown for various values of positron concentration γ, while considering other fixed values M = 0.9, σ = 0.1, Ω = 0.3, α = 0.8, p_‖ = 0.2 and p_⊥ = 0.1. We note that as γ increases, the depth and root of the Sagdeev potential increases. It is clear from Figure 3B that, the amplitude of the solitary pulse increases while its width decreases with higher value of γ. Therefore, solitary structure gets taller and narrower with the increase of positron concentration in a magnetized anisotropic e − p − i plasma. The same effect has been shown in Ref. [30] while studying these waves in unmagnetized isotropic plasma. It is clearly seen that in the absence of positron concentration γ = 0, the amplitude of solitary structure reduced as shown in Figure 3 by solid orange curve.

FIGURE 3

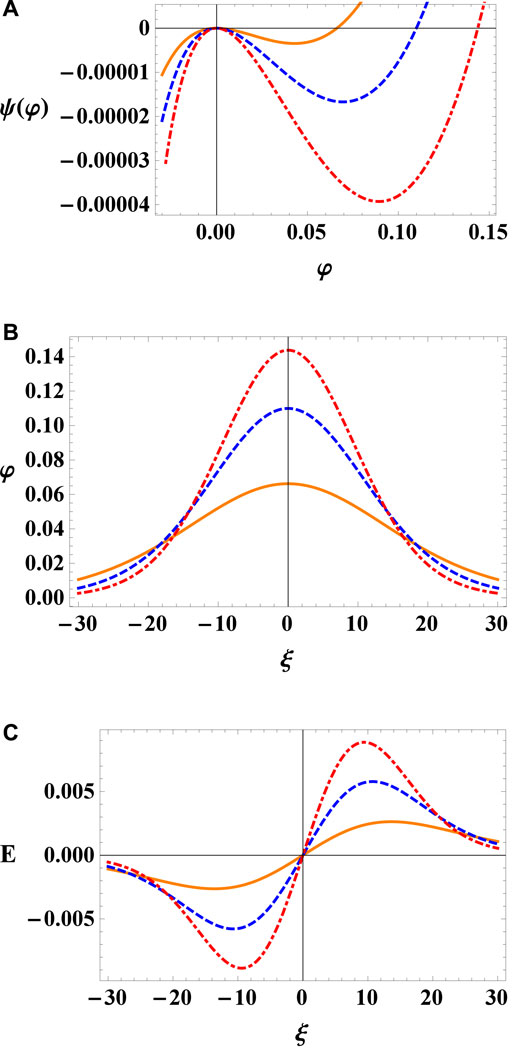
FIGURE 3. Plot of (A) Sagdeev potential ψ(φ) vs. φ, (B) Electrostatic potential φ and (C) Electric field E for different values of γ = 0.00 (solid curve), 0.05 (dashed curve) and 0.10 (dot-dashed curve) with M = 0.9, Ω = 0.3, p_‖ = 0.2, p_⊥ = 0.1, α = 0.80, and σ = 0.1.

To study the effect of pressure anisotropy on the solitary waves, we have shown the variation of Sagdeev potential ψ(φ) along with the corresponding electrostatic potential and electric field profiles with p_‖ = 0.20 (solid curve), 0.25 (dashed curve) and 0.30 (dot-dashed curve) while considering M = 0.9, γ = 0.2, Ω = 0.3, α = 0.8, σ = 0.1, and p_⊥ = 0.1in Figure 4. It has been noted that the ion parallel pressure p_‖ variation is quite effective (i.e., a minor change in p_‖ causes a significant changes in the Sagdeev potential). Thereby increasing values of p_‖ result in the decrease of depth and root of Sagdeev potential as well as in the amplitude of associated soliton pulses. The changing values of perpendicular ion pressure p_⊥ have no discernible influence on the amplitude of the solitary waves as shown in Figure 5. In Figure 6 we have considered three different cases, mainly p_‖ = p_⊥ = 0, p_‖ > p_⊥ and p_⊥ > p_‖ with fixed values of M = 0.85, γ = 0.1, Ω = 0.3, α = 0.8, σ = 0.1. For p_‖ > p_⊥ the amplitude of solitary pulse decreases while in case of p_⊥ > p_‖ the amplitude of solitary pulses is not significantly effected as compared to p_‖. In the absence of pressure anisotropy p_‖ = p_⊥ = 0, the amplitude of soliton increases as shown in Figure 6 by orange solid curve. We can infer from this Figure 6 that, in comparison to p_⊥, the characteristics of IASWs are more sensitive to variations in p_‖ as compared to p_⊥. Similar results have been demonstrated in Ref. [35].

FIGURE 4

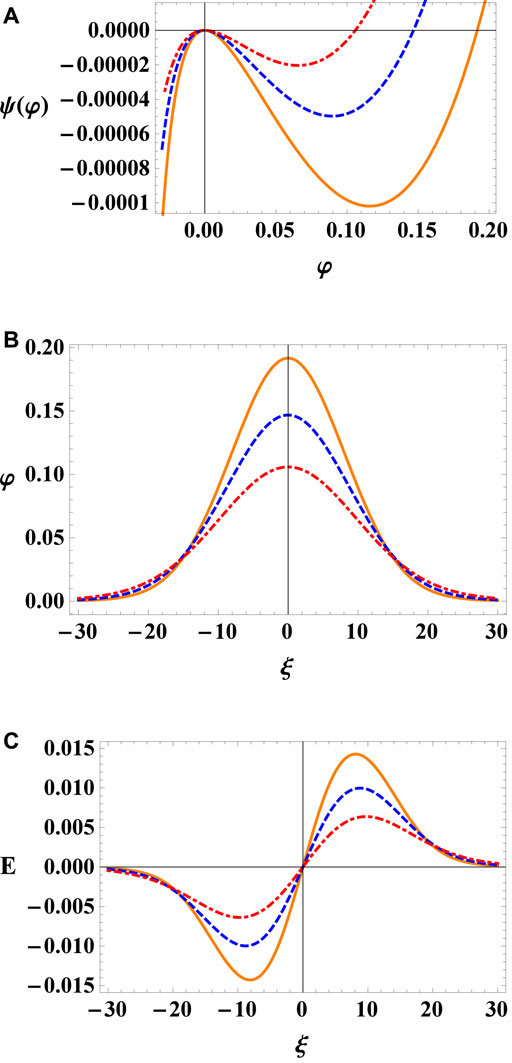
FIGURE 4. Plot of (A) Sagdeev potential ψ(φ) vs. φ, (B) Electrostatic potential φ and (C) Electric field E for different values of p_‖ = 0.20 (solid curve), 0.25 (dashed curve) and 0.30 (dot-dashed curve) with M = 0.9, Ω = 0.3, γ = 0.2, p_⊥ = 0.1, α = 0.80, and σ = 0.1.

FIGURE 5

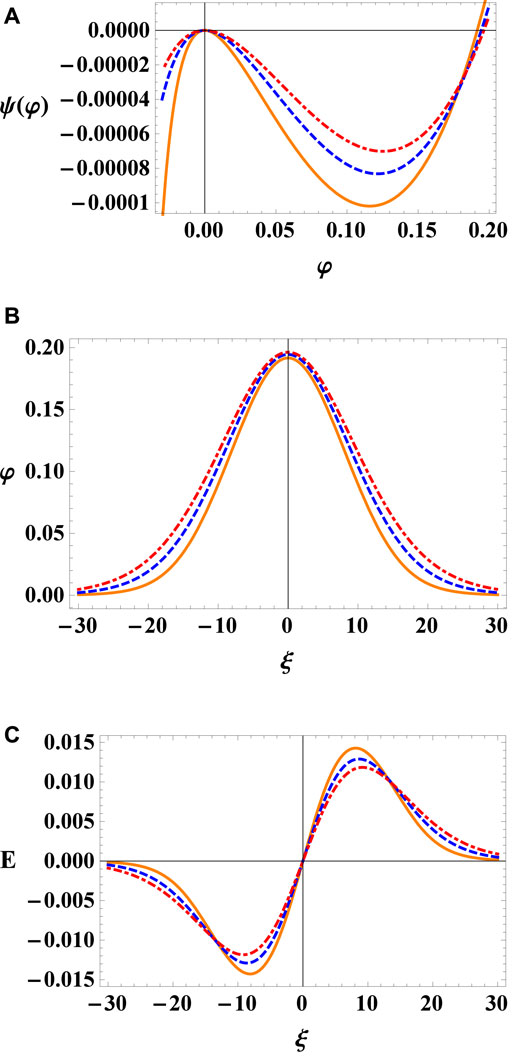
FIGURE 5. Plot of (A) Sagdeev potential ψ(φ) vs. φ, (B) Electrostatic potential φ and (C) Electric field E for different values of p_⊥ = 0.1 (solid curve), 0.5 (dashed curve) and 0.9 (dot-dashed curve) with M = 0.9, Ω = 0.3, γ = 0.2, p_‖ = 0.2, α = 0.80, and σ = 0.1.

FIGURE 6

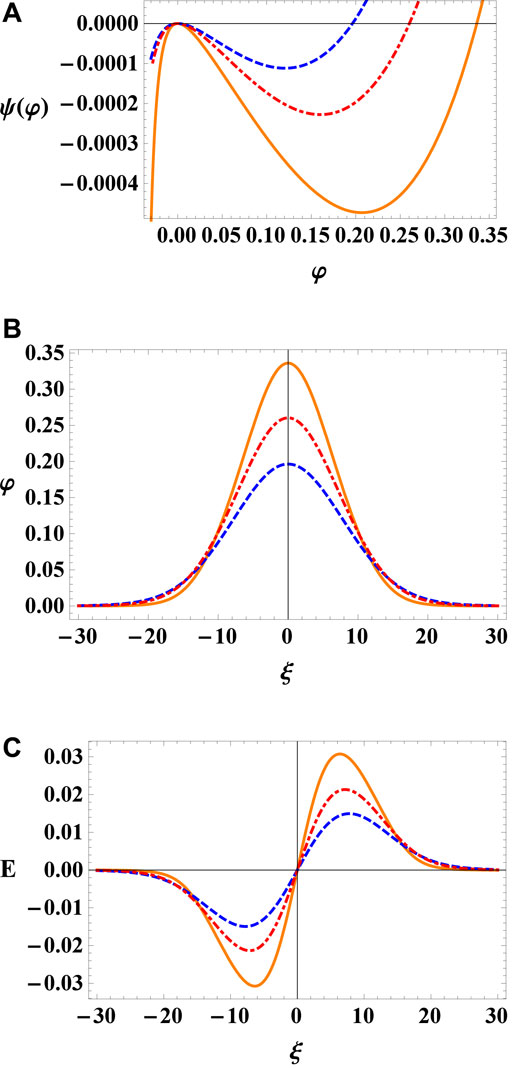
FIGURE 6. Plot of (A) Sagdeev potential ψ(φ) vs. φ, (B) Electrostatic potential φ and (C) Electric field E for different pressure anisotropy cases p_‖ = p_⊥ = 0 (solid curve), p_‖ > p_⊥ (dashed curve) and p_⊥ > p_‖ (dot-dashed curve) with M = 0.85, Ω = 0.3, γ = 0.2, α = 0.80, and σ = 0.1.

7 Conclusion

We have presented a study of the properties of arbitrary amplitude non-linear IASWs, propagating in a magnetized plasma characterized by anisotropic ions and Maxwellian distributed electrons and positrons. The linear analysis gives two modes, the IA and the ion-cyclotron modes, whose characteristics depends on the Maxwellian electron and positron and on the pressure anisotropy of the ions. We have shown that the frequency of the acoustic mode decreases with increasing obliqueness of propagation. In the non-linear regime, Sagdeev approach is used for the investigation of the properties of arbitrary amplitude IASWs. A parametric analysis was carried out for studying the characteristics of these waves, which can be summarize as follows.

• The amplitude of solitary pulses increases with rising values of positron concentration γ.

• The amplitude of solitary pulses reduced with higher values of parallel ion pressure p_‖.

• Finally, we found that the characteristics of IASWs are more sensitive to the parallel ion pressure p_‖ than perpendicular ion pressure p_⊥.

These results are general and might be applied to astrophysical plasma environments like the polar cups region of pulsars and near active galactic nuclei, where magnetized e − p − i plasma and ions with aniotropic pressure can exist.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rees MJ, Gibbons GW, Hawking SW, Siklas S. The very early universe. Cambridge: Cambridge University Press (1983).

Google Scholar

2. Kozlovsky B, Murphy RJ, Share GH. Positron-emitter production in solar flares from 3He reactions. J Astrophy (2004) 604:892–9. doi:10.1086/381969

CrossRef Full Text | Google Scholar

3. Miller H, Witta P. Active galactic nuclei. Berlin: Springer-Verlag (1987).

Google Scholar

4. Michel FC. Theory of pulsar magnetospheres. Rev Mod Phys (1982) 54:1–66. doi:10.1103/revmodphys.54.1

CrossRef Full Text | Google Scholar

5. Zeba I, Moslem WM, Shukla PK. Ion solitary pulses in warm plasmas with ultrarelativistic degenerate electrons and positrons. J Astrophy (2012) 750:72. doi:10.1088/0004-637x/750/1/72

CrossRef Full Text | Google Scholar

6. Berezhiani VI, Mahajan SM. Large amplitude localized structures in a relativistic electron-positron ion plasma. Phys Rev Lett (1994) 73:1110–3. doi:10.1103/physrevlett.73.1110

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Surko CM, Murphy TJ. Use of the positron as a plasma particle. Phys Fluids (1990) 2:1372–5. doi:10.1063/1.859558

CrossRef Full Text | Google Scholar

8. Surko CM, Leventhal M, Crane WS, Passner A, Wysocki F, Murphy TJ, et al. Use of positrons to study transport in tokamak plasmas (invited). Rev Sci Instrum (1986) 57:1862–7. doi:10.1063/1.1139154

CrossRef Full Text | Google Scholar

9. Pakzad HR. Ion acoustic solitary waves in plasma with nonthermal electron and positron. Phys Lett A (2009) 373:847–50. doi:10.1016/j.physleta.2008.12.066

CrossRef Full Text | Google Scholar

10. Krall NA, Trivelpiece AW. Principles of plasm physics. USA: McGraw-Hill (1973).

Google Scholar

11. Hasegawa A. Plasma instabilities and nonlinear effects. New York: Springer (1975).

Google Scholar

12. Davidson RC. Methods in nonlinear plasma theory. New York: Academic (1972).

Google Scholar

13. Nicolson DR. Introduction to plasma theory. New York: Wiley (1983).

Google Scholar

14. Popel SI, Vladimirov SV, Shukla PK. Ion-acoustic solitons in electron–positron–ion plasmas. Phys Plasmas (1995) 2:716–9. doi:10.1063/1.871422

CrossRef Full Text | Google Scholar

15. Alinejad H, Mamun AA. Oblique propagation of electrostatic waves in a magnetized electron-positron-ion plasma with superthermal electrons. Phys Plasmas (2011) 18:112103. doi:10.1063/1.3656982

CrossRef Full Text | Google Scholar

16. Ullah G, Saleem M, Khan M, Khalid M, Rahman A, Nabi S. Ion acoustic solitary waves in magnetized electron–positron–ion plasmas with Tsallis distributed electrons. Contrib Plasma Phys (2020) 60:e202000068. doi:10.1002/ctpp.202000068

CrossRef Full Text | Google Scholar

17. Nejoh YN. The effect of the ion temperature on large amplitude ion-acoustic waves in an electron–positron–ion plasma. Phys Plasmas (1996) 3:1447–51. doi:10.1063/1.871734

CrossRef Full Text | Google Scholar

18. Mahmood S, Mushtaq A, Saleem H. Ion acoustic solitary wave in homogeneous magnetized electron-positron-ion plasmas. New J Phys (2003) 5:28. doi:10.1088/1367-2630/5/1/328

CrossRef Full Text | Google Scholar

19. Washimi H, Taniuti T. Propagation of ion-acoustic solitary waves of small amplitude. Phys Rev Lett (1966) 17:996–8. doi:10.1103/physrevlett.17.996

CrossRef Full Text | Google Scholar

20. Kazeminezhad F, Kuhn S, Tavakoli A. Vlasov model using kinetic phase point trajectories. Phys Rev E (2003) 67:026704. doi:10.1103/physreve.67.026704

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sagdeev RZ. Cooperative phenomena and shock waves in collisionless plasmas. Rev Plasma Phys (1966) 4:23.

Google Scholar

22. Berthomier M, Pottelette R, Malingre M. Solitary waves and weak double layers in a two-electron temperature auroral plasma. J Geophys Res Space Phys (1998) 103:4261–70. doi:10.1029/97ja00338

CrossRef Full Text | Google Scholar

23. Verheest F. Nonlinear dust-acoustic waves in multispecies dusty plasmas. Planet Space Sci (1992) 40:1–6. doi:10.1016/0032-0633(92)90145-e

CrossRef Full Text | Google Scholar

24. Chew GF, Goldberger ML, Low FE. The Boltzmann equation an d the one-fluid hydromagnetic equations in the absence of particle collisions. Proc R Soc London, Ser A (1956) 236:112–8.

Google Scholar

25. Denton RE, Anderson BJ, Gary SP, Fuselier SA. Bounded anisotropy fluid model for ion temperatures. J Geophys Res (1994) 99:11225–41. doi:10.1029/94ja00272

CrossRef Full Text | Google Scholar

26. Parks GK. Physics of space plasmas. USA: Perseus (1991).

Google Scholar

27. Chatterjee P, Saha T, Ryu CM. Obliquely propagating ion acoustic solitary waves and double layers in a magnetized dusty plasma with anisotropic ion pressure. Phys Plasmas (2008) 15:123702. doi:10.1063/1.2996114

CrossRef Full Text | Google Scholar

28. Sultana S, Kourakis I, Saini NS, Hellberg MA. Oblique electrostatic excitations in a magnetized plasma in the presence of excess superthermal electrons. Phys Plasmas (2010) 17:032310. doi:10.1063/1.3322895

CrossRef Full Text | Google Scholar

29. Khalid M, El-Tantawy SA, Rahman AU. Oblique ion acoustic excitations in a magnetoplasma having κ-deformed Kaniadakis distributed electrons. Astrophys Space Sci (2020) 365:1–9.

CrossRef Full Text | Google Scholar

30. El-Awady EI, El-Tantawy SA, Moslem WM, Shukla PK. Electron–positron–ion plasma with kappa distribution: Ion acoustic soliton propagation. Phys Lett A (2010) 374:3216–9. doi:10.1016/j.physleta.2010.05.053

CrossRef Full Text | Google Scholar

31. Mahmood S, Akhtar N. Ion acoustic solitary waves with adiabatic ions in magnetized electron-positron-ion plasmas. Eur Phys J D (2008) 49:217–22. doi:10.1140/epjd/e2008-00165-4

CrossRef Full Text | Google Scholar

32. Choi CR, Ryu CM, Lee DY, Lee NC, Kim YH. Dust ion acoustic solitary waves in a magnetized dusty plasma with anisotropic ion pressure. Phys Lett A (2007) 364:297–303. doi:10.1016/j.physleta.2006.12.014

CrossRef Full Text | Google Scholar

33. Adnan M, Williams G, Qamar A, Mahmood S, Kourakis I. Pressure anisotropy effects on nonlinear electrostatic excitations in magnetized electron-positron-ion plasmas. Eur Phys J D (2014) 68:247–15. doi:10.1140/epjd/e2014-50384-y

CrossRef Full Text | Google Scholar

34. Adnan M, Mahmood S, Qamar A. Effect of anisotropic ion pressure on solitary waves in magnetized dusty plasmas. Contrib Plasma Phys (2014) 54:724–34. doi:10.1002/ctpp.201300061

CrossRef Full Text | Google Scholar

35. Adnan M, Qamar A, Mahmood S, Kourakis I. On the characteristics of obliquely propagating electrostatic structures in non-Maxwellian plasmas in the presence of ion pressure anisotropy. Phys Plasmas (2017) 24:032114. doi:10.1063/1.4978613

CrossRef Full Text | Google Scholar

36. Khalid M, Hadi F, Rahman A. Modulation of multi-dimensional waves in anisotropic magnetized plasma. Eur Phys J Plus (2021) 136:1061. doi:10.1140/epjp/s13360-021-02063-x

CrossRef Full Text | Google Scholar

37. Alyousef H, Khalid M, Rahman A, Tantawy SA. Large amplitude electrostatic (Un)modulated excitations in anisotropic magnetoplasmas: Solitons and Freak waves. Braz J Phys (2022) 52:202. doi:10.1007/s13538-022-01199-0

CrossRef Full Text | Google Scholar

38. Khalid M. Oblique ion-acoustic solitary waves in anisotropic plasma with Tsallis distribution. EPL (2022) 138:53003. doi:10.1209/0295-5075/ac6a08

CrossRef Full Text | Google Scholar

39. Singh SV, Devanandhan S, Lakhina GS, Bharuthram R. Effect of ion temperature on ion-acoustic solitary waves in a magnetized plasma in presence of superthermal electrons. Phys Plasmas (2013) 20:012306. doi:10.1063/1.4776710

CrossRef Full Text | Google Scholar

Appendix: Potential functions used in Eq. 36 are given as

${\delta }_1\left(\phi \right)=\eta e^{\phi }+\frac{\gamma }{\sigma }{e}^{-\sigma \phi }-\left(\eta +\frac{\gamma }{\sigma }\right)$

${\delta }_2\left(\phi \right)={\left(\eta e^{\phi }+\frac{\gamma }{\sigma }{e}^{-\sigma \phi }\right)}^2-{\left(\eta +\frac{\gamma }{\sigma }\right)}^2$

$\begin{array}{ll}\hfill {\delta }_3\left(\phi \right)& =\left(\begin{array}{c}\hfill \frac{{\eta }^4}{4}{e}^{4\phi }-\frac{4{\eta }^3\gamma }{3-\sigma }{e}^{\left(3-\sigma \right)\phi }+\frac{6{\eta }^2{\gamma }^2}{2-2\sigma }{e}^{\left(2-2\sigma \right)\phi }-\hfill \\ \hfill \frac{4\eta {\gamma }^3}{1-3\sigma }{e}^{\left(1-3\sigma \right)\phi }-\frac{{\gamma }^4}{4\sigma }{e}^{-4\sigma \phi }\hfill \end{array}\right)\hfill \\ \hfill & -\left(\frac{{\eta }^4}{4}-\frac{4{\eta }^3\gamma }{3-\sigma }+\frac{6{\eta }^2{\gamma }^2}{2-2\sigma }-\frac{4\eta {\gamma }^3}{1-3\sigma }-\frac{{\gamma }^4}{4\sigma }\right)\hfill \end{array}$

${\delta }_4\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^{-1}-{\left(\eta -\gamma \right)}^{-1}$

${\delta }_5\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^{-2}-{\left(\eta -\gamma \right)}^{-2}$

${\delta }_6\left(\phi \right)=\left(\eta e^{\phi }+\frac{\gamma }{\sigma }{e}^{-\sigma \phi }\right){\left(\eta e^{\varphi }-\gamma e^{-\sigma \phi }\right)}^{-1}-\left(\eta +\frac{\gamma }{\sigma }\right){\left(\eta -\gamma \right)}^{-1}$

${\delta }_7\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^2-{\left(\eta -\gamma \right)}^2$

${\delta }_8\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^3-{\left(\eta -\gamma \right)}^3$

${\delta }_9\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^3\left(\eta e^{\phi }+\frac{\gamma }{\sigma }{e}^{-\sigma \phi }\right)-{\left(\eta -\gamma \right)}^3\left(\eta +\frac{\gamma }{\sigma }\right)$

${\delta }_{10}\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^6-{\left(\eta -\gamma \right)}^6$

${\delta }_{11}\left(\phi \right)=\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)-\left(\eta -\gamma \right)$

${\delta }_{12}\left(\phi \right)=\log \left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)-\log \left(\eta -\gamma \right)$

${\delta }_{13}\left(\phi \right)=\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)\left(\eta e^{\phi }+\frac{\gamma }{\sigma }{e}^{-\sigma \phi }\right)-\left(\eta -\gamma \right)\left(\eta +\frac{\gamma }{\sigma }\right)$

${\delta }_{14}\left(\phi \right)=\left(\frac{{\eta }^2{e}^{2\phi }}{2}-\frac{{\gamma }^2{e}^{-2\sigma \phi }}{2\sigma }-\frac{2\eta \gamma e^{\left(1-\sigma \right)\phi }}{\left(1-\sigma \right)}\right)-\left(\frac{{\eta }^2}{2}-\frac{{\gamma }^2}{2\sigma }-\frac{2\eta \gamma }{\left(1-\sigma \right)}\right)$

${\delta }_{15}\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^4-{\left(\eta -\gamma \right)}^4$

${\delta }_{16}\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^{-3}\left(\eta e^{\phi }+\gamma \sigma e^{-\sigma \phi }\right)$

${\delta }_{17}\left(\phi \right)=\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)\left(\eta e^{\phi }+\gamma \sigma e^{-\sigma \phi }\right)$

${\delta }_{18}\left(\phi \right)={\left(\eta e^{\phi }-\gamma e^{-\sigma \phi }\right)}^{-1}\left(\eta e^{\phi }+\gamma \sigma e^{-\sigma \phi }\right)$