A model for fermionic dark matter addressing both the CDF MW and the (g − 2)μ anomalies

We explore a simple and renormalizable model which incorporates a new stable fermion that accounts for the dark matter in the universe and which, at the same time, provides an interpretation of two recent measurements that deviate from the expectation in the Standard Model: the muon anomalous magnetic moment and the mass of the W boson recently recorded by the CDF collaboration. The model has a fermionic sector that involves singlet and doublet fields, in which the lightest state is the DM and interacts mainly through the Higgs portal. Two realizations of such a possibility are considered: one in which the Higgs sector is minimal and another in which it is extended to contain two doublet fields.

1 Introduction

There is a large consensus that the Standard Model (SM) of particle physics, although chiefly confirmed by the recent campaign of direct and indirect searches performed at the CERN LHC [1, 2], cannot be the ultimate theory and should only be valid at currently explored energies. One of the main reasons is that it does not involve an electrically neutral, weakly interacting massive particle (WIMP) that could account for the dark matter that apparently forms 25% of the energy budget of the universe [3]. New physics beyond the SM that incorporates such a particle is thus highly expected [4, 5]. Most interesting are the scenarios in which this WIMP interacts mainly or exclusively through the Higgs sector of the theory, the so-called Higgs portal models; see Ref. 6 for a recent review.

The need for new physics beyond the SM recently received a further boost with some unexpected experimental results performed at Fermilab and which cannot be interpreted strictly within the context of the model. The most surprising one is a new and more precise determination of the mass of the W boson performed by the CDF collaboration [7]

$M_W=80.4335\pm 0.0094\mathrm{G}\mathrm{e}\mathrm{V},(1)$

which not only deviates by about 7σ with respect to the SM value but is also in conflict with similar measurements performed at other colliders, such as LEP and LHC [8]. Another less surprising result is the latest Fermilab measurement of the anomalous magnetic moment of the muon, $a_{\mu }=\frac{1}{2}{(g-2)}_{\mu }$, which was found to be [9–24]

$a_{\mu }^{\text{EXP}}=\left(116592061\pm 41\right)\times 10^{-11},(2)$

confirming and magnifying the long-standing (g − 2)_μ anomaly [10], as the deviation from the consensus theory prediction in the SM [25] is now 4.2σ, $\mathrm{\Delta }{a}_{\mu }=a_{\mu }^{\text{EXP}}-a_{\mu }^{\text{SM}}=(251\pm 59)\times 10^{-11}$. Again, there is an ongoing debate about the validity of the SM prediction, and the possibility that the discrepancy could partly be due to unknown uncertainties, as suggested by a recent conflicting lattice calculation [26], should not be overlooked.

Despite the fact that these two results are still controversial and require further experimental and theoretical scrutiny, it is tempting to interpret them as the first of the long-awaited hints of new physics beyond the SM. Nevertheless, one should at least try to relate the two anomalies and explore the possibility of embedding them into model extensions that address also some important shortcomings of the SM, in particular, those which include a viable DM candidate. This is what we attempt and explore in the present work.

We consider a rather simple particle physics scenario dubbed the singlet–doublet model [27–29] in which the DM is the lightest electrically neutral state of a new fermionic sector consisting of an admixture of SU(2) singlet and doublet fields. The new fermions obey a discrete symmetry which forces the DM to be stable and to interact with the SM particle mainly through the Higgs sector. This singlet–doublet model is thus an economical and renormalizable realization of a Higgs portal to a fermionic DM [6]. The SM extension with these fermions charged under the SU(2) group implies new contributions that could provide a theoretical interpretation of the $M_W^{\text{CDF}}$ measurement [30–32].¹

Two realizations of this possibility will be considered. In the first and minimal one, the DM state interacts with the SM via the single SM Higgs particle [36] with a mass of 125 GeV observed at the LHC. We will show that, although it could lead to a correct DM cosmological relic abundance assuming the freeze-out paradigm [4, 5], the model is severely constrained, in particular, by direct DM detection in astroparticle physics experiments, which excludes most of its parameter space. In addition, such a minimal extension, while it can indeed address the M_W anomaly, does not explain the (g − 2)_μ value. Therefore, we also consider an extension of the model in which the Higgs sector is enlarged and includes two Higgs-doublet fields to break the electroweak symmetry. This two-Higgs-doublet model (2HDM) [37] allows evading the constraints from DM direct searches while leading to a correct DM relic density and, at the same time, addressing both the M_W and (g − 2)_μ anomalies via the new contributions of the richer Higgs sector.

The paper is organized as follows: we introduce the fermionic singlet–doublet model with the minimal SM Higgs sector in the next section and the 2HDM extension in Section 3. In both sections, we discuss the impact on DM phenomenology and attempt to explain the values of $M_W^{\text{CDF}}$ and eventually (g − 2)_μ. A short conclusion is given in Section 4.

2 The singlet–doublet model with an SM-like Higgs sector

2.1 The theoretical setup

The so-called fermionic singlet–doublet model [27–29] [6, 38, 39] is one of the most minimal ultraviolet-complete realizations of the Higgs portal framework for dark matter, enabling the possibility of renormalizable interactions between a fermionic DM candidate and the SM Higgs doublet field. In this scenario, the spectrum of the SM is extended by two additional SU(2)_L doublet fields and one singlet fermionic field

$D_L=\left(\begin{array}{c}\hfill N_L\hfill \\ \hfill E_L\hfill \end{array}\right),D_R=\left(\begin{array}{c}\hfill -E_R\hfill \\ \hfill N_R\hfill \end{array}\right),S,(3)$

which are described by the following Lagrangian

$\mathcal{L}=-\frac{1}{2}{m}_S{S}^2-m_D{D}_L{D}_R-y_1{D}_L\mathrm{\Phi }S-y_2{D}_R\tilde{\mathrm{\Phi }}S+\text{h.c.},(4)$

with the implicit assumption that the new states are odd under a Z₂ symmetry that forbids mixing with the SM fermions. Φ is the SM Higgs doublet which, in the unitary gauge, is

$\mathrm{\Phi }=\frac{1}{\sqrt{2}}\left(\begin{array}{c}\hfill 0\hfill \\ \hfill v+H\hfill \end{array}\right),v\simeq 246\mathrm{G}\mathrm{e}\mathrm{V}.(5)$

After electroweak symmetry breaking, mixing occurs between the electrically neutral components of the new fermionic fields. The mass eigenstates will be assumed to be three Majorana fermions², whose masses are obtained by diagonalizing the mass matrix

$\mathcal{M}=\left(\begin{array}{ccc}\hfill m_S\hfill & \hfill y_{1}v/\sqrt{2}\hfill & \hfill y_{2}v/\sqrt{2}\hfill \\ \hfill y_{1}v/\sqrt{2}\hfill & \hfill 0\hfill & \hfill m_D\hfill \\ \hfill y_{2}v/\sqrt{2}\hfill & \hfill m_D\hfill & \hfill 0\hfill \end{array}\right).(6)$

The mass eigenstates, using the unitary 3 × 3 matrix U diagonalizing $\mathcal{M}$, are defined as

${\chi }_i=S{U}_{i1}+N_L{U}_{i2}+N_R{U}_{i3},(7)$

with, by convention, $m_{{\chi }_1}<m_{{\chi }_2}<m_{{\chi }_3}$. The electrically charged components of the new fermionic fields form a Dirac fermion instead, which we denote as ψ^± and with a mass $m_{{\psi }^{\pm }}\simeq m_D$. If $m_{{\chi }_1}<m_{{\psi }^{\pm }}$, the lightest Majorana fermion will be the DM candidate as, by virtue of the Z₂ discrete symmetry, it will be absolutely stable.

In the physical basis, the interaction Lagrangian of the new fermions reads [5]

$\begin{array}{ll}\hfill \mathcal{L}& ={\bar{\chi }}_i{\gamma }^{\mu }\left(g_{Z{\chi }_i{\chi }_j}^V-g_{Z{\chi }_i{\chi }_j}^A{\gamma }_5\right){\chi }_j{Z}_{\mu }+{\bar{\psi }}^{-}{\gamma }^{\mu }\left(g_{W^{\mp }{\psi }^{\pm }{\chi }_i}^V-g_{W^{\mp }{\psi }^{\pm }{\chi }_i}^A{\gamma }_5\right)W_{\mu }^{-}{\chi }_i-e{\bar{\psi }}^{-}{\gamma }^{\mu }{\psi }^{-}{A}_{\mu }\hfill \\ \hfill & -\frac{g}{2{\cos }^2{\theta }_W}\left(1-2{\sin }^2{\theta }_W\right){\bar{\psi }}^{-}{\gamma }^{\mu }{\psi }^{-}{Z}_{\mu }+g_{H{\chi }_i{\chi }_j}H{\bar{\chi }}_i{\chi }_j+\text{h.c.},\hfill \end{array}(8)$

with g the SU(2)_L gauge coupling and ${\cos }^2{\theta }_W=1-{\sin }^2{\theta }_W=M_W^2/M_Z^2$. The couplings of the new fermions with the gauge and Higgs bosons can be written, in terms of the elements of the mixing matrix U, as

$\begin{array}{ll}\hfill & g_{H{\chi }_i{\chi }_j}=\frac{1}{\sqrt{2}}\left(y_1{U}_{i2}^{*}{U}_{j1}^{*}+y_2{U}_{j2}^{*}{U}_{i1}^{*}\right),g_{W^{\mp }{\psi }^{\pm }{N}_i}^{V/A}=\frac{g}{2\sqrt{2}}\left(U_{i3}\mp U_{i2}^{*}\right),\hfill \\ \hfill & g_{Z{\chi }_i{\chi }_j}^{V/A}=c_{Z{\chi }_i{\chi }_j}\mp c_{Z{\chi }_i{\chi }_j}^{*},c_{Z{\chi }_i{\chi }_j}=\frac{g}{4\cos {\theta }_W}\left(U_{i3}{U}_{j3}^{*}-U_{i2}{U}_{j2}^{*}\right).\hfill \end{array}(9)$

From the aforestated equations, one notices in particular that given its Majorana nature, the DM couples in pairs with the Z boson only via the vector–axial interaction; there are also couplings to the W boson. The model is thus not strictly of the Higgs portal type, and this will have an impact on the phenomenology, as will be seen shortly. Following Ref. 29, we will trade the parameters y₁, y₂ with a single coupling y and a mixing angle θ

$y_1=y\cos \theta ,y_2=y\sin \theta .(10)$

With these elements, one can start discussing the phenomenology of the model and, in particular, the way it addresses the DM issue and the CDF measurement of M_W.

2.2 The DM relic density and constraints from direct detection

In order to be a viable DM candidate, the lightest Majorana fermion should have a primordial abundance which is compatible with the measurement Ω_DMh² ≈ 0.12 ± 0.0012 performed by the Planck experiment [3]. Throughout this work, we will assume that the DM relic density is accounted for in the standard thermal freeze-out paradigm in which it is related to a thermally averaged annihilation cross-section of the order of ⟨σv⟩∝ 10⁻²⁶cm³s⁻¹ [4, 5]. In our singlet–doublet model, the DM annihilates mostly into SM fermion pairs via s-channel exchange of the H and Z bosons and, for larger DM masses, into WW, ZZ and Zh final states. The latter channels occur not only through Z and H boson exchange but also through t-channel exchange of the new fermions.

It is of note that if the DM is very close in mass to some of its fermionic partners, coannihilation processes involving the DM and these fermions, or these fermions alone, come as a supplement to DM annihilation and could, in any case, provide the correct relic density. In order to determine it with sufficient accuracy and match it with the Planck value, we have implemented the model into the numerical package micrOMEGAs [40, 41], which includes all (co)annihilation channels and all relevant effects.

There are other constraints on the DM mass and couplings beyond the one from the relic density, and the strongest one comes from direct detection in astroparticle experiments, i.e., in elastic scattering of the DM with nuclei. Our singlet–doublet DM model features both spin-independent (SI) and spin-dependent (SD) interactions. The former are due to the interaction of the DM with the Higgs boson and are described by the following DM-nucleon scattering cross-section (for simplicity, we explicitly report only the more important proton case).

${\sigma }_{{\chi }_{1}p}^{\text{SI}}=\frac{{\mu }_{{\chi }_{1}p}^2}{\pi M_H^4}|g_{H{\chi }_1{\chi }_1}{|}^2\frac{m_p^2}{v^2}{\left[f_{p}Z/A+f_n\left(1-Z/A\right)\right]}^2,(11)$

where ${\mu }_{{\chi }_{1}p}=m_{{\chi }_1}{m}_p/(m_{{\chi }_1}+m_p)$ is the DM/proton reduced mass. f_p ≃ f_n ≈ 0.3 are the effective couplings of the DM with the nucleons. A, Z represent the atomic number and the number of protons of the element/material composing a given detector; at the moment, the reference constraints are provided by xenon-based experiments such as LZ and XENON. It is useful to report the explicit expression of the DM–Higgs coupling

$g_{H{\chi }_1{\chi }_1}=-\frac{y^{2}v\left(m_{{\chi }_1}+m_D\sin 2\theta \right)}{m_D^2+2m_D{m}_{{\chi }_1}-3m_{{\chi }_1}^2+y^2{v}^2/2},(12)$

from which one can see that it can be set to zero if the term $m_{{\chi }_1}+m_D\sin 2\theta$ vanishes. If it is indeed the case, a so-called blind spot [42, 43] occurs for these spin-independent interactions. Spin-dependent interactions are due to the DM axial–vector interactions with the Z boson. The corresponding cross-section is given by

${\sigma }_{N_{1}p}^{\mathrm{SD}}=\frac{{\mu }_{{\chi }_{1}p}^2}{\pi M_Z^4}|g_{Z{\chi }_1{\chi }_1}^A{|}^2{\left[A_u^Z{\mathrm{\Delta }}_u^p+A_d^Z\left({\mathrm{\Delta }}_d^p+{\mathrm{\Delta }}_s^p\right)\right]}^2.(13)$

A blind spot $g_{Z{\chi }_1{\chi }_1}^A=0$ can also occur for spin-dependent interactions when |U₁₂| = |U₁₃|. Even if the singlet–doublet model is potentially testable in indirect detection also, as some of the relevant annihilation processes, like those into W/Z bosons, are s-wave dominated, the corresponding limits are not in competition with the ones from direct detection. Thus, they will not be explicitly reported here; for more details, see –Refs. 5, 29.

2.3 The CDF W-mass anomaly and the new fermionic sector

We come now to the discussion of the new contributions to the W boson mass and confront them with the recent CDF measurement. In leading order, the variation of the electroweak observables and, in particular, M_W with respect to the SM prediction can be related to a deviation from the custodial limit Δρ = 1/(ρ − 1) = 0 of the ρ parameter, which measures the strength of the neutral to charged currents ratio at zero-momentum transfer [44, 45]: $\mathrm{\Delta }{M}_W/M_W\approx \frac{3}{4}\mathrm{\Delta }\rho$. The contribution to Δρ (and hence to ΔM_W and other observables) of two particles of an SU(2) doublet with masses that have a large splitting can be rather large as it is quadratic in the mass of the heaviest particle [44].

To also take into account subleading contributions to ΔM_W, one can, e.g., consider the Peskin–Takeuchi approach with the S, T, U parameters [46]. In this scheme, the largest contribution T is, in fact, simply Δρ, T ∝Δρ − Δρ|_SM, while S describes new contributions from neutral current processes at different energies and U is the contribution to M_W from new charged currents (this last correction is in general small and we will neglect it here). In our singlet–doublet model, the contributions to the S and T parameters originate from the new fermionic sector that couples to the W and Z bosons [47–51].

The new fermion (NF) contributions can be schematically written as [50]

$\begin{array}{ccc}\hfill \mathrm{\Delta }{S}_{\text{NF}}& =\hfill & {\mathrm{\Sigma }}_{i,j=1}^3{\left(U_{1i}{U}_{2j}+U_{2i}{U}_{1j}\right)}^{2}F\left(m_{{\chi }_i},-m_{{\chi }_j}\right)-F\left(m_D,m_D\right),\hfill \\ \hfill \mathrm{\Delta }{T}_{\text{NF}}& =\hfill & {\mathrm{\Sigma }}_{i=1}^3\left[{\left(U_{1i}\right)}^{2}G\left(m_S,m_{{\chi }_i}\right)+{\left(U_{2i}\right)}^{2}G\left(m_S,-m_{{\chi }_i}\right)\right],\hfill \end{array}(14)$

where the functions F and G are given by (α_EM is the fine structure constant)

$\begin{array}{ll}\hfill F\left(m_A,m_B\right)=& \frac{1}{6\pi {\left(m_A^2-m_B^2\right)}^2}[m_A{m}_B\left(3m_A^2\right.-4m_A{m}_B+3m_B^2+\frac{1}{m_A-m_B}\times [m_A^6+m_B^6-3m_A^2{m}_B^2\left(m_A^2+m_B^2\right)+6m_A^3{m}_B^3]],\hfill \end{array}(15)$

$G\left(m_A,m_B\right)=\frac{1}{16{\pi }^2{\alpha }_{\text{EM}}{v}^2}\left[-2m_A{m}_B+\frac{2m_A{m}_B\left(m_A^2+m_B^2\right)-m_A^4-m_B^4}{m_A^2-m_B^2}\log \frac{m_A^2}{m_B^2}\right].$

As an illustration, in Figure 1, we show the regions of the [m_D, m_S] and [y, tan θ] planes, which provide a viable fit of the $M_W^{\text{CDF}}$ anomaly. The three different colors of the contours correspond to the three assignments of the (y, tan θ) pairs, namely, (1, − 6), (1, − 10), and (1, − 20), in the left plot and (m_S, m_D) pairs, namely, (10, 120), (50, 100), and (100, 200), [in GeV] on the right plot. We restricted to mass values m_D ≥ 100 GeV to comply with limits on charged leptons from the LEP experiment [8]. The reason for the negative values of tan θ is that they allow for a blind spot in DM direct detection, as will be seen later.

FIGURE 1

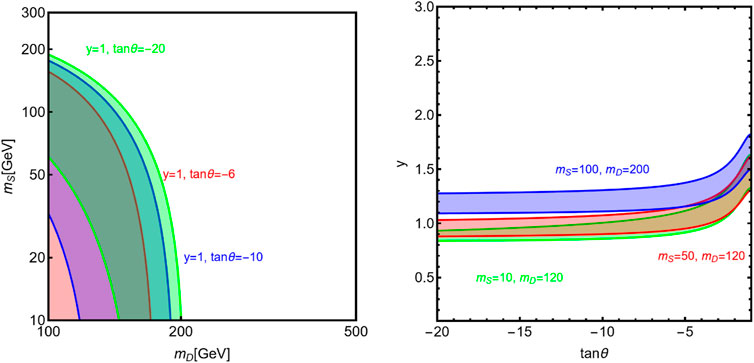
FIGURE 1. Regions of the [m_D, m_S] (left) and [tan θ, y] (right) planes for the singlet–doublet model with an SM-like Higgs sector which comply with the $M_W^{\text{CDF}}$ anomaly. The different colors correspond to the choices of (y, tan θ) or (m_S, m_D) given in the plots.

As evidenced by Figure 1, the CDF M_W measurement seems to favor relatively low values of the masses m_S and m_D, implying a rather light DM candidate. In such a case, a relevant complementary constraint would be represented by the invisible widths of the Z and H bosons, as both particles can decay into a pair of the escaping DM candidate if such processes are kinematically allowed, i.e., when $m_{{\chi }_1}<\frac{1}{2}{M}_Z$ and $m_{{\chi }_1}<\frac{1}{2}{M}_H$, respectively.

Additional decay processes of the Z boson are strongly constrained by precision measurements performed at LEP, which can be summarized by the upper bound Γ(Z → inv) < 2.3 MeV for m_S ≤ 45 GeV [8]. Likewise, extra exotic decays of the 125 GeV Higgs boson are disfavored by LHC measurements of the H couplings to fermions and gauge bosons. The most recent results lead to an upper bound on the Higgs invisible decay branching ratio of BR(H → inv) < 0.11 [1, 2]. Additional constraints on the masses m_S and m_D, and on the parameters y and θ, could come from direct searches at LEP2 and at the LHC, but they are model dependent and we will ignore them here for simplicity.

Before moving to the combination of our results, we note that as the new fermionic sector does not couple or mix with SM fermions, it does not contribute to (g − 2)_μ and, thus, the anomalous Fermilab result cannot be explained in this minimal model.

2.4 Combined numerical results

We now have all the elements to discuss our main numerical results that combine all collider and astroparticle physics constraints, which are reported in Figure 2. The figure compares the regions of parameter space in the [m_D, m_S] plane accounting for the $M_W^{\text{CDF}}$ anomaly and including the different constraints. More precisely, the black isocontours represent the viable relic density according to the standard WIMP paradigm, while the hatched regions correspond to the various experimental exclusion bounds. The blue and purple regions are excluded, respectively, by limits from spin-independent and spin-dependent DM interactions according to the most recent determination made by the LZ [52] and XENON1T [53] experiments. It is of note that the particular shape of the excluded region by spin-independent interactions is represented by two “islands” separated by a narrow band of allowed parameter space. This narrow band correspond to values of the (m_S, m_D) pair that satisfy, exactly or very closely, the blind spot condition, $m_{{\chi }_1}+m_D\sin 2\theta =0$.

FIGURE 2

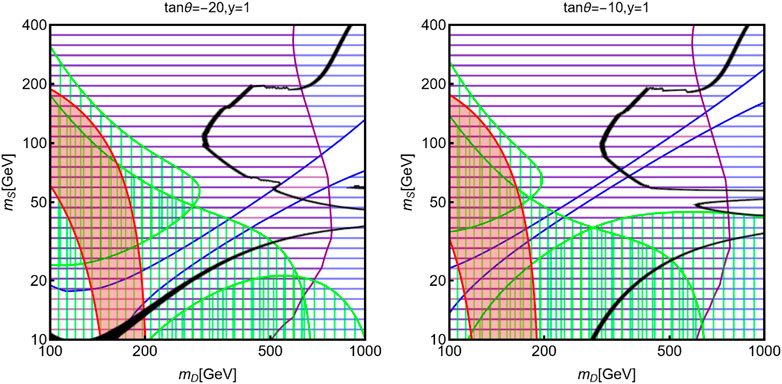
FIGURE 2. Summary of constraints for the singlet–doublet model: the black isocontour corresponds to the correct relic density, while the red regions provide a viable interpretation of the $M_W^{\text{CDF}}$ discrepancy. The hatched regions correspond to different experimental exclusions, namely, limits from spin-independent interactions (blue), spin-dependent interactions (purple), and the invisible widths of the H/Z bosons (green).

The green regions are, instead, excluded by searches of invisible decay branching fractions of the SM Higgs and Z bosons. A given benchmark will be regarded as viable if there is a non-zero intersecting area between the red and black contours and outside the colored regions corresponding to the experimental exclusions. As can be seen, this is not the case for the benchmarks shown in the figure. This is mostly due to the very strong constraints from DM detection, which rule out most of the [m_D, m_S] plane. Indeed, given the different interactions responsible for the spin-independent and spin-dependent cross-sections, it is very difficult to achieve blind spots for both of them at the same time. Given also the low m_S and m_D values needed to reproduce the $M_W^{\text{CDF}}$ value, at least one of the two limits (together with the ones from invisible H/Z decays) becomes effective.

To assess our results in a more systematic way, we have conducted a parameter scan over the following ranges for the model parameters

$m_S\in \left[\mathrm{10,300}\right]\text{GeV},m_D\in \left[\mathrm{100,1000}\right]\text{GeV},tan\theta \in \left[-\mathrm{20,20}\right],y\in \left[10^{-2},10\right],(16)$

retaining the points complying with the CDF anomaly, the correct DM relic density, and the constraints from the Z/H invisible decay widths. The lower limit of 100 GeV on m_D has been chosen to account for the LEP bound on exotic charged particle searches. These model points are shown in Figure 3 in the $(m_{{\chi }_1},{\sigma }_{{\chi }_{1}p}^{\text{SI}})$ and $(m_{{\chi }_1},{\sigma }_{{\chi }_{1}p}^{\mathrm{SD}})$ planes. The regions above the corresponding experimental exclusions have been marked in blue.

FIGURE 3

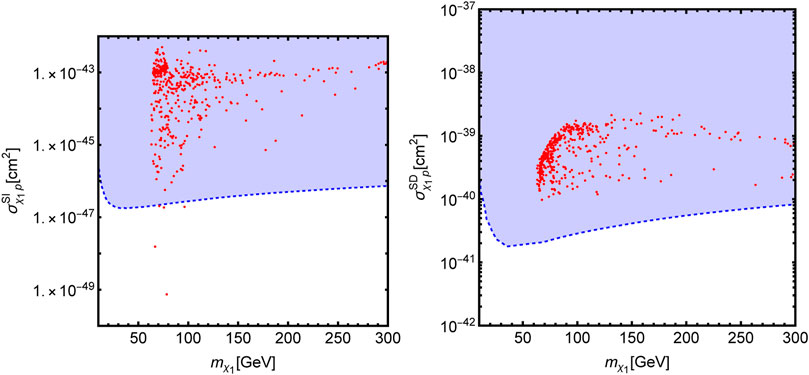
FIGURE 3. Model points of the minimal singlet–doublet model complying with CDF excess and DM relic density shown in the $(m_{{\chi }_1},{\sigma }_{{\chi }_{1}p}^{\text{SI}})$ and $(m_{{\chi }_1},{\sigma }_{{\chi }_{1}p}^{\mathrm{SD}})$ planes. The blue regions are experimentally excluded.

As one can see, even if it is possible to achieve a small population of points, mostly around the Higgs pole $m_{{\chi }_1}\simeq \frac{1}{2}{M}_H$ via the already-mentioned blind spots to evade the constraint on spin-independent DM interactions, the constraint on the spin-dependent cross-section feature a very strong complementarity, ruling out these fine-tuned configurations.

An extension of the model is thus required to bypass these limitations. An interesting possibility would be a Higgs sector with two doublets to which we turn our attention now.

3 The singlet–doublet fermion case in a 2HDM

3.1 The 2HDM and its ingredients

We consider the case that the scalar sector of the theory is composed of two doublet fields Φ₁ and Φ₂$,$ which lead to the CP-conserving Z₂ invariant potential [54]

$\begin{array}{ll}\hfill V\left({\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2\right)& =m_{11}^2{\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_1+m_{22}^2{\mathrm{\Phi }}_2^{†}{\mathrm{\Phi }}_2-m_{12}^2\left({\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_2+\mathrm{h}.\mathrm{c}.\right)\hfill \\ \hfill & +\frac{{\lambda }_1}{2}{\left({\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_1\right)}^2+\frac{{\lambda }_2}{2}{\left({\mathrm{\Phi }}_2^{†}{\mathrm{\Phi }}_2\right)}^2+{\lambda }_3\left({\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_1\right)\left({\mathrm{\Phi }}_2^{†}{\mathrm{\Phi }}_2\right)\hfill \\ \hfill & +{\lambda }_4\left({\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_2\right)\left({\mathrm{\Phi }}_2^{†}{\mathrm{\Phi }}_1\right)+\frac{{\lambda }_5}{2}\left[{\left({\mathrm{\Phi }}_1^{†}{\mathrm{\Phi }}_2\right)}^2+\mathrm{h}.\mathrm{c}.\right].\hfill \end{array}(17)$

After electroweak symmetry breaking, the two doublets can be decomposed as

${\mathrm{\Phi }}_i=\left(\begin{array}{c}\hfill {\varphi }_i^{+}\hfill \\ \hfill \left(v_i+{\rho }_i+i{\eta }_i\right)/\sqrt{2}\hfill \end{array}\right),i=\mathrm{1,2},(18)$

with v₁ and v₂ vacuum expectation values satisfying $\sqrt{v_1^2+v_2^2}=v\simeq 246$ and tan β = v₂/v₁. The physical mass eigenstates emerge via rotations with angles α and β

$\left(\begin{array}{c}\hfill {\varphi }_1^{+}\hfill \\ \hfill {\varphi }_2^{+}\hfill \end{array}\right)={\mathfrak{R}}_{\beta }\left(\begin{array}{c}\hfill G^{+}\hfill \\ \hfill H^{+}\hfill \end{array}\right),\left(\begin{array}{c}\hfill {\eta }_1\hfill \\ \hfill {\eta }_2\hfill \end{array}\right)={\mathfrak{R}}_{\beta }\left(\begin{array}{c}\hfill G^0\hfill \\ \hfill A\hfill \end{array}\right),\left(\begin{array}{c}\hfill {\rho }_1\hfill \\ \hfill {\rho }_2\hfill \end{array}\right)={\mathfrak{R}}_{\alpha }\left(\begin{array}{c}\hfill H\hfill \\ \hfill h\hfill \end{array}\right),(19)$

with ${\mathfrak{R}}_{X,X=\alpha ,\beta }$ being the rotation matrices of angle X with elements given in terms of cos X and sin X. The states h, H are the neutral CP-even Higgs bosons, with h being identified with the observed 125 GeV Higgs state; throughout this work, we will assume the hierarchy M_h < M_H. A is a CP-odd Higgs eigenstate, while H^± are the electrically charged Higgs states. Finally, G⁰ and G⁺ are the Goldstone bosons that make the longitudinal degrees of freedom of the Z and W bosons.

In order to be theoretically consistent, the parameters of the scalar potential should comply with a series of constraints (see, for instance, Ref. 55): i) the scalar potential should be bound from below, ii) it obeys s-wave unitarity at the tree level, iii) the electroweak vacuum should be a stable global minimum, and finally, iv) the couplings should stay perturbative, i.e., |λ_i| ≤ 4π. These constraints have been discussed in the literature, and a recent account has been given, e.g., in Ref. 35. They can be translated into constraints on the masses of the various Higgs mass eigenstates using relations also given in Ref. 35. We will include all these constraints in our numerical analysis.

Turning to the couplings between the physical Higgs bosons and the SM fermions, they are described by the following Yukawa-type Lagrangian:

$\begin{array}{ll}\hfill -{\mathcal{L}}_{\text{Yuk}}^{\text{SM}}& ={\mathrm{\Sigma }}_{f=u,d,l}\frac{m_f}{v}\left[g_{\mathit{hff}}\bar{f}fh+g_{\mathit{Hff}}\bar{f}fH-i{g}_{\mathit{Aff}}\bar{f}{\gamma }_{5}fA\right]\hfill \\ \hfill & -\left(\sqrt{2}/v\right)\left[\bar{u}\left(m_u{g}_{\mathit{Auu}}{P}_L+m_d{g}_{\mathit{Add}}{P}_R\right)d{H}^{+}+m_l{g}_{\mathit{All}}\bar{\nu }{P}_R\ell H^{+}+\mathrm{h}.\mathrm{c}.\right],\hfill \end{array}(20)$

with $P_{L/R}=\frac{1}{2}(1\mp {\gamma }_5)$ and g_ϕff being the reduced couplings of the ϕ boson to up- and down-type quarks and charged leptons normalized to the SM couplings, $g_{\varphi ff}=g_{\varphi ff}^{2\text{HDM}}/g_{Hff}^{\text{SM}}$.

To avoid the emergence of tree-level flavor-changing neutral currents, only four possible sets of assignments of the couplings can be considered [37, 56]; they are dubbed type-I, type-II, type-X (or lepton-specific), and type-Y (or flipped) 2HDMs. The corresponding couplings are summarized in Table 1. It is of note that the angle α, which determines the mixing between the neutral CP-even states h and H, is constrained by the measurement of the couplings of the h state at the LHC, which should be SM-like. The statement is enforced quantitatively by allowing only small deviations from the so-called alignment limit $\beta -\alpha =\frac{\pi }{2}$, see, e.g., Ref. 57. As for the couplings of the other Higgs states, it can be seen from the table that they can be strongly enhanced or suppressed with respect to the SM values, depending on the value of tan β and the considered configuration. Consequently, different experimental limits should apply in the different cases, and we refer to, e.g., Ref. 6 for a review. As discussed in Refs. 33, 34, in order to comply with the (g − 2)_μ and $M_W^{\text{CDF}}$ anomalies, one should focus on the lepton-specific or type-X 2HDM, with large values of the parameter tan β to enhance the lepton couplings. It allows to achieve a relatively light spectrum for the additional Higgs states while still complying with most of the bounds coming from collider searches and flavor physics.

TABLE 1

TABLE 1. Couplings of the 2HDM Higgs bosons to fermions, normalized to those of the SM-like Higgs boson, as a function of the angles α and β. In the case of the CP-even Higgs states, their values in the alignment limit $\beta -\alpha \to \frac{\pi }{2}$.

Considering the interactions of the Higgs sector with the singlet–doublet fermionic states, the relevant Lagrangian is a straightforward generalization of the one presented in the previous section and can be written as (a, b = 1, 2) [39, 58]

$\mathcal{L}=-\frac{1}{2}{m}_S{S}^2-m_D{D}_L{D}_R-y_1{D}_L{\mathrm{\Phi }}_{a}S-y_2{D}_R{\tilde{\mathrm{\Phi }}}_b{S}^{+}\text{h.c}.(21)$

The fermionic physical eigenstates will be still represented by three neutral Majoranas and one electrically charged Dirac fermion. This time, the neutral mixing matrix will depend on the two different vacuum expectation values: v₁ and v₂. Consequently, the singlet and doublet components of the DM and its couplings will also be sensitive to the angles α and β, in addition to the masses m_S and m_D. In the fermion mass basis, the interaction Lagrangian reads

$\begin{array}{ll}\hfill \mathcal{L}& =\stackrel{-}{{\psi }^{-}}{\gamma }^{\mu }\left(g_{W^{\mp }{\psi }^{\pm }{\chi }_i}^V-g_{W^{\mp }{\psi }^{\pm }{N}_i}^A{\gamma }_5\right){\chi }_i{W}_{\mu }^{-}+\frac{1}{2}{\mathrm{\Sigma }}_{i,j=1}^3\overline{{\chi }_i}{\gamma }^{\mu }\left(g_{Z{\chi }_i{\chi }_j}^V-g_{Z{\chi }_i{\chi }_j}^A{\gamma }_5\right){\chi }_j{Z}_{\mu }\hfill \\ \hfill & +\frac{1}{2}{\mathrm{\Sigma }}_{i,j=1}^3\overline{{\chi }_i}\left(y_{h{\chi }_i{\chi }_j}h+y_{H{\chi }_i{\chi }_j}H+y_{A{\chi }_i{\chi }_j}{\gamma }_{5}A\right){\chi }_j+\stackrel{-}{{\psi }^{-}}\left(g_{H^{\pm }\psi {\chi }_i}^S-g_{H^{\pm }\psi {\chi }_i}^P{\gamma }_5\right){\chi }_i{H}^{-}\hfill \\ \hfill & -e{A}_{\mu }\stackrel{-}{{\psi }^{-}}{\gamma }^{\mu }{\psi }^{-}-\frac{g}{2\cos {\theta }_W}\left(1-2{\sin }^2{\theta }_W\right)Z_{\mu }\stackrel{-}{{\psi }^{-}}{\gamma }^{\mu }{\psi }^{-}+\text{h.c.},\hfill \end{array}(22)$

where the Higgs couplings in the case of ϕ = h, H, A and H^± are given by

$\begin{array}{ll}\hfill y_{\varphi {\chi }_i{\chi }_j}& =\frac{{\delta }_{\varphi }}{2\sqrt{2}}\left[U_{i1}\left(y_1{R}_a^{\varphi }{U}_{i2}+y_2{R}_b^{\varphi }{U}_{i3}\right)+\left(i\leftrightarrow j\right)\right],\hfill \\ \hfill g_{H^{\pm }\psi {\chi }_i}^{S/P}& =\frac{1}{2}{U}_{i1}\left(y_1{R}_1^{H^{\pm }}\pm y_2{R}_2^{H^{\pm }}\right),\hfill \end{array}(23)$

with δ_h = δ_H = −1 and δ_A = −i. Similar to what occurs for the SM fermions, one should not assume arbitrary couplings of the new fermions with the Φ₁ and Φ₂ doublet fields. The simplest way to proceed would consist of extending to the new fermionic sector the same symmetries which define the four flavor-conserving 2HDMs defined earlier [39, 58]. This leads to two possible assignments of the $R_{a,b}^{\varphi }$ parameters:

$R_1^h=R_2^h=-\sin \alpha ,R_1^H=R_2^H=\cos \alpha ,R_1^A=R_2^A=-\sin \beta ,R_1^{H^{\pm }}=R_2^{H^{\pm }}=-\sin \beta ,(24)$

$R_1^h=-R_2^H=-\sin \alpha ,R_2^h=R_1^H=\cos \alpha ,R_1^A=R_1^{H^{\pm }}=-\sin \beta ,R_2^A=R_2^{H^{\pm }}=\cos \beta .(25)$

which will be dubbed type-A for the first one and type-B for the second configuration.

This completes the necessary ingredients to study the phenomenology of the model.

3.2 The DM sector

The phenomenology of the DM particle in the present case bears many similarities with the already-discussed minimal singlet–doublet model. We thus simply point out the additional features that are due to the extended Higgs sector. Starting with DM direct detection, the spin-independent cross-section receives an additional contribution from the t-channel exchange of the heavy CP-even H state and will be then given by [39, 58]

${\sigma }_{\chi p}^{\text{SI}}=\frac{{\mu }_{\chi p}^2}{\pi }\frac{m_p^2}{v^2}{\left|{\displaystyle \sum _q}{f}_q\left(\frac{y_{h{\chi }_1{\chi }_1}{g}_{\mathit{hqq}}}{M_h^2}+\frac{y_{H{\chi }_1{\chi }_1}{g}_{\mathit{Hqq}}}{M_H^2}\right)\right|}^2.(26)$

In contrast, the functional form of the spin-dependent cross-section is unchanged with respect to the one in the minimal model presented in Section 2.2. Again, the spin-independent cross-section can be set to zero at the tree level by choosing vanishing Higgs couplings $y_{h{\chi }_1{\chi }_1}=y_{H{\chi }_1{\chi }_1}=0$ by imposing the relation m_S + m_D sin 2θ ≃ 0. A blind spot can also be generated with a destructive interference between the h/H-exchange contributions.

For what concerns the relic density, there are mostly two relevant changes with respect to the minimal model. First, we have the possibility of the extra s-channel exchange of the pseudoscalar boson A (in addition to that of the H state) in DM annihilation into SM fermion final states. This additional contribution has no counterpart in the interactions relevant to DM direct detection and, hence, could potentially alleviate the tensions that are present in the minimal model. A further relevant impact on the DM relic density would appear when one of the extra Higgs bosons is lighter than the DM particle, implying the possibility of additional annihilation channels for the latter.

Finally, there are also bounds on the DM mass and couplings from collider searches, as already discussed in the previous section when we considered the invisible decay widths of the h and Z bosons that would also apply in the 2HDM realization. One additional feature not presented earlier is that, in the case of a light pseudoscalar state, the width of the 125 GeV Higgs boson can get additional exotic contributions corresponding to the h → ZA and h → AA channels. The former is absent in the alignment limit as g_hZA = 0, and the latter is subject to a very active search program at the LHC, see, e.g., Refs. 59–61.

The partial decay width of the 125 Higgs into two light pseudoscalars is given by [62]

$\mathrm{\Gamma }\left(h\to AA\right)=\frac{{\left|{\lambda }_{\mathit{hAA}}\right|}^2}{32\pi M_h}\sqrt{1-4M_A^2/M_h^2},(27)$

where, using the abbreviation $M^2\equiv m_{12}^2/(\sin \beta \cos \beta )$ with m₁₂ appearing in the 2HDM scalar potential given in Eq. 17, one has

${\lambda }_{\mathit{hAA}}=\frac{1}{2v}\left[\left(2M^2-2M_A^2-M_h^2\right)\sin \left(\beta -\alpha \right)+\left(M^2-M_h^2\right)\left(\cot \beta -\tan \beta \right)\cos \left(\beta -\alpha \right)\right].(28)$

One can see that it is possible to set the λ_hAA coupling to zero, i.e., to achieve a kind of blind spot, by imposing the relation [63]

$\tan \left(\beta -\alpha \right)=\frac{M^2-M_h^2}{2M^2-2M_A^2-M_h^2}\left(\tan \beta -\cot \beta \right).(29)$

3.3 Interpreting the CDF W-mass anomaly

We now come to the contributions of the new particles of this extended singlet–doublet scenario to the electroweak observables and, in particular, to the mass M_W. In addition to the new fermion contributions to the S and T parameters, which have exactly the same functional form given in Section 2.3, one needs to include those of the extended Higgs sector. The contribution to the S and T parameters from a 2HDM can be written as [48]

$\begin{array}{c}{S}_{2\text{HDM}}=F\left(M_h,M_Z\right)+M_Z^{2}G\left(M_h,M_Z\right)+F\left(M_A,M_H\right)-F\left(M_{H^{\pm }},M_{H^{\pm }}\right),\hfill \\ T_{2\text{HDM}}=-3\left[A\left(M_h,M_W\right)-A\left(M_h,M_Z\right)\right]+F\left(M_A,M_H\right)-F\left(M_{H^{\pm }},M_{H^{\pm }}\right),\hfill \end{array}(30)$

where we have assumed the alignment limit $\alpha =\beta -\frac{\pi }{2}$ and used the functions

$\begin{array}{c}A\left(m_A,m_B\right)=\frac{1}{32{\pi }^2{\alpha }_{\text{EM}}{v}^2}\left[\frac{m_A^2+m_B^2}{2}-\frac{m_A^2{m}_B^2}{m_A^2-m_B^2}\log \frac{m_A^2}{m_B^2}\right],\hfill \\ F\left(m_A,m_B\right)=\frac{1}{24\pi }\left[\frac{4m_A^2{m}_B^2}{{\left(m_A^2-m_B^2\right)}^2}+\frac{m_A^6+m_B^6-3m_A^2{m}_B^2\left(m_A^2+m_B^2\right)}{{\left(m_A^2-m_B^2\right)}^3}\log \frac{m_A^2}{m_B^2}\right],\hfill \\ G\left(m_A,m_B\right)=\frac{1}{2\pi }\left[\frac{2m_A^2{m}_B^2}{{\left(m_A^2-m_B^2\right)}^3}\log \frac{m_A^2}{m_B^2}-\frac{m_A^2+m_B^2}{{\left(m_A^2-m_B^2\right)}^2}\right].\hfill \end{array}(31)$

We show in Figure 4 how a viable fit of the $M_W^{\text{CDF}}$ anomaly is obtained for two benchmark assignments of the model parameters. The two panels show the $[M_H,M_{H^{\pm }}]$ plane for two values of M_A, namely, 70 GeV and 300 GeV, with tan β = 10 in both cases.

FIGURE 4

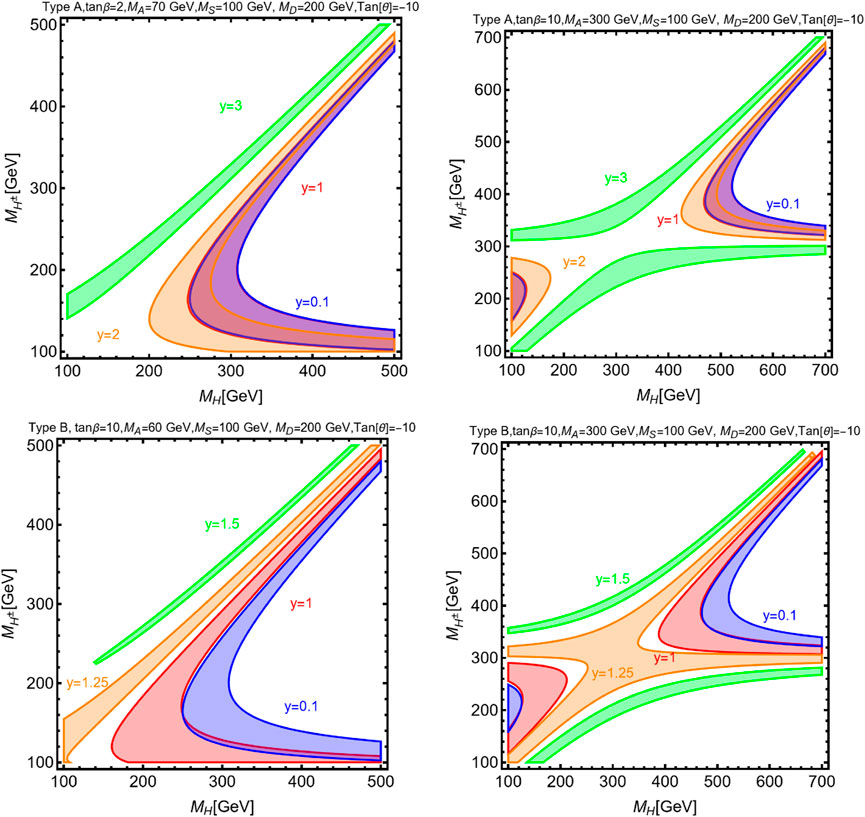
FIGURE 4. Regions in the $[M_H,M_{H^{\pm }}]$ plane providing a viable fit of the $M_W^{\text{CDF}}$ measurement for some benchmarks of the 2HDM singlet–doublet model. The different colors correspond to the different values of the Yukawa coupling y reported on the panels. The first row refers to the type-A configuration of the couplings of the DM, while the second row corresponds to the type-B configuration.

For what concerns the fermionic sector, we have taken for panels m_S = 100 GeV, m_D = 200 GeV, and tan θ = −10 and considered four values of y, corresponding to the different colored contours. We have focused again on a negative value for tan θ so that a blind spot can be enforced in DM direct detection.

The pattern in the figures can be understood as follows. For the lowest values of the DM Yukawa coupling y, the contributions of the new fermions to the electroweak observables and, hence, to M_W are very small. The $M_W^{\text{CDF}}$ result is accounted for mainly by the scalar sector. In agreement with the findings of Refs. 34, 35, this result is achieved by taking an appropriate mass splitting between the H and H^± states. When the Yukawa coupling y increases, the impact of the new fermions on M_W is more significant. Consequently, one has to reduce the contribution for the extra Higgs bosons by having a smaller mass splitting. As it should be clear from the parameter assignment, it is necessary to consider small values of tan β in the type-A scenario (the DM Yukawa couplings are suppressed with tan β) and values of y greater than unity to have a substantial contribution from the new fermions to the CDF anomaly. In the type-B case, the strength of the DM interactions increases with tan β and, consequently, lower values of y are required.

3.4 Addressing the muon g-2 anomaly

In contrast to the minimal singlet–doublet model discussed in the previous section, the presence of an extended Higgs sector also allows to generate an additional contribution to the anomalous magnetic moment of the muon, which could potentially reproduce the recent experimental result. Such a contribution actually emerges from the combination of two types of terms. The first one, which appears at the one-loop level, scales as $m_{\mu }^2/M_{\varphi }^2$ with ϕ being an electrically neutral state of the model. Consequently, it is strongly suppressed unless ϕ is very light, and we will consider such a possibility only for the CP-even A boson. The corresponding contributions can be approximately written as [64, 65]

$\mathrm{\Delta }{a}_{\mu }^{1-\text{loop}}\approx -\frac{{\alpha }_{\text{EM}}}{8\pi {\sin }^2{\theta }_W}\frac{m_{\mu }^4}{M_W^2{M}_A^2}{g}_{A\mu \mu }^2\left[\log \left(\frac{M_A^2}{m_{\mu }^2}\right)-\frac{11}{6}\right].(32)$

Given the already-mentioned suppression, a proper computation of Δa_μ should also include the two-loop level contribution which arises from Barr–Zee-type diagrams [66] in which there is a heavy fermion loop with an enhanced $m_f^2/M_{\varphi }^2$ term that compensates the higher α_EM power suppression. In the case of the A state, it can be written as [67–69]

$\mathrm{\Delta }{a}_{\mu }^{2-\text{loop}}=\frac{{\alpha }_{\text{EM}}^2}{8{\pi }^2{\sin }^2{\theta }_W}\frac{m_{\mu }^2}{M_W^2}{g}_{A\mu \mu }{\displaystyle \sum _f}{g}_{\mathit{Aff}}{N}_c^f{Q}_f\frac{m_f^2}{M_A^2}H\left(\frac{m_f^2}{M_A^2}\right),(33)$

$H\left(r\right)={\int }_0^1\mathrm{d}x\frac{\log \left(r\right)-\log \left[x\left(1-x\right)\right]}{r-x\left(1-r\right)}.(34)$

Our numerical determination of Δa_μ is nonetheless obtained by considering the full computation, as given, for example, in Ref. 69, which includes the contribution of all Higgs bosons of the 2HDM. It is arguable from the aforestated expressions that sizable couplings of the new Higgs bosons with the muons are needed to account for the (g − 2)_μ anomaly; for a more detailed discussion, see, for example, Ref. 33. This requirement selects the type-II and the type-X among the flavor-preserving Yukawa configurations as they involve enhanced Higgs couplings to muons at high tan β values, g_Aℓℓ ∝ tan β. However, in the type-II scenario, the presence of light neutral Higgs bosons is disfavored by direct Higgs searches at the LHC, in particular, in the production processes $pp\to gg/b\bar{b}\to H/A$ and the subsequent decays H/A → τ⁺τ⁻ [70, 71] and eventually also H/A → μ⁺μ⁻ [72–74]; see the discussion of the next subsection.

We show in Figure 5 the regions of the [M_A, tan β] plane which provide a viable fit of the (g − 2)_μ anomaly at the 1σ (green) and 2σ (yellow) levels. The two panels differ by the assignments of the $(M_H,M_{H^{\pm }})$ pair, which have been chosen, in agreement with the outcome of Figure 4, to provide a good fit of $M_W^{\text{CDF}}$. Furthermore, to overcome the constraint from the h width at low M_A values, we have fixed the value of the angle α as in Eq. 29. As can be seen, a viable fit of the (g − 2)_μ anomaly is achieved for very high tan β values and M_A ≲ 60 GeV. The sizable mass splitting between the pseudoscalar state A and the other 2HDM states is also constrained by violation of lepton universality in decays of the SM Z and τ particles [75]. The corresponding bounds are represented as dot-dashed isocontours in the figure, and the regions above the contours are ruled out.

FIGURE 5

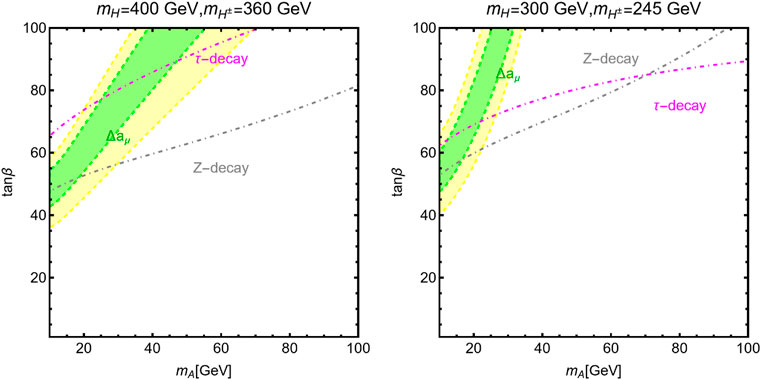
FIGURE 5. Regions providing a viable fit of the (g − 2)_μ anomaly at 1σ(green) and 2σ (yellow) in the plane [M_A, tan β] for two assignments of $(M_H,M_{H^{\pm }})$, namely, (400,350) and (300, 245) GeV. The dot-dashed lines represent the bounds from violation of lepton universality in decays of the Z boson and τ-lepton (regions above the lines are excluded).

The different shapes of the (g − 2)_μ contours can be explained as follows. The value of a_μ in the 2HDM is due to a non-trivial interplay between 1- and 2-loop contributions, as the latter one can potentially exceed the former since the suppression by the factor α_EM is compensated by an $m_f^2/m_{\mu }^2$ enhancement for m_f ≫ m_μ. It is of note that the A boson gives a negative (positive) contribution to a 1-loop (2-loop), while the opposite occurs for the CP-even h, H bosons. Thus, a good fit of (g − 2)_μ is obtained with the 2-loop A contribution. In the type-X case, this occurs for $\mathcal{O}(10\text{GeV})<M_A<M_h$ and very high tan β values. The H state should be heavy enough for its negative 2-loop contribution to be reduced. The two panels of Figure 5 also differ because of the different values of the angle α obtained from the condition Eq. 29, which modifies the couplings of the CP-even h, H states.

It is of note that the constraints from Z-decays are stronger when the hierarchy between M_A and M_H increases, while constraints from τ decays become weaker with increasing $M_{H^{\pm }}$ and have more impact in the right panel. In all cases, these constraints are strong, reducing to a narrow strip the regions in which the (g − 2)_μ value can be reproduced at the 1σ level.

3.5 LHC searches of additional Higgs bosons

Additional Higgs bosons are actively searched by the ATLAS and CMS collaborations. The strongest constraints are typically associated with searches of electrically neutral resonances. Among them, the most constraining and typically most relevant in our context are the ones coming from the processes H/A → τ⁺τ⁻; see, e.g., Ref. 70 for the most recent results. As discussed in, e.g., Refs. 33, 35 and mentioned previously, these bounds are generally rather severe in the type-II scenario at sufficiently high tan β values. Indeed, in this case, both the production cross-sections in the fusion processes gg → H/A (mediated by loops of b-quark with strongly enhanced couplings), $b\bar{b}\to H/A$, and the branching ratios for the H/A → ττ decays (about 10% in this case) are large. H/A masses above the TeV range are, in principle, excluded by these LHC searches.

In turn, these bounds sensitively weaken in the case of the type-X or the lepton-specific scenario in which the H/A couplings to b-quarks are not enhanced, thus lowering the production cross-section rates (albeit also increasing the decay branching ratios). For this reason, bounds from processes not involving fermions in the final state, such as H → ZZ [76], H → AZ [77], A → HZ [78], and A → hZ [79], could become more relevant.

We have therefore computed the production cross-sections’ time decay branching ratios of all the processes mentioned previously as function of the model parameters. We have used the numerical package SuSHI [80, 81] and compared the obtained results with the corresponding bounds given by the two LHC teams. The outcome of such a comparison, when combined with other constraints, will be discussed at the end of the next subsection.

3.6 Combined results

We are now ready to combine the individual constraints previously discussed to obtain the global picture that is shown in Figure 6. We have considered three benchmarks for the singlet–doublet 2HDM model in the type-X configuration and with the tan β and M_ϕ values listed on each plot and imposed the various constraints in the [m_D, m_S] plane. The color code is the same as the one adopted in the minimal singlet–doublet case (Figure 2). A combined fit of the correct relic density and of the $M_W^{\text{CDF}}$ result is achieved at the crossing of the black line (relic density) and red area (M_W). Such an intersection should lie outside the experimental exclusions, represented by the hatched colored regions.

FIGURE 6

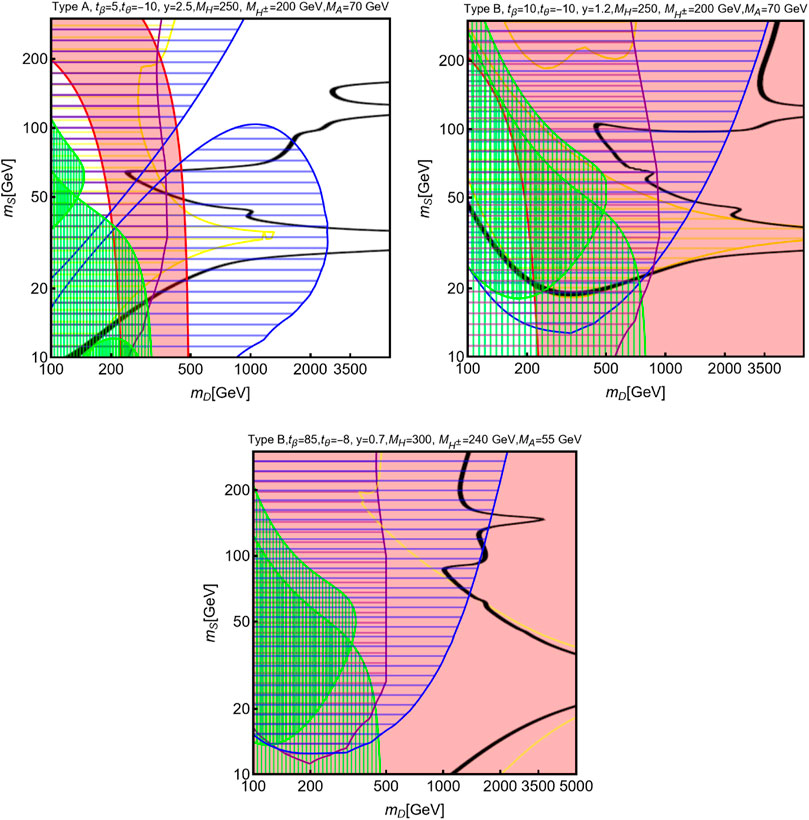
FIGURE 6. Combined constraints on the singlet–double 2HDM scenario in the [m_D, m_S] plane for three benchmarks in the type-X configuration, with input parameters given on top of each plot. The color convention is the same as that in Figure 2.

In the three selected benchmarks, the first two allow simply combining the CDF result for M_W with DM phenomenology, and similar parameter assignments as in Figure 1 of the minimal singlet–doublet model have been adopted. Comparing the outcome with the analogous one given in the previous section, one first notices that the relic density contours have a richer pattern. This is due to the presence of the possibly light extra Higgs bosons which could meet the resonance condition, $m_{{\chi }_1}\simeq \frac{1}{2}{M}_{\varphi }$, for the relic density.

A second notable difference with respect to the minimal model is that due to the dependence of the entries of the Majorana mixing matrix U on tan β, it is possible to further reduce the impact of the bounds from DM direct detection and from the invisible Higgs decay branching ratio, in addition to the blind spot condition (the latter is particularly evident in the first panel of the figure, showing similarly to the previous section, the excluded regions separated in two “islands”) for negative tan θ values. It is of note that for these first two benchmarks, we have considered only values $M_A>\frac{1}{2}{M}_h$ so that the “invisible” width of the h state is due only to the decay into DM pairs. In the figures, in addition to the limits from direct detection [52, 53], we have also explicitly shown the parameter space excluded by DM indirect detection, represented by the negative results of the searches of γ-ray signals performed by the FERMI-LAT experiment [82, 83].

In turn, the third benchmark of Figure 6 is characterized by a very high value of tan β and a light A boson, tan β = 85 (which allows a perturbativity of all couplings in the type-X case) and M_A = 55 GeV (which is not excluded by pp → A → ττ, μμ searches). As can be seen from the last panel of Figure 6, this benchmark leads at the same time to a correct DM relic density and provides viable interpretations of both the (g − 2)_μ and $M_W^{\text{CDF}}$ anomalies.

In addition to the study of these three specific benchmarks, we have conducted a parameter scan to provide a more complete and systematic illustration of our results. The model parameters have been varied within the following ranges:

$\begin{array}{c}{M}_H\in \left[\mathrm{125,500}\right]\text{GeV},M_{H^{\pm }}\in \left[\mathrm{80,500}\right]\text{GeV},M_A\in \left[62.5,500\right]\text{GeV},\hfill \\ \left|\cos \left(\beta -\alpha \right)\right|<0.1,\tan \beta \in \left[\mathrm{1,50}\right],\hfill \\ m_S\in \left[\mathrm{10,300}\right]\text{GeV},m_D\in \left[\mathrm{100,3500}\right]\text{GeV},y\in \left[0.01,10\right],\tan \theta \in \left[-20,-1\right].\hfill \end{array}(35)$

Again, the ranges of the parameters associated with the new fermionic sector have been limited to automatically encompass the LEP bound on new charged particles, m_D > 100 GeV. Furthermore, we have limited ourselves to negative values of tan θ to more easily evade DM direct detection constraints. For what concerns the 2HDM sector, we have again accounted for the LEP bound on the mass of the charged Higgs and considered only the value of M_A above $\frac{1}{2}{M}_h$ for the pseudoscalar Higgs to avoid h → AA decays without a fine-tuned hAA coupling. To increase the efficiency of the parameter scan, we considered only the range tan β ≲ 50. As a result, one could reproduce only the $M_W^{\text{CDF}}$ value and DM phenomenology since, as discussed in the dedicated section, one can obtain only a 2σ agreement with the measured (g − 2)_μ value at the price of fine-tuning the model parameters, which renders our numerical scan rather inefficient. The scan has been repeated for both the type-A and type-B configurations of the new fermion couplings with the 2HDM sector. Two sets of constrains have been applied to the model points.

The first one consists of imposing a viable fit of $M_W^{\text{CDF}}$, a correct DM relic density, and compatibility with DM direct and indirect detection constraints and with the invisible widths of the Higgs and the Z bosons. The model points passing such a set of constraints in the (m_D, m_S) and $(m_{{\chi }_1},y)$ planes are shown in Figure 7. The red (blue) points correspond to the type-A (type-B) coupling configuration. Looking at the (m_S, m_D) plane, one notices immediately that no model points appear when m_D < m_S. Indeed, in such a case, the DM is mostly doublet-like, featuring a very efficient annihilation into gauge bosons which makes it under-abundant unless its mass is set at around 1 TeV; we have not considered such a scenario in our analysis. In addition, one notices an increased density of points for m_S ≃ m_D. This corresponds to a scenario in which the correct relic density is achieved via co-annihilations among the DM and the other new fermions. A final remark is that for the type-B configuration, there is a preference for values of m_D above 1 TeV. This is due to the fact that in this configuration, for a given value of y, the DM couplings are enhanced by tan β. To avoid constraints from DM detection, we need to reduce its doublet component. In addition to these features, the viable model points tend to be distributed uniformly in the (m_S, m_D) plane. This is due to the fact that it is always possible to achieve the correct relic density by a suitable choice of the $\left|m_{{\chi }_1}-\frac{1}{2}{M}_{Z,h,H,A}\right|$ value.

FIGURE 7

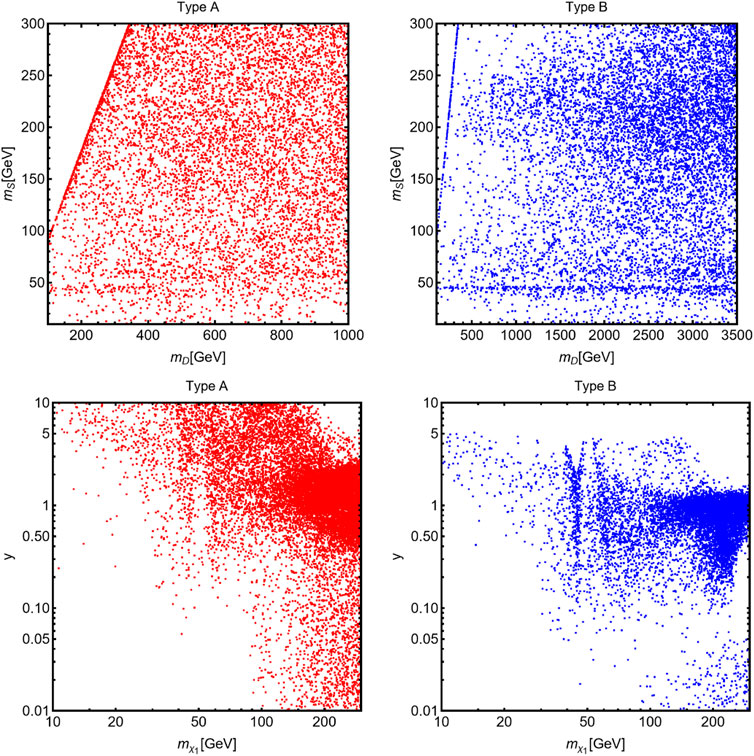
FIGURE 7. Outcome of the large parameter scan of the singlet–doublet fermionic model coupled with two Higgs-doublet fields. The model points compatible with the CDF M_W value and the DM constraints are shown in the (m_D, m_S) plane (first row) and $(m_{{\chi }_1},y)$ plane (second row). The two columns refer, respectively, to the type-A and type-B configurations of the couplings of the fermions with the Higgs doublets.

In an analogous fashion, we see that the viable model points span large regions of the $(m_{{\chi }_1},y)$ bidimensional plane. For the already-mentioned tan β enhancement in the type-B scenario, lower values of y appear to be preferred. We further notice the viable region occurring for $m_{{\chi }_1}\gtrsim 100\text{GeV}$ and very low values of y. This corresponds to the coannihilation region already observed in the (m_S, m_D) plane.

To complete our analysis, we have therefore applied the constraints from the searches of neutral Higgs bosons at the LHC to the model points already shown in Figure 7, the impact of which is illustrated in Figure 8. In the left panel of the figure, we show all the model points (marked in red) already reported in Figure 7 but, this time, in the $(M_H-M_A,M_{H^{\pm }}-M_A)$ bidimensional plane. These points are compared with the points (marked in green) which are compatible with the LHC constraints from additional Higgs searches. On general grounds, the distribution of the model points resembles the shapes already seen in Figure 4. We notice, nevertheless, a preference for the scenario in which the M_W CDF value is mostly accounted for through a mass splitting between the additional 2HDM bosons, including the LHC constraints from Higgs searches having a very strong impact as these exclude the regions in which the pseudoscalar A boson is heavier than the CP-even H state.

FIGURE 8

FIGURE 8. Another view of the model points that have been shown in Figure 7 (red points) and those that are also complying with the LHC constraints from additional Higgs boson searches (green points) in the $(M_H-M_A,M_{H^{\pm }}-M_A)$ plane (left panel) and in the (M_A, tan β) plane (right panel). Details are given in the text.

A clearer picture is provided by the right panel of Figure 8, which shows the viable model points after applying the LHC Higgs search constraints in the (M_A, tan β) bidimensional plane. From this figure, one can argue that the most relevant constraints are the ones coming from searches of A → Zh and A → ZH decay channels, as the viable points lie mostly in areas in which such decay processes are kinematically forbidden. From the figure, one can thus conclude that dedicated searches for additional Higgs bosons with couplings, as in the type-X or lepton-specific configurations, have the highest potential in constraining the scenario under investigation.

4 Conclusion

In this work, we have considered the relatively simple fermionic singlet–doublet model for dark matter, first with a minimal Higgs sector and then with an extended one to include two doublets. We have explored the possibility of simultaneously fulfilling the collider and astroparticle physics constraints that allow us to obtain a successful DM candidate with the correct relic density and addressing two recent experimental anomalies, namely, the discrepancies with respect to the prediction in the SM of the muon anomalous magnetic moment (g − 2)_μ and the mass of the W boson M_W measured by the CDF collaboration.

We have shown that in the minimal singlet–doublet model with an SM-like Higgs sector, as a result of the presence of a new fermionic sector coupled with the SM gauge bosons, one can address only the $M_W^{\text{CDF}}$ anomaly while having a DM with the correct relic density. The extra particle spectrum does not couple to SM fermions and cannot explain the experimental (g − 2)_μ value. Nevertheless, the model parameter space is almost entirely excluded by the constraints on the DM particle that arise from direct detection.

Extending the Higgs sector of the singlet–doublet model to contain a second scalar doublet field is doubly beneficial. On the one hand, it allows one to evade the constraints from DM direct detection, and, on the other hand, one can also achieve a viable interpretation of the muon (g − 2) anomaly, besides the interpretation of the CDF M_W measurement. This is carried out by means of a light pseudoscalar A boson that strongly couples to muons. In this case, significant parts of the parameter space of the model are still allowed, but they will be challenged by the next round of collider and astroparticle physics experiments.

Author contributions

GA, as the corresponding author, proposed the idea of the manuscript and contributed to the analysis of dark matter phenomenology and to the fit of the anomalies. AD contributed to the building of the model and assessment of theoretical constraints and constraints from Higgs physics, due to his expertise in the field. Both authors contributed equivalent amounts to the editing of the text.

Funding

AD is supported by the Estonian Research Council (ERC) grant MOBTT86 and by the Junta de Andalucia through the Talentia Senior program grants PID2021-128396NB-I00, A-FQM-211-UGR18, and P18-FR-4314 with ERDF.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Other extensions, for instance, the ones discussed Refs. 33–35, in which the DM is an isosinglet fermion and the Higgs sector is enlarged to contain two doublet fields and a singlet pseudoscalar Higgs field, can also achieve this goal.

²The possibility of Dirac fermions was proposed in Ref. 38 and leads to a similar picture compared to the Majorana case.

References

1.The ATLAS Collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature (2022) 607:52–9. [Erratum: Nature 612, E24 (2022)]. doi:10.1038/s41586-022-04893-w

PubMed Abstract | CrossRef Full Text | Google Scholar

2.The CMS Collaboration. A portrait of the Higgs boson by the CMS experiment ten years after the discovery. Nature (2022) 607:60–8. doi:10.1038/s41586-022-04892-x

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. Astron Astrophys (2020) 641:A6. [Erratum: Astron.Astrophys. 652, C4 (2021)]. doi:10.1051/0004-6361/201833910

CrossRef Full Text | Google Scholar

4. Bertone G, Hooper D, Silk J. Particle dark matter: Evidence, candidates and constraints. Phys Rept (2005) 405:279–390. doi:10.1016/j.physrep.2004.08.031

CrossRef Full Text | Google Scholar

5. Arcadi G, Dutra M, Ghosh P, Lindner M, Mambrini Y, Pierre M, et al. The waning of the WIMP? A review of models, searches, and constraints. Eur Phys J C (2018) 78:203. doi:10.1140/epjc/s10052-018-5662-y

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Arcadi G, Djouadi A, Raidal M. Dark matter through the Higgs portal. Phys Rept (2020) 842:1–180. doi:10.1016/j.physrep.2019.11.003

CrossRef Full Text | Google Scholar

7. Aaltonen T, Amerio S, Amidei D, Anastassov A, Annovi A, Antos J, et al. High-precision measurement of the W boson mass with the CDF II detector. Science (2022) 376:170–6. doi:10.1126/science.abk1781

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zyla PA, Barnett RM, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. Review of particle physics. PTEP (2020) 2020:083C01. doi:10.1093/ptep/ptaa104

CrossRef Full Text | Google Scholar

9. Abi B, Albahri T, Al-Kilani S, Allspach D, Alonzi L, Anastasi A, et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys Rev Lett (2021) 126:141801. doi:10.1103/PhysRevLett.126.141801

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. Final report of the E821 muon anomalous magnetic moment measurement at BNL. Phys Rev D (2006) 73:072003. doi:10.1103/PhysRevD.73.072003

CrossRef Full Text | Google Scholar

11. Davier M, Hoecker A, Malaescu B, Zhang Z. Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon g − 2 and ${\alpha (m_{Z}^2)}$ using newest hadronic cross-section data. Eur Phys J (2017) C77:827. doi:10.1140/epjc/s10052-017-5161-6

CrossRef Full Text | Google Scholar

12. Keshavarzi A, Nomura D, Teubner T. Muon g − 2 and $\alpha(M_{Z}^2)$: A new data-based analysis. Phys Rev (2018) D97:114025. doi:10.1103/PhysRevD.97.114025

CrossRef Full Text | Google Scholar

13. Colangelo G, Hoferichter M, Stoffer P. Two-pion contribution to hadronic vacuum polarization. J High Energ Phys (2019) 02:006. doi:10.1007/JHEP02(2019)006

CrossRef Full Text | Google Scholar

14. Hoferichter M, Hoid BL, Kubis B. Three-pion contribution to hadronic vacuum polarization. J High Energ Phys (2019) 08:137. doi:10.1007/jhep08(2019)137

CrossRef Full Text | Google Scholar

15. Davier M, Hoecker A, Malaescu B, Zhang Z. A new evaluation of the hadronic vacuum polarisation contributions to the muon anomalous magnetic moment and to $\boldsymbol{\alpha}(\mathbf{m}_{\spmathbf{Z}}^{\spmathbf{2}})$. Eur Phys J (2020) C80:241. [Erratum: Eur. Phys. J. C80, 410 (2020)]. doi:10.1140/epjc/s10052-020-7792-2

CrossRef Full Text | Google Scholar

16. Keshavarzi A, Nomura D, Teubner T. The g − 2 of charged leptons, $\alpha(M_{Z}^2)$ and the hyperfine splitting of muonium. Phys Rev (2020) D101:014029. doi:10.1103/PhysRevD.101.014029

CrossRef Full Text | Google Scholar

17. Kurz A, Liu T, Marquard P, Steinhauser M. Hadronic contribution to the muon anomalous magnetic moment to next-to-next-to-leading order. Phys Lett (2014) B734:144–7. doi:10.1016/j.physletb.2014.05.043

CrossRef Full Text | Google Scholar

18. Melnikov K, Vainshtein A. Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment revisited. Phys Rev (2004) D70:113006. doi:10.1103/PhysRevD.70.113006

CrossRef Full Text | Google Scholar

19. Masjuan P, Sánchez-Puertas P. Pseudoscalar-pole contribution to the (g_μ − 2): A rational approach. Phys Rev (2017) D95:054026. doi:10.1103/PhysRevD.95.054026

CrossRef Full Text | Google Scholar

20. Colangelo G, Hoferichter M, Procura M, Stoffer P. Dispersion relation for hadronic light-by-light scattering: Two-pion contributions. J High Energ Phys (2017) 04:161. doi:10.1007/jhep04(2017)161

CrossRef Full Text | Google Scholar

21. Hoferichter M, Hoid BL, Kubis B, Leupold S, Schneider SP. Dispersion relation for hadronic light-by-light scattering: Pion pole. J High Energ Phys (2018) 10:141. doi:10.1007/jhep10(2018)141

CrossRef Full Text | Google Scholar

22. Gérardin A, Meyer HB, Nyffeler A. Lattice calculation of the pion transition form factor with N_f = 2 + 1 Wilson quarks. Phys Rev (2019) D100:034520. doi:10.1103/PhysRevD.100.034520

CrossRef Full Text | Google Scholar

23. Bijnens J, Hermansson-Truedsson N, Rodríguez-Sánchez A. Short-distance constraints for the HLbL contribution to the muon anomalous magnetic moment. Phys Lett (2019) B798:134994. doi:10.1016/j.physletb.2019.134994

CrossRef Full Text | Google Scholar

24. Colangelo G, Hagelstein F, Hoferichter M, Laub L, Stoffer P. Longitudinal short-distance constraints for the hadronic light-by-light contribution to (g − 2)_μ with large-N_c Regge models. J High Energ Phys (2020) 03:101. doi:10.1007/jhep03(2020)101

CrossRef Full Text | Google Scholar

25. Aoyama T, Asmussen N, Benayoun M, Bijnens J, Blum T, Bruno M, et al. The anomalous magnetic moment of the muon in the Standard Model. Phys Rept (2020) 887:1–166. doi:10.1016/j.physrep.2020.07.006

CrossRef Full Text | Google Scholar

26. Borsanyi S, Fodor Z, Guenther JN, Hoelbling C, Katz SD, Lellouch L, et al. Leading hadronic contribution to the muon magnetic moment from lattice QCD. Nature (2021) 593:51–5. doi:10.1038/s41586-021-03418-1

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Cohen T, Kearney J, Pierce A, Tucker-Smith D. Singlet-doublet dark matter. Phys Rev D (2012) 85:075003. doi:10.1103/PhysRevD.85.075003

CrossRef Full Text | Google Scholar

28. Cheung C, Sanford D. Simplified models of mixed dark matter. J Cosmology Astroparticle Phys (2014) 02:011. doi:10.1088/1475-7516/2014/02/011

CrossRef Full Text | Google Scholar

29. Calibbi L, Mariotti A, Tziveloglou P. Singlet-Doublet Model: Dark matter searches and LHC constraints. J High Energ Phys (2015) 10:116. doi:10.1007/jhep10(2015)116

CrossRef Full Text | Google Scholar

30. Crivellin A, Heeck J, Stoffer P. Perturbed lepton-specific two-Higgs-doublet model facing experimental hints for physics beyond the standard model. Phys Rev Lett (2016) 116:081801. doi:10.1103/PhysRevLett.116.081801

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Crivellin A, Kirk M, Kitahara T, Mescia F. Large t→cZ as a sign of vectorlike quarks in light of the W mass. Phys Rev D (2022) 106:L031704. doi:10.1103/PhysRevD.106.L031704

CrossRef Full Text | Google Scholar

32. de Giorgi A, Merlo L, Pokorski S. The low-scale seesaw solution to the M_W and (g − 2)_μ anomalies. Fortschritte der Physik (2022). doi:10.1002/prop.202300020

CrossRef Full Text | Google Scholar

33. Arcadi G, Djouadi A, Queiroz FDS. Models with two Higgs doublets and a light pseudoscalar: A portal to dark matter and the possible (g−2)μ excess. Phys Lett B (2022) 834:137436. doi:10.1016/j.physletb.2022.137436

CrossRef Full Text | Google Scholar

34. Arcadi G, Djouadi A. 2HD plus light pseudoscalar model for a combined explanation of the possible excesses in the CDF MW measurement and (g-2)μ with dark matter. Phys Rev D (2022) 106:095008. doi:10.1103/PhysRevD.106.095008

CrossRef Full Text | Google Scholar

35. Arcadi G, Benincasa N, Djouadi A, Kannike K. The 2HD+a model: Collider, dark matter and gravitational wave signals. arXiv (2022). doi:10.48550/arXiv.2212.14788

CrossRef Full Text | Google Scholar

36. Djouadi A. The Anatomy of electro-weak symmetry breaking. I: The Higgs boson in the standard model. Phys Rept (2008) 457:1–216. doi:10.1016/j.physrep.2007.10.004

CrossRef Full Text | Google Scholar

37. Branco GC, Ferreira PM, Lavoura L, Rebelo MN, Sher M, Silva JP. Theory and phenomenology of two-Higgs-doublet models. Phys Rept (2012) 516:1–102. doi:10.1016/j.physrep.2012.02.002

CrossRef Full Text | Google Scholar

38. Yaguna CE. Singlet-doublet Dirac dark matter. Phys Rev D (2015) 92:115002. doi:10.1103/PhysRevD.92.115002

CrossRef Full Text | Google Scholar

39. Arcadi G. 2HDM portal for singlet-doublet dark matter. Eur Phys J C (2018) 78:864. doi:10.1140/epjc/s10052-018-6327-6

CrossRef Full Text | Google Scholar

40. Belanger G, Boudjema F, Pukhov A, Semenov A. MicrOMEGAs: A program for calculating the relic density in the MSSM. Comput Phys Commun (2002) 149:103–20. doi:10.1016/S0010-4655(02)00596-9

CrossRef Full Text | Google Scholar

41. Belanger G, Boudjema F, Pukhov A, Semenov A. micrOMEGAs 2.0.7: A program to calculate the relic density of dark matter in a generic model. Comput Phys Commun (2007) 177:894–5. doi:10.1016/j.cpc.2007.08.002

CrossRef Full Text | Google Scholar

42. Choudhury A, Kowalska K, Roszkowski L, Sessolo EM, Williams AJ. Less-simplified models of dark matter for direct detection and the LHC. J High Energ Phys (2016) 04:182. doi:10.1007/JHEP04(2016)182

CrossRef Full Text | Google Scholar

43. Choudhury A, Kowalska K, Roszkowski L, Sessolo EM, Williams AJ. Blind spots for direct detection with simplified DM models and the LHC. Universe (2017) 3:41. doi:10.3390/universe3020041

CrossRef Full Text | Google Scholar

44. Veltman MJG. Limit on mass differences in the weinberg model. Nucl Phys B (1977) 123:89–99. doi:10.1016/0550-3213(77)90342-X

CrossRef Full Text | Google Scholar

45. Toussaint D. Renormalization effects from superheavy Higgs particles. Phys Rev D (1978) 18:1626–31. doi:10.1103/PhysRevD.18.1626

CrossRef Full Text | Google Scholar

46. Peskin ME, Takeuchi T. Estimation of oblique electroweak corrections. Phys Rev D (1992) 46:381–409. doi:10.1103/PhysRevD.46.381

CrossRef Full Text | Google Scholar

47. He HJ, Polonsky N, Su SF. Extra families, Higgs spectrum and oblique corrections. Phys Rev D (2001) 64:053004. doi:10.1103/PhysRevD.64.053004

CrossRef Full Text | Google Scholar

48. Barbieri R, Hall LJ, Nomura Y, Rychkov VS. Supersymmetry without a light Higgs boson. Phys Rev D (2007) 75:035007. doi:10.1103/PhysRevD.75.035007

CrossRef Full Text | Google Scholar

49. Enberg R, Fox PJ, Hall LJ, Papaioannou AY, Papucci M. LHC and dark matter signals of improved naturalness. J High Energ Phys (2007) 11:014. doi:10.1088/1126-6708/2007/11/014

CrossRef Full Text | Google Scholar

50. D’Eramo F. Dark matter and Higgs boson physics. Phys Rev D (2007) 76:083522. doi:10.1103/PhysRevD.76.083522

CrossRef Full Text | Google Scholar

51. Joglekar A, Schwaller P, Wagner CEM. Dark matter and enhanced Higgs to di-photon rate from vector-like leptons. J High Energ Phys (2012) 12:064. doi:10.1007/JHEP12(2012)064

CrossRef Full Text | Google Scholar

52. Aalbers J, Akerib DS, Akerlof CW, Al Musalhi AK, Alder F, Alqahtani A, et al. First dark matter search results from the LUX-ZEPLIN (LZ) experiment (2022).

Google Scholar

53. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro F, et al. Constraining the spin-dependent WIMP-nucleon cross sections with XENON1T. Phys Rev Lett (2019) 122:141301. doi:10.1103/PhysRevLett.122.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Davidson S, Haber HE. Erratum: Basis-independent methods for the two-Higgs-doublet model [Phys. Rev. D72, 035004 (2005)]. Phys Rev D (2005) 72:035004. [Erratum: Phys.Rev.D 72, 099902 (2005)]. doi:10.1103/PhysRevD.72.099902

CrossRef Full Text | Google Scholar

55. Barroso A, Ferreira PM, Ivanov IP, Santos R. Metastability bounds on the two Higgs doublet model. J High Energ Phys (2013) 06:045. doi:10.1007/JHEP06(2013)045

CrossRef Full Text | Google Scholar

56. Glashow SL, Weinberg S. Natural conservation laws for neutral currents. Phys Rev D (1977) 15:1958–65. doi:10.1103/PhysRevD.15.1958

CrossRef Full Text | Google Scholar

57. Pich A, Tuzon P. Yukawa alignment in the two-Higgs-doublet model. Phys Rev D (2009) 80:091702. doi:10.1103/PhysRevD.80.091702

CrossRef Full Text | Google Scholar

58. Berlin A, Gori S, Lin T, Wang LT. Pseudoscalar portal dark matter. Phys Rev D (2015) 92:015005. doi:10.1103/PhysRevD.92.015005

CrossRef Full Text | Google Scholar

59. Aad G, Abbott B, Abbott D, Abed Abud A, Abeling K, Abhayasinghe D, et al. Search for Higgs boson decays into two new low-mass spin-0 particles in the 4b channel with the ATLAS detector using pp collisions at \sqrt{s}= 13 TeV. Phys Rev D (2020) 102:112006. doi:10.1103/PhysRevD.102.112006

CrossRef Full Text | Google Scholar

60.The CMS collaboration Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, et al. Search for a light pseudoscalar Higgs boson in the boosted μμττ final state in proton-proton collisions at $\sqrt{s}=$ 13 TeV. J High Energ Phys (2020) 08:139. doi:10.1007/JHEP08(2020)139

CrossRef Full Text | Google Scholar

61. Tumasyan A, Adam W, Bergauer T, Dragicevic M, Ero J, Valle AED, et al. Search for low-mass dilepton resonances in Higgs boson decays to four-lepton final states in proton–proton collisions at $$\sqrt{s}=13\,\text {TeV}. Eur Phys J C (2022) 82:290. doi:10.1140/epjc/s10052-022-10127-0

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Djouadi A. The anatomy of electroweak symmetry breaking Tome II: The Higgs bosons in the Minimal Supersymmetric Model. Phys Rept (2008) 459:1–241. doi:10.1016/j.physrep.2007.10.005

CrossRef Full Text | Google Scholar

63. Abe T, Sato R, Yagyu K. Lepton-specific two Higgs doublet model as a solution of muon g − 2 anomaly. J High Energ Phys (2015) 07:064. doi:10.1007/JHEP07(2015)064

CrossRef Full Text | Google Scholar

64. Dedes A, Haber HE. Can the Higgs sector contribute significantly to the muon anomalous magnetic moment? J High Energ Phys (2001) 05:006. doi:10.1088/1126-6708/2001/05/006

CrossRef Full Text | Google Scholar

65. Djouadi A, Kohler T, Spira M, Tutas J. (e t) type leptoquarks at e p colliders. Z Phys C (1990) 46:679–86. doi:10.1007/BF01560270

CrossRef Full Text | Google Scholar

66. Barr SM, Zee A. Electric dipole moment of the electron and of the neutron. Phys Rev Lett (1990) 65:21–4. [Erratum: Phys.Rev.Lett. 65, 2920 (1990)]. doi:10.1103/PhysRevLett.65.21

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Chang D, Chang WF, Chou CH, Keung WY. Large two-loop contributions tog−2from a generic pseudoscalar boson. Phys Rev D (2001) 63:091301. doi:10.1103/PhysRevD.63.091301

CrossRef Full Text | Google Scholar

68. Larios F, Tavares-Velasco G, Yuan CP. Very lightCP-odd scalar in the two-Higgs-doublet model. Phys Rev D (2001) 64:055004. doi:10.1103/PhysRevD.64.055004

CrossRef Full Text | Google Scholar

69. Ilisie V. New Barr-Zee contributions to (g −2)_μ in two-Higgs-doublet models. J High Energ Phys (2015) 04:077. doi:10.1007/JHEP04(2015)077

CrossRef Full Text | Google Scholar

70. Aad G, Abbott B, Abbott D, Abed Abud A, Abeling K, Abhayasinghe D, et al. Search for heavy Higgs bosons decaying into tau leptons with the ATLAS detector using pp collisions at \sqrt{s}=13 TeV. Phys Rev Lett (2020) 125:051801. doi:10.1103/PhysRevLett.125.051801

PubMed Abstract | CrossRef Full Text | Google Scholar

71.CMS Collaboration. Searches for additional Higgs bosons and vector leptoquarks in ττ final states in proton-proton collisions at $\sqrt{s}=13∼\mathrm{TeV}$ (2022).

Google Scholar

72. Argyropoulos S, Haisch U. Benchmarking LHC searches for light 2HDM+a pseudoscalars. Scipost Phys (2022) 13:007. doi:10.21468/SciPostPhys.13.1.007

CrossRef Full Text | Google Scholar

73. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, Dragicevic M, et al. Search for a narrow resonance lighter than 200 GeV decaying to a pair of muons in proton-proton collisions at s=13 TeV. Phys Rev Lett (2020) 124:131802. doi:10.1103/PhysRevLett.124.131802

CrossRef Full Text | Google Scholar

74.The LHCb collaboration Aaij R, Abellán Beteta C, Ackernley T, Adeva B, Adinolfi M, et al. Searches for low-mass dimuon resonances. J High Energ Phys (2020) 10:156. doi:10.1007/JHEP10(2020)156

CrossRef Full Text | Google Scholar

75. Chun EJ, Kim J. Leptonic precision test of leptophilic two-Higgs-doublet model. J High Energ Phys (2016) 07:110. doi:10.1007/jhep07(2016)110

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Aad G, Abbott B, Abbott DC, Abud AA, Abeling K, et al. ATLAS Collaboration Search for heavy resonances decaying into a pair of Z bosons in the ℓ⁺ℓ⁻ℓ′⁺ℓ′⁻ and \ell ^+\ell ^-\nu {{\bar{\nu }}} final states using 139 fb−1 of proton–proton collisions at \sqrt{s} = 13TeV with the ATLAS detector. Eur Phys J C (2021) 81:332. doi:10.1140/epjc/s10052-021-09013-y

CrossRef Full Text | Google Scholar

77.The CMS collaboration Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Bergauer T, et al. Search for new neutral Higgs bosons through the H → ZA $\to \ell^{+}\ell^{-} \mathrm{b}\bar{\mathrm{b}}$ process in pp collisions at $\sqrt{s} =$ 13 TeV. J High Energ Phys (2020) 03:055. doi:10.1007/JHEP03(2020)055

CrossRef Full Text | Google Scholar

78. Aad G, Abbott B, Abbott DC, Abed Abud A, Abeling K, Abhayasinghe DK, et al. Search for a heavy Higgs boson decaying into a Z boson and another heavy Higgs boson in the ℓℓbb and ℓℓWW final states in pp collisions at \sqrt{s}=13\ \text {TeV} with the ATLAS detector. Eur Phys J C (2021) 81:396. doi:10.1140/epjc/s10052-021-09117-5

CrossRef Full Text | Google Scholar

79.ATLAS Collaboration. Search for heavy resonances decaying into a Z or W boson and a Higgs boson in final states with leptons and b-jets in 139 fb⁻¹ of pp collisions at $\sqrt{s}=13∼$TeV with the ATLAS detector (2022).

Google Scholar

80. Harlander RV, Liebler S, Mantler H. SusHi: A program for the calculation of Higgs production in gluon fusion and bottom-quark annihilation in the standard model and the MSSM. Comput Phys Commun (2013) 184:1605–17. doi:10.1016/j.cpc.2013.02.006

CrossRef Full Text | Google Scholar

81. Harlander RV, Liebler S, Mantler H. SusHi Bento: Beyond NNLO and the heavy-top limit. Comput Phys Commun (2017) 212:239–57. doi:10.1016/j.cpc.2016.10.015

CrossRef Full Text | Google Scholar

82. Ackermann M, Ajello M, Albert A, Atwood WB, Baldini L, Ballet J, et al. Search for gamma-ray emission from the Coma Cluster with six years of Fermi-LAT data. Astrophys J (2016) 819:149. [Erratum: Astrophys.J. 860, 85 (2018)]. doi:10.3847/0004-637X/819/2/149

CrossRef Full Text | Google Scholar

83. Ackermann M, Ajello M, Albert A, Anderson B, Atwood W, Baldini L, et al. Updated search for spectral lines from Galactic dark matter interactions with pass 8 data from the Fermi Large Area Telescope. Phys Rev D (2015) 91:122002. doi:10.1103/PhysRevD.91.122002

CrossRef Full Text | Google Scholar