- 1Graphene and Advanced 2D Materials Research Group (GAMRG), School of Engineering and Technology, Sunway University, Petaling Jaya, Selangor, Malaysia
- 2Department of Basic Science, Hamedan University of Technology, Hamedan, Iran
- 3State Key Laboratory of Precision Spectroscopy, Quantum Institute for Light and Atoms, Department of Physics, East China Normal University, Shanghai, China
- 4Department of Physics, Government College University, Faisalabad, Pakistan
- 5Advanced Communication Engineering (ACE) Centre of Excellence, Universiti Malaysia Perlis, Kangar, Perlis, Malaysia
The weak force sensing based on a coherent quantum noise cancellation (CQNC) scheme is presented in a hybrid cavity optomechanical system containing a trapped ensemble of ultracold atoms and an optical parametric amplifier (OPA). In the proposed system, the back-action noise can be completely eliminated at all frequencies and through the proper choice of the OPA parameters, and the noise spectral density can also be reduced at lower frequencies. This leads to a significant enhancement in the sensitivity of the cavity optomechanical weak force sensor, and the noise spectral density also surpasses the standard quantum limit (SQL) even for the small input power at the lower detection frequency. Furthermore, the experimental feasibility of this scheme is also briefly discussed. This study can be used for the realization of a force sensor based on hybrid cavity optomechanical systems and for the coherent quantum control in macroscopic systems.
1 Introduction
Cavity optomechanics is an emerging research area which explores the coherent coupling between the optical mode and the mechanical mode through the radiation pressure of photons trapped inside an optical cavity [1–3]. It has also made significant advances in this modern era of quantum technology such as ultrahigh-precision measurement [4], gravitation-wave detection [5], quantum information processing (QIP) [6], non-classical photon statistics [7–10], quantum entanglement [11–19], macroscopic quantum coherence [20–22], ground-state cooling of mechanical oscillator [23, 24], and optomechanically induced transparency (OMIT) [25–32] including quantum teleportation [33, 34] and quantum communication [33–35]. Moreover, the measurement of weak forces at the quantum limit of sensitivity is of particular importance [36, 37] and also leads to major developments in cavity optomechanical sensors [38, 39]. In particular, one of the greatest applications of optomechanical sensors is the detection of gravitational waves [40], which directly leads to the rapid development of sensors based on cavity optomechanical systems [1, 41, 42]. In addition, optomechanical sensors can also give accurate results to measure various physical quantities like mass [43–45], acceleration [46–49], displacement [50–53] and force [54–58], magnetometry [59–61], and acoustic sensing [62, 63]. However, such kind of optomechanical sensors have limitations due to the presence of the shot noise and the back-action noise, and the competition between them leads to the notion of the standard quantum limit (SQL) [56, 64]. The quantum non-demolition measurement [65] through quantum entanglement [66] or squeezing [67–69] can be used to surpass the SQL, e.g., some pioneering theoretical works suggest that the squeezed states can be used to detect the gravitational waves using supersensitive interferometry [38, 70, 71]. Furthermore, a few experimental protocols to investigate possible quantum gravity effects on macroscopic mechanical oscillators that are preliminarily prepared in a high purity state are given [72].
In the optomechanical sensor, as we increase the input power to enhance the measurement strength and to decrease the shot noise, it also increases the unwanted measurement back-action noise. This means that both these noises have opposite scaling with the input laser power and we need to reduce or completely eliminate the back-action noise to increase the force sensitivity, that is why the complete elimination of back-action noise is the most important goal for all the optomechanical sensing based platforms. Except for the quantum thermometry using sideband asymmetry of a laser-cooled mechanical resonator, where back-action is not unwanted, but desirable [2, 73]. It has been shown that back-action-evading measurements of a single quadrature of nanomechanical motion can increase the force sensitivity [74], whereas two-mode back-action-evading measurements in a single-mode cavity can also surpass the SQL [75]. Another approach for obtaining the sub-SQL is based on the CQNC of the back-action noise through quantum interference. In this approach, an anti-noise path in the system is introduced through the addition of an ancillary oscillator which manifests an equal and opposite response to the light field, and it cancels the back-action noise [76–78]. So, the CQNC scheme can delete the back-action noise induced due to the radiation pressure at all frequencies and surpass the SQL [79, 80]. In recent developments, hybrid optomechanical systems containing atomic ensembles significantly improve the optomechanical cooling [81–85], the realization of quantum squeezing of the motion of mechanical oscillators [86], and provide entangled Einstein–Podolsky–Rosen (EPR) states and squeezed states [76, 87–89]. Interestingly, it is possible to enhance the precision of a position measurement inside an optomechanical cavity with the optical parametric amplifier (OPA) [90] and force sensitivity in a simple [91] and hybrid optomechanical system with trapped atomic ensemble [92, 93]. Very recently, a study on Zeptonewton force sensing with squeezed quadratic optomechanics was proposed, and the results showed that by optimizing the system, a force sensitivity seven orders of magnitude higher than any conventional linear cavity optomechanical sensors could be achieved [94].
Based on these works, the present work aims to study the CQNC scheme-based weak force sensing in a hybrid optomechanical system containing both the degenerate OPA and the trapped atomic ensemble inside the cavity. In this way, we have investigated the effects of the amplitude and phase of the OPA on the spectral force sensing. The coupling between the optomechanical cavity and the atomic ensemble is necessary for the CQNC process. On the other hand, tuning the OPA parameters can improve the precision of force sensing and reach the sub-SQL sensitivity. This system can also create wider spacing in the normal mode splitting (NMS) and a greater degree of the squeezing spectrum as compared with just an OPA or an atomic ensemble [95].
The present paper is organized as follows. In Section 2, we present the hybrid optomechanical system and its model Hamiltonian for the optomechanical force sensor. We obtain the linearized equations of motion in Section 3. In Section 4, we have discussed the enhancement of CQNC and subsequently weak force sensing under different conditions. We have also briefly discussed the experimental feasibility of this proposed scheme. Finally, we have given a conclusion in Section 5.
2 The model Hamiltonian
We consider the hybrid optomechanical system as shown in Figure 1, which consists of a single-mode optical cavity with resonance frequency ωa and a mechanical oscillator (MO) with mass, m; frequency, ωm; and damping rate, γm. This mechanical oscillator is coupled to the cavity mode through the radiation pressure and is simultaneously subjected to an external force Fext. Furthermore, this hybrid optomechanical system contains an ensemble of N number of two-level ultracold atoms trapped inside it and interacts non-resonantly with the intracavity field and a classical control field. For a sufficiently large value of N, this trapped atomic ensemble behaves effectively as a negative-mass oscillator (NMO) [92, 93, 96–99]. The cavity mode is also coherently driven by a classical field of frequency, ωL,; input power, PL; and wavelength, λL. Moreover, the cavity mode is also coupled to a degenerate OPA. The total Hamiltonian of this hybrid system can be written as the following:
where
where
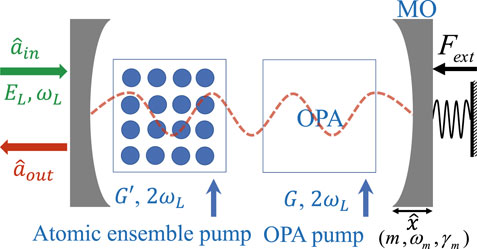
FIGURE 1. Overview of the hybrid optomechanical system which consists of an optomechanical cavity, a degenerate optical parametric amplifier (OPA), and an ensemble of two-level ultracold atoms. The atomic ensemble behaves effectively as a negative-mass oscillator (NMO) under the bosonization process [92, 93, 96]. An external force Fext is applied on the MO acting as a force sensor. The cavity is also driven by an external classical field with power PL and frequency ωL.
3 Dynamics of the system
The linearized quantum Langevin equations (QLEs) of this system can be obtained from the Hamiltonian given in Eq. 2 and simultaneously adding the noise and damping terms in these QLEs [64],
where γm and Γ are the mechanical damping rate and the collective atomic dephasing rate, respectively. The mechanical noise term is
Here, Δ = Δa + g0Xs is the effective cavity detuning, and αs is the steady-state value of the intracavity field amplitude which can always be taken as real and positive with an appropriate chosen phase of the driving field EL. Furthermore, we define the optical and atomic quadrature operators
Here,
where
Therefore, Eq. 5 can be given in the Fourier space as follows:
where
4 Force sensing and CQNC
Solving Eq. 8, we can find the phase quadrature of the cavity field,
Furthermore, the detected output phase quadrature of the cavity field mode can be expressed in terms of the input noises as follows:
where
For applying the CQNC conditions we have considered here
for all frequencies, and the back-action term will be canceled in Eq. 11, but the small term will remain and contribute as the shot noise which is the effect of the OPA. In the CQNC scheme, we should have g = G′ and
whereas the added force noise
The aforementioned Eq. 15 contains the thermal Langevin force coupled with a thermal reservoir at temperature T (first term), the shot noise in the phase quadrature of the optical field (second term), the noise injected into the system through the OPA (third term), and the atomic noise (fourth term). Furthermore, we can find the sensitivity of the force measurement by using the definition of spectral density SF,add(ω) of the added noise [77, 100] as follows:
Using the conditions of the CQNC and for ω ≪ κ (this is not difficult to achieve experimentally, since it is easy to prepare bad cavities), this approximation is also used in earlier works [91–93, 96]; further, we find the spectral noise as follows:
where the back-action noise term scaled to g2 is notably deleted. Furthermore, our obtained result can be compared to the standard optomechanical system, discussed in Refs. [1, 77, 93], as the following equation
which contains the shot noise and the back-action noise terms proportional to 1/g2 and g2, respectively. The thermal Brownian noise results in a constant background noise to the force sensitivity independent of the input laser power. At T = 0, we can minimize the right hand side of Eq. 18 with respect to g2, or proportionally, the input laser power
and equivalently, the minimized noise spectral density for the CQNC at T = 0 is given as follows:
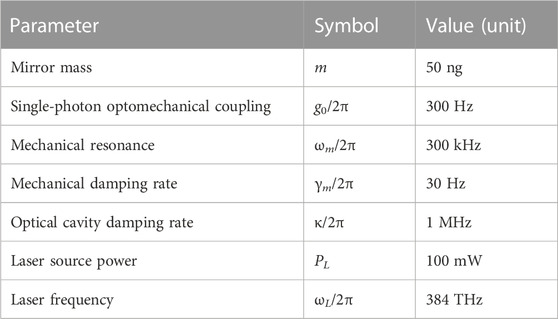
We will compare the noise spectrum in our proposed scheme with a bare standard optomechanical system formed by an optical cavity coupled with a MO [1]. The SQL for stationary force detection comes from the minimization of the force spectrum of the standard optomechanical system at a given frequency over the driving power as given in Refs. [1, 92, 93, 96]. Next, we use a set of parameters to simulate the noise spectral densities of the current research system, the fixed parameters are given in Table 1, and the rest of the parameters are taken as the phase of the OPA, 0⩽θ⩽2π; the gain of OPA, 0⩽G⩽0.3κ; and also three values for detuning, Δ/ωm = 0, 1, 2.
The noise spectral densities for the standard optomechanical system (SQL, black solid line), the proposed hybrid optomechanical system with OPA, and atomic ensemble (dashed lines) including CQNC schemes (red solid line) are shown in Figure 2, where the black solid line is obtained using Eq. 18, the dashed lines, namely, G/κ = 0, 0.1, 0.3, and θ = 0, ±π/2, ±π, ±3π/2 correspond to Eq. 17, and the solid red line corresponds to Eq. 20. The spectral density for the CQNC scheme is limited to the shot noise term over the whole detection bandwidth and is the main advantage of the CQNC scheme. In this context, the variation of the noise spectral density of the hybrid optomechanical system with the detection frequency for the different values of the OPA pump gain G and the phase angle θ = π is shown in Figure 2A. At the mechanical resonance condition $\left (\omega = \omega_{m} \right)$ and for effective cavity detuning Δ = 0, the noise spectral density of the standard optomechanical system (SQL) and that of the hybrid optomechanical system with the OPA pump is equal to the noise spectral density of the CQNC scheme. With the gradual increase in the OPA pump gain, G, the noise spectral density can be suppressed almost nearly by two orders of magnitude at frequencies below and above the mechanical resonance condition as shown in Figure 2A. In addition, we find that in the case of G = 0, the dashed purple and the black solid line almost coincide. This is because, in this case, the first two terms in both Eqs 17, 18 are much bigger than their later terms, and consequently, they have almost the same behavior. Then, we have the same result obtained by a conventional CQNC scheme [93]. However, if we take non-zero values for G, we have smaller values for SF as can be seen for G = 0.1 and G = 0.3 in Figure 2A. In fact, it shows that present scheme has much better results than conventional CQNC scheme such as those in Ref. [93]. Furthermore, an experimental scheme to expand the detection bandwidth for gravitational-wave observation in which quantum uncertainty can be squeezed inside one of the optical resonators at high frequencies while keeping the low-frequency sensitivity unchanged [102]. However, for a given value of G, the noise spectral density gets suppressed only for θ = π, whereas for other values of θ, its values increase beyond the SQL as shown in Figure 2B.
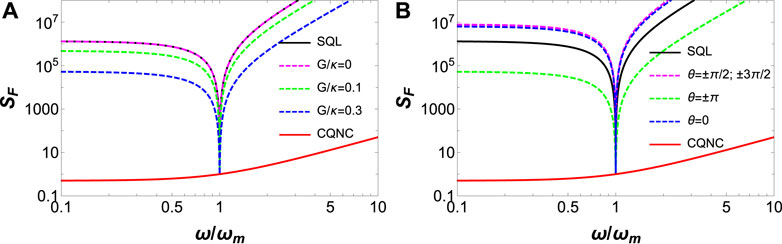
FIGURE 2. Noise power spectral densities for the standard optomechanical system SSQL (black solid line), the hybrid optomechanical system with the OPA (colored dashed line), and the coherent quantum noise cancellation SCQNC (red solid line) as a function of frequency ω/ωm. The spectral densities are normalized to ℏmωmγm. The OPA parameters are given as (A) θ = π and (B) G/κ = 0.3 and the rest of the parameters are given in Table 1. Here, we have taken Q = ωm/γm =104.
The noise spectral densities as functions of the laser driving power PL (scaled to the optomechanical coupling strength g2) for on-resonance
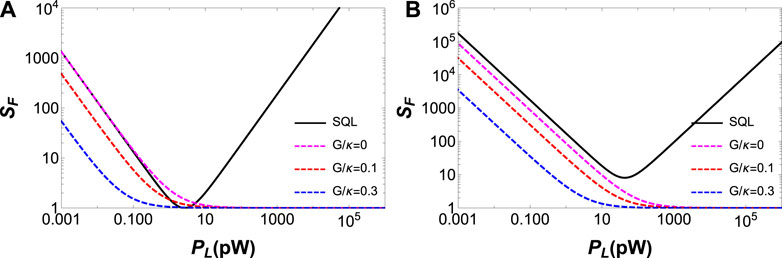
FIGURE 3. Noise spectral density (A) on mechanical resonance
In Figure 4, we have plotted the noise spectral density of force measurement in mechanical on-resonance and off-resonance conditions for different values of the effective detuning, Δ. For on-resonance case (ω = ωm), it can be seen that resonant CQNC with Δ = 0 gives better sensitivity for force measurement than heterodyne CQNC with Δ = ωm and Δ = 2ωm, as shown in Figure 4A. Moreover, for a higher value of cavity detuning, Δ = 2ωm, noise spectral density can even surpass the SQL, and so, it degrades force sensitivity. Furthermore, for off-resonance case (ω = ωm + 4γm), again, Δ = 0 gives better force sensitivity as compared to heterodyne CQNC as shown in Figure 4B. However, this resonant CQNC gives much better results for on-resonance cases only. This is because in case of on-resonance condition, the anti-Stokes process dominates within the system which leads to a significant cooling of the mechanical oscillator and facilitates a better force sensitivity.
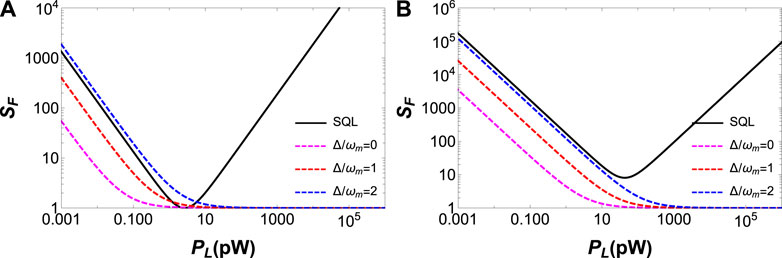
FIGURE 4. Noise spectral density (A) on mechanical resonance (ω = ωm) and (B) off-resonance
We have studied the effect of
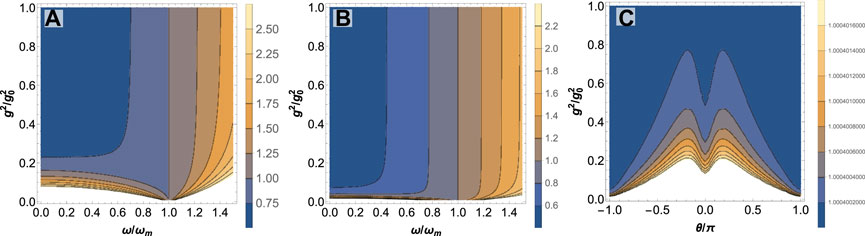
FIGURE 5. Contour plot of noise spectral density for weak force measurement as function of (A) the relative squared optomechanical coupling strength
Based on our research results, we would like to add here that unlike earlier work cited in Ref. [96] where all the numerical results were studied for only one optimal value of squeezing phase minimizing the shot noise contribution, we have explored the most generalized scenario with different non-linear gain and phase angle of the OPA; in fact, in our scheme, both the parameters of OPA can significantly reduce the measurement of weak force sensing. So, our numerical results are more generalized and are easily implemented in comparison to that of Ref. [96]. This is because, as in the work given by Ref. [96], they need an infinite bandwidth value and very high squeezing parameters for the externally coupled squeeze vacuum reservoir to the cavity mode; this is still very challenging from the experimental and integrated photonics points of view as their scheme cannot avoid the detrimental effects of the inevitable major losses in the transmission and injection of the squeezed light from the external squeezed reservoir into the optomechanical cavity. Furthermore, from the analytical point of view, these squeezing bandwidth parameters related to the external vacuum reservoir should ideally be infinite; only then will the Markovian approximation hold valid for the input noise terms related to cavity field operators in Ref. [96], whereas in our case, OPA parameters are almost of the order of the cavity decay rate which again makes our scheme easily feasible in future experiments. Another important advantage of adding squeezed OPA within an optomechanical system is that it provides significant ground state cooling as shown in our earlier work [24], which is very difficult for the scheme given in Ref. [96], and hence, our scheme will give better quantum measurement due to the cooling effect even in unresolved sideband regime of cavity optomechanics.
4.1 Experimental feasibility and measurement of weak force
Finally, it is necessary to discuss the experimental feasibility and detection of the weak force in the cavity optomechanical system. Here, we need to admit that implementing our proposal experimentally is challenging. Fortunately, Hertzberg et al. demonstrated back-action-evading measurements of a single quadrature of nanomechanical motion can increase the force sensitivity [74]. Furthermore, Møller et al. in 2017 demonstrated destructive or constructive interference of the quantum back-action for the two mechano-oscillators, further showing that the back-action-evading measurement in the hybrid system leads to an enhancement of displacement sensitivity in a negative mass reference frame [103]. This suggests that the quantum back-action noise can be eliminated experimentally by some quantum physical mechanism. In addition, a recent study reported that they observed quantum back-action noise due to optomechanical coupling leading to correlated mechanical fluctuations of the two mechanical oscillators in a driven optical cavity [104]. The observed quantum back-action noise undoubtedly provides a solid foundation for the realization of our scheme. Moreover, Daniel et al. reported that the collective motion of atoms can be driven through quantum noises in the radiation pressure and that the quantum back-action of this motion onto the cavity field produces ponderomotive squeezing. In turn, they detected this quantum phenomenon by measuring sub-wave-noise optical squeezing [105].
In particular, the ensembles of ultracold atoms are used for atomic clocks [106], quantum simulation [107], quantum information processing [108], dynamical phase transitions in an optical cavity [109], and coherent quantum noise cancellation [93, 96]. According to the purpose in these works, a large range of the number of atoms has been used. In the optomechanical CQNC schemes, in one hand the cavity field is strongly driven but on the other hand there is a weak coupling between the atom-field modes which consequently there is the low-excitation limit for atomic ensemble. In fact, under the conditions of large atom number N, weak atom-cavity coupling, and the low-excitation limit, the dynamics of the atomic ensemble can be described in terms of a collective bosonic operators. For example, the total number of atoms are approximately large such as N ≈ 1 × 1013 used to show Einstein-Podolsky-Rosen paradox [110], and N ≈ 1 × 1013 used in the CQNC force sensing [93] as we have assumed in the present scheme. Note that the number of excited atoms can be quantified by
On the other hand, quantum systems that exhibit dynamic quantum back-action of radiation pressure have to address a range of design considerations, including physical size and dissipation [2]. Fortunately, recent experimental progress in the fabrication technology of cavity optomechanical systems is very mature and perfect, opening up enormous possibilities in the design and integration of hybrid quantum interfaces based on optical cavities [111], for example, the optomechanical resonator with a micromechanical membrane coupled simultaneously with atomic gas [112, 113]. In particular, this also lays the foundation for the conditions under which CQNC can be realized. In addition, these hybrid systems that combine optomechanical resonators with the best features of atomic (or atom like) systems to develop experimentally feasible approaches based on CQNC are given in Refs. [89, 103].
In order to better promote the experiment realization of the present scheme, we briefly give the reference ranges for the key parameters in the experiment according to the current experimental ability. It is worth noting that these parameter values are mainly collected by Aspelmeyer et al. [1]. When selecting experimental parameters, we need to comprehensively consider the stability of the system, the difficulty of device processing, the experimental cost, etc. Specifically, the mass of the moving mirror m is chosen as 10–22 kg
5 Conclusion
We theoretically investigate the weak force sensing through the CQNC scheme in a hybrid optomechanical system containing an ensemble of trapped ultracold atoms and the OPA. For a sufficiently large number of atoms, this trapped ensemble of ultracold atoms acts as a negative-mass oscillator, which destructively interacts with the optical cavity mode leading to the cancellation of the back-action noise. In addition, the presence of OPA reduces the shot noise in the regime of the low driving power and also gives a broad range of detection frequency. In particular, the CQNC and shot noise reduction occur when the effective linear optomechanical coupling strength g and the collective atomic coupling with the optical cavity mode given by G are both equal to each other. Furthermore, it can be seen that in case of resonance CQNC, i.e., effective cavity detuning Δ = 0, a comparable value of G, and suitable value of phase angle θ leads to the suppression of the noise spectral density significantly at frequencies below and above the mechanical resonance condition. Our study provides a promising platform for weak force sensing and can also be explored in other systems of quantum sensing with waveguide, interferometer, or parity-time symmetric microcavity.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
MK thanks and acknowledges the International Research Network Grant Scheme (STR-IRNGS-SET-GAMRG-01-2021).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics: Nano-and micromechanical resonators interacting with light. Springer (2014).
2. Kippenberg TJ, Vahala KJ. Cavity optomechanics: Back-action at the mesoscale. science (2008) 321(5893):1172–6. doi:10.1126/science.1156032
4. Teufel JD, Donner T, Castellanos-Beltran MA, JenniferHarlow W, Lehnert KW. Nanomechanical motion measured with an imprecision below that at the standard quantum limit. Nat nanotechnology (2009) 4(12):820–3. doi:10.1038/nnano.2009.343
5. Arvanitaki A, Geraci AA. Detecting high-frequency gravitational waves with optically levitated sensors. Phys Rev Lett (2013) 110(7):071105. doi:10.1103/physrevlett.110.071105
6. Mancini S, Vitali D, Tombesi P. Scheme for teleportation of quantum states onto a mechanical resonator. Phys Rev Lett (2003) 90(13):137901. doi:10.1103/physrevlett.90.137901
7. Rabl P. Photon blockade effect in optomechanical systems. Phys Rev Lett (2011) 107(6):063601. doi:10.1103/physrevlett.107.063601
8. Singh SK, Raymond Ooi CH. Quantum correlations of quadratic optomechanical oscillator. JOSA B (2014) 31(10):2390–8. doi:10.1364/josab.31.002390
9. Singh SK, Muniandy SV. Temporal dynamics and nonclassical photon statistics of quadratically coupled optomechanical systems. Int J Theor Phys (2016) 55(1):287–301. doi:10.1007/s10773-015-2661-8
10. Kundu A, Singh SK. Heisenberg-angevin formalism for squeezing dynamics of linear hybrid optomechanical system. Int J Theor Phys (2019) 58(8):2418–27. doi:10.1007/s10773-019-04133-4
11. Hofer SG, Wieczorek W, Aspelmeyer M, Hammerer K. Quantum entanglement and teleportation in pulsed cavity optomechanics. Phys Rev A (2011) 84(5):052327. doi:10.1103/physreva.84.052327
12. De Chiara G, Paternostro M, Massimo Palma G. Entanglement detection in hybrid optomechanical systems. Phys Rev A (2011) 83(5):052324. doi:10.1103/physreva.83.052324
13. Wang Y-D, Chesi S, Clerk AA. Bipartite and tripartite output entanglement in three-mode optomechanical systems. Phys Rev A (2015) 91(1):013807. doi:10.1103/physreva.91.013807
14. Barzanjeh SH, Naderi MH, Soltanolkotabi M. Steady-state entanglement and normal-mode splitting in an atom-assisted optomechanical system with intensity-dependent coupling. Phys Rev A (2011) 84(6):063850. doi:10.1103/physreva.84.063850
15. Vitali D, Gigan S, Anderson F, Böhm HR, Tombesi P, Guerreiro A, et al. Optomechanical entanglement between a movable mirror and a cavity field. Phys Rev Lett (2007) 98(3):030405. doi:10.1103/physrevlett.98.030405
16. Asjad M, Tombesi P, Vitali D. Quantum phase gate for optical qubits with cavity quantum optomechanics. Opt Express (2015) 23(6):7786–94. doi:10.1364/oe.23.007786
17. Singh SK, Peng J-X, Asjad M, Mazaheri M. Entanglement and coherence in a hybrid laguerre–Gaussian rotating cavity optomechanical system with two-level atoms. J Phys B: At Mol Opt Phys (2021) 54(21):215502. doi:10.1088/1361-6455/ac3c92
18. Mazaheri M, Jamasb S. Pulsed entanglement and quantum steering in a three-mode electro-optomechanical system. Quan Inf Process (2020) 19(8):222–19. doi:10.1007/s11128-020-02721-6
19. Gebremariam T, Mazaheri M, Zeng Y, Li C. Dynamical quantum steering in a pulsed hybrid opto-electro-mechanical system. JOSA B (2019) 36(2):168–77. doi:10.1364/josab.36.000168
20. Jin L, Peng J-X, Yuan Q-Z, Feng X-L. Macroscopic quantum coherence in a spinning optomechanical system. Opt Express (2021) 29(25):41191–205. doi:10.1364/oe.443486
21. Peng J-X, Jin C, Jin L, Liu Z-X. Quantum coherence regulated by nanoparticles in a whispering-gallery-mode microresonator. Annalen der Physik (2021) 533(11):2100210. doi:10.1002/andp.202100210
22. Zheng Q, Xu J, Yao Y, Li Y. Detecting macroscopic quantum coherence with a cavity optomechanical system. Phys Rev A (2016) 94(5):052314. doi:10.1103/physreva.94.052314
23. Wilson-Rae I, Nooshi N, Zwerger W, Kippenberg TJ. Theory of ground state cooling of a mechanical oscillator using dynamical backaction. Phys Rev Lett (2007) 99(9):093901. doi:10.1103/physrevlett.99.093901
24. Asjad M, Abari NE, Zippilli S, Vitali D. Optomechanical cooling with intracavity squeezed light. Opt Express (2019) 27(22):32427–44. doi:10.1364/oe.27.032427
25. Agarwal GS, Huang S. Electromagnetically induced transparency in mechanical effects of light. Phys Rev A (2010) 81(4):041803. doi:10.1103/physreva.81.041803
26. Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Albert S. Optomechanically induced transparency. Science (2010) 330(6010):1520–3. doi:10.1126/science.1195596
27. Lin Q, Rosenberg J, Chang D, Ryan C, Eichenfield M, Vahala KJ, et al. Coherent mixing of mechanical excitations in nano-optomechanical structures. Nat Photon (2010) 4(4):236–42. doi:10.1038/nphoton.2010.5
28. Safavi-Naeini AH, Alegre TP, Chan J, Eichenfield M, Winger M, Lin Q, et al. Electromagnetically induced transparency and slow light with optomechanics. Nature (2011) 472(7341):69–73. doi:10.1038/nature09933
29. Peng J-X, Chen Z, Yuan Q-Z, Feng X-L. Optomechanically induced transparency in a laguerre-Gaussian rotational-cavity system and its application to the detection of orbital angular momentum of light fields. Phys Rev A (2019) 99(4):043817. doi:10.1103/physreva.99.043817
30. Peng J-X, Chen Z, Yuan Q-Z, Feng X-L. Double optomechanically induced transparency in a laguerre-Gaussian rovibrational cavity. Phys Lett A (2020) 384(7):126153. doi:10.1016/j.physleta.2019.126153
31. Singh SK, Asjad M, Ooi CH. Tunable optical response in a hybrid quadratic optomechanical system coupled with single semiconductor quantum well. Quan Inf Process (2022) 21(2):47–18. doi:10.1007/s11128-021-03401-9
32. Singh SK, Parvez M, Abbas T, Peng J-X, Mazaheri M, Asjad M. Tunable optical response and fast (slow) light in optomechanical system with phonon pump. Phys Lett A (2022) 442:128181. doi:10.1016/j.physleta.2022.128181
33. Asjad M, Zippilli S, Tombesi P, Vitali D. Large distance continuous variable communication with concatenated swaps. Physica Scripta (2015) 90(7):074055. doi:10.1088/0031-8949/90/7/074055
34. Asjad M, Tombesi P, Vitali D. Feedback control of two-mode output entanglement and steering in cavity optomechanics. Phys Rev A (2016) 94(5):052312. doi:10.1103/physreva.94.052312
35. Manninen J, Asjad M, Ojajärvi R, Kuusela P, Massel F. Clauser-horne-shimony-holt bell inequality test in an optomechanical device. Phys Rev A (2018) 98(4):043831. doi:10.1103/physreva.98.043831
36. Braginsky VB, Vorontsov YI, Thorne KS. Quantum nondemolition measurements. Science (1980) 209(4456):547–57. doi:10.1126/science.209.4456.547
38. Aasi J, Abadie J, Abbott BP, Abbott R, Abbott TD, Abernathy MR, et al. Enhanced sensitivity of the ligo gravitational wave detector by using squeezed states of light. Nat Photon (2013) 7(8):613–9.
39. Li B-B, Ou L, Lei Y, Liu Y-C. Cavity optomechanical sensing. Nanophotonics (2021) 10(11):2799–832. doi:10.1515/nanoph-2021-0256
40. Yu H, McCuller L, Tse M, Kijbunchoo N, Barsotti L, Mavalvala N, et al. Quantum correlations between light and the kilogram-mass mirrors of ligo. Nature (2020) 583(7814):43–7. doi:10.1038/s41586-020-2420-8
41. McClelland DE, Mavalvala N, Chen Y, Schnabel R. Advanced interferometry, quantum optics and optomechanics in gravitational wave detectors. Laser Photon Rev (2011) 5(5):677–96. doi:10.1002/lpor.201000034
42. Miao H, Ma Y, Zhao C, Chen Y. Enhancing the bandwidth of gravitational-wave detectors with unstable optomechanical filters. Phys Rev Lett (2015) 115(21):211104. doi:10.1103/physrevlett.115.211104
43. Shang-Wu B, Xin-You L, Yin T-S, Zhu G-L, Qian B, Wu Y. Mass sensing by quantum criticality. Opt Lett (2019) 44(3):630–3. doi:10.1364/ol.44.000630
44. Liu S, Liu B, Wang J, Sun T, Yang W-X. Realization of a highly sensitive mass sensor in a quadratically coupled optomechanical system. Phys Rev A (2019) 99(3):033822. doi:10.1103/physreva.99.033822
45. Sansa M, Defoort M, Brenac A, Hermouet M, Banniard L, Alexandre F, et al. Optomechanical mass spectrometry. Nat Commun (2020) 11(1):3781–7. doi:10.1038/s41467-020-17592-9
46. Krause AG, Winger M, TimBlasius D, Lin Q, Painter O. A high-resolution microchip optomechanical accelerometer. Nat Photon (2012) 6(11):768–72. doi:10.1038/nphoton.2012.245
47. Qvarfort S, Serafini A, Barker PF, Bose S. Gravimetry through non-linear optomechanics. Nat Commun (2018) 9(1):3690–11. doi:10.1038/s41467-018-06037-z
48. Zhou F, Bao Y, Madugani R, Long DA, Gorman JJ, LeBrun TW. Broadband thermomechanically limited sensing with an optomechanical accelerometer. Optica (2021) 8(3):350–6. doi:10.1364/optica.413117
49. Cheng L, Yang B, Zheng X, Guo X, Sun Z, Zhou L, Huang X. 2
50. Wilson DJ, Sudhir V, Piro N, Ryan S, Ghadimi A, Kippenberg TJ. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature (2015) 524(7565):325–9. doi:10.1038/nature14672
51. Rossi M, Mason D, Chen J, Tsaturyan Y, Albert S. Measurement-based quantum control of mechanical motion. Nature (2018) 563(7729):53–8. doi:10.1038/s41586-018-0643-8
52. Brawley GA, Vanner MR, Larsen PE, Schmid S, Boisen A, Bowen WP. Nonlinear optomechanical measurement of mechanical motion. Nat Commun (2016) 7(1):10988–7. doi:10.1038/ncomms10988
53. Liu T, Pagliano F, van Veldhoven R, Pogoretskiy V, Jiao Y, Fiore A. Integrated nano-optomechanical displacement sensor with ultrawide optical bandwidth. Nat Commun (2020) 11(1):2407–7. doi:10.1038/s41467-020-16269-7
54. CarltonCaves M, Thorne KS, Drever RWP, Sandberg VD, Zimmermann M. On the measurement of a weak classical force coupled to a quantum-mechanical oscillator. i. issues of principle. Rev Mod Phys (1980) 52(2):341–92. doi:10.1103/revmodphys.52.341
55. Gavartin E, Verlot P, Kippenberg TJ. A hybrid on-chip optomechanical transducer for ultrasensitive force measurements. Nat nanotechnology (2012) 7(8):509–14. doi:10.1038/nnano.2012.97
56. Schreppler S, Spethmann N, Nathan B, Botter T, Barrios M, Stamper-Kurn DM. Optically measuring force near the standard quantum limit. Science (2014) 344(6191):1486–9. doi:10.1126/science.1249850
57. Ghobadi R, Gholizadeh S, Mazaheri M. Weak force measurement in bistable optomechanical system. Int J Opt Photon (2015) 9(1):19–26.
58. Liu Z, Wei Y, Chen L, Li J, Dai S, Zhou F, et al. Phonon-laser ultrasensitive force sensor. Phys Rev Appl (2021) 16(4):044007. doi:10.1103/physrevapplied.16.044007
59. Forstner S, Prams S, Knittel J, Van Ooijen ED, Swaim JD, Harris GI, et al. Cavity optomechanical magnetometer. Phys Rev Lett (2012) 108(12):120801. doi:10.1103/physrevlett.108.120801,
60. Forstner S, Sheridan E, Knittel J, Humphreys CL, Brawley GA, Rubinsztein-Dunlop H, et al. Micrometry: Ultrasensitive optomechanical magnetometry (adv. Mater. 36/2014). Adv Mater (2014) 26(36):6355. doi:10.1002/adma.201470249
61. Li B-B, Jan B, Hoff UB, Madsen LS, Forstner S, Prakash V, et al. Quantum enhanced optomechanical magnetometry. Optica (2018) 5(7):850–6. doi:10.1364/optica.5.000850
62. Basiri-Esfahani S, Armin A, Forstner S, Bowen WP. Precision ultrasound sensing on a chip. Nat Commun (2019) 10(1):132–9. doi:10.1038/s41467-018-08038-4
63. Guggenheim JA, Jing L, Allen TJ, Colchester RJ, Noimark S, Ogunlade O, et al. Ultrasensitive plano-concave optical microresonators for ultrasound sensing. Nat Photon (2017) 11(11):714–9. doi:10.1038/s41566-017-0027-x
65. Thorne KS, Drever RWP, CarltonCaves M, Zimmermann M, Sandberg VD. Quantum nondemolition measurements of harmonic oscillators. Phys Rev Lett (1978) 40(11):667–71. doi:10.1103/physrevlett.40.667
66. Ma Y, Miao H, Pang BH, Evans M, Zhao C, Harms J, et al. Proposal for gravitational-wave detection beyond the standard quantum limit through epr entanglement. Nat Phys (2017) 13(8):776–80. doi:10.1038/nphys4118
67. Clark JB, Lecocq F, Simmonds RW, Aumentado J, Teufel JD. Observation of strong radiation pressure forces from squeezed light on a mechanical oscillator. Nat Phys (2016) 12(7):683–7. doi:10.1038/nphys3701
68. Alexander O, Sedlmeir F, Vogl U, Dirmeier T, Schunk G, DmitryStrekalov V, et al. Squeezed vacuum states from a whispering gallery mode resonator. Optica (2019) 6(11):1375–80. doi:10.1364/optica.6.001375
69. Min JY, Cripe J, Mansell GL, McRae TG, Ward RL, BramSlagmolen JJ, et al. Broadband reduction of quantum radiation pressure noise via squeezed light injection. Nat Photon (2020) 14(1):19–23. doi:10.1038/s41566-019-0527-y
70. Hollenhorst JN. Quantum limits on resonant-mass gravitational-radiation detectors. Phys Rev D (1979) 19(6):1669–79. doi:10.1103/physrevd.19.1669
71. Dodonov VV, Man’ko VI, Rudenko VN, Zamolodchikov AIB, Kopeliovich BZ, Lapidus LI, et al. Nondemolition measurements in gravitational-wave experiments. Sov Phys JETP (1980) 51:443.
72. Bonaldi M, Borrielli A, Chowdhury A, Di Giuseppe G, Li W, Marino F, et al. Probing quantum gravity effects with quantum mechanical oscillators. The Eur Phys J D (2020) 74(9):178–9. doi:10.1140/epjd/e2020-10184-6
73. Safavi-Naeini AH, Chan J, Hill JT, Gröblacher S, Miao H, Chen Y, et al. Laser noise in cavity-optomechanical cooling and thermometry. New J Phys (2013) 15(3):035007. doi:10.1088/1367-2630/15/3/035007
74. Hertzberg JB, Rocheleau T, Ndukum T, Savva M, Clerk AA, Schwab KC. Back-action-evading measurements of nanomechanical motion. Nat Phys (2010) 6(3):213–7. doi:10.1038/nphys1479
75. Woolley MJ, Clerk AA. Two-mode back-action-evading measurements in cavity optomechanics. Phys Rev A (2013) 87(6):063846. doi:10.1103/physreva.87.063846
76. Hammerer K, Aspelmeyer M, Simon Polzik E, Zoller P. Establishing einstein-poldosky-rosen channels between nanomechanics and atomic ensembles. Phys Rev Lett (2009) 102(2):020501. doi:10.1103/physrevlett.102.020501
77. Wimmer MH, Steinmeyer D, Hammerer K, Heurs M. Coherent cancellation of backaction noise in optomechanical force measurements. Phys Rev A (2014) 89(5):053836. doi:10.1103/physreva.89.053836
78. Schweer J, Steinmeyer D, Hammerer K, Heurs M. All-optical coherent quantum-noise cancellation in cascaded optomechanical systems. Phys Rev A (2022) 106(3):033520. doi:10.1103/PhysRevA.106.033520
79. Tsang M, CarltonCaves M. Coherent quantum-noise cancellation for optomechanical sensors. Phys Rev Lett (2010) 105(12):123601. doi:10.1103/physrevlett.105.123601
80. Tsang M, CarltonCaves M. Evading quantum mechanics: Engineering a classical subsystem within a quantum environment. Phys Rev X (2012) 2(3):031016. doi:10.1103/physrevx.2.031016
81. Genes C, Ritsch H, Vitali D. Micromechanical oscillator ground-state cooling via resonant intracavity optical gain or absorption. Phys Rev A (2009) 80(6):061803. doi:10.1103/physreva.80.061803
82. Hammerer K, Stannigel K, Genes C, Zoller P, Treutlein P, Camerer S, et al. Optical lattices with micromechanical mirrors. Phys Rev A (2010) 82(2):021803. doi:10.1103/physreva.82.021803
83. Genes C, Ritsch H, Michael Drewsen A, Dantan A. Atom-membrane cooling and entanglement using cavity electromagnetically induced transparency. Phys Rev A (2011) 84(5):051801. doi:10.1103/physreva.84.051801
84. Camerer S, Korppi M, Jöckel A, Hunger D, Hänsch TW, Treutlein P. Realization of an optomechanical interface between ultracold atoms and a membrane. Phys Rev Lett (2011) 107(22):223001. doi:10.1103/physrevlett.107.223001
85. Gebremariam T, Zeng Y-X, Mazaheri M, Li C. Enhancing optomechanical force sensing via precooling and quantum noise cancellation. SCIENCE CHINA Phys Mech Astron (2020) 63(1):210311–1. doi:10.1007/s11433-019-9424-y
86. Edwina Wollman E, Lei CU, Weinstein AJ, Suh J, Kronwald A, Marquardt F, et al. Quantum squeezing of motion in a mechanical resonator. Science (2015) 349(6251):952–5. doi:10.1126/science.aac5138
87. Wasilewski W, Jensen K, Hanna K, Jan Renema J, Balabas MV, Simon Polzik E. Quantum noise limited and entanglement-assisted magnetometry. Phys Rev Lett (2010) 104(13):133601. doi:10.1103/physrevlett.104.133601
88. Muschik CA, Eugene SP, Cirac JI. Dissipatively driven entanglement of two macroscopic atomic ensembles. Phys Rev A (2011) 83(5):052312. doi:10.1103/physreva.83.052312
89. EugenePolzik S, Hammerer K. Trajectories without quantum uncertainties. Annalen der Physik (2015) 527(1-2):A15–20. A15–A20. doi:10.1002/andp.201400099
90. Peano V, Schwefel HGL, Marquardt CH, Marquardt F. Intracavity squeezing can enhance quantum-limited optomechanical position detection through deamplification. Phys Rev Lett (2015) 115(24):243603. doi:10.1103/physrevlett.115.243603
91. Wen Z, Zhang S-D, Adam M, Jing H. Weak-force sensing with squeezed optomechanics. SCIENCE CHINA Phys Mech Astron (2020) 63(2):224211. doi:10.1007/s11433-019-9451-3
92. Ali M, Dalafi A, Bemani F, Naderi MH. Force sensing in hybrid bose-einstein-condensate optomechanics based on parametric amplification. Phys Rev A (2019) 100(2):023815. doi:10.1103/physreva.100.023815
93. Bariani F, Seok H, Singh S, Vengalattore M, Meystre P. Atom-based coherent quantum-noise cancellation in optomechanics. Phys Rev A (2015) 92(4):043817. doi:10.1103/physreva.92.043817
94. Zhang S-D, Wang J, Jiao Y-F, Zhang H, Li Y, Zuo Y-L. Zeptonewton force sensing with squeezed quadratic optomechanics. arXiv preprint arXiv:2202.08690 (2022).
95. He Q, Badshah F, Basit A, Guo P, Zhang X, Zhou Z, et al. Normal-mode splitting and ponderomotive squeezing in a nonlinear optomechanical system assisted by an atomic ensemble. JOSA B (2020) 37(4):911–20. doi:10.1364/josab.381878
96. Ali M, Bemani F, Naderi MH, Roknizadeh R, Vitali D. Force sensing based on coherent quantum noise cancellation in a hybrid optomechanical cavity with squeezed-vacuum injection. New J Phys (2016) 18(7):073040. doi:10.1088/1367-2630/18/7/073040
97. Bemani F, Černotík O, Ruppert LDV, Filip R. Force sensing in an optomechanical system with feedback-controlled in-loop light. Phys Rev Appl (2022) 17(3):034020. doi:10.1103/physrevapplied.17.034020
98. Sadat Ebrahimi M, Ali M, Harouni MB. Single-quadrature quantum magnetometry in cavity electromagnonics. Phys Rev A (2021) 103(6):062605. doi:10.1103/physreva.103.062605
99. Ali M, Dalafi A, Naderi MH. Ultraprecision quantum sensing and measurement based on nonlinear hybrid optomechanical systems containing ultracold atoms or atomic bose–einstein condensate. AVS Quan Sci (2021) 3(2):024701. doi:10.1116/5.0035952
100. Satya Sainadh U, Anil Kumar M. Force sensing beyond standard quantum limit with optomechanical “soft” mode induced by nonlinear interaction. Opt Lett (2020) 45(3):619–22. doi:10.1364/OL.384751
101. Chakram S, Patil YS, Chang L, Vengalattore M. Dissipation in ultrahigh quality factor sin membrane resonators. Phys Rev Lett (2014) 112(12):127201. doi:10.1103/physrevlett.112.127201
102. Korobko M, Ma Y, Chen Y, Schnabel R. Quantum expander for gravitational-wave observatories. Light: Sci Appl (2019) 8(1):118–8. doi:10.1038/s41377-019-0230-2
103. Christoffer BM, Thomas RA, Vasilakis G, Zeuthen E, Tsaturyan Y, Eugene SP, et al. Quantum back-action-evading measurement of motion in a negative mass reference frame. Nature (2017) 547(7662):191–5. doi:10.1038/nature22980
104. Spethmann N, Kohler J, Schreppler S, Buchmann L, Stamper-Kurn DM. Cavity-mediated coupling of mechanical oscillators limited by quantum back-action. Nat Phys (2016) 12(1):27–31. doi:10.1038/nphys3515
105. Brooks DWC, Botter T, Schreppler S, Purdy TP, Nathan B, Stamper-Kurn DM. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature (2012) 488(7412):476–80. doi:10.1038/nature11325
106. Ludlow AD, Boyd MM, Ye J, Peik E, Schmidt PO. Optical atomic clocks. Rev Mod Phys (2015) 87(2):637. doi:10.1103/RevModPhys.87.637
107. Cazalilla MA, Rey AM. Ultracold fermi gases with emergent su (n) symmetry. Rep Prog Phys (2014) 77(12):124401. doi:10.1088/0034-4885/77/12/124401
108. Daley AJ. Quantum computing and quantum simulation with group-ii atoms. Quantum Inf Process (2011) 10:865–84. doi:10.1007/s11128-011-0293-3
109. Muniz JA, Barberena D, Lewis-Swan RJ, Young DJ, Cline JRK, Rey AM, et al. Exploring dynamical phase transitions with cold atoms in an optical cavity. Nature (2020) 580(7805):602–7. doi:10.1038/s41586-020-2224-x
110. He QY, Reid MD. Towards an einstein–podolsky–rosen paradox between two macroscopic atomic ensembles at room temperature. New J Phys (2013) 15(6):063027. doi:10.1088/1367-2630/15/6/063027
111. Kurizki G, Bertet P, Kubo Y, Mølmer K, Petrosyan D, Rabl P, et al. Quantum technologies with hybrid systems. Proc Natl Acad Sci (2015) 112(13):3866–73. doi:10.1073/pnas.1419326112
112. Ian H, Gong ZR, Liu Y-X, Sun CP, Nori F. Cavity optomechanical coupling assisted by an atomic gas. Phys Rev A (2008) 78(1):013824. doi:10.1103/physreva.78.013824
113. Hunger D, Camerer S, Korppi M, Jockel A, Hansch T. Coupling ultracold atoms to mechanical oscillators. Comptes Rendus Physique (2011) 12(9-10):871–87. doi:10.1016/j.crhy.2011.04.015
114. Murch KW, Moore KL, Gupta S, Stamper-Kurn DM. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat Phys (2008) 4(7):561–4. doi:10.1038/nphys965
115. Arcizet O, Cohadon P-F, Briant T, Pinard M, Antoine H. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature (2006) 444(7115):71–4. doi:10.1038/nature05244
116. Guha B, Allain PE, Lemaitre A, Leo G, Favero I. Force sensing with an optomechanical self-oscillator. Phys Rev Appl (2020) 14(2):024079. doi:10.1103/physrevapplied.14.024079
117. Chan J, Alegre TP, Safavi-Naeini AH, Hill JT, Krause A, Gröblacher S, et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature (2011) 478(7367):89–92. doi:10.1038/nature10461
118. Kleckner D, Pepper B, Jeffrey E, Sonin P, Thon SM, Bouwmeester D. Optomechanical trampoline resonators. Opt express (2011) 19(20):19708. doi:10.1364/oe.19.019708
Keywords: quantum noise cancellation, optical parametric amplifier, standard quantum limit, optomechanical force sensor, ultracold atoms
Citation: Singh SK, Mazaheri M, Peng J-X, Sohail A, Khalid M and Asjad M (2023) Enhanced weak force sensing based on atom-based coherent quantum noise cancellation in a hybrid cavity optomechanical system. Front. Phys. 11:1142452. doi: 10.3389/fphy.2023.1142452
Received: 11 January 2023; Accepted: 14 March 2023;
Published: 07 April 2023.
Edited by:
Q. H. Liu, Hunan University, ChinaReviewed by:
Xiu-Min Lin, Fujian Normal University, ChinaMa Hongyang, Qingdao University of Technology, China
Zia Uddin, COMSATS University, Islamabad Campus, Pakistan
Copyright © 2023 Singh, Mazaheri, Peng, Sohail, Khalid and Asjad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jia-Xin Peng, MTgyMTc2OTYxMjdAMTYzLmNvbQ==
†These authors have contributed equally to this work and share first authorship
 S. K. Singh1†
S. K. Singh1† Jia-Xin Peng
Jia-Xin Peng A. Sohail
A. Sohail Mohammad Khalid
Mohammad Khalid M. Asjad
M. Asjad