Smoothed particle hydrodynamics method for free surface flow based on MPI parallel computing

In the field of computational fluid dynamics (CFD), smoothed particle hydrodynamics (SPH) is very suitable for simulating problems with large deformation, free surface flow and other types of flow scenarios. However, traditional smoothed particle hydrodynamics methods suffer from the problem of high computation complexity, which constrains their application in scenarios with accuracy requirements. DualSPHysics is an excellent smoothed particle hydrodynamics software proposed in academia. Based on this tool, this paper presents a largescale parallel smoothed particle hydrodynamics framework: parallelDualSPHysics, which can solve the simulation of large-scale free surface flow. First, an efficient domain decomposition algorithm is proposed. And the data structure of DualSPHysics in a parallel framework is reshaped. Secondly, we proposed a strategy of overlapping computation and communication to the parallel particle interaction and particle update module, which greatly improves the parallel efficiency of the smoothed particle hydrodynamics method. Finally, we also added the pre-processing and post-processing modules to enable parallelDualSPHysics to run in modern high performance computers. In addition, a thorough evaluation shows that the 3 to 120 million particles tested can still maintain more than 90% computing efficiency, which demonstrates that the parallel strategy can achieve superior parallel efficiency.

1 Introduction

With the fast development of computer hardware and the rapid improvement of computing performance, computational fluid dynamics (CFD) provides an alternative tool for investigating scientific problems and has been successfully applied to solving practical engineering problems. Historically, CFD solvers have been dominated by mesh-based methods, including finite element method (FEM), finite volume method (FVM), and the finite difference method (FDM). For quite a long time, these mesh-based methods have been applied to industry problems (e.g., aerospace [1], chip packaging [2], etc.). However, due to the pre-defined mesh, mesh-based methods present some important limitations when solving problems with complex boundary, high-speed impact response of materials and large deformation. Meshless methods, which replace meshes with a set of arbitrarily distributed particles, are demonstrated to be advantageous over mesh-based methods [3]. Recently, the academia and industry communities have seen an exponential growth of meshless methods in the use of CFD solvers. Among many meshless methods, the smoothed particle hydrodynamics (SPH) method [4] is the most popular one. Compared with the traditional methods, the SPH method uses a series of particles to describe the field variables (such as position, velocity and density) in space. There is no dependency between particles, and it does not need to set the background mesh associated with each other in the solution area. Therefore, it can better describe the behavior of fluid at complex boundaries. The meshless characteristic makes SPH the primary choice for simulating problems of free surface flow, multiphase flow and impact load.

SPH was originally proposed by Monaghan in 1977 [4] to solve astrophysics problems. Then it was successfully applied to the simulation of polytropic stellar models for astrophysics. SPH uses Lagrangian perspective to describe the motion of fluid particles. Therefore it does not need to follow the constraints of Euler method. Particles can move freely with each other in the solution region according to the update rules. As a result, SPH can well describe the physical scene with complex motion boundary. Besides the ability to deal with problems that are difficult to solve by traditional mesh-based methods, SPH has its own drawbacks, such as tension instability and difficulty to deal with boundary conditions. The main obstacle that prevents its application to solving large scale real world problems is its computation complexity. Over the last several decades, a lot of research effort [5]; [6]; [7]; [8]; [9]; [10]; [11] has been devoted to improving the computation efficiency of SPH. In SPH, particles only interacts with neighboring particles within a specific range. Therefore, the computation of SPH shows simple data dependence relations and good data locality. This feature makes it possible to accelerate SPH with different levels of parallelization. The original SPH code was developed to run on single-core CPUs. Compared with the single core CPU, multi-core shared memory CPUs integrate multiple computing cores into the same chip. They interact with data through the internal bus, and the task allocation is uniformly scheduled through the Operating System (OS). Therefore, it is easy to execute tasks on multiple cores. At present, many SPH codes based on multithreading acceleration technology have been proposed. They use OpenMP to explicitly allocate computing tasks to each core of CPU. Thus accelerating SPH with thread-level parallelism. For example, Daisuke et al. systematically discussed the impact of different computing core architecture organizations on the computational efficiency of SPH method. Their experiments showed that processor using Many Integrated Core (MIC) had obvious acceleration effect on the parallel SPH method [12]. Then, their other work is based on the successful application of shared memory multiprocessors in the Discrete Element Method (DEM), which showed the universality of multi-core processors parallel computing framework [13]. Luo et al. used OpenMP to discuss the computational efficiency of simulating dam-break flow in different threads under the framework of multi-core parallelism. Their work showed that under the condition of more than 2 million particle size, the increase of data exchange overhead between CPU cores reduced the computational efficiency when the number of threads increases [14]. In addition to thread-level parallelism, data-level parallelism can be realized with Single Instruction Multiple Data (SIMD) technology. Intel provides the support of the intrinsics¹ instruction set macro package for SIMD technology. This macro package provided instruction sets with different vector widths such as Streaming SIMD Extensions (SSE), Advanced Vector Extensions (AVX) and AVX-512, and there are rich documents attached, developers only need to follow the instruction specification to realize the vectorization parallelism of SPH (support C/C++). Its principle is to convert the SPH code to the vectorization unit of the CPU through the vectorization instruction set for calculation, and then calculate n data at a time according to the width of the vector register (the vector width is n), so as to accelerate the simulation process of SPH. At present, Willis et al. showed that using AVX-512 to optimize the serial SPH code can obtain up to 4 speedups [5]. Therefore, vectorization acceleration is also an important parallel scheme in CPU. With the development of hardware technology, the computational efficiency of SPH has been greatly improved. For example, the Graphics Computing Unit (GPU) originally used for graphics processing integrates many computing units and extremely long pipelines. In addition, the NVIDIA has launched Compute Unified Device Architecture (CUDA) as a new computing framework and had gained more and more extensive applications and attention in industry and academia. Developers can write code using C/C++/FORTRAN language and run it with ultra-high performance on GPU supporting CUDA, which makes it more convenient to transplant SPH code to GPU. Therefore, data intensive tasks are very suitable for computing using GPU. Harada and Kawaguchi first used GPU to improve SPH calculation efficiency to simulate the flow procedure of more than 4 million fluid particles, but they only put part of SPH on GPU for calculation at first [6]. The disadvantage of this method is that it will lead to frequent data exchange between GPU and CPU in the system update stage, which will lead to great communication overhead. Then, they implemented the whole SPH method on GPU by introducing a three-dimensional grid structure [7], and achieved up to 28.5x speedups, since then, more GPU based optimizations have made great progress [8]; [9]; [10].

We have discussed the progress of multi threading, vectorization and GPU acceleration in SPH methods, but they are all implemented on a single node architecture. However, the computing power of supercomputers composed of multiple computing nodes far exceeds that of single node computers. Regardless of using homogeneous pure CPU/GPU and heterogeneous CPU + GPU/DSP (accelerator) supercomputers, the SPH codes can be transplanted to clusters with one million cores through MPI communication. At present, Frontier is the fastest in the TOP500 List² of global supercomputing, it is equipped with 8,730,112 AMD Optimized 3rd Generation EPYC 64C 2 GHz processors, and the peak performance of floating-point operation reaches 1102 Petaflops/s (1.1 Exaflop/s). And supercomputers have new breakthroughs in computing power every few years, which undoubtedly provides strong computing resource support for the CFD field. The “E” level (1 Exaflop/s) computing era will greatly promote the development of CFD. The parallel SPH method based on MPI has made great progress. For example, Oger et al. successfully used 32,768 processes to simulate the ball falling experiment of 100 million fluid particles through MPI library, and clearly captured the details of liquid splash, and it can maintain more than 90% computational efficiency [3]. Many studies have shown that the key to the high efficiency of large-scale parallel SPH method is how to deal with the load balancing problem of particles [15]; [16]; [17], so that each process can be evenly distributed to the same number of particles as much as possible. Guo et al. uses the open-source software Zoltan as the evaluation weight solution to solve the load balancing problem of the SPH method in large-scale cases [18], they used 12,000 processes to simulate the incompressible flow problem and still achieved 43% efficiency [19]. Domínguez et al. solved the load balancing problem and applied non-blocking communication to hide the communication. Finally, they simulated nearly 1 billion particles for Weakly Compressible SPH (WCSPH) using up to 64 GPUs in modern supercomputing system [20].

At present, the SPH method attracts researchers from all over the world because of its superior performance. Therefore, there are many excellent open source software, which are widely spread in academic circles and industry, these software can available at www.spheric-sph.org. Among them, the influential SPH open-source software are SWIFT [21], GADGET [22], PYSPH [23], DualSPHysics [24] and SPlisHSPlasH [25]. SWIFT and GADGET are mainly used to simulate cosmology and astrophysics. Both of them integrate asynchronous MPI communication optimization technology, so they can run directly on supercomputer for large-scale simulation. PYSPH had been written using Python language and is developed by Indian Institute of Technology (IIT). Because the software architecture is effectively encapsulated, developers can efficiently design various SPH variant algorithms without paying attention to the specific implementation of the bottom layer. SPlisHSPlasH realizes the pressure solver and multi-phase flow algorithm through OpenMP, Vectorization and CUDA optimization. DualSPHysics (dual.sphysics.org) was jointly developed by Manchester University and Vigo University based on practical engineering applications. It can provide solutions for simulating free surface flow, multiphase flow and fluid-structure coupling problems. In addition, the software also couples the Discrete Element Method (DEM) [26]; [27], and also has a perfect pre-processing software gencase and post-processing module, so that developers can quickly establish their own simulation scenarios according to rich description documents. DualSPHysics software that is originated from SPHysics is written in FORTRAN. Because the code did not optimize the computational performance, the software can only solve small-scale physical problems. Therefore, in order to optimize the low computational efficiency of the traditional SPH method, DualSPHysics has been developed. Developers have implemented the CPU/GPU version of DualSPHysics using OpenMP and CUDA optimization respectively. However, they initially worked on a single node. Then, Domínguez et al. implemented DualSPHysics with multiple GPU versions and successfully applied the parallel SPH code to the interaction analysis of underwater drilling platforms and ocean waves [20]. However, up to date, the multi-CPUs version of DualSPhysics program has not been released. Therefore, the motivation of this paper is to implement the multi-CPUs version of DualSPhysics on a large-scale cluster through MPI for simulation experiments, so as to further optimize the CPU version of DualSPhysics. In summary, this paper makes the following contributions:

• We implemented the parallel version of DualSPHysics based on multiple CPUs through MPI. Among them, we improved the pre-processing and post-processing functions of the parallel version of the software. It is extended to fluid simulation that can support large-scale engineering cases.

• We use packaging operation and asynchronous communication to hide between computing and communication, and improve the scalability of large-scale parallel SPH code.

• The parallel version of SPH code we developed can run on large-scale clusters with superior performance, and it can simulate the physical scene of practical engineering applications.

The remaining module structure of this paper are as follows: Section 2 introduces the theory and development of smooth particle hydrodynamics method, and Section 3 introduces the procedure of implementing parallelDualSPHysics using MPI. Section 4 tests the performance of the parallel version of parallelDualSPHysics, and tests the strong scalability and weak scalability respectively, an engineering simulation example is given.

2 Smoothed particle hydrodynamics method

Unlike mesh-based methods, the SPH method is a typical particle method, which uses a series of nodes as interpolation points. These nodes carry the information of physical variables, such as position, velocity and density, and then use these particles to discretize the Navier-Stokes (N-S) equation. In SPH method, the fluid particles after the N-S equation is discretized are regarded as weakly compressible, and then, the update of particles is based on the interpolation of all particles within the smooth length h. The 2D example corresponds to a circle in the support domain, and the 3D example corresponds to a sphere in space. In the definition domain Ω, any continuous field function in space can be represented by the following equation:

$F\left(\mathit{r}\right)=\int F\left({\mathit{t}}^{\prime }\right)\delta \left(\mathit{t}-{\mathit{t}}^{\prime }\right)d{\mathit{t}}^{\prime }(1)$

Where δ(t − t′) is a Dirac function, according to the basic principle of SPH introduced above, the field function (Eq. 1) of any variable in space can be approximated by integration. So the field function in space can be expressed by the following Eq. 2.

$F\left(\mathit{t}\right)=\int F\left({\mathit{t}}^{\prime }\right)W\left(\mathit{t}-{\mathit{t}}^{\prime },h\right)d{\mathit{t}}^{\prime }(2)$

Where t is the vector variable in space (e.g., velocity, density and position), W is the smooth kernel function, which needs to meet many characteristics, such as the smooth kernel function must be sufficiently smooth and always greater than or equal to 0. By interpolating the continuous function F in Eq. 2 with discrete particles, the value of particle a can be calculated by interpolation of all neighboring particles in the support domain.

$F\left({\mathit{t}}_a\right)\approx {\displaystyle \sum _b}F\left({\mathit{t}}_b\right)W\left({\mathit{t}}_a-{\mathit{t}}_b,h\right)\mathrm{\Delta }{V}_b(3)$

The volume ΔV_b of particles b is used in particle approximation in order to replace the infinitesimal volume element dt’ as shown in Eq. 3. Then, the mass of particle b can be expressed by the following formula: m_b = ΔV_bρ_b. Therefore, Eq. 3 is further converted to the following form.

$F\left({\mathit{t}}_a\right)\approx {\displaystyle \sum _b}F\left({\mathit{t}}_b\right)\frac{m_b}{{\rho }_b}W\left({\mathit{t}}_a-{\mathit{t}}_b,h\right)(4)$

Eq. 4 is the discrete procedure of SPH method, and Figure 1 shows the particle approximation process of the SPH method, the calculation of particle i can be interpolated according to its corresponding neighbor particles in the support domain. Therefore, it can be used to discrete the momentum conservation equation, and finally obtain the discrete form of acceleration solved by Eq. 5.

$\frac{d{\mathit{v}}_a}{dt}=-{\displaystyle \sum _b}{m}_b\left(\frac{P_b}{{\rho }_b^2}+\frac{P_a}{{\rho }_a^2}+{\mathrm{\Pi }}_{ab}\right){\nabla }_a{W}_{ab}+\mathit{g}(5)$

FIGURE 1

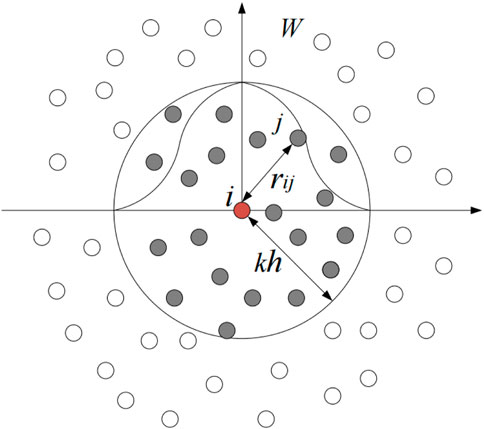
FIGURE 1. Interpolation principle of the smoothed particle hydrodynamics method, including kernel approximation and particle approximation.

Where P is the pressure, v_a is the velocity of particle a, ρ is the density, m is mass of the particle, g is the acceleration of gravity (g = 9.8 m/s²), Π_ab is the given artificial viscosity, Monaghan proposed the idea of artificial viscosity because of its simplicity, and the viscosity term Π_ab is defined as follows:

${\mathrm{\Pi }}_{ab}=\left\{\begin{array}{c}1\frac{-\lambda {{\displaystyle \bar{c}}}_{ab}{\mu }_{ab}}{{{\displaystyle \bar{\rho }}}^{ab}},v_{ab}\cdot r_{ab}<0\hfill \\ 0,v_{ab}\cdot r_{ab}>0\hfill \end{array}\right.(6)$

The viscosity term Π_ab is given by Eq. 6, where r_ab = r_a − r_b, v_ab = v_a − v_b represent the position and velocity of particles (a and b) respectively, λ represent the coefficient to be adjusted, and ${\mu }_{ab}=h{v}_{ab}\cdot r_{ab}/\left(r_{ab}^2+{\eta }^2\right),{\eta }^2=0.01h^2$, ${\bar{c}}_{ab}=0.5\left(c_a+c_b\right)$ is the speed of sound transmission.

Similarly, because the mass of particles is the same, the calculation formula of fluid density can only be obtained by discretizing the continuity equation through Eq. 4.

$\frac{d{\rho }_a}{dt}={\displaystyle \sum _b}{m}_b{\mathit{v}}_{ab}{\nabla }_a{W}_{ab}(7)$

Where v_ab = v_a − v_b and ∇_aW_ab = ∇_aW(r_a − r_b, h).

In the discrete solution of the SPH method, the fluid particles are generally assumed to be weakly compressible, the pressure calculation of particles is determined by Eq. 7 and equation of state. Therefore, the pressure calculation of particles can be described by Eq. 8.

$P=B\left[{\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }-1\right](8)$

Where γ = 7 for water, ρ₀ = 1000 kg/m³, $B=c_0^2{\rho }_0/\gamma$, and $c_0=c({\rho }_0)=\sqrt{(\partial P)/(\partial \rho )}$ when ρ = ρ₀, c₀ represents the speed of local sound.

In addition, three common kernel functions are provided showing as Eqs 9–11, where q = t/h, t is the distance between particle a and particle b arbitrarily in the influence domain, h is the smooth length.

1. Gaussian kernel

$W\left(t,h\right)={\alpha }_D{e}^{-q^2}(9)$

Where α_D is equal to $\frac{1}{{\pi }^{\frac{1}{2}}h}$, $\frac{1}{\pi h^2}$ and $\frac{1}{\pi \frac{3}{2}{h}^3}$ in one/two/three dimension, respectively. Gaussian kernel function has good mathematical properties, including its smoothness and high accuracy. Therefore, it is very suitable for solving higher-order derivatives.

2. Cubic spline kernel

$W\left(t,h\right)={\alpha }_D\left\{\begin{array}{c}\hfill 1-\frac{3}{2}{q}^2+\frac{3}{4}{q}^3,0\le q\le 1\hfill \\ \hfill \frac{1}{4}{\left(2-q\right)}^3,1\le q\le 2\hfill \end{array}\right.(10)$

Where α_D is equal to $\frac{10}{7}\pi h^2$, $\frac{1}{\pi h^3}$ in two dimensions and three dimensions, respectively. Compared with other kernel functions, Cubic spline is the most widely used kernel function.

3. Quintic kernel

$W\left(t,h\right)={\alpha }_D{\left(1-\frac{q}{2}\right)}^4\left(2q+1\right),0\le q\le 2(11)$

Where α_D is equal to $\frac{7}{4\pi h^2}$, $\frac{21}{16\pi h^3}$ in two dimensions and three dimensions, respectively. The kernel function has good stability and high interpolation accuracy.

In the process of SPH calculation, each particle has to interact with multiple neighbor particles, which will lead to the low computational efficiency of SPH method. Obviously, finding neighbor particles is also a time-consuming step. At present, the more efficient neighbor search algorithms of SPH method are Cell Linked list [28] and Verlet list algorithm [9]. The two algorithms are widely used in various mainstream SPH open source software. The CLL method is simple to implement and consumes less memory. In contrast, Verlet list algorithm uses the strategy of consuming memory in exchange for time. It needs to save the information of particles in the previous step, so the memory consumption is large. DualSPHysics uses the cell linked list method to search for neighbor particles.

3 ParallelDualSPHysics

This section describes the parallel version based on DualSPHysics code implemented by MPI in multi-core CPU cluster architecture, which is named parallelDualSPHysics. In DualSPhysics software, Neighbor List (NL), Particle Interaction (PI) and System Update (SU) are the three calculation modules of the SPH method. [29] showed that particle interaction accounts for more than 90% of the calculation time on single core CPU. Therefore, the key to achieve the ideal acceleration effect is to evenly distribute the computing load of the particle interaction part to each processor. In addition, with the increase of particle size, the processor communication overhead also needs to be controlled within a reasonable range, so that it cannot become the main factor restricting the computing overhead. Therefore, the communication mode needs to be optimized.

3.1 Storage structure of particles

As mentioned earlier, the calculation process of serial SPH method consists of three steps: neighbor list search, particle interaction and system update. In the process of calculation, the simulation results are output in the form of Bi4 binary file every fixed time step. Then performance of the subsequent rendering on the simulation result output file are shown in Figure 2.

FIGURE 2

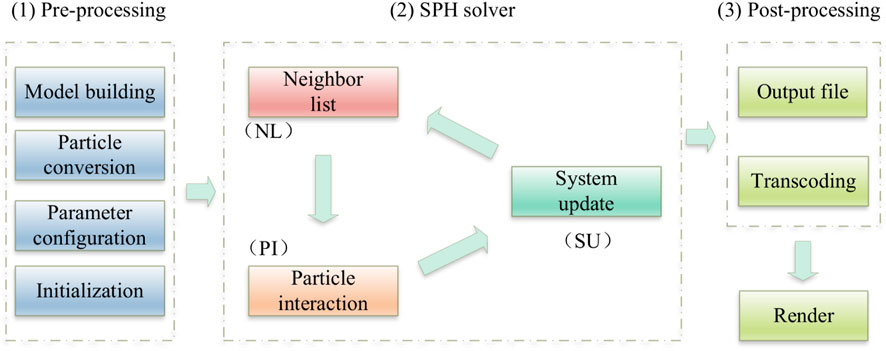
FIGURE 2. In DualSPHysics, pre-processing, SPH solver and post-processing are the three main functional modules of the software.

In DualSPHysics, there are three steps to create a simulation example, which are pre-processing, solver calculation and post-processing to show the simulation results. As shown in Figure 2, the preprocessing part is responsible for the establishment of the model, and parse the model file (VTK, STL file format) into particle information. In addition, the software also provides XML files for parameter setting, after the GenCase module completes the configuration of the preprocessing part, particles can be calculated by SPH solver. This part will realize the fluid simulation process, the result file at that time is output every fixed time step, these output files contain information such as position, velocity and density of particles. When the simulation is finished, all the output files are post-processed, and the particle information in the result file is rendered. Finally, the whole procedure of simulation can be displayed by visualization software such as ParaView.

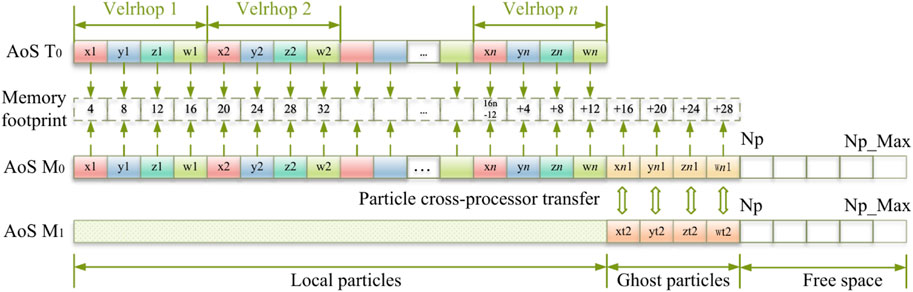
We introduce the program architecture of serial version DualSPHysics. However, the parallel version of the SPH method will face many different challenges, one of which is the storage of particle information. In order to realize the distributed storage of particles, we designed a particle parallel storage framework as shown in Figure 3. We take the storage of particle velocity and density as an example to explain in detail. In the object-oriented programming paradigm, the storage of particles is based on the Array of Structure (SoA). x, y, z and w represent the three components of velocity and density of T₀(x, y, z, w), and their memory gradually increases in 4-bits according to Figure 3.

FIGURE 3

FIGURE 3. The particle storage structure for parallelDualSPHysics.

In parallelDualSPHysics, the number of particles transferred across processes is variable, therefore the array for storing particles must be dynamic. However, dynamic array will slow down the whole simulation process due to its frequent allocation and assignment each time. Therefore, this paper adopts the strategy of sacrificing space for time, which replaces the dynamic array structure with a fixed-length array. The principle is as follows: First, we create an array with a fixed length of Np_Max. Np_Max should be greater than Np, which is the total number of particles in the current process. The Np_Max array consists of three parts, which store local particles, ghost particles and reserved space respectively. Local particles do not transfer across processes, so they are stored at the top of the array, followed by ghost particles. When particles transfer across processes, the reserved space will receive ghost particles transferred from adjacent processes. In this way, the problem of particle storage across processes can be solved and the cost of time is also considered.

3.2 Domain decomposition

Domain decomposition algorithm uses the idea of divide and conquer to divide the computing region into several subregions, and then assign each subregion to the corresponding processor. When the whole problem scale remains unchanged, the computing load borne by each processor will decrease with the increase of processor. Ideally, their computing time will show a linear decrease. Similarly, in the parallel process of SPH, in order to obtain the ideal acceleration effect, each processor is required to allocate the same number of fluid particles as much as possible.

In the parallel computing structure of the SPH method, in order to evenly distribute the computing tasks to their respective processes at the start time, this paper proposes a domain decomposition (DD) algorithm, as shown in Figure 4. All particles are distributed in the whole solution domain. To evenly distribute all the particles to their corresponding processes, we first divide the particles into two parts by dichotomy. Then each part is divided repeatedly until all processes receive the same number of particles. At last, the whole solution domain is evenly divided into sub-regions from 1 to n. Each sub-region corresponds to particle block j. And these particle blocks are also stored in the corresponding process as a preparation for following calculation. The specific implementation details of the domain decomposition (DD) algorithm are shown in Algorithm 1.

FIGURE 4

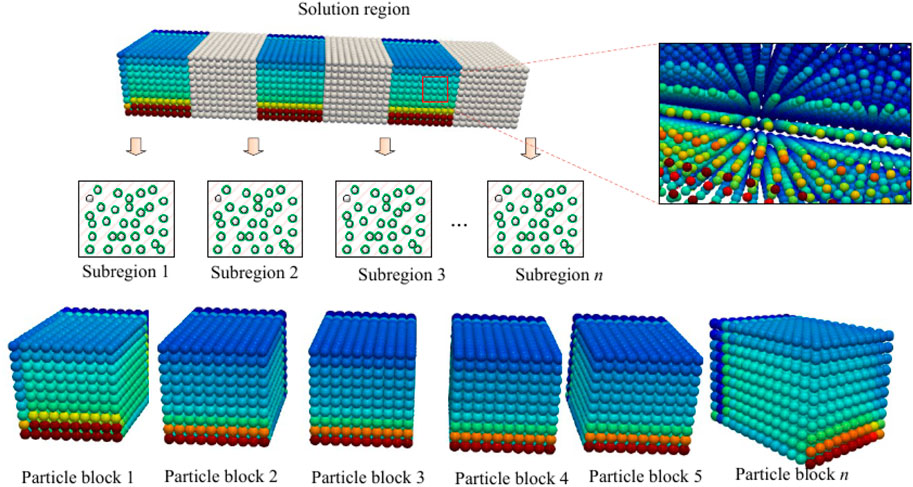
FIGURE 4. According to the principle of domain decomposition, particles are equally distributed to different subsets as computing tasks.

Algorithm 1. Domain decomposition (DD).

As described in Algorithm 1, the whole solution region is divided into several sub-regions corresponding to the number of processes. First of all, the algorithm divides the particles in lines 1 to 4. Because the particles are stored in an array that is unordered, the particles need to be sorted before dividing the sub-regions. This procedure is completed by the root process ${\mathbb{P}}_{\mathit{root}}$. Then the sorting results are divided according to the sub-regions responsible for the process by dichotomy and stored in the index, which can largely avoid the exhaustion of computing resources caused by the overall movement of particles. Then, in line 5, the partition result is sent to the corresponding process through the Scatter() function. At this time, each process obtains the particles it needs to store. The particles are only stored in the form of an index (the range is P_init to P_finish). Its particle information is stored in the arranged particle array (e.g., Pos[p]/Velrhop[p]/Code[p]), so the particle information stored by each process after domain decomposition can be obtained according to the index range obtained. Finally, the position, velocity, density, and other information of particles are stored in the corresponding process in lines 7 to 11.

3.3 Parallelized particle interaction

In DualSPHysics open source software, according to the analysis in Figure 2. Among them, the most time-consuming part is the procedure of SPH solution, which requires continuous iteration until all time steps are completed. Therefore, to design an efficient SPH parallel algorithm, it is necessary to solve the particle communication problem. When the particle size to be simulated expands, the communication time overhead will greatly exceed the time overhead of particle computing, this will become a bottleneck restricting the parallel efficiency of programs, and an effective way to solve this bottleneck is the overlap of computing and communication. Its basic principle is that in the calculation process, the data that needs communication at the boundary is sent out by non-blocking communication, and the central part of data that does not need communication is calculated at the same time. Ideally, when the data in the central part is calculated, the boundary data is received, and then the data in the boundary part is calculated. Therefore, the communication time is effectively hidden, which will greatly improve the performance of parallel scalability.

Algorithm 2. parallel particle interaction (PPI).

Particle interaction is the most time consuming module in the SPH method. This module calculates the force of each particle through the interpolation of neighbor particles and presents it in the form of acceleration. Because of its computation complexity, this module accounts for over 90% of the total execution time. Therefore, in order to achieve an efficient acceleration effect, we need to solve the parallel scalability problem of the particle interaction module. As shown in Figure 5, this paper proposes a strategy for overlapping computation and communication to hide communication latency and optimize the parallelization of particle interaction modules. First, it divides particles into two groups: boundary ghost particles and central particles, according to the smooth radius of 2h away from the process boundary. Then, according to the calculation rules of the SPH method on the support domain (only the neighbor particles within the smooth radius are calculated), the corresponding neighbor particles of the central part of the particles completely fall into the process. So it can complete the calculation of particle interaction without communicating with the adjacent process. Ghost particles need to communicate with neighboring processes. Therefore, in order to minimize the communication overhead, we first send ghost particles to adjacent processes through asynchronous transmission. At the same time, we calculate particles located in the central part. When the center particle calculation is completed, the boundary particles are also sent and received. Finally, we calculate the ghost particles that fall into the boundary part. This strategy makes full use of the idle waiting computing resources caused by the transmission of ghost particles. Therefore it effectively alleviates the parallel efficiency of programs.Therefore, in the parallel framework, the calculation process of particle interaction is divided into two processes: ghost boundary particle and central particle. According to this particle partition method, we propose a parallelized particle interaction (PPI) algorithm based on communication hiding to realize the parallelization of the SPH method.The PPI Algorithm 2 describes the particle interaction method based on our communication hiding strategy. Firstly, lines 2-3 divide the process boundary according to the smooth radius of 2 h. Then, in lines 4-10, all particles are divided into central particles and ghost particles according to their distances from the process boundary. Then the number of ghost particles to be communicated is sent through the MPI_Sendrecv() function to apply for enough memory to store the ghost particles. In order to reduce the number of communications and save memory resources, this paper also uses the Pack/Unpack() function to implement the packaging operation of particle information in lines 13 and 19. According to the principle of particle division, we send ghost particles to adjacent processes in the way of asynchronous transmission in lines 14 and 15. Then we calculate central particles in line 17. When the central particle calculation is completed, we use the Waitall() function to check whether the ghost particle transmission is complete, after which we calculate the ghost particle. Finally, the interaction force of all particles is calculated and its acceleration is output to the subsequent particle update module. The algorithm realizes the overlap of computation and communication, and theoretically meets the design requirements of efficient parallel programs.

FIGURE 5

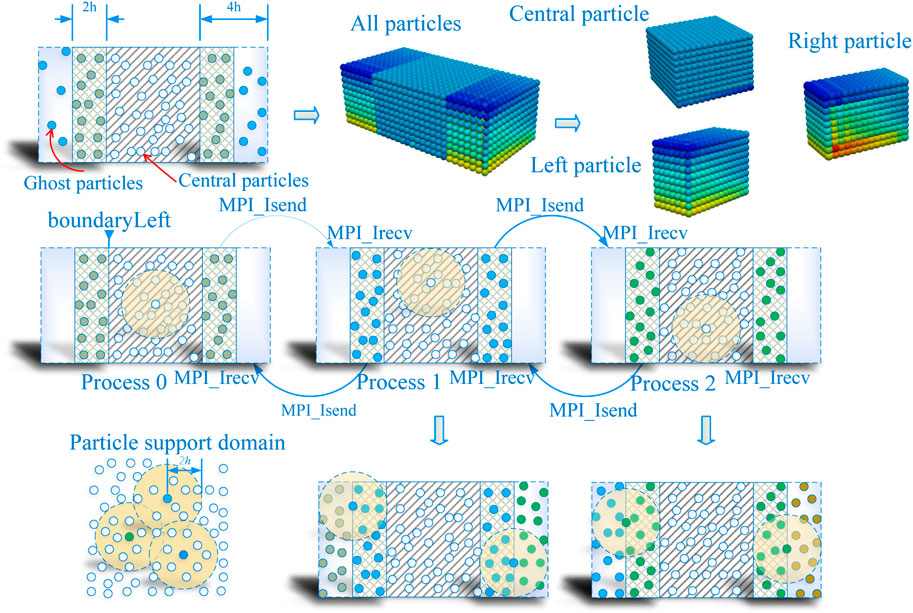
FIGURE 5. In the particle interaction module, particles use non-blocking communication to achieve the overlap between computation and communication.

Algorithm 3. Parallel system update (PSU).

3.4 Parallelized system update

Unlike the serial SPH system update module, the parallel system update module not only needs to deal with the update of particle information, but also needs to consider the situation of cross-process transfers of particles caused by the change of position. Similarly, handling the communication of particles is still the primary task to optimize parallel efficiency. Therefore, this paper proposes a parallel system update (PSU) method as shown in Algorithm 3.

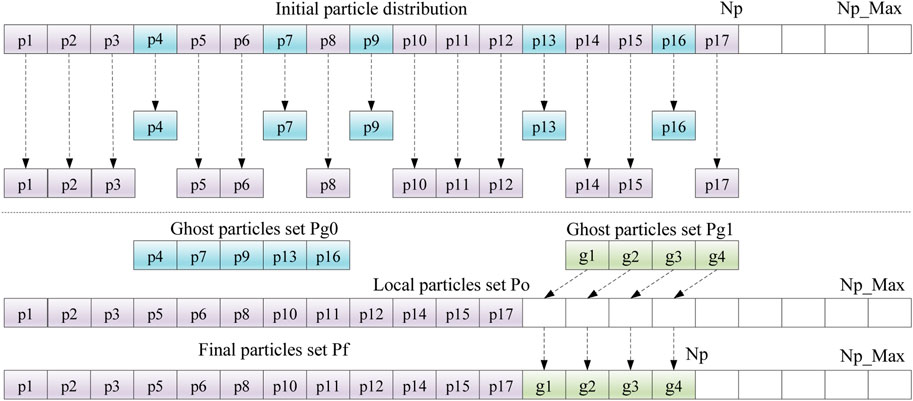
The serial version of SPH does not need to consider the problem of particles moving across processes in the system update module, which is a unique feature of the parallel version of SPH code. Therefore, particle storage needs to use the storage structure presented in Figure 3. The back end of the array can store ghost particles transferred from adjacent processes. It ensures the cross-process transfer of ghost particles. First of all, the algorithm updates the position, velocity, and density information of particles in lines 4-5 according to the acceleration. Then, in lines 6-10, particles outside the process boundary are detected. These particles are called ghost particles and will be transferred across the process. Particles that are within the process boundary are called local particles, which do not require cross-process transfer. Partitioning of particles has become the basic requirement to implement communication hiding and improve the scalability of parallel programs. In lines 14-16, the algorithm sends the ghost particles to the destination process by asynchronous transmission. Then the algorithm reorders the local particles and stores them in the local process in order (the transfer of ghost particles will leave enough room for array elements). In line 17, the algorithm calls the MPI_Waitall function to check whether the ghost particles have been transferred. When the return value of status is true, we store the ghost particles received from the neighboring processes behind the local particles. Finally, we get all the particle information after the cross-process transfer of particles. The hidden strategy of computation and communication is an effective way to solve the problem that the program enters the parallel performance bottleneck prematurely.

The PSU algorithm can be described in Figure 6, and p1-p17 is used to represent the particles in process Proc_m. After the particles update the position coordinate information, the ghost particle set that needs to cross the process is detected. For example, the set Pg0 = {p4, p7, p9, p13, p16} represents the ghost particles that will cross the process. When the particles cross the processor, the Pg0 is first sent to the adjacent processes through asynchronous transmission. At the same time, the ghost particles are eliminated and the local particles are reorganized. The set Po = {p1, p2, … , p15, p17} represents the reorganized local particle set. Finally, add the ghost particle set Pg1 = {g1, g2, g3, g4} from the adjacent process to the local particle set. Therefore, the Pf particle set is the final stored particles of process Proc_m, which also shows that the number of particles of process Proc_m is equal to local particles plus ghost particles sent by adjacent processes in a given time step. Obviously, the communication is also hidden in the phase of ghost particle asynchronous communication and local particle reorganization.

FIGURE 6

FIGURE 6. The entire procedure of parallelizing the particle update module.

3.5 Dynamic load balancing

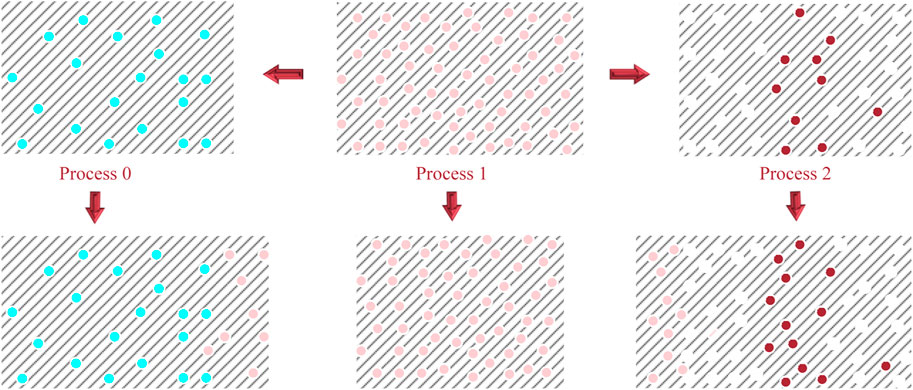
In the particle update stage, due to the existence of ghost particles across the process, there will be a major load imbalance problem for the fluid particles allocated by the process, which will lead to excessive computational load in some processes and idle waiting in other processes, slowing down the whole simulation process. In order to alleviate the imbalance of particle load in the calculation procedure of SPH, we locally adjust the particles of adjacent processes.

Load balancing is a common problem in parallel computing [15]. At present, many studies have shown that using Zoltan open source framework to realize resource allocation can achieve significant results [30]. However, due to the complexity of the software, this paper adopts local adjustment algorithm to realize particle dynamic load balancing. As shown in Figure 7, due to particle update, the number of particles in process 1 is much smaller than that in process 0/2. When the difference in the number of particles between the two processes reaches a given threshold, the program can determine that the calculation load is unbalanced. Therefore, it needs to move t particles from process 1 to process 0/2 to alleviate the problem of calculation load imbalance. The adjustment of local algorithm is simple to implement, and can also obtain good performance.

FIGURE 7

FIGURE 7. The principle of dynamic adjustment of particles in three adjacent processes.

3.6 Parallel SPH framework

Previously, we gave the parallelization method of particle interaction and particle update module, which is combined with the whole SPH. Therefore, this paper describes the calculation flow of parallel SPH as shown in Figure 8. We show six processes as an example. First, we use the domain decomposition algorithm to divide the whole SPH region, and store the particles in the corresponding processor. Then, the CLL algorithm is used to sort the fluid particles and store them in the corresponding cell they belong to. At the same time, it can be seen that communication needs to be carried out in the part of particle interaction and particle update. When processes need to communicate, each process sends boundary data to adjacent processes. However, as the size of simulated particles increases, the time spent communicating between processes will be much longer than the time spent computing, thus becoming a major constraint on parallel scalability. Therefore, communication optimization is needed to obtain efficient parallel programs. In this paper, communication hiding is used to alleviate the impact of communication on parallel efficiency. Their principle is to send out the data of the boundary part first, and then calculate the central data irrelevant to the boundary part. In this way, the computation and communication can be hidden, and the parallel efficiency of SPH can be improved.

FIGURE 8

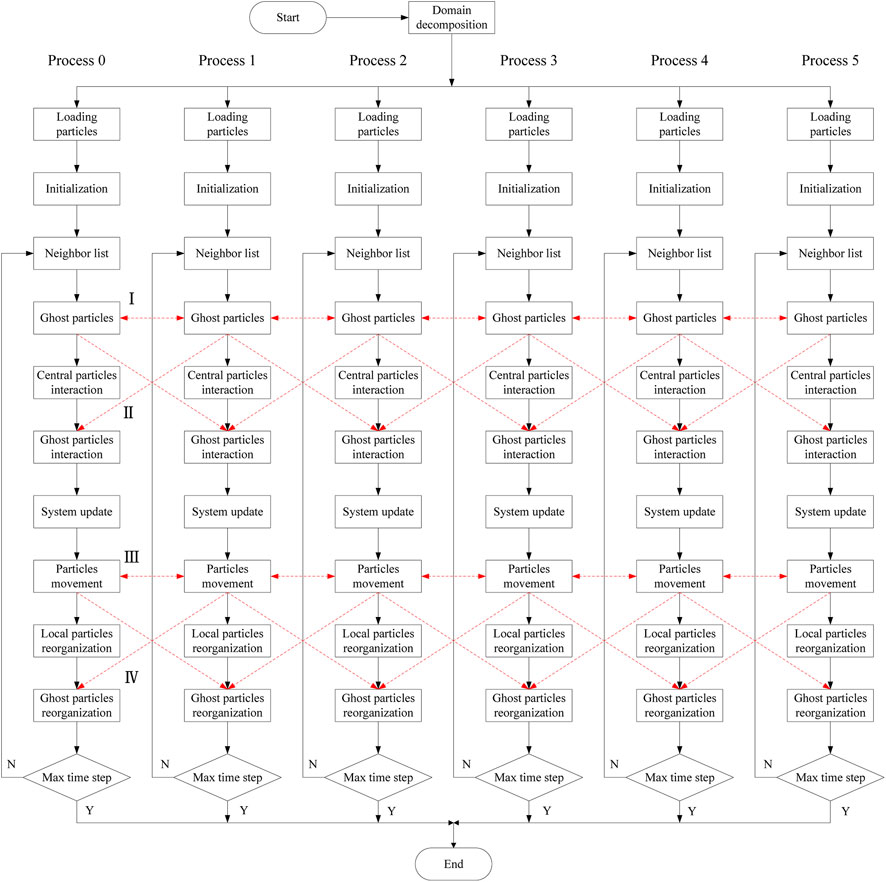
FIGURE 8. A parallel workflow of the parallelDualSPHysics with six processes, where dashed lines represent data communication, there are four communication stages: I, II, III, and IV.

4 Experiment

This section evaluates the performance of our parallel SPH method, including strong scalability and weak scalability. The feasibility of the parallel method in this paper is fully verified. In addition, we also give an example of practical engineering application.

4.1 TestCases and hardware

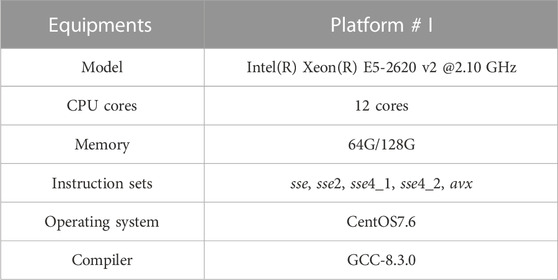
The configuration information of the supercomputer CPU node is shown in Table 1. Among them, the CPU with hardware configuration uses Intel(R) Xeon(R) E5-2620 v2, which carries 12 cores in one node. It also supports vectorization instruction set based on SIMD technology. In addition, their memory configurations are 64G and 128G. Our platform runs CentOS7.6 and the compiler we used is GCC-8.3.0.

TABLE 1

TABLE 1. The configuration information of the experimental platform.

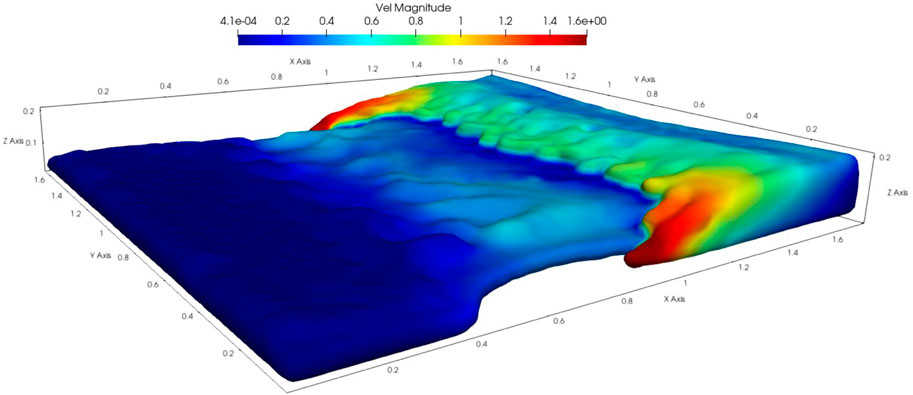
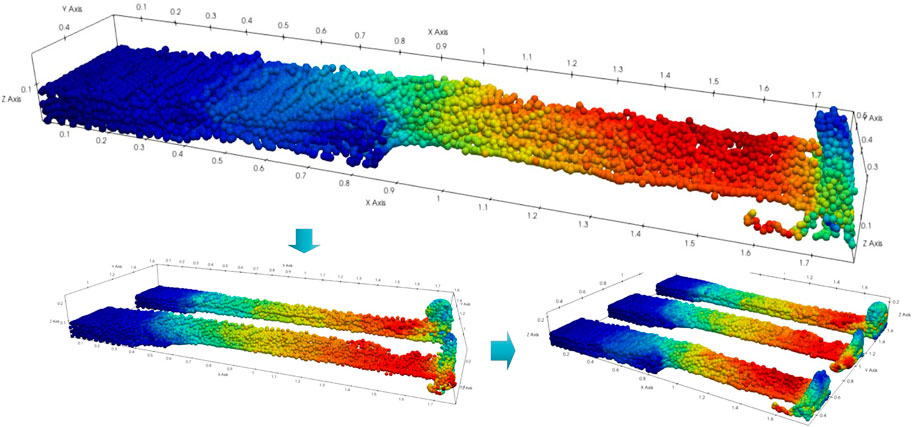
Fluid flow is ubiquitous in nature. The rapid development of CFD makes it possible to simulate the fluid mechanics of complex fluids, such as blood flow behavior in blood vessels [31], meteorological monitoring [32], tsunami prevention and control [33], etc. In order to evaluate the parallel performance of the large-scale SPH code proposed in this paper. We used the testcase shown in Figures 9, 10. This testcase simulates the flow procedure of pure fluid. In this testcase, the parallel performance of the program has a great relationship with the number of particles calculated. Figure 10 describes the use of different processes to solve the whole task. It can be seen that each process is only responsible for a small part of the task. Particle communication occurs within the range of 2 h away from the process boundary, which is also the using scope of the communication hiding strategy.

FIGURE 9

FIGURE 9. Test case shows the flow of pure fluid.

FIGURE 10

FIGURE 10. Fluid particles calculated by different processes.

4.2 Efficiency and scalability

Parallel scalability is usually used to evaluate the parallel performance of large-scale programs. Under the condition that the overall computing scale remains unchanged, the computing time of a program with superior parallel efficiency will decrease linearly with the increase of computing nodes. This rule is also known as the strong scalability of programs. In the same way, weak scalability describes the internal law that the computing scale and nodes increase equally while the computing time remains unchanged. We first evaluate the parallel efficiency of 3 million particles at 128G nodes shown in Figure 11.

FIGURE 11

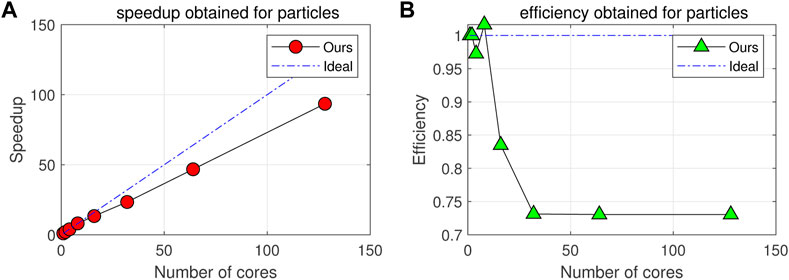
FIGURE 11. (A,B) respectively describe the acceleration and computational efficiency obtained in different processes for 128G memory nodes with fixed particle number, and it also increases the benchmark under ideal conditions for comparison.

Figure 11 describes the parallel efficiency of simulating 3 million particles with 128 processes. When the number of processes is less than 20, a better linear acceleration ratio can be obtained. At this time, the parallel efficiency is close to 80%. But when the number of processes increases to 128, the parallel efficiency of the program drops sharply to 70%. The reason for this phenomenon is that the ratio of boundary particles to central particles is too large. And it is assumed that the ratio is τ. With the increase of the number of processes, τ becomes larger and larger due to the continued segmentation of the whole solution domain by the domain decomposition algorithm (the number of central particles decreases with the increase of the number of processes). In an ideal case, we give a threshold of τ₀. Which represents the critical proportion that the center particle just completes the calculation when the boundary particle completes the transmission. In order to obtain the linear acceleration ratio, obviously, according to the strategy of communication hiding, we know that in the phase of particle interaction and system update, the transmission of boundary ghost particles always ends before the completion of the calculation of the central particle. So the CPU can always perform the calculation task of particles continuously. This principle is the key to ensuring that parallel programs obtain the linear acceleration ratio. Therefore, the value of τ of this testcase is greater than the threshold τ₀, which violates the principle of efficient parallelism.

Figure 12 evaluates the parallel efficiency of two testcases on a 64G memory node. Among them, Figures 12A, B present a testcase with 3 million particles. While Figures 12C, D present a testcase with 70 million particles. [19] showed that the number of particles will affect the parallel efficiency of the program. According to the previous analysis, we know that when the ratio τ of the boundary ghost particles and the center particles is greater than the critical value τ₀, the time spent on particle transmission is greater than its calculation time, which will lead to the reduction of parallel efficiency. By analyzing Figure 12B, we find that the parallel efficiency drops sharply when the number of processes exceeds 200. Its efficiency drops further to 20% when 1024 processes are used. In order to alleviate the parallel efficiency of the program, it is necessary to increase the number of particles to obtain an efficient linear acceleration ratio. Figures 12C, D show the linear acceleration ratio obtained when the number of particles is 70 million. Over 90% of the parallel efficiency can be achieved when the number of processes is 1024, which shows that under the requirements of efficient parallel efficiency (the ratio of ghost and central particles is less than the threshold τ₀). This paper realizes the development of SPH large-scale parallel program by implementing the strategy of communication hiding. At the same time, we can also see that the superlinear acceleration ratio can be obtained when the number of processes is relatively small, which is caused by the reading and writing of the simulation results and the disturbance of the system.

FIGURE 12

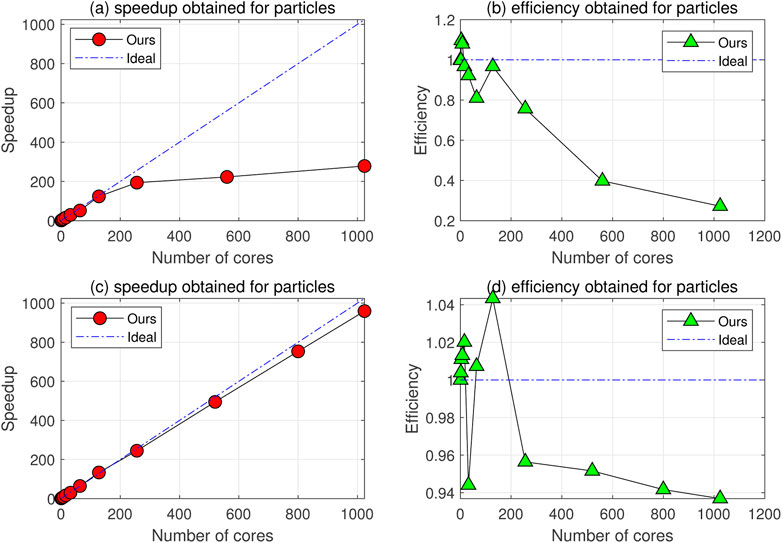
FIGURE 12. Speedup and computational efficiency for 64G memory nodes, the particle size of (A) and (B) is 3 million, and that of (C) and (D) is 70 million.

The weak scalability of parallel software is also an important standard for parallel performance. It reveals the impact of the increase of computing scale and computing nodes on the whole parallel system. Figure 13 shows the parallel weak scalability results of the SPH code. We evaluated the weak scalability of 50,000 and 100,000 particles per node, increasing from 100 to 1024 processes. The number of calculated particles can exceed 120 million particles at most. The results show that with the increase of the computing scale and the equal proportion of computing nodes, the time consumed by each computing node has no significant difference in the acceptable range. This result shows that the parallel SPH code developed in this paper achieves efficient parallel scalability. It also proves the effectiveness of our communication hiding strategy in the development of large-scale parallel SPH code.

FIGURE 13

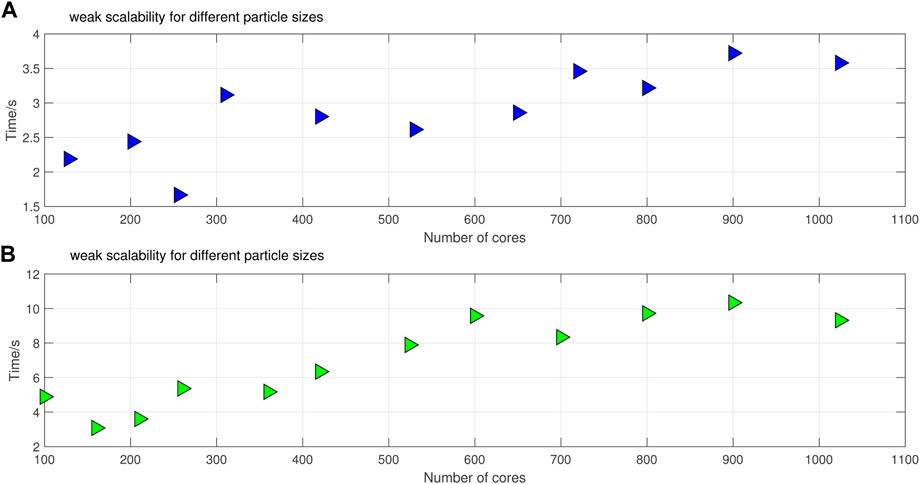
FIGURE 13. (A) and (B) assign an average of 50,000 and 100,000 particles to each processor for weak scalability testing, respectively.

4.3 Engineering simulation

In the field of engineering practice, it is often necessary to model and simulate the scene of fluid flow. This part presents a simulation case with actual scale, which shows the impact process of bridge subjected to flood. As shown in Figure 14, the bridge model used in this paper has eight piers. The length, width and height of the bridge are 70m, 5m and 9m, respectively.

FIGURE 14

FIGURE 14. The bridge model used in this paper.

The application uses more than 7 million fluid particles to simulate the flood. The actual physical time for simulating 10 s is 2.5, 3.7, 5.2, 6.1, 7.4, 8.2, 9.1 and 10 s respectively. Considering the calculation efficiency, the smooth length of this example cannot be reduced without limitation. At the same time, in order to ensure that the proportion of boundary particles to central particles is within a reasonable range, we use 256 processes to conduct the simulation. It took nearly 17 h to obtains the results. The simulation results (Figure 15) clearly capture the flow of water after passing through the pier. Many flow details can be successfully captured as the number of particles exceeds ten million. It can give the corresponding simulation results as an aid and reference before engineering practice, which shows that the parallel SPH method developed in this paper can have the potential for practical engineering application.

FIGURE 15

FIGURE 15. Simulation procedure of flood impact on bridge.

It can be seen from the simulation results (Figure 16) that it captures the splash image of the water flowing through the pier. And the velocity of the fluid particles above the bridge pier is slowed down (the color of the fluid particles represents the magnitude of the velocity). Particles that do not touch the pier pass by the pier, and the velocity is not significantly reduced. Through the analysis of the simulation results, it can clearly capture the details of the interaction between the water flow and the pier. It can also calculate the impact force of the current on the pier at the moment, which is of great significance for engineering application.

FIGURE 16

FIGURE 16. Simulation details of water flow (fluid particle) after passing through the pier.

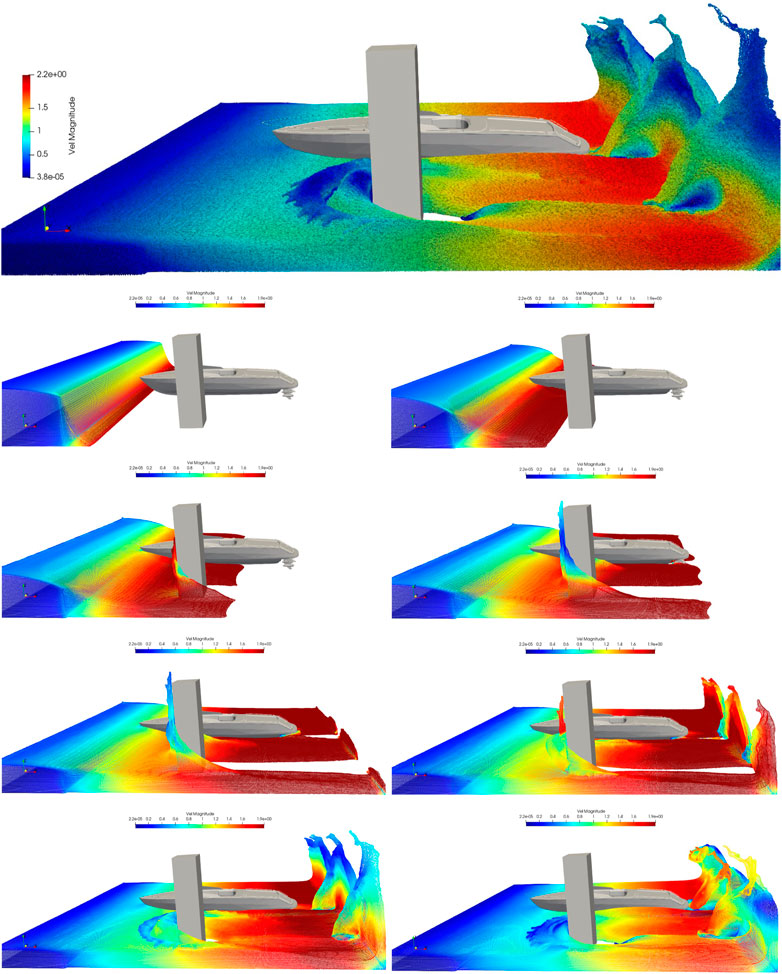
Mesh-based methods such as the finite element method, finite volume method, and finite difference method have no advantages over the particle method in dealing with large deformation problems, they are not good at capturing the simulation procedure of free surface flow. Therefore, in order to further verify the parallel method presented in this paper. As shown in Figure 17, we show the procedure of interaction between water flowing through a ship and a square cylinder, which further demonstrates the unique advantages of the SPH method for simulating free surface flow. The test case simulates the flow process of actual physical time from 2 to 16 s, and each time interval is 2 s. Also based on the consideration of calculation efficiency, the calculation time of 512 processes in this paper is nearly 9 h. This test case calculates a total of 50 million fluid particles. Obviously, it clearly shows a series of changes from the beginning of the flow to the contact with obstacles (ships and cylinders). And it can capture the details of the surrounding flow and reflected flow formed after the water contacts the cylinder, at the same time, the water contact boundary is reflected back. The simulation results show that the increase in particle number can improve the calculation accuracy. Therefore, it is of great significance to develop a large-scale parallel SPH method for practical engineering applications.

FIGURE 17

FIGURE 17. Simulation procedure of water flow through ship and square cylinder.

5 Conclusion

This paper gives a large-scale parallel program named parallelDualSPHysics based on the single-CPU version. Firstly, we give a domain decomposition algorithm, which distributes the solution region equally to each process, so each processor can get the same number of particles and complete the initialization configuration of the parameters. Secondly, we present a parallel version of the particle interaction algorithm, which divides each region into a boundary part and a center part. Based on this division, we achieve overlap between calculation and communication, which greatly improves the parallel efficiency of the program. In addition, we have parallelized the system update module, which rearranges local particles to hide communication when ghost particles are sent. Finally, we have improved the initialization of particles and the output module of results under the parallel framework, which further enhances the functionality of parallelDualSPHysics. To verify its parallel performance, we tested its scalability, When the number of simulated particles exceeds 70 million, we still get more than 90% computational efficiency with 1024 cores. On the weak scalability test, we tested 120 million particles and the statistical time overhead remained within a reasonable range. Therefore, through the scalability analysis of parallel programs, it is found that the parallelDualSPHyiscs software given in this paper can achieve high parallel efficiency. In the future plan, we will carry out the following research. On the one hand, we combine OpenMP multi-core parallel and SIMD vectorization optimization techniques within a single node to further improve the computational efficiency of SPH codes. On the other hand, based on the concurrency of large-scale programs, we will develop methods that couple other physical fields to efficiently apply to the study of fluid-structure interactions to solve large-scale engineering applications with complex boundaries.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SL: paper writing, experimental testing, KW: provide ideas. XF: language polishing. XG: Build an experimental scheme. CY: writing, revising and put forward innovation points. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2020YFA0709803), Research on Key Technologies of Numerical Simulation of Explosion Shock (Grant No. 22-TDRCJH-02-001), and the National Natural Science Foundation of China (Grant No. 61902413 and No. 62002367).

Acknowledgments

Thank the reviewers and editors for their valuable comments, which have greatly improved the quality of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹www.intel.com/content/www/us/en/docs/intrinsics-guide.

²www.top500.org.

References

1. Spalart PR, Venkatakrishnan V. On the role and challenges of cfd in the aerospace industry. Aeronaut J (2016) 120:209–32. doi:10.1017/aer.2015.10

CrossRef Full Text | Google Scholar

2. Yao XJ, Wang ZD, Zhang WJ. A new analysis of the capillary driving pressure for underfill flow in flip-chip packaging. IEEE Trans Components Packaging Manufacturing Tech (2017) 4:1534–44. doi:10.1109/TCPMT.2014.2339493

CrossRef Full Text | Google Scholar

3. Oger G, Le Touzé D, Guibert D, De Leffe M, Biddiscombe J, Soumagne J, et al. On distributed memory mpi-based parallelization of sph codes in massive hpc context. Comp Phys Commun (2016) 200:1–14. doi:10.1016/j.cpc.2015.08.021

CrossRef Full Text | Google Scholar

4. Gingold RA, Monaghan JJ. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Monthly notices R astronomical Soc (1977) 181:375–89. doi:10.1093/mnras/181.3.375

CrossRef Full Text | Google Scholar

5. Willis JS, Schaller M, Gonnet P, Bower RG, Draper PW. An efficient simd implementation of pseudo-verlet lists for neighbour interactions in particle-based codes (2018). arXiv:1804.06231.

Google Scholar

6. Harada T, Koshizuka S, Kawaguchi Y. Smoothed particle hydrodynamics on gpus. In: Proc. Computer Graphics Int.; May 30-Jun. 2, 2007; Rio de Janeiro, Brazil (2007). p. 671–91.

Google Scholar

7. Amada T, Imura M, Yasumuro Y, Manabe Y, Chihara K. Particle-based fluid simulation on gpu. In: ACM workshop on general-purpose computing on graphics processors (Citeseer), 41. Springer (2004). p. 42.

Google Scholar

8. Crespo AC, Dominguez JM, Barreiro A, Gomez-Gesteira M, Rogers BD, Langowski J. Gpus, a new tool of acceleration in cfd: Efficiency and reliability on smoothed particle hydrodynamics methods. PLoS ONE (2011) 6:e20685. doi:10.1371/journal.pone.0020685

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Winkler D, Rezavand M, Rauch W. Neighbour lists for smoothed particle hydrodynamics on gpus. Comp Phys Commun (2018) 225:140–8. doi:10.1016/j.cpc.2017.12.014

CrossRef Full Text | Google Scholar

10. Khrapov S, Khoperskov A. Smoothed-particle hydrodynamics models: Implementation features on gpus. Cham: Springer (2017).

Google Scholar

11. Long S, Fan X, Li C, Liu Y, Fan S, Guo X-W, et al. Vecdualsphysics: A vectorized implementation of smoothed particle hydrodynamics method for simulating fluid flows on multi-core processors. J Comput Phys (2022) 463:111234. doi:10.1016/j.jcp.2022.111234

CrossRef Full Text | Google Scholar

12. Nishiura D, Furuichi M, Sakaguchi H. Computational performance of a smoothed particle hydrodynamics simulation for shared-memory parallel computing. Comp Phys Commun (2015) 194:18–32. doi:10.1016/j.cpc.2015.04.006

CrossRef Full Text | Google Scholar

13. Nishiura D, Sakaguchi H. Parallel-vector algorithms for particle simulations on shared-memory multiprocessors. J Comput Phys (2011) 230:1923–38. doi:10.1016/j.jcp.2010.11.040

CrossRef Full Text | Google Scholar

14. Luo Z, Wu Q, Zhang L. Parallel simulation of dam-break flow by openmp-based sph method. J Phys Conf (2017) 916:012042. doi:10.1088/1742-6596/916/1/012042

CrossRef Full Text | Google Scholar

15. Verma K, Szewc K, Wille R. Advanced load balancing for sph simulations on multi-gpu architectures. In: Proceeding of the 2017 IEEE High Performance Extreme Computing Conference (HPEC); September 2017; Waltham, MA, USA. IEEE (2017). p. 1–7.

CrossRef Full Text | Google Scholar

16. Egorova MS, Dyachkov SA, Parshikov AN, Zhakhovsky V. Parallel sph modeling using dynamic domain decomposition and load balancing displacement of voronoi subdomains. Comp Phys Commun (2019) 234:112–25. doi:10.1016/j.cpc.2018.07.019

CrossRef Full Text | Google Scholar

17. Chaussonnet G, Dauch T, Keller M, Okraschevski M, Ates C, Schwitzke C, et al. Influence of the flow physics on the load balancing during sph simulations. In: High performance computing in science and Engineering’19. Berlin, Germany: Springer (2021). p. 463–77.

CrossRef Full Text | Google Scholar

18. Devine K, Hendrickson B, Boman E, St. John M, Vaughan C (2000). Design of dynamic load-balancing tools for parallel applications. In Proceedings of the 14th international conference on Supercomputing. Santa Fe New Mexico: US Department of Energy March 2000 United States 110–8.

CrossRef Full Text | Google Scholar

19. Guo X, Rogers BD, Lind S, Stansby PK. New massively parallel scheme for incompressible smoothed particle hydrodynamics (isph) for highly nonlinear and distorted flow. Comp Phys Commun (2018) 233:16–28. doi:10.1016/j.cpc.2018.06.006

CrossRef Full Text | Google Scholar

20. Domínguez JM, Crespo AJ, Valdez-Balderas D, Rogers BD, Gómez-Gesteira M. New multi-gpu implementation for smoothed particle hydrodynamics on heterogeneous clusters. Comp Phys Commun (2013) 184:1848–60. doi:10.1016/j.cpc.2013.03.008

CrossRef Full Text | Google Scholar

21. Schaller M, Gonnet P, Draper PW, Chalk AB, Bower RG, Willis J, et al. Swift: Sph with inter-dependent fine-grained tasking. Astrophysics Source Code Library (2018). ascl–1805.

Google Scholar

22. Nori M, Baldi M. Ax-gadget: A new code for cosmological simulations of fuzzy dark matter and axion models. Monthly Notices R Astronomical Soc (2018) 478:3935–51. doi:10.1093/mnras/sty1224

CrossRef Full Text | Google Scholar

23. Ramachandran P, Bhosale A, Puri K, Negi P, Muta A, Dinesh A, et al. Pysph: A python-based framework for smoothed particle hydrodynamics. ACM Trans Math Softw (Toms) (2021) 47:1–38. doi:10.1145/3460773

CrossRef Full Text | Google Scholar

24. Domínguez JM, Fourtakas G, Altomare C, Canelas RB, Tafuni A, García-Feal O, et al. Dualsphysics: From fluid dynamics to multiphysics problems. Comput Part Mech (2021) 1–29:867–95. doi:10.1007/s40571-021-00404-2

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Dan K, Bender J, Solenthaler B, Teschner M. Smoothed particle hydrodynamics techniques for the physics based simulation of fluids and solids (2020). arXiv:2009.06944.

Google Scholar

26. Yu J, Yao W, Duan K, Liu X, Zhu Y. Experimental study and discrete element method modeling of compression and permeability behaviors of weakly anisotropic sandstones. Int J Rock Mech Mining Sci (2020) 134:104437. doi:10.1016/j.ijrmms.2020.104437

CrossRef Full Text | Google Scholar

27. Wong KK. Three-dimensional discrete element method for the prediction of protoplasmic seepage through membrane in a biological cell. J Biomech (2017) 65:115–24. doi:10.1016/j.jbiomech.2017.10.023

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gómez-Gesteira M, Crespo AJ, Rogers BD, Dalrymple RA, Dominguez JM, Barreiro A. Sphysics–development of a free-surface fluid solver–part 2: Efficiency and test cases. Comput Geosciences (2012) 48:300–7. doi:10.1016/j.cageo.2012.02.028

CrossRef Full Text | Google Scholar

29. Domínguez J, Crespo A, Gómez-Gesteira M, Marongiu J. Neighbour lists in smoothed particle hydrodynamics. Int J Numer Methods Fluids (2011) 67:2026–42. doi:10.1002/fld.2481

CrossRef Full Text | Google Scholar

30. Puri K, Ramachandran P, Godbole P. Load balancing strategies for sph. In: Proceeding of the 2013 National Conference on Parallel Computing Technologies (PARCOMPTECH); February 2013; Bangalore, India. IEEE (2013). p. 1–5.

CrossRef Full Text | Google Scholar

31. Sigalotti LDG, Klapp J, Pedroza K, Nathal E, Alvarado-Rodríguez CE. Numerical simulation of the blood flow through a brain vascular aneurysm with an artificial stent using the sph method. Engineering (2018) 10:891–912. doi:10.4236/eng.2018.1012062

CrossRef Full Text | Google Scholar

32. Gissler C, Band S, Peer A, Ihmsen M, Teschner M. Approximate air-fluid interactions for sph. In: Proceedings of the 13th Workshop on Virtual Reality Interactions and Physical Simulations. Lyon, France: The Eurographics Association (2017). p. 29–38.

Google Scholar

33. Hasanpour A, Istrati D, Buckle I. Coupled sph–fem modeling of tsunami-borne large debris flow and impact on coastal structures. J Mar Sci Eng (2021) 9:1068. doi:10.3390/jmse9101068

CrossRef Full Text | Google Scholar