Analysis of the consensus of double-layer chain networks

The multi-layer network topology structures directly affect the robustness of network consensus. The different positions of edges between layers will lead to a great difference in the consensus of double-layer chain networks. Finding the optimal positions of edges for consensus can help to design the network topology structures with optimal robustness. In this paper, we first derive the coherence of double-layer chain networks with one and two connected edges between layers by graph theory. Secondly, the optimal and worst connection edges positions of the two types of networks are simulated. When there is one edge between layers, the optimal edge connection position is found at 1/2 of each chain, and the worst edge connection position is found at the end node of the chain. When there are two edges between layers, the optimal edges connection positions are located at 1/5 and 4/5 of each chain respectively, and the worst edges connection positions are located at the end node of the chain and its neighbor node. Furthermore, we find that the optimal edge connection positions are closely related to the number of single-layer network nodes, and obtain their specific rules.

1 Introduction

In recent years, the research on complex networks has attracted extensive attention from interdisciplinary scholars, such as physics, chemistry, ecology and information science [1, 2]. The study of complex networks has not only profound theoretical significance but also has a wide range of practical applications. With the deepening of research, scholars have made new progress in synchronization and propagation of complex networks [3, 4], consensus and robustness [5–11], fractal networks [12, 13], cascading failures [14].

The traditional single-layer networks do not consider the interaction between networks, which greatly reduces the applicability of single-layer network models. Therefore, the study of multi-layer networks is one of the current research focuses [15–18], which breaks the limitation of homogeneity of nodes and connected edges in single-layer networks, and considers multiple types of nodes and their connected edge relationships. He studied the additive coupling and Markov switching coupling to capture the synchronization of layered connected multi-layer networks, and verified the effectiveness of the conclusions through examples [16]. Li analyzed the synchronizability of the double-layer dumbbell networks under different inter-layer coupling modes, and compared the synchronizability under three inter-layer connection modes [17].

The topological structures of multi-layer networks are closely related to the robustness of network consensus. The connection modes between nodes will affect the consensus of the network. The study of the influence of network topology structures on consensus will help to better understand the robustness of network consensus, and then design the network structures with the optimal anti-interference ability. The consensus of the network means that each node has a single state subject to noise. It is measured by network coherence and Laplacian characteristic spectrum [19]. Zhang analyzed the consensus of networks with special structures under the influence of white noise, and obtained an analytical expression for network coherence in the Sierpinski gaskets [20]. Gao used the relationships between Laplacian polynomial and determinant to obtain the coherence of weighted corona networks [21]. Huang obtained the Laplacian spectrum of several kinds of double-layer networks by graph operation, and compared the advantages and disadvantages of the first-order coherence of several kinds of networks [22].

The chain network is a classic network structure, which is widely used in network monitoring [23], system control [24], etc. The research usually abstracts the physically composed networks into double-layer chain networks, and selects the appropriate nodes for interference to get the optimal control with the same cost. Wu analyzed the synchronizability of double-layer chain networks with two connected edges between layers, and found the optimal positions of the two connected edges [25]. Deng studied the synchronizability of two different types of multi-layer chain networks using the master stability function method, and obtained the main factors affecting the synchronizability of the two types of networks [26]. At present, the research on multi-layer chain networks mainly focuses on synchronization, and there is less research on consensus. This paper firstly obtains the coherence of double-layer chain networks with one and two connected edges between layers. Furthermore, through conjecture, calculation, simulation and analysis of the consensus of two types of networks, the optimal and the worst inter-layer edges connection modes are obtained. We summarize the novelty and main contributions as follows.

1. This paper presents double-layer chain network model with partial inter-layer connection, which is different from the inter-layer fully connected network in that it will save more costs and have more practicability.

2. Since the Laplacian spectrum of partially connected double-layer chain network is difficult to solve, we apply the new method to obtain the analytic formula of the coherence of the double-layer chain networks.

3. We obtained the optimal and worst connected edge positions of the double-layer chain networks based on the analytic formula of the coherence, and the results are very regular and verified by experiments.

In Section 2, the preliminaries required in this paper are given. Section 3 deduces the first-order coherence of the double-layer chain networks, and gives some conjectures about the networks coherence. Section 4 shows the numerical simulation experiment and analysis.

2 Preliminaries

2.1 The definition of first-order network coherence

The network dynamics model with v nodes is described as follows [12]:

$\dot{x}\left(t\right)=-Lx\left(t\right)+\phi \left(t\right),(1)$

where L is the Laplacian matrix of the network, φ(t) ∈ R^v represents the interference of Gaussian white noise at time t. The network coherence is defined as robustness to noise:

$H^{\left(1\right)}=\frac{1}{v}\sum _{i=1}^v\underset{t\to \infty }{\lim }\mathit{var}\left\{x_i\left(t\right)-\frac{1}{v}\sum _{j=1}^v{x}_j\left(t\right)\right\}.(2)$

The output of system (1) is written as follows:

$y=Sx,(3)$

where S is the projection operator, $S=I-\frac{1}{v}\mathbf{1}{\mathbf{1}}^{\mathit{T}}$, 1 is the v-vector of all ones.

By Formula 1, Formula 2, Formula 3,

$H^{\left(1\right)}=\frac{1}{v}tr\left({\int }_0^{\infty }{e}^{-L^{T}t}S{e}^{-Lt}dt\right).(4)$

According to the literature [12], the first-order coherence is measured by H⁽¹⁾,

$H^{\left(1\right)}=\frac{1}{2v}\sum _{\kappa =2}^v\frac{1}{{\lambda }_{\kappa }}.(5)$

2.2 The double-layer chain networks

A double-layer chain network is composed of two chains with n nodes. In this paper, the double-layer chain network G^s is shown in Figure 1 a, where one edge is connected between layers of the network model. We assume that the ith (1 ≤ i ≤ n) node pair has a connected edge. The double-layer chain model G^d is shown in Figure 1 b, where two edges are connected between layers of the network model. We assume that the ith and jth (1 ≤ i < j ≤ n) node pairs are connected to edges, the edge connection method is abbreviated as i@j.

FIGURE 1

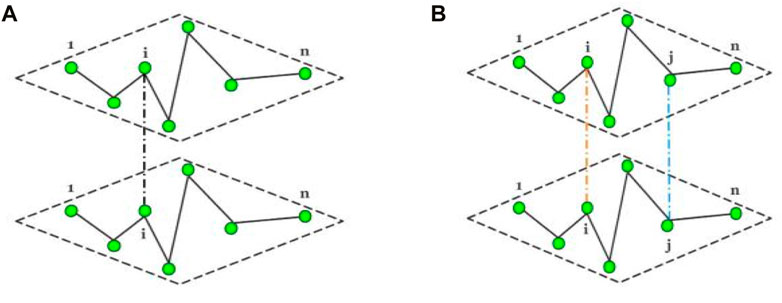
FIGURE 1. (A) Schematic diagram of a double-layer chain network G^s. (B) Schematic diagram of a double-layer chain network G^d.

2.3 Lemma of correlation

Lemma 1 [17] Let M, N be n × n square matrices, then

$\left|\begin{array}{cc}\hfill M\hfill & \hfill N\hfill \\ \hfill N\hfill & \hfill M\hfill \end{array}\right|=|M+N\Vert M-N|.$

Lemma 2 [10] Let the corresponding characteristic polynomial of matrix Q_n be Q_n(λ) = q_nλⁿ + q_n−1λⁿ⁻¹ + ⋯ + q₁λ + q₀,

${Q_n=\left(\begin{array}{cccccccc}\hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill \end{array}\right)}_{n\times n}$

then q₀ = (−1)ⁿ (n + 1), $q_1={(-1)}^{n-1}\frac{n(n+1)(n+2)}{6}$, $q_2={(-1)}^{n-2}\frac{(n-1)n(n+1)(n+2)(n+3)}{120}$.

3 The first-order coherence and conjectures

3.1 The first-order coherence H^(1s) of G^s

Let the Laplacian matrix of G^s be L₁, $L_1=\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill B\hfill & \hfill A\hfill \end{array}\right)$, B = diag (b₁₁, b₂₂, … , b_nn), b_ii = −1, b_jj = 0 (1 ≤ i ≤ n, j ≠ i),

${A+B=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right)}_{n\times n}.$

According to lemma 1, the characteristic polynomial of G^s is

$P_1\left(\lambda \right)=|\lambda I_{2n}-L_1|=|\lambda I_n-A-B\Vert \lambda I_n-A+B|.$

We expand determinant |λI_n − A− B| by the first row and the nth row, and determinant |λI_n − A+ B| by the ith row,

$|\lambda I_n-A-B|=Q_n\left(\lambda \right)+2Q_{n-1}\left(\lambda \right)+Q_{n-2}\left(\lambda \right),$

|λI_n − A+ B| = Q_n(λ) + 2Q_n−1(λ) + Q_n−2(λ) − 2 [Q_i−1(λ) + Q_i−2(λ)][Q_n−i(λ) + Q_n−i−1(λ)].

Let 0 = θ₁ < θ₂ ≤ ⋯ ≤ θ_n and 0 < ρ₁ ≤ ρ₂ ≤ ⋯ ≤ ρ_n be the Laplacian eigenvalues of |λI_n − A− B| and |λI_n − A+ B|, respectively. By formula (5),

$H^{\left(1s\right)}=\frac{1}{4n}\left(\sum _{\kappa =2}^n\frac{1}{{\theta }_{\kappa }}+\sum _{l=1}^n\frac{1}{{\rho }_l}\right).(6)$

For the sake of calculation, let Q_m (0), Q_m (1), Q_m (2) be the constant term, first-order coefficient and quadratic coefficient of the characteristic polynomial of Q_m(λ).

Claim 1

$\sum _{\kappa =2}^n\frac{1}{{\theta }_{\kappa }}=\frac{n^2-1}{6}.(7)$

Proof. Let 0 = θ₁ < θ₂ ≤ ⋯ ≤ θ_n be the Laplacian eigenvalues of Q_n(λ) + 2Q_n−1(λ) + Q_n−2(λ), according to Vieta theorem and lemma 2,

$\sum _{\kappa =2}^n\frac{1}{{\theta }_{\kappa }}=-\frac{Q_n\left(2\right)+2Q_{n-1}\left(2\right)+Q_{n-2}\left(2\right)}{Q_n\left(1\right)+2Q_{n-1}\left(1\right)+Q_{n-2}\left(1\right)}=\frac{n^2-1}{6}.$

Claim 2

$\sum _{l=1}^n\frac{1}{{\rho }_l}=\frac{n^2}{2}-ni+n+i^2-i.(8)$

Proof. Let 0 < ρ₁ ≤ ρ₂ ≤ ⋯ ≤ ρ_n be the Laplacian eigenvalues of Q_n(λ) + 2Q_n−1(λ) + Q_n−2(λ) − 2 [Q_i−1(λ) + Q_i−2(λ)][Q_n−i(λ) + Q_n−i−1(λ)], according to Vieta theorem and lemma 2,

$\sum _{l=1}^n\frac{1}{{\rho }_l}=-\frac{Q_n\left(1\right)+2Q_{n-1}\left(1\right)+Q_{n-2}\left(1\right)-2F\left(0\right)H\left(1\right)-2F\left(1\right)H\left(0\right)}{Q_n\left(0\right)+2Q_{n-1}\left(0\right)+Q_{n-2}\left(0\right)-2F\left(0\right)H\left(0\right)},$

where F (0) = Q_i−1 (0) + Q_i−2 (0), F (1) = Q_i−1 (1) + Q_i−2 (1), H (0) = Q_n−i (0) + Q_n−i−1 (0), H (1) = Q_n−i (1) + Q_n−i−1 (1), then

$\sum _{l=1}^n\frac{1}{{\rho }_l}=\frac{n^2}{2}-ni+n+i^2-i.$

Theorem 1 Let the number of single-layer chain network nodes in G^s be n, if the edge connection position is located at i, then the first-order coherence of G^s is

$H^{\left(1s\right)}=\frac{1}{4n}\left(\frac{4n^2-1}{6}-ni+n+i^2-i\right).$

Proof. By formula 6, formula 7, formula 8, theorem 1 can be easily obtained.

3.2 The first-order coherence H^(1d) of G^d

Let the Laplacian matrix of G^d be L₂, $L_2=\left(\begin{array}{cc}\hfill C\hfill & \hfill D\hfill \\ \hfill D\hfill & \hfill C\hfill \end{array}\right)$, D = diag (d₁₁, d₂₂, … , d_nn), d_ii = d_jj = −1, d_rr = 0 (1 ≤ i < j ≤ n, r ≠ i, j),

${C+D=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill -1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right)}_{n\times n}.$

According to lemma 1, the characteristic polynomial of G^d is

$P_2\left(\lambda \right)=|\lambda I_{2n}-L_2|=|\lambda I_n-C-D\Vert \lambda I_n-C+D|.$

$|\lambda I_n-C-D|=|\lambda I_n-A-B|=Q_n\left(\lambda \right)+2Q_{n-1}\left(\lambda \right)+Q_{n-2}\left(\lambda \right),$

|λI_n − C + D| = Q_n(λ) + 2Q_n−1(λ) + Q_n−2(λ) − 2 [Q_j−1(λ) +Q_j−2(λ)][Q_n−j(λ) + Q_n−j−1(λ)] − 2 [Q_i−1(λ) + Q_i−2(λ)]{Q_n−i(λ) + Q_n−i−1(λ) − 2Q_j−i−1(λ)[Q_n−j(λ) + Q_n−j−1(λ)]}.

Let 0 < σ₁ ≤ σ₂ ≤ ⋯ ≤ σ_n be the Laplacian eigenvalues of |λI_n − C + D|, by formula 5,

$H^{\left(1d\right)}=\frac{1}{4n}\left(\sum _{\kappa =2}^n\frac{1}{{\theta }_{\kappa }}+\sum _{p=1}^n\frac{1}{{\sigma }_p}\right).(9)$

Similar to the proof of lemma 4, we have

$\sum _{p=1}^n\frac{1}{{\sigma }_p}=\frac{n+\left(n-j\right)\left(n-j+1\right)+i\left(i-1\right)}{2}-\frac{n}{4\left(j-i+1\right)}+\frac{\left(j-i-1\right)\left(j-i\right)}{6}.(10)$

Theorem 2 Let the number of single-layer chain network nodes in G^d be n, if the edges connection positions are located at i and j, then the first-order coherence of G^d is

$H^{\left(1d\right)}=\frac{1}{4n}\left[\frac{n^2-1}{6}+\frac{n+\left(n-j\right)\left(n-j+1\right)+i\left(i-1\right)}{2}\right]$

$+\frac{1}{4n}\left[\frac{\left(j-i-1\right)\left(j-i\right)}{6}-\frac{n}{4\left(j-i+1\right)}\right].$

Proof. By formula 7, formula 9 and formula 10, theorem 2 can be easily obtained.

3.3 Conjecture

Conjecture 1 The conjectures for the effect of edge connection position i (1 ≤ i ≤ n) on the consensus of G^s are as follows:

(1) When n = 2k + 1 (k ≥ 1), the optimal edge connection position is located at k + 1, the worst edges connection positions are located at 1 and 2k + 1.

(2) When n = 2k (k ≥ 1), the optimal edges connection positions are located at k and k + 1, the worst edges connection positions are located at 1 and 2k.

Conjecture 2 The conjectures for the effect of edge connection method i@j (i < j)on the consensus of G^d are as follows:

(1) The worst edges connection methods are 1@2 and n − 1@n.

(2) When i is fixed, given the symmetry of the double-layer chain network, we assume that 1 ≤ i ≤ [n/2]. The worst edge connection method is i@i + 1. When n = 4k, n = 4k + 1, n = 4k + 2, n = 4k + 3, the optimal edges connection methods are i@3k + [(i + 3)/4], i@3k + [(i + 6)/4], i@3k + 1 + [(i + 5)/4], i@3k + 2 + [(i + 4)/4], respectively.

Conjecture 3 For the impact of the number of nodes n on the consensus of G^d, the conjectures are as follows:

When n = 5k, the optimal edges connection methods are k@4k and k + 1@4k + 1, n = 5k + x (x = 1, 2, 3, 4), the optimal edge connection method is k + 1@4k + x.

4 Numerical simulation experiment and analysis

In this section, the three conjectures proposed in Section 3 are numerically simulated to verify the rationality of the conjectures.

4.1 The influence of edge connection position i on the consensus of G^s

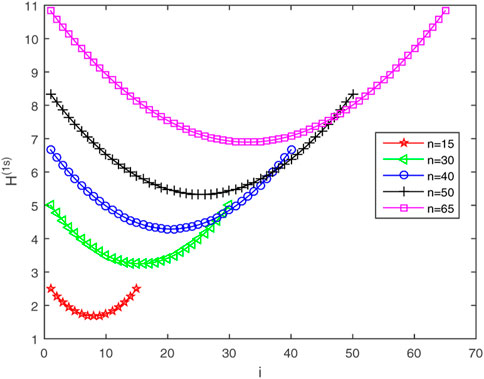
When n = 15, 30, 40, 50, 65, Figure 2 shows the relationships between the first-order coherence H^(1s) and i. With the increase of i, H^(1s) first decreases and then increases, and reaches the minimum value at [i = (n + 1)/2], and the maximum value at i = 1 and i = n. Since the consensus of the network is inversely proportional to the first-order coherence, the optimal edge connection position of G^s is located at [i = (n + 1)/2], and the worst edges connection positions of G^s are located at i = 1, n. It is consistent with the conclusion of conjecture 1.

FIGURE 2

FIGURE 2. The relationship between the coherence of G^s and the edge connection position i.

4.2 The influence of edge connection method i@j (i < j) on the consensus of G^d

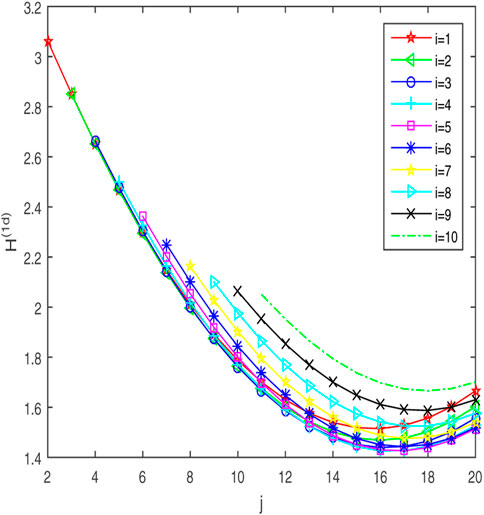
When n = 20, 1 ≤ i ≤ 10, i + 1 ≤ j ≤ 20, Figure 3 traverses all the connection methods i@j of G^d. It is found that H^(1d) reaches its maximum at i = 1, j = 2. Therefore, G^d has the worst consensus at the edges connection methods 1@2 and n − 1@n.

FIGURE 3

FIGURE 3. The relationship among the coherence of G^d and the edge connection position i,j.

When i is fixed, H^(1d) decreases first and then increases with the increase of j, and reaches its maximum value at j = i + 1. The worst edge connection method is i@i + 1. Figure 3 shows that H^(1d) will reach the minimum value with the increase of j, and j is not only related to i, but also related to the value of n. Through the analysis of MATLAB, it is found that the value of j is related to [3n/4] and [(i + x)/4](x = 0, 1, 2, 3). When n = 4k, n = 4k + 1, n = 4k + 2, n = 4k + 3, H^(1d) will reach the minimum value at j = 3k + [(i + 3)/4], j = 3k + [(i + 6)/4], j = 3k + 1 + [(i + 5)/4], j = 3k + 2 + [(i + 4)/4], respectively. It is consistent with the conclusion of conjecture 2.

4.3 The influence of the number of single-layer nodes n on the consensus of G^d

The values of i and j corresponding to the minimum coherence H^(1d) are obtained by MATLAB software, and the edges connection methods i@j of G^d with n (5 ≤ n ≤ 104) are calculated ergodically when the consensus is optimal, and the correctness of conjecture 3 is verified.

Figure 4 shows the variation of the optimal edges connected positions i, j and n and their linear fitting lines under the condition that n = 5k + x (1 ≤ k ≤ 20, x = 0, 1, 2, 3, 4).

FIGURE 4

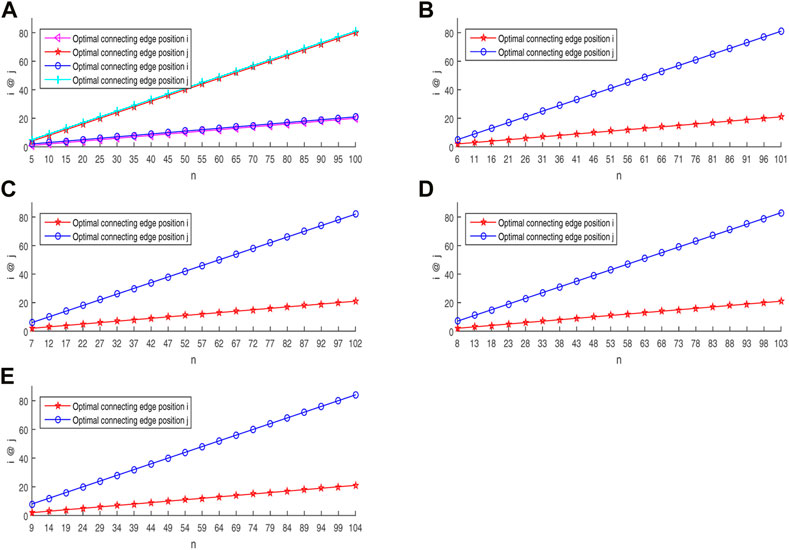
FIGURE 4. The optimal edge connection positions i and j vary with the number of single-layer network nodes n. (A) n = 5k; (B) n = 5k + 1; (C) n = 5k + 2; (D) n = 5k + 3; (E) n = 5k + 4.

From Figure 4A, when n = 5k, there exist two cases of optimal edges connection methods, and the corresponding i and j are distributed on the lines i = k, j = 4k and i = k + 1, j = 4k + 1. Therefore, n = 5k, the edges connection methods k@4k and k + 1@4k + 1 have optimal consensus.

From Figures 4B–E, when n = 5k + x (x = 1, 2, 3, 4), the optimal edge connection method is unique. The corresponding i and j are distributed on i = k + 1, j = 4k + 1, j = 4k + 2, j = 4k + 3 and j = 4k + 4, respectively. Therefore, when n = 5k + x (x = 1, 2, 3, 4), the edge connection method k + 1@4k + x have the optimal consensus. The above simulation results are consistent with the conclusion of conjecture 3.

5 Conclusion

In this paper, using the relationship between the Laplacian eigenvalues and characteristic polynomials, we calculate the coherence of double-layer chain networks with one and two connecting edges between layers. On this basis, the numerical simulations are carried out for the optimal/worst connection positions of the consensus of double-layer chain networks. If there are n nodes in a single layer, the optimal edge connection position of double-layer chain networks with one edge between layers is in the middle, and the worst edge connection position is located at the end node of the chain. The optimal edges connection positions of double-layer chain networks with two edges between layers are located at near n/5 and 4n/5 of each chain respectively, and the worst edges connection positions are located at the end node of the chain and its neighbor node. When i (1 ≤ i ≤ [n/2]) is fixed, the optimal edge connection method i@j (i + 1 ≤ j ≤ n) of double-layer chain networks with two edges between layers is near i@3n/4 + i/4, and the worst edge connection method is i@i + 1. Further, when the number of nodes n is subdivided into 5k, 5k + 1, 5k + 2, 5k + 3, 5k + 4, in the case of n = 5k, the optimal edges connection positions are k and 4k, k + 1 and 4k + 1. In the case of n = 5k + x (x = 1, 2, 3, 4), the optimal edges connection positions are k + 1 and 4k + x.

At present, the research on the optimal inter-layer connection position of double-layer networks mostly adopts numerical methods, and it is difficult to get the results in theory. In this paper, we get the optimal edge connection method when the number of double-layer chain networks between layers is 2. However, when the number of edge connections between layers is greater than 2, how the optimal edge connection method changes in position is worthy of our in-depth study.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, HG and YD; methodology, HG and JZ; software, YD; validation, YD and JZ; formal analysis, QL and RG; writing—original draft preparation, HG and YD; writing—review and editing, JZ; supervision, YD; and project administration, HG All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (no.2022D01A246) and Xinjiang Uygur Autonomous Region University Basic Research Business Fund Research Project (no.XJEDU2022P129), the National Science Foundation of Xinjiang (NSFXJ) (no.2021D01A65), the National Science Foundation of Xinjiang (NSFXJ) (no.2021D01B35), National innovation and entrepreneurship training program for College Students (no.202210994014), National innovation and entrepreneurship training program for College Students (no.202110994006). School level project of Xinjiang institute of Light industry Technology (no. XJQG2023S94), Xinjiang Higher Education Development Research Center (no. ZK202285B).

Acknowledgments

We express our sincere gratitude to the persons who gave us valuable comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tang L, Wu X, Lu J, Lu JA, D’Souza RM. Master stability functions for complete, intra-layer, and inter-layer synchronization in multiplex networks of coupled Rossler oscillators. Phys Rev E (2019) 99(1):012304. Article ID 012304. doi:10.1103/physreve.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gelbrecht M, Boers N, Kurths J. Variability of the low-level circulation of the South American monsoon analysed with complex networks. Eur Phys J Spec Top (2021) 230(14):3101–20. doi:10.1140/epjs/s11734-021-00187-w

CrossRef Full Text | Google Scholar

3. Skardal S, Arola-Fernndez L, Taylor D, Arenas A. Higher-order interactions can better optimize network synchronization. Phys Rev Res (2021) 3(4):043193. Article ID 043193. doi:10.1103/physrevresearch.3.043193

CrossRef Full Text | Google Scholar

4. Wu X, Li Y, Wei J, Zhao J, Feng J, Lu J. Inter-layer synchronization in two-layer networks via variable substitution control. J Franklin Inst (2020) 357(4):2371–87. doi:10.1016/j.jfranklin.2019.12.019

CrossRef Full Text | Google Scholar

5. Shang Y. On connectivity and robustness of random graphs with inhomogeneity. J Appl Probab (2022) 60:284–94. doi:10.1017/jpr.2022.32

CrossRef Full Text | Google Scholar

6. Sun W, Li Y, Liu S. Noisy consensus dynamics in windmill-type graphs. Chaos (2020) 30(12):123131. Article ID 123131, 2020. doi:10.1063/5.0020696

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Shang Y. Practical consensus for heterophilous multiagent networks with constrained states. J Franklin Inst (2022) 359:10931–48. doi:10.1016/j.jfranklin.2022.04.037

CrossRef Full Text | Google Scholar

8. Chen J, Sun W, Wang J. Topology design for leader-follower coherence in noisy asymmetric networks. Physica Scripta (2023) 98(1):015215. Article ID 015215. doi:10.1088/1402-4896/aca9a3

CrossRef Full Text | Google Scholar

9. Shang Y. Constrained consensus in state-dependent directed multiagent networks. IEEE Trans Netw Sci Eng (2022) 9(6):4416–25. doi:10.1109/tnse.2022.3201187

CrossRef Full Text | Google Scholar

10. Gao H, Zhu J, Chen X, Zhang L, Li X. Coherence analysis of symmetric star topology networks. Front Phys (2022) 10:2022. Article ID 876994. doi:10.3389/fphy.2022.876994

CrossRef Full Text | Google Scholar

11. Sun W, Hong M, Liu S, Fan K. Leader-follower coherence in noisy ring-trees networks. Nonlinear Dyn (2020) 102(3):1657–65. doi:10.1007/s11071-020-06011-9

CrossRef Full Text | Google Scholar

12. Liu J, Bao Y, Zheng W, Hayat S. Network coherence analysis on a family of nested weighted n-polygon networks. Fractals (2021) 29(08). Article ID 2150260, 2021. doi:10.1142/s0218348x21502601

CrossRef Full Text | Google Scholar

13. Qi Y, Zhang Z, Yi Y, Li H. Consensus in self-similar hierarchical graphs and sierpinski graphs: Convergence speed, delay robustness, and coherence. IEEE Trans Cybernetics (2018) 49(2):592–603. doi:10.1109/tcyb.2017.2781714

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yang Q, Caterina M, Gruenbacher M. Gruenbacher. Robustness of supply chain networks against underload cascading failures. Physica A: Stat Mech its Appl (2021) 563. Article ID 125466, 2021.

CrossRef Full Text | Google Scholar

15. Jalan S, Kumar A, Leyva I. Explosive synchronization in frequency displaced multiplex networks. Chaos: Interdiscip J Nonlinear Sci (2019) 29(4):041102. Article ID 041102. doi:10.1063/1.5092226

PubMed Abstract | CrossRef Full Text | Google Scholar

16. He W, Chen G, Han Q, Du W, Cao J, Qian F. Multiagent systems on multilayer networks: Synchronization analysis and network design. IEEE Trans Syst Man, Cybernetics: Syst (2017) 47(7):1655–67. doi:10.1109/tsmc.2017.2659759

CrossRef Full Text | Google Scholar

17. Li J, Luan Y, Wu X, Lu J. Synchronizability of double-layer dumbbell networks. Chaos: Interdiscip J Nonlinear Sci (2021) 31(7):073101. Article ID 073101. doi:10.1063/5.0049281

CrossRef Full Text | Google Scholar

18. Zhu J, Huang D, Yu Z, Pei P. Synchronizability of multi-layer dual-center coupled star networks. Front Phys (2021) 9. Article ID 782607, 2021. doi:10.3389/fphy.2021.782607

CrossRef Full Text | Google Scholar

19. Patterson S, Bamieh B. Consensus and coherence in fractal networks. IEEE Trans Control Netw Syst (2014) 1(4):338–48. doi:10.1109/tcns.2014.2357552

CrossRef Full Text | Google Scholar

20. Xu W, Wu B, Zhang Z, Zhang Z, Kan H, Chen G. Coherence scaling of noisy second-order scale-free consensus networks. IEEE Trans Cybernetics (2022) 52(7):5923–34. doi:10.1109/tcyb.2021.3052519

CrossRef Full Text | Google Scholar

21. Du W, Zhu J, Gao H, Li X. Consensus analysis of the weighted corona networks. Front Phys (2022) 10. Article ID 948247. doi:10.3389/fphy.2022.948247

CrossRef Full Text | Google Scholar

22. Huang D, Bian J, Jiang H, Yu Z. Consensus indices of two layered multi-star networks: An application of laplacian spectrum. Front Phys (2021) 9. Article ID 803941, 2021. doi:10.3389/fphy.2021.803941

CrossRef Full Text | Google Scholar

23. Tang F, You I, Guo S, Guo M, Ma Y. A chain-cluster based routing algorithm for wireless sensor networks. J Intell Manufacturing (2012) 23(4):1305–13. doi:10.1007/s10845-010-0413-4

CrossRef Full Text | Google Scholar

24. Zi S, Lin W. Intelligent street light control system based on long chain sensor network. China Illuminating Eng J (2015) 26:48–56.

Google Scholar

25. Wu X, Meng H, Lu J, Jie J, Han X. Analysis of the synchronizability of two-layer chain networks with two inter-layer edges. Scientia Sinica Informationis (2021) 51:1931–45.

Google Scholar

26. Deng Y, Zhen J, Deng G, Zhang Q. Eigenvalue spectrum and synchronizability of multiplex chain networks. Physica A: Stat Mech its Appl (2020) 537:122631. Article ID 122631, 2020. doi:10.1016/j.physa.2019.122631

CrossRef Full Text | Google Scholar