
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 24 March 2023
Sec. Condensed Matter Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1140286
 Kouta Kondou1,2*
Kouta Kondou1,2* Yoshichika Otani1,2,3
Yoshichika Otani1,2,3Spin–charge conversion (SCC) leads to the driving principle of spintronics devices, such as non-volatile magnetic memory and energy harvesting devices from light, sound, and heat to charge current. Recently, controllable SCCs have emerged in materials with spatial- and time-reversal asymmetry as a new route for efficient manipulation and realization of novel functionalities of future spintronics devices. This study overviews the SCC from the fundamental mechanism to the recent research progress in novel materials, such as topological magnets and atomically layered materials. Additionally, we discuss the chiral organic materials from the viewpoint of a new pathway for the emergence of spin functionalities.
Spin and charge degrees of freedom can be converted by the spin Hall effect (SHE), which was theoretically predicted by Dyakonov and Perel [1]. Approximately 3 decades later, Hirsch re-predicted and introduced it as SHE [2]. Since the 2000s, high-quality film preparation and microfabrication technologies for semiconductors and metals have been developed, leading to the first observation of spin accumulation in GaAs by optical technique in 2004 [3]. After the pioneering works, systematic experiments in semiconductors have clarified the fundamental properties of SHE, such as carrier type [4], amount of dopant [5], and intervalley transition dependence [6]. These findings might lead to the establishment of fundamental technology for a novel integration platform that combines photonic, magnetic, and electronic components.
Moreover, intensive experimental research on the SHE in metallic materials [7–10] established the so-called spin–orbit torque (SOT) that enables switching magnetization and driving magnetic domain wall for magnetic memory applications [11, 12] and auto-oscillation for microwave generators [13], among others. Thus, SHE is currently one of the indispensable phenomena in spintronic devices.
An essential characteristic of the SHE is that it can act as a spin source by producing the flow of spin angular momentum (spin-current), perpendicular to the charge current, as shown in Figures 1A, B. Thus, the SHE contributes to simplifying the device structure, for example, ferromagnetic metal/spin Hall material bilayer for magnetization switching [11–13]. It has also been developed to extract electrical charge current from heat, sound, and light using the inverse effect. Accordingly, this technique draws attention from the standpoint of energy harvesting [14, 15].
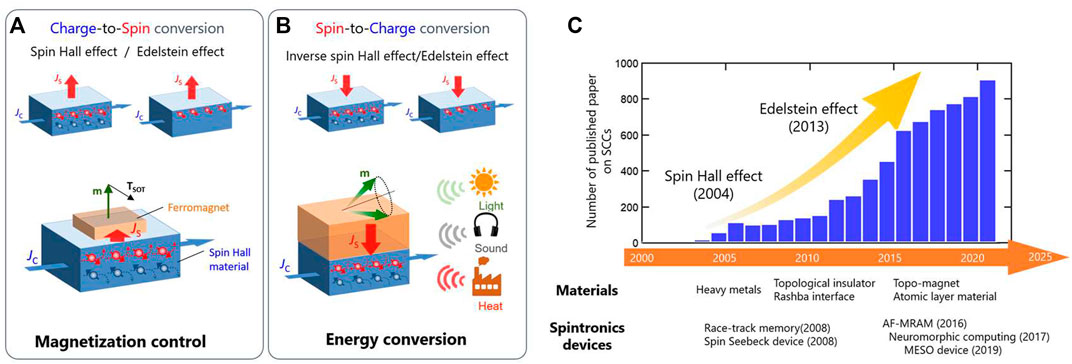
FIGURE 1. Spin–charge interconversion and its applications. (A) Charge-to-spin conversion due to spin Hall and Edelstein effects. In both cases, spins accumulate at the interface by applying the charge current. The spin accumulation gives rise to the spin–orbit torques (SOTs) to the adjacent ferromagnet. It is the working principle for SCC-based spintronic devices, such as magnetic memory, spin-torque nano-oscillator, and spin-wave logic. (B) Spin-to-charge conversion due to inverse spin Hall and inverse Edelstein effects. The inverse effects convert light, sound, and heat-to-charge currents via spin currents. (C) The number of studies on SCCs and proposed spintronics devices as a function of year. Searches for keywords, such as spin–charge conversion, spin Hall effect (SHE), Edelstein effect, and spin–orbit torque, on the Web of Science database. After the first experimental observation of the SHE in 2004 and the Edelstein effect in 2013, the number of SCC studies increased yearly since fundamental research of SCCs began to trigger novel spintronics device concepts and applications.
The spin–charge conversion (SCC) efficiency, defined as the ratio of the spin current density and the charge current density, called the spin Hall angle, determines the performance of such SHE-based spintronic devices. The SHE relies on spin–orbit interactions and can be generated by intrinsic or extrinsic mechanisms. So far, systematic theoretical and experimental works reveal that SHE in 4d and 5d transition metals comes from the intrinsic mechanism based on the degeneracy of d-orbitals via spin–orbit coupling (SOC) [16–19]. However, the extrinsic SHE relies on scattering, namely, skew scattering [20] and side jump [21] by impurities causing strong spin–orbit interactions. However, the maximum conversion efficiency of these materials is only in the range of a few tens of percent [19] [11, 22, 23]. Thus, it was required to discover and establish the technology for novel conversion phenomena to improve efficiency.
Recently, as a new type of spin conversion principle instead of the SHE, the Edelstein effect (EE) in the two-dimensional electron systems with spin-splitting surface states has been actively studied [24, 25]. Unlike the bulk SHE, this effect generates spin accumulation via spin momentum locking linked to the charge current flow at material interfaces. Such spin-splitting surface and interface states caused by the spatial inversion asymmetry have been observed at the surface of the topological insulator and Rashba interface by means of angle-resolved photoemission spectroscopy (ARPES) [26, 27]. In the surface states, the polarization vector of electron spins depends on the direction of electron flows, called spin-momentum locking [27]. The application of an electric field gives rise to spin accumulation at the interfaces, a behavior known as the Edelstein effect (EE). The large spin splitting at the surface of the topological insulator and Rashba interface realizes more efficient SCC than transition metals, at several orders of magnitude smaller current densities than for transition metals [28–31].
These experimental demonstrations of SCCs via SHE and EE led to the novel concepts of spintronics devices [32–36], such as a racetrack memory driven by high-speed magnetic domain wall motion [32] and a magnetoelectric spin–orbit (MESO) device based on interfacial SCCs [33]. Since the first observation of SHE in 2004 and EE in 2013, the number of studies on SCCs has been increasing every year, as shown in Figure 1C. Thus, not only are SCCs interesting as a fundamental science, but they also attract attention in terms of applications and are expected to have practical applications.
From such research backgrounds, to realize lower power consumption and higher speed operation of spintronics devices, it is desired to develop a method to control the spin polarization vector and the conversion efficiency freely. This review article overviews the recent research trend of the emergence of SCC functionalities utilizing symmetry, such as space, time, and chirality, as shown in Figure 2.
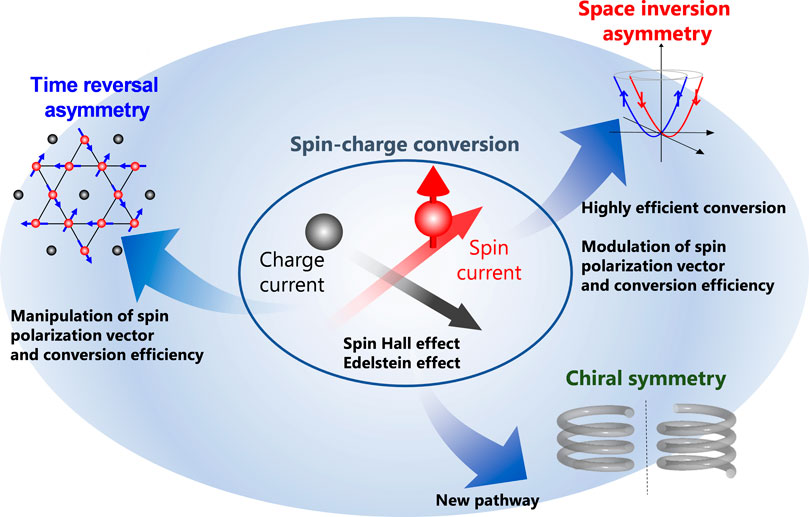
FIGURE 2. Explore spin–charge conversion functionality by focusing on spatial asymmetry, time-reversal asymmetry, and chiral symmetry.
At material interfaces, spin-splitting surface states appear due to spatial inversion asymmetry. When an electric field is applied to such an interface, non-equilibrium spin accumulation occurs [24, 25]. Edelstein predicted such spin accumulation in 1990 [24]. In the 2000s, by utilizing the spin-resolved ARPES technique, the surface states were investigated intensively. In 2007, a large spin splitting of ∼200 meV was observed in Ag/Bi surface alloys. Interestingly, it is much larger than the Bi surface (∼14 meV) [26, 37, 38]. Around the same time, it was experimentally discovered that the linear Dirac dispersion exhibits 100% spin polarization in the topological insulator surface [27].
The spin accumulation at the surface state can exert SOTs consisting of field-like and spin-transfer (anti-damping) torques on adjacent magnets. Thus, effective utilization of EE-induced spin accumulation has been desired for spintronics study. High-quality thin film preparation technologies, including molecular beam epitaxy and sputter deposition, are now ready to fabricate devices for quantitative evaluation of spin generation at the interface. These achievements have enabled low-power efficient magnetization reversal [28, 31, 39, 40].
The amplitude of spin splitting, proportional to Rashba parameter αR, characterizes the efficiency of the EE-induced SCCs. Thus, the charge-to-spin conversion efficiency q and spin-to-charge conversion λ are described by q = αR/(ħτsvF2) and λ = αRτs/ħ, where ħ and τs are plank constant and spin relaxation time at the surface state, respectively [25, 28, 31]. There is a trade-off relation between conversion efficiencies q and λ through τs, which is determined by the strength of the hybridization between bulk and interface states [41]. Indeed, highly efficient spin-to-charge conversion has been observed at the oxide interface of LaAlO3/SrTiO3, as its interface exhibits a spin relaxation time several orders of magnitude longer than metal interfaces due to weak hybridization between bulk and interface states [42].
Since one of the origins of a large αR is known as the asymmetric electron distribution at the interface [37, 43], the large αR can be induced not only by the surface alloy such as Ag/Bi but also by many kinds of material interfaces [41, 44–47]. From this point of view, recently, novel SCCs have emerged by modifying the interfacial state of metal/organic molecules depending on the molecular structure, polarity, and arrangement. By utilizing the highly spin-to-charge conversion at the molecule/metal interfaces, electrical detection of ultra-thin molecules absorption less than a single layer has been reported [41]. These research directions have drawn much attention as a new aspect of molecular spintronics [41, 47].
Unique features of these interfacial SCCs are the realization of highly efficient conversion, improvement of material selectivity, and the ability to modulate the conversion efficiency by the external electric field significantly. So far, several methods by utilizing an external electric field have been reported for 1) Fermi level tuning [48], 2) lattice strain [49], 3) oxygen transfer [50], and 4) electric polarity reversal in ferroelectric materials [51]. Especially for the latter two methods, it is possible to remain in the state even after the external electric field is turned off (i.e., non-volatile control). These modulation techniques are essential for future applications, such as magnetoelectric spin–orbit (MESO) devices based on interfacial SCCs [33].
Furthermore, spatial inversion asymmetry in crystals is also important for the emergence of SCC functions. Figure 3B shows the symmetry-dependent SOT magnetization switching in low-symmetry crystals, such as CuPt. Notably, out-of-plane spin polarization can be generated in such low-symmetry crystals by breaking lateral mirror symmetry [52–55] but not the conventional SHE in transition metals. In the inverse conversion (i.e., spin-to-charge conversion), the spin polarization and the charge current are parallel. In addition, the conventional conversion where the spin polarization is orthogonal to the charge current has been observed [56].
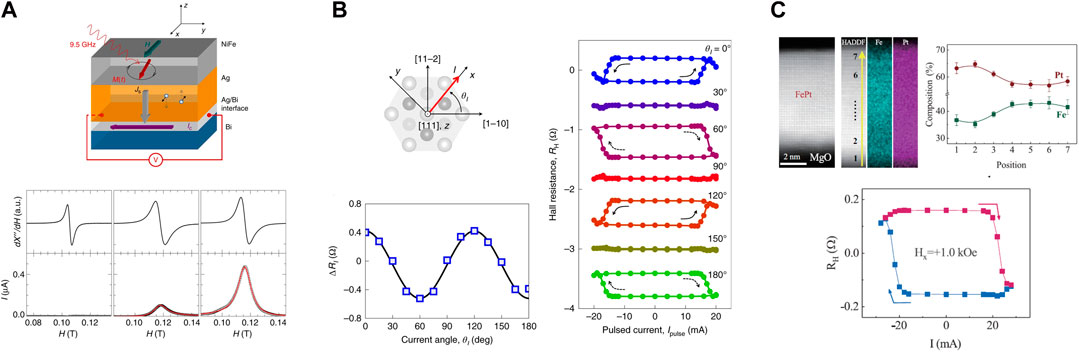
FIGURE 3. Emergence of SCCs due to spatial inversion symmetry breaking. (A) Spin-to-charge conversion at Ag/Bi Rashba interface in [44]. The bottom figure corresponds to FMR and spin pumping spectra in NiFe/Ag, NiFe/Bi, and NiFe/Ag/Bi films. A clear enhancement appears due to spin-to-charge conversion at Ag/Bi. (B) CuPt/CoPt Hall devices for symmetry-dependent SOT-induced magnetization switching in [52]. Plane view of the L11 hexagon projected along the [111] direction, where the Pt atomic layer (grey color) is sandwiched between two Cu (Co) atomic layers. The polarity of magnetization switching (clockwise and anti-clockwise) depends on the current angle θl from the low-symmetry axis [1–10] of CuPt. (C) Self-induced SOT switching in a single ferromagnetic layer in [57]. A composition gradient exists in FePt along the thickness direction.
Additionally, spatial inversion asymmetry in the magnetic materials is also interesting because current-induced magnetization reversal has been observed in a single magnetic layer i.e., a spin source layer like Pt is unnecessary for magnetization control [57–61]. It might be caused by “self-induced SOT,” which is induced by current-induced spin accumulation inside the magnetic material due to spatial asymmetry. For example, such self-induced SOTs have been observed in the gradient composition magnet in Figure 3C [57–59] and low symmetry van der Waals magnetic crystal Fe3GeTe2 [60]. In particular, in the F3GeTe2, the critical current density for magnetization reversal is approximately two orders of magnitude smaller than that in the conventional transition metal/ferromagnetic metal bilayer. Thus, the elucidation of the mechanism has attracted attention [61].
These fundamental research developments regarding the SCC functionalities induced by spatial inversion asymmetry are promising to contribute to more efficient and faster magnetization control in spintronics devices.
This study focuses on SCCs in magnetic materials with time-reversal asymmetry. Magnetic materials have also been studied using the same experimental methods for non-magnetic metal such as non-local spin valves, spin-torque ferromagnetic resonance (FMR), and spin pumping, among others [62, 63]. So far, SHE and ISHE on magnetic materials have been investigated regarding a correlation with the anomalous Hall effect (AHE) because SHE shares the scattering mechanism, such as skew scattering and side jump with AHE [64, 65]. From this point of view, utilizing scattering enhancement due to spin fluctuation near the magnetic phase transition temperature is also a promising way to attribute the amplitude of SHE [66–71].
Recently, there have been remarkable developments in experimental research on the magnetization direction-dependent SHE [70–82]. Figure 4A shows the SHE caused by AHE in a ferromagnet, which was first predicted by theoretical study and demonstrated experimentally later [72, 73, 75], called spin-AHE. In addition, spin precession along a ferromagnetic moment was found to tilt a spin polarization vector inside the ferromagnet shown in Figure 4B [76] and at the ferromagnetic/non-magnetic interface [77]. The spin polarization vector can be controlled by adjusting the magnetic moment in these phenomena.
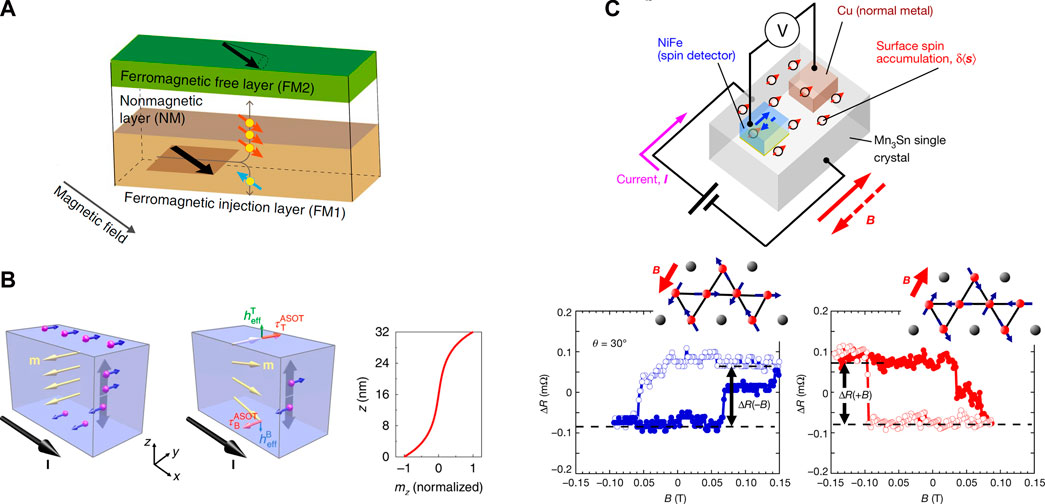
FIGURE 4. Emergence of SCCs due to time-reversal symmetry breaking. (A) Spin-AHE in ferromagnetic metal (FM)1/non-magnetic metal (NM)/FM2 tri-layer structure magnetic damping constant in FM2 is modulated by SOT due to spin-AHE in FM1 in [74]. (B) Tilting spin polarization vector about the magnetic moment in ferromagnetic metal in [76]. (C) Spin accumulation in the non-collinear antiferromagnet Mn3Sn due to magnetic SHE in [79]. The chemical potential measurement detects the current-induced spin accumulation via a voltage drop across NiFe and Cu electrodes. Polarity changes of the magnetoresistance loop indicate the sign change of the accumulated spin polarization vector.
Furthermore, this concept has been extended to SHE in antiferromagnets [78–82]. Notably, the non-collinear antiferromagnets Mn3X (X = Sn, Ge) draw much attention as a candidate material for next-generation ultra-fast spintronic devices. It is a Weyl magnet displaying a huge response comparable to ferromagnets at room temperature [83]. Such a non-collinear antiferromagnet has a tiny magnetization, approximately 1/1,000 of a ferromagnet, so the time-reversal symmetry is broken, and the spin structure of the Mn3X can be reversed by a small external magnetic field or electric current via SOT [83–85].
In contrast to the ferromagnetic dipole, the spin structure of the Mn3X generates a magnetic octupole moment consisting of multiple Mn spins. In the Mn3X, octupole direction-dependent SHE and ISHE caused by the momentum-dependent spin polarization produced by the non-collinear magnetic order were discovered and named magnetic SHE (MSHE) and magnetic ISHE, as shown in Figure 4C [79].
In the MSHE, the spin-polarization vector is perpendicular to the direction of the magnetic octupole moment. Very recently, unconventional SOT and field-free magnetization switching of adjacent ferromagnets due to the MSHE in non-collinear antiferromagnets have been reported [80–82].
Compared with the spatial asymmetry-induced SCC functionalities, the SCCs caused by the time-reversal asymmetry can be tuned more freely by controlling the magnetization direction by an external magnetic field. This section focused on SCCs generating a steady spin state in magnetic materials. The emergence of novel functionalities of SHE under magnetization dynamics might be an attractive research topic in the near future [66, 86].
Chirality is a common property in wide branches of science, such as biology, chemistry, physics, and cosmology, for the emergence of any functionality. Molecular chirality is essential to induce spin functionalities in organic materials. Indeed, the spin polarization of electrons passing through chiral molecules such as DNA chains has been observed [87], implying an interaction between chiral structure and passing electron spins. This property is called chiral-induced spin selectivity (CISS), of which phenomena have been investigated using various experimental techniques, such as photoelectron spectroscopy, conductive atomic force microscope (AFM), and magnetoresistance measurement [87–96]. Surprisingly, a considerably large spin polarization [90, 91] comparable to that of ferromagnets such as Fe (∼0.4) appears at room temperature despite the weak SOC of light elements in chiral organic molecules.
However, the physical origin of the large spin polarization due to CISS remains elusive. In particular, significantly large SOC of approximately several 100 meV, which is several orders higher than that of organic materials such as graphene (∼10 μeV [97]), is necessary to realize such large spin polarization [90–92]. Recent theoretical work revealed that the geometric SOC due to molecule structure, such as curvature, gives rise to large SOC even in organic materials such as DNA [98]. Furthermore, as another degree of freedom, the contribution of orbital texture in chiral molecules has also been discussed [99, 100]. Quantitative and systematic experimental and theoretical works are indispensable to reveal the microscopic origin of large spin polarization due to CISS in molecules.
Conversely, several experimental studies have recently reported the CISS-like effect without bias current in chiral molecules [101–104]. For instance, a chiral molecule adsorbed on a superconductor surface exhibits Shiba states similar to the magnetic impurity-induced state in the tunneling spectra, as shown in Figure 5B [103]. Moreover, a chirality-dependent effective magnetic field has occurred at room temperature [101, 102]. Remarkably, no bias charge current flows through the chiral molecules, implying that spontaneous spin polarization may emerge in the chiral molecules. More recently, current-in-plane MR (CIP-MR) effects have been observed in chiral molecule/ferromagnetic metal bilayers at room temperature, as shown in Figure 5C [104]. The temperature dependence of the MR suggests the existence of thermally driven spontaneous spin polarization in the chiral molecules [104–107].
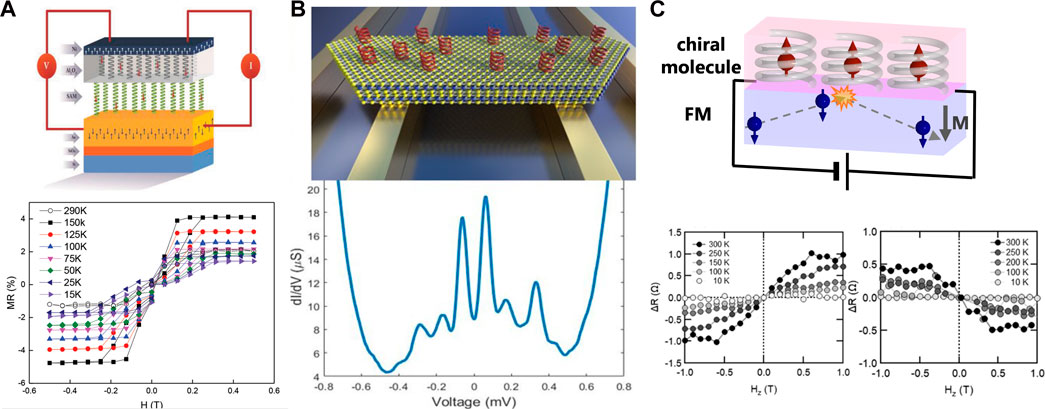
FIGURE 5. Molecular chirality-induced spin functionalities. (A) Chirality-dependent current perpendicular to the plane magnetoresistance against the external perpendicular magnetic field. Charge current flows in the chiral molecules in [94]. (B) Magnetic impurity-like state in superconductor induced by chiral molecules in [101]. (C) Chirality-dependent current-in-plane magnetoresistance in ferromagnetic metal/chiral molecule bilayer without bias charge current in the chiral molecule in [104]. Magnetoresistance decrease with decreasing the measurement temperature.
Recently, in the chiral inorganic crystals, systematic experiments regarding the CISS effect have been reported [108, 109]. Spin polarization due to the CISS effect has been observed by applying a charge current along the c-axis in chiral crystal CrNb3S6. The inverse CISS has also been detected in the same device, confirming the CISS effect’s reciprocal relationship [108]. Furthermore, exciting phenomena beyond conventional spintronics physics, such as chirality-induced spin polarization over millimeters, have been reported in the chiral crystals despite the strong SOC (chiral) materials [109]. It is highly desirable to comprehensively understand such chirality-induced spin phenomena across a range of materials and scales.
We have reviewed recent SCCs research regarding the emergence of novel functionality caused by spatial asymmetry, time-reversal asymmetry, and chiral symmetry. These symmetries enable us to control the conversion efficiency of the SCCs and the spin polarization vector. Importantly, such a concept for the emergence of SCCs functionality incorporates the viewpoint of symmetry will progress remarkably the design of the material, device, and its function [104].
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work was supported by JST-CREST (no. JPMJCR18T3) and JST-Mirai (no. JPMJMI20A1) and by Grants-in-Aid for Scientific Research (19H02586 and 19H05629).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Dyakonov MI, Perel VI. Possibility of orienting electron spins with current. Sov Phys JETP (1971) 13:467.
3. Kato YK, Myers RC, Gossard AC, Awschalom DD. Observation of the spin Hall effect in semiconductors. Science (2004) 306(5703):1910–3. doi:10.1126/science.1105514
4. Ando K, Saitoh E. Observation of the inverse spin Hall effect in silicon. Nat Commun (2012) 3:629. doi:10.1038/ncomms1640
5. Zucchetti C, Bottegoni F, Isella G, Finazzi M, Rortais F, Vergnaud C, et al. Spin-to-Charge conversion for hot photoexcited electrons in germanium. Phys Rev B (2018) 97(12):125203. doi:10.1103/PhysRevB.97.125203
6. Okamoto N, Kurebayashi H, Trypiniotis T, Farrer I, Ritchie DA, Saitoh E, et al. Electric control of the spin Hall effect by intervalley transitions. Nat Mater (2014) 13(10):932–7. doi:10.1038/nmat4059
7. Wunderlich J, Kaestner B, Sinova J, Jungwirth T. Experimental observation of the spin-Hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys Rev Lett (2005) 94(4):047204. doi:10.1103/PhysRevLett.94.047204
8. Saitoh E, Ueda M, Miyajima H, Tatara G. Conversion of spin current into charge current at room temperature: Inverse spin-Hall effect. Appl Phys Lett (2006) 88(18):182509. doi:10.1063/1.2199473
9. Valenzuela SO, Tinkham M. Direct electronic measurement of the spin Hall effect. Nature (2006) 442(7099):176–9. doi:10.1038/nature04937
10. Kimura T, Otani Y, Sato T, Takahashi S, Maekawa S. Room-temperature reversible spin Hall effect. Phys Rev Lett (2007) 98(15):156601. doi:10.1103/PhysRevLett.98.156601
11. Liu L, Pai CF, Li Y, Tseng HW, Ralph DC, Buhrman RA. Spin-torque switching with the giant spin Hall effect of tantalum. Science (2012) 336(6081):555–8. doi:10.1126/science.1218197
12. Haazen PP, Mure E, Franken JH, Lavrijsen R, Swagten HJ, Koopmans B. Domain wall depinning governed by the spin Hall effect. Nat Mater (2013) 12(4):299–303. doi:10.1038/nmat3553
13. Demidov VE, Urazhdin S, Ulrichs H, Tiberkevich V, Slavin A, Baither D, et al. Magnetic nano-oscillator driven by pure spin current. Nat Mater (2012) 11(12):1028–31. doi:10.1038/nmat3459
14. Otani Y, Shiraishi M, Oiwa A, Saitoh E, Murakami S. Spin conversion on the nanoscale. Nat Phys (2017) 13(9):829–32. doi:10.1038/nphys4192
15. Puebla J, Hwang Y, Kondou K, Otani Y. Progress in spinconversion and its connection with band crossing. Annalen der Physik (2022) 534(4):2100398. doi:10.1002/andp.202100398
16. Mosendz O, Pearson JE, Fradin FY, Bauer GE, Bader SD, Hoffmann A. Quantifying spin Hall angles from spin pumping: Experiments and theory. Phys Rev Lett (2010) 104(4):046601. doi:10.1103/PhysRevLett.104.046601
17. Kontani H, Naito M, Hirashima D S, Yamada K, Inoue J-i. Study of intrinsic spin and orbital Hall effects in Pt based on a (6s, 6p, 5d) tight-binding model. J Phys Soc Jpn (2007) 76(10):103702. doi:10.1143/jpsj.76.103702
18. Tanaka T, Kontani H, Naito M, Naito T, Hirashima DS, Yamada K, et al. Intrinsic spin Hall effect and orbital Hall effect in4dand5dtransition metals. Phys Rev B (2008) 77(16):165117. doi:10.1103/PhysRevB.77.165117
19. Morota M, Niimi Y, Ohnishi K, Wei DH, Tanaka T, Kontani H, et al. Indication of intrinsic spin Hall effect in4dand5dtransition metals. Phys Rev B (2011) 83(17):174405. doi:10.1103/PhysRevB.83.174405
20. Smit J. The spontaneous Hall effect in ferromagnetics ii. Physica (1958) 24(1-5):39–51. doi:10.1016/s0031-8914(58)93541-9
21. Berger L. Side-jump mechanism for the Hall effect of ferromagnets. Phys Rev B (1970) 2(11):4559–66. doi:10.1103/PhysRevB.2.4559
22. Pai C-F, Liu L, Li Y, Tseng HW, Ralph DC, Buhrman RA. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl Phys Lett (2012) 101(12):122404. doi:10.1063/1.4753947
23. Niimi Y, Kawanishi Y, Wei DH, Deranlot C, Yang HX, Chshiev M, et al. Giant spin Hall effect induced by skew scattering from bismuth impurities inside thin film cubi alloys. Phys Rev Lett (2012) 109(15):156602. doi:10.1103/PhysRevLett.109.156602
24. Edelstein VM. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun (1990) 73(3):233–5. doi:10.1016/0038-1098(90)90963-c
25. Shen K, Vignale G, Raimondi R. Microscopic theory of the inverse Edelstein effect. Phys Rev Lett (2014) 112(9):096601. doi:10.1103/PhysRevLett.112.096601
26. Ast CR, Henk J, Ernst A, Moreschini L, Falub MC, Pacile D, et al. Giant spin splitting through surface alloying. Phys Rev Lett (2007) 98(18):186807. doi:10.1103/PhysRevLett.98.186807
27. Hsieh D, Xia Y, Qian D, Wray L, Dil JH, Meier F, et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature (2009) 460(7259):1101–5. doi:10.1038/nature08234
28. Sanchez JC, Vila L, Desfonds G, Gambarelli S, Attane JP, De Teresa JM, et al. Spin-to-Charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat Commun (2013) 4:2944. doi:10.1038/ncomms3944
29. Mellnik AR, Lee JS, Richardella A, Grab JL, Mintun PJ, Fischer MH, et al. Spin-transfer torque generated by a topological insulator. Nature (2014) 511(7510):449–51. doi:10.1038/nature13534
30. Fan Y, Upadhyaya P, Kou X, Lang M, Takei S, Wang Z, et al. Magnetization switching through giant spin-orbit torque in a magnetically doped topological insulator heterostructure. Nat Mater (2014) 13(7):699–704. doi:10.1038/nmat3973
31. Kondou K, Yoshimi R, Tsukazaki A, Fukuma Y, Matsuno J, Takahashi KS, et al. Fermi-level-dependent charge-to-spin current conversion by Dirac surface states of topological insulators. Nat Phys (2016) 12(11):1027–31. doi:10.1038/nphys3833
32. Ryu KS, Thomas L, Yang SH, Parkin S. Chiral spin torque at magnetic domain walls. Nat Nanotechnol (2013) 8(7):527–33. doi:10.1038/nnano.2013.102
33. Manipatruni S, Nikonov DE, Lin CC, Gosavi TA, Liu H, Prasad B, et al. Scalable energy-efficient magnetoelectric spin-orbit logic. Nature (2019) 565(7737):35–42. doi:10.1038/s41586-018-0770-2
34. Uchida K, Takahashi S, Harii K, Ieda J, Koshibae W, Ando K, et al. Observation of the spin seebeck effect. Nature (2008) 455(7214):778–81. doi:10.1038/nature07321
35. Jungwirth T, Marti X, Wadley P, Wunderlich J. Antiferromagnetic spintronics. Nat Nanotechnol (2016) 11(3):231–41. doi:10.1038/nnano.2016.18
36. Grollier J, Querlioz D, Camsari KY, Everschor-Sitte K, Fukami S, Stiles MD. Neuromorphic spintronics. Nat Electron (2020) 3(7):360–70. doi:10.1038/s41928-019-0360-9
37. Petersen L, Hedegård P. A simple tight-binding model of spin–orbit splitting of sp-derived surface states. Surf Sci (2000) 459(1-2):49–56. doi:10.1016/s0039-6028(00)00441-6
38. Bian G, Wang X, Miller T, Chiang TC. Origin of giant Rashba spin splitting in Bi/Ag surface alloys. Phys Rev B (2013) 88(8):085427. doi:10.1103/PhysRevB.88.085427
39. Khang NHD, Ueda Y, Hai PN. A conductive topological insulator with large spin Hall effect for ultralow power spin-orbit torque switching. Nat Mater (2018) 17(9):808–13. doi:10.1038/s41563-018-0137-y
40. Yasuda K, Tsukazaki A, Yoshimi R, Kondou K, Takahashi KS, Otani Y, et al. Current-nonlinear Hall effect and spin-orbit torque magnetization switching in a magnetic topological insulator. Phys Rev Lett (2017) 119(13):137204. doi:10.1103/PhysRevLett.119.137204
41. Isshiki H, Kondou K, Takizawa S, Shimose K, Kawabe T, Minamitani E, et al. Realization of spin-dependent functionality by covering a metal surface with a single layer of molecules. Nano Lett (2019) 19(10):7119–23. doi:10.1021/acs.nanolett.9b02619
42. Lesne E, Fu Y, Oyarzun S, Rojas-Sanchez JC, Vaz DC, Naganuma H, et al. Highly efficient and tunable spin-to-charge conversion through Rashba coupling at oxide interfaces. Nat Mater (2016) 15(12):1261–6. doi:10.1038/nmat4726
43. Bentmann H, Kuzumaki T, Bihlmayer G, Blügel S, Chulkov EV, Reinert F, et al. Spin orientation and sign of the Rashba splitting in Bi/Cu(111). Phys Rev B (2011) 84(11):115426. doi:10.1103/PhysRevB.84.115426
44. Shao Q, Li P, Liu L, Yang H, Fukami S, Razavi A, et al. Roadmap of spin–orbit torques. IEEE Trans Magnetics (2021) 57(7):1–39. doi:10.1109/tmag.2021.3078583
45. Karube S, Kondou K, Otani Y. Experimental observation of spin-to-charge current conversion at non-magnetic metal/Bi2o3 interfaces. Appl Phys Express (2016) 9(3):033001. doi:10.7567/apex.9.033001
46. Asami A, An H, Musha A, Gao T, Kuroda M, Ando K. Spin absorption at a ferromagnetic-metal/platinum-oxide interface. Phys Rev B (2019) 99(2):024432. doi:10.1103/PhysRevB.99.024432
47. Nakayama H, Yamamoto T, An H, Tsuda K, Einaga Y, Ando K. Molecular engineering of Rashba spin-charge converter. Sci Adv (2018) 4(3):eaar3899. doi:10.1126/sciadv.aar3899
48. Fan Y, Kou X, Upadhyaya P, Shao Q, Pan L, Lang M, et al. Electric-field control of spin-orbit torque in a magnetically doped topological insulator. Nat Nanotechnol (2016) 11(4):352–9. doi:10.1038/nnano.2015.294
49. Liu E, Fache T, Cespedes-Berrocal D, Zhang Z, Petit-Watelot S, Mangin S, et al. Strain-enhanced charge-to-spin conversion in Ta/Fe/Pt multilayers grown on flexible mica substrate. Phys Rev Appl (2019) 12(4):044074. doi:10.1103/PhysRevApplied.12.044074
50. Mishra R, Mahfouzi F, Kumar D, Cai K, Chen M, Qiu X, et al. Electric-field control of spin accumulation direction for spin-orbit torques. Nat Commun (2019) 10(1):248. doi:10.1038/s41467-018-08274-8
51. Varotto S, Nessi L, Cecchi S, Sławińska J, Noël P, Petrò S, et al. Room-temperature ferroelectric switching of spin-to-charge conversion in germanium telluride. Nat Electro (2021) 4(10):740–7. doi:10.1038/s41928-021-00653-2
52. Liu L, Zhou C, Shu X, Li C, Zhao T, Lin W, et al. Symmetry-dependent field-free switching of perpendicular magnetization. Nat Nanotechnol (2021) 16(3):277–82. doi:10.1038/s41565-020-00826-8
53. MacNeill D, Stiehl GM, Guimaraes MHD, Buhrman RA, Park J, Ralph DC. Control of spin–orbit torques through crystal symmetry in wte2/ferromagnet bilayers. Nat Phys (2016) 13(3):300–5. doi:10.1038/nphys3933
54. Kao IH, Muzzio R, Zhang H, Zhu M, Gobbo J, Yuan S, et al. Deterministic switching of a perpendicularly polarized magnet using unconventional spin-orbit torques in wte(2). Nat Mater (2022) 21(9):1029–34. doi:10.1038/s41563-022-01275-5
55. Yu G, Upadhyaya P, Fan Y, Alzate JG, Jiang W, Wong KL, et al. Switching of perpendicular magnetization by spin-orbit torques in the absence of external magnetic fields. Nat Nanotechnol (2014) 9(7):548–54. doi:10.1038/nnano.2014.94
56. Safeer CK, Ontoso N, Ingla-Aynes J, Herling F, Pham VT, Kurzmann A, et al. Large multidirectional spin-to-charge conversion in low-symmetry semimetal mote(2) at room temperature. Nano Lett (2019) 19(12):8758–66. doi:10.1021/acs.nanolett.9b03485
57. Tang M, Shen K, Xu S, Yang H, Hu S, Lu W, et al. Bulk spin torque-driven perpendicular magnetization switching in L1(0) fept single layer. Adv Mater (2020) 32(31):e2002607. doi:10.1002/adma.202002607
58. Zheng Z, Zhang Y, Lopez-Dominguez V, Sanchez-Tejerina L, Shi J, Feng X, et al. Field-free spin-orbit torque-induced switching of perpendicular magnetization in a ferrimagnetic layer with a vertical composition gradient. Nat Commun (2021) 12(1):4555. doi:10.1038/s41467-021-24854-7
59. Zhu L, Ralph DC, Buhrman RA. Unveiling the mechanism of bulk spin-orbit torques within chemically disordered Fe x Pt 1-x single layers. Adv Funct Mater (2021) 31(36):2103898. doi:10.1002/adfm.202103898
60. Zhang K, Han S, Lee Y, Coak MJ, Kim J, Hwang I, et al. Gigantic current control of coercive field and magnetic memory based on nanometer-thin ferromagnetic van der Waals Fe(3) gete(2). Adv Mater (2021) 33(4):e2004110. doi:10.1002/adma.202004110
61. Saunderson TG, Go D, Blügel S, Kläui M, Mokrousov Y. Hidden interplay of current-induced spin and orbital torques in bulk Fe3GeTe2. Phys Rev Res (2022) 4(4):L042022. doi:10.1103/PhysRevResearch.4.L042022
62. Miao BF, Huang SY, Qu D, Chien CL. Inverse spin Hall effect in a ferromagnetic metal. Phys Rev Lett (2013) 111(6):066602. doi:10.1103/PhysRevLett.111.066602
63. Du C, Wang H, Yang F, Hammel PC. Systematic variation of spin-orbit coupling withd-orbital filling: Large inverse spin Hall effect in3dtransition metals. Phys Rev B (2014) 90(14):140407. doi:10.1103/PhysRevB.90.140407
64. Zimmermann B, Chadova K, Ködderitzsch D, Blügel S, Ebert H, Fedorov DV, et al. Skew scattering in dilute ferromagnetic alloys. Phys Rev B (2014) 90(22):220403. doi:10.1103/PhysRevB.90.220403
65. Omori Y, Sagasta E, Niimi Y, Gradhand M, Hueso LE, Casanova F, et al. Relation between spin Hall effect and anomalous Hall effect in 3d ferromagnetic metals 3 d Ferromagnetic Metals. Phys Rev B (2019) 99(1):014403. doi:10.1103/PhysRevB.99.014403
66. Wei DH, Niimi Y, Gu B, Ziman T, Maekawa S, Otani Y. The spin Hall effect as a probe of nonlinear spin fluctuations. Nat Commun (2012) 3:1058. doi:10.1038/ncomms2063
67. Varotto S, Cosset-Cheneau M, Grezes C, Fu Y, Warin P, Brenac A, et al. Independence of the inverse spin Hall effect with the magnetic phase in thin nicu films. Phys Rev Lett (2020) 125(26):267204. doi:10.1103/PhysRevLett.125.267204
68. Wang Y, Decker MM, Meier TNG, Chen X, Song C, Grunbaum T, et al. Spin pumping during the antiferromagnetic-ferromagnetic phase transition of iron-rhodium. Nat Commun (2020) 11(1):275. doi:10.1038/s41467-019-14061-w
69. Zhang S, Xia S, Li Q, Yang B, Li J, Cao Q, et al. Identification of spin-dependent thermoelectric effects in metamagnetic ferh/heavy-metal bilayers. Appl Phys Lett (2021) 118(14):142401. doi:10.1063/5.0038150
70. Qu G, Nakamura K, Hayashi M. Magnetization direction dependent spin Hall effect in 3d ferromagnets 3d Ferromagnets. Phys Rev B (2020) 102(14):144440. doi:10.1103/PhysRevB.102.144440
71. Mook A, Neumann RR, Johansson A, Henk J, Mertig I. Origin of the magnetic spin Hall effect: Spin current vorticity in the Fermi sea. Phys Rev Res (2020) 2(2):023065. doi:10.1103/PhysRevResearch.2.023065
72. Taniguchi T, Grollier J, Stiles MD. Spin-transfer torques generated by the anomalous Hall effect and anisotropic magnetoresistance. Phys Rev Appl (2015) 3(4):044001. doi:10.1103/PhysRevApplied.3.044001
73. Das KS, Schoemaker WY, van Wees BJ, Vera-Marun IJ. Spin injection and detection via the anomalous spin Hall effect of a ferromagnetic metal. Phys Rev B (2017) 96(22):220408. doi:10.1103/PhysRevB.96.220408
74. Iihama S, Taniguchi T, Yakushiji K, Fukushima A, Shiota Y, Tsunegi S, et al. Spin-transfer torque induced by the spin anomalous Hall effect. Nat Electro (2018) 1(2):120–3. doi:10.1038/s41928-018-0026-z
75. Hibino Y, Taniguchi T, Yakushiji K, Fukushima A, Kubota H, Yuasa S. Giant charge-to-spin conversion in ferromagnet via spin-orbit coupling. Nat Commun (2021) 12(1):6254. doi:10.1038/s41467-021-26445-y
76. Wang W, Wang T, Amin VP, Wang Y, Radhakrishnan A, Davidson A, et al. Anomalous spin-orbit torques in magnetic single-layer films. Nat Nanotechnol (2019) 14(9):819–24. doi:10.1038/s41565-019-0504-0
77. Baek SC, Amin VP, Oh YW, Go G, Lee SJ, Lee GH, et al. Spin currents and spin-orbit torques in ferromagnetic trilayers. Nat Mater (2018) 17(6):509–13. doi:10.1038/s41563-018-0041-5
78. Chen X, Shi S, Shi G, Fan X, Song C, Zhou X, et al. Observation of the antiferromagnetic spin Hall effect. Nat Mater (2021) 20(6):800–4. doi:10.1038/s41563-021-00946-z
79. Kimata M, Chen H, Kondou K, Sugimoto S, Muduli PK, Ikhlas M, et al. Magnetic and magnetic inverse spin Hall effects in a non-collinear antiferromagnet. Nature (2019) 565(7741):627–30. doi:10.1038/s41586-018-0853-0
80. Kondou K, Chen H, Tomita T, Ikhlas M, Higo T, MacDonald AH, et al. Giant field-like torque by the out-of-Plane magnetic spin Hall effect in a topological antiferromagnet. Nat Commun (2021) 12(1):6491. doi:10.1038/s41467-021-26453-y
81. You Y, Bai H, Feng X, Fan X, Han L, Zhou X, et al. Cluster magnetic octupole induced out-of-Plane spin polarization in antiperovskite antiferromagnet. Nat Commun (2021) 12(1):6524. doi:10.1038/s41467-021-26893-6
82. Hu S, Shao DF, Yang H, Pan C, Fu Z, Tang M, et al. Efficient perpendicular magnetization switching by a magnetic spin Hall effect in a noncollinear antiferromagnet. Nat Commun (2022) 13(1):4447. doi:10.1038/s41467-022-32179-2
83. Nakatsuji S, Kiyohara N, Higo T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature (2015) 527(7577):212–5. doi:10.1038/nature15723
84. Tsai H, Higo T, Kondou K, Nomoto T, Sakai A, Kobayashi A, et al. Electrical manipulation of a topological antiferromagnetic state. Nature (2020) 580(7805):608–13. doi:10.1038/s41586-020-2211-2
85. Higo T, Kondou K, Nomoto T, Shiga M, Sakamoto S, Chen X, et al. Perpendicular full switching of chiral antiferromagnetic order by current. Nature (2022) 607(7919):474–9. doi:10.1038/s41586-022-04864-1
86. Ou Y, Ralph DC, Buhrman RA. Strong enhancement of the spin Hall effect by spin fluctuations near the curie point of FexPt1−x alloys. Phys Rev Lett (2018) 120(9):097203. doi:10.1103/PhysRevLett.120.097203
87. Ray K, Ananthavel SP, Waldeck DH, Naaman R. Asymmetric scattering of polarized electrons by organized organic films of chiral molecules. Science (1999) 283(5403):814–6. doi:10.1126/science.283.5403.814
88. Gohler B, Hamelbeck V, Markus TZ, Kettner M, Hanne GF, Vager Z, et al. Spin selectivity in electron transmission through self-assembled monolayers of double-stranded DNA. Science (2011) 331(6019):894–7. doi:10.1126/science.1199339
89. Mishra S, Mondal AK, Pal S, Das TK, Smolinsky EZB, Siligardi G, et al. Length-dependent electron spin polarization in oligopeptides and DNA. The J Phys Chem C (2020) 124(19):10776–82. doi:10.1021/acs.jpcc.0c02291
90. Al-Bustami H, Khaldi S, Shoseyov O, Yochelis S, Killi K, Berg I, et al. Atomic and molecular layer deposition of chiral thin films showing up to 99% spin selective transport. Nano Lett (2022) 22(12):5022–8. doi:10.1021/acs.nanolett.2c01953
91. Naaman R, Paltiel Y, Waldeck DH. Chiral molecules and the electron spin. Nat Rev Chem (2019) 3(4):250–60. doi:10.1038/s41570-019-0087-1
92. Kiran V, Mathew SP, Cohen SR, Hernandez Delgado I, Lacour J, Naaman R. Helicenes-a new class of organic spin filter. Adv Mater (2016) 28(10):1957–62. doi:10.1002/adma.201504725
93. Kulkarni C, Mondal AK, Das TK, Grinbom G, Tassinari F, Mabesoone MFJ, et al. Highly efficient and tunable filtering of electrons' spin by supramolecular chirality of nanofiber-based materials. Adv Mater (2020) 32(7):e1904965. doi:10.1002/adma.201904965
94. Mondal PC, Kantor-Uriel N, Mathew SP, Tassinari F, Fontanesi C, Naaman R. Chiral conductive polymers as spin filters. Adv Mater (2015) 27(11):1924–7. doi:10.1002/adma.201405249
95. Suda M, Thathong Y, Promarak V, Kojima H, Nakamura M, Shiraogawa T, et al. Light-driven molecular switch for reconfigurable spin filters. Nat Commun (2019) 10(1):2455. doi:10.1038/s41467-019-10423-6
96. Senthil Kumar K, Kantor-Uriel N, Mathew SP, Guliamov R, Naaman R. A device for measuring spin selectivity in electron transfer. Phys Chem Chem Phys (2013) 15(42):18357–62. doi:10.1039/c3cp53089b
97. Sichau J, Prada M, Anlauf T, Lyon TJ, Bosnjak B, Tiemann L, et al. Resonance microwave measurements of an intrinsic spin-orbit coupling gap in graphene: A possible indication of a topological state. Phys Rev Lett (2019) 122(4):046403. doi:10.1103/PhysRevLett.122.046403
98. Shitade A, Minamitani E. Geometric spin–orbit coupling and chirality-induced spin selectivity. New J Phys (2020) 22(11):113023. doi:10.1088/1367-2630/abc920
99. Utsumi Y, Entin-Wohlman O, Aharony A. Spin selectivity through time-reversal symmetric helical junctions. Phys Rev B (2020) 102(3):035445. doi:10.1103/PhysRevB.102.035445
100. Liu Y, Xiao J, Koo J, Yan B. Chirality-driven topological electronic structure of DNA-like materials. Nat Mater (2021) 20(5):638–44. doi:10.1038/s41563-021-00924-5
101. Ben Dor O, Yochelis S, Radko A, Vankayala K, Capua E, Capua A, et al. Magnetization switching in ferromagnets by adsorbed chiral molecules without current or external magnetic field. Nat Commun (2017) 8:14567. doi:10.1038/ncomms14567
102. Miwa S, Kondou K, Sakamoto S, Nihonyanagi A, Araoka F, Otani Y, et al. Chirality-induced effective magnetic field in a phthalocyanine molecule. Appl Phys Express (2020) 13(11):113001. doi:10.35848/1882-0786/abbf67
103. Alpern H, Yavilberg K, Dvir T, Sukenik N, Klang M, Yochelis S, et al. Magnetic-related states and order parameter induced in a conventional superconductor by nonmagnetic chiral molecules. Nano Lett (2019) 19(8):5167–75. doi:10.1021/acs.nanolett.9b01552
104. Kondou K, Shiga M, Sakamoto S, Inuzuka H, Nihonyanagi A, Araoka F, et al. Chirality-induced magnetoresistance due to thermally driven spin polarization. J Am Chem Soc (2022) 144(16):7302–7. doi:10.1021/jacs.2c00496
105. Fransson J. Charge redistribution and spin polarization driven by correlation induced electron exchange in chiral molecules. Nano Lett (2021) 21(7):3026–32. doi:10.1021/acs.nanolett.1c00183
106. Du G-F, Fu H-H, Wu R. Vibration-enhanced spin-selective transport of electrons in the DNA double helix. Phys Rev B (2020) 102(3):035431. doi:10.1103/PhysRevB.102.035431
107. Fransson J. Vibrational origin of exchange splitting and ”chiral-induced spin selectivity. Phys Rev B (2020) 102(23):235416. doi:10.1103/PhysRevB.102.235416
108. Inui A, Aoki R, Nishiue Y, Shiota K, Kousaka Y, Shishido H, et al. Chirality-induced spin-polarized state of a chiral crystal CrNb3S6. Phys Rev Lett (2020) 124(16):166602. doi:10.1103/PhysRevLett.124.166602
Keywords: spin-charge conversion, chirality-induced spin selectivity, spatial inversion asymmetry, time-reversal asymmetry, spin Hall effect, Edelstein effect
Citation: Kondou K and Otani Y (2023) Emergence of spin–charge conversion functionalities due to spatial and time-reversal asymmetries and chiral symmetry. Front. Phys. 11:1140286. doi: 10.3389/fphy.2023.1140286
Received: 08 January 2023; Accepted: 01 March 2023;
Published: 24 March 2023.
Edited by:
Carlo Zucchetti, Politecnico di Milano, ItalyCopyright © 2023 Kondou and Otani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kouta Kondou, a2tvbmRvdUByaWtlbi5qcA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.