Joint DOD and DOA detection for MIMO radar based on signal subspace reconstruction and matching

In this study, the Direction Of Departure (DOD) and Direction Of Arrival (DOA) of signals detection for Multi-Input Multi-Output (MIMO) radar is discussed. A novel signal subspace reconstruction model to match the signal subspace obtained based on the covariance matrix of the array output is developed to enhance the performance of the DOD and DOA detection. In the developed scheme, the technology of beamforming is first introduced to define an objective space in mathematics for the targets to be detected. By considering the orthogonality between the signal subspace and the noise subspace and defining a reconstruction index of the signal subspace, a multi-dimensional objective function of the DOD and DOA is established. Therefore, the problem of DOD and DOA detection is transformed into an optimization of the multi-dimensional objective function. Subsequently, the Quantum-Behaved Particle Swarm Optimization (QPSO) is employed to optimize the multi-dimensional objective function and to determine an optimal signal subspace. At the same time the DOD and DOA can be fast captured. A series of simulations demonstrate that the proposed method provides significant accuracy improvements in DOD and DOA detection, especially for low signal-to-noise ratio thresholds and small snapshots.

Introduction

Multi-Input Multi-Output (MIMO) radar [1–3] is a new type of radar in recent years. Compared with traditional antenna arrays, the MIMO radars have potential advantages. The reason is that the MIMO radars make use of multiple antenna elements to transmit diverse waveforms and receive echo signals simultaneously in similar ways [4–6]. The detection of Direction Of Departure (DOD) and Direction Of Arrival (DOA) for MIMO radars has been actively studied and widely applied in many technical fields [7–10]. Subspace-based algorithms are an important kind of methods for DOD and DOA detection, which has the advantages of strong resolution and high detection accuracy [11, 12].

Among the subspace-based methods the most representative ones are the MUltiple SIgnal Classification (MUSIC) [13] and the Estimation Signal Parameter via Rotational Invariance Techniques (ESPRIT) [14]. The MUSIC approach is well-known for its high-resolution capability, and can be used for arrays with any form of geometry to detect DOA and DOA of each target [15, 16]. However, the massive spectral peak search makes it difficult to popularize this algorithm in the engineering field. Without spectral peak search (search-free detection), the ESPRIT algorithm can detect the DOA and DOA in a closed form solution [8, 17–19]. However, this type of methods can only be applied to the Uniform Linear antenna Array (ULA), or the antenna arrays themselves possess a same structure of (shift invariant) subarrays. This limitation makes it difficult to extend such algorithms to practical applications [20–22].

Thus, fast detection of the DOD and DOA in the MIMO radar system with an arbitrary antenna array has always been the pursuit for researchers. In [18], an ambiguity function-based algorithm is designed to detect the DOD and DOA in a MIMO Radar system. By constructing a spatial time-frequency distribution matrix, this method uses ESPRIT and Root-MUSIC to realize the joint DOD and DOA fast detection. This process does not involve multiple-dimensional spectrum peak searching and the parameters can also be paired automatically. In [20], a robust method for joint DOD and DOA detection in a non-Gaussian noise environment is proposed. This method uses a robust M-estimator to form an estimate of the covariance matrix of the array output and then utilizes the random matrix theory and polynomial rooting method to capture the DOD and DOA in a large scale MIMO radar system. By exploiting the banded complex symmetric Toeplitz structure of the mutual coupling matrices [21], a robust sparse Bayesian learning algorithm for DOD and DOA detection is also developed, and this method is demonstrated to work well and have better detection performance in unknown non-uniform noise and mutual coupling.

In this study, a joint DOD and DOA detection scheme through signal subspace optimal reconstruction is developed. In the developed scheme, we first use the beamforming [23–25] to set an objective space in mathematics for the targets to be detected. Then, we randomly select a collection of DODs and DOAs from the objective space to establish a potential signal subspace with the steering matrix of the MIMO array. Considering of the orthogonality between the signal subspace and the noise subspace and a reconstruction error of the signal subspace, we build a multi-dimensional objective function, which contains all information of DODs and DOAs. Subsequently, the Quantum-Behaved Particle Swarm Optimization (QPSO) [26, 27] is employed to optimize the multi-dimensional objective function so as to obtain the optimal reconstruction of the signal subspace. Finally, the DOD and DOA can be fast detected with a high accuracy. A detailed derivation and comprehensive analysis of the proposed method are presented. The simulation results verify that the proposed algorithm outperforms the other methods, especially under low signal to noise ratio (SNR) and small snapshots. To the best of our knowledge, the proposed scheme has not been considered in previous studies.

This paper is structured as follows. The signal model for a MIMO array is formulated in Section 2. A fast DOD and DOA detection method is discussed in detail in Section 3. Section 4 includes experimental setup and analysis of simulation results. Finally, Section 5 concludes the paper.

Signal model of the MIMO array

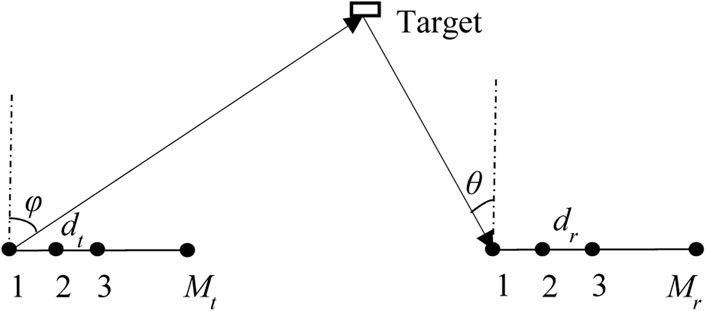
Consider a bistatic MIMO radar array composed of M_t transmitter sensors and M_r receiver sensors, in the transmit array and receive array, respectively. Both of these arrays are ULAs, and the inter-element spacings of adjacent sensor elements are d_t and d_r (not larger than half wavelength of the signals), respectively. Assume that there are P far-field uncorrelated targets with the DODs and DOAs $\left({\phi }_p,{\theta }_p\right),p=\mathrm{1,2},\text{L},P$ in the target space. Figure 1 shows the signal model of the bistatic MIMO array. The output of the matched filters at the receiver can be expressed in the following manner:

$\begin{array}{l}\mathit{X}\left(t\right)=\left[{\mathit{a}}_r\left({\phi }_1\right)\otimes {\mathit{a}}_t\left({\theta }_1\right),{\mathit{a}}_r\left({\phi }_2\right)\otimes {\mathit{a}}_t\left({\theta }_2\right),\text{L},{\mathit{a}}_r\left({\phi }_P\right)\otimes {\mathit{a}}_t\left({\theta }_P\right)\right]\mathit{b}\left(t\right)+\mathit{n}\left(t\right)\\ =\mathit{A}\mathit{b}\left(t\right)+\mathit{n}\left(t\right)\end{array}(1)$

where A is the direction matrix (steering matrix), $\mathit{b}\left(t\right)={\left[b_1\left(t\right),b_2\left(t\right),\text{L},b_P\left(t\right)\right]}^T$ is a vector containing the reflection coefficients and Doppler phase shifts of the targets, and $\mathit{n}\left(t\right)$ is the complex additive white gaussian noise vector. ${\mathit{a}}_r$ and ${\mathit{a}}_t$ are receive and transmit steering vectors which have the following structures:

$\begin{array}{l}{\mathit{a}}_r\left({\phi }_p\right)={\left[1,e^{j\frac{\pi d_r\sin {\phi }_p}{\lambda }},\mathrm{L},e^{j\frac{\pi \left(M_r-1\right)d_r\sin {\phi }_P}{\lambda }}\right]}^T\\ {\mathit{a}}_t\left({\theta }_p\right)={\left[1,e^{j\frac{\pi d_t\sin {\theta }_p}{\lambda }},\mathrm{L},e^{j\frac{\pi \left(M_t-1\right)d_r\sin {\theta }_p}{\lambda }}\right]}^T\end{array}(2)$

where T stands for the transpose operation, and λ is the wavelength of the signals. The covariance matrix of the array output is computed by

${\mathit{R}}_X=E\left[\mathit{X}\left(t\right){\mathit{X}}^H\left(t\right)\right](3)$

where H represents the complex conjugate transpose. The signal and noise subspaces are commonly obtained through the eigenvalue decomposition of the covariance matrix of the array output. That is, the eigenvectors corresponding to the P largest eigenvalues span the signal subspace U_s, and the remainder eigenvectors form the noise subspace U_n. The MUSIC method detects the DOD and DOA by constructing and optimizing the following spatial spectrum function

$f_{MUSIC}=\frac{1}{{\left[{\mathit{a}}_r\left({\phi }_i\right)\otimes {\mathit{a}}_t\left({\theta }_i\right)\right]}^H{\mathit{U}}_n{\mathit{U}}_n^H\left[{\mathit{a}}_r\left({\phi }_i\right)\otimes {\mathit{a}}_t\left({\theta }_i\right)\right]}(4)$

FIGURE 1

FIGURE 1. Signal model of the bistatic MIMO array.

The spatial spectrum function is expected to show a large positive value if φ and θ are a true DOD and DOA, which is due to the orthogonality between the signal subspace and noise subspace. Obviously, the peak search implies a huge amount of computation. How to reduce the amount of computation generated in the search process has always been the goal of researchers.

Joint DOD and DOA detection scheme through signal subspace optimal reconstruction and matching

In this section, a fast joint DOD and DOA detection scheme through signal subspace optimal reconstruction and matching will be developed in detail. The developed scheme, as we will demonstrate, has excellent detection performance under the scenarios of low SNR and small snapshot.

To reduce the search scope, we firstly use the beamforming to capture the potential regions (including the DODs and DOAs) of the targets. Let Ω_k (k = 1, 2, … , K) be the K spectrum peaks determined by the beamforming. We take the neighbourhoods of the K spectrum peaks in mathematics as the potential regions of the targets, and the following searching will be carried out on these regions (observation space).

Then, we randomly select P (P can obtained by the Minimum Descriptive Length, MDL) criterion directions to form a direction vector $\stackrel{\sim }{\mathit{\Omega }}$ to construct an initial steering matrix $\stackrel{\sim }{\mathit{A}}$ according to Eq. 2, with which an initial signal subspace can be reconstructed in the following way:

${\stackrel{\sim }{\mathit{U}}}_s=\stackrel{\sim }{\mathit{A}}\left(\stackrel{\sim }{\mathit{\Omega }}\right){\left[{\stackrel{\sim }{\mathit{A}}}^H\left(\stackrel{\sim }{\mathit{\Omega }}\right)\stackrel{\sim }{\mathit{A}}\left(\stackrel{\sim }{\mathit{\Omega }}\right)\right]}^{-\frac{1}{2}}(5)$

Ideally, we consider that this signal subspace and the estimated signal subspace with the eigenvalue decomposition of the covariance matrix of the array output should be equal, i.e.,

${‖{\stackrel{\sim }{\mathit{U}}}_s{\stackrel{\sim }{\mathit{U}}}_s^H-{\mathit{U}}_s{\mathit{U}}_s^H‖}_2\to 0(6)$

where ${‖\mathrm{g}‖}_2$ denotes l₂ norm. On the other hand, consider the orthogonality between the signal and noise subspaces, the following equation should also hold:

${‖{\stackrel{\sim }{\mathit{U}}}_s^H{\mathit{U}}_n‖}_2=0(7)$

In order to detect more accurate DODs and DOAs, the above two equations should hold at the same time. Thus, we build a multi-dimensional objective function in the following form:

$J={‖{\stackrel{\sim }{\mathit{U}}}_s{\stackrel{\sim }{\mathit{U}}}_s^H-{\mathit{U}}_s{\mathit{U}}_s^H‖}_2+{‖{\stackrel{\sim }{\mathit{U}}}_s^H{\mathit{U}}_n‖}_2(8)$

The DODs and DOAs can be obtained through optimizing the objective function in a 2P dimensional space. In this study, we use the Quantum-Behaved Particle Swarm Optimization (QPSO) as an optimization method to minizine the multi-dimensional objective function and to solve the DODs and DOAs of the signals. Suppose there are N particles, and the optimization process can be described as:

1) Initialize the particle position vector ${\stackrel{\sim }{\mathit{\Omega }}}^{\left(n\right)}$ (n = 1, 2, … , N) and the best previous position ${\stackrel{\sim }{\mathit{\Omega }}}_{best}^{\left(n\right)}$ of each particle.

2) Capture the mean of the best position $\mathit{m}\mathit{b}\mathit{e}\mathit{s}\mathit{t}\left(t\right)$ according to

$\mathit{m}\mathit{b}\mathit{e}\mathit{s}\mathit{t}=\frac{1}{N}{\displaystyle \sum }_{n=1}^N{\stackrel{\sim }{\mathit{\Omega }}}_n^{pbest}\left(t\right)(9)$

3) Substitute the particle position vector ${\stackrel{\sim }{\mathit{\Omega }}}^{\left(n\right)}$ into the objective function 8) that is being optimized and at the same time compare it with the particle’s previous best value so as to determine the current fitness value.

4) Determine the current global best (gbest) position through comparing it with the previous one and determine whether to update it or not.

5) Modify the positions of particles to make all of them fall within the definition domain.

6) Repeat steps (2) to (5) until the termination condition or the number of executions has been saturated.

In the implementation of the QPSO, the approach is run for nmax = 300 iterations with 30 particles by considering the dimension of the target space. However, we allow the method to be terminated if no changes in gbest is 20%nmax consecutive iterations. The particle position vector generated at algorithm termination is the DODs and DOAs we want to detect.

Experimental studies:

In order to evaluate the performance of the developed scheme, in this section we present two groups of simulations to assess the DOD and DOA detection performance of our algorithm in comparison with the other two commonly methods (MUSIC and ESPRIT). In the comparison, the Root-Mean-Square Error (RMSE) criterion [28, 29] is used as an evaluation indicator which is define as

$\sqrt{\frac{1}{N_s}{\displaystyle \sum }_{n=1}^{N_s}\left\{\frac{1}{P}{\displaystyle \sum }_{p=1}^P{\left[{\widehat{\alpha }}_p\left(n\right)-\alpha \right]}^2\right\}}(10)$

where N_s denotes the number of the independent simulations, ${\alpha }_p$ is the pth DOD or DOA of the P impinging sources, and ${\widehat{\alpha }}_p$ is the estimate value of ${\alpha }_p$ captured in the nth simulation.

In the simulation, we normally adopt the bistatic MIMO radar system with 𝑀_t = 8 and M_r = 8, and assume that there are three non-coherent signals located at $\left({\phi }_1,{\theta }_1\right)=\left(5^{\circ },{15}^{\circ }\right)$, $\left({\phi }_2,{\theta }_2\right)=\left({10}^{\circ },{30}^{\circ }\right)$, and $\left({\phi }_3,{\theta }_3\right)=\left({30}^{\circ },{10}^{\circ }\right)$, respectively.

Simulation 1

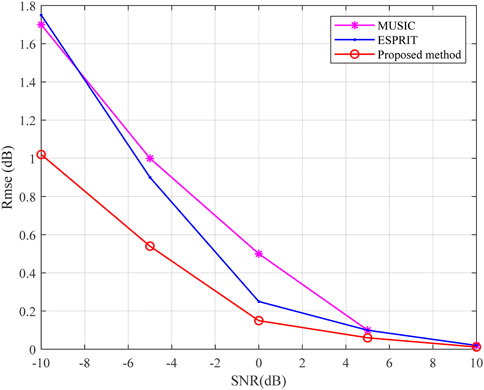
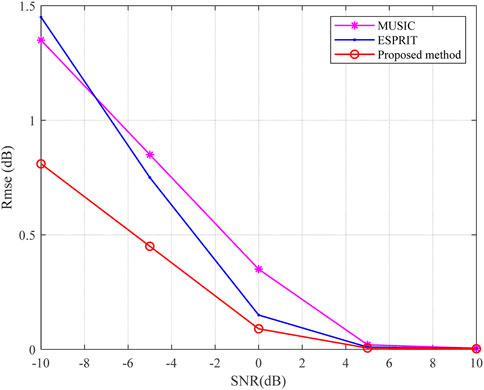
This simulation quantifies the performance of the RMSE versus SNR. In the simulation, the number of snapshots is fixed as 50, and 100 Monte Carlo experiments are completed. Figures 2, 3 visualize the experimental results of the DOD and DOA detection. It can be seen that these methods can all achieve DOD and DOA detection when the SNR is high (say >0 dB). The RMSE drops with the SNR decreasing, and the proposed method outperforms the other methods under most situations.

FIGURE 2

FIGURE 2. DOD estimation performance with different SNR.

FIGURE 3

FIGURE 3. DOA estimation performance with different SNR.

Simulation 2

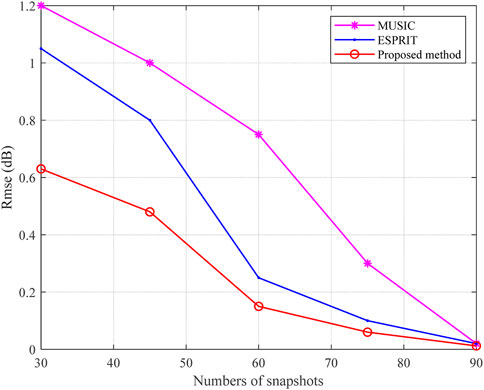
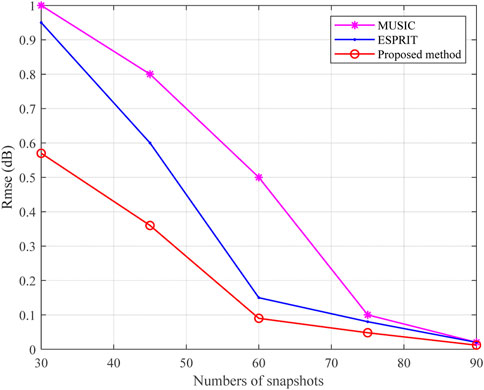
In the second simulation, we test the RMSE of different methods versus the numbers of snapshots. In this simulation, the SNR is fixed as -5dB, and 100 Monte Carlo experiments are carried out. Figures 4, 5 show the plot of the performance of RMSE of the DOD and DOA detection versus the numbers of snapshots. It is apparent that the developed scheme outperforms the other approaches and becomes insensitive to the changes of the numbers of snapshots.

FIGURE 4

FIGURE 4. DOD estimation performance with different snapshots.

FIGURE 5

FIGURE 5. DOA estimation performance with different snapshots.

The principles of MUSIC and ESPRIT imply that their detection performance is mainly dependent on the covariance matrix of the array output and the signal and noise subspaces. At the situation of low SNR and small number of snapshots, their performance deteriorates significantly or even fails largely due to the inaccuracy of the covariance matrix of the array output and signal and noise subspaces. However, the proposed method detects the DOD and DOA through exploiting a signal subspace reconstruction model to match the signal subspace obtained based on the covariance matrix of the array output, which eliminates the dependence on the covariance matrix to a certain extent.

Conclusion

In this paper, we put forward a novel signal subspace reconstruction model to match the signal subspace obtained based on the covariance matrix of the array output to enhance the performance of the DOD and DOA detection. In the design progress, the problem of DOD and DOA detection is transformed into a signal subspace reconstruction and matching problem. A multi-dimensional objective function is built and optimized to solve the DOD and DOA. Simulation results prove the performance of the developed algorithm compared with the other subspace-based methods.

At the current stage, we have completed a theoretical analysis and offered a comprehensive suite of experiments. Some practical experiments (including hardware) would be an interesting avenue to explore in future studies.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All the authors made significant contributions to the work. The idea was proposed by WM; YL and YC simulated the algorithm, analysed the data designed the experiments; WM, YC and YL polished the English and wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Shaanxi Provincial Fund for Distinguished Young Scholars under Grant 2021JC-23.

Conflict of interest

WM was employed by Beijing Jianzhu Technology Co., LTD

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sempere Chaves C, Geschke RH, Shargorodskyy M, Herschel R, Kose S, Leuchs S, et al. Multisensor polarimetric MIMO radar network for disaster scenario detection of persons. IEEE Microwave Wireless Components Lett (2022) 32(3):238–40. doi:10.1109/lmwc.2021.3132788

CrossRef Full Text | Google Scholar

2. Han K, Hong S. High-resolution phased-subarray MIMO radar with grating lobe cancellation technique. IEEE Trans Microwave Theor Tech (2022) 70(5):2775–85. doi:10.1109/tmtt.2022.3151633

CrossRef Full Text | Google Scholar

3. Niu S, Zhu D, Jin G, Cheng Y, Wang Y. A novel transmitter-interpulse phase coding MIMO-radar for range ambiguity separation. IEEE Trans Geosci Remote Sensing (2022) 60:1–16. doi:10.1109/tgrs.2022.3221406

CrossRef Full Text | Google Scholar

4. Norrdine A, Cetinkaya H, Herschel R. Radar wave based positioning of spatially distributed MIMO radar antenna systems for near-field nondestructive testing. IEEE Sensors Lett (2020) 4(5):1–4. doi:10.1109/lsens.2020.2989546

CrossRef Full Text | Google Scholar

5. Dontamsetti SG, Kumar RVR. A distributed MIMO radar with joint optimal transmit and receive signal combining. IEEE Trans Aerospace Electron Syst (2021) 57(1):623–35. doi:10.1109/taes.2020.3027103

CrossRef Full Text | Google Scholar

6. Liu Y, Xu X, Xu G. MIMO radar calibration and imagery for near-field scattering diagnosis. IEEE Trans Aerospace Electron Syst (2018) 54(1):442–52. doi:10.1109/taes.2017.2760758

CrossRef Full Text | Google Scholar

7. Schüßler C, Hoffmann M, Bräunig J, Ullmann I, Ebelt R, Vossiek M. A realistic radar ray tracing simulator for large MIMO-arrays in automotive environments. IEEE J Microwaves (2021) 1(4):962–74. doi:10.1109/jmw.2021.3104722

CrossRef Full Text | Google Scholar

8. Liao Y, Zhao R, Gao L. Joint DOD and DOA estimation in bistatic MIMO radar with distributed nested arrays. IEEE Access (2019) 7:50954–61. doi:10.1109/access.2019.2904613

CrossRef Full Text | Google Scholar

9. Xu F, Vorobyov SA, Yang X. Joint DOD and DOA estimation in slow-time MIMO radar via PARAFAC decomposition. IEEE Signal Process. Lett (2020) 27:1495–9. doi:10.1109/lsp.2020.3018904

CrossRef Full Text | Google Scholar

10. Xu J, Wang WQ, Gui R. Computational efficient DOA, DOD, and Doppler estimation algorithm for MIMO radar. IEEE Signal Process. Lett (2019) 26(1):44–8. doi:10.1109/lsp.2018.2879546

CrossRef Full Text | Google Scholar

11. Zhang Y, Wang Y, Tian Z, Leus G, Zhang G. Efficient angle estimation for MIMO systems via redundancy reduction representation. IEEE Signal Process. Lett (2022) 29:1052–6. doi:10.1109/lsp.2022.3164850

CrossRef Full Text | Google Scholar

12. Cui C, Xu J, Gui R, Wang W, Wu W. Search-free DOD, DOA and range estimation for bistatic FDA-MIMO radar. IEEE Access (2018) 6:15431–45. doi:10.1109/access.2018.2816780

CrossRef Full Text | Google Scholar

13. Xu KJ, Quan YH, Bie BW, Xing MD, Nie WK, Hanyu E. Fast direction of arrival estimation for uniform circular arrays with a virtual signal subspace. IEEE Trans Aerospace Electron Syst (2021) 57(3):1731–41. doi:10.1109/taes.2021.3050667

CrossRef Full Text | Google Scholar

14. Chen Z, Chen P. Compressed sensing-based DOA and DOD estimation in bistatic co-prime MIMO arrays. In: 2017 IEEE Conference on Antenna Measurements & Applications (CAMA); 4-6 Dec. 2017; Tsukuba, Japan (2017). p. 297–300.

CrossRef Full Text | Google Scholar

15. Roy R, Kailath T. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Trans Acoust Speech, Signal Process (1989) 37(7):984–95. doi:10.1109/29.32276

CrossRef Full Text | Google Scholar

16. Shi W, He C, Huang J, Zhang Q. Fast MUSIC algorithm for joint DOD-DOA estimation based on Gibbs Sampling in MIMO array. In: 2016 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC); 5-8 Aug. 2016; Hong Kong, China (2016). p. 1–4.

CrossRef Full Text | Google Scholar

17. Li Z, Zhou C, Jia Y, Wang G, Yan C, Lv Y. DOD and DOA Estimation for bistatic co-prime MIMO array based on correlation matrix augmentation. In: 2019 International Conference on Control, Automation and Information Sciences (ICCAIS); 23-26 October 2019; Chengdu, China (2019). p. 1–5.

CrossRef Full Text | Google Scholar

18. Fan T, Jiang H, Sun J. Ambiguity function-based ESPRIT-Root-MUSIC algorithm for DOD-DOA estimation in MIMO radar. In: International Conference on Radar Systems (Radar 2017); 23-26 Oct. 2017; Belfast, UK (2017). p. 1–4.

Google Scholar

19. Zhao X, Guo C, Chu S, Zhang W. DOD and DOA estimation of coherent targets in bistatic MIMO radar based on DFSS_ESPRIT. In: 2021 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE); Jan 12, 2021-Apr 12, 2021; Zhuhai, China (2021). p. 1–3.

CrossRef Full Text | Google Scholar

20. Jiang H, Lu Y, Yao S. Random matrix based method for joint DOD and DOA estimation for large scale MIMO radar in non-Gaussian noise. In: 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 20-25 March 2016; Shanghai, China (2016). p. 3031–5.

CrossRef Full Text | Google Scholar

21. Tang WG, Jiang H, Zhang Q. Robust DOD and DOA estimation for bistatic MIMO radar in unknown mutual coupling and non-uniform noise. In: 2022 IEEE 12th Sensor Array and Multichannel Signal Processing Workshop (SAM); June 20-23, 2022; Trondheim, Norway (2022). p. 116–20.

CrossRef Full Text | Google Scholar

22. Wen F, Zhang Z, Zhang G. Joint DOD and DOA estimation for bistatic MIMO radar: A covariance trilinear decomposition perspective. IEEE Access (2019) 7:53273–83. doi:10.1109/access.2019.2912842

CrossRef Full Text | Google Scholar

23. Xu K, Xing M, Zhang R, Hanyu E, Sha M, Nie W, et al. High-accuracy DOA estimation algorithm at low SNR through exploiting a supervised index. IEEE Trans Aerospace Electron Syst (2022) 58(4):3658–65. doi:10.1109/taes.2022.3144121

CrossRef Full Text | Google Scholar

24. Han J, Ng BP, Er MH. An adaptive orientational beamforming technique for narrowband interference rejection. In: 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 22 May 2022 – 27 May 2022; Singapore (2022). p. 4908–12.

CrossRef Full Text | Google Scholar

25. Zhu D, Li B, Liang P. A novel hybrid beamforming algorithm with unified analog beamforming by subspace construction based on partial csi for massive MIMO-OFDM Systems. IEEE Trans Commun (2017) 65(2):594–607. doi:10.1109/tcomm.2016.2625794

CrossRef Full Text | Google Scholar

26. Sun J, Fang W, Wu X, Palade V, Xu W. Quantum-behaved particle swarm optimization: Analysis of individual particle behavior and parameter selection. Evol Comput (2012) 20:349–93. doi:10.1162/evco_a_00049

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Luo J, Shao Y, Liao X, Liu J, Zhang J. Complex permittivity estimation for cloths based on QPSO method over (40 to 50) GHz. IEEE Trans Antennas Propagation (2021) 69(1):600–5. doi:10.1109/tap.2020.3005032

CrossRef Full Text | Google Scholar

28. Yu X, Liu B, Qiu G, Tian C. 2D-DOA efficient estimation algorithm based on IRD-MUSIC for frequency hopping signal. In: 2022 IEEE 4th International Conference on Civil Aviation Safety and Information Technology (ICCASIT); 12-14 October 2022; Dali, China (2022). p. 675–9.

CrossRef Full Text | Google Scholar

29. Wu R, Zhang Y, Ni L, Zhang K, Liu N, Wan Q. DOA estimation for beam scanning radar based on sparse signal reconstruction with incomplete pulse. In: 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC); October 25-27, 2022; Xi'an, Shaanxi, China (2022). p. 1–6.

CrossRef Full Text | Google Scholar