- Xi’an Research Institute of High Technology, Xi’an, Shaanxi, China
Communication networks are used as an important guarantee for information interaction and efficient collaboration within many fields and systems; however, under information technology conditions, the destruction of a number of nodes in a network may have a great impact on the overall operation of the network. Therefore, it is important to accurately determine the critical nodes in the network to enhance the network’s resistance to destruction. Combining the characteristic attributes of the communication network, a node contribution evaluation matrix is proposed based on the efficiency matrix, from the perspective of node receiving information; a node value evaluation matrix is proposed from the perspective of a node providing information to neighboring nodes, and node importance is calculated by integrating the evaluation results of the two matrices and the node’s own attributes. The algorithm is suitable for directed-weighted network node value evaluation, and the effectiveness and accuracy of the algorithm are verified by comparing other algorithms for a small-scale network. In further experimental validation, a hybrid weighted communication network evolution model based on organizational structured networks is proposed, and networks of different sizes are generated for experimental simulation. The results show that when nodes with high importance are removed from the network, they can cause a rapid decrease in the network efficiency and maximum connectivity, confirming the accuracy of the algorithm in evaluating the importance of nodes and identifying critical nodes in the network.
1 Introduction
Following the rapid development of information technology, communication networks have become an indispensable and important part of many systems and fields [1, 2]. A communication network refers to a complex network with topology and specific functions and is composed of multiple nodes with information transmission functions that are interconnected by communication links. The communication network is the basis for information transmission, close collaboration, and efficient cooperation among the components within the system [3, 4]. Differences in hierarchical relationships, location effects, and information interaction capabilities of the nodes in a communication network result in nodes having different values and varying influence on the whole network [5–7]. Evaluating the importance of nodes in communication networks, detecting critical nodes in the network, and protecting them are important for improving networks’ resilience to damage [8].
At present, evaluating the importance of network nodes is generally based on complex network theory, mainly focusing on the study of undirected and unweighted networks, while results from the study of directed-weighted networks are rare [9–13]. The connection between communication network nodes represents a link for information transmission and defines the direction of information flow; the strength of information interaction between nodes; and the connectivity of communication links, transmission rate, communication capacity, and other various indicators [14, 15]. This causes specificity of the connected edges between nodes, which need to be assigned different weights for consideration; therefore, evaluation methods in undirected and unweighted networks cannot be simply applied to communication networks.
[16] proposed the DWCN_NodeRank metric to evaluate the importance of nodes in directed-weighted networks from the perspective of information transmission based on the idea of the PageRank algorithm. However, the algorithm was not well-distinguished for partial nodes and it converged slowly, making it difficult to guarantee accuracy. Wang et al. [17] constructed multiple influence matrices for directed-weighted networks; however, the algorithm needed to calculate both the shortest path and the number of path entries between nodes, making it highly time-consuming, complex, and difficult to apply to large-scale networks. Ma et al. [3] introduced a mutual information (MI) algorithm [18] to communication networks to measure node importance; however, the algorithm did not take the mutual influence between non-adjacent nodes into account, while the consideration of edge weights was neglected in the calculation process and the measured results were unconvincing. The literature [19–22] used a node importance contribution matrix and a network efficiency matrix to evaluate the value of nodes; however, the former only considered the influence between neighboring nodes, while the latter ignored the weakening effect of intermediate nodes on information transmission when considering the interaction between non-adjacent nodes, and both did not take the directedness of the network into account.
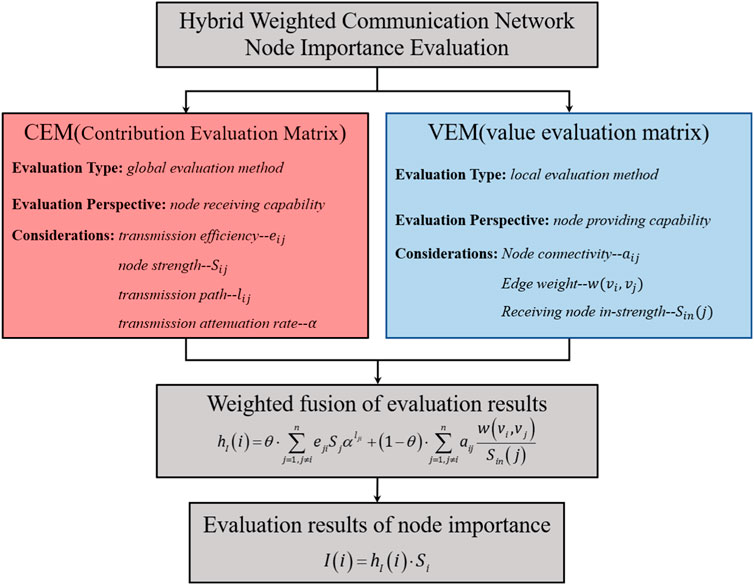
In this article, complex network theory is used to evaluate the importance of nodes in communication networks. To address the problem that most current node importance evaluation algorithms are not applicable to directed-weighted networks, we combine the characteristics of communication networks and, first, complete the construction of a topological model of a communication network. Second, considering the directedness of the network, the importance of nodes in the network is divided into the importance of receiving information from other nodes and the importance generated by providing information to adjacent nodes. From the above two different perspectives, CEM and VEM are proposed to measure the node importance. Finally, a hybrid weighted communication network evolution model based on OSN is proposed to determine the characteristics of communication network hierarchy, and experimental simulations are performed in the model to verify the effectiveness of the algorithm.
2 Communication network and its node importance
2.1 Communication network topology model construction
In communication networks, information transmission between nodes occurs both bidirectionally and unidirectionally, and the weights of two edges in bidirectional communication transmission may not be the same. Based on this, the communication network is abstracted as a hybrid weighted network with both undirected and directed edges [3].
For the convenience of research, the bidirectional link in the communication network, i.e., the undirected edges in the network, is transformed into two directed edges with opposite directions, thus transforming the hybrid weighted network into a directed-weighted network with only directed edges. The weights of communication links represent the flow of information transmitted between nodes, so the principle of similar weights is used [23], i.e., the larger the weight, the stronger the connection between nodes. On this basis, the nodes in the network can then be studied using a directed-weighted network node importance assessment method.
In the directed-weighted network model,
2.2 Related metrics
Based on the network model constructed above and considering the operational characteristics of the communication network [15, 24, 25], the following definitions are given to measure the individual nodes in the network as well as the network globally.
2.2.1 Node importance metrics
Metric 1: Node efficiency
where
where
Metric 2: DWCN_NodeRank (NR). Zhang et al. [16] proposed the NR method, an evaluation metric for the importance of nodes in directed-weighted network; the
where
2.2.2 Network global efficiency metrics
Metric 3: Maximum connectivity
where
Metric 4: Network efficiency
The higher the efficiency of the network, the smoother the transmission of information in the network and the stronger the connectivity of the network.
3 Node importance evaluation method based on importance evaluation matrix
In complex communication networks, nodes interact with each other through paths composed of directed edges to complete an information interaction. The variability of node connectivity in the network and the fact that the edges connecting nodes have different weights and directions cause the strength of interaction between different nodes and their contribution to the overall information flow efficiency of the network to be strong or weak. The node importance contribution matrix [20] mainly describes the contribution of nodes to adjacent nodes without taking the interaction effects between non-adjacent nodes into account, and it is only researched for undirected networks. The efficiency matrix [22] takes the influence of non-adjacent nodes through the shortest path between nodes into account. However, this method just considers the influence of the nodes in the shortest path on network information transmission and only for undirected networks.
In this article, we believe that the importance of nodes in the process of information transmission in the network is mainly reflected in two aspects: one is the contribution value from other nodes in the network. In a directed network, when there exists a path from node
In this article, CEM and VEM are proposed to measure the value of nodes in the above two aspects in directed-weighted networks.
4 Node contribution evaluation matrix (CEM)
For directed-weighted networks, the transmission efficiency between nodes forms the network efficiency matrix
where
where
A larger value of node
4.1 Node value evaluation matrix (VEM)
The CEM measures the node importance from the point of view that the node receives contributions from other nodes. In this section, the node value is measured from the point of view that the node provides information for its adjacent nodes, and the VEM is proposed as follows:
In this matrix,
A higher
4.2 Evaluation the node importance
CEM and VEM measure the importance of nodes from different perspectives, and obtain the contribution evaluation vector
Combining Eq. 11–13, the above equation can be expressed as:
where
After obtaining the comprehensive importance of the node, it is also necessary to take the node’s own strength information into consideration in the calculation of the node importance. The importance of the node
4.3 Algorithm steps and complexity analysis
In a communication network, the most direct form of information exchange and dissemination exists between adjacent nodes; however, when the strength of a node and the efficiency of information transmission are high, this will also have a greater influence on non-adjacent nodes, which makes the evaluation results inaccurate if only node importance is evaluated in terms of nodes receiving or outputting information. Therefore, this article comprehensively considers the characteristics of the above two aspects in a directed-weighted network. The information flow and interaction of the communication network, CEM, and VEM are proposed. Combining the node importance obtained by the two matrixes, a comprehensive evaluation of the node importance is finally realized. The specific steps of the algorithm are as follows.
Step 1:. Preparation stage. According to the network edge weight matrix
Step 2:. Constructing CEM and calculating the node contribution importance. Fill the obtained
Step 3:. Constructing VEM and calculating the node value importance. Fill the elements
Step 4:. Importance integration. Normalize the vectors
Step 5:. Node importance calculation. The importance of the node
5 Experiment analysis
5.1 Algorithm effectiveness analysis
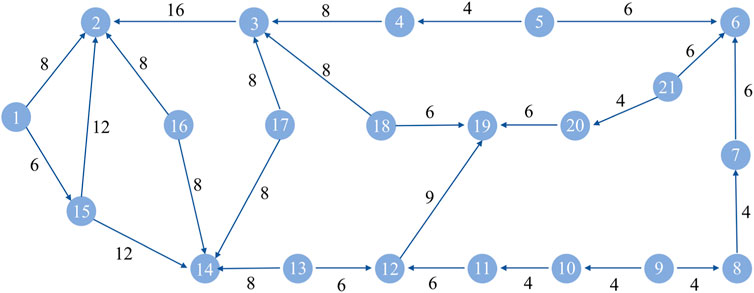
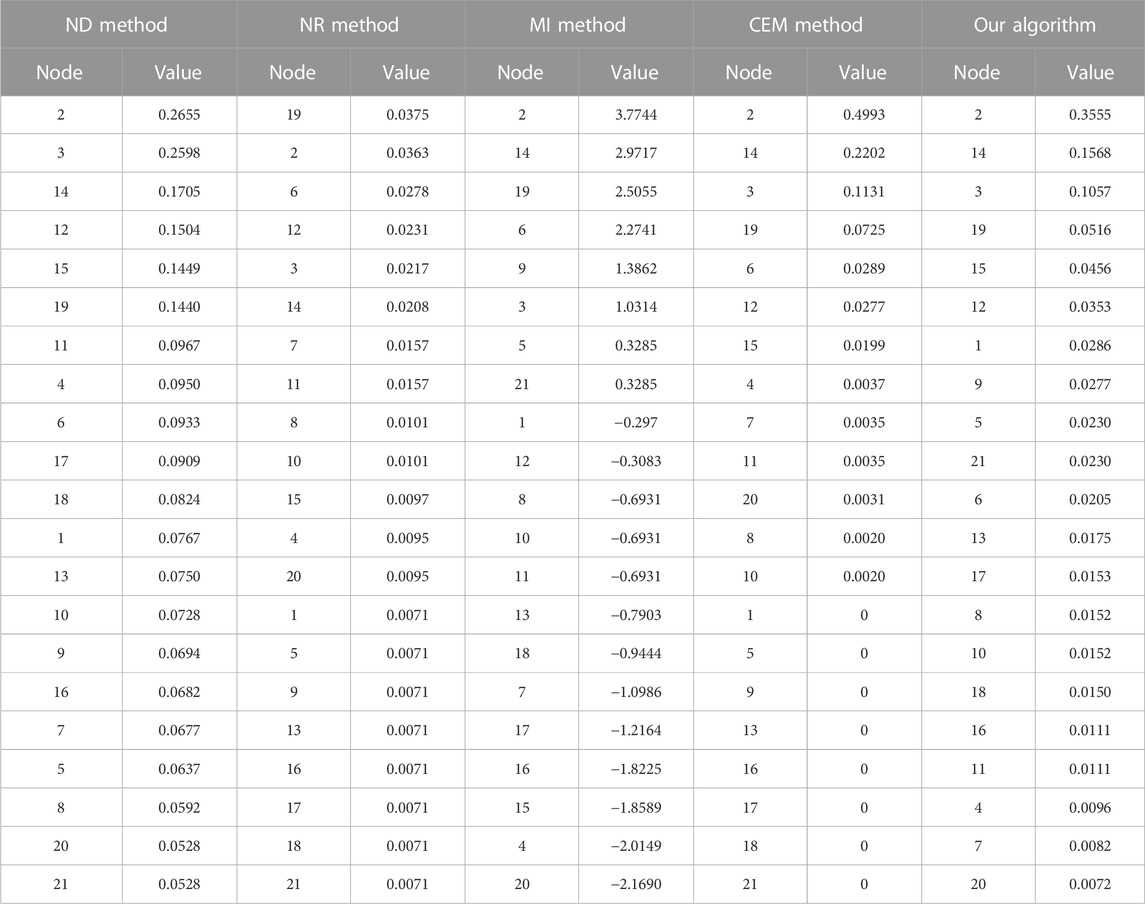
The ARPA (advanced research project agency) network is a typical network model, which is often used to verify the evaluation results of the importance of complex networks. As shown in Figure 2 the network has 21 nodes and 26 edges. This article takes the directed-weighted ARPA network as an example to analyze the effectiveness of the algorithm employed here. The node deletion (ND) method, NR method (σ = 0.85) [16], MI method [3], our algorithm (α = 0.8, θ = 0.7), and only the evaluation results of the CEM method are used for comparison. The experimental results are shown in Table 1.
From the comparison results in Table 1, the calculation results of the algorithm in this study have a higher distinguishing effect for nodes than the NR method and only the CEM method; the above two methods have the same evaluation results for 8 nodes with an in-degree of 0 in the network, especially for the evaluation of nodes 1, 5, 9, and 16. The above four nodes are located in different positions in the network, and the edge weights of the nodes are different. However, the NR values of the four nodes and the evaluation results using only the CEM cannot effectively distinguish them. Therefore, it is not comprehensive enough to consider the importance of nodes in directed-weighted communication network only from the perspective of nodes receiving contributions from other nodes. Comparing the algorithm in this study with the evaluation results using only the CEM, the first four nodes with the highest importance are the same, and they are all nodes 2, 14, 3, and 19. For the node ranked fifth in importance, the CEM considered to be node 6, and the algorithm in this study considered to be node 15 after the comprehensive VEM. Comparing the evaluation of the above two nodes by the node deletion method, the importance of node 15 is obviously better than node 6. Therefore, the algorithm in this study considers the importance of two aspects of the node, which not only strengthens the distinction of the algorithm for node identification, but also makes the evaluation results more accurate. At the same time, taking the evaluation results of the node deletion method as a reference, comparing our algorithm with the MI method, the evaluation result of our algorithm is more relevant to the node deletion method.
The algorithm based on CEM and VEM measures the importance of nodes from the two aspects of receiving information and outputting information. We proved using examples that the algorithm has better applicability to the directed-weighted network, and the accuracy of measuring the importance of nodes.
5.2 Further analysis in simulated network
5.2.1 Construction of hybrid weighted communication network
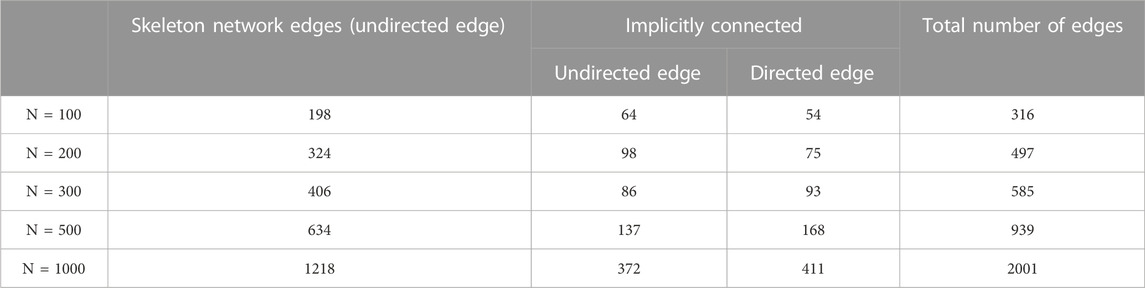
Most of the real-world communication networks have an obvious organizational hierarchy [28], such as the combat command network, which has obvious hierarchical characteristics between nodes and contains tree skeletons and implicit connections [29, 30]. Such networks can be classified as Organizational Structure Networks (OSNs) [31]. In order to better simulate the hybrid weighted communication network with organizational structure characteristics, this study proposes an OSN-based hybrid weighted network evolution model for the characteristics of the communication network. The construction process of the model is as follows.
Step 1:. Generate nodes and establish a communication network skeleton with a hierarchical structure. First, add a central node to the network and randomly generate m
Step 2:. Assign weights to the skeleton network and define the edge connecting the node and the parent node in the skeleton network as an undirected edge. The edge weight is
Step 3:. Generate implicit connections for the skeleton network and assign edges between nodes according to the probability given by the following formula:
where
Step 4:. Determine the direction and weight of implied edges. The direction of the edge is divided into the following three cases: i) when
5.2.2 Simulation experiment analysis
Taking the parameters
In order to further verify the effectiveness of the algorithm, according to the ranking results of the importance of the nodes, the nodes in the network are deleted in turn, and the changes of the maximum connectivity
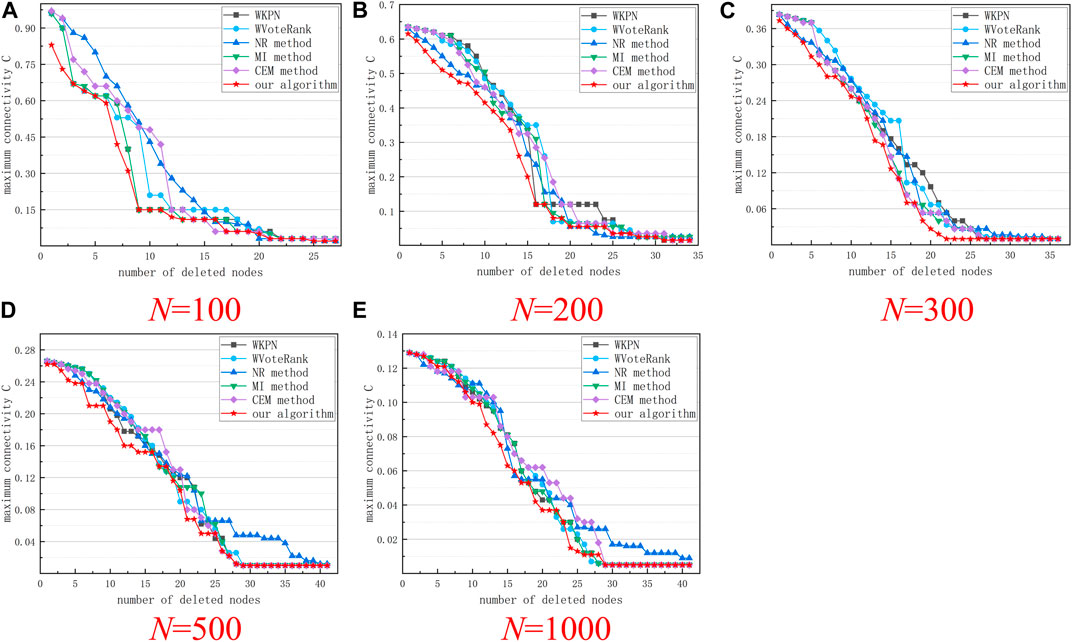
FIGURE 4. Maximum connectivity curves of the network after removing nodes according to the ranking results of different algorithms. (A–E) respectively show the results of five groups of experiments with a network size of 100 to 1000.
As can be seen from Figure 4, removing the nodes in the network according to the sorting results of the algorithm in this study (α = 0.8, θ = 0.7) can rapidly decreases the network connectivity, which has a significant impact on the transmission of information in the network. Compared with other algorithms, this algorithm also has certain advantages. As can be seen from Figure 5, in networks of different scales, the network efficiency decline curves obtained by our algorithm can maintain a rapid downward trend in the initial stage, indicating that after these nodes are removed from the network, the network will be rapidly destroy.
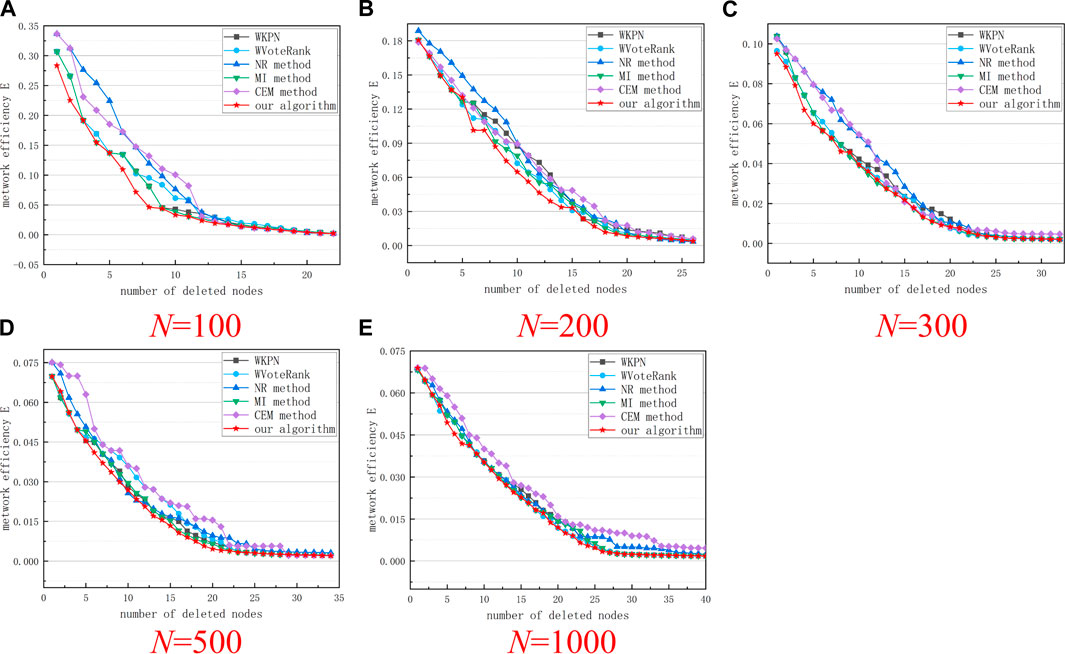
FIGURE 5. Network efficiency changing curves after removing nodes according to the ranking results of different algorithms. (A–E) respectively show the results of five groups of experiments with a network size of 100 to 1000.
As shown in Figures 4, 5, the algorithm in this study deletes the same number of nodes in most cases, which can cause greater damage to the network. Therefore, using the algorithm in this article, and considering the importance of the two aspects of the node, the node can be measured more accurately.
6 Conclusion
In this article, a communication network is abstracted as a hybrid weighted network for analysis and the CEM and the VEM are respectively proposed to evaluate the importance of nodes from the perspective of nodes receiving and output information. The effectiveness of the algorithm is proved in a small network. A hybrid weighted network evolution model based on OSN is proposed to verify the efficacy of the algorithm.
The experimental results show that the algorithm proposed in this study can better distinguish the nodes in the network and is more suitable for evaluating the importance of different types of nodes in a directed network. The validity of the algorithm is verified in the ARPA network. Compared with other directed-weighted network node value evaluation algorithms, the measurement results of the node value of the algorithm in this study have a higher correlation with the measurement results based on the ND method, indicating that the algorithm is more accurate in identifying key nodes in the network. At the same time, according to the sorting result of the algorithm in this study, when the node is deleted from the OSN-based hybrid weighted network model, the maximum connectivity and network efficiency drop rapidly, which shows that the important nodes identified by our algorithm have great value in the network. Through experimental simulation, the accuracy of the algorithm in discovering critical nodes in the network is further verified, which has certain application value for improving the invulnerability of communication networks.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
GT and XY performed the analysis. GT validated the analysis and drafted the manuscript. ZY reviewed the manuscript. YL and GC designed the research. All authors have read and approved the content of the manuscript.
Funding
This work was financially supported by the regional foundation of the Shaanxi Natural Science Foundation (2021JM-250).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ren D, Lin Z. Analysis of computer communication network and its security technology framework. In: Innovative computing: Proceedings of the 4th international conference on innovative computing (IC 2021). Singapore: Springer (2022).
2. Chen G, Sun P, Zhang J. Repair strategy of military communication network based on discrete artificial bee colony algorithm. IEEE Access (2020) 8:73051–60. doi:10.1109/access.2020.2987860
3. Yang Y-Z, Hu M, Huang T-Y. Influential nodes identification in complex networks based on global and local information. Chin Phys B (2020) 29(8):088903. doi:10.1088/1674-1056/ab969f
4. Lu Y, Zhao Y-J, Sun F-C, Liang R. Measuring and improving communication robustness of networks. IEEE Commun Lett (2019) 23(12):2168–71. doi:10.1109/lcomm.2019.2941940
5. Hu T-R, Wang R, Huang X-H. Node importance evaluation method for command information system communication network. Command Inf Syst Tech (2019) 10(5):95–100.
6. Lü L, Zhang YC, Yeung CH, Zhou T. Leaders in social networks, the delicious case. PloS one (2011) 6(6):e21202. doi:10.1371/journal.pone.0021202
7. Li C, Wang L, Sun S, Xia C. Identification of influential spreaders based on classified neighbors in real-world complex networks. Appl Math Comput (2018) 320:512–23. doi:10.1016/j.amc.2017.10.001
8. Wang Z-Q, Zhang Y, Zhang S, Guo Q-Q, Chen S-D. DJ-1 can inhibit microtubule associated protein 1 B formed aggregates. J Beijing Univ Posts Telecommunications (2011) 34(4):38–42. doi:10.1186/1750-1326-6-38
9. Sun H, Chen D, He J, Ch’ng E. A voting approach to uncover multiple influential spreaders on weighted networks. Physica A: Stat Mech its Appl (2019) 519:303–12. doi:10.1016/j.physa.2018.12.001
10. Gao L, Cao J-H, Song T-L, Xing B, Yan X. Evolution model of equipment support system of systems based on complex network theory. Acta Armamentarii (2017) 38(10):2019–30.
11. Tang P-C, Song C-C, Ding W-W, Ma J, Dong J, Huang L. Research on the node importance of a weighted network based on the K-Order propagation number algorithm. Entropy (2020) 22(3):364. doi:10.3390/e22030364
12. Li Z-Y, Xiong F, Wang X-M, Chen H-S, Xiong X. Topological influence-aware recommendation on social networks. New York: John Wiley (2019). Complexity.
13. Xiong F, Shen W, Chen H, Pan S, Wang X, Yan Z. Exploiting implicit influence from information propagation for social recommendation. IEEE Trans Cybernetics (2019) 50(10):4186–99. doi:10.1109/tcyb.2019.2939390
14. Yang Z-R, Zhang H, Liu J. Optimization algorithm of military communication network structure under node attack strategy. Syst Eng Elect (2021) 43(7):1848–55.
15. Chandrasekharan S, Gomez K, Al-Hourani A, Kandeepan S, Rasheed T, Goratti L, et al. Designing and implementing future aerial communication networks. IEEE Commun Mag (2016) 54(5):26–34. doi:10.1109/mcom.2016.7470932
16. Zhang K, Li P, Zhu B, Hu M. Evaluation method for node importance in directed-weighted complex networks based on PageRank. J Nanjing Univ Aeronautics Astronautics (2013) 45(3):429–34.
17. Wang Y, Guo J-L. Evaluation method of node importance in directed-weighted complex network based on multiple influence matrix. Acta Physica Sinica (2017) 66(5):050201. doi:10.7498/aps.66.050201
18. Liu Y, Jin J, Zhang Y, Xu C. A new clustering algorithm based on data field in complex networks. The J Supercomputing (2014) 67(3):723–37. doi:10.1007/s11227-013-0984-x
19. Xuan Z, Zhang F-M, Li K-W, Hui X-B, Wu H-S. Finding vital node by node importance evaluation matrix in complex networks. Acta Physica Sinica (2012) 61(5):1–7.
20. Zhou X, Zhang J-W. A new node importance evaluating method for complex weighted networks. Acta Armamentarii (2015) 36(S2):268–73.
21. Fan W-L, Liu Z-G. An evaluation method for node importance based on efficiency matrix. Chin J Comput Phys (2013) 30(5):714–9.
22. Fan W-L, Liu Z-G. Ranking method for node importance based on efficiency matrix. J Southwest Jiaotong Univ (2014) 49(2):337–42.
23. Zhong C, Xiong F, Pan S, Wang L, Xiong X. Hierarchical attention neural network for information cascade prediction. Inf Sci (2023) 622:1109–27. doi:10.1016/j.ins.2022.11.163
24. Zhang H, Lü Y-J. Vulnerability of vehicular ad hoc network based on complex network. J Beijing Univ Aeronautics Astronautics (2021) 47(8):1543–9.
25. Liu J, Xiong Q, Shi W, Shi X, Wang K. Evaluating the importance of nodes in complex networks. Physica A: Stat Mech its Appl (2016) 452:209–19. doi:10.1016/j.physa.2016.02.049
26. Liu J-X. A regulative arithmetic on the contingency communication in the damaged military communication networks. Appl Mech Mater (2014) 364:571–2.
27. Yu J, Xiao B, Cui Y. Cascading failure model and robustness of heterogeneous interdependent combat network. arXiv preprint arXiv:2205.04099 (2022).
28. Wang W, Mosse D, Cole D, Pickel J-G. Dynamic wireless network reconfiguration for control system applied to a nuclear reactor case study. Proc 26th Int Conf Real-Time Networks Syst (2018) 30–40.
29. Li J-C, Jiang J, Yang K-W, Chen Y. Research on functional robustness of heterogeneous combat networks. IEEE Syst J (2019) 13(2):1487–95. doi:10.1109/jsyst.2018.2828779
30. Qiu T, Liu J, Si W, Wu DO. Robustness optimization scheme with multi-population Co-evolution for scale-free wireless sensor networks. IEEE/ACM Trans Networking (2019) 27(3):1028–42. doi:10.1109/tnet.2019.2907243
31. Li E-Y, Gong J-X, Huang J, Kong J-T. Node importance analysis of complex networks for combat systems based on function chain. J Command Control (2018) 4(1):42–9.
Keywords: communication networks, directed-weighted network, node importance, evaluation matrix, network destruction resistance, vulnerabilities
Citation: Tian G, Yang X, Li Y, Yang Z and Chen G (2023) Hybrid weighted communication network node importance evaluation method. Front. Phys. 11:1133250. doi: 10.3389/fphy.2023.1133250
Received: 28 December 2022; Accepted: 17 April 2023;
Published: 19 June 2023.
Edited by:
Jiang Zhu, Netskope Inc., United StatesReviewed by:
Chengyi Xia, Tiangong University, ChinaFei Xiong, Beijing Jiaotong University, China
Zhenjiang Zhang, Beijing Jiaotong University, China
Copyright © 2023 Tian, Yang, Li, Yang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinzhi Yang, MjgyMzEyOTQxMUBxcS5jb20=
 Gan Tian
Gan Tian Xinzhi Yang
Xinzhi Yang