- 1Aviation and Automobile School, Chongqing Youth Vocational and Technical College, Chongqing, China
- 2College of Physics, Chongqing University, Chongqing, China
Weyl semimetals, classified as solid-state crystals and whose Fermi energy is accurately situated at Weyl points (WPs), have received much attention in condensed matter physics over the past 10 years. Weyl quasiparticles have been observed in the electronic and bosonic regimes, in addition to the extensive amount of theoretical and numerical predictions for the Weyl semimetals. This study demonstrates that 12 single Weyl phonons with linear dispersion and six double Weyl phonons with quadratic dispersion coexist between two specific phonon branches in real material P4332 BaSi2. The 12 single Weyl phonons and the six double Weyl phonons can form a Weyl complex phonon, which hosts a zero net chirality.
Introduction
Condensed-matter systems with inherent topological orders have received a great deal of attention lately. On the one hand, since quasiparticle excitations in realistic materials provide analogs of relativistic fermions or bosons in quantum field theory, these topological systems offer exotic platforms to study elementary particles and their related phenomena in high-energy physics. However, non-trivial topology, which is characterized by topological invariants, gives rise to topological quasiparticles in crystalline solids [1], providing an intriguing way to study symmetry-protected topological orders. Additionally, the crystal symmetry rather than the Poincare symmetry constraints quasiparticles in crystalline solids. There is therefore a possibility of discovering unusual topological quasiparticles [2–10] without high-energy physics counterparts in condensed-matter physics in addition to the traditional Dirac, Weyl, and Majorana particles in the standard model.
Numerous conventional and non-conventional topological quasiparticles have been proposed up to this point. For instance, intense research focuses on topological bosons in crystalline solids and various non-trivial fermions in topological semimetals [11–29]. Weyl-type excitations stand out among these non-trivial quasiparticles as being particularly significant. A quantized chiral charge, also known as the Chern number C, is what defines the topology of a Weyl point (WP). WPs are present in a system by shattering either the time-reversal or inversion symmetry because of the twofold-degenerate feature.
However, the crystal symmetries of crystalline solids are more intricate and may contain unusual Weyl-type quasiparticles. For example, the screw rotational symmetry can protect double WPs or WPs with the higher Chern number C. The 4-fold or 6-fold rotational symmetry can protect quadratic-double or cubic-triple WPs [28, 30–39].
This work identifies a Weyl complex composed of 12 C-1 WPs and 6 C-2 WPs in the phonon dispersion for P4332 BaSi2. Note that P4332 BaSi2 is a prepared experiential material [40]. BaSi2 crystallizes in the cubic P43232 space group. Ba2+ is bonded in an 8-coordinate geometry to eight equivalent Si1− atoms. Si1− is bonded in a 7-coordinate geometry to four equivalent Ba2+ and three equivalent Si1− atoms. The optimized lattice constants for P4332 BaSi2 are a = b = c = 6.771 Å, which are in good agreement with the experimental data, i.e., a = b = c = 6.715 Å [40]. The crystal structure of the relaxed BaSi2 is shown in Figure 1A.

FIGURE 1. (A) The crystal structure for BaSi2. (B) 3D bulk and 2D surface BZs. (C) Phonon dispersion for BaSi2. P1 and P2 are two obvious crossing points.
Methods
Using the Vienna ab initio Simulation Package [41] and the DFT framework, computations for the realistic material BaSi2 were carried out. The calculation’s energy and force convergence conditions were set to 10−6 eV and −0.01 eV/Å, respectively. A 5 × 5 × 5 Monkhorst-Pack grid was used to sample the whole BZ after the plane-wave expansion was truncated at 500 eV. We used the density functional perturbation theory to obtain the force constants for phonon spectrum calculations, and then we used the PHONOPY package [42] to calculate the phonon dispersion spectrum. We obtained the phonon Hamiltonian of the tight-binding model and the surface local DOSs with the open-source software WANNIER TOOLS [50] and surface Green’s functions.
Results and discussion
We determine the phonon spectra using first-principles calculations and verify that the two obvious phonon crossing points are present in the optical phonon branches of P4332 BaSi2. The absence of an imaginary frequency in the phonon spectrum, as seen in Figure 1C, demonstrates the P4332 BaSi2’s dynamical stability. We mainly focus on the frequencies around 8 THz and find two obvious phonon crossing points, P1 and P2, on Γ-X and Γ-M, respectively (see Figure 1B).
Figures 2A, B display the three-dimensional plot of the twofold degenerate phonon bands around the P1 and P2 points, respectively. From Figure 2A, one finds that the WP at P1 is a Charge-two WP. The charge-2 Weyl point (C-2 WP) is a topologically charged 0D two-fold band degeneracy with a charge of 2. It has a quadratic energy splitting in the plane perpendicular to the Γ-X direction and a linear dispersion in one direction (Γ-X). On a high-symmetry line or at a high-symmetry point in the BZ, the C-2 WP can happen. Figure 2B shows that the WP at P2 is a Charge-one WP. The charge-1 Weyl point (C-1 WP) is a degeneracy of the 0D two-fold band. It can occur at a generic k point in BZ and features a linear energy splitting in any direction in momentum space.
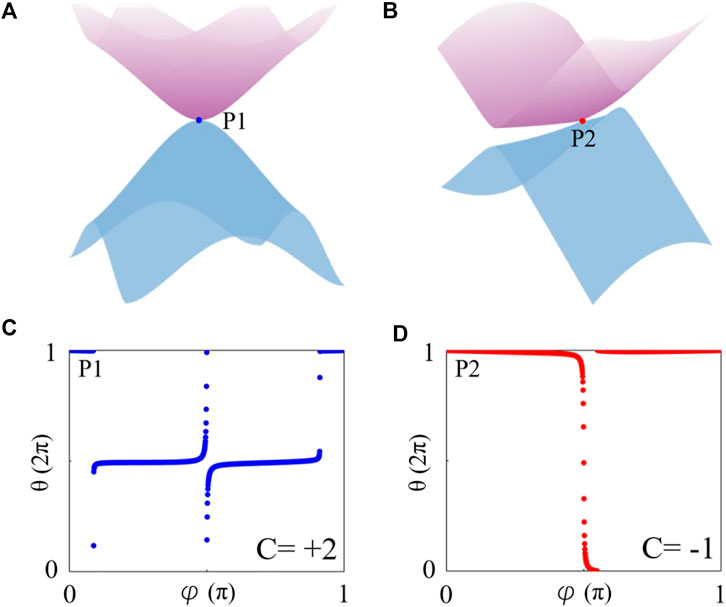
FIGURE 2. (A) and (B) 3D plots of the phonon bands around P1 and P2 points. (C) and (D) Evolutions of the average position of the Wannier center for the WP with C = +2 at P1 and the WP with C = −1 at P2.
Note that C-2 WP and C-1 WP are also named as double WP and single WP, respectively. In the scientific literature, double-Weyl points with greater topological ordering and emerging in particular crystals with particular symmetries have been discovered. Because double-Weyl points result from the coalescence of two single-Weyl points, their topological charge values are equal to 2 and −2.
In order to determine the chirality of Weyl phonons, we employ the Wilson-loop method within the evolution of the average position of Wannier centers. Figures 2C, D show the evolution of the average position of the Wannier centers for the P1 WP with positive chirality and the evolution of the average position of the Wannier centers for the P2 WP with negative chirality, respectively. These findings suggest that the WP at P1 (or P2) forms a double phonon WP with chiral charge 2 (or a single WP with chiral charge −1).
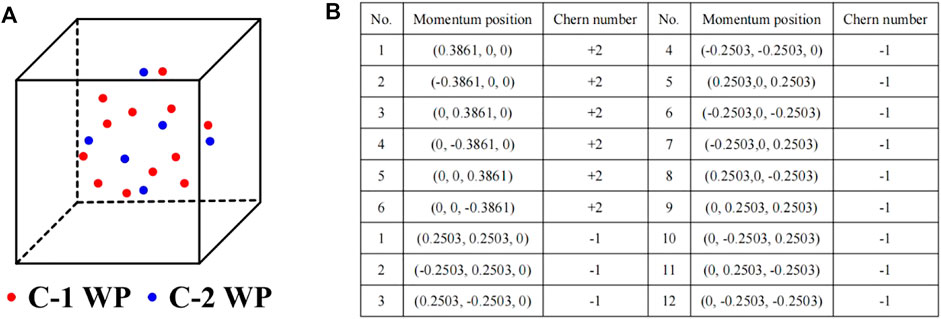
As shown in Figure 3A, one finds a total of 12 single WPs with C = −1 and 6 double WPs with C = +2 in the 3D BZ. The positions for all these multiple C-1 and C-2 WPs are shown in Figure 3B. These 12 C-1 WPs and 6 C-2 WPs will form a Weyl complex, which has a zero net chiral charge and obeys the Nielsen-Ninomiya no-go theorem [51, 52]. Note that the Weyl compelx has also be predicted by series research groups [53–56].
Therefore, our findings present ideal candidates for C-1 and C-2 WP phonons to form phononic Weyl complexes. Moreover, our findings are applicable to fermionic systems.
Unique non-trivial surface states are associated with the exotic C-2 and C-1 WP phonons. We build a phonon tight-binding Hamiltonian in the Wannier representation using second-order interatomic force constants to demonstrate this. The iterative Green’s function method is used to calculate phonon surface states in this model. Figure 4 depicts the local phonon density of states (LDOS) projected on a semi-infinite (001) surface of P4332 BaSi2. As anticipated, there are two visible phonon surface states, each of which begins at the projection of the double WP and ends at the projections of two single WPs. The lack of trivial bulk states on the (001) surface of P4332 BaSi2 substantially simplifies experimental detection and subsequent applications [43–49].
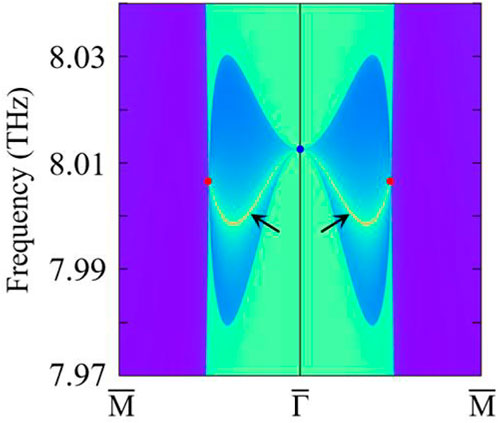
FIGURE 4. The phonon LDOS projected on the (001) surface. The phonon surface states are marked by black arrows.
Summary
We demonstrated that in real material P4332 BaSi2, there are 12 single WPs with C = −1 and 6 double WPs with C = +2 in the 3D BZ. These Weyl phonons create a Weyl complex with zero net charge number, and their non-trivial surface states connect the projections of phonon WPs are visible.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
Investigations and writing: YL.
Funding
This work is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant Nos. KJZD-K202104101 and KJQN202204104) and the school-level Scientific Research Project of Chongqing Youth Vocational and Technical College (Grant No. CQY2021KYZ03).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Yu ZM, Zhang Z, Liu GB, Wu W, Li XP, Zhang RW, et al. Encyclopedia of emergent particles in three-dimensional crystals. Sci Bull (2022) 67(4):375–80. doi:10.1016/j.scib.2021.10.023
2. Yan B, Felser C. Topological materials: Weyl semimetals. Annu Rev Condensed Matter Phys (2017) 8:337–54. doi:10.1146/annurev-conmatphys-031016-025458
3. Lv BQ, Weng HM, Fu BB, Wang XP, Miao H, Ma J, et al. Experimental discovery of weyl semimetal TaAs. Phys Rev X (2015) 5(3):031013. doi:10.1103/physrevx.5.031013
4. Soluyanov AA, Gresch D, Wang Z, Wu Q, Troyer M, Dai X, et al. Type-ii weyl semimetals. Nature (2015) 527(7579):495–8. doi:10.1038/nature15768
5. Hosur P, Qi X. Recent developments in transport phenomena in Weyl semimetals. Comptes Rendus Physique (2013) 14(9-10):857–70. doi:10.1016/j.crhy.2013.10.010
6. Chan CK, Lindner NH, Refael G, Lee PA. Photocurrents in weyl semimetals. Phys Rev B (2017) 95(4):041104. doi:10.1103/physrevb.95.041104
7. Wang HX, Lin ZK, Jiang B, Guo GY, Jiang JH. Higher-order weyl semimetals. Phys Rev Lett (2020) 125(14):146401. doi:10.1103/physrevlett.125.146401
8. Ruan J, Jian SK, Zhang D, Yao H, Zhang H, Zhang SC, et al. Ideal weyl semimetals in the ChalcopyritesCuTlSe2,AgTlTe2,AuTlTe2, andZnPbAs2. Phys Rev Lett (2016) 116(22):226801. doi:10.1103/physrevlett.116.226801
9. Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90(1):015001. doi:10.1103/revmodphys.90.015001
10. Young SM, Kane CL. Dirac semimetals in two dimensions. Phys Rev Lett (2015) 115(12):126803. doi:10.1103/physrevlett.115.126803
11. Zhang X, Jin L, Dai X, Liu G. Topological type-II nodal line semimetal and Dirac semimetal state in stable kagome compound Mg3Bi2. J Phys Chem Lett (2017) 8(19):4814–9. doi:10.1021/acs.jpclett.7b02129
12. Wang L, Yang Y, Wang J, Liu W, Liu Y, Gong J, et al. Excellent catalytic performance toward the hydrogen evolution reaction in topological semimetals. EcoMat (2022) 2022:e12316. doi:10.1002/eom2.12316
13. Tian L, Liu Y, Meng W, Zhang X, Dai X, Liu G. Spin–orbit coupling-determined topological phase: Topological insulator and quadratic Dirac semimetals. J Phys Chem Lett (2020) 11(24):10340–7. doi:10.1021/acs.jpclett.0c03103
14. Meng W, Zhang X, He T, Jin L, Dai X, Liu Y, et al. Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J Adv Res (2020) 24:523–8. doi:10.1016/j.jare.2020.05.026
15. Chen DY, Wu Y, Jin L, Li Y, Wang X, Duan J, et al. Superconducting properties in a candidate topological nodal line semimetal SnTaS2 with a centrosymmetric crystal structure. Phys Rev B (2019) 100(6):064516. doi:10.1103/physrevb.100.064516
16. Liu G, Jin L, Dai X, Chen G, Zhang X. Topological phase with a critical-type nodal line state in intermetallic CaPd. Phys Rev B (2018) 98(7):075157. doi:10.1103/physrevb.98.075157
17. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J Adv Res (2020) 23:95–100. doi:10.1016/j.jare.2020.01.017
18. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J Adv Res (2020) 22:137–44. doi:10.1016/j.jare.2019.12.001
19. Wang X, Cheng Z, Zhang G, Kuang M, Wang XL, Chen H. Strain tuning of closed topological nodal lines and opposite pockets in quasi-two-dimensional α-phase FeSi2. Phys Chem Chem Phys (2020) 22(24):13650–8. doi:10.1039/d0cp02334e
20. Yang T, Jin L, Liu Y, Zhang X, Wang X. Spin-polarized type-II nodal loop and nodal surface states in hexagonal compounds XTiO2 (X= Li, Na, K, Rb). Phys Rev B (2021) 103(23):235140. doi:10.1103/physrevb.103.235140
21. Zhou F, Liu Y, Kuang M, Wang P, Wang J, Yang T, et al. Time-reversal-breaking Weyl nodal lines in two-dimensional A3C2 (A= Ti, Zr, and Hf) intrinsically ferromagnetic materials with high Curie temperature. Nanoscale (2021) 13(17):8235–41. doi:10.1039/d1nr00139f
22. Wang X, Cheng Z, Zhang G, Yuan H, Chen H, Wang XL. Spin-gapless semiconductors for future spintronics and electronics. Phys Rep (2020) 888:1–57. doi:10.1016/j.physrep.2020.08.004
23. Zhou F, Liu Y, Wang J, Kuang M, Yang T, Chen H, et al. Intersecting topological nodal ring and nodal wall states in superhard superconductor FeB4. Phys Rev Mater (2021) 5(7):074201. doi:10.1103/physrevmaterials.5.074201
24. Xie C, Yuan H, Zhang Z, Wang X. Magnetic Weyl and quadratic nodal lines in inverse-Heusler-based fully compensated ferrimagnetic half-metals. Phys Rev Mater (2022) 6(9):094406. doi:10.1103/physrevmaterials.6.094406
25. Gao H, Venderbos JW, Kim Y, Rappe AM. Topological semimetals from first principles. Annu Rev Mater Res (2019) 49:153–83. doi:10.1146/annurev-matsci-070218-010049
26. Bernevig A, Weng H, Fang Z, Dai X. Recent progress in the study of topological semimetals. J Phys Soc Jpn (2018) 87(4):041001. doi:10.7566/jpsj.87.041001
27. Fang C, Lu L, Liu J, Fu L. Topological semimetals with helicoid surface states. Nat Phys (2016) 12(10):936–41. doi:10.1038/nphys3782
28. Fang C, Gilbert MJ, Dai X, Bernevig BA. Multi-Weyl topological semimetals stabilized by point group symmetry. Phys Rev Lett (2012) 108(26):266802. doi:10.1103/physrevlett.108.266802
29. Ding G, Wang J, Yu ZM, Zhang Z, Wang W, Wang X. Single pair of type-III weyl points half-metals: BaNiIO6 as an example. Phys Rev Mater (2023) 7(1):014202. doi:10.1103/physrevmaterials.7.014202
30. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401
31. Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302
32. Lai HH. Correlation effects in double-Weyl semimetals. Phys Rev B (2015) 91(23):235131. doi:10.1103/physrevb.91.235131
33. Jian SK, Yao H. Correlated double-Weyl semimetals with Coulomb interactions: Possible applications to HgCr2Se 4 and SrSi2. Phys Rev B (2015) 92(4):045121. doi:10.1103/physrevb.92.045121
34. Chen Q, Fiete GA. Thermoelectric transport in double-Weyl semimetals. Phys Rev B (2016) 93(15):155125. doi:10.1103/physrevb.93.155125
35. Wang YT, Tsai YW. Multiple Weyl and double-Weyl points in an elastic chiral lattice. New J Phys (2018) 20(8):083031. doi:10.1088/1367-2630/aada55
36. Zhong M, Han Y, Wang J, Liu Y, Wang X, Zhang G. Material realization of double-Weyl phonons and phononic double-helicoid surface arcs with P213 space group. Phys Rev Mater (2022) 6(8):084201. doi:10.1103/physrevmaterials.6.084201
37. Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303
38. Singh B, Chang G, Chang TR, Huang SM, Su C, Lin MC, et al. Tunable double-Weyl Fermion semimetal state in the SrSi2 materials class. Scientific Rep (2018) 8(1):10540–9. doi:10.1038/s41598-018-28644-y
39. He H, Qiu C, Cai X, Xiao M, Ke M, Zhang F, et al. Observation of quadratic Weyl points and double-helicoid arcs. Nat Commun (2020) 11(1):1820–6. doi:10.1038/s41467-020-15825-5
40. Evers J, Oehlinger G, Weiss A. Eine neue hochdruckphase von Bariumdisilicid. Angew Chem (1978) 90(7):562–3. doi:10.1002/ange.19780900724
41. Hafner J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J Comput Chem (2008) 29(13):2044–78. doi:10.1002/jcc.21057
42. Togo A, Tanaka I. First principles phonon calculations in materials science. Scripta Materialia (2015) 108:1–5. doi:10.1016/j.scriptamat.2015.07.021
43. Singh S, Wu Q, Yue C, Romero AH, Soluyanov AA. Topological phonons and thermoelectricity in triple-point metals. Phys Rev Mater (2018) 2(11):114204. doi:10.1103/physrevmaterials.2.114204
44. Liu Y, Chen X, Xu Y. Topological phononics: From fundamental models to real materials. Adv Funct Mater (2020) 30(8):1904784. doi:10.1002/adfm.201904784
45. Wang X, Zhou F, Yang T, Kuang M, Yu ZM, Zhang G. Symmetry-enforced ideal lanternlike phonons in the ternary nitride Li6WN4. Phys Rev B (2021) 104(4):L041104. doi:10.1103/physrevb.104.l041104
46. Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148
47. Zhou F, Zhang Z, Chen H, Kuang M, Yang T, Wang X. Hybrid-type nodal ring phonons and coexistence of higher-order quadratic nodal line phonons in an AgZr alloy. Phys Rev B (2021) 104(17):174108. doi:10.1103/physrevb.104.174108
48. Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303
49. Feng Y, Xie C, Chen H, Liu Y, Wang X. Dirac point phonons at high-symmetry points: Towards materials realization. Phys Rev B (2022) 106(13):134307. doi:10.1103/physrevb.106.134307
50. Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: An open-source software package for novel topological materials. Comp Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033
51. Nielsen HB, Ninomiya M. Absence of neutrinos on a lattice:(I). Proof by homotopy theory. Nucl Phys B (1981) 185(1):20–40. doi:10.1016/0550-3213(81)90361-8
52. Nielsen HB, Ninomiya M. Absence of neutrinos on a lattice:(II). Intuitive topological proof. Nucl Phys B (1981) 193(1):173–94. doi:10.1016/0550-3213(81)90524-1
53. Wang X, Zhou F, Zhang Z, Yu ZM, Yao Y. Hourglass charge-three Weyl phonons. Phys Rev B (2022) 106(21):214309. doi:10.1103/physrevb.106.214309
54. Liu QB, Wang Z, Fu HH. Charge-four weyl phonons. Phys Rev B (2021) 103(16):L161303. doi:10.1103/physrevb.103.l161303
55. Wang R, Xia BW, Chen ZJ, Zheng BB, Zhao YJ, Xu H. Symmetry-protected topological triangular Weyl complex. Phys Rev Lett (2020) 124(10):105303. doi:10.1103/physrevlett.124.105303
Keywords: DFPT calculation, phonon, Weyl point, DFT, topological feature
Citation: Li Y (2023) Multiple Weyl and double-Weyl points in the phonon dispersion of P4332 BaSi2. Front. Phys. 11:1129933. doi: 10.3389/fphy.2023.1129933
Received: 22 December 2022; Accepted: 23 January 2023;
Published: 10 February 2023.
Edited by:
Xiaoming Zhang, Hebei University of Technology, ChinaCopyright © 2023 Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Li, bGl5YW5nX3BoeXNpY3NAMTI2LmNvbQ==
 Yang Li
Yang Li