A heuristic approach to the prediction of a periodic solution for a damping nonlinear oscillator with the non-perturbative technique

The present work attracts attention to obtaining a new result of the periodic solution of a damped nonlinear Duffing oscillator and a damped Klein–Gordon equation. It is known that the frequency response equation in the Duffing equation can be derived from the homotopy analysis method only in the absence of the damping force. We suggest a suitable new scheme successfully to produce a periodic solution without losing the damping coefficient. The novel strategy is centered on establishing an alternate equation apart from any difficulty in handling the influence of the linear damped term. This alternative equation was obtained with the rank upgrading technique. The periodic solution of the problem is presented using the non-perturbative method and validated by the modified homotopy perturbation technique. This technique is successful in obtaining new results toward a periodic solution, frequency equation, and the corresponding stability conditions. This methodology yields a more effective outcome of the damped nonlinear oscillators. With the help of this procedure, one can analyze many problems in the domain of physical engineering that involve oscillators and a linear damping influence. Moreover, this method can help all interested plasma authors for modeling different nonlinear acoustic oscillations in plasma.

1 Introduction

In the range of differential equations, various physical manifestations, such as acoustic waves in plasma physics, and many engineering problems are modeled. A lot of scientists have made magnificent efforts to evaluate the solution of these differential equations. Different techniques have been utilized to evaluate the corresponding solutions. Modeling different biological, physical, and biochemical engineering problem occurrences, in general, yields nonlinear partial differential equations (PDEs). Moreover, plasma physics is one of the most fertile fields for many researchers interested in studying nonlinear phenomena. To perform modeling, the nonlinear phenomena that propagate in different plasma systems and many ordinary and partial differential equations must be solved. For this purpose, different mathematical approaches have been introduced for modeling several physical problems. Recently, a damped nonlinear oscillator model has been widely considered in practical engineering, general physics, and in plasma physics. For mathematical scientists, an article on nonlinear PDEs, which are addressed in most engineering and science domains, is extremely important. Many authors have offered a survey of the literature with numerous references using various analytical techniques for dealing with the damped nonlinear oscillation problems. Nonlinear systems remain a challenge, and its interest has fundamentally concentrated on specific changes in system instability and bifurcations.

Duffing oscillators are permanently connected with engineering and physical situations, especially plasma physics. The damping force is an impact on an oscillatory system that has the action of restricting, reducing, or averting its oscillation. Damping is created by operations of losing the energy stored in an oscillation. Examples include resistance in electronic oscillators, viscous pull in mechanical systems and plasma physics, osmosis, and expansion of light in visual oscillators. Damping, which did not build from vanishing energy, may be significant in other vibrating systems like those that subsist in some biological systems. A system’s damping may be categorized as one of the following:

• Overdamped: The system reaches equilibrium as an exponential decay.

• Critically damped: The system reaches equilibrium as soon as possible without vibrating.

• Underdamped: The system vibrates with amplitude slowly lessening to zero (at low frequency compared to the nondamped case).

• Undamped: The system resonantly oscillates at its native frequency.

See [1] for additional instances for the aforementioned categories.

Over the current decades, a lot of physical phenomena have been described utilizing nonlinear ordinary differential equations (ODEs). One of the simplest of these oscillators called a Duffing equation has received significant interest in light of its classical applications in engineering, biology, plasma physics, and sciences. The history of nonlinear proceedings in engineering sciences has been observed since [2] employed the hardening spring model to investigate the vibration of the electromagnetic vibrating beam in 1918. Therefore, the Duffing equation has been extensively utilized in structural dynamics and in mathematics to determine the existence of oscillatory motions of second-order nonlinear PDEs. The oscillation/non-oscillation theorems of Meissner’s equation were investigated by [3]. [4] utilized the multiple-scale perturbation approach to develop and calculate an analytic periodic solution of oscillating movements in damping Duffing oscillators. [5] used perturbation techniques for nonlinear structural vibrations using Duffing oscillators. Consequently, perturbation analysis is still used to obtain an analytic solution for oscillating movements. The HPM was first introduced by the famous mathematician [6]. Recently, it has been employed in numerous investigations in engineering and physics. In contrast, this technique failed in analyzing damping nonlinear oscillators [7]. There are many modifications made by many researchers to improve HPM to be a more functioning method. [8] employed the parameter-expanding technique as a modification to HPM in solving strongly nonlinear oscillators. [9] and [10] developed HPM by connecting it with Laplace transform for solving nonlinear oscillators. [11] obtained a periodic solution for the Fangzhu oscillator by HPM.

Next, several of the latest developments of this technique are briefly mentioned; for instance, the combination of the multiple-scale method and HPM [12–15], the parameterized HPM [16], and nonlinearities distribution HPM was applied to solve Troesch’s problem [17]. Numerical and approximate techniques can be utilized for the treatment of nonlinear oscillators. Numerous estimates were used in trying to solve linear and nonlinear oscillators, for example, the reproducing kernel method [18]. Moreover, an iterative procedure is employed to evaluate a numerical solution of the optimal control issues of the Duffing oscillators [19]. Also, [20] applied the finite difference technique to investigate an oscillatory model. Furthermore, by substituting a suitable linear auxiliary operator for the linear operator in [21] analysis of nonlinear equations with restoring force, among other changes, they created a new version of HPM. By using the modified homotopy perturbation procedure, [22] also introduced an analytic solution for a nonconservative parametric quintic-cubic Duffing oscillator. A damped Mathieu equation was solved using a modulation for HPM by [23]. The Newell–Whitehead–Segel (NWS) equation’s periodic solution was also estimated by [24] using the HPM. [25] introduced a simple frequency formulation to study a tangent oscillator. An analytic solution of Burgers’ equation with time-fraction has been introduced by [26]. A variational principle for a nonlinear equation that appears in several micro-electro-mechanical systems was developed by [27]. Furthermore, a jerk Duffing oscillator was solved using the lowering rank approach by him and [28]. Luo and Jin have used the lower-order technique in numerical approaches [29]. Recently, [30] applied the non-perturbative technique to solve a damping Helmholtz–Rayleigh–Duffing oscillator.

It is common knowledge that some nonlinear differential equations do not have exact solutions. Then, the analysis of approximate solutions for some kinds of these systems plays a significant role in investigating nonlinear physical phenomena [31]. The damping Duffing oscillator refers to these kinds of equations, and it is represented by the following equation:

$\ddot{y}+2\mu \dot{y}+{\omega }_0^{2}y+Q{y}^3=0;y=y\left(t\right)(1)$

It is thought to observe that a Duffing oscillator is a simple model which displays various kinds of vibrations, such as chaos and limit cycles. The term $\dot{y}\left(t\right)$ in Eq. 1 represents a damping oscillation, and $\mu$ refers to viscous damping. The part $\left({\omega }_0^{2}y+Q{y}^3\right)$ refers to a nonlinear restoring force acting as a hard spring (with ${\omega }_0^2$ rules, the size of stiffness, and $Q$ dominants, the size of nonlinearity). This equation illustrates a wonderful area of well-known nonlinear dynamical system behavior. It was used by a lot of scientists to illustrate such behaviors. Numerous problems in both engineering and physics drive to nonlinear Duffing oscillators (Eq. 1) from oscillations of a simple pendulum, including nonlinear electrical circuits. It has been approved in various applications in image processing [4, 5]. The approximate periodic response for the un-damped equation, obtained by various analytical methods, has been discussed in almost all textbooks on nonlinear vibration. Eq. 1, with a non-zero damping term, has received attention in many domains of physical engineering problems. The investigation of new techniques which drive the solution of the damped Duffing equation was of vital significance since these solutions can be used for a cubic Schrodinger/damping Klein–Gorden equation that has numerous uses in nonlinear optics, plasma physics, and fluid mechanics.

Other related works have been included in this study, yielding a good understanding of the present analysis. A fractionally damped beam has been analyzed by [32]. The influence of dispersion force and squeezed film damping was incorporated in the dynamic instability of the nanowire-fabricated sensor subjected to centrifugal and constant acceleration [33, 34]. Even though Eq. 1 appears straightforward at a first glance, it contains several complex elements. The classical perturbation approach has a lot of drawbacks. Moreover, the following damping nonlinear Klein–Gorden equation has the same shortcoming when using the classical HPM:

$y_{tt}+P{y}_{xx}+2\mu y_t+2\eta y_x+\sigma y=Q{y}^3;y=y\left(x,t\right)(2)$

The real constant coefficients $P,\eta ,\mu ,\sigma ,$ and $Q$ can be defined as a second-order spatial derivative coefficient, spatial damped coefficient, temporal damped coefficient, natural frequency, and cubic stiffness parameter, respectively. The classical nonlinear Klein–Gordon equation, which appears in several scientific domains such as nonlinear optics, solid physics, fluid mechanics, quantum mechanics, and plasma physics, is derived from Eq. 2 when the values of the coefficients $\mu$ and $\eta$ vanish. In addition to its applications in plasma physics, it can be used for modeling many nonlinear structures in plasma. It transforms into the one-dimensional time-nonlinear damped Klein–Gordon equation when $\mu >0$ and $\eta =0$ [35–38]. The aforementioned damping Klein–Gordon equation can be transformed into a damping Duffing oscillator by using the technique of the traveling wave approaches. Traveling waves engender multiple physical systems spontaneously, typically qualified by PDEs. Then, by including the following traveling wave’s next variable $\zeta \left(x,t\right)$, one can create an alternative oscillatory form of Eq. 2.

$\zeta \left(x,t\right)=2\eta x+2P\mu t.(3)$

Such transformation was applied to the nonlinear Klein–Gordon Eq. 2 without damping by [39]. According to the stated novel independent variable, one obtains

$y_t=2P\mu y^{\prime }\left(\zeta \right),y_x=2\eta y^{\prime }\left(\zeta \right),y_{tt}=4P^2{\mu }^2{y}^{″}\left(\zeta \right),\text{and}{y}_{xx}=4{\eta }^2{y}^{″}\left(\zeta \right),(4)$

where the prime denotes the total derivative concerning the variable $\zeta$. By utilizing Eq. 4 with Eq. 2, it will be transformed into the following damping Duffing equation:

$P{y}^{″}\left(\zeta \right)+y^{\prime }\left(\zeta \right)+{\omega }_0^{2}y\left(\zeta \right)=R{y}^3\left(\zeta \right),(5)$

where ${\omega }_0^2$ and $R$ are given through the subsequent notations:

${\omega }_0^2=\frac{\sigma }{4\left(P{\mu }^2+{\eta }^2\right)},\mathrm{a}\mathrm{n}\mathrm{d}R=\frac{Q}{4\left(P{\mu }^2+{\eta }^2\right)}.(6)$

The solution of Eq. 5 gives the traveling wave solution of the original nonlinear Klein–Gordon equation as given in Eq. 2. Suppose that Eq. 5 has been subjected to these initial conditions $y\left(0\right)=A\mathrm{a}\mathrm{n}\mathrm{d}{y}^{\prime }\left(0\right)=0$.

A fresh perturbation strategy is required to address the drawbacks. Unexpectedly, the flaw in Eq. 1 has been fixed by using the fractional derivative in conjunction with HPM [40, 41].

In the present research, a new suitable idea is presented successfully to produce a periodic solution for oscillators containing the damping coefficient without losing this damping force. The main idea is based on the rank upgrading technique by upgrading the linear operator to a higher order and using the original equation to replace what is equivalent to the linear damped term [42, 43]. The outcome is an alternative fourth-order differential equation devoid of any damping difficulties. The comparison between this alternative equation and the original equation showed that the obtained equation is corrected and can be used to perform the periodic solution. The periodic solution of the problem is presented using the non-perturbative method and validated by the modified homotopy perturbation technique.

2 Methodology

To overcome the difficulty in solving the damping nonlinear oscillator, one can employ the rank upgrading mechanism to annihilate the damping term “$y^{\prime }$”. This method is used for upgrading the order of the derivatives of Eq. 5 to become

$P{y}^{‴}+y^{″}+{\omega }_0^2{y}^{\prime }=3R{y}^2{y}^{\prime },(7)$

$P{y}^{\left(4\right)}=-y^{‴}+\left(3R{y}^2-{\omega }_0^2\right)y^{″}+6Ry{y^{\prime }}^2.(8)$

By removing $y^{\prime }$ from Eq. 7 with the help of Eq. 5 and replacing $y^{‴}$ in Eq. 8 yields

$P^2{y}^{\left(4\right)}-\left(1+2P\left(3R{y}^2-{\omega }_0^2\right)\right)y^{″}-6PRy{y^{\prime }}^2+\left(3R{y}^2-{\omega }_0^2\right)\times \left(R{y}^2-{\omega }_0^2\right)y=0.(9)$

This is a fourth-order equation with cubic-quintic nonlinearity which represents an alternative form of the original damping Eq. 5. This new form will be subject to the initial conditions listed as follows:

$y\left(0\right)=A,y^{\prime }\left(0\right)=0,y^{″}\left(0\right)=\frac{A}{P}\left(R{A}^2-{\omega }_0^2\right),\mathrm{a}\mathrm{n}\mathrm{d}{y}^{‴}\left(0\right)=-\frac{A}{P^2}\left(R{A}^2-{\omega }_0^2\right).(10)$

It can be ensured that Eq. 9 represents an alternative form of the original Eq. 5 through the comparison of the numerical solutions.

3 Introducing the periodic solution

The periodic solution can be introduced from Eq. 9 analytically which can be illustrated as follows, with the non-perturbative approach and with the homotopy perturbation method:

It is noted that Eq. 9 can be rearranged in the following form:

$y^{\left(4\right)}-g\left(y,y^{\prime },y^{″}\right)+f\left(y\right)=0,(11)$

where the two odd functions $g\left(y,y^{\prime },y^{″}\right)$ and $f\left(y\right)$ are selected to have $y^{″}$ and $y$ as a common factor, respectively. Here,

$\left.\begin{array}{l}g\left(y,y^{\prime },y^{″}\right)=\frac{1}{P^2}\left(1+2P\left(3R{y}^2-{\omega }_0^2\right)+6\mathit{PR}\frac{y{y^{\prime }}^2}{y^{″}}\right)y^{″},\\ f\left(y\right)=\frac{1}{P^2}\left(3R{y}^2-{\omega }_0^2\right)\left(R{y}^2-{\omega }_0^2\right)y.\end{array}\right\}.(12)$

Consequently, Eq. 11 in the non-perturbative approach can be sought in the form

$y^{\left(4\right)}-{\beta }^2{y}^{″}+{\mathit{\varpi }}^{4}y=0.(13)$

The efficient frequency formula given by El-Dib [44–46] can be used to evaluate both ${\beta }^2$ and ${\varpi }^4$ as follows:

Introducing the trial solution to Eq. 13 in the form

$\widehat{y}\left(\zeta \right)=A\cos \omega \zeta ,(14)$

where $A$ and $\omega$ represent the amplitude and the unknown frequency of the oscillation, respectively. Accordingly, both ${\varpi }^4\left(A\right)$ and ${\beta }^2\left(A\right)$ read

${\varpi }^4\left(A\right)=\frac{\underset{0}{\overset{T}{{\displaystyle \int }}}\widehat{y}\left(\zeta \right)f\left(\widehat{y}\right)d\zeta }{\underset{0}{\overset{T}{{\displaystyle \int }}}{\widehat{y}}^2\left(\zeta \right)d\zeta }=\frac{1}{8P^2}\left(15A^4{R}^2-24A^{2}R{\omega }_0^2+8{\omega }_0^4\right);T=\frac{\pi }{2\omega },(15)$

${\beta }^2\left(A\right)=\frac{\underset{0}{\overset{T}{{\displaystyle \int }}}{\widehat{y}}^{″}\left(\zeta \right)g\left(\widehat{y},{\widehat{y}}^{\prime },{\widehat{y}}^{″}\right)d\zeta }{\underset{0}{\overset{T}{{\displaystyle \int }}}{{\widehat{y}}^{″}}^2\left(\zeta \right)d\zeta }=\frac{1}{P^2}\left(1+3A^2\mathit{PR}-2P{\omega }_0^2\right).(16)$

Employing Eq. 14 with the linear fourth-order Eq. 13 yields the frequency equation in the form

${\omega }^4+{\beta }^2\left(A\right){\omega }^2+{\varpi }^4\left(A\right)=0.(17)$

At this stage, the solution of Eq. 13 has the form

$y\left(\zeta \right)=A\cos \omega \zeta ,(18)$

with

$\omega =\frac{1}{\sqrt{2}}\sqrt{-{\beta }^2+\sqrt{{\beta }^4-4{\varpi }^4}}.(19)$

4 Validation with the homotopy perturbation approach

By utilizing the technique of the auxiliary equivalent [21, 40, 47, 48] by introducing ($P^2{\omega }^{4}y$) into Eq. 9 and then building the corresponding homotopy equation, one obtains

$y^{\left(4\right)}-{\omega }^{4}y=\frac{\rho }{P^2}\left[-P^2{\omega }^{4}y+y^{″}-\left(3R{y}^2-{\omega }_0^2\right)\left(R{y}^3-{\omega }_0^{2}y-P{y}^{″}\right)+P\left(3R{y}^2-{\omega }_0^2\right)y^{″}+6PRy{y^{\prime }}^2\right];\rho \in \left[\mathrm{0,1}\right].(20)$

The new frequency parameter $\omega$ is unknown to determine the latter.

By operating both sides of Eq. 20 with the inverse $\left(D_{\zeta }^2-{\omega }^2\right)$, one can reduce the artificial higher power and obtain

$\left(D_{\zeta }^2+{\omega }^2\right)y=\frac{\rho }{P^2\left(D_{\zeta }^2-{\omega }^2\right)}\left[-P^2{\omega }^{4}y+y^{″}-\left(3R{y}^2-{\omega }_0^2\right)\left(R{y}^3-{\omega }_0^{2}y-P{y}^{″}\right)+P\left(3R{y}^2-{\omega }_0^2\right)y^{″}+6PRy{y^{\prime }}^2\right].(21)$

This equation is an alternative to Eq. 5; it is free of difficulty due to the linear damping effects. At this stage, the application of HPM is easy without any shortcomings. Typically, introducing the homotopy expansion [6], one finds

$y\left(\zeta ;\rho \right)=y_0\left(\zeta \right)+\rho y_1\left(\zeta \right)+{\rho }^2{y}_2\left(\zeta \right)+...,(22)$

where the unknowns $y_0\left(\zeta \right)\text{and}{y}_1\left(\zeta \right)$ are given by substituting from Eq. 22 into Eq. 21; following the same procedure as given in HPM, the abovementioned unknowns may be determined by the simpler differential equations as follows:

$y_0^{″}+{\omega }^2{y}_0=0,(23)$

which is the linear harmonic equation having the general solution in the form

$y_0\left(\zeta \right)=A\cos \left(\omega \zeta \right),(24)$

where $A$ is the amplitude of the oscillation. Furthermore, we have

$\left(D_{\zeta }^2+{\omega }^2\right)y_1=\frac{1}{P^2\left(D_{\zeta }^2-{\omega }^2\right)}[-P^2{\omega }^4{y}_0+y_0^{″}-\left(3R{y}_0^2-{\omega }_0^2\right)\left(R{y}_0^3-{\omega }_0^2{y}_0-P{y}_0^{″}\right)+P\left(3R{y}_0^2-{\omega }_0^2\right)y_0^{″}+6\mathit{PR}{y}_0{y^{\prime }}_0^2].(25)$

The zero-order solution Eq. 24 is introduced into Eq. 25, and the cancellation of the secular terms requires

$P^2{\omega }^4-\left(2P{\omega }_0^2-3\mathit{PR}{A}^2-1\right){\omega }^2+{\omega }_0^4-3R{\omega }_0^2{A}^2+\frac{15}{8}{R}^2{A}^4=0.(26)$

Consequently, the frequency–amplitude equation is given by

${\omega }^2=\frac{1}{2P^2}\left[\left(2P{\omega }_0^2-3\mathit{PR}{A}^2-1\right)\pm \sqrt{\frac{3}{2}{P}^2{R}^2{A}^4-4P{\omega }_0^2+6\mathit{PR}{A}^2+1}\right].(27)$

It is noted that the frequency equation derived by the homotopy perturbation method is equivalent to that obtained before by the non-perturbative approach in Eq. 17.

Without secular terms, the solution of Eq. 25 arises in the form

$y_1\left(\zeta \right)=\frac{R{A}^3}{80P^2{\omega }^4}\left({\omega }_0^2-3P{\omega }^2-\frac{15}{16}R{A}^2\right)\cos \left(3\omega \zeta \right)-\frac{R^2{A}^5}{3328P^2{\mathrm{\Omega }}^4}\cos \left(5\omega \zeta \right).(28)$

Accordingly, the final first-order approximate solution gives

$y\left(\zeta \right)=A\cos \left(\omega \zeta \right)+\frac{R{A}^3}{80P^2{\omega }^4}\left({\omega }_0^2-3P{\omega }^2-\frac{15}{16}R{A}^2\right)\cos \left(3\omega \zeta \right)-\frac{R^2{A}^5}{3328P^2{\omega }^4}\cos \left(5\omega \zeta \right).(29)$

It should be noted that solution Eq. 29 is superior to known asymptotic periodic solutions of Eq. 5. See, for illustration, the recent study demonstrated by [49]. In his work, he applied the Laplace Adomian decomposition method to a damping Duffing equation and obtained an asymptotic solution in terms of a power series. However, the abovementioned solution cannot be obtained using HPM without applying the rank upgrading technique.

The stability criteria of the frequency–amplitude Eq. 26 become

$P\left(2{\omega }_0^2-3R{A}^2\right)>1,{\omega }_0^4-3R{\omega }_0^2{A}^2+\frac{15}{8}{R}^2{A}^4>0,\text{and}\frac{3}{2}{P}^2{R}^2{A}^4-4P{\omega }_0^2+6\mathit{PR}{A}^2+1>0.(30)$

These criteria ensure the positivity of ${\omega }^2.$

By employing the value of $\zeta$ as a function of $x$ and $y$ from Eq. 3 into the asymptotic solution of Eq. 29, consequently, this asymptotic solution is converted in terms of the original Klein–Gordon Eq. 2; therefore, one obtains

$\begin{array}{l}y\left(x,t\right)=A\cos \left(2\eta \omega x+2P\mu \omega t\right)+\frac{R{A}^3}{80P^2{\omega }^4}\left({\omega }_0^2-3P{\omega }^2-\frac{15}{16}R{A}^2\right)\cos \left(3\eta \omega x+6P\mu \omega t\right)\\ -\frac{R^2{A}^5}{3328P^2{\omega }^4}\cos \left(10\eta \omega x+10P\mu \omega t\right).\end{array}(31)$

For more convenience, a numerical calculation will be represented to confirm the previous approximate analytic solution of the damping Duffing oscillator 5).

5 Numerical illustrations

In this section, the comparison between the numerical solutions for both the original Eq. 5 and alternative Eq. 9is explained. The Runge–Kutta approach built in Mathematica software will be used in this comparison. The numerical values of the parameters are selected in the form $P=5,R=0.1,{\omega }_0=2$ and $A=1$. In Figure 1, the numerical solution for the original equation is represented by the solid red line, while the alternative equation is plotted with a blue dashed line. In this calculation, the error between these solutions is $8.671\times {10}^{-8}$. This means that the two curves are identical. This graph shows that Eq. 9 is another face of Eq. 5. This means that any solution of Eq. 9 represents a solution of Eq. 5. Therefore, the periodic solution obtained by the non-perturbative technique or that obtained by the modified HPM represents a periodic solution of the original Eq. 5.

FIGURE 1

FIGURE 1. Comparison of the numerical solution between Eq. 5 and Eq. 9.

It is worthwhile to observe that the periodic solution Eq. 18, that obtained by the non-perturbative method, and the periodic solution Eq. 29, performed by the modified homotopy perturbation approach, are required for comparing the periodic solution that can be produced from Eq. 5 directly. It is easy to employ the Galerkin’s method directly to Eq. 5 to perform the following periodic solution:

$y\left(\zeta \right)=A\cos \mathrm{\Omega }\zeta ,(32)$

where $\mathrm{\Omega }$ is given by

$\mathrm{\Omega }=\frac{1}{2P}\left(-1+\sqrt{1-3A^2\mathit{PR}+4P{\omega }_0^2}\right).(33)$

Figure 2 represents the periodic solution obtained by three different methods. These are as follows: Galerkin’s solution (Eq. 32), which is plotted by the solid red line; the non-perturbative solution (Eq. 18),which is represented by the blue dashed line; and the HPM solution (Eq. 29), which is represented by the dotted green curve. The calculations are made for the system having $P=2.6,R=1,{\omega }_0=1.5$, and $A=1$. The investigation of this graph shows that there is an excellent agreement between the three curves. The relative error between the Galerkin solution (Eq. 32) and the non-perturbative solution (Eq. 18) is $0.0007843$, while the error between the Galerkin solution (Eq. 32) and the HPM solution (Eq. 29) is found to be $0.004467$. This comparison also shows that the non-perturbative solution (Eq. 18) is closer than the HPM solution (Eq. 29) to Galerkin’s solution (Eq. 32).

FIGURE 2

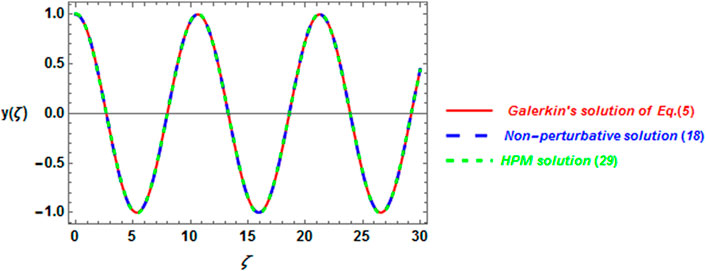
FIGURE 2. Comparison between the analytical periodic solutions by the non-perturbative and homotopy perturbation approaches (18) and (29), respectively, with Galerkin’s solution (Eq. 32).

The approximate solution, as given in Eq. 32, is sketched versus the parameter $\zeta$ for the amplitude $A=1$ and $R=0.1,P=5{\omega }_0=2.$ This calculation is displayed in Figures 3–5. These three graphs show a periodic solution for the damping Duffing Eq. 5. Moreover, the influence of the parameters $P$ and $R$ and the linear frequency ${\omega }_0$ on the periodic solution is shown in these graphs. The growth in these coefficients reduces the time cycle of the wave solution.

FIGURE 3

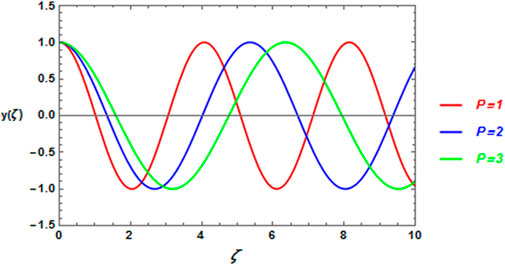
FIGURE 3. Influence of the parameter P on the periodic solution Eq. 32.

FIGURE 4

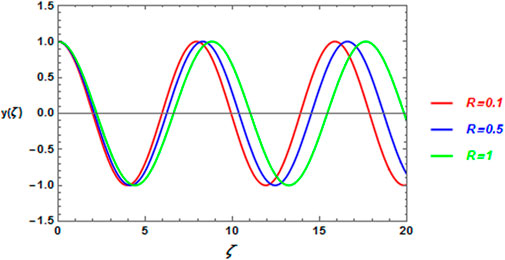
FIGURE 4. Influence of the parameter R on the periodic solution Eq. 32.

FIGURE 5

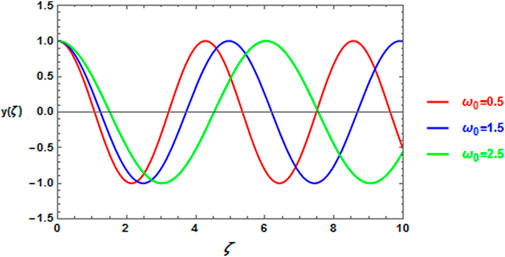
FIGURE 5. Influence of the parameter ${\omega }_0$ on the periodic solution Eq. 32.

The calculations are performed under the stability conditions that are given in Eq. 30. The stable distribution is located in the plane $\left({\omega }_0^2-A\right).$ The numerical outcomes are illustrated in Figures 6–9, where the stable region is colored in red. These stable regions have satisfied the three inequalities in Eq. 30. In Figure 6, the natural frequency ${\omega }_0^2$ is plotted versus the amplitude $A$ for the Duffing coefficient $R=2$ at $P=0.1$. When the parameter $P$ was increased to the value of $P=0.2$ (i.e., the damping coefficient is decreased), the stable region was decreased, as shown in Figure 7. The continued raise in $P$ results in reducing the stable region, as shown in Figure 8, for $P=0.3$. This shows the increase in the damping coefficient plays a stabilizing influence. This agreement is with those obtained in [11]. The examination of the increase in the Duffing coefficient is the subject of Figure 9. It is observed that as $R$ increased, the width of the stable region decreased. This ensures that the nonlinear coefficient plays a destabilizing influence.

FIGURE 6

FIGURE 6. Stability distribution of the conditions for a system of $R=2$ and $P=0.1.$

FIGURE 7

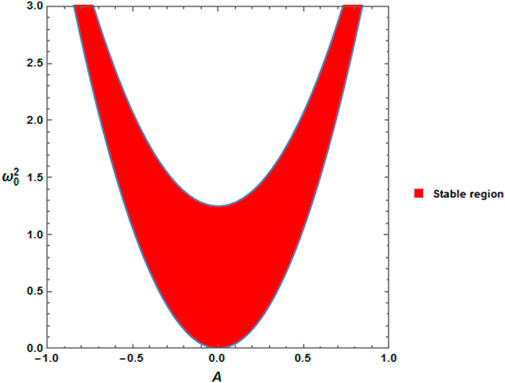
FIGURE 7. Stability distribution of the same system, as given in Figure 6, except that $P=0.2.$

FIGURE 8

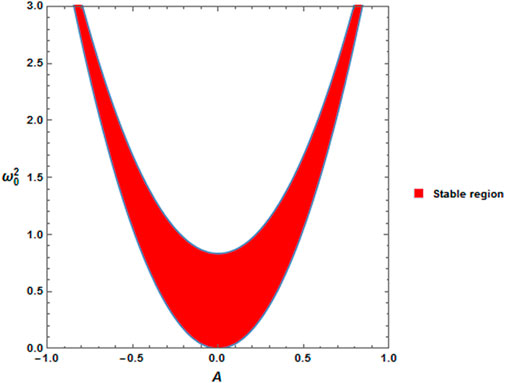
FIGURE 8. Stability distribution of the same system, as given in Figure 6, except that $P=0.3.$

FIGURE 9

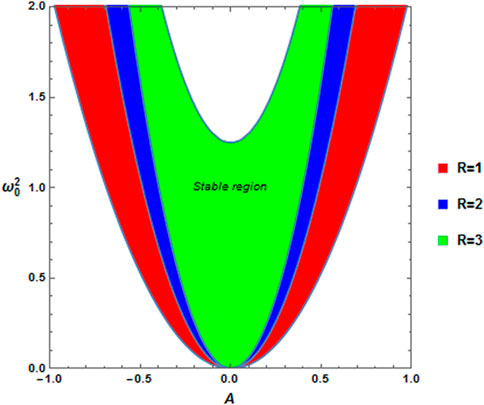
FIGURE 9. Stability distribution of the same system, as given in Figure 7, of $P=0.2.$

6 Conclusion

Away from the regular investigation of the nonlinear oscillators, the present article has been explained. This article deals with the nonlinear Duffing equation and obtains a new result of the periodic solution of a damped nonlinear Duffing oscillator and the damped Klein–Gordon equation by using a new technique named the rank upgrading technique. This technique first increases the order of the partial differential equation by differentiating the original differential equation. The alternative equation is obtained. The comparison between this alternative equation and the original equation shows that the obtained equation is corrected and can be used to perform the periodic solution. Its solution has been validated by applying the HPM to the alternative equation, in which the oscillation frequency obtained by the non-perturbative approach has been identical to that frequency obtained by the HPM. This frequency has been used to discuss stability behavior. A comparison of the periodic solutions’ curves was obtained using three different methods. Non-perturbative, modified homotopy perturbation, and Galerkin solutions showed an excellent agreement. This comparison also shows that the non-perturbative solution is closer to Galerkin’s solution than the HPM solution. Furthermore, this scheme is a new technique. Therefore, the present numerical method can be used for analyzing different acoustic waves and oscillations in plasma and different physical systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author contributions

YE: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal). NE: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal). HA: conceptualization (equal), formal analysis (equal), investigation (equal), and methodology (equal).

Acknowledgments

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R17), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Alciatore DG. Introduction to mechatronics and measurement. 3rd ed New York: McGraw-Hill (2007). ISBN 978-0-07-296305-2.

Google Scholar

2. Duffing G. Erzwunge Schweingungen bei Veränderlicher Eigenfrequenz. Braunschweig): F. Viewig u. Sohn (1918).

Google Scholar

3. Yamanaka Y, Yamaoka N. Oscillation and non-oscillation theorems for Meissner's equation. Appl Math Comput (2021) 388:125526. doi:10.1016/j.amc.2020.125526

CrossRef Full Text | Google Scholar

4. Nayfeh AH. Perturbation methods. New York, USA: John Wily & Sons (1973).

Google Scholar

5. Nayfeh AH, Mook DT. Non-linear oscillations. New York, USA: John Wily & Sons (1979).

Google Scholar

6. He JH. Homotopy perturbation technique. Comput Methods Appl Mech Eng (1999) 178:257–62. doi:10.1016/s0045-7825(99)00018-3

CrossRef Full Text | Google Scholar

7. He JH, El-Dib YO. Homotopy perturbation method with three expansions. J Math Chem (2021) 59:1139–50. doi:10.1007/s10910-021-01237-3

CrossRef Full Text | Google Scholar

8. He JH. New interpretation of homotopy perturbation method. Int J Mod Phys B (2006) 20(18):2561–8. doi:10.1142/s0217979206034819

CrossRef Full Text | Google Scholar

9. Liu ZJ, Adamu MY, Suleiman E, He JH. Hybridization of homotopy perturbation method and Laplace transformation for the partial differential equations. Therm Sci (2017) 21(4):1843–6. doi:10.2298/tsci160715078l

CrossRef Full Text | Google Scholar

10. Filobello-Nino U, Vazquez-Leal H, Herrera-May AL, Ambrosio-Lazaro RC, Jimenez-Fernandez VM, Sandoval-Hernandez M, et al. The study of heat transfer phenomena by using modified homotopy perturbation method coupled by Laplace transform. Therm Sci (2020) 24(2B):1105–15. doi:10.2298/tsci180108204f

CrossRef Full Text | Google Scholar

11. He JH, El-Dib YO. Homotopy perturbation method for Fangzhu oscillator. J Math Chem (2020) 58(10):2245–53. doi:10.1007/s10910-020-01167-6

CrossRef Full Text | Google Scholar

12. El-Dib YO. Stability approach for periodic delay Mathieu equation by the He-multiple-scales method. Alexandria Eng J (2018) 57:4009–20. doi:10.1016/j.aej.2018.01.021

CrossRef Full Text | Google Scholar

13. El-Dib YO. Modified multiple scale technique for the stability of the fractional delayed nonlinear oscillator. Pramana - J Phys (2020) 94:56. doi:10.1007/s12043-020-1930-0

CrossRef Full Text | Google Scholar

14. El-Dib YO. Multiple scales homotopy perturbation method for Non-Linear Oscillators. Nonlinear Sci Lett A (2017) 8(4):352–64.

Google Scholar

15. El-Dib YO. Periodic solution of the cubic nonlinear Klein–Gordon equation, and the stability criteria via the He-multiple-scales method. Pramana - J Phys (2019) 92:7. doi:10.1007/s12043-018-1673-3

CrossRef Full Text | Google Scholar

16. Adamu MY, Ogenyi P. Parameterized homotopy perturbation method. Nonlinear Science Letters A (2017) 8(2):240–3.

Google Scholar

17. Vazquez-Leal H. Non-linearities distribution homotopy perturbation method to find solution for Troesch problem. Nonlinear Science Letters A (2018) 9(3):279–91.

Google Scholar

18. Akgül A, Ahmad H. Reproducing kernel method for Fangzhu's oscillator for water collection from air. Math Methods Appl Sci (2020). doi:10.1002/mma.6853

CrossRef Full Text | Google Scholar

19. Liu C, Kuo C, Chang J. Solving the optimal control problems of nonlinear Duffing oscillators by using an iterative shape functions method. Comp Model Eng Sci (2020) 122(1):33–48. doi:10.32604/cmes.2020.08490

CrossRef Full Text | Google Scholar

20. Liu X, Chen X, Kang R, Shen X, Ni B. A coupled cavitation model in an oscillatory oil squeeze film. Comp Model Eng Sci (2020) 123(1):129–52. doi:10.32604/cmes.2020.07836

CrossRef Full Text | Google Scholar

21. Shen Y, El-Dib YO. A periodic solution of the fractional sine-Gordon equation arising in architectural engineering. J Low Frequency Noise, Vibration Active Control (2021) 40(2):683–91. doi:10.1177/1461348420917565

CrossRef Full Text | Google Scholar

22. El-Dib YO, Elgazery NS, Mady AA, Alyousef HA. On the modeling of a parametric cubic-quintic non-conservative Duffing oscillator via the modified homotopy perturbation method. Z für Naturforschung A (2022) 77(5):475–86. doi:10.1515/zna-2021-0354

CrossRef Full Text | Google Scholar

23. El-Dib YO, Elgazery NS. Damped Mathieu equation with a modulation property of the homotopy perturbation method. J Sound Vibration (2022) 56:21–36. doi:10.32604/sv.2022.014166

CrossRef Full Text | Google Scholar

24. Elgazery NS. A periodic solution of the newell-whitehead-segel (NWS) wave equation via fractional calculus. J Appl Comput Mech (2020) 6(SI):1293–300.

Google Scholar

25. He JH, Yang Q, He CH, Khan Y. A simple frequency formulation for the tangent oscillator. Axioms (2021) 10:320. doi:10.3390/axioms10040320

CrossRef Full Text | Google Scholar

26. Shokhanda R, Goswami P, He JH, Althobaiti A. An approximate solution of the time-fractional two-mode coupled Burgers equation. Fractal and Fractional (2021) 5:196. doi:10.3390/fractalfract5040196

CrossRef Full Text | Google Scholar

27. He JH, Anjum N, Skrzypacz P. A variational principle for a nonlinear oscillator arising in the microelectromechanical system. J Appl Comput Mech (2021) 7(1):78–83.

Google Scholar

28. He JH, El-Dib YO. The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer Methods Partial Differential Equations (2021) 37(2):1800–8. doi:10.1002/num.22609

CrossRef Full Text | Google Scholar

29. Luo Z, Jin S. A reduced-order extrapolated Crank–Nicolson collocation spectral method based on proper orthogonal decomposition for the two-dimensional viscoelastic wave equations. Numer Methods Partial Differential Equations (2020) 36:49–65. doi:10.1002/num.22397

CrossRef Full Text | Google Scholar

30. El-Dib YO. The damping Helmholtz–Rayleigh–Duffing oscillator with the non-perturbative approach. Mathematics Comput Simulation (2022) 194:552–62. doi:10.1016/j.matcom.2021.12.014

CrossRef Full Text | Google Scholar

31. He JH, El-Dib YO. The enhanced homotopy perturbation method for axial vibration of strings. Fact universitatis, Ser Mech Eng (2021) 19:735. doi:10.22190/FUME210125033H

CrossRef Full Text | Google Scholar

32. Jena RM, Chakraverty S, Jena SK. Dynamic response analysis of fractionally damped beams subjected to external loads using homotopy analysis method. J Appl Comput Mech (2019) 5(2):355–66. doi:10.22055/jacm.2019.27592.1419

CrossRef Full Text | Google Scholar

33. Atabak R, Sedighi HM, Reza A, Mirshekari E. Analytical investigation of air squeeze film damping for biaxial micro-scanner using eigenfunction expansion method. Math Methods Appl Sci (2020). doi:10.1002/mma.6658

CrossRef Full Text | Google Scholar

34. Yekrangisendi A, Yaghobi M, Riazian M, Koochi A. Scale-dependent dynamic behavior of nanowire-based sensor in accelerating field. J Appl Comput Mech (2019) 5(2):486–97. doi:10.22055/jacm.2018.27302.1393

CrossRef Full Text | Google Scholar

35. Lin Y, Cui M. A new method to solve the damped nonlinear Klein-Gordon equation. Sci China Ser A: Math (2008) 51:304–13. doi:10.1007/s11425-008-0030-2

CrossRef Full Text | Google Scholar

36. Pang Y, Yang Y. A note on finite time blowup for dissipative Klein–Gordon equation. Nonlinear Anal (2020) 195:111729. doi:10.1016/j.na.2019.111729

CrossRef Full Text | Google Scholar

37. Parka JY, Jeong U. Optimal control of damped Klein–Gordon equations with state constraints. J Math Anal Appl (2007) 334:11–27. doi:10.1016/j.jmaa.2006.12.042

CrossRef Full Text | Google Scholar

38. Côte R, Martel Y, Yuan X. Long-time asymptotics of the one-dimensional damped nonlinear Klein–Gordon equation. Archive Rational Mech Anal (2021) 239(3):1837–74. doi:10.1007/s00205-020-01605-4

CrossRef Full Text | Google Scholar

39. Dehghan M, Ghesmati A. Application of the dual reciprocity boundary integral equation technique to solve the nonlinear Klein–Gordon equation. Comp Phys Commun (2010) 181(8):1410–8. doi:10.1016/j.cpc.2010.04.008

CrossRef Full Text | Google Scholar

40. El-Dib YO, Elgazery NS. Effect of fractional derivative properties on the periodic solution of the nonlinear oscillations. Fractals (2020) 28(4):2050095. doi:10.1142/S0218348X20500954

CrossRef Full Text | Google Scholar

41. El-Dib YO. Stability approach of a fractional-delayed duffing oscillator. Discontinuity, Nonlinearity, and Complexity (2020) 9(3):367–76.

CrossRef Full Text | Google Scholar

42. El-Dib YO. Homotopy perturbation method with rank upgrading technique for the superior nonlinear oscillation. Math Comput Simulation (2021) 182:555–65. doi:10.1016/j.matcom.2020.11.019

CrossRef Full Text | Google Scholar

43. El-Dib YO, Matoog RT. The rank upgrading technique for a harmonic restoring force of nonlinear oscillators. J Appl Comput Mech (2021) 7(2):782–9.

Google Scholar

44. El-Dib YO. Immediate solution for fractional nonlinear oscillators using the equivalent linearized method. J Low Frequency Noise Vibration Active Control (2022) 41(4):1411–25. doi:10.1177/14613484221098788

CrossRef Full Text | Google Scholar

45. El-Dib YO. Insightful and comprehensive formularization of frequency amplitude formula for strong or singular nonlinear oscillators. J Low Frequency Noise, Vibration Active Control (2023) 146134842211181. doi:10.1177/14613484221118177

CrossRef Full Text | Google Scholar

46. El-Dib YO, Elgazery NS, Gad NS. A novel technique to obtain a time-delayed vibration control analytical solution with simulation of He’s formula. J Low Frequency Noise (2023). Vibration & Active Control. doi:10.1177/14613484221149518

CrossRef Full Text | Google Scholar

47. He JH, El-Dib YO, Mady AA. Homotopy perturbation method for the fractal toda oscillator. Fractal and Fractional (2021) 5:93. doi:10.3390/fractalfract5030093

CrossRef Full Text | Google Scholar

48. El-Dib YO. Criteria of vibration control in delayed third-order critically damped Duffing oscillation. Archive of Applied Mechanics (2021) 92(1):1–19. doi:10.1007/s00419-021-02039-4

CrossRef Full Text | Google Scholar

49. Nnaji DU. Application of Laplace adomian decomposition method (LADM) to duffing equation. APLAMBERT Academic Publishing (2020).

Google Scholar