Numerical simulations of MHD generalized Newtonian fluid flow effects on a stretching sheet in the presence of permeable media: A finite difference-based study

Casson–Williamson (CW) nanofluid flows and mass transfer characteristics are explored in this study. Furthermore, the velocity slip condition and viscous dissipation affect or are taken to examine the changes in mass and heat transfer caused by a stretching surface integrated into permeable media with heat conversion beneath the effect of a magnetic field and consistent thermal radiation. All the physicochemical characteristics of the non-linear fluids are regarded massive. Whether or not the concentration of nanofluids remains stable is investigated. When particles of a nanofluid are in motion, chemical reactions can occur, and this motion can be used to study the concentration of the nanofluid. One must first examine a set of non-linear partial differential equations with boundary conditions as a base equation to obtain the necessary BVP mathematical model. The approximate solution for differential equations was found using the finite difference method, which also considered the necessary boundary conditions. The numerical analysis results are then represented visually to demonstrate how different governing parameters affect velocity, temperature, and concentration. Although the heat transmission exhibits a reverse manner, the non-Newtonian nanofluid moves more quickly in the non-appearance of a magnetic domain than it does in one. Additionally, as the porosity parameter increased, the heat transmission rate decreased, whereas the skin friction coefficient increased. The novel parts of this study come from the simulation findings of a non-Newtonian CW nanofluid model in porous media subjected to a magnetic field, heat radiation, and slip velocity phenomena.

1 Introduction

One of the most challenging areas of the latest research is nanotechnology. Nanotechnology has been a major contributor to the advancement of computing and electronics, allowing for the creation of faster, smaller, and more legacy systems that can process and hold ever-increasing amounts of data. Its significance and uses highlight the most recent developments and advancements in the field of nanoscience and nanotechnology, as well as their numerous applications in fields such as energy, cosmetics, biology, biotechnology, drug delivery, tissue engineering, environmental protection, information technology, food and agriculture, and future prospects. Thiruvangadam et al. [1] investigated the food industry’s potential uses for nanotechnology in the future. Roco et al. [2] studied the future of nanotechnology research for social purposes.

A relatively recent area of science and technology is nano-medicine. Nikalje studied the classification of nanomaterials based on their size and provided a brief explanation of the many forms of pharmaceutical nano-systems [3]. Mahpatra and Gupta conducted research on heat transmission in stagnation point flow in the direction of a stretching sheet [4]. A heat transfer study for Casson fluid flow over a stretching sheet with Newtonian heating and viscous dissipation was invented by Ahmad et al. [5]. Khan and Pop examined the flow of a nanofluid past a stretched sheet in the boundary layer [6]. Analytical modeling of entropy generation for Casson nanofluid flow caused by a stretching surface was studied by Abolbashari et al. [7].

There are numerous uses for magnetohydrodynamics (MHD) in physics, chemistry, and engineering. From biological systems to astronomical phenomena such as the formation of magnetic fields and solar flares, MHD addresses essential physical processes across several length scales. MHD also outlines bring down the heat applications, such as electric arc welding and joining operations, as well as other technologically significant applications, such as the magnetic confinement of fusion plasma and the interaction of fusion plasmas with projected liquid metal blankets [8].

Nadeem et al. investigated Casson nanofluid flow past a linearly stretching sheet in a three-dimensional MHD boundary layer with convective boundary conditions and a model for Casson nanofluid flow across a non-linearly stretched sheet considering magnetic field effects by Mustafa et al. [9, 10]. In a computer investigation of the thermal transmission of electromagnetic fluid across a stretched surface, Hussain et al. [11] studied the form factor performance of solid particles. Specifically, they investigated how well solid particles acted as shape factors. Hayat et al. [12] examined the features of nanofluid convection flow across a stretched sheet in combination with a convectively heated chemical process and a heat source/sink. Afify studied Casson nanofluid flow over a stretching sheet under slip boundary conditions when there is viscous dissipation and chemical reaction [13]. Nanofluid flow over a non-linearly stretching sheet through a porous medium with chemical reaction and thermal radiation was investigated by Khan et al. [14]. Ibrahim et al. [15] studied the effects of a chemical reaction and a heat source on a Casson nanofluid’s dissipative MHD mixed convection flow across a non-linear permeable stretching sheet. The effects of viscosity dissipation and chemical reaction on nanofluid flow through a permeable surface were examined by Dero et al. [16]. Goud et al. [17] investigated the impact of thermal radiation and joule heating hydrodynamic Casson nanofluid flow through a non-linear inclined porous stretching sheet when the chemical reaction was considered.

Williamson nanofluid flow yielded by an inclined Lorentz force across a non-linear stretching sheet was explored by Khan et al. [18]. Researchers led by Reddy et al. [19] investigated the MHD flow and heat transfer capabilities of Williamson nanofluid over a stretching sheet with varying thicknesses and varying levels of heat capacity. The parabolic velocity of MHD Casson–Williamson (CW) fluids with cross-diffusion was investigated by Kumaran and Sandeep [20]. For MHD Williamson fluid, Parmar [21] investigated the behavior in an unstable convective boundary layer with a permeable stretched surface, non-linear radiation, and a heater. Radiative MHD thin film flow of Williamson fluid across an erratic permeable stretching sheet was examined by Shah et al. [22]. Lund et al. [23] conducted research on the evaluation of a dual solution for the MHD flow of Williamson fluid while accounting for slipping. Statistical investigation of stagnation-point heat flow in Williamson fluid with viscous dissipation and exponential heat source effects was studied by Mahanthesh et al. [24]. Hall current and nth-order thermochemical flow of 3D radiative Williamson fluid across an inclined stretched sheet were the subjects of an investigation conducted by Shamshuddin et al. [25]. Ullah investigated the MHD radiative flow of a stretching sheet of Williamson nanofluid in a porous medium with convective boundary conditions [26]. Saravana et al. [27] learned that the fluid flowing across a thin stretched surface in MHD Williamson and Casson exhibits thermal radiation and diffusion effects. Sivanandam researched Cattaneo-Christov dual flux entropy optimization of MHD CW fluid flow over a convectively heated stretchable sheet [28]. Using a porous stretching surface, Humane et al. [29] explored the effects of the chemical reaction and thermal radiation on the magnetohydrodynamic flow of CW nanofluid. Yousuf et al. [30] considered the impacts of chemical reactions on the flow of a CW nanofluid over a slippery stretched sheet in a porous medium. MHD Williamson nanofluid flow across a permeable stretched sheet with thermal radiation and chemical reaction was investigated by Patil et al. [31]. The characteristics of chemical reaction, suction/injection, and MHD radiative flow of Williamson nanofluid with the Cattaneo–Christov model over a stretching sheet over permeable media studied by Reddy et al. [32]. Falodun et al. [33] investigated the effects of magneto-thermal and chemical processes on the flow of the CW nanofluid boundary layer under the Soret–Dufour mechanism. In addition, information could be discovered on the significance of the heat transfer process that occurs through nanofluids in industrial applications [34–40].

The innovative aspects of this research result from a simulation of a non-Newtonian CW nanofluid model subjected to a magnetic field, thermal radiation, slip velocity phenomenon, and porous media. In this study, the literature review is presented in the Introduction section and the mathematical structure is presented in the mathematical model section. In the Numerical procedure section, we discuss the details of the solution methodology. The Results and discussion section provides a detailed breakdown and explanation of the variables that govern fluid flow. Finally, the expected results are presented in the Conclusion section.

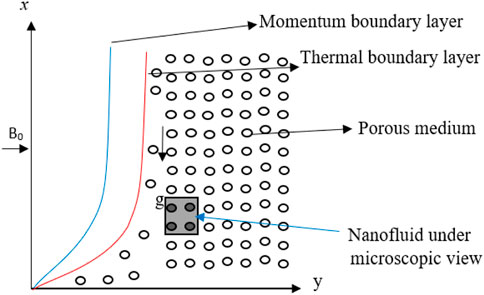
2 Flow configurations and modeling

To simulate a non-linear fluid flow, we employed the CW model equations first presented by Patil et al. [31]. Shear stress association ${\tau }_{ij}$ and the fundamental governing equations of the Williamson product, which is focused on the Cauchy Stress tensor, are presented as follows:

${\tau }_{ij}=\mu \left(\frac{\partial u}{\partial y}-\frac{\mathrm{\Gamma }}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right),(1)$

when the fluid viscosity is $\mu$ and the time constraint is $\mathrm{\Gamma }=0$. It is easy to see that this is a non-linear model, and the Newtonian form may be deduced because it is a special situation when $\mathrm{\Gamma }=0$. Since there is no time constant in the Newtonian model, the first component of the shear stress gives us a good description of the system. The yield stress is the shear stress above which flow begins for a given fluid with infinite viscosity at a zero shear rate; the following statement illustrates how the Newtonian model becomes closer to the Casson model in this particular scenario:

${\tau }_{ij}=\mu \left(\left(1+\frac{1}{\beta }\right)\frac{\partial u}{\partial y}\right),(2)$

where $\beta$ is a Casson parameter. Last but not least, it is important to determine whether the properties of the liquid are a combination of Williamson and Casson characteristics. Therefore, the CW framework can be used to describe these fluids:

${\tau }_{ij}=\mu \left(\left(1+\frac{1}{\beta }\right)\frac{\partial u}{\partial y}-\frac{\mathrm{\Gamma }}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right).(3)$

It is expected that the magnetic field strength $B_0$ is homogeneous along the y-axis. Furthermore, the magnetic Reynolds number of the flow is believed to be extremely small, making the induced magnetic field inconsequential. We use this model because it accurately describes a large class (perhaps the majority) of non-Newtonian nanofluids throughout a broad shear rate range. The initial flow conditions are imposed by the effects of the magnetic field, heat radiation, and chemical reactions. Here, u and v denote two different components of the nanofluid velocity, T represents the nanofluid temperature, and C is its concentration. The nanofluid density $\rho$ and its heat conductivity $\kappa$ will be treated as uniform. Figure 1 shows the flow’s physical representation in Cartesian coordinates.

FIGURE 1

FIGURE 1. Flow pattern of the problem.

An expression of the governing differential equations for the suggested CW model for stable laminar flow in two dimensions is expressed as follows [41]:

$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0,(4)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=v\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}u}{\partial y^2}+\sqrt{2}v\mathrm{\Gamma }\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma {\beta }_0^{2}u}{\rho }-\frac{v}{k}u+g\beta \left(T-T_{\infty }\right),(5)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k}{\rho c_p}\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}}\right)\frac{{\partial }^{2}T}{\partial y^2}+\tau \{\left.\left(D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}-\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right.\right\}-\frac{\mu }{\rho c_p}\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}u}{\partial y^2}+\frac{\mathrm{\Gamma }}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^3+\frac{Q_0}{\rho c_p}\left(T-T_{\infty }\right),(6)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2-K_r\left(C-C_{\infty }\right),(7)$

considering the particular structural boundary constraints to match the preceding model:

$u=ax+{\lambda }_1\left(\left(1+\frac{1}{\beta }\right)\frac{\partial u}{\partial y}-\frac{\mathrm{\Gamma }}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right),(8)$

$T=T_w,C=C_{w}aty=0,$

$u\to 0,T\to T_{\infty },C\to C_{\infty }asy\to \infty .(9)$

In addition, the first portion of Eq. 8 is a symbol for the phenomenon known as slip velocity. Slip can have significant repercussions on the physical state of a few microscopic fluxes, comparable to literature that occur in a microelectromechanical system. In addition, leakage at the microdevice walls, which are the conduits across which liquid is transported, may have a considerable influence on the amount of temperature and mass transferred by the system. In addition, this might play a part in the consequences of spurts, hysteresis, and shear skin. In addition, boundary-dragging fluids have a variety abounding of applications in technology, including the polishing of arbitrary valves and inner hollows. The following form of similarity variables was chosen to transform the set of governing equations to ODEs. This also made all quantities dimensionless:

$\eta =\sqrt{\frac{a}{y}}y,u=a{f}^{\prime }\left(\eta \right),v=-\sqrt{av}f\left(\eta \right),$

$\theta \left(\eta \right)=\frac{{T-T}_{\theta }}{{T_w-T}_{\theta }},\varphi \left(\eta \right)=\frac{{C-C}_{\infty }}{{C_w-C}_{\infty }}.(10)$

Through the use of the similarity transformation in Eq. 10, we can obtain the reducing ODEs from Eqs 4–9:

$\left(1+\frac{1}{\beta }\right)f^{‴}+W_c{f}^{″}{f}^{‴}+f^2-Mf-K_{p}f+∆\theta =0,(11)$

$\frac{1}{\mathit{Pr}}\left(1+R\right){\theta }^{″}+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{\left({\theta }^{\prime }\right)}^2+f{\theta }^{\prime }+EC\left[\left(1+\frac{1}{\beta }\right)f^2+\frac{W_c}{2}{f}^3\right]+Q\theta =0,(12)$

${\varphi }^{″}+Scf{\varphi }^{\prime }-ScG\varphi +\frac{Nt}{Nb}{\theta }^{″}=0,(13)$

together with the applicable boundary conditions listed as follows:

$f\left(0\right)=0,f^{\prime }\left(0\right)=1+\lambda \left[\left(1+\frac{1}{\beta }\right)f^{″}+\frac{W_c}{2}f{″}^2\right],$

$\theta \left(0\right)=1,\varphi \left(0\right)=1,(14)$

$f\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0,\varphi \left(\eta \right)\to 0asn\to \infty .(15)$

The following measurements are considered the problem governing constraints: the Weissenberg parameter, the slip velocity constraint, the porosity constraint, the magnetic constraint, the Prandtl number, the radiation, mixed convection, Eckert number, thermophoresis, Schmidt number, Brownian movement, energy formation, and chemical interaction. Their respective values are recorded as follows:

$W_c=\frac{\mathrm{\Gamma }x\sqrt{2a^3}}{v},\lambda =\sqrt{\frac{a}{m}},M=\frac{\sigma B_0^2}{a\rho },\mathit{Pr}=\frac{\mu c_p}{k},$

$Ec=\frac{{\left(ax\right)}^2}{c_p\left(T_w-T_{\infty }\right)},$

$R=\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}k},∆=\frac{g{\beta }^{\infty }\left(T_w-T_{\infty }\right)}{a^{2}x},K_p=\frac{v}{ka},$

$Nt=\frac{\tau D_t\left(T_w-T_{\infty }\right)}{T_{\infty }v},$

$Nb=\frac{\tau D_B\left(C_W-C_{\infty }\right)}{\nu },{\mathrm{S}}_c=\frac{\upsilon }{D_B},\mathrm{G}=\frac{K_r}{a}.$

As can be seen, the local parameters based on the length scale $x$ are $W_e,\Delta$, and $E_c$. The fact that these parameters depend on $x$ and that their qualities fluctuate locally during the flow movement means that the equations provided are only applicable to locally similar solutions. Using Eq. 10, it is possible to account for shear stress, energy, and mass transmission at the stretching sheet in this study (10). These results are frequently expressed using the local Sherwood number $shx$, the local Nusselt number $Nux$, and the non-dimensional skin friction coefficient $Cf$. Eq. 10, in this task, produces

$C_f\sqrt{{\mathrm{R}\mathrm{e}}_x}=-\left[\left(1+\frac{1}{\beta }\right)f^{″}\left(0\right)+\frac{We}{2}{f}^{\prime }{\prime }^2\left(0\right)\right],$

$\frac{N{u}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-\left(1+R\right){\theta }^{\prime }\left(0\right),$

$\frac{S{h}_x}{\sqrt{{\mathrm{R}\mathrm{e}}_x}}=-{\varphi }^{\prime }\left(0\right),$

where ${\mathrm{R}\mathrm{e}}_x=\frac{u_{w}x}{v}$.

3 Numerical approach

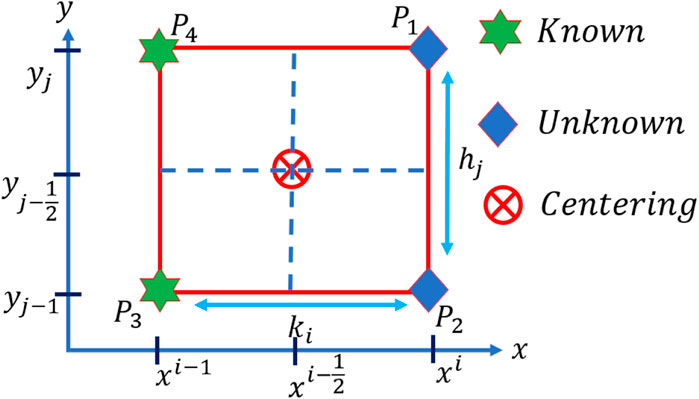
The objective of this segment is to detail the foundational procedures that led to the development of the Keller-Box approach, a finite differencing numerical method, as depicted in Figure 2. Because similarity transformations are used to turn the governing equation of the model into a set of coupled ordinary differential structuring equations, important boundary conditions associated with the velocity and energy are provided in the equations in a dimensionless form. Finding solutions to the resulting system of differential equations using analytical methods is an exceedingly time-consuming and difficult process due to the complexity of the resulting system.

FIGURE 2

FIGURE 2. Schematic diagram of FDM discretization.

Therefore, numerical methods are often considered the best approach to finding problem-specific simulations. We opted for the computational approach due to the many advantages offered by numerical approaches, such as the elimination of unnecessary computational and time-related costs. When considering the available numerical approaches, the Keller-Box approach [42–44] is the best fit for our modeled differential system:

$f^{\prime }=u,(16)$

$u^{\prime }=w,(17)$

${\theta }^{\prime }=p,(18)$

${\varphi }^{\prime }=q,(19)$

$\left(1+\frac{1}{\beta }\right)w^{\prime }+W_{c}w{w}^{\prime }+fw-u^2-\left(M+K\right)u+\Delta \theta =0,(20)$

$\frac{1}{P_r}\left(1+R\right)p^{\prime }+Nbpq+Nt{p}^2+E_c\left[\left(1+\frac{1}{\beta }\right)w^2+\frac{W_c}{2}{w}^3\right]+Q\theta =0,(21)$

$q^{\prime }+S_{c}fq-S_{c}G\varphi +\frac{Nt}{Nb}{p}^{\prime }=0,(22)$

$\frac{f_j-f_{j-1}}{h}=\frac{u_j-u_{j-1}}{2},$

$\rho f_j-\rho f_{j-1}-\frac{h}{2}\left(\rho u_j+\rho u_{j-1}\right)=f_{j-1}-f_j+\frac{h}{2}\left(u_j-u_{j-1}\right)=r_1,$

$\rho u_j-\rho u_{j-1}-\frac{h}{2}\left(\rho w_j+\rho w_{j-1}\right)=u_{j-1}-u_j+\frac{h}{2}\left(w_j+w_{j-1}\right)=r_5,$

$\rho {\theta }_j-\rho {\theta }_{j-1}-\frac{h}{2}\left(\rho p_j+\rho p_{j-1}\right)={\theta }_{j-1}-{\theta }_j+\frac{h}{2}\left(p_j+p_{j-1}\right)=r_6,$

$\rho {\varphi }_j-\rho {\varphi }_{j-1}-\frac{h}{2}\left(\rho q_j+\rho q_{j-1}\right)={\varphi }_{j-1}-{\varphi }_j+\frac{h}{2}\left(q_j+q_{j-1}\right)=r_7,$

${\psi }_1{\rho f}_j+{\psi }_2\rho f_{j-1}+{\psi }_3\rho u_j+{\psi }_4\rho u_{j-1}+{\psi }_5\rho w_j+{\psi }_6\rho w_{j-1}+{\psi }_7\rho {\theta }_j+{\psi }_8{\rho }_{j-1}{=r}_2,$

${\chi }_1{\rho f}_j+{\chi }_2\rho f_{j-1}+{\chi }_3\rho w_j+{\chi }_4\rho w_{j-1}+{\chi }_5\rho {\theta }_j+{\chi }_6\rho {\theta }_j+{\chi }_7\rho p_j+{{\chi }_8}_{\rho p_j}+{\chi }_9\rho q_j+{\chi }_{10}\rho q_{j-1}{=r}_3,$

${\eta }_1{\rho f}_j+{\eta }_2\rho f_{j-1}+{\eta }_3\rho p_j+{\eta }_4\rho p_{j-1}+{\eta }_5\rho {\varphi }_j+{\eta }_6\rho {\varphi }_j+{\eta }_7\rho q_j+{{\eta }_8}_{\rho q_{j-1}}=r_4,$

$\left\{\begin{array}{l}{\psi }_1={\psi }_2=\frac{h}{4}\left(w_j+w_{j-1}\right)\\ {\psi }_3={\psi }_4=-\frac{h}{4}\left(f_j+f_{j-1}\right)-\left(\frac{m+k}{2}\right)h\\ {\psi }_5=\left(1+\frac{1}{\beta }\right)+\frac{w_c}{2}\left(w_j-w_{j-1}\right)+\frac{w_c}{2}\left(w_j+w_{j-1}\right)+\frac{h}{4}\left(f_j+f_{j-1}\right)\\ {\psi }_6=-\left(1+\frac{1}{\beta }\right)+\frac{w_c}{2}\left(w_j-w_{j-1}\right)+\frac{w_c}{2}\left(w_j+w_{j-1}\right)+\frac{h}{4}\left(f_j+f_{j-1}\right)\\ {\psi }_7={\psi }_8=\frac{\Delta h}{2}\end{array}\right\},(23)$

$\left\{\begin{array}{l}{\chi }_1={\chi }_2=\frac{h}{4}\left(p_j+p_{j-1}\right)\\ {\chi }_3={\chi }_4=E_c\left(1+\frac{1}{\beta }\right)\frac{\hslash }{2}\left(w_j+w_{j-1}\right)+E_c\frac{\left(1+\frac{1}{\beta }\right)}{2}h{\left(w_j+w_{j-1}\right)}^2\\ {\chi }_5={\chi }_6=\frac{Qh}{2}\\ {\chi }_7=\frac{1}{\mathit{pr}}\left(1+R\right)+\frac{Nbh}{4}\left(q_j+q_{j-1}\right)+\frac{h}{2}\left(f_j+f_{j-1}\right)\\ {\chi }_8=-\frac{1}{\mathit{pr}}\left(1+R\right)+\frac{Nbh}{4}\left(q_j+q_{j-1}\right)+\frac{h}{2}\left(f_j+f_{j-1}\right)\\ {\chi }_9={\chi }_{10}=\frac{Nbh}{4}\left(p_j+p_{j-1}\right)\end{array}\right\},(24)$

$\left\{\begin{array}{l}{\eta }_1={\eta }_2=S_{c}h\left(q_j+q_{j-1}\right)\\ {\eta }_5={\eta }_6=\frac{S_{c}hG}{g}\\ {\eta }_3=\frac{Nt}{gNb},{\eta }_4=-\frac{N_t}{N_b}\\ {\eta }_7=1+\frac{S_{c}h}{4}\left(f_j+f_{j-1}\right)\\ {\eta }_8=-1+\frac{S_{c}h}{4}\left(f_j+f_{j-1}\right)\\ {\chi }_9={\chi }_{10}=\frac{Nbh}{4}\left(p+p_{j-1}\right)\end{array}\right\},(25)$

$r_2=\left(1+\frac{1}{\beta }\right)\left(w_{j-1}-w_j\right)-\frac{W_c}{2}\left(w_j+w_{j-1}\right)\left(w_j-w_{j-1}\right)-\frac{h}{4}\left(f_j+f_{j-1}\right)\left(w_j+w_{j-1}\right)$

$+\frac{h}{4}{\left(u_j+u_{j-1}\right)}^2+\left(\frac{M+k}{2}\right)h\left(u_j+u_{j-1}\right)+\frac{\Delta h}{2}\left({\theta }_j+{\theta }_{j-1}\right),$

$r_3=\frac{1}{P_r}\left(1+R\right)p_{j-1}-\frac{1}{P_r}\left(1+R\right)p_j-\frac{Nbh}{4}\left(p_j+p_{j-1}\right)\left(q_j+q_{j-1}\right)-\frac{Nth}{4}\left(p_j+p_{j-1}\right)-\frac{h}{4}\left(f_j+f_{j-1}\right)\left(p_j+p_{j-1}\right)$

$+E_c\left[\left(1+\frac{1}{\beta }\right)\frac{h}{4}\left(w_j+w_{j-1}\right)\right]+E_c\left(1+\frac{1}{\beta }\right)\frac{h}{8}{\left(w_j+w_{j-1}\right)}^3,$

${\chi }_4=q_{j-1}-q_j-\frac{S_{c}h}{4}\left(f_j+f_{j-1}\right)\left(q_j+q_{j-1}\right)-S_c\frac{Gh}{2}\left({\varphi }_j+{\varphi }_{j-1}\right)-\frac{Nb}{Nt}\left(p_j+p_{j-1}\right).$

In most cases, the block-tridiagonal structure of the linearized difference equation will be composed of variables or constants. However, in this particular instance, it will be composed of block matrices. The following is a definition of each member of the matrix that pertains to our scenario:

$\left[\begin{array}{cccccc}\left[{\mathbf{A}}_{\mathbf{1}}\right]& \left[{\mathbf{C}}_{\mathbf{2}}\right]& \bullet & \bullet & \bullet & \bullet \\ \left[{\mathbf{B}}_{\mathbf{2}}\right]& \left[{\mathbf{A}}_{\mathbf{2}}\right]& \left[{\mathbf{C}}_{\mathbf{2}}\right]& \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \left[{\mathbf{B}}_{{\mathbf{j}}_{-\mathbf{1}}}\right]& \left[{\mathbf{A}}_{{\mathbf{j}}_{-\mathbf{1}}}\right]& \left[{\mathbf{C}}_{\mathbf{j}-\mathbf{1}}\right]\\ \bullet & \bullet & \bullet & \bullet & \left.{\left[\mathbf{B}\right.}_{\mathbf{j}}\right]& \left[{\mathbf{A}}_{\mathbf{j}}\right]\end{array}\right]\left[\begin{array}{c}\left[{\delta }_1\right]\\ \left[{\delta }_2\right]\\ \bullet \\ \bullet \\ \bullet \\ \left[{\delta }_{j-1}\right]\\ \left[{\delta }_j\right]\end{array}\right]=\left[\begin{array}{c}\left[r_1\right]\\ \left[r_2\right]\\ \bullet \\ \bullet \\ \bullet \\ \left[r_{j-1}\right]\\ \left[r_j\right]\end{array}\right],$

that is,

$\left[A\right]\left[\delta \right]=\left[r\right],$

where

$A_1=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& r_4& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& -1& -\frac{h}{2}& 0& 0& 0& 0\\ 0& 0& 0& -1& -\frac{h}{2}& 0& 0\\ 0& 0& 0& 0& 0& -1& -\frac{h}{2}\end{array}\right],$

$C_j=\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 1& -\frac{h}{2}& 0& 0& 0& 0\\ 0& 0& 0& 1& -\frac{h}{2}& 0& 0\\ 0& 0& 0& 0& 0& A& -\frac{h}{2}\end{array}\right],$

$B_2=\left[\begin{array}{ccccccc}-1& -\frac{h}{2}& 0& 0& 0& 0& 0\\ {\psi }_2& {\psi }_4& {\psi }_6& {\psi }_8& 0& 0& 0\\ {\chi }_2& 0& {\chi }_4& {\chi }_6& {\chi }_8& 0& {\chi }_1\\ {\eta }_2& 0& 0& 0& {\eta }_4& {\eta }_6& {\eta }_8\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right],$

$A_j=\left[\begin{array}{ccccccc}1& -\frac{h}{2}& 0& 0& 0& 0& 0\\ {\psi }_1& {\psi }_3& {\psi }_5& {\psi }_7& 0& 0& 0\\ {\chi }_1& 0& {\chi }_3& {\chi }_5& {\chi }_7& 0& {\chi }_9\\ {\eta }_1& 0& 0& 0& {\eta }_3& {\eta }_5& {\eta }_7\\ 0& -1& -\frac{h}{2}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -1& -\frac{h}{2}\end{array}\right],$

$A_J=\left[\begin{array}{ccccccc}1& -\frac{h}{2}& 0& 0& 0& 0& 0\\ {\psi }_1& {\psi }_3& {\psi }_5& {\psi }_7& 0& 0& 0\\ {\chi }_1& 0& {\chi }_3& {\chi }_5& {\chi }_7& 0& {\chi }_9\\ {\eta }_1& 0& 0& 0& {\eta }_3& {\eta }_5& {\eta }_7\\ 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right].$

These computations are performed again and over again until a certain convergence criterion is reached, at which point the process is terminated when $\left|\delta v_0^{\left(i\right)}\right|\le {\epsilon }_1,$ where ${\epsilon }_1$ is a small prescribed value.

4 Results and discussion

In this study, we introduced a model for the flow of non-Newtonian CW nanofluids, which is regulated by the momentum $\left(f^{\prime }\right)$, temperature $\left(\theta \right)$, and concentration $\left(\varphi \right)$ equations and affected by energy radiation, magnetic field, slip velocity, viscous dissipation, energy creation, and chemical reaction. In order to resolve the highly non-linear ODE in Eqs 11–13 and boundary conditions in Eqs 14 and 15, we adopt the Keller-Box approach. The rest of parameters for the simulations are defined as $M=\beta =Nb=Wc=0.5,Kp=1.0,G=\lambda =∆=0.2,Ec=Q=0.1,R=0.2$, and $\mathit{Pr}=2.0$, respectively (Table 1) (Figure 3).

TABLE 1

TABLE 1. Comparisons of Mahmoud’s result with those of the current work for $-f^{″}\left(0\right)$.

FIGURE 3

FIGURE 3. Variation of M on (A) $f^{\prime }\left(\eta \right)$, (B) $\theta \left(\eta \right)$, and (C) $\varphi \left(\eta \right)$.

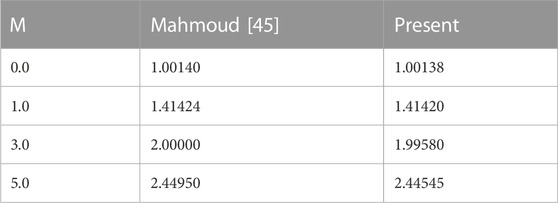
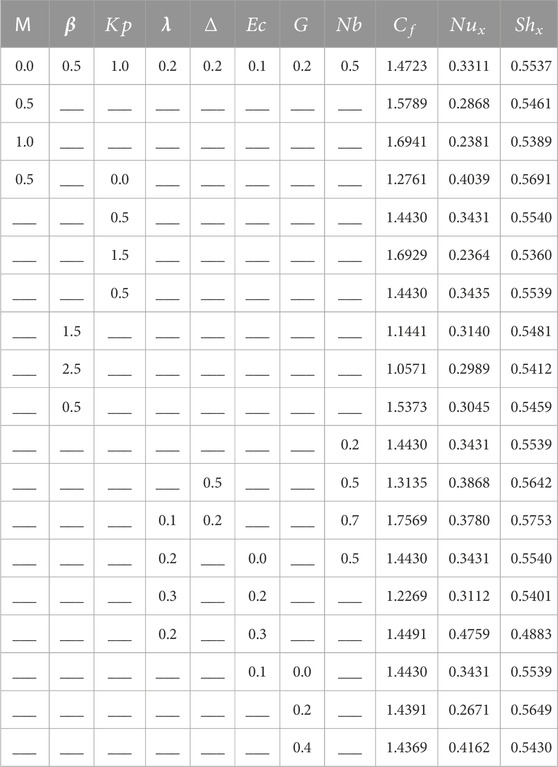
The data presented in Table 1 have been validated against prior research. The conclusions that can be drawn from these findings are very congruent with Mahmoud’s conclusions [45]. Whenever the physicochemical parameters were altered, the obeying diagrams were constructed to demonstrate the findings of $f^{\prime }$, $\theta$, and $\varphi$. Figure 3 depicts the consequences M has on $f^{\prime }$, $\theta$, and $\varphi$. When M is enhanced in this diagram, $\theta$ and nanoparticle $\varphi$ rise; however, the velocity distributions tend to get larger, which contradicts what you would expect to see. Due to the presence of M, the motion of the nanofluid will be affected by a force that acts as propagation. It will be a physical event. This force can slow down the nanofluid that makes it so useful. This causes the nanofluid to soak up some of the heat emitted by the same force that created it.

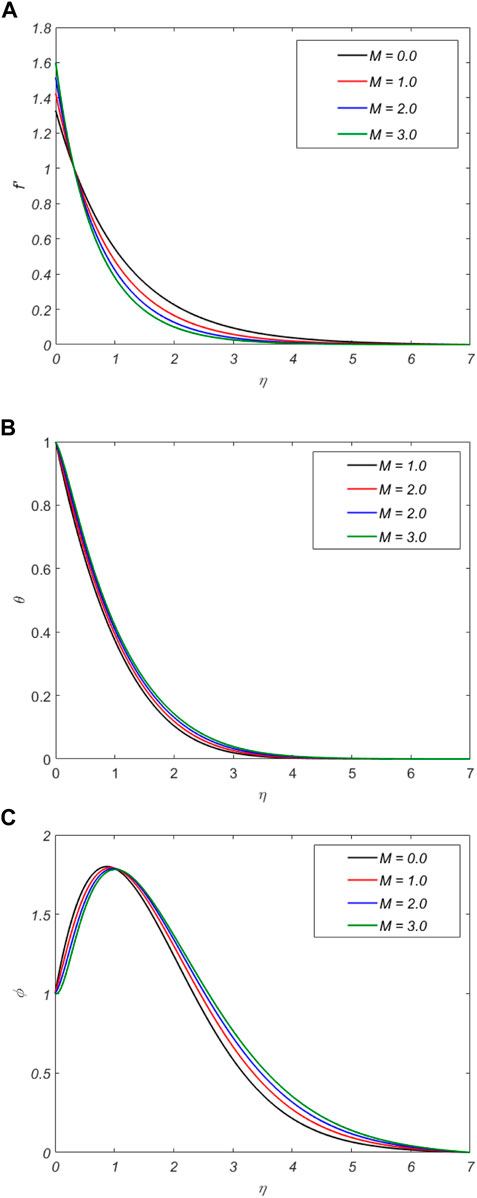
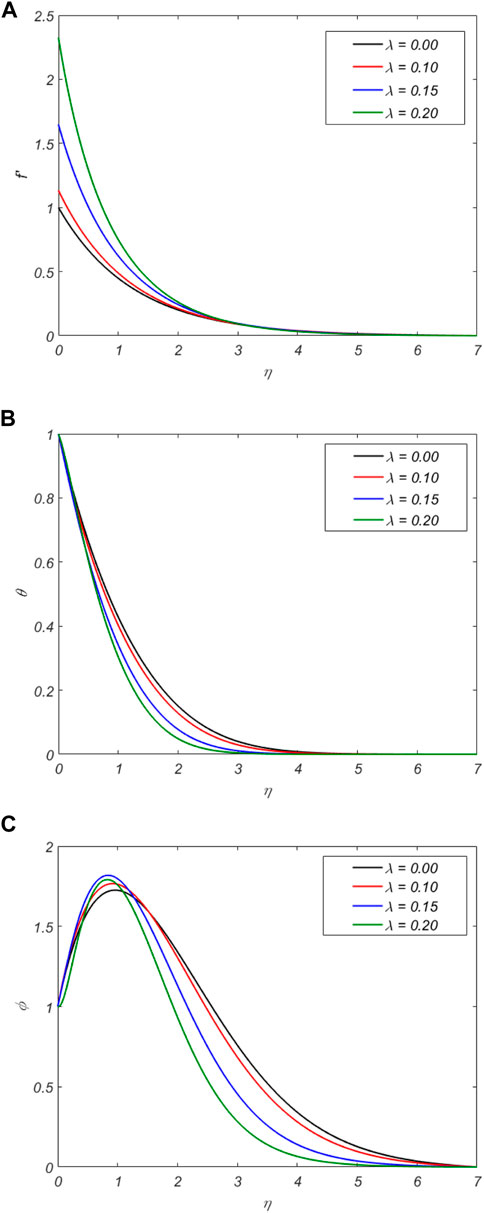
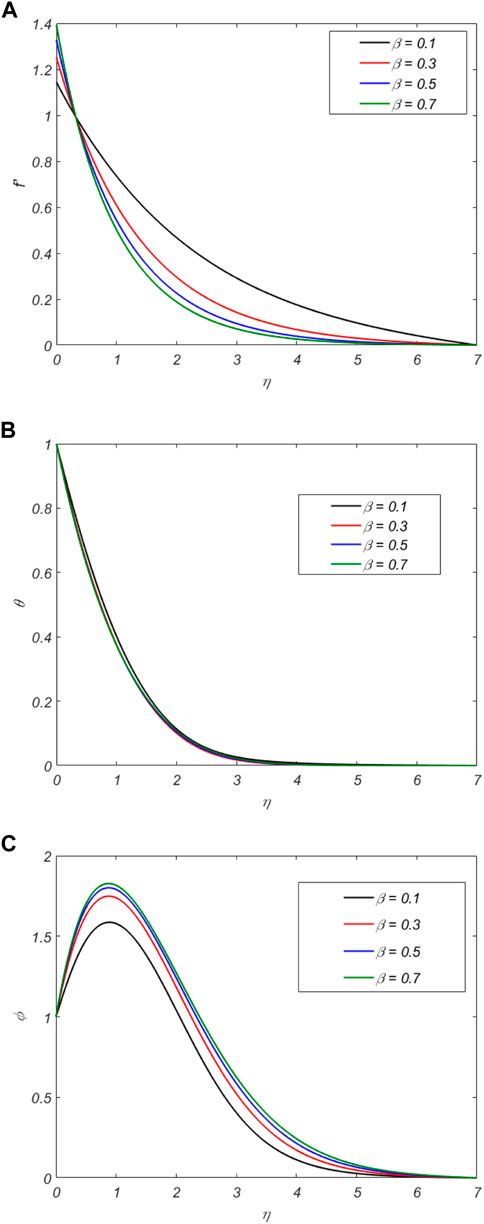
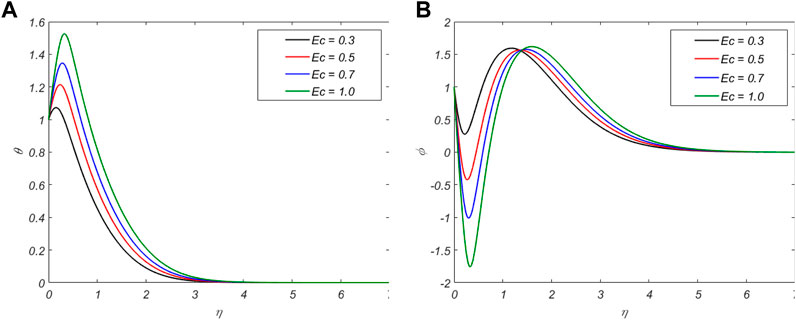
Figure 4 shows the significant properties of the slip velocity factor $\lambda$ and its influence on $f^{\prime }$, θ, and ϕ of the non-Newtonian nanofluid. When the slip velocity parameter is given a larger value, it is possible to anticipate a significant reduction in the nanofluid velocity, which will reduce the width of the boundary coat. Consequently, occurrences of phenomena related to slip velocity being present result in a significant improvement to $\theta$ and $\varphi$.

FIGURE 4

FIGURE 4. Variation of $\lambda$ on (A) $f^{\prime }\left(\eta \right)$, (B) $\theta \left(\eta \right)$, and (C) $\varphi \left(\eta \right)$.

Figure 5 depicts the effects of $\beta$ on the profiles of $f^{\prime }$, $\theta$, and $\varphi$. As a direct consequence, the nanofluid flow slows down as it moves away from the sheet, making the boundary layer finer in proportion to the growing value of $\beta$. Conversely, when $\beta$ is large, $\varphi$ and $\theta$ are greater than they are when the Casson value is small.

FIGURE 5

FIGURE 5. Variation of $\beta$ on (A) $f^{\prime }\left(\eta \right)$, (B) $\theta \left(\eta \right)$, and (C) $\varphi \left(\eta \right)$.

Figure 6 illustrates the discrepancy between $\theta$ and $\varphi$ through the use of numerous quantities of the Brownian motion constraint $Nb$. Importantly, the appearance of $Nb\ne 0$ for nanoparticles significantly drops the rate of propagation in ϕ, although θ exhibits the reverse pattern. This is a factor that needs to be considered. From a purely physical perspective, an increase in the Brownian motion component may cause substantial movement of nanofluid molecules. As a result, the quantity of heat generated in the boundary layer region increases, as does the kinetic energy.

FIGURE 6

FIGURE 6. Variation of $Nb$ on (A) $\theta \left(\eta \right)$ and (B) $\varphi \left(\eta \right)$.

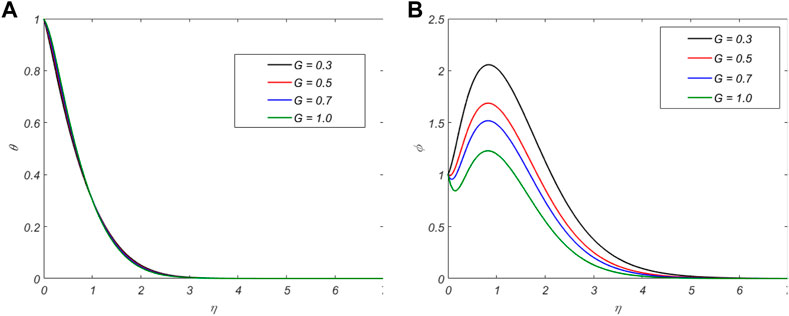
The impact of G on $\theta$ of the nanofluid and $\varphi$ of its nanoparticles is shown in Figure 7. When $\varphi$ is lower, the value of G increases. Additionally, there is a minor expansion in $\theta$ and the thickness of the thermal boundary layer. As might be observed in the diagram that follows, a sizeable G implies a high chemical transformation rate between nanofluid molecules. This, in turn, causes a considerable latency in the accumulation of nanofluid concentration. The effect of the Eckert number Ec on the values of $\theta$ and $\varphi$ is illustrated in Figure 8. As anticipated, a considerable expansion of the thermal layer occurs as Ec moves forward. Due to viscous dissipation mechanisms, certain amounts of nanofluid kinetic energy are transformed into heat, which supports an enhancement in $\theta$ of the fluid at all locations within the appropriate boundary layer. In addition, $\varphi$ displays the same minor tendency when the Eckert number Ec rises (Table 2).

FIGURE 7

FIGURE 7. Variation of $G$ on (A) $\theta \left(\eta \right)$ and (B) $\varphi \left(\eta \right)$.

FIGURE 8

FIGURE 8. Variation of $Ec$ on (A) $\theta \left(\eta \right)$ and (B) $\varphi \left(\eta \right)$.

TABLE 2

TABLE 2. Variation of numerous constraints on $C_f$, ${Nu}_x$, and ${Sh}_x$.

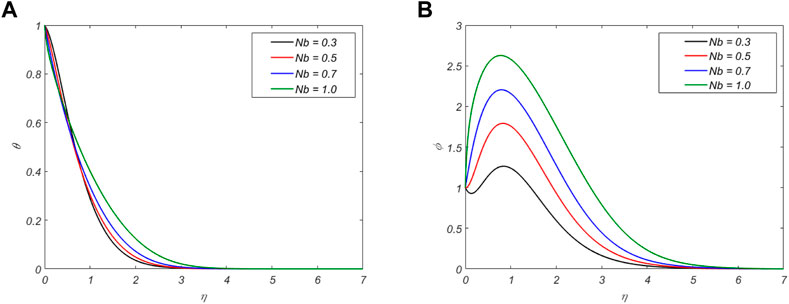
Statistical representations are utilized to display the results of the numerical simulations. Table 2 illustrates how the various physical properties of nanofluids affect not only the rates of temperature and mass transport, but also the $C_f$ coefficient. Notably, $C_f$ goes up when the magnetic and porous parameters increase. Meanwhile, ${Nu}_x$ and ${Sh}_x$ increase in the other way. This is something that should be kept in mind. Furthermore, $\beta$ and the slip velocity component produce a decline in $C_f$, a decrease in ${Nu}_x$, and a decrease in ${Sh}_x$. When the mixed convection parameter increases, ${Nu}_x$ speeds up and simultaneously the rate of mass transmission increases. Similarly, the rising values of Ec, $Nb$, and G result in a drop in ${Nu}_x$. Conversely, ${Sh}_x$ tends to exhibit the reverse trend.

5 Conclusion

A novel concept of the cumulative effects of slip velocity and the viscous dissipation feature is used to describe the flow of a non-Newtonian CW nanofluid caused by a stretching sheet. This concept is used to represent the flow. In addition, the chemical reactions between magnetic fields, thermal radiation, nanoparticles, and heat creation are considered. Moreover, the physical model is submerged in a material that is porous and saturated. The numerical investigation is presented in a graphically displayed form using the finite difference method, and it is discussed in some detail. The results are presented in detail as follows:

❖ $Ec$, G, and the Brownian parameter are all factors that contribute to an increase in ${Sh}_x$, whereas ${Nu}_x$ is impacted in a reverse manner.

❖ When M and the permeable media parameter increase, it increases the skin friction coefficient and decreases the flow rate of the nanofluid.

❖ Increasing $Ec$, mixed convection parameter, chemical reaction rate, or the Brownian parameter worsens the concentration distribution, whereas increasing $\beta$ or the slip velocity parameter improves it.

❖ When the slip velocity is increased, there is a corresponding drop in the mass flux rate, the rate of heat transmission, and the wall shear stress.

❖ Temperature rises when there is an improvement in the porous parameter, $\beta$, slip velocity, and M.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AM computed the results; SI wrote the original draft; HS and AM wrote the review draft. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Thiruvengadam M, Rajakumar G, Chung IM. Nanotechnology: Current uses and future applications in the food industry. 3 Biotech (2018) 8(1):74–13. doi:10.1007/s13205-018-1104-7

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Roco MC, Mirkin CA, Hersam MC. Nanotechnology research directions for societal needs in 2020: Summary of international study. J nanoparticle Res (2011) 13(3):897–919. doi:10.1007/s11051-011-0275-5

CrossRef Full Text | Google Scholar

3. Nikalje AP. Nanotechnology and its applications in medicine. Med Chem (2015) 5(2):081–9. doi:10.4172/2161-0444.1000247

CrossRef Full Text | Google Scholar

4. Mahapatra T, Gupta AS. Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transfer (2002) 38(6):517–21. doi:10.1007/s002310100215

CrossRef Full Text | Google Scholar

5. Ahmad K, Wahid Z, Hanouf Z. Heat transfer analysis for Casson fluid flow over stretching sheet with Newtonian heating and viscous dissipation. J Phys Conf Ser (2019) 1127:012028. IOP Publishing. doi:10.1088/1742-6596/1127/1/012028

CrossRef Full Text | Google Scholar

6. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat mass transfer (2010) 53(11-12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Abolbashari M. H., Freidoonimehr N., Nazari F., Rashidi M. M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Advanced Powder Technology (2015) 26(2):542–52. doi:10.1016/j.apt.2015.01.003

CrossRef Full Text | Google Scholar

Flint T. F., Smith M. C., Shanthraj P. Magneto-hydrodynamics of multi-phase flows in heterogeneous systems with large property gradients. Scientific Reports (2021) 11(1):18998–15. doi:10.1038/s41598-021-97177-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadeem S., Haq R. U., Akbar N. S. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Transactions on Nanotechnology (2013) 13(1):109–15. doi:10.1109/tnano.2013.2293735

CrossRef Full Text | Google Scholar

10. Mustafa M, Khan JA. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv (2015) 5(7):077148. doi:10.1063/1.4927449

CrossRef Full Text | Google Scholar

11. Hussain SM, Jamshed W, Kumar V, Kumar V, Nisar KS, Eid MR, et al. Computational analysis of thermal energy distribution of electromagnetic Casson nanofluid across stretched sheet: Shape factor effectiveness of solid-particles. Energ Rep (2021) 7:7460–77. doi:10.1016/j.egyr.2021.10.083

CrossRef Full Text | Google Scholar

12. Hayat T, Bilal Ashraf M, Shehzad SA, Alsaedi A. Mixed convection flow of Casson nanofluid over a stretching sheet with convectively heated chemical reaction and heat source/sink. J Appl Fluid Mech (2015) 8(4):803–13. doi:10.18869/acadpub.jafm.67.223.22995

CrossRef Full Text | Google Scholar

13. Afify AA. The influence of slip boundary condition on Casson nanofluid flow over a stretching sheet in the presence of viscous dissipation and chemical reaction. Math Probl Eng (2017) 2017:1–12. doi:10.1155/2017/3804751

CrossRef Full Text | Google Scholar

14. Ullah I, Khan I, Shafie S. MHD natural convection flow of Casson nanofluid over nonlinearly stretching sheet through porous medium with chemical reaction and thermal radiation. Nanoscale Res Lett (2016) 11(1):527–15. doi:10.1186/s11671-016-1745-6

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ibrahim SM, Lorenzini G, Kumar PV, Raju CSK. Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transfer (2017) 111:346–55. doi:10.1016/j.ijheatmasstransfer.2017.03.097

CrossRef Full Text | Google Scholar

16. Dero S, Mohd Rohni A, Saaban A. Effects of the viscous dissipation and chemical reaction on Casson nanofluid flow over the permeable stretching/shrinking sheet. Heat Transfer (2020) 49(4):1736–55. doi:10.1002/htj.21688

CrossRef Full Text | Google Scholar

17. Goud BS, Reddy YD, Rao VS. Thermal radiation and Joule heating effects on a magnetohydrodynamic Casson nanofluid flow in the presence of chemical reaction through a non-linear inclined porous stretching sheet. J Naval Architecture Mar Eng (2020) 17(2):143–64. doi:10.3329/jname.v17i2.49978

CrossRef Full Text | Google Scholar

18. Khan M, Malik MY, Salahuddin T, Hussian A. Heat and mass transfer of Williamson nanofluid flow yield by an inclined Lorentz force over a nonlinear stretching sheet. Results Phys (2018) 8:862–8. doi:10.1016/j.rinp.2018.01.005

CrossRef Full Text | Google Scholar

19. Reddy S, Naikoti K, Rashidi MM. MHD flow and heat transfer characteristics of Williamson nanofluid over a stretching sheet with variable thickness and variable thermal conductivity. Trans A. Razmadze Math Inst (2017) 171(2):195–211. doi:10.1016/j.trmi.2017.02.004

CrossRef Full Text | Google Scholar

20. Kumaran G, Sandeep N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J Mol Liquids (2017) 233:262–9. doi:10.1016/j.molliq.2017.03.031

CrossRef Full Text | Google Scholar

21. Parmar A. Unsteady convective boundary layer flow for MHD Williamson fluid over an inclined porous stretching sheet with non-linear radiation and heat source. Int J Appl Comput Math (2017) 3(1):859–81. doi:10.1007/s40819-017-0387-4

CrossRef Full Text | Google Scholar

22. Shah Z, Bonyah E, Islam S, Khan W, Ishaq M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon (2018) 4(10):e00825. doi:10.1016/j.heliyon.2018.e00825

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lund LA, Omar Z, Khan I. Analysis of dual solution for MHD flow of Williamson fluid with slippage. Heliyon (2019) 5(3):e01345. doi:10.1016/j.heliyon.2019.e01345

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mahanthesh B, Mackolil J, Shehzad SA. Statistical analysis of stagnation-point heat flow in Williamson fluid with viscous dissipation and exponential heat source effects. Heat Transfer (2020) 49(8):4580–91. doi:10.1002/htj.21842

CrossRef Full Text | Google Scholar

25. Shamshuddin MD, Mabood F, Salawu SO. Flow of three-dimensional radiative Williamson fluid over an inclined stretching sheet with Hall current and nth-order chemical reaction. Heat Transfer (2021) 50(6):5400–17. doi:10.1002/htj.22130

CrossRef Full Text | Google Scholar

26. Ullah I. MHD radiative flow of Williamson nanofluid along stretching sheet in a porous medium with convective boundary conditions. Proc Inst Mech Eng E: J Process Mech Eng (2022) 236(3):1144–52. doi:10.1177/09544089211058093

CrossRef Full Text | Google Scholar

27. Saravana R, Hemadri Reddy R, Narasimha Murthy KV, Makinde OD. Thermal radiation and diffusion effects in MHD Williamson and Casson fluid flows past a slendering stretching surface. Heat Transfer (2022) 51(4):3187–200. doi:10.1002/htj.22443

CrossRef Full Text | Google Scholar

28. Sivanandam S, Eswaramoorthi S. Entropy optimization of MHD Casson-Williamson fluid flow over a convectively heated stretchy sheet with Cattaneo-Christov dual flux. Scientia Iranica (2022) 0:0. doi:10.24200/sci.2022.58291.5654

CrossRef Full Text | Google Scholar

29. Humane PP, Patil VS, Patil AB. Chemical reaction and thermal radiation effects on magnetohydrodynamics flow of Casson–Williamson nanofluid over a porous stretching surface. Proc Inst Mech Eng Part E: J Process Mech Eng (2021) 235(6):2008–18. doi:10.1177/09544089211025376

CrossRef Full Text | Google Scholar

30. Yousef NS, Megahed AM, Ghoneim NI, Elsafi M, Fares E. Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alexandria Eng J (2022) 61(12):10161–70. doi:10.1016/j.aej.2022.03.032

CrossRef Full Text | Google Scholar

31. Patil VS, Humane PP, Patil AB. MHD Williamson nanofluid flow past a permeable stretching sheet with thermal radiation and chemical reaction. Int J Model Simulation (2022) 1–15. doi:10.1080/02286203.2022.2062166

CrossRef Full Text | Google Scholar

32. Reddy MV, Lakshminarayana P. MHD radiative flow of Williamson nanofluid with Cattaneo-Christov model over a stretching sheet through a porous medium in the presence of chemical reaction and suction/injection. J Porous Media (2022) 25:1–15. doi:10.1615/jpormedia.2022041423

CrossRef Full Text | Google Scholar

33. Falodun BO, Ige EO. Linear and quadratic multiple regressions analysis on magneto-thermal and chemical reactions on the Casson-Williamson nanofluids boundary layer flow under Soret-Dufour mechanism. Arab J Basic Appl Sci (2022) 29(1):269–86. doi:10.1080/25765299.2022.2115688

CrossRef Full Text | Google Scholar

34. Akram J, Akbar NS, Alansari M, Tripathi D. Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Int Commun Heat Mass Transfer (2022) 136:106208. doi:10.1016/j.icheatmasstransfer.2022.106208

CrossRef Full Text | Google Scholar

35. Akram J, Akbar NS, Tripathi D. A theoretical investigation on the heat transfer ability of water-based hybrid (Ag–Au) nanofluids and Ag nanofluids flow driven by electroosmotic pumping through a microchannel. Arabian J Sci Eng (2021) 46(3):2911–27. doi:10.1007/s13369-020-05265-0

CrossRef Full Text | Google Scholar

36. Khan U, Zaib A, Abu Bakar S, Ishak A. Stagnation-point flow of a hybrid nanoliquid over a non-isothermal stretching/shrinking sheet with characteristics of inertial and microstructure. Case Stud Therm Eng (2021) 26(5):101150. doi:10.1016/j.csite.2021.101150

CrossRef Full Text | Google Scholar

37. Khan U, Zaib A, Ishak A. Magnetic field effect on sisko fluid flow containing gold nanoparticles through a porous curved surface in the presence of radiation and partial slip. Mathematics (2021) 9(9):921. doi:10.3390/math9090921

CrossRef Full Text | Google Scholar

38. Khan U, Zaib A, Ishak A, Waini I, Pop I, Elattar S, et al. Stagnation point flow of a water-based graphene-oxide over a stretching/shrinking sheet under an induced magnetic field with homogeneous-heterogeneous chemical reaction. J Magnetism Magn Mater (2023) 565(2022):170287. doi:10.1016/j.jmmm.2022.170287

CrossRef Full Text | Google Scholar

39. Maraj EN, Akbar NS, Iqbal Z, Azhar E. Framing the MHD mixed convective performance of CNTs in rotating vertical channel inspired by thermal deposition: Closed form solutions. J Mol Liquids (2017) 233:334–43. doi:10.1016/j.molliq.2017.03.041

CrossRef Full Text | Google Scholar

40. Sher Akbar N, Maraj EN, Noor NFM, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35(5):102124. doi:10.1016/j.csite.2022.102124

CrossRef Full Text | Google Scholar

41. HumanePatilPatil PPVSAB. Chemical reaction and thermal radiation effects on magnetohydrodynamics flow of Casson-Williamson nanofluid over a porous stretching surface. J Process Mech Eng (2021) 235:2008–18.

CrossRef Full Text | Google Scholar

42. BilalMajeedMahmoodKhanSeikh SAHRIAH, Sherif E-SM, Khan I, Sherif ESM. Heat and mass transfer in hydromagnetic second-grade fluid past a porous inclined cylinder under the effects of thermal dissipation, diffusion and radiative heat flux. Energies (2020) 13:278. doi:10.3390/en13010278

CrossRef Full Text | Google Scholar

43. MajeedBilalMahmood AHSR, Malik MY. Heat transfer analysis of viscous fluid flow between two coaxially rotated disks embedded in permeable media by capitalizing non-Fourier heat flux model. Physica A: Stat Mech its Appl (2020). doi:10.1016/j.physa.2019.123182

CrossRef Full Text | Google Scholar

44. BilalTassaddiqMajeedNisarAli SAAHKSF, Malik MY, Nisar KS, Malik MY. Computational and physical examination about the aspects of fluid flow between two coaxially rotated disks by capitalizing non-fourier heat flux theory: Finite difference approach. Front Phys (2020) 7. doi:10.3389/fphy.2019.00209

CrossRef Full Text | Google Scholar

45. Mahmoud MAA. Thermal radiation effects on MHD flow of a micropolar fluid over a stretching surface with variable thermal conductivity. Phys A (2007) 375:401–10. doi:10.1016/j.physa.2006.09.010

CrossRef Full Text | Google Scholar

Nomenclature

$T_W$ surface temperature ($K$)

$B_0$ strength of the magnetic field ($T$)

$T_{\infty }$ ambient temperature ($K$)

($u,v$) velocity components (m/s)

$C$ nanoparticle concentration ($mol{L}^{-1}$)

$C_f$ skin friction coefficient

$W_e$ local Weissenberg numbers

$C_w$ surface nanoparticle concentration ($mol{L}^{-1}$)

$D_B$ Brownian diffusion coefficient ($m^2{s}^{-1}$)

$\rho$ density of the fluid ($kg{m}^{-3}$)

$D_T$ thermophoresis diffusion coefficient ($m^2{s}^{-1}$)

$Ec$ Eckert number

$\mu$ coefficient of viscosity ($kg{m}^{-1}{s}^{-1}$)

$\nu$ kinematic viscosity ($m^2{s}^{-1}$)

$g$ gravitational acceleration ($m{s}^{-2}$)

$\varphi$ dimensionless concentration

${\lambda }_1$ slip velocity factor ($m$)

$\lambda$ slip velocity parameter

$\sigma$ electrical conductivity ($s{m}^{-1}$)

$M$ magnetic parameter

${\sigma }^{*}$ Stefan–Boltzmann constant ($W{m}^{-1}{K}^{-4}$)

$Nb$ Brownian motion parameter

$\eta$ similarity variable

$\beta$ Casson parameter

$Nt$ thermophoresis parameter

$N{u}_x$ local Nusselt number

$\mathrm{\Gamma }$ Williamson parameter ($s$)

$Q_0$ heat generation (absorption) coefficient

$Q$heat generation parameter$R$ heat generation parameter $R$radiation parameter

${\mathrm{R}\mathrm{e}}_x$ local Reynolds number