
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 09 February 2023
Sec. Fusion Plasma Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1117543
This article is part of the Research TopicAdvances in Fusion and Low-Temperature Plasma PhysicsView all 3 articles
Non-linear inverse Compton scattering (NICS) is of significance in laser-plasma physics and for application-relevant laser-driven photon sources. Given this interest, we investigated this synchrotron-like photon emission in a promising configuration achieved when an ultra-intense laser pulse interacts with a double-layer target (DLT). Numerical simulations with two-dimensional particle-in-cell codes and analytical estimates are used for this purpose. The properties of NICS are shown to be governed by the processes characterizing laser interaction with the near-critical and solid layers composing the DLT. In particular, electron acceleration, laser focusing in the low-density layer, and pulse reflection on the solid layer determine the radiated power, the emitted spectrum, and the angular properties of emitted photons. Analytical estimates, supported by simulations, show that quantum effects are relevant at laser intensities as small as
In the field of ultra-high intensity (
Photon emission by electrons in the laser–plasma interaction occurs mainly through two processes: bremsstrahlung mediated by high-Z atoms in dense-plasma regions [15, 16], and non-linear inverse Compton scattering (NICS) mediated by strong electromagnetic fields [5]. NICS is expected to be the dominant emission process at very high intensities when a0 = eE0/(meω0c) ≥ 100, where a0 is the normalized vector potential defined with the electron charge e, the electric field peak amplitude E0, the electron mass me, the laser frequency ω0, and the speed of light c. Instead, bremsstrahlung strongly depends on the target atomic number Z, density, and geometry. Thus, it is expected to dominate for thick enough, high-Z-material targets [17].
NICS is the process in which an electron absorbing multiple laser photons emits a high-energy photon [5]. It is the quantum version of synchrotron emission important in the regime in which the ultra-high intensities of the electromagnetic fields and the high energy of the electron make relevant spin effects and the discrete stochastic nature of the emitted radiation [3, 4]. The main parameter to describe this emission is a Lorentz invariant, usually referred to as the electron quantum parameter:
where γ is the emitting electron Lorentz factor,
The first experiments on NICS have been performed by colliding a high-intensity laser pulse with a relativistic electron beam from a conventional linear accelerator [19]. In all-optical setups, NICS has been observed in several cases exploiting laser wakefield acceleration (LWFA) with either two counter-propagating laser beams [1, 2] or only one laser beam reflected from a plasma mirror [20]. However, the low density of the gas target in these schemes and, consequently, the limited number of high-energy electrons (bunch charge around tens of pC) limit the conversion efficiency from laser to photons [21, 22]. Higher efficiencies would be possible at higher densities in solid foils [6] or, even better, in near-critical targets [23], that is, targets approaching the critical density
A highly developed target concept, like a double-layer target (DLT), could allow exploiting NICS more efficiently than the LWFA case and performing more accessible studies for current laser facilities. The DLT we consider here consists of a low-density layer placed on a solid substrate. The low-density layer is near-critical at a laser wavelength of around 1 µm and can be obtained by growing a nanostructured material (foam) on the substrate [33–35]. Laser propagating against electrons is achieved in DLTs thanks to the substrate acting as a plasma mirror like in [20]. At the same time, the near-critical layer enhances the hot-electron generation producing a high-charge (tens of nC) population of energetic electrons during the interaction [36]. The substrate reflects the laser pulse creating an overlap between the reflected field and the hot electrons efficiently accelerated before reflection by the laser itself. The fulfilment of the counter-propagation condition makes the DLT a promising scheme for NICS, as proved by some numerical studies [37–42] and preliminarily investigated by some of us as supervisors of [43]. Consequently, as demonstrated in [44], DLTs could become interesting for electron-positron pair generation at extreme intensities (
The micrometric target case and the time scales of NICS, which follow the typical laser pulse time scales of tens of fs, are accessible to particle-in-cell (PIC) simulations. PIC codes, well-established tools to simulate collisionless plasmas in self-consistent electromagnetic fields, have been recently enriched with several packages to simulate additional physics, including synchrotron-like emission. One of the most feasible and accurate ways to simulate photon emission via NICS inside PIC codes is a Monte Carlo method [48]. This strategy adopts a semi-classical approach using emission rates calculated in the locally constant crossed field approximation (LCFA), which assumes only first-order QED processes and is now standard in many PIC codes [49–51].
An in-depth numerical investigation of NICS during the laser–DLT interaction is preparatory to any experimental campaign. Some numerical studies of NICS in DLTs or similar targets [37, 38, 41, 44] focus on the very high-intensity regime, a0 ∼ 100–300, which is not ordinary in current laser facilities and was only recently achieved experimentally [52]. For these reasons, in this work, we study NICS in DLTs at non-extreme intensities (a0 ∼ 20–60) with a sizeable numerical scan of 2D PIC simulations performed with Smilei [53], a PIC code capable of simulating NICS. Some existing studies focus on non-extreme intensities similar to ours but with different objectives or target properties [39, 40, 42]. We want to contribute novel aspects with respect to these investigations, specifying that, on the comparable parts, our findings are compatible with the results of these works. We focus first on the physical aspects of interaction and, in particular, of emission. Second, we reconstruct some photon emission properties analytically to test the numerical tool and evaluate the impact of quantum effects in this regime. Then, we compare NICS and bremsstrahlung in some selected cases to estimate the possible competition between the two processes in an experimental framework. Finally, we analyze the emission properties considering all the laser intensities and target parameters (foam density and length) studied in the simulation scan.
We have investigated NICS in DLTs with the PIC code Smilei. This code embarks a Monte Carlo module for NICS based on the approach presented in [50]. This approach relies on the emission rates obtained within the LCFA (see discussion in [3]) and allows treating high-energy photons as macro-photons. When emitted, these macro-photons are created with a momentum pointing in the direction of the emitting electron, an approximation valid in the relativistic limit [54].
We have performed 2D simulations of a laser pulse interacting with a DLT. The simulation resolution is 62.5 points per µm in a box of 40.96 µm in y and variable in x from 34 to 74 µm according to the target length. The simulation duration also changes according to the target length from 138 fs to 272 fs. The laser pulse peak enters the simulation box from the x = 0 boundary nearly 20 fs after the beginning of the simulation. The laser pulse has wavelength λ = 2πc/ω0 = 0.8 µm, a sin2 temporal profile in intensity with FWHM = 20 fs and a Gaussian spatial profile with a waist (radius at which the field amplitudes fall to 1/e) of 3 μm, corresponding approximately to an f/4 focusing aperture. The laser is linearly polarized in the y plane of the box. These laser parameters have been chosen to be a characteristic of forthcoming experiments on multi-petawatt, ultrashort, Ti:Sapphire laser systems such as Apollon [55]. The target is a DLT with a fully ionized homogeneous carbon (Z = 6, A = 12) foam on top of a fully ionized aluminum (Z = 13, A = 27) layer of 2 µm thickness and density 450 nc. The choice of fully ionized target layers results from having tested, considering field ionization in additional simulations, that the target atoms involved in the interaction rapidly get fully ionized at a0 ≥ 20. The foam electrons are represented with up to 10 particles per cell (ppc) according to the layer density, foam ions with 1 ppc, substrate electrons with 32 ppc, and substrate ions with 3 ppc. Electrons are initialized with a temperature of 10 eV, and ions are initialized cold. Photon generation via NICS is switched on only for photon energies above 0.25 mec2 and for χ > 10–4. NICS is simulated with the default tables of Smilei, and pair production is neglected. We have performed 80 simulations exploring all the combinations of the following parameters: foam density ne = 1, 2, 5, 10 nc, foam thickness = 5, 10, 15, 20, 25 μm, and intensity I = 0.87, 3.46, 5.41, 7.79 ⋅ 1021 W/cm2 (a0 = 20, 40, 50, 60). A special simulation, called simulation A, characterized by a0 = 50, foam thickness = 15 µm and foam density = 2 nc was performed with a high temporal resolution of the diagnostics. We will use it in Section 3 to describe the physics of the interaction and the main properties of NICS in DLTs.
We start reporting the results of simulation A (see Section 2). We use this simulation to describe the main aspects of the laser–DLT interaction and the consequent NICS emission. Figure 1 helps visualize the behavior of the laser and hot electrons during the simulation.
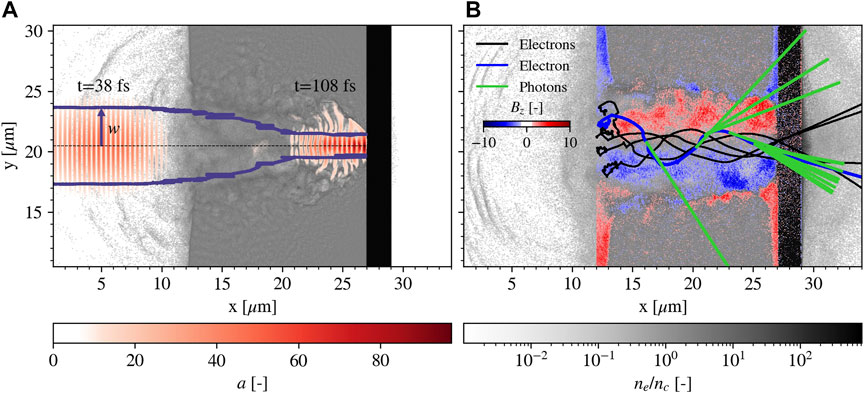
FIGURE 1. Evolution of the laser and trajectories of some electrons in simulation A. Plot (A) shows in blue lines the laser waist limits, calculated as the points where the field amplitude falls to 1/e of its maximum, and two snapshots of a = e|E|/(meω0c) at 38 fs and 108 fs. The black dashed line indicates the center of the box in y. Plot (B) shows some trajectories of electrons and photons and the field Bz normalized to the code units at 204 fs. The represented electrons (black and blue lines) are characterized by a final value of kinetic energy above 60 MeV. The photons (green lines) are emitted by the electron represented in blue. In the background of both plots, the electron density normalized to nc at 108 fs in (A) and 204 fs in (B).
Before the interaction, the laser pulse focused on the target left boundary undergoes free-propagation (Figure 1A laser snapshot at 38 fs). When the interaction with the low-density layer starts, the pulse experiences a progressive alteration of its spatial and temporal shape, and a gradual absorption [56]. The near-critical plasma behaves as a lens causing relativistic self-focusing [57–59]. This phenomenon induces the reduction of the laser spot size, the increase of the laser pulse intensity, and, consequently, the pulse confinement in a channel in which the electron density is depleted because of the ponderomotive force. As shown by the blue line in Figure 1A, the laser waist is decreased symmetrically inside the foam from 3 µm down to nearly 1 µm. During the interaction with the near-critical layer, a = e|E|/(meω0c) increases from 50 to 70 and goes above 100 when the laser is reflected on the substrate (Figure 1A laser snapshot at 108 fs). As a consequence of reflection, the electromagnetic field strength is further enhanced due to the superposition of the incident and reflected pulse. A temporary standing wave builds in front of the substrate, and the peaks of the normalized electric field e|E|/(meω0c) and magnetic field e|B|/(meω0) alternatively grow up to 150 at the nodes and antinodes of this wave. Self-focusing and superposition can thus significantly boost NICS. Another phenomenon is the magnetization of the channel [60]: following the laser pulse propagation, the Bz component of the field fills the channel in two symmetric regions of opposite signs (Figure 1B).
The channel dug by the laser inside the plasma has a variable diameter that follows the reduction of the laser size during propagation. Hot electrons are generated in this channel with a broad energy spectrum with maximum energies up to 460 MeV. Indeed, when the interaction starts, electrons are rapidly accelerated via direct laser acceleration [61]. The trajectories of the most energetic electrons, black and blue lines in Figure 1B, show that, at the beginning of the interaction, the electrons are pushed backwards and then are accelerated into the channel following the laser pulse and co-moving with it. Simultaneously, the electrons experience betatron oscillations in the transverse direction driven by the magnetization of the channel, which, in addition, constrains electrons to be confined in the channel itself [61].
Some examples of the higher-energy emission are presented in Figure 1B, where the emitted photons are shown in green, and the emitting electron appears in blue. In general, we can distinguish two emission phases. Photons are produced firstly during the laser propagation through the foam; we call this the ramp phase [43] because emission occurs at a constant rate and the energy radiated away grows linearly. Then, a peak of emission happens in front of the substrate (burst phase [43]) when electrons see the counterpropagating reflected laser field. In Figure 2A, the number density of all emitted photons is reported. The emission occurs predominantly in the channel region of the foam, where most energetic electrons are confined. In Figure 2B, all the emitted photons are represented as arrows directed according to their momentum and colored according to their energy. We can recognize low-energy backward emitted photons, especially in the early phase of interaction (left side of the channel), and higher-energy forward emission due to oscillating electrons in the channel. Most photons and the most energetic ones are emitted before the substrate during the burst phase. The distributions in Figure 2C describe the directionality of photon emission in more detail. Although a background of emission is present at all angles due to the chaotic motion of electrons, photons are mainly emitted backwards during the ramp phase (blue curve) and in a cone of 30° around the forward direction during the burst phase (green curve). The energy distribution in the ramp phase (yellow curve) shows a more relevant contribution in energy by the forward emission due to electrons undergoing oscillations and following the laser pulse, as recognized in Figure 2B. During the burst phase, the emission shows two lobes peaked at 15°. This bilobal structure is typically observed when emitting electrons accelerated by a linearly polarized laser undergo oscillations in a near-critical plasma channel [23, 25, 27, 29, 62, 63]. The peak angle of the bilobal structure is determined by the angular deviation of betatron oscillations at the instant of copious burst emission. This angle is given by ϕ ∼ rβωβ/c [63, 64], where rβ is the amplitude of the oscillations which is approximately given by the channel radius, and
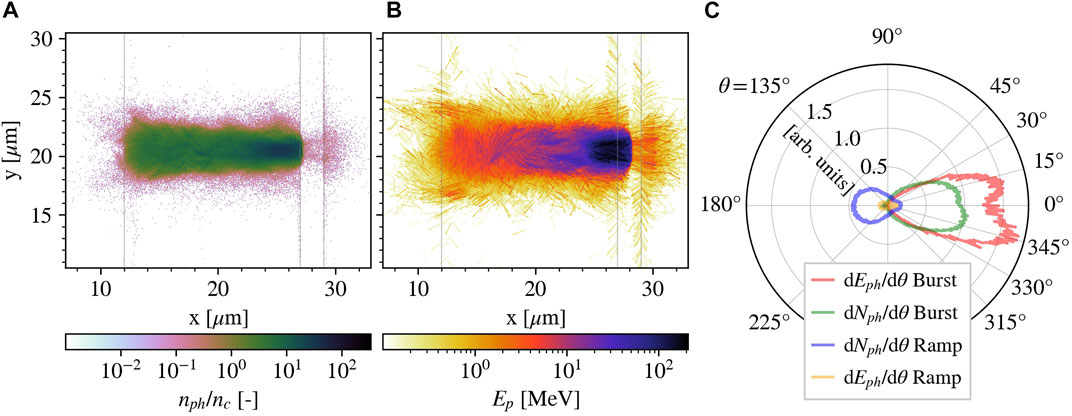
FIGURE 2. Spatial and angular information on photon emission: the distribution in space of photon number density normalized to nc (A), the emitted photons represented as arrows directed according to their momentum and colored according to their energy Ep (B), and the photon angular distribution in number and energy (C) for the two phases of emission, that is, ramp (before 110 fs) and burst (after 110 fs). The three plots consider all the photons emitted in simulation A. In plots (A) and (B), photons are fixed in their emission position and grey lines indicate the target limits at the beginning of the simulation. The angle θ of the distribution in (C) is zero in the laser propagation direction.
The maximum values of χ reached by electrons are around 0.04 in the ramp phase and up to 0.33 in the burst phase. Since electron χ goes above 0.1 in this phase, we expect to see the impact of quantum effects [3, 48]. Using the approximation for χ mentioned in Section 1 for the counterpropagation condition, we can simply estimate the maximum value for this parameter in the burst phase using χ ≈ 2γafℏω0/(mec2), where af is the maximum normalized vector potential achieved by self-focusing. We can check that using γ ≈ 800 and af ≈ 75, which are reasonable values for simulation A, this formula gives a χ value around 0.33. More insights are gained by discussing a more specific approximation for χ. Since the most relevant fields in the physical system are the laser ones, Ey and Bz, and the electrons are mainly accelerated in the forward direction, we can evaluate χ using this approximation of formula 1:
where as = mc2/(ℏω0), βx = vx/c with vx the electron velocity component in the laser propagation direction, and Ey and Bz are normalized by meω0c/e and meω0/e, respectively. As shown in Figure 3A by the red line, this approximated formula describes well the maximum value of χ achieved during the simulation. An improvement in the agreement is obtained considering also the term
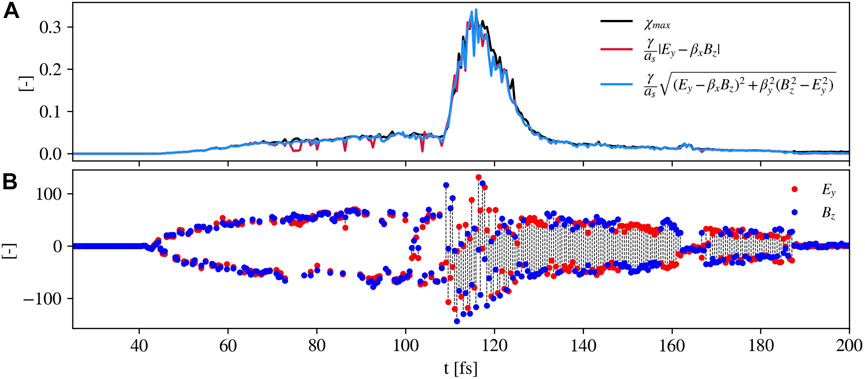
FIGURE 3. In (A), maximum values of χ obtained during the simulation: in black, the simulation values; in red, the values computed with formula 2 considering the macroelectrons with the maximum χ, and in blue the values calculated in the same way but with an additional correction. In (B), the electric field normalized by meω0c/e in the y direction (red dots) and the magnetic field normalized by meω0/e in the z direction (blue dots) felt by the macroelectron with the maximum χ at each timestep of the simulation diagnostic. The two field values for each macroelectron are connected with a dashed black line.
We compare some properties of emitted photons in simulation A with analytical results. Since Smilei simulates emission according to the LCFA and, thus, using the results for NICS in constant crossed fields, that is, when E⊥B and |E| = c|B|, we can use the results of this theory [3, 65–68] to estimate the evolution of the emitted power and the final spectrum of all emitted photons. We rearrange the formulas of this theory as functions of macro-electron properties: parameter χ, kinetic energy Ee, and numerical weight we. The instantaneous emitted power by all electrons is given by the summation of their contributions at a given time:
where
where Kv are the modified Bessel functions of the second kind, and ξ is the variable of integration. In Figure 4A, we have plotted the evolution of the emitted power in the simulation (black) compared with the same quantity obtained from formula 3 in the classical case (red) and with the quantum correction of formula 4 (blue). More precisely, the plotted quantities are power densities due to the reduced dimensionality of the simulations. The evolution of emitted power shows the two distinct phases we have highlighted in Section 3.1. The emitted power is nearly constant from 60 fs to 110 fs; thus, the energy converted in photons linearly increases: ramp phase. Instead, around 120 fs, the peak of emission characteristic of the burst phase occurs. While emission in the ramp phase is well-described in a classical framework of synchrotron emission, the emission peak in front of the substrate needs quantum corrections to be estimated correctly. This fact indicates that the quantum regime of synchrotron emission is observed here. The plot confirms that the quantum effects arising when χ approaches one reduce the emitted power against the classical case.
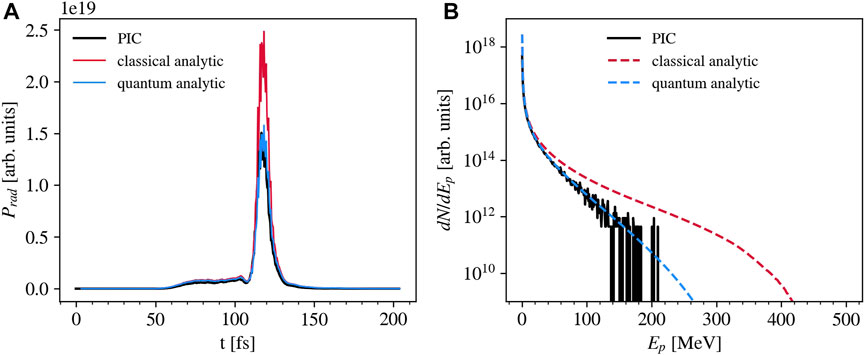
FIGURE 4. Comparison among emission properties obtained in simulation A and estimated analytically considering synchrotron emission classically or including quantum effects. Plot (A) shows the evolution in time of the emitted power densities. Plot (B) shows the final photon spectrum.
The energy spectrum of all emitted photons during the simulation is given analytically by a summation of electrons contributions integrated in time:
where t0 and t1 are the starting and ending time of the simulation, respectively, Ep is the photon energy, and y is given by the following equation:
It is worth noting that Ee, χ, and, consequently, y are time-dependent quantities. The classical limit, corresponding to the usual synchrotron emission formula [54], is obtained neglecting the recoil of the radiating electrons, that is, by taking Ep ≪ Ee in Eqs. 5, 6:
In Figure 4B, we compare the spectrum obtained in the simulation (solid black line) with those analytically estimated in the classical case (dashed red line) and with quantum corrections (dashed blue line). The NICS spectrum is broad with an exponential shape. This shape is expected considering the typically broad, nearly exponential spectra obtained for electrons in DLTs [69–71]. The quantum corrections change the slope and cut-off of the estimated spectrum at high energy since the most energetic emission is expected to come from electrons with higher χ and thus more affected by these corrections. The cut-off of the simulated spectrum is not present in the estimated ones. This effect is due to the reduced number of particles per cell used for macro-electrons in our simulations. If this number is low, reduced sampling affects the high-energy electrons and the photons they emit. We have tested that a visible improvement in the high-energy sampling in this plot occurs only by strongly increasing the number of macro-electrons by at least two orders of magnitude, making the simulation more expensive in computational resources.
The procedure described in this section is similar to some strategies reported in literature [72, 73] evaluating photon emission without using a Monte Carlo approach. Our estimates were performed after the simulation using the macro-electron properties saved by the diagnostics with a high time resolution. Even if the stochasticity of emission is not considered, formulas 3 and 5 can be valuable tools to check and estimate emission after PIC simulations in any case of interest and not only in the DLT case. Furthermore, this procedure can be used to recognize and evaluate the impact of quantum effects of NICS emission according to the laser and target configurations, as we have demonstrated in the DLT case.
Using analytical formulas and simulations, we can compare NICS and bremsstrahlung in the range of parameters explored in this work. Similarly to Eq. 5, we can estimate bremsstrahlung generated in the substrate, which is the target region with higher density and atomic number, thus the most relevant for this type of emission. We use a generalization of Eq. 7 of Ref. [46]:
where ni is the ion density of the substrate, dN/dEe is the time-dependent spectrum in energy of electrons inside the substrate, a = 11 ⋅ 10–31 m2 and b = 0.83. In Figure 5, we report NICS-bremsstrahlung comparisons in the case of foam thickness 25 µm and foam density 1 nc varying the parameter a0 (20–40-50–60). We show the NICS spectra obtained with Smilei (green), the bremsstrahlung spectra from analogous simulations using the PIC code EPOCH [74] that allows for Monte Carlo evaluation of bremsstrahlung [46] (blue), and the analytical estimates of bremsstrahlung using formula 9 (red). Due to the lower efficiencies of the two processes, we consider them independent, and we do not activate NICS emission in EPOCH. When a0 = 40, 50, 60, bremsstrahlung is lower than NICS by at least two orders of magnitudes on the whole range of the spectrum. Instead, at a0 = 20, NICS contribution is strongly reduced due to the relatively low laser intensity and becomes closer to the bremsstrahlung contribution. In this case, the two processes contribute similarly: the high-energy spectrum is dominated by bremsstrahlung, while in the low-energy portion, synchrotron radiation prevails. Overall, we deduce that the impact of NICS in our DLTs in non-extreme laser regimes is remarkably relevant. The results of Figure 5 can be discussed considering that NICS and bremsstrahlung have a different dependence on laser intensity. Bremsstrahlung depends on the electron energy achieved during the laser-driven acceleration of electrons and, thus, indirectly on laser intensity. On the other hand, NICS has an explicit dependence on intensity and the production yield goes approximately as
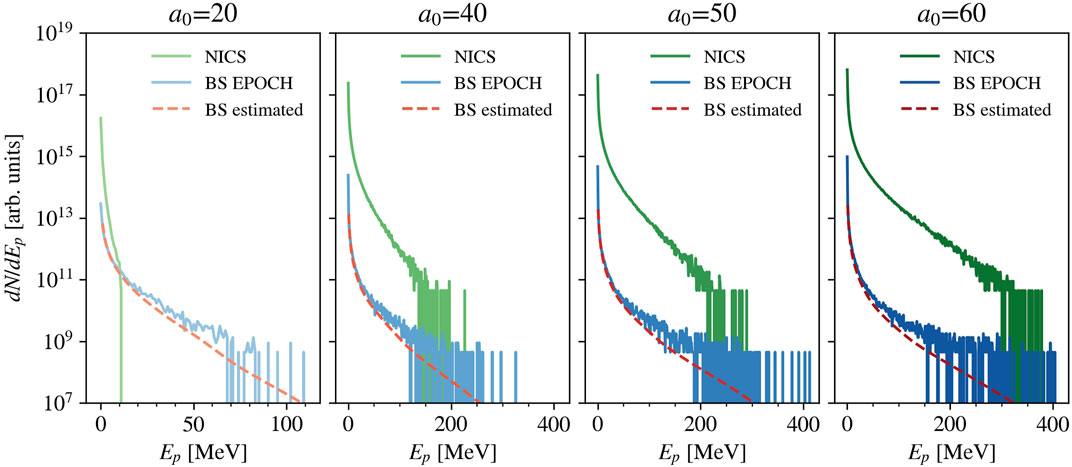
FIGURE 5. Spectra of emitted photons in the case of foam thickness 25 µm and foam density 1 nc varying the parameter a0 (20–40–50–60). The reported spectra refer to NICS emission from Smilei simulations (solid lines in green), bremsstrahlung (BS) emission simulated with the PIC code EPOCH (solid lines in blue) and estimated analytically (dashed lines in red).
We report results from the whole simulation scan focusing on the dependencies of NICS emission properties on the laser and target parameters. We have chosen two properties for this analysis: the conversion efficiency from laser energy into photon energy and the average energy of all emitted photons (Figure 6). These quantities are expected to be useful in assessing the feasibility of applications and can be quantitatively evaluated in 2D simulations avoiding units altered by the reduced dimensionality. The conversion efficiencies represent the ratio between the energy in photons generated in the simulation, which have energy above 0.25 mec2, and the laser energy. The presence of this cut-off reduces the conversion efficiency since only the high-energy portion of the electromagnetic spectrum is considered but avoids generating a lot of low-energy photons, which can be computationally heavy to handle. Furthermore, as noted in Section 3.2, low-energy emission is not affected by quantum effects and, thus, less relevant to be simulated with a Monte Carlo approach.
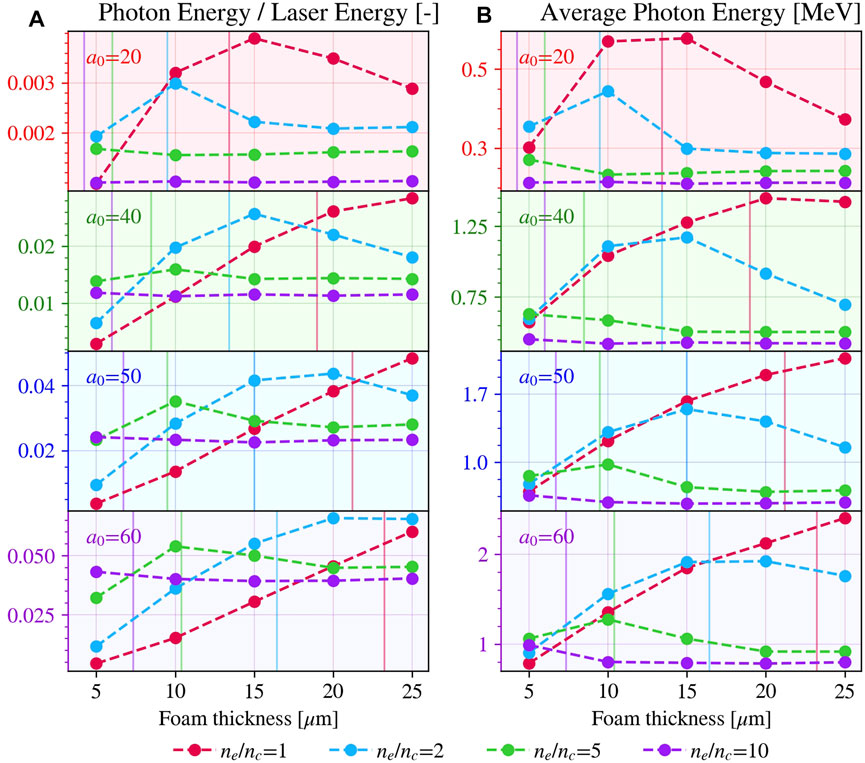
FIGURE 6. Conversion efficiency of photon energy in laser energy (A) and average energy of all emitted photons (B) in all the simulations performed varying a0, foam thickness and density (ne/nc). Every circle represents a simulation. Vertical lines colored according to the density values indicate the self-focusing length.
In Figure 6A, we observe that the conversion efficiencies tend to show an optimum case in thickness for fixed a0 and the foam density. Exceptions are the low-density cases at high a0 where probably the scan is not covering the optimal cases corresponding to higher foam lengths, as shown by [40]. By decreasing a0 or increasing the foam density, this optimum tends to shift toward lower lengths, and its value decreases. This effect is due to the lower transparency of the plasma to the laser. Shorter foams grant that the laser can reach the reflection on the substrate and thus the counter-propagation condition of the burst phase that enhances the efficiency and energy of emission. Contrarily, the cases with dense and long foams tend to suppress the burst emission because of relevant laser absorption during the propagation, a phenomenon evidenced in [78]. Because of this, the conversion efficiencies in long foam cases increase by lowering the density. However, denser cases can become optimal at shorter foam lengths.
The average photon energy (Figure 6B) shows similar optimal lengths once fixed a0 and the density. The same comments on efficiencies are valid for the average photon energy, although dense foam cases have lower performance considering this parameter even in thinner foams.
The processes involving the laser pulse, in particular, the self-focusing and the consequent electron heating, directly impact NICS and its dependence on target parameters. 3D PIC simulations have revealed that the self-focusing effect generated by the near-critical target is representable as the action of a lens [56]. A thin-lens model can be used to obtain the focal length f of the near-critical layer and to describe the self-focusing process. This model gives
Figure 7 reports the conversion efficiency, panel (A), and the average photon energy, panel (B), varying a0, thus making identifiable their dependence on this parameter. The simulations considered here are only those with foam thickness closest to the self-focusing length once fixed a0 and ne/nc. This plot confirms a general trend reported in the literature according to which the conversion efficiency from the laser in photon energy goes approximately as
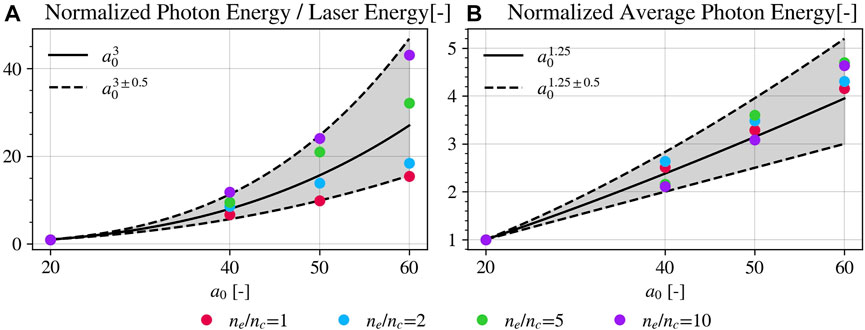
FIGURE 7. Normalized conversion efficiency of photon energy in laser energy (A) and average energy of all emitted photons (B) in the simulations with foam thickness closest to the self-focusing length f. Normalization is achieved by dividing by the value at a0 = 20 once fixed the foam density ne/nc. Solid and dashed black lines represent powers of a0 approximately matching the simulation point dependence.
Considering a nanostructured morphology for the target, the quantitative results reported in this section and the previous ones would be different. Alteration of the interaction processes due to the presence of the nanostructure is expected [79]. We mention that, as reported in [39, 43], including a nanostructured morphology for the foam in 2D simulations has mainly the impact of reducing the photon yield and maximum photon energy due to density dishomogeneities and more chaotic motion of electrons with respect to the uniform case, albeit remaining more efficient than the single layer. For this work, based on 2D simulations, we focus on something other than the detailed morphology expecting it to be worthy of consideration in more realistic 3D simulations. In addition, relatively high laser intensities tend to homogenize the nanostructure [79], and, if the laser contrast is not very high, the laser prepulse is expected to ionize and make the foam uniform before the interaction with the main laser peak.
In this work, we have investigated NICS occurring during the interaction of an intense laser pulse (
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
MGa, AF, MGr, and MP contributed to the conception and design of the study. MGa and AF performed the PIC simulations and the data analysis. MGa wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
This work was carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). This work was funded by the European Union (ERC, PANTANI, 101069171).
The authors thank Rafael Caprani for his master’s thesis [43] supervised by MGr, MP, and AF, which set the basis of this work and was preparatory to the analysis of results. They acknowledge the agreement between the Department of Energy at Politecnico di Milano and the Cineca consortium (Casalecchio di Reno, Italy) for access to the high-performance computing machines Marconi, Galileo, Galileo100, and Marconi100.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Cole J, Behm K, Gerstmayr E, Blackburn T, Wood J, Baird C, et al. Experimental evidence of radiation reaction in the collision of a high-intensity laser pulse with a laser-wakefield accelerated electron beam. Phys Rev X (2018) 8:011020. doi:10.1103/physrevx.8.011020
2. Poder K, Tamburini M, Sarri G, Piazza AD, Kuschel S, Baird C, et al. Experimental signatures of the quantum nature of radiation reaction in the field of an ultraintense laser. Phys Rev X (2018) 8:031004. doi:10.1103/physrevx.8.031004
3. Niel F, Riconda C, Amiranoff F, Duclous R, Grech M. From quantum to classical modeling of radiation reaction: A focus on stochasticity effects. Phys Rev E (2018) 97:043209. doi:10.1103/physreve.97.043209
4. Blackburn TG. Radiation reaction in electron–beam interactions with high-intensity lasers. Rev Mod Plasma Phys (2020) 4:5. doi:10.1007/s41614-020-0042-0
5. Piazza AD, Müller C, Hatsagortsyan KZ, Keitel CH. Extremely high-intensity laser interactions with fundamental quantum systems. Rev Mod Phys (2012) 84:1177–228. doi:10.1103/revmodphys.84.1177
6. Ridgers CP, Brady CS, Duclous R, Kirk JG, Bennett K, Arber TD, et al. Dense electron-positron plasmas and ultraintense γ rays from laser-irradiated solids. Phys Rev Lett (2012) 108:165006. doi:10.1103/physrevlett.108.165006
7. Zhang P, Bulanov SS, Seipt D, Arefiev AV, Thomas AGR. Relativistic plasma physics in supercritical fields. Phys Plasmas (2020) 27:050601. doi:10.1063/1.5144449
8. Daykin TS, Sawada H, Sentoku Y, Beg FN, Chen H, McLean HS, et al. Characterization of fast electron divergence and energy spectrum from modeling of angularly resolved bremsstrahlung measurements. Phys Plasmas (2018) 25:123103. doi:10.1063/1.5055257
9. Geddes CG, Rykovanov S, Matlis NH, Steinke S, Vay JL, Esarey EH, et al. Compact quasi-monoenergetic photon sources from laser-plasma accelerators for nuclear detection and characterization. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2015) 350:116–21. doi:10.1016/j.nimb.2015.01.013
10. Courtois C, Edwards R, Fontaine ACL, Aedy C, Barbotin M, Bazzoli S, et al. High-resolution multi-MeV x-ray radiography using relativistic laser-solid interaction. Phys Plasmas (2011) 18:023101. doi:10.1063/1.3551738
11. Ma Y, Hua J, Liu D, He Y, Zhang T, Chen J, et al. Region-of-interest micro-focus computed tomography based on an all-optical inverse compton scattering source. Matter Radiat Extremes (2020) 5:064401. doi:10.1063/5.0016034
12. Gruse JN, Streeter M, Thornton C, Armstrong C, Baird C, Bourgeois N, et al. Application of compact laser-driven accelerator x-ray sources for industrial imaging. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2020) 983:164369. doi:10.1016/j.nima.2020.164369
13. Habs D, Tajima T, Schreiber J, Barty CP, Fujiwara M, Thirolf PG. Vision of nuclear physics with photo-nuclear reactions by laser-driven γ beams. The Eur Phys J D (2009) 55:279–85. doi:10.1140/epjd/e2009-00101-2
14. Mirani F, Calzolari D, Formenti A, Passoni M. Superintense laser-driven photon activation analysis. Commun Phys (2021) 4:185. doi:10.1038/s42005-021-00685-2
15. Kmetec JD, Gordon CL, Macklin JJ, Lemoff BE, Brown GS, Harris SE. MeV x-ray generation with a femtosecond laser. Phys Rev Lett (1992) 68:1527–30. doi:10.1103/physrevlett.68.1527
16. Gahn C, Pretzler G, Saemann A, Tsakiris GD, Witte KJ, Gassmann D, et al. MeV γ-ray yield from solid targets irradiated with fs-laser pulses. Appl Phys Lett (1998) 73:3662–4. doi:10.1063/1.122855
17. Martinez B, d'Humières E, Gremillet L. Synchrotron radiation from ultrahigh-intensity laser-plasma interactions and competition with bremsstrahlung in thin foil targets. Phys Rev Res (2020) 2:043341. doi:10.1103/physrevresearch.2.043341
18. Bulanov SS, Schroeder CB, Esarey E, Leemans WP. Electromagnetic cascade in high-energy electron, positron, and photon interactions with intense laser pulses. Phys Rev A (2013) 87:062110. doi:10.1103/physreva.87.062110
19. Bula C, McDonald KT, Prebys EJ, Bamber C, Boege S, Kotseroglou T, et al. Observation of nonlinear effects in compton scattering. Phys Rev Lett (1996) 76:3116–9. doi:10.1103/physrevlett.76.3116
20. Phuoc KT, Corde S, Thaury C, Malka V, Tafzi A, Goddet JP, et al. All-optical compton gamma-ray source. Nat Photon (2012) 6:308–11. doi:10.1038/nphoton.2012.82
21. Esarey E, Schroeder CB, Leemans WP. Physics of laser-driven plasma-based electron accelerators. Rev Mod Phys (2009) 81:1229–85. doi:10.1103/revmodphys.81.1229
22. Chen S, Powers ND, Ghebregziabher I, Maharjan CM, Liu C, Golovin G, et al. MeV-energy x rays from inverse compton scattering with laser-wakefield accelerated electrons. Phys Rev Lett (2013) 110:155003. doi:10.1103/physrevlett.110.155003
23. Brady CS, Ridgers CP, Arber TD, Bell AR. Gamma-ray emission in near critical density plasmas. Plasma Phys Controlled Fusion (2013) 55:124016. doi:10.1088/0741-3335/55/12/124016
24. Nerush EN, Kostyukov IY, Ji L, Pukhov A. Gamma-ray generation in ultrahigh-intensity laser-foil interactions. Phys Plasmas (2014) 21:013109. doi:10.1063/1.4863423
25. Ji LL, Pukhov A, Nerush EN, Kostyukov IY, Shen BF, Akli KU. Energy partition, γ-ray emission, and radiation reaction in the near-quantum electrodynamical regime of laser-plasma interaction. Phys Plasmas (2014) 21:023109. doi:10.1063/1.4866014
26. Brady CS, Ridgers CP, Arber TD, Bell AR. Synchrotron radiation, pair production, and longitudinal electron motion during 10-100 PW laser solid interactions. Phys Plasmas (2014) 21:033108. doi:10.1063/1.4869245
27. Wang HY, Liu B, Yan XQ, Zepf M. Gamma-ray emission in near critical density plasmas at laser intensities of 1021 w/cm2. Phys Plasmas (2015) 22:033102. doi:10.1063/1.4913991
28. Wu D, Qiao B, He XT. The radiation reaction effects in the ultra-intense and ultra-short laser foil interaction regime. Phys Plasmas (2015) 22:093108. doi:10.1063/1.4930111
29. Huang TW, Robinson APL, Zhou CT, Qiao B, Liu B, Ruan SC, et al. Characteristics of betatron radiation from direct-laser-accelerated electrons. Phys Rev E (2016) 93:063203. doi:10.1103/physreve.93.063203
30. Serebryakov DA, Nerush EN. Efficient gamma-ray generation by ultra-intense laser pulses obliquely incident on a planar plasma layer. Quan Elect (2016) 46:299–304. doi:10.1070/qel16051
31. Chang HX, Qiao B, Zhang YX, Xu Z, Yao WP, Zhou CT, et al. Ultraintense laser absorption and γ-ray synchrotron radiation in near critical density plasmas. Phys Plasmas (2017) 24:043111. doi:10.1063/1.4981213
32. Chang HX, Qiao B, Huang TW, Xu Z, Zhou CT, Gu YQ, et al. Brilliant petawatt gamma-ray pulse generation in quantum electrodynamic laser-plasma interaction. Scientific Rep (2017) 7:45031. doi:10.1038/srep45031
33. Zani A, Dellasega D, Russo V, Passoni M. Ultra-low density carbon foams produced by pulsed laser deposition. Carbon (2013) 56:358–65. doi:10.1016/j.carbon.2013.01.029
34. Maffini A, Pazzaglia A, Dellasega D, Russo V, Passoni M. Growth dynamics of pulsed laser deposited nanofoams. Phys Rev Mater (2019) 3:083404. doi:10.1103/physrevmaterials.3.083404
35. Maffini A, Orecchia D, Pazzaglia A, Zavelani-Rossi M, Passoni M. Pulsed laser deposition of carbon nanofoam. Appl Surf Sci (2022) 599:153859. doi:10.1016/j.apsusc.2022.153859
36. Yang Y, Jiao J, Tian C, Wu Y, Dong K, Zhou W, et al. Near-microcoulomb multi-MeV electrons generation in laser-driven self-formed plasma channel. Laser Part Beams (2017) 35:476–82. doi:10.1017/s0263034617000490
37. Gong Z, Hu RH, Lu HY, Yu JQ, Wang DH, Fu EG, et al. Brilliant GeV gamma-ray flash from inverse compton scattering in the QED regime. Plasma Phys Controlled Fusion (2018) 60:044004. doi:10.1088/1361-6587/aaa9b1
38. Gu YJ, Klimo O, Bulanov SV, Weber S. Brilliant gamma-ray beam and electron–positron pair production by enhanced attosecond pulses. Commun Phys (2018) 1:93. doi:10.1038/s42005-018-0095-3
39. Huang TW, Kim CM, Zhou CT, Ryu CM, Nakajima K, Ruan SC, et al. Tabletop laser-driven gamma-ray source with nanostructured double-layer target. Plasma Phys Controlled Fusion (2018) 60:115006. doi:10.1088/1361-6587/aadbeb
40. Huang TW, Kim CM, Zhou CT, Cho MH, Nakajima K, Ryu CM, et al. Highly efficient laser-driven compton gamma-ray source. New J Phys (2019) 21:013008. doi:10.1088/1367-2630/aaf8c4
41. Xue K, Dou ZK, Wan F, Yu TP, Wang WM, Ren JR, et al. Generation of highly-polarized high-energy brilliant γ-rays via laser-plasma interaction. Matter Radiat Extremes (2020) 5:054402. doi:10.1063/5.0007734
42. Jirka M, Klimo O, Gu YJ, Weber S. Enhanced photon emission from a double-layer target at moderate laser intensities. Scientific Rep (2020) 10:8887. doi:10.1038/s41598-020-65778-4
43. Caprani R. Compact photon sources in multi-PetaWatt facilities: A kinetic numerical investigation. Master’s thesis. Milano, Italy: University Politecnico di Milano (2020).
44. Liu JX, Ma YY, Yu TP, Zhao J, Yang XH, Gan LF, et al. Enhanced electron–positron pair production by ultra intense laser irradiating a compound target. Plasma Phys Controlled Fusion (2016) 58:125007. doi:10.1088/0741-3335/58/12/125007
45. Prencipe I, Metzkes-Ng J, Pazzaglia A, Bernert C, Dellasega D, Fedeli L, et al. Efficient laser-driven proton and bremsstrahlung generation from cluster-assembled foam targets. New J Phys (2021) 23:093015. doi:10.1088/1367-2630/ac1fcd
46. Formenti A, Galbiati M, Passoni M. Modeling and simulations of ultra-intense laser-driven bremsstrahlung with double-layer targets. Plasma Phys Controlled Fusion (2022) 64:044009. doi:10.1088/1361-6587/ac4fce
47. Shou Y, Wang P, Lee SG, Rhee YJ, Lee HW, Yoon JW, et al. Brilliant femtosecond-laser-driven hard x-ray flashes from carbon nanotube plasma. Nat Photon (2022) 17:137–142. doi:10.1038/s41566-022-01114-8
48. Ridgers C, Kirk J, Duclous R, Blackburn T, Brady C, Bennett K, et al. Modelling gamma-ray photon emission and pair production in high-intensity laser–matter interactions. J Comput Phys (2014) 260:273–85. doi:10.1016/j.jcp.2013.12.007
49. Gonoskov A, Bastrakov S, Efimenko E, Ilderton A, Marklund M, Meyerov I, et al. Extended particle-in-cell schemes for physics in ultrastrong laser fields: Review and developments. Phys Rev E (2015) 92:023305. doi:10.1103/physreve.92.023305
50. Lobet M, d'Humières E, Grech M, Ruyer C, Davoine X, Gremillet L. Modeling of radiative and quantum electrodynamics effects in PIC simulations of ultra-relativistic laser-plasma interaction. J Phys Conf Ser (2016) 688:012058. doi:10.1088/1742-6596/688/1/012058
51. Blackburn TG, Seipt D, Bulanov SS, Marklund M. Benchmarking semiclassical approaches to strong-field QED: Nonlinear compton scattering in intense laser pulses. Phys Plasmas (2018) 25:083108. doi:10.1063/1.5037967
52. Yoon JW, Kim YG, Choi IW, Sung JH, Lee HW, Lee SK, et al. Realization of laser intensity over 1023 w/cm2. Optica (2021) 8:630. doi:10.1364/optica.420520
53. Derouillat J, Beck A, Pérez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comp Phys Commun (2018) 222:351–73. doi:10.1016/j.cpc.2017.09.024
55. Cros B, Paradkar B, Davoine X, Chancé A, Desforges F, Dobosz-Dufrénoy S, et al. Laser plasma acceleration of electrons with multi-PW laser beams in the frame of CILEX. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 740:27–33. doi:10.1016/j.nima.2013.10.090
56. Wang HY, Lin C, Sheng ZM, Liu B, Zhao S, Guo ZY, et al. Laser shaping of a relativistic intense, short Gaussian pulse by a plasma lens. Phys Rev Lett (2011) 107:265002. doi:10.1103/physrevlett.107.265002
57. Sun GZ, Ott E, Lee YC, Guzdar P. Self-focusing of short intense pulses in plasmas. Phys Fluids (1987) 30:526. doi:10.1063/1.866349
58. Ren C, Duda BJ, Hemker RG, Mori WB, Katsouleas T, Antonsen TM, et al. Compressing and focusing a short laser pulse by a thin plasma lens. Phys Rev E (2001) 63:026411. doi:10.1103/physreve.63.026411
59. Pazzaglia A, Fedeli L, Formenti A, Maffini A, Passoni M. A theoretical model of laser-driven ion acceleration from near-critical double-layer targets. Commun Phys (2020) 3:133. doi:10.1038/s42005-020-00400-7
60. Pukhov A, ter Vehn JM. Relativistic magnetic self-channeling of light in near-critical plasma: Three-dimensional particle-in-cell simulation. Phys Rev Lett (1996) 76:3975–8. doi:10.1103/physrevlett.76.3975
61. Arefiev AV, Khudik VN, Robinson APL, Shvets G, Willingale L, Schollmeier M. Beyond the ponderomotive limit: Direct laser acceleration of relativistic electrons in sub-critical plasmas. Phys Plasmas (2016) 23:056704. doi:10.1063/1.4946024
62. Stark D, Toncian T, Arefiev A. Enhanced multi-MeV photon emission by a laser-driven electron beam in a self-generated magnetic field. Phys Rev Lett (2016) 116:185003. doi:10.1103/physrevlett.116.185003
63. Shen XF, Pukhov A, Günther MM, Rosmej ON. Bright betatron x-rays generation from picosecond laser interactions with long-scale near critical density plasmas. Appl Phys Lett (2021) 118:134102. doi:10.1063/5.0042997
64. Esarey E, Shadwick BA, Catravas P, Leemans WP. Synchrotron radiation from electron beams in plasma-focusing channels. Phys Rev E (2002) 65:056505. doi:10.1103/PhysRevE.65.056505
65. Ritus VI. Quantum effects of the interaction of elementary particles with an intense electromagnetic field. J Soviet Laser Res (1985) 6:497–617. doi:10.1007/bf01120220
66. Baier VN, Katkov VM, Strakhovenko VM. Electromagnetic processes at high energies in oriented single crystals. Singapore, Singapore: World Scientific Publishing (1998). doi:10.1142/2216
67. Sokolov A, Ternov I, Kilmister C. Radiation from relativistic electrons. American Institute of physics translation series. New York, NY: American Institute of Physics (1986).
68. Berestetskii V, Lifshitz E, Pitaevskii L. Quantum Electrodynamics. 2nd ed. Translated by J. B. Sykes and J. S. Bell. Oxford, England: Butterworth-Heinemann (1982).
69. Cialfi L, Fedeli L, Passoni M. Electron heating in subpicosecond laser interaction with overdense and near-critical plasmas. Phys Rev E (2016) 94:053201. doi:10.1103/physreve.94.053201
70. Passoni M, Sgattoni A, Prencipe I, Fedeli L, Dellasega D, Cialfi L, et al. Toward high-energy laser-driven ion beams: Nanostructured double-layer targets. Phys Rev Acc Beams (2016) 19:061301. doi:10.1103/physrevaccelbeams.19.061301
71. Passoni M, Arioli FM, Cialfi L, Dellasega D, Fedeli L, Formenti A, et al. Advanced laser-driven ion sources and their applications in materials and nuclear science. Plasma Phys Controlled Fusion (2019) 62:014022. doi:10.1088/1361-6587/ab56c9
72. Martins JL, Vranic M, Grismayer T, Vieira J, Fonseca RA, Silva LO. Modelling radiation emission in the transition from the classical to the quantum regime. Plasma Phys Controlled Fusion (2015) 58:014035. doi:10.1088/0741-3335/58/1/014035
73. Niel F, Riconda C, Amiranoff F, Lobet M, Derouillat J, Pérez F, et al. From quantum to classical modeling of radiation reaction: A focus on the radiation spectrum. Plasma Phys Controlled Fusion (2018) 60:094002. doi:10.1088/1361-6587/aace22
74. Arber TD, Bennett K, Brady CS, Lawrence-Douglas A, Ramsay MG, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Controlled Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001
75. Vyskočil J, Gelfer E, Klimo O. Inverse compton scattering from solid targets irradiated by ultra-short laser pulses in the 1022-1023 w/cm2 regime. Plasma Phys Controlled Fusion (2020) 62:064002. doi:10.1088/1361-6587/ab83cb
76. Wan F, Lv C, Jia M, Sang H, Xie B. Photon emission by bremsstrahlung and nonlinear compton scattering in the interaction of ultraintense laser with plasmas. Eur Phys J D (2017) 71:236. doi:10.1140/epjd/e2017-70805-7
77. Chintalwad S, Krishnamurthy S, Ramakrishna B, Ridgers CP. Photon emission enhancement studies from the interaction of ultraintense laser pulses with shaped targets. Phys Rev E (2022) 105:025205. doi:10.1103/physreve.105.025205
78. Fedeli L, Formenti A, Bottani CE, Passoni M. Parametric investigation of laser interaction with uniform and nanostructured near-critical plasmas. Eur Phys J D (2017) 71:202. doi:10.1140/epjd/e2017-80222-7
Keywords: laser, plasma, non-linear inverse Compton scattering, particle-in-cell, numerical simulation, double-layer target, laser-driven photons
Citation: Galbiati M, Formenti A, Grech M and Passoni M (2023) Numerical investigation of non-linear inverse Compton scattering in double-layer targets. Front. Phys. 11:1117543. doi: 10.3389/fphy.2023.1117543
Received: 06 December 2022; Accepted: 19 January 2023;
Published: 09 February 2023.
Edited by:
Wei-Min Wang, Renmin University of China, ChinaReviewed by:
Huai-Hang Song, Institute of Physics (CAS), ChinaCopyright © 2023 Galbiati, Formenti, Grech and Passoni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marta Galbiati, bWFydGEuZ2FsYmlhdGlAcG9saW1pLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.