- 1Department of Applied Mathematics and Statistics, Institute of Space Technology, Islamabad, Pakistan
- 2Department of Mathematics of Applied Sciences, Umm-Al-Qura University, Makkah, Saudi Arabia
- 3Department of Basic Sciences, College of Science and Theoretical Studies, Saudi Electronic University, Riyadh, Saudi Arabia
- 4School of Mathematical Sciences, Universiti Sains Malaysia, Penang, Malaysia
- 5Department of Mathematical Sciences, Faculty of Sciences, Universiti Teknologi Malaysia, Johor Bahru, Malaysia
Determining the non-linear traveling or soliton wave solutions for variable-order fractional evolution equations (VO-FEEs) is very challenging and important tasks in recent research fields. This study aims to discuss the non-linear space–time variable-order fractional shallow water wave equation that represents non-linear dispersive waves in the shallow water channel by using the Khater method in the Caputo fractional derivative (CFD) sense. The transformation equation can be used to get the non-linear integer-order ordinary differential equation (ODE) from the proposed equation. Also, new exact solutions as kink- and periodic-type solutions for non-linear space–time variable-order fractional shallow water wave equations were constructed. This confirms that the non-linear fractional variable-order evolution equations are natural and very attractive in mathematical physics.
1 Introduction
Fractional calculus is a generalization of traditional integer-order integration and derivation actions onto non-integer order. The idea of fractional calculus is as old as classical calculus; it was discussed for the first time by Leibniz and L’Hospital in 1965. The fractional- and variable-order VO fractional models gained more attention because these models describe the physical phenomenon properly as compared to integer-order differential models. The non-linear FEEs define different phenomena in various areas, such as signal preparation, medication, biology, and organic framework [1, 2]. Many strategies have been produced to solve integer/fractional-order problems. Various fractional-order literature works directed that the memory and/or non-locality of the system may change with time, space, or other conditions. So, here our focus is on VO fractional differential models, which describe the physical models that vary with time or space or space–time. For example, Akgül et al. [3] solved the VO FPDE numerically and presented numerical experiments to confirm the efficiency and feasibility. Katsikadelis [4] developed a numerical method for linear and non-linear VO FPDEs in the Caputo sense. The resultant numerical values demonstrated the accuracy of the proposed method. Sahoo et al. [5] reviewed the VO operator definitions and properties. They discussed the new transfer function and investigated the model of a dynamic viscoelastic oscillator. Sing et al. [6] suggested an SEIR model that modeled the 2014–2015 outbreak of the Ebola virus in Africa. They discussed the system of VO FDEs and estimated its parameters for one or more variables. Semary et al. [7] approximated the solution of Liouville–Caputo VO FPDEs with
The aforementioned cited literature reported that so far only numerical studies have been discussed for VO models and no attempt has been made to find the closed form for such types of VO-FEEs. The objective of this paper is to discuss the closed-form solution of the non-linear VO-FEEs. Here, we solve the non-linear VO fractional shallow water wave equation with CFD using the Khater method. The VO fractional problems are more complex computationally than a constant fractional order, and the evolution of a system can be furthermore clearly and accurately described. This contribution seems natural and simple and models many systems with VO [36]. The traveling wave solutions for the VO physical models are not known to the authors.
2 The outline of the Khater method
The non-linear variable-order
where
Also, the important property is given as follows:
Eq. 1 involved the linear and non-linear highest-order derivatives. A brief explanation of the proposed method is as follows [37]:
Convert the variable-order FPDE into an ordinary differential equation (ODE) by taking the transformation as
The obtained ODE is as follows:
where
where
The aforementioned equation has 27 possible solutions [33], which are derived by formulating various traveling wave solutions. Furthermore, the balancing principle is used to find
The solutions to Eq. 7:
When
or
When
or
When
or
When
or
When
or
When
or
When
When
or
When
When
When
When
When
When
When
When
When
When
When
When
The exact solutions for Eq. 1 are obtained by substituting unknown constants and Eq. 7 in Eq. 6.
3 Formulation for the solutions of shallow water wave equations
Shallow water waves arise in the ocean when the waves move from the center of the ocean to the shore or beach known as shallow water waves. Most of the ocean waves are produced by wind, tsunamis, earthquakes, tides, etc. [38], which carry energy. Tsunamis and tides are both shallow water waves. The shallow water wave equation has been derived from the Navier–Stokes equations. Here, we apply the proposed method to study the non-linear space–time fractional VO shallow water wave equation and construct a traveling wave solution based on the Khater method.
3.1 The non-linear space–time variable-order fractional shallow water wave equation
We consider the space–time VO fractional shallow water wave equation as follows [39]:
Using the wave variable
By balancing the highest-order non-linear term
Substituting Eq. 37 into Eq. 36 yields a polynomial equation for
Solving the aforementioned system of algebraic equations by using computer algebra, we obtain
where
Substituting Eq. 38 into Eq. 37, we obtain
Now, substituting the solutions of Eq. 7, we obtain the following 27 distinct traveling wave solutions for space–time fractional variable-order shallow water wave Eq. 35:
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
When
4 Graphical representation
This section focuses on the graphical representation of some specific findings. Marwan and Aminah [40] solved the generalized shallow water equation by the (G′/G)-expansion and constructed a new exact solution for the proposed method. Bagchi et al. [41] extended the elliptic function method and found the traveling wave solution for the generalized shallow water wave equation. The obtained solutions are in the form of singular and periodic soliton solutions. Here, in this study, the graphical results obtained for different values of VO
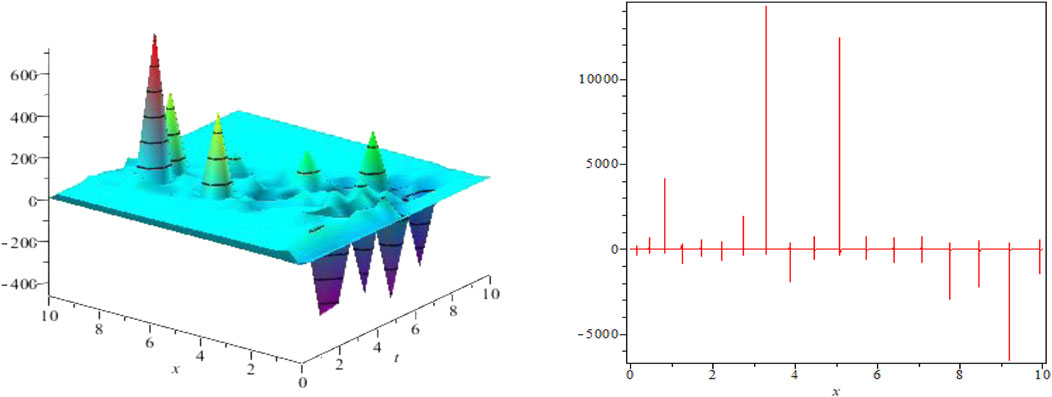
FIGURE 1. Periodic solution for Eq. 35 for
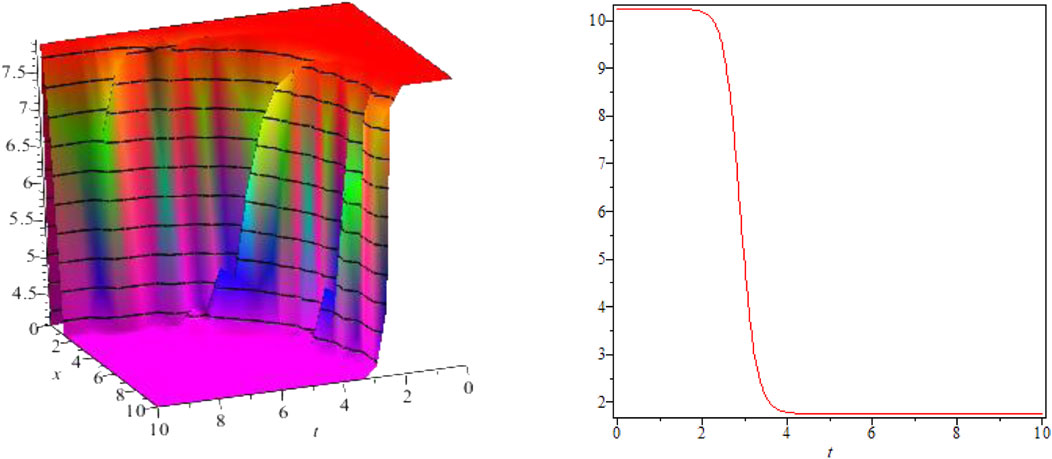
FIGURE 2. Kink-shaped solution for Eq. 35 for
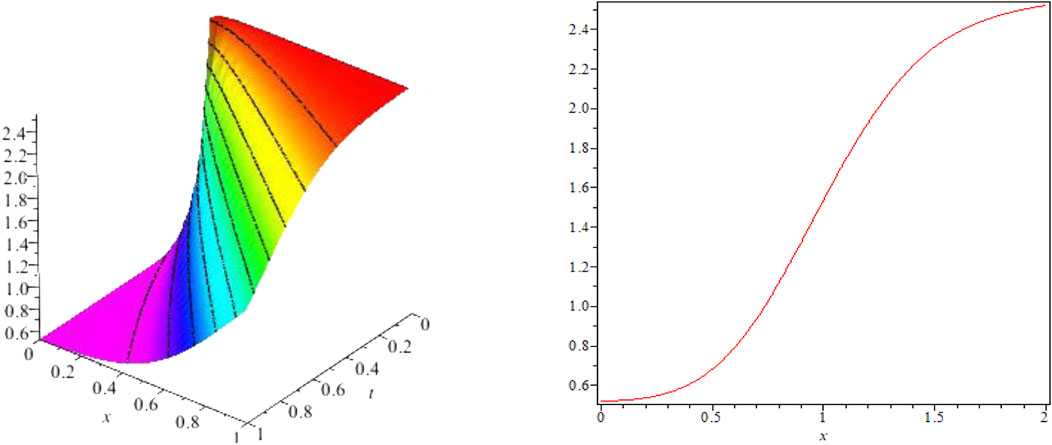
FIGURE 3. Kink-shaped solution for Eq. 35 for
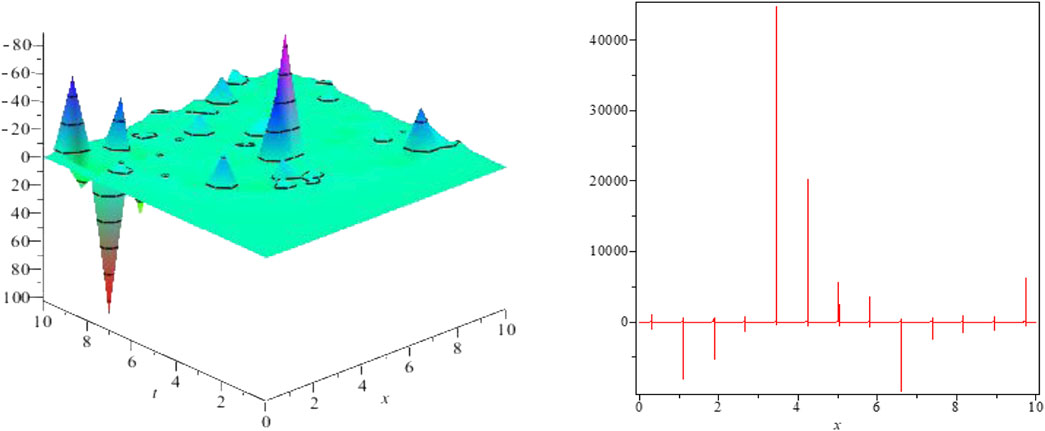
FIGURE 4. Kink-shaped solution for Eq. 35 for
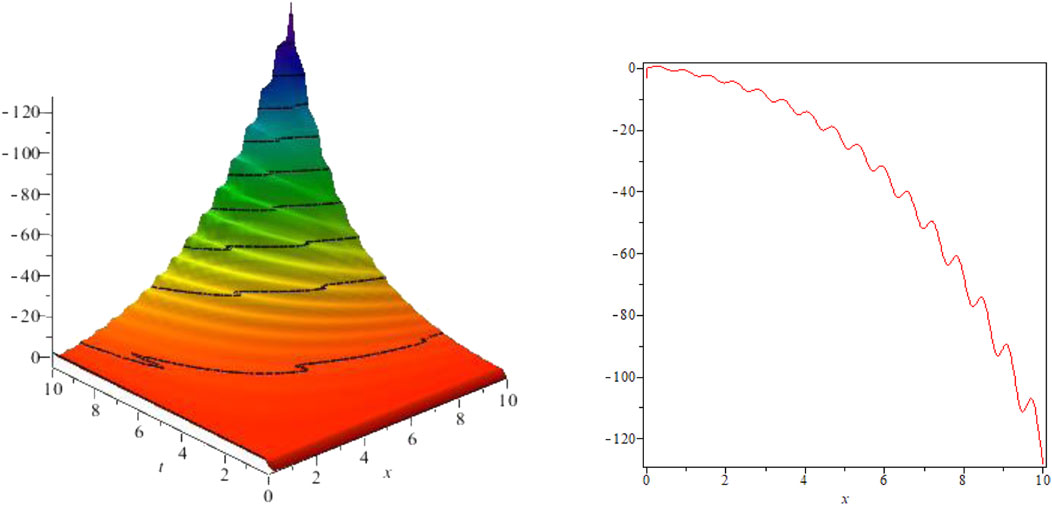
FIGURE 5. Kink-shaped solution for Eq. 35 for
5 Conclusion
In this paper, we solved the non-linear VO fractional evolution equation successfully in the Caputo fractional derivative sense and obtained new exact traveling wave solutions. The VO fractional evolution equation is discussed quite efficiently and accurately by using the Khater method. Here, 27 exact solutions having Kink and singular soliton-type solutions are obtained for different values of VO
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work under grant code: 22UQU4310396DSR54.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
ADI, alternating direction implicit scheme; EW, equal width; FPDE, fractional partial differential equation; GEW, generalized equal width; ODE, ordinary differential equation; SRLW, symmetric regularized long wave; VO, variable order; 2D, two-dimensional; 3D, three-dimensional.
References
1. Bekir A, Güner Ö. The G′G-expansion method using modified Riemann–Liouville derivative for some space-time fractional differential equations. Ain Shams Eng J (2014) 5(3):959–65. doi:10.1016/j.asej.2014.03.006
2. Bin Z. (G′/G)-expansion method for solving fractional partial differential equations in the theory of mathematical physics. Communic Theor Phys (2012) 58:623–30. doi:10.1088/0253-6102/58/5/02
3. Akgül A, Baleanu D. On solutions of variable-order fractional differential equations. Int J Optimization Control Theories Appl (Ijocta) (2017) 7(1):112–6. doi:10.11121/ijocta.01.2017.00368
4. Katsikadelis JT. Numerical solution of variable order fractional differential equations (2018). Available at: https://arXiv.org/abs/preprint.arXiv:1802.00519.
5. Sahoo S, Saha Ray S, Das S, Bera RK. The formation of dynamic variable order fractional differential equation. Int J Mod Phys C (2016) 27(07):1650074. doi:10.1142/s0129183116500741
6. Singh AK, Mehra M, Gulyani S. Learning parameters of a system of variable order fractional differential equations. Numer Methods Partial Differential Equations (2021) num.22796. doi:10.1002/num.22796
7. Semary MS, Hassan HN, Radwan AG. The minimax approach for a class of variable order fractional differential equation. Math Methods Appl Sci (2019) 42(8):2734–45. doi:10.1002/mma.5545
8. Taghipour M, Aminikhah H. A new compact alternating direction implicit method for solving two-dimensional time fractional diffusion equation with Caputo-Fabrizio derivative. Filomat (2020) 34(11):3609–26. doi:10.2298/fil2011609t
9. Ali U, Sohail M, Usman M, Abdullah FA, Khan I, Nisar KS. Fourth-order difference approximation for time-fractional modified sub-diffusion equation. Symmetry (2020) 12(5):691. doi:10.3390/sym12050691
10. Ali U, Kamal R, Mohyud-Din ST. On nonlinear fractional differential equations. Int J Mod Math Sci (2012) 3:3., no.
11. Zhao Z, Yue J, He L. New type of multiple lump and rogue wave solutions of the (2+ 1)-dimensional Bogoyavlenskii–Kadomtsev–Petviashvili equation. Appl Math Lett (2022) 133:108294. doi:10.1016/j.aml.2022.108294
12. Zubair T, Usman M, Ali U, Mohyud-Din ST. Homotopy analysis method fa or system of partial differential equations. Int J Mod Eng Sci (2012) 1(2):67–79.
13. Zhao Z, He L. A new type of multiple-lump and interaction solution of the Kadomtsev–Petviashvili I equation. Nonlinear Dyn (2022) 109:1033–46. doi:10.1007/s11071-022-07484-6
14. Hu W, Deng Z, Han S, Zhang W. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs. J Comput Phys (2013) 235:394–406. doi:10.1016/j.jcp.2012.10.032
15. Hu W, Xu M, Song J, Gao Q, Deng Z. Coupling dynamic behaviors of flexible stretching hub-beam system. Mech Syst Signal Process (2021) 151:107389. doi:10.1016/j.ymssp.2020.107389
16. Zhao Z, He L. Lie symmetry, nonlocal symmetry analysis, and interaction of solutions of a (2+ 1)-dimensional KdV–mKdV equation. Theor Math Phys (2021) 206(2):142–62. doi:10.1134/s0040577921020033
17. Uddin MH, Khatun MA, Arefin MA, Akbar MA. Abundant new exact solutions to the fractional nonlinear evolution equation via Riemann-Liouville derivative. Alexandria Eng J (2021) 60(6):5183–91. doi:10.1016/j.aej.2021.04.060
18. Barman HK, Seadawy AR, Roy R, Akbar MA, Raddadi MH. Rational closed form soliton solutions to certain nonlinear evolution equations ascend in mathematical physics. Results Phys (2021) 27:104450. doi:10.1016/j.rinp.2021.104450
19. Barman HK, Akbar MA, Osman MS, Nisar KS, Zakarya M, Abdel-Aty AH, et al. Solutions to the Konopelchenko-Dubrovsky equation and the Landau-Ginzburg-Higgs equation via the generalized Kudryashov technique. Results Phys (2021) 24:104092. doi:10.1016/j.rinp.2021.104092
20. Roy R, Akbar MA, Seadawy AR, Baleanu D. Search for adequate closed form wave solutions to space–time fractional nonlinear equations. Partial Differential Equations Appl Math (2021) 3:100025. doi:10.1016/j.padiff.2021.100025
21. Kumar S, Niwas M, Osman MS, Abdou MA. Abundant different types of exact soliton solution to the (4+1)-dimensional Fokas and (2+1)-dimensional breaking soliton equations. Commun Theor Phys (2021) 73:105007. doi:10.1088/1572-9494/ac11ee
22. Ali U, Mastoi S, Othman WAM, Khater MM, Sohail M. Computation of traveling wave solution for nonlinear variable-order fractional model of modified equal width equation. AIMS Math (2021) 6(9):10055–69. doi:10.3934/math.2021584
23. Akhtar J, Seadawy AR, Tariq KU, Baleanu D. On some novel exact solutions to the time fractional (2+ 1) dimensional Konopelchenko–Dubrovsky system arising in physical science. Open Phys (2020) 18(1):806–19. doi:10.1515/phys-2020-0188
24. Islam T, Akbar MA, Azad AK. Traveling wave solutions to some nonlinear fractional partial differential equations through the rational (G′/G)-expansion method. J Ocean Eng Sci (2018) 3(1):76–81. doi:10.1016/j.joes.2017.12.003
25. Mamun Miah M, Shahadat Ali HM, Ali Akbar M, Majid Wazwaz A. Some applications of the (G′/G, 1/G)-expansion method to find new exact solutions of NLEEs. The Eur Phys J Plus (2017) 132(6):252–15. doi:10.1140/epjp/i2017-11571-0
26. Islam MS, Khan K, Akbar MA, Mastroberardino A. A note on improved F-expansion method combined with Riccati equation applied to nonlinear evolution equations. R Soc Open Sci (2014) 1(2):140038. doi:10.1098/rsos.140038
27. Hu W, Huai Y, Xu M, Feng X, Jiang R, Zheng Y, et al. Mechanoelectrical flexible hub-beam model of ionic-type solvent-free nanofluids. Mech Syst Signal Process (2021) 159:107833. doi:10.1016/j.ymssp.2021.107833
28. Hu W, Xu M, Zhang F, Xiao C, Deng Z. Dynamic analysis on flexible hub-beam with step-variable cross-section. Mech Syst Signal Process (2022) 180:109423. doi:10.1016/j.ymssp.2022.109423
29. Ali U, Ahmad H, Abu-Zinadah H. Soliton solutions for nonlinear variable-order fractional Korteweg–de Vries (KdV) equation arising in shallow water waves. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.06.011
30. Gulalai SA, Rihan FA, Ullah A, Al-Mdallal QM, Akgul A. Nonlinear analysis of a nonlinear modified KdV equation under Atangana Baleanu Caputo derivative. AIMS Math (2022) 7(5):7847–65. doi:10.3934/math.2022439
31. Hu W, Wang Z, Zhao Y, Deng Z. Symmetry breaking of infinite-dimensional dynamic system. Appl Math Lett (2020) 103:106207. doi:10.1016/j.aml.2019.106207
32. Zayed Elsayed ME, Amer Yasser A, Shohib Reham MA. Exact traveling wave solution for nonlinear fractional partial differential equation using the improved (G’/G)-expansion method. Int J Engin (2014) 4(7):18–31.
33. Ali U, Ganie AH, Khan I, Alotaibi F, Kamran K, Muhammad S, et al. Traveling wave solutions to a mathematical model of fractional order (2+ 1)-dimensional breaking soliton equation. Fractals (2022). p. 2240124.
34. Hu W, Zhang C, Deng Z. Vibration and elastic wave propagation in spatial flexible damping panel attached to four special springs. Commun Nonlinear Sci Numer Simulation (2020) 84:105199. doi:10.1016/j.cnsns.2020.105199
35. Ali U, Ahmad H, Baili J, Botmart T, Aldahlan MA. Exact analytical wave solutions for space-time variable-order fractional modified equal width equation. Results Phys (2022) 33:105216. doi:10.1016/j.rinp.2022.105216
36. Hu W, Huai Y, Xu M, Deng Z. Coupling dynamic characteristics of simplified model for tethered satellite system. Acta Mechanica Sinica (2021) 37(8):1245–54. doi:10.1007/s10409-021-01108-9
37. Nayfeh AH, Balachandran B. Applied nonlinear dynamics: Analytical, computational, and experimental methods. John Wiley & Sons (2008).
38. Pushkarev AN, Zakharov VEE. Nonlinear amplification of ocean waves in straits. Theor Math Phys (2020) 203(1):535–546.
39. Rezazadeh H, Korkmaz A, Khater MM, Eslami M, Lu D, Attia RA. New exact traveling wave solutions of biological population model via the extended rational sinh-cosh method and the modified Khater method. Mod Phys Lett B (2019) 33(28):1950338. doi:10.1142/s021798491950338x
40. Clarkson PA, Mansfield EL. On a shallow water wave equation. Nonlinearity (1994) 7(3):975–1000. doi:10.1088/0951-7715/7/3/012
Keywords: space-time variable-order fractional shallow water wave equation, variable-order Caputo fractional derivative, Khater method, closed-form solution, graphical representation
Citation: Ali U, Naeem M, Alahmadi R, Abdullah FA, Khan MA and Ganie AH (2023) An investigation of a closed-form solution for non-linear variable-order fractional evolution equations via the fractional Caputo derivative. Front. Phys. 11:1114319. doi: 10.3389/fphy.2023.1114319
Received: 02 December 2022; Accepted: 23 January 2023;
Published: 14 February 2023.
Edited by:
Gangwei Wang, Hebei University of Economics and Business, ChinaReviewed by:
Weipeng Hu, Northwestern Polytechnical University, ChinaZhonglong Zhao, North University of China, China
Copyright © 2023 Ali, Naeem, Alahmadi, Abdullah, Khan and Ganie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Umair Ali, dW1haXJraGFubWF0aEBnbWFpbC5jb20=; Abdul Hamid Ganie, YS5nYW5pZUBzZXUuZWR1LnNh
 Umair Ali
Umair Ali Muhammad Naeem
Muhammad Naeem Reham Alahmadi3
Reham Alahmadi3 Farah Aini Abdullah
Farah Aini Abdullah