Energy and information flows in autonomous systems

Multi-component molecular machines are ubiquitous in biology. We review recent progress on describing their thermodynamic properties using autonomous bipartite Markovian dynamics. The first and second laws can be split into separate versions applicable to each subsystem of a two-component system, illustrating that one can not only resolve energy flows between the subsystems but also information flows quantifying how each subsystem’s dynamics influence the joint system’s entropy balance. Applying the framework to molecular-scale sensors allows one to derive tighter bounds on their energy requirement. Two-component strongly coupled machines can be studied from a unifying perspective quantifying to what extent they operate conventionally by transducing power or like an information engine by generating information flow to rectify thermal fluctuations into output power.

1 Introduction

Livings things are fundamentally out of thermodynamic equilibrium [1]. Maintaining this state requires a constant flow of energy into them accompanied by dissipation of heat into their environment. Quantifying these flows is straightforward for macroscopic systems but much less so on the small scales of molecular machinery. The advent of ever-more-refined experimental equipment capable of probing small-scale thermodynamics has led to the burgeoning field of stochastic thermodynamics [2–5]. Within this theory, energy flows are deduced from the thermally influenced stochastic dynamics of small-scale systems, permitting quantification of heat dissipation and energetic requirements of diverse experimental setups as well as molecular biological machinery.

1.1 Information thermodynamics

Information plays an interesting and, at times, adversarial role in thermodynamics. At the dawn of statistical mechanics, Maxwell illustrated the counterintuitive role of information by arguing that an intelligent demon could separate gas molecules according to their velocity with seemingly no expense of energy, apparently contradicting the second law [6]. Resolving this paradox plagued physicists for a century [6, 7], leading to well-known contributions from Szilard [8], Landauer [9], and Bennett [10] ultimately showing that acquiring, processing, and storing information incurs thermodynamic costs that balance or exceed any benefit gained from it.

Within the theory of stochastic thermodynamics, information has been incorporated in various ways, including measurement and feedback [11–17] performed by an experimenter on a system, and a system interacting with information reservoirs [18–21]; this established information as a proper thermodynamic resource [22] that sets limits on system capabilities similar to work and free energy. Diverse theoretical works [23–29] and experimental realizations [30–48] illustrate information-powered engines.

1.2 Autonomous and complex systems consisting of subsystems

Small-scale information thermodynamics is also relevant for biological systems such as molecular machines and molecular-scale sensors [49, 50]. Understanding living systems at small scales and advancing the design of nanotechnology [51] requires extending thermodynamics beyond conventional contexts: Instead of the scripted experimental manipulation of time-dependent control parameters, living systems are autonomous, driven out of equilibrium by steady-state nonequilibrium boundary conditions.

Moreover, embracing more of the complexity of biology, we seek understanding beyond the interactions of a system with weakly coupled baths, to encompass interactions among strongly coupled subsystems [52–55]. Lacking a clear separation between a measurement that collects information about a system and feedback that acts on this information [56], in autonomous systems it is more practical to differentiate between subsystems: An upstream system that generates information for a downstream system to react to or exploit.

While in the non-autonomous setup apparent second-law violations result from not correctly accounting for non-autonomous interventions by an experimenter [12–17, 28], in autonomous multi-component systems they can be traced back to thermodynamic accounting that ignores the strong coupling [56–59].

In its simplest form such an autonomous setup is realized by a downstream molecular sensor that reacts to an independent upstream signal [60–65]. More complex interactions are realized by two-component strongly coupled molecular machines in which the dynamics of each component is influenced by the other [54, 66, 67] and by assemblies of molecular transport motors that collectively pull cargo [68, 69].

Here we focus on such autonomous systems, collecting results that extend information thermodynamics to contexts lacking explicit external measurement and feedback, and showcase that bipartite Markovian dynamics and information flow are versatile tools to understand the thermodynamics and performance limits of these systems.

1.3 Objectives and organization

Our aims with this review are to:

1. Build on stochastic thermodynamics to give a gentle introduction to the information-flow formalism, deriving all necessary equalities and inequalities and relating the different names and concepts for similar quantities that appear throughout the literature. Section 2 introduces bipartite dynamics and establishes the notation. Section 3 and Section 4 deal with energy and information flows in these bipartite systems in general, while Section 5.1 compares various similar information-flow measures.

2. Collect results valid for biomolecular sensors, for which the information-flow formalism produces a tighter second law. These are contained in Section 5.

3. Address engine setups and show that the information-flow formalism advances understanding of autonomous two-component engines simultaneously as work and information transducers (Section 6).

1.4 Related reviews

The information-flow formalism is firmly rooted in the theory of stochastic thermodynamics. Recent reviews include a comprehensive one by Seifert [2] and reviews by Jarzynski [3] (focusing on non-equilibrium work relations), Van den Broeck and Esposito [4] (explicitly dealing with jump processes), and Ciliberto [70] (on experiments in stochastic thermodynamics). The recent book by Peliti and Pigolotti [5] also gives a pedagogical introduction to the field. Information thermodynamics itself has recently been reviewed by Parrondo et al. [22].

Turning to molecular machinery, the working principles of Brownian motors have been reviewed by Reimann [71]. General aspects of molecular motors can be found in the reviews by Chowdhury [72] and Kolomeisky [73]. Brown and Sivak [74] focus on the transduction of free energy by nanomachines, while reviews by Silverstein [75] and Li and Toyabe [76] specifically treat the efficiencies of molecular motors.

2 Bipartite dynamics

We consider a mesoscopic composite system whose state at time t is denoted by z(t). Due to thermal fluctuations, its dynamics are described by a Markovian stochastic process defined by a Master equation [77, 78]:

$\frac{\mathrm{d}}{\mathrm{d}t}{p}_t\left(z\right)={\displaystyle \sum _{z^{\prime }}}\left[R\left(z|z^{\prime };t\right)p_t\left(z^{\prime }\right)-R\left(z^{\prime }|z;t\right)p_t\left(z\right)\right],(1)$

where p_t(z) is the probability to find the composite system in state z at time t and the transition rates R(z|z′;t) (sometimes also called the generator) encode the jump rates from state z′ to state z. For convenience, we assume a discrete state space; however, all results can easily be translated into continuous state-space dynamics, as we allude to in Section 2.3. If multiple paths between states z′ and z are possible, the RHS in Eq. (1) needs to include a sum over all possible jump paths.

We assume that one can meaningfully divide the state space into distinct parts, e.g., z = {x, y}, where two subsystems X and Y are identified as distinct units interacting with each other. The process z(t) is bipartite if the transition rates can be written as

$R\left(z|z^{\prime };t\right)=R_y^{x{x}^{\prime }}\left(t\right){\delta }_{y,y^{\prime }}+R_{y{y}^{\prime }}^x\left(t\right){\delta }_{x,x^{\prime }},(2)$

meaning that transitions cannot happen simultaneously in multiple subsystems. Note that this does not imply that the processes x(t) and y(t) are independent of each other; rather their influence on each other is restricted to modifying the other process’s transition rates.

When the dynamics of the joint system are not bipartite, the dissection of energy and information flows presented in the following is more challenging. Chétrite, et al. have investigated this case [79]. Moreover, information flows for quantum systems (without bipartite structure) have also been analyzed [80]. Here, we exclusively cover classical bipartite systems.

2.1 Paradigmatic examples

Bipartite dynamics should be expected whenever two systems (that possess their own dynamics) are combined such that each fluctuation can be decomposed into independent contributions. The dynamics of systems studied in cellular biology can often be approximated as bipartite.

Two paradigmatic examples that have been well studied are molecular motors (such as F_o−F₁ ATP synthase) with strongly coupled interacting sub-components, or cellular sensors that react to a changing external concentration. The joint dynamics of such systems can be decomposed into the distinct fluctuations of each subsystem, each of which is influenced by the other subsystem (in the case of a strongly coupled molecular machine) or into dynamics strongly influenced by an independent process (in the case of a sensor). Figure 1 shows examples and associated simplified state graphs.

FIGURE 1

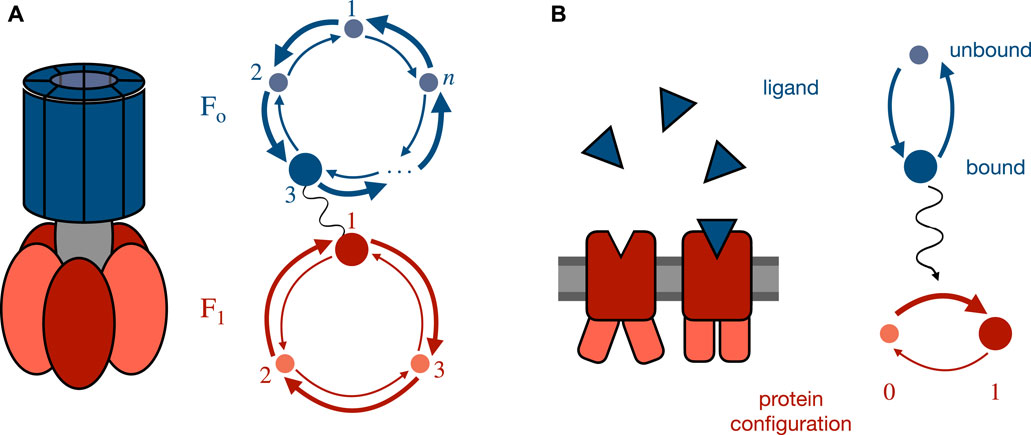
FIGURE 1. Paradigmatic example systems and their simplified state graphs. (A) Simplified model for F_o−F₁ ATP synthase. Upstream F_o dynamics are cyclically driven by a proton gradient while downstream F₁ dynamics are driven in the opposite direction by ATP hydrolysis [54, 66, 67]. Through their coupling, the joint system can transduce work by driving the downstream system against its natural gradient, thereby converting one chemical fuel into another. (B) Simplified model of a biochemical sensor, e.g., involved in E. coli chemotaxis [60–65]. The upstream signal is the binding state (bound or unbound) of the receptor which is reflected in the downstream protein conformation by modifying its potential-energy landscape and thereby influencing the transition rates between configurations.

2.2 Notation

To keep the notation concise and unambiguous, we adopt the following conventions:

1. Random variables are denoted with small letters. Occasionally the more explicit notation p(X_t = x) is used to avoid ambiguity.

2. The joint probability of two random variables taking values x and y, respectively, is denoted by p(x, y). The conditional probability of x given y is denoted by p(x|y).

3. Time arguments are dropped for probabilities and transition rates unless distinct times appear in a single expression, as in p(x_t, y_t′).

4. Total time derivatives are denoted with a dot. The bipartite assumption ensures that rates of change of various quantities can be split into separate contributions due to the X and Y dynamics, respectively. Those individual rates of change are indicated with a dot and the corresponding superscript, i.e., ${\dot{E}}^X$ is the rate of change of energy E due to X-dynamics and $\dot{E}={\dot{E}}^X+{\dot{E}}^Y$ [see Eqs (16a)–(16c)].

5. When no argument is given, symbols represent global quantities, whereas capitalized arguments in square brackets indicate different subsystem-specific quantities, e.g., S ≔ −∑_x,yp(x, y) ln p(x, y) is the joint entropy, while S[X] ≔ − ∑_x p(x) ln p(x) and S[X|Y] ≔ − ∑_xyp(x, y) ln p(x|y) are marginal and conditional entropies, respectively [81, Chap. 2].

2.3 Continuous state spaces

The framework outlined below can also be applied to continuous state spaces. For continuous diffusion processes described by a Fokker-Planck equation (82) this has been done in [58].

For diffusion-type dynamics, Eq. (2) corresponds to the statement that the diffusion matrix must be block-diagonal, such that the Fokker-Planck equation can be written as

$\frac{\partial p_t\left(x,y\right)}{\partial t}=-\frac{\partial }{\partial x}\left[{\mu }^X\left(x,y;t\right)-D^X\frac{\partial }{\partial x}\right]p_t\left(x,y\right)-\frac{\partial }{\partial y}\left[{\mu }^Y\left(x,y;t\right)-D^Y\frac{\partial }{\partial y}\right]p_t\left(x,y\right),(3)$

for respective subsystem drift coefficients μ^X and μ^Y and subsystem diffusion coefficients D^X and D^Y. The corresponding coupled Langevin equations (78) are.

$\dot{x}={\mu }^X\left(x,y;t\right)+\sqrt{D^X}{\xi }^X\left(t\right)(\mathrm{4a})$

$\dot{y}={\mu }^Y\left(x,y;t\right)+\sqrt{D^Y}{\xi }^Y\left(t\right),(\mathrm{4b})$

where ξ^X(t) and ξ^Y(t) are independent Gaussian white-noise terms for which $⟨{\xi }^X(t){\xi }^X(t^{\prime })⟩=2\delta (t-t^{\prime })$, and similarly for Y, and $⟨{\xi }^X(t){\xi }^Y(t^{\prime })⟩=0$. Therefore the two components X and Y are indeed influenced by independent fluctuations, which is often a reasonable approximation for most systems studied here, e.g., two-component molecular machines.

3 Energy flows

As a first step towards a thermodynamic interpretation of the stochastic dynamics described above, we relate stochastic transitions to energy exchanges between the two subsystems and between individual subsystems and the environment as represented by baths/reservoirs of various kinds. For the systems considered here it is safe to assume that all processes are isothermal and that their stochasticity is due to thermal fluctuations.

For systems relaxing to equilibrium the transition rates in Eqs (1) and (2) are related to thermodynamic potentials through the detailed-balance relation. This relation follows from demanding that, in the absence of any driving, the distribution of system states must relax to the equilibrium distribution with no net flux along any transition,

$0=R_{y{y}^{\prime }}^{x{x}^{\prime }}{p}_{\text{eq}}\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}{p}_{\text{eq}}\left(x,y\right).(5)$

The equilibrium distribution is the Boltzmann distribution $p_{\text{eq}}(x,y)=\exp \left[-\left({ϵ}_{xy}-F_{\text{eq}}\right)/k_{\text{B}}T\right]$, where ϵ_xy is the potential energy of the system state (x, y), k_B is Boltzmann’s constant, T the temperature, and F_eq the equilibrium free energy. Consequently, the transition rates are related by

$\ln \frac{R_{y{y}^{\prime }}^{x{x}^{\prime }}}{R_{y^{\prime }y}^{x^{\prime }x}}=\frac{{ϵ}_{x^{\prime }{y}^{\prime }}-{ϵ}_{xy}}{k_{\text{B}}T}.(6)$

When each system state is a mesostate composed of many microstates, as is common for modeling small biological systems, the potential energy ϵ_xy must be replaced by a mesostate free energy [83]. The following thermodynamic formalism remains unchanged, however.

The systems we consider here are driven by chemical reactions and external loads and do not obey the detailed-balance relation. Consequently they do not, in general, relax to equilibrium. Conceptually, we could include the state of the other reservoirs (chemical and work reservoirs) into the microstate Z of the system and then describe a non-equilibrium steady state as a very slow relaxation to global equilibrium, driving cyclical processes in the system of interest; however, such a description would be unnecessarily cumbersome. Assuming that these reservoirs are large compared to the system of interest and weakly coupled to it, we split the free energy of the supersystem into contributions from the reservoirs and the system of interest. Then, energy exchanges between all reservoirs and the system of interest are treated in the same way as energy exchanges with a heat bath, giving a local detailed-balance relation [4, 83–85]:

$\ln \frac{R_{y{y}^{\prime }}^{x{x}^{\prime }}}{R_{y^{\prime }y}^{x^{\prime }x}}=\frac{{ϵ}_{x^{\prime }{y}^{\prime }}-{ϵ}_{xy}-{\sum }_{\nu }{\left(\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^{x{x}^{\prime }}\right)}^{\left(\nu \right)}+f^X{\mathrm{\Delta }}^{x{x}^{\prime }}+f^Y{\mathrm{\Delta }}_{y{y}^{\prime }}}{k_{\text{B}}T},(7)$

where ${\left(\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^{x{x}^{\prime }}\right)}^{(\nu )}$ is the free-energy change in the reservoir ν associated with system transition (x′, y′) → (x, y), f ^X and f ^Y are external forces (here assumed constant) acting on the respective subsystems, and Δ^xx′ and Δ_yy′ are the respective lengths the subsystems undertake against their respective external forces when stepping from (x′, y′) to (x, y). The RHS of Eq. (7) is sometimes called entropy flow associated with a transition [4]. Importantly, if multiple paths connect the states {x′, y′} and {x, y}, local detailed-balance relations hold separately for each of these paths [86].

3.1 Global energy balance

Armed with the local detailed-balance relation (7), we identify different energy flows in the system. Below, we state the usual conventions of stochastic thermodynamics [2, 4] to identify the different contributions (heat and work) associated with each transition. The average rate $\dot{Q}(t)$ of heat exchanged with the thermal environment is given by averaging the log-ratio of transition rates over the net flux for all transitions in the system:

$\dot{Q}≔-k_{\text{B}}T{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_{y{y}^{\prime }}^{x{x}^{\prime }}}{R_{y^{\prime }y}^{x^{\prime }x}},(8)$

where we assume that the states x and y are consecutively numbered, so that the notation x > x′ indicates a sum over transitions between distinct states, omitting the reverse transitions. Throughout this review all energy flows into the system are positive by convention.

Two types of work can be identified, $\dot{W}={\dot{W}}_{\text{chem}}+{\dot{W}}_{\text{mech}}$. These are the average rate of chemical work associated with the influx of energy from the chemical reservoirs,

${\dot{W}}_{\text{chem}}≔-{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]{\displaystyle \sum _{\nu }}{\left(\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^{x{x}^{\prime }}\right)}^{\left(\nu \right)},(9)$

and the average rate of mechanical work due to the subsystems’ responses to external forces,

${\dot{W}}_{\text{mech}}≔{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\left(f^X{\mathrm{\Delta }}^{x{x}^{\prime }}+f^Y{\mathrm{\Delta }}_{y{y}^{\prime }}\right).(10)$

Finally, we identify the rate of change of average internal energy as

$\dot{E}≔{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\left({ϵ}_{xy}-{ϵ}_{x^{\prime }{y}^{\prime }}\right).(11)$

With Eqs (7)-(10), we verify the global first law, representing the global energy balance:

$\dot{E}=\dot{Q}+{\dot{W}}_{\text{chem}}+{\dot{W}}_{\text{mech}},(12)$

which retrospectively justifies identifying the log-ratio of transition rates as heat (8).

3.2 Subsystem-specific energy balances

Due to the bipartite assumption (2), we also find subsystem-specific versions of this balance equation by splitting all energy flows into contributions from the respective subsystems: First the heat flow

$\dot{Q}={\dot{Q}}^X+{\dot{Q}}^Y(\mathrm{13a})$

splits into subsystem-specific heat flows

${\dot{Q}}^X≔-k_{\text{B}}T{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_y^{x{x}^{\prime }}}{R_y^{x^{\prime }x}}(\mathrm{13b})$

${\dot{Q}}^Y≔-k_{\text{B}}T{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\ln \frac{R_{y{y}^{\prime }}^x}{R_{y^{\prime }y}^x}.(\mathrm{13c})$

Similarly, the chemical work

${\dot{W}}_{\text{chem}}={\dot{W}}_{\text{chem}}^X+{\dot{W}}_{\text{chem}}^Y(\mathrm{14a})$

splits into

${\dot{W}}_{\text{chem}}^X≔-{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]{\displaystyle \sum _{\nu }}{\left(\mathrm{\Delta }{\mu }_y^{x{x}^{\prime }}\right)}^{\left(\nu \right)}(\mathrm{14b})$

${\dot{W}}_{\text{chem}}^Y≔-{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]{\displaystyle \sum _{\nu }}{\left(\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^x\right)}^{\left(\nu \right)},(\mathrm{14c})$

where $\mathrm{\Delta }{\mu }_y^{x{x}^{\prime }}$ is equal to $\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^{x{x}^{\prime }}$ evaluated for y = y′ and similarly for $\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^x$. The bipartite assumption (2) ensures that these two functions together cover all applicable $\mathrm{\Delta }{\mu }_{y{y}^{\prime }}^{x{x}^{\prime }}$.

Finally, the mechanical work

${\dot{W}}_{\text{mech}}={\dot{W}}_{\text{mech}}^X+{\dot{W}}_{\text{mech}}^Y(\mathrm{15a})$

splits into

${\dot{W}}_{\text{mech}}^X≔{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}{p}_t\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]f^X{\mathrm{\Delta }}^{x{x}^{\prime }}(\mathrm{15b})$

${\dot{W}}_{\text{mech}}^Y≔{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^x{p}_t\left(x,y^{\prime }\right)-R_{y^{\prime }y}^x{p}_t\left(x,y\right)\right]f^Y{\mathrm{\Delta }}_{y{y}^{\prime }}.(\mathrm{15c})$

Moreover, we formally split the change in the joint potential energy

$\dot{E}={\dot{E}}^X+{\dot{E}}^Y(\mathrm{16a})$

into contributions due to the respective dynamics of each particular subsystem,

${\dot{E}}^X≔{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\left({ϵ}_{xy}-{ϵ}_{x^{\prime }y}\right)(\mathrm{16b})$

${\dot{E}}^Y≔{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\left({ϵ}_{xy}-{ϵ}_{x{y}^{\prime }}\right),(\mathrm{16c})$

where a positive rate indicates that the joint potential energy increases due to the respective subsystem’s dynamics.

We obtain the subsystem-specific first laws as the balances of energy flows into the respective subsystems:

${\dot{E}}^X={\dot{Q}}^X+{\dot{W}}_{\text{chem}}^X+{\dot{W}}_{\text{mech}}^X(\mathrm{17a})$

${\dot{E}}^Y={\dot{Q}}^Y+{\dot{W}}_{\text{chem}}^Y+{\dot{W}}_{\text{mech}}^Y.(\mathrm{17b})$

With Eqs (2), (7)–(11), and (13a)–(16c), we verify that the sum of the subsystem-specific first laws in Eqs (17a) and (17b) yields the global first law (12).

3.3 Work done by one subsystem on the other

The subsystem-specific first laws in Eqs (17a) and (17b) stem from a formal argument. Ideally, we would like to identify internal energy flows that the subsystems communicate between each other; i.e., we would like to identify transduced work in the manner of [55]. However, with no clear prescription on how to split the energy landscape into X-, Y-, and interaction components,

${ϵ}_{xy}={ϵ}_x+{ϵ}_y+{ϵ}_{xy}^{\text{int}},(18)$

the identification of energy flowing from one subsystem to the other remains ambiguous: For example, how much has a change in the X-coordinate changed the potential energy of the X-subsystem and how much has it changed the interaction energy? The ambiguity has already been pointed out in [87], where the authors propose to settle it through physical arguments by identifying a clear interaction term in the Hamiltonian and asking that the splitting leaves constant the average subsystem energy.

We propose a different approach to define an input work into one subsystem. Conventionally work is defined for interactions between a work reservoir (e.g., an experimentalist’s external power source) and a system. Interactions between the work reservoir and the system are mediated by a control parameter influencing the system’s potential-energy landscape. Crucially, there is negligible feedback from the system state to the dynamics of the control parameter. To define work between subsystems, imagine treating subsystem Y as if it were an externally manipulated control parameter influencing the potential-energy landscape of X. Then, the power done by the control parameter Y on system X would be supplied externally and equal the rate of change of internal energy due to the dynamics of the control parameter:

${\dot{W}}^{Y\to X}≔{\dot{E}}^Y.(\mathrm{19a})$

Consequently, we define ${\dot{W}}^{Y\to X}$ as the transduced work from Y to X, which is positive when Y increases the potential energy available to X. Similarly we define

${\dot{W}}^{X\to Y}≔{\dot{E}}^X(\mathrm{19b})$

as the transduced work from X to Y. Thus, an externally manipulated control parameter could be understood as the limiting case of a negligible back-action from the downstream system to the (possibly deterministic) dynamics of the upstream system. This identification of energy flows communicated between the systems becomes useful when singling out one subsystem that is driven (possibly with feedback) by another one (see Section 6).

Figure 2 summarizes the splitting of the first law presented in this section and illustrates how energy moves between the subsystems.

FIGURE 2

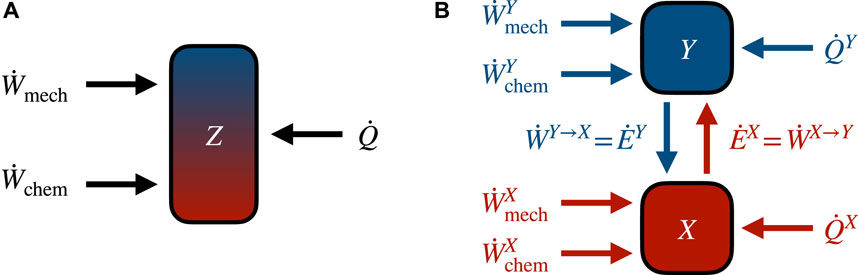
FIGURE 2. Energy flows in autonomous bipartite systems. (A) Global energy flows can be distinguished between work (mechanical and chemical) and heat. Since at steady state the average global internal energy stays constant, average flows of work and heat must cancel. (B) The bipartite assumption (2) allows decomposition of energy flows into contributions from each subsystem. Color and direction of arrows reflect the subsystem-specific first laws (17a) in red and (17b) in blue.

4 Entropy and free-energy balance

As always in thermodynamics, energetics are only half of the picture. We therefore next consider entropic quantities. Together, the rate $\dot{E}$ of change of global internal energy E (11), and the rate $\dot{S}$ of change of global entropy S (defined in the following) determine the rate of change of nonequilibrium (or “generalized”) free energy [88–91],

$\dot{F}≔\dot{E}-k_{\text{B}}T\dot{S}.(20)$

4.1 Global entropy balance

Following Ref. [4], we explicitly write the rate of change of system entropy:

$\dot{S}=-{\displaystyle \sum _{x,y}}\frac{\mathrm{d}}{\mathrm{d}t}p\left(x,y\right)\ln p\left(x,y\right)(\mathrm{21a})$

$=-{\displaystyle \sum _{x,x^{\prime },y,y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln p\left(x,y\right)(\mathrm{21b})$

$=-{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x^{\prime },y^{\prime }\right)}(\mathrm{21c})$

$\begin{array}{ll}\hfill & =\underset{≕\dot{\mathrm{\Sigma }}}{\underbrace{{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{{yy}^{\prime }}^{{xx}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_{{yy}^{\prime }}^{{xx}^{\prime }}p\left(x^{\prime },y^{\prime }\right)}{R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)}}}\hfill \\ \hfill & -\underset{=-\dot{Q}/k_{\text{B}}T}{\underbrace{{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{{yy}^{\prime }}^{{xx}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_{{yy}^{\prime }}^{{xx}^{\prime }}}{R_{y^{\prime }y}^{x^{\prime }x}}}},\hfill \end{array}(\mathrm{21d})$

where we have used the Master equation (1) in Eq. (21b), the fact that Eq. (21b) sums over every transition twice in Eq. (21c), and the definition of the heat flow (8) in Eq. (21d).

Rearranging the terms gives the global second law:

$\dot{\mathrm{\Sigma }}=\dot{S}-\frac{\dot{Q}}{k_{\text{B}}T}(\mathrm{22a})$

$={\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)}{R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)}(\mathrm{22b})$

$\ge 0,(\mathrm{22c})$

where $\dot{\mathrm{\Sigma }}$ is the rate of global entropy production, i.e., the rate at which entropy is produced in the whole system and attached baths. Its nonnegativity follows from the fact that, in each term of the sum in Eq. (22b), the two factors are always either both positive or both negative.

Using the definition of nonequilibrium free energy (20) and the global first law (12), we rewrite the global second law as

${\dot{W}}_{\text{mech}}+{\dot{W}}_{\text{chem}}-\dot{F}\ge 0.(23)$

4.1.1 Marginal and hidden entropy production

An interesting digression covers related research on inferring total entropy production from the dynamics of only one subsystem. Prominent examples of such systems with hidden degrees of freedom are molecular transport-motor experiments [73, 92] in which only trajectories of an attached cargo are observed while the motor dynamics are hidden. Assessing motor efficiency, however, necessitates a detailed knowledge of the internal motor dynamics. Hence thermodynamic inference [83] is required to infer hidden system properties.

Alongside dynamics on masked Markovian networks [93–102], bipartite systems have been used to model situations in which one sub-component of the full system is hidden. One common strategy consists of mapping the observed dynamics of one subsystem onto a Markov model, which generally produces a lower bound on the total entropy production rate [86] that can subsequently be augmented with any information available about the hidden dynamics [103]. However, the observed process is non-Markovian which results, e.g., in modifications of fluctuation theorems [104–106]. Another approach is to use thermodynamic uncertainty relations [107–111] to produce a bound on the total entropy production using observable currents.

Importantly, the formalism laid out here requires full observability of the dynamics of both subsystems; recent efforts have explored when one can infer the kind of driving mechanism from observations of just one degree of freedom, e.g., the dynamics of probe particles attached to unobserved molecular motors [92, 112].

4.2 Subsystem-specific entropy balance

In analogy to subsystem-specific versions of the first law (17a), (17b) which introduce energy flows between the different subsystems, subsystem-specific versions of the second law introduce an entropic flow between the systems, called information flow.

The bipartite assumption (2) splits the global entropy production (22b) into two nonnegative contributions, $\dot{\mathrm{\Sigma }}={\dot{\mathrm{\Sigma }}}^X+{\dot{\mathrm{\Sigma }}}^Y$:

${\dot{\mathrm{\Sigma }}}^X≔{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)}{R_y^{x^{\prime }x}p\left(x,y\right)}\ge 0(\mathrm{24a})$

${\dot{\mathrm{\Sigma }}}^Y≔{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\ln \frac{R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)}{R_{y^{\prime }y}^{x}p\left(x,y\right)}\ge 0.(\mathrm{24b})$

To make contact with the form of the global second law (22a), we identify different contributions to the subsystem-specific entropy productions ${\dot{\mathrm{\Sigma }}}^X$ and ${\dot{\mathrm{\Sigma }}}^Y$:

${\dot{\mathrm{\Sigma }}}^X={\dot{S}}^X-\frac{{\dot{Q}}^X}{k_{\text{B}}T}(\mathrm{25a})$

${\dot{\mathrm{\Sigma }}}^Y={\dot{S}}^Y-\frac{{\dot{Q}}^Y}{k_{\text{B}}T},(\mathrm{25b})$

where ${\dot{Q}}^X$ and ${\dot{Q}}^Y$ are the heat flows (13b) and (13c) into the respective subsystems and, in accordance with the identification of rates of change of energy in Eqs (16b) and (16c), we identify the rates of change of total entropy due to the individual subsystem dynamics.

${\dot{S}}^X≔-{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x^{\prime },y\right)}(\mathrm{26a})$

${\dot{S}}^Y≔-{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x,y^{\prime }\right)}.(\mathrm{26b})$

Importantly, these rates are not the rates of change of marginal entropies S[X] = −∑ _x p(x) ln p(x) and S[Y] = −∑_yp(y) ln p(y). Rewriting the subsystem-specific entropy productions with these marginal rates leads to the identification of an information flow, as we show in Section 4.3.

Substituting the subsystem-specific first laws (17a), (17b) gives subsystem-specific second laws in terms of work and free energy,

${\dot{W}}_{\text{mech}}^X+{\dot{W}}_{\text{chem}}^X-{\dot{F}}^X\ge 0(\mathrm{27a})$

${\dot{W}}_{\text{mech}}^Y+{\dot{W}}_{\text{chem}}^Y-{\dot{F}}^Y\ge 0,(\mathrm{27b})$

where ${\dot{F}}^X={\dot{E}}^X-k_{\text{B}}T{\dot{S}}^X$ is the rate of change of nonequilibrium free energy due to the dynamics of X, and similarly for ${\dot{F}}^Y$. Their sum gives the rate of change $\dot{F}$ of the nonequilibrium free energy.

While formally appealing, the rate of change of nonequilibrium free energy due to one subsystem’s dynamics has little utility. Often, one only knows the free energy for one subsystem (e.g., by having constructed a potential-energy landscape for one of the subsystems as done in [113] for the F₁-component of ATP synthase) or the free energy of one subsystem is unknown or undefined (e.g., for the external environment process in a sensing setup). To this end, we next present other ways of writing (and interpreting) the subsystem-specific second laws.

4.3 Subsystem-specific second laws with information flows

We express the rate ${\dot{S}}^X$ of change of total entropy due to the dynamics of X (26a) in terms of the rate of change of marginal entropy,

$\dot{S}\left[X\right]=-{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x\right)}{p\left(x^{\prime }\right)},(28)$

and similarly for ${\dot{S}}^Y$ to rewrite Eqs (25a), (25b) as

$0\le {\dot{\mathrm{\Sigma }}}^X=\dot{S}\left[X\right]-\frac{{\dot{Q}}^X}{k_{\text{B}}T}-{\dot{I}}^X(\mathrm{29a})$

$0\le {\dot{\mathrm{\Sigma }}}^Y=\dot{S}\left[Y\right]-\frac{{\dot{Q}}^Y}{k_{\text{B}}T}-{\dot{I}}^Y.(\mathrm{29b})$

Here, we have identified the remaining terms as the information flows [87],

${\dot{I}}^X≔\underset{\text{d}t\to 0}{\lim }\frac{I\left[X_{t+\mathrm{d}t};Y_t\right]-I\left[X_t;Y_t\right]}{\mathrm{d}t}(\mathrm{30a})$

${\dot{I}}^Y≔\underset{\text{d}t\to 0}{\lim }\frac{I\left[X_t;Y_{t+\mathrm{d}t}\right]-I\left[X_t;Y_t\right]}{\mathrm{d}t},(\mathrm{30b})$

i.e., the rate of change of mutual information between the subsystems that is due only to the dynamics of one of them. Information flow is positive when the dynamics of the corresponding subsystem increase the mutual information between the two subsystems. In Supplementary Appendix S1 we show that for bipartite Markovian dynamics this definition leads to

${\dot{I}}^X={\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(y|x\right)}{p\left(y|x^{\prime }\right)},(\mathrm{31a})$

${\dot{I}}^Y={\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)},(\mathrm{31b})$

i.e., the form used in [57] with which we can verify the equality of Eq. (25a) and Eq. (29a) and similarly of Eq. (25b) and Eq. (29b). Equations (29a), (29b) express the same subsystem-specific entropy productions as Eqs (25a), (25b). The latter contain subsystem-specific changes ${\dot{S}}^X$ and ${\dot{S}}^Y$ of the global (joint) entropy S. In contrast, the former contain changes of the marginal entropies S[X] and S[Y]. Joint entropy not only contains the sum of marginal entropies, but also the mutual information, S = S[X] + S[Y] − I[X; Y] [81, Chap. 2.3]. Consequently, changes in joint entropy not only contain contributions from the changes of marginal entropies, but also the change in mutual information. The information flows I^X and I^Y distribute this rate of change symmetrically across the two subsystem-specific entropy productions. Summing (30a) and (30b) yields the total change in mutual information between X and Y. For Markovian bipartite dynamics this reads explicitly.

${\dot{I}}^X+{\dot{I}}^Y={\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\left[\ln \frac{p\left(y|x\right)}{p\left(y|x^{\prime }\right)}+\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)}\right](\mathrm{32a})$

$={\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\left[\ln \frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\frac{p\left(x^{\prime }\right)p\left(y^{\prime }\right)}{p\left(x^{\prime },y^{\prime }\right)}+\ln \frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\frac{p\left(x^{\prime }\right)p\left(y^{\prime }\right)}{p\left(x^{\prime },y^{\prime }\right)}\right](\mathrm{32b})$

$={\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}\frac{p\left(x^{\prime }\right)p\left(y^{\prime }\right)}{p\left(x^{\prime },y^{\prime }\right)}(\mathrm{32c})$

$=\dot{I},(\mathrm{32d})$

where the bipartite assumption (2) ensures that there is no contribution from transitions in which x and y change simultaneously.

The term information flow was first used in the context of non-equilibrium thermodynamics by Allahverdyan et al. [87] and was later taken up by Horowitz and Esposito [57]. Section 5.1 compares information flow with conceptually similar quantities called nostalgia [114] and learning rate [65].

Notice the appealing structure of the subsystem-specific entropy productions in Eqs (29a) and (29b): For interacting subsystems, it is not enough to consider marginal entropy changes and heat flows into one subsystem, because to obtain a non-negative entropy production rate, one needs an additional term due to correlations between the interacting subsystems. Expressed differently: When one explicitly neglects or is unaware of other subsystems strongly coupled to the subsystem of interest, erroneous conclusions about the entropy production are possible, either overestimating it or perhaps even finding it to be negative, leading to a Maxwell-demon-like paradox.

We next present two alternative representations of the same subsystem-specific entropy production that rely on rewriting the rate of change of global entropy ${\dot{S}}^X$ due to X dynamics in terms of the time-derivative of conditional entropy, $\dot{S}[X|Y]$, instead of the time-derivative of marginal entropy, $\dot{S}[X]$.

4.3.1 Alternative representation of subsystem-specific entropy production in terms of conditional entropy

In addition to the formulation in Eq. (29a), the subsystem-specific entropy production in Eq. (25a) can also be rewritten in terms of the rate of change $\dot{S}[X|Y]=-\frac{\mathrm{d}}{\mathrm{d}t}{\sum }_{x,y}p(x,y)\ln p(x|y)$ of conditional entropy, since.

${\dot{S}}^X=-{\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x^{\prime },y\right)}(\mathrm{33a})$

$=-{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x,y\right)}{p\left(x^{\prime },y\right)}(\mathrm{33b})$

$=-{\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(x|y\right)}{p\left(x^{\prime }|y^{\prime }\right)}\frac{p\left(x^{\prime }|y^{\prime }\right)}{p\left(x^{\prime }|y\right)}(\mathrm{33c})$

$=\dot{S}\left[X|Y\right]-{\displaystyle \sum _{x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x^{\prime }}p\left(x^{\prime },y^{\prime }\right)-R_{y^{\prime }y}^{x^{\prime }}p\left(x^{\prime },y\right)\right]\ln \frac{p\left(x^{\prime }|y^{\prime }\right)}{p\left(x^{\prime }|y\right)}(\mathrm{33d})$

$=\dot{S}\left[X|Y\right]+{\dot{I}}^Y,(33e)$

where line (33b) uses the bipartite assumption (2) along with the fact that, due to the log-ratio in Eq. (33b), all terms y ≠ y′ are zero. Line (33e) follows from the definition (31b) of ${\dot{I}}^Y$. This leads to

$0\le {\dot{\mathrm{\Sigma }}}^X=\dot{S}\left[X|Y\right]-\frac{{\dot{Q}}^X}{k_{\text{B}}T}+{\dot{I}}^Y.(34)$

Comparing with Eq. (25a), which expresses the same subsystem-specific entropy production, we observe a difference in interpretation: If one interprets Y not as a subsystem on equal footing with X but instead as a stochastic control protocol for system X, the subsystem-specific second law in Eq. (34) seems more natural. Such stochastic control protocols arise naturally in the context of sensors, where a changing environment effectively acts as a stochastic protocol [114], and in contexts with measurement-feedback loops where a stochastic measurement of the system state dictates the statistics of the future control protocol [11–15, 115].

4.3.2 Subsystem-specific second law with conditional free energy

In cases where the nonequilibrium free energy of subsystem X is known, we define a conditional nonequilibrium free energy of system X given a control parameter Y as the average energy of X given the particular control-parameter value y less (k_BT times) the average entropy of X given the control-parameter value y, all averaged over Y.

$F\left[X|Y\right]≔{⟨{⟨{ϵ}_{xy}⟩}_{p\left(x|y\right)}-k_{\text{B}}T(-{\displaystyle \sum _x}p\left(x|y\right)\ln p\left(x|y\right))⟩}_{p\left(y\right)}(\mathrm{35a})$

$=E-k_{\text{B}}TS\left[X|Y\right].(\mathrm{35b})$

Thus, this free energy is averaged over all stochastic control-parameter values.

With the splitting of the first law in Eq. (16a), the subsystem-specific first law in Eq. (17a), and the identification of transduced work ${\dot{W}}^{Y\to X}$ in Eq. (19a), we rewrite the subsystem-specific second law in Eq. (34) as.

$0\le k_{\text{B}}T{\dot{\mathrm{\Sigma }}}^X={\dot{W}}^{Y\to X}+{\dot{W}}_{\text{mech}}^X+{\dot{W}}_{\text{chem}}^X-\dot{F}\left[X|Y\right]+k_{\text{B}}T{\dot{I}}^Y(\mathrm{36a})$

$={\dot{W}}^{\to X}-\dot{F}\left[X|Y\right]+k_{\text{B}}T{\dot{I}}^Y,(\mathrm{36b})$

where ${\dot{W}}^{\to X}≔{\dot{W}}^{Y\to X}+{\dot{W}}_{\text{mech}}^X+{\dot{W}}_{\text{chem}}^X$ is the total input work into subsystem X. Again, compared to the regular second law, there is an additional information flow modifying the entropy balance.

4.4 Steady-state flows

At steady state, average energy, entropy, and mutual information are all constant, $\dot{E}=\dot{S}=\dot{S}[X]=\dot{S}[X|Y]=\dot{I}[X;Y]=0$. However, this does not imply that the subsystem-specific rates of change vanish, too; but the energy and information flows do simplify, giving

${\dot{E}}^X={\dot{W}}^{X\to Y}=-{\dot{W}}^{Y\to X}=-{\dot{E}}^Y(\mathrm{37a})$

${\dot{I}}^X=-{\dot{I}}^Y,(\mathrm{37b})$

i.e., if one subsystem’s dynamics increase the average energy or mutual information, the dynamics of the other must compensate this change accordingly, to ensure constant energy and mutual information at steady state. These relations are especially useful for the dynamics of biological systems which can often be modelled as at steady state.

4.5 Marginal and conditional entropy productions

Note that the subsystem-specific entropy productions ${\dot{\mathrm{\Sigma }}}^X$ and ${\dot{\mathrm{\Sigma }}}^Y$ are neither marginal nor conditional entropy productions, i.e., they do not result from the time-reversal statistics of the non-Markovian marginal processes obtained by only observing the X- or Y-dynamics or of the statistics of trajectories of one subsystem conditioned on the trajectory of the other.

It is possible to define such marginal and conditional entropy productions for bipartite Markov processes. As shown by Crooks and Still [116], the total entropy production $\dot{\mathrm{\Sigma }}$ is then split into non-negative marginal and conditional contributions. Similarly to the subsystem-specific entropy production rates in (29a), (29b), which contain the information flows ${\dot{I}}^X$ and ${\dot{I}}^Y$, the resulting marginal and conditional entropy productions contain information-theoretic exchange terms. Unlike the information-flow formalism presented here, such a splitting is not symmetric: this may be natural when there is a clear distinction between the subsystems, e.g., in the context of a sensor influenced by an external environment signal (Section 5), but perhaps less so when one has reason to treat the subsystems on equal footing.

4.6 Tighter second laws and information engines

Historically, the question of how to incorporate information into a thermodynamic theory so as to restore the second law’s validity has attracted much interest. Discussions ranged around the thought experiment of Maxwell’s demon [6, 7], with well-known contributions from Szilard [8], Landauer [9], and Bennett [10]. Within stochastic thermodynamics, Maxwell’s demon has been formalized as a process with (repeated) feedback [11–15] and interactions with an information reservoir (often modeled as a tape of bits) [18–21].

The advent of increasingly refined experimental techniques for microscale manipulation has enhanced the prospect of finding realizations of Maxwell’s thought experiment in real-world molecular machinery, stimulating a formalization of the thermodynamics of information [22]. The bulk of the experimental realizations demonstrating the possibility of information engines utilize some kind of time-dependent external control [32, 34, 37–39, 41, 43–46]. In a recent example, an optically trapped colloidal particle X is ratcheted against gravity without the trap Y transducing any work W^Y→X to it, thus enabling the complete conversion of heat to actual mechanical output work $-W_{\text{mech}}^X$ in the gravitational potential [27, 47].

The picture of autonomous interacting subsystems does not naturally allow such a clear distinction between measurement and feedback, or between system and tape [56]. Instead, continuous Maxwell demons are identified by current reversals, apparently making heat flow against the direction indicated by the second law [35, 59, 117, 118]. In this context the information-flow formalism produces a bound on apparent second-law violations in one subsystem using an information-theoretic quantity.

We are now in a position to assess the role of information flows in the operation of two-component systems and make contact with Maxwell’s demon. We focus on the specific second law applied to the X-subsystem. Rearranging (34), we obtain:

$\dot{S}\left[X|Y\right]-\frac{{\dot{Q}}^X}{k_{\text{B}}T}\ge -{\dot{I}}^Y,(38)$

where the LHS is a conventional expression for the entropy production due to system X (entropy change of the system state X at fixed Y, minus heat flow ${\dot{Q}}^X$ into the system) and the RHS is an information-theoretic quantity measuring an aspect of correlation between X and another system Y.

Let us distinguish two cases: 1) If ${\dot{I}}^Y<0$—naturally arising whenever there is no feedback from X to Y—(38) represents an improved lower bound on the traditional expression for entropy production.

2) If ${\dot{I}}^Y>0$, (38) states that the traditional expression for entropy production can become negative, in apparent contradiction to the second law. This can reasonably be interpreted as a Maxwell-demon setup, and in this continuous-time formalism can immediately be applied to autonomous Maxwell demons such as [35, 59, 117, 118].

In Section 5 and Section 6 we discuss both cases in detail.

5 Sensors: External Y-dynamics

The performance limits of biomolecular sensors such as those found in Escherichia coli have gained attention [119–122]. As observed by Berg and Purcell [123], the main challenge faced by sensors tasked with measuring concentrations in the microscopic world is the stochastic nature of their input signal, i.e., the irregular arrival and binding of diffusing ligands; different strategies can improve inference of ligand concentration [124–126].

Sensing has also been studied from an information-thermodynamics perspective, where the main question revolves around the minimum thermodynamic cost to achieve a given sensor accuracy. Maintaining correlation between an internal downstream signalling network and an external varying environment is costly [62, 127–131] and involves erasing and rewriting a memory, analogous to a Maxwell demon [132]. Here, we focus on a high-level characterization of biomolecular sensing that uses bipartite Markov processes.

Specifically, in a sensor setup, the stochastic dynamics of one of the subsystems (the environmental signal) are independent of the other (the sensor). Figure 1B shows an example of a sensor setup inspired by the signaling network involved in E. coli chemotaxis. Let Y be an external process (e.g., whether a ligand is bound to the receptor) that influences the transition rates of the sensor X, but whose transition rates are independent of X: $R_{y{y}^{\prime }}^x=R_{y{y}^{\prime }}$. This implies the nonpositivity of the Y-information flow in (31b):

${\dot{I}}^Y={\displaystyle \sum _{x,y>y^{\prime }}}{R}_{y{y}^{\prime }}p\left(x,y^{\prime }\right)\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)}-{\displaystyle \sum _{x,y>y^{\prime }}}{R}_{y^{\prime }y}p\left(x,y\right)\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)}(\mathrm{39a})$

$={\displaystyle \sum _{x,y^{\prime }>y}}{R}_{y^{\prime }y}p\left(x,y\right)\ln \frac{p\left(x|y^{\prime }\right)}{p\left(x|y\right)}-{\displaystyle \sum _{x,y>y^{\prime }}}{R}_{y^{\prime }y}p\left(x,y\right)\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)}(\mathrm{39b})$

$=-{\displaystyle \sum _{y\ne y^{\prime }}}{R}_{y^{\prime }y}p\left(y\right)\underset{\ge 0}{\underbrace{\sum _{x}p\left(x|y\right)\ln \frac{p\left(x|y\right)}{p\left(x|y^{\prime }\right)}}}(\mathrm{39c})$

$\le 0,(\mathrm{39d})$

where in Eq. (39b) we swapped summation indices y ↔ y′ in the first sum, and in Eq. (39c) the term with an underbrace is a relative entropy and hence is nonnegative [81, Chap. 2.3].

Equation (34) thus implies a stronger second-law inequality:

$\dot{S}\left[X|Y\right]-\frac{{\dot{Q}}^X}{k_{\text{B}}T}\ge -{\dot{I}}^Y\ge 0.(40)$

The LHS represents the sensor’s entropy production, which is lower-bounded by an information-theoretic quantity that has various interpretations in the literature. In the following we will build intuition about this quantity and comment on its relation to the sensor’s measuring performance.

5.1 Nostalgia and learning rate

The first inequality in Eq. (40) was originally pointed out by Still, et al. in a discrete-time formalism [114] and for possibly non-Markovian external processes. In that formalism, $-{\dot{I}}^Y$ is interpreted as nostalgia quantifying the share of the mutual information between X and Y that is not predictive of the immediate future of Y or, equivalently, the rate at which information between X and Y becomes irrelevant due to Y dynamics. A sensor that predicts the future signal worse—in the sense of storing more information that is useless for predicting the next signal state—thus produces more entropy than one that is more predictive, raising the possibility that evolution selects for sensors that make parsimonious predictions.

A second related quantity is the learning rate ℓ_x introduced by Barato et al. [65]. Originally defined for systems in steady state, it is exactly the information flow ${\dot{I}}^X$ in Eq. (31a):

${\ell }_{\text{x}}={\dot{I}}^X.(41)$

The learning rate quantifies how the uncertainty in an external signal Y is reduced by the dynamics of X, i.e., how much X learns about Y:

${\ell }_{\text{x}}={\displaystyle \sum _{x>x^{\prime },y}}\left[R_y^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_y^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(y|x\right)}{p\left(y|x^{\prime }\right)}(\mathrm{42a})$

$\begin{array}{ll}\hfill & ={\displaystyle \sum _{x>x^{\prime },y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x{x}^{\prime }}p\left(x^{\prime },y\right)-R_{y^{\prime }y}^{x^{\prime }x}p\left(x,y\right)\right]\ln \frac{p\left(y|x\right)}{p\left(y^{\prime }|x^{\prime }\right)}\hfill \\ \hfill & -{\displaystyle \sum _{x,y>y^{\prime }}}\left[R_{y{y}^{\prime }}^{x}p\left(x,y^{\prime }\right)-R_{y^{\prime }y}^{x}p\left(x,y\right)\right]\ln \frac{p\left(y|x\right)}{p\left(y^{\prime }|x\right)}\hfill \end{array}(\mathrm{42b})$

$=-\dot{S}\left[Y|X\right]+{\dot{S}}^Y\left[Y|X\right].(\mathrm{42c})$

We used the bipartite assumption (2) in the second line. Here ${\dot{S}}^Y[Y|X]$ is the rate of change of S [Y|X] that is due to the Y-dynamics [65, 133].

In the special case of a steady state $(\dot{S}[Y|X]=0)$, the information flows cancel $({\ell }_x={\dot{I}}^X=-{\dot{I}}^Y)$ and inequality (40) reduces to

$-\frac{{\dot{Q}}^X}{k_{\text{B}}T}\ge {\ell }_{\text{x}}.(43)$

This motivated Barato et al. to define an informational efficiency [65], $\eta ≔-k_{\text{B}}T{\ell }_{\text{x}}/{\dot{Q}}^X$, measuring the share of a sensor’s dissipation that is used to actually track the environmental signal.

The following series of (in-)equalities sums up the relations between the different measures of information flow:

${\dot{I}}^X=\underset{\text{learning}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}}{\underbrace{{\ell }_{\text{x}}}}(\mathrm{44a})$

$=\underset{\text{d}t\to 0}{\lim }\frac{I\left[X_{t+\mathrm{d}t};Y_t\right]-I\left[X_t;Y_t\right]}{\mathrm{d}t}\left[(30a)\right](\mathrm{44b})$

$=\dot{I}-{\dot{I}}^Y\left[(32d)\right](\mathrm{44c})$

$=\underset{(\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{o}\mathrm{f})\mathrm{n}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{g}\mathrm{i}\mathrm{a}}{\underbrace{-{\dot{I}}^Y}}\left[\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\right](\mathrm{44d})$

$\ge 0.\left[\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}Y-\mathrm{d}\mathrm{y}\mathrm{n}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{s}\right](44e)$

5.2 Other information-theoretic measures of sensor performance

While information flow bounds sensor dissipation and has intuitive interpretations in terms of predictive power [114] and learning rate [65], other information-theoretic quantities seem more natural to measure sensor performance.

For example, Tostevin and ten Wolde [134] have calculated the rate of mutual information between a sensor’s input and output; however, Barato et al. [64] have shown that this rate is not bounded by the thermodynamic entropy production rate. (The desired inequality requires both the time-forward trajectory mutual information rate and its time-reversed counterpart [135].)

Another commonly used quantity to infer causation is the (rate of) transfer entropy [136], which in turn is a version of directed information [137, 138] (for a gentle introduction see, e.g. [139], section 15.2.2). Much like information flow, this rate also bounds the sensor’s entropy production rate [133]; however, in general, it represents a looser bound than the information flow. The transfer-entropy rate measures the growth rate of mutual information between the current environmental signal and the sensor’s past trajectory. This motivated Hartich et al. [140] to define sensory capacity as the ratio of learning rate and transfer-entropy rate, measuring the share of total information between environmental signal and the entire sensor’s past that the sensor’s instantaneous state carries. It is maximal if the sensor is an optimal Bayesian filter [141, 142].

Finally, a natural quantity to measure a sensor’s performance is the static mutual information between its state and the environmental signal. Brittain et al. [143] have shown that in simple setups, learning rate and mutual information change in qualitatively similar ways when system parameters are varied; however, in more complex setups with structured environmental processes or feedback from the sensor to the environment, maximizing the learning rate might produce a suboptimal sensor. They rationalize this result by noting that the rate at which the sensor must obtain new information to maintain a given level of static mutual information does not necessarily coincide with the magnitude of that static mutual information.

6 Engine setups: Feedback from X to Y

Here, we consider the more general case of an engine setup in which the two components X and Y cannot be qualitatively distinguished as an external and an internal process; instead, both components X and Y form a joint system. On a formal level, there now is feedback from X to Y, such that (39d) no longer holds in general and it is not possible to make model-independent statements about the direction of information flow. To make contact with analyses of multi-component molecular machines, we present a few conceptual differences between external control by an experimenter and what we call autonomous control by another coupled stochastic system.

6.1 External vs autonomous control

There is a long history of nonequilibrium statistical mechanics motivated by single-molecule experiments. A hallmark of these experiments is dynamical variation by an external apparatus of control parameters such as the position or force of an optical trap [144], magnetic trap [145], or atomic-force microscope [146]. This external control allows an unambiguous identification of work done on a system as the change in internal energy achieved through the variation of control parameters, and heat as the complementary change of internal energy due to the system’s dynamics. Sekimoto [147, 148] has identified heat and work for diffusive dynamics described by a Langevin equation; this identification readily carries over to discrete dynamics [2, 4] and even Hamiltonian dynamics [3].

The notion of a deterministic control-parameter trajectory allows, e.g., the derivation of fluctuation theorems [149–151] and the study of how to optimize such a trajectory to minimize the average work done on the system [152–157] or its fluctuations [158, 159]. Feedback can also be included in the analysis by considering measurements and subsequent modifications to the control-parameter trajectory that depend on measurement outcome [11–15].

However, in biological systems, there is generally no dynamical variation of external control parameters. Instead, these systems are autonomous, and stochastic thermodynamics occurs in the context of relatively constant but out-of-equilibrium “boundary conditions”: a single temperature and a variety of chemical potentials that are mutually inconsistent with a single equilibrium system distribution, thus leading to free-energy transduction [74] when the coupling is sufficiently strong such that not all currents flow in the direction of their driving force. Increasingly, researchers are modeling molecular machines as multi-component systems with internal flows of energy and information. Examples are the molecular motor F_o−F₁ ATP synthase [66, 160, 161] that can be modeled using two strongly coupled subsystems [54, 162–166], or molecular motor-cargo collective systems where sometimes hundreds of motors (such as kinesin, dynein [167], and myosin [168]) work in concert [68, 69], leading to different performance trade-offs [169–174].

Nonetheless, multi-component systems can be interpreted as if the dynamics of one component provide a variation of external control parameters to the other. In this context, it can be useful to identify an upstream (more strongly driven by nonequilibrium boundary conditions) system Y and a downstream (more strongly driven by the coupled upstream system than by the nonequilibrium boundary conditions) system X, although the identification of these components may sometimes be ambiguous. This type of autonomous control differs from external control in two important aspects: 1) It is stochastic since the dynamics of the upstream system are itself stochastic; 2) There is feedback from the downstream to the upstream system because the upstream system’s dynamics obey local detailed balance (7). Both aspects can lead to counterintuitive results when one naively applies stochastic energetics to one subsystem that is strongly coupled to others [55].

6.2 Conventional and information engines

Let us more closely examine two-component engines, e.g., the F_o−F₁ ATP synthase sketched in Figure 1A. Such a molecular machine can be regarded as a kind of chemical-work transducer using a stronger upstream chemical gradient to drive a downstream chemical reaction against its natural direction [49, 175]. Recently, the coupling characteristics and energy flows in such systems have received attention [54, 55, 67, 166].

It is natural to consider direct energy flows from an input (chemical) reservoir (e.g., ${\dot{W}}_{\text{chem}}^Y$) through the transduced work (e.g., ${\dot{W}}^{Y\to X}$) between subsystems to an output reservoir (e.g., $-{\dot{W}}_{\text{chem}}^X$), with two intermediate heat losses ($-{\dot{Q}}^Y$ and $-{\dot{Q}}^X$), see Figure 3A. However, a completely different mode of operation is also possible where the input work is not used to transduce energy from Y to X but to rectify thermal fluctuations of X, hence converting input heat ${\dot{Q}}^X$ into output work $-{\dot{W}}_{\text{chem}}^X$, see Figure 3B. The second setup can be interpreted as an information engine, a realization of a Maxwell demon [7], where X is the thermodynamic system controlled by the demon Y. Focusing on the energy flows into and out of system X alone would lead an observer to the erroneous conclusion that heat is entirely converted into useful work, a process forbidden by the second law. However this apparent second-law violation results from neglecting the other part of the machine (Y), which, to restore the second law, must dissipate more heat into the environment than X converts into work. As discussed in Section 4, the bipartite assumption gives the information flow as a measure to assess the extent to which a given system acts as an information engine.

FIGURE 3

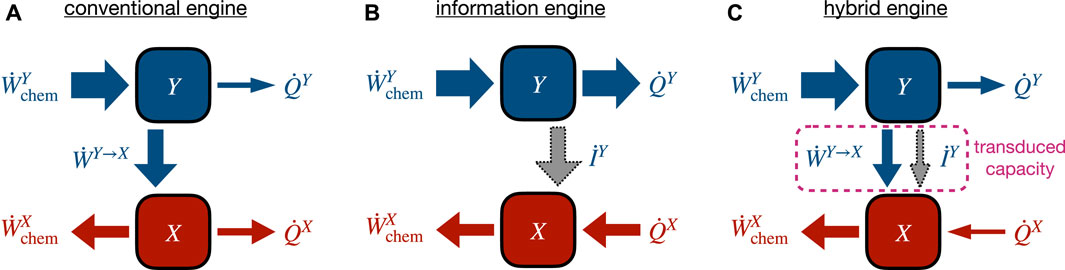
FIGURE 3. Different operational modes of a two-component engine converting chemical input power ${\dot{W}}_{\text{chem}}^Y$ to chemical output power $-{\dot{W}}_{\text{chem}}^X$. Arrow direction and thickness respectively indicate the net energy flow’s direction and magnitude. (A) In a conventional engine, input power ${\dot{W}}^{Y\to X}$ is transduced from the upstream component to the downstream component to end up as output power, with heat losses $-{\dot{Q}}^Y$ and $-{\dot{Q}}^X$ in the process. (B) An information engine uses the input power into the upstream component to rectify thermal fluctuations in the downstream component into output power. To achieve this, the upstream component must create information flow ${\dot{I}}^Y$ that the downstream component can exploit. (C) A hybrid engine uses a mixture of both operation modes. Transduced power and information flow sum to give the transduced capacity.

6.3 Steady-state transduced capacity

Our discussion indicates that conventional and information engines can be treated with a common framework, as in [49] where a synthetic molecular motor was analyzed, identifying distinct flows of information and energy with which the upstream subsystem drives the downstream subsystem. For concreteness, let Y be the upstream and X be the downstream subsystem. As shown in [67, 176], combining the subsystem-specific second laws at steady state leads to a simultaneous bound on input and output power in terms of an intermediate quantity, called transduced capacity in [67]. Substituting the steady-state identities $\dot{S}[X]=0=\dot{S}[Y]$ and ${\dot{I}}^X=\dot{I}-{\dot{I}}^Y=-{\dot{I}}^Y$ into the subsystem-specific entropy productions (29a) and (29b) gives

$-\frac{{\dot{Q}}^X}{k_{\text{B}}T}+{\dot{I}}^Y\ge 0(\mathrm{45a})$

$-\frac{{\dot{Q}}^Y}{k_{\text{B}}T}-{\dot{I}}^Y\ge 0.(\mathrm{45b})$

Using the subsystem-specific first laws in Eqs (17a) and (17b) and identifying the transduced power in Eq. (19a) gives ${\dot{E}}^Y=-{\dot{E}}^X={\dot{W}}^{Y\to X}$, so that

$\underset{\text{input}\mathrm{p}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}}{\underbrace{\frac{{\dot{W}}_{\text{chem}}^Y+{\dot{W}}_{\text{mech}}^Y}{k_{\text{B}}T}}}\ge \underset{\text{transduced\hspace{0.17em}\hspace{0.17em}capacity}}{\underbrace{\frac{{\dot{W}}^{Y\to X}}{k_{\text{B}}T}+{\dot{I}}^Y}}\ge \underset{\text{output}\mathrm{p}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}}{\underbrace{-\frac{{\dot{W}}_{\text{chem}}^X+{\dot{W}}_{\text{mech}}^X}{k_{\text{B}}T}}}.(46)$

This relation suggests that the transduced capacity acts as a bottleneck for the conversion of input to output power. The capacity of this bottleneck consists of two distinct pathways, a conventional energetic component ${\dot{W}}^{Y\to X}$, with which the upstream subsystem drives the downstream subsystem by doing work on it, as well as an information-theoretic component ${\dot{I}}^Y$, with which the upstream subsystem creates information between the two subsystems that the downstream subsystem can exploit to generate output power. This hybrid setup is illustrated in Figure 3C.

We expect efficient work transducers to come as close as possible to saturating both inequalities to minimize dissipative losses during their operation. It would be interesting to investigate under which circumstances each of the two pathways leads to the most efficient work transducers and whether real-world biomolecular machinery has evolved to preferentially exploit one over the other.

7 Conclusion, extensions, and outlook

7.1 Summary

In this review we focused on the thermally influenced stochastic dynamics of two-component autonomous systems which are commonly found in biological machinery. We assumed that the dynamics are Markovian and bipartite such that only one subsystem changes its state at a time.

We collected results that show how the bipartite assumption enables the first and second laws of thermodynamics to be split into subsystem-specific versions. The subsystem-specific first laws lead to energy flows between the individual subsystems and the environment and to the transduced power—the energy flow between the subsystems. The subsystem-specific second laws reveal information flows as specific entropic quantities that quantify how the dynamics of a single subsystem change the mutual information shared between the subsystems.

Sensors are a setup to which the formalism applies naturally because an external signal influences the stochastic dynamics of the sensor. Within the framework, the sensor’s dissipation (the energy flow) is bounded by an information-theoretic quantity (the information flow) measuring aspects of the influence of the environmental signal on the sensor.

Studying strongly coupled molecular machines within this framework reveals that the more conventional transduced power (the energy flow) from one subsystem to the other is accompanied by the less conventional information flow, which can be interpreted as a hallmark of information engines. Both flows are capable of supporting energy transduction through the coupled system such that conventional and information engines can be studied from the same perspective.

7.2 More than two subsystems

The question naturally arises whether the information-flow framework can be extended to systems with more than two subsystems. For such systems, Horowitz [58] defined an information flow ${\dot{I}}^{X;Z_{-X}}$, i.e., the information flow between X and all other subsystems Z_−X that together compose the global system. This flow is then further refined by identifying which other subsystems can directly interact with X, and subsystem-specific second laws of the form of (25a), (25b) follow.

However, defining unambiguous directed energy flows as transduced work from one subsystem to another remains challenging for more than two subsystems. Recall that in Section 3.3 we argued that in a bipartite system the dynamics of one subsystem at a fixed state of the other can be interpreted as a control-parameter variation on the fixed subsystem. Hence, any potential-energy changes can be interpreted as work done on the fixed subsystem by the dynamic evolution of the other subsystem. Applying this logic to multipartite systems still permits definition of how much work one subsystem contributes to changing the global potential energy, but not the explicit flow between two subsystems.

Working out conditions under which exact transduced energy flows can be resolved would be an interesting extension and could lead to useful insights for multipartite systems such as energy flows in collections of motors transporting cargoes.

7.3 Optimizing coupled work transducers

In Section 6.3 we illustrated that the sum of transduced power and information flows acts as a kind of bottleneck for the transduction of work in two-component engines. Optimizing a given two-component work transducer and studying which of the two pathways maximize throughput seems like an interesting extension.

A first step towards this goal was accomplished in [67] for a specific model capturing aspects of F_o−F₁ ATP synthase. It was found that both transduced power and information flow are required to maximize output power and that maximal power tends to lead to equal subsystem entropy productions ${\dot{\mathrm{\Sigma }}}^X$ and ${\dot{\mathrm{\Sigma }}}^Y$ (29a, 29b).

7.4 Application to real-world machinery

Finally, it would be interesting to see the information-flow formalism applied to real-world machinery. This would involve measuring and modeling the dynamics of two components of a biomolecular system, e.g., both units of F_o−F₁ ATP synthase, instead of only the dynamics of F₁ as is conventionally done in most single-molecule experiments and theory [53, 113, 177–179]. This can be accomplished, e.g., by observing two components of a biomolecular system and explicitly calculating information flow, possibly revealing the ratchet mechanism of a Maxwell’s demon at work. A first step towards this is found in [49] where a synthetic chemical information motor is analyzed: the authors bridge their information-flow analysis to a chemical-reaction analysis [180] and identify regimes in which energy or information is the dominant driving mechanism. Another recent contribution in this direction is [50] where information flow has been calculated explicitly for dimeric molecular motors. Finally, Freitas and Esposito recently suggested [181] a macroscopic Maxwell demon based on CMOS technology and analyzed the information flow between its components [182].

Author contributions

JE and DS conceived the review and wrote and edited the manuscript. Both authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was supported by grant FQXi-IAF19-02 from the Foundational Questions Institute Fund, a donor-advised fund of the Silicon Valley Community Foundation. Additional support was from a Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant (DS) and a Tier-II Canada Research Chair (DS).

Acknowledgments

We thank Matthew Leighton and John Bechhoefer (SFU Physics) and Mathis Grelier (Grenoble Physics) for helpful conversations and feedback on the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1108357/full#supplementary-material

References

1. Schrödinger E. What is Life? Cambridge: Cambridge University Press (1992).

Google Scholar

2. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys (2012) 75:126001. doi:10.1088/0034-4885/75/12/126001

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Jarzynski C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu Rev Condens Matter (2011) 2:329–51. doi:10.1146/annurev-conmatphys-062910-140506

CrossRef Full Text | Google Scholar

4. Van den Broeck C, Esposito M. Ensemble and trajectory thermodynamics: A brief introduction. Physica A (2015) 418:6–16. doi:10.1016/j.physa.2014.04.035

CrossRef Full Text | Google Scholar

5. Peliti L, Pigolotti S. Stochastic thermodynamics: An introduction. Princeton, NJ and Oxford: Princeton University Press (2021).

Google Scholar

6. Knott CG. Life and Scientific Work of Peter Guthrie Tait. London: Cambridge University Press (1911). p. 213.

Google Scholar

7. Leff HS, Rex AF. Maxwell’s demon 2. Bristol: IOP Publishing (2003).

Google Scholar

8. Szilard L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z Phys (1929) 53:840–856. doi:10.1007/BF01341281

CrossRef Full Text | Google Scholar

9. Landauer R. Irreversibility and heat generation in the computing process. IBM J Res Dev (1961) 5:183–91. doi:10.1147/rd.53.0183

CrossRef Full Text | Google Scholar

10. Bennett CH. The thermodynamics of computation—A review. Int J Theor Phys (1982) 21:905–40. doi:10.1007/bf02084158

CrossRef Full Text | Google Scholar

11. Cao FJ, Feito M. Thermodynamics of feedback controlled systems. Phys Rev E (2009) 79:041118. doi:10.1103/PhysRevE.79.041118

CrossRef Full Text | Google Scholar

12. Sagawa T, Ueda M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys Rev Lett (2010) 104:090602. doi:10.1103/PhysRevLett.104.090602

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ponmurugan M. Generalized detailed fluctuation theorem under nonequilibrium feedback control. Phys Rev E (2010) 82:031129. doi:10.1103/PhysRevE.82.031129

CrossRef Full Text | Google Scholar

14. Horowitz JM, Vaikuntanathan S. Nonequilibrium detailed fluctuation theorem for repeated discrete feedback. Phys Rev E (2010) 82:061120. doi:10.1103/PhysRevE.82.061120

CrossRef Full Text | Google Scholar

15. Sagawa T, Ueda M. Nonequilibrium thermodynamics of feedback control. Phys Rev E (2012) 85:021104. doi:10.1103/PhysRevE.85.021104

CrossRef Full Text | Google Scholar

16. Sagawa T, Ueda M. Fluctuation theorem with information exchange: Role of correlations in stochastic thermodynamics. Phys Rev Lett (2011) 109:180602. doi:10.1103/PhysRevLett.109.180602

CrossRef Full Text | Google Scholar

17. Sagawa T, Ueda M. Role of mutual information in entropy production under information exchanges. New J Phys (2013) 15:125012. doi:10.1088/1367-2630/15/12/125012

CrossRef Full Text | Google Scholar

18. Mandal D, Jarzynski C. Work and information processing in a solvable model of Maxwell’s demon. Proc Nat Acad Sci (2012) 109:11641–5. doi:10.1073/pnas.1204263109

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mandal D, Quan HT, Jarzynski C. Maxwell’s refrigerator: An exactly solvable model. Phys Rev Lett (2013) 111:030602. doi:10.1103/PhysRevLett.111.030602

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Barato A, Seifert U. Unifying three perspectives on information processing in stochastic thermodynamics. Phys Rev Lett (2014) 112:090601. doi:10.1103/PhysRevLett.112.090601

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Barato A, Seifert U. Stochastic thermodynamics with information reservoirs. Phys Rev E (2014) 90:042150. doi:10.1103/PhysRevE.90.042150

CrossRef Full Text | Google Scholar

22. Parrondo JMR, Horowitz JM, Sagawa T. Thermodynamics of information. Nat Phys (2015) 11:131–9. doi:10.1038/NPHYS3230

CrossRef Full Text | Google Scholar

23. Bauer M, Abreu D, Seifert U. Efficiency of a Brownian information machine. J Phys A: Math Theo (2012) 45:162001. doi:10.1088/1751-8113/45/16/162001

CrossRef Full Text | Google Scholar

24. Schmitt RK, Parrondo JMR, Linke H, Johansson J. Molecular motor efficiency is maximized in the presence of both power-stroke and rectification through feedback. New J Phys (2015) 17:065011. doi:10.1088/1367-2630/17/6/065011

CrossRef Full Text | Google Scholar

25. Bechhoefer J. Hidden Markov models for stochastic thermodynamics. New J Phys (2015) 17:075003. doi:10.1088/1367-2630/17/7/075003

CrossRef Full Text | Google Scholar

26. Still S. Thermodynamic cost and benefit of memory. Phys Rev Lett (2020) 124:050601. doi:10.1103/PhysRevLett.124.050601

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lucero JNE, Ehrich J, Bechhoefer J, Sivak DA. Maximal fluctuation exploitation in Gaussian information engines. Phys Rev E (2021) 104:044122. doi:10.1103/PhysRevE.104.044122

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ehrich J, Still S, Sivak DA. Energetic cost of feedback control. arXiv:2206.10793 (2022).

Google Scholar

29. Still S, Daimer D. Partially observable Szilard engines. New J Phys (2022) 24:073031. doi:10.1088/1367-2630/ac6b30

CrossRef Full Text | Google Scholar

30. Serreli V, Lee CF, Kay ER, Leigh DA. A molecular information ratchet. Nature (2007) 445:523–7. doi:10.1038/nature05452

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Bannerman ST, Price GN, Viering K, Raizen MG. Single-photon cooling at the limit of trap dynamics: Maxwell’s demon near maximum efficiency. New J Phys (2009) 11:063044. doi:10.1088/1367-2630/11/6/063044

CrossRef Full Text | Google Scholar

32. Toyabe S, Sagawa T, Ueda M, Muneyuki E, Sano M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat Phys (2010) 6:988–92. doi:10.1038/NPHYS1821

CrossRef Full Text | Google Scholar

33. Koski JV, Maisi VF, Sagawa T, Pekola JP. Experimental observation of the role of mutual information in the nonequilibrium dynamics of a Maxwell demon. Phys Rev Lett (2014) 113:030601. doi:10.1103/PhysRevLett.113.030601

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Koski JV, Maisi VF, Pekola JP, Averin DV. Experimental realization of a Szilard engine with a single electron. Proc Natl Acad Sci U.S.A (2014) 111:13786–9. doi:10.1073/pnas.1406966111

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Koski JV, Kutvonen A, Khaymovich IM, Ala-Nissila T, Pekola JP. On-chip Maxwell’s demon as an information-powered refrigerator. Phys Rev Lett (2015) 115:260602. doi:10.1103/PhysRevLett.115.260602

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Vidrighin MD, Dahlsten O, Barbieri M, Kim SM, Vedral V, Walmsley IA. Photonic Maxwell’s demon. Phys Rev Lett (2016) 116:050401. doi:10.1103/PhysRevLett.116.050401

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Camati PA, Peterson JPS, Batalhao TB, Micadei K, Souza AM, Sarthour RS, et al. Experimental rectification of entropy production by Maxwell’s demon in a quantum system. Phys Rev Lett (2016) 117:240502. doi:10.1103/PhysRevLett.117.240502

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Chida K, Desai S, Nishiguchi K, Fujiwara A. Power generator driven by Maxwell’s demon. Nat Commun (2017) 8:15310. doi:10.1038/ncomms15301

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cottet N, Jezouin S, Bretheau L, Campagne-Ibarcq P, Ficheux Q, Anders J, et al. Observing a quantum Maxwell demon at work. Proc Natl Acad Sci USA (2017) 114:7561–4. doi:10.1073/pnas.1704827114

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Paneru G, Lee DY, Tlusty T, Pak HK. Lossless Brownian information engine. Phys Rev Lett (2018) 120:020601. doi:10.1103/PhysRevLett.120.020601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Masuyama Y, Funo K, Murashita Y, Noguchi A, Kono S, Tabuchi Y, et al. Information-to-work conversion by Maxwell’s demon in a superconducting circuit quantum electrodynamical system. Nat Commun (2018) 9:1291. doi:10.1038/s41467-018-03686-y

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Naghiloo M, Alonso JJ, Rmotio A, Lutz E, Murch KW. Information gain and loss for a quantum Maxwell’s demon. Phys Rev Lett (2018) 121:030604. doi:10.1103/PhysRevLett.121.030604

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Admon T, Rahav S, Roichman Y. Experimental realization of an information machine with tunable temporal correlations. Phys Rev Lett (2018) 121:180601. doi:10.1103/PhysRevLett.121.180601

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Paneru G, Lee DY, Park JM, Park JT, Noh JD, Pak HK. Optimal tuning of a Brownian information engine operating in a nonequilibrium steady state. Phys Rev E (2018) 98:052119. doi:10.1103/PhysRevE.98.052119

CrossRef Full Text | Google Scholar

45. Ribezzi-Crivellari M, Ritort F. Large work extraction and the Landauer limit in a continuous Maxwell demon. Nat Phys (2019) 15:660–4. doi:10.1038/s41567-019-0481-0

CrossRef Full Text | Google Scholar

46. Paneru G, Dutta S, Sagawa T, Tlusty T, Pak HK. Efficiency fluctuations and noise induced refrigerator-to-heater transition in information engines. Nat Commun (2020) 11:1012–8. doi:10.1038/s41467-020-14823-x

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Saha TK, Lucero JNE, Ehrich J, Sivak DA, Bechhoefer J. Maximizing power and velocity of an information engine. Proc Natl Acad Sci USA (2021) 118:e2023356118. doi:10.1073/pnas.2023356118

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Saha TK, Lucero JNE, Ehrich J, Sivak DA, Bechhoefer J. Bayesian information engine that optimally exploits noisy measurements. Phys Rev Lett (2022) 129:130601. doi:10.1103/PhysRevLett.129.130601

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Amano S, Esposito M, Kreidt E, Leigh DA, Penocchio E, Roberts BMW. Insights from an information thermodynamics analysis of a synthetic molecular motor. Nat Chem (2022) 14:530–7. doi:10.1038/s41557-022-00899-z

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Takaki R, Mugnai ML, Thirumalai D. Information flow, gating, and energetics in dimeric molecular motors. Proc Nat Acad Sci USA (2022) 119:e2208083119. doi:10.1073/pnas.2208083119

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Wilson MR, Solà J, Carlone A, Goldup SM, Lebrasseur N, Leigh DA. An autonomous chemically fuelled small-molecule motor. Nature (2016) 534:235–40. doi:10.1038/nature18013

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Feniouk BA, Cherepanov DA, Junge W, Mulkidjanian AY. Atp-synthase of Rhodobacter capsulatus: Coupling of proton flow through Fo to reactions in F1 under the ATP synthesis and slip conditions. FEBS Lett (1999) 445:409–14. doi:10.1016/S0014-5793(99)00160-X

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Toyabe S, Watanabe-Nakayama T, Okamoto T, Kudo S, Muneyuki E. Thermodynamic efficiency and mechanochemical coupling of F1-ATPase. Proc Natl Acad Sci USA (2011) 108:17951–6. doi:10.1073/pnas.1106787108

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Lathouwers E, Lucero JN, Sivak DA. Nonequilibrium energy transduction in stochastic strongly coupled rotary motors. J Phys Chem Lett (2020) 11:5273–8. doi:10.1021/acs.jpclett.0c01055

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Large SJ, Ehrich J, Sivak DA. Free energy transduction within autonomous systems. Phys Rev E (2021) 103:022140. doi:10.1103/PhysRevE.103.022140

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Shiraishi N, Ito S, Kawaguchi K, Sagawa T. Role of measurement-feedback separation in autonomous Maxwell’s demons. New J Phys (2015) 17:045012. doi:10.1088/1367-2630/17/4/045012

CrossRef Full Text | Google Scholar

57. Horowitz JM, Esposito M. Thermodynamics with continuous information flow. Phys Rev X (2014) 4:031015. doi:10.1103/PhysRevX.4.031015

CrossRef Full Text | Google Scholar

58. Horowitz JM. Multipartite information flow for multiple Maxwell demons. J Stat Mech (2015) 2015:P03006. doi:10.1088/1742-5468/2015/03/P03006

CrossRef Full Text | Google Scholar

59. Freitas N, Esposito M. Characterizing autonomous Maxwell demons. Phys Rev E (2021) 103:032118. doi:10.1103/PhysRevE.103.032118

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Barkai N, Leibler S. Robustness in simple biochemical networks. Nature (1997) 387:913–7. doi:10.1038/43199

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Sourjik V, Wingreen NS. Responding to chemical gradients: Bacterial chemotaxis. Curr Op Cel Bio. (2012) 24:262–8. doi:10.1016/j.ceb.2011.11.008

CrossRef Full Text | Google Scholar

62. Mehta P, Schwab DJ. Energetic costs of cellular computation. Proc Nat Acad Sci USA (2012) 109:17978–82. doi:10.1073/pnas.1207814109

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Barato AC, Hartich D, Seifert U. Rate of mutual information between coarse-grained non-markovian variables. J Stat Phys (2013) 153:460–78. doi:10.1007/s10955-013-0834-5

CrossRef Full Text | Google Scholar

64. Barato AC, Hartich D, Seifert U. Information-theoretic versus thermodynamic entropy production in autonomous sensory networks. Phys Rev E (2013) 87:042104. doi:10.1103/PhysRevE.87.042104

CrossRef Full Text | Google Scholar

65. Barato AC, Hartich D, Seifert U. Efficiency of cellular information processing. New J Phys (2014) 16:103024. doi:10.1088/1367-2630/16/10/103024

CrossRef Full Text | Google Scholar

66. Junge W, Nelson N. ATP synthase. Annu Rev Biochem (2015) 84:631–57. doi:10.1146/annurev-biochem-060614-034124

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Lathouwers E, Sivak DA. Internal energy and information flows mediate input and output power in bipartite molecular machines. Phys Rev E (2022) 105:024136. doi:10.1103/PhysRevE.105.024136

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Leopold PL, McDowall AW, Pfister KK, Bloom GS, Brady ST. Association of Kinesin with characterized membrane-bounded organelles. Cell Motil. Cytoskeleton (1992) 23:19–33. doi:10.1002/cm.970230104

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Rastogi K, Puliyakodan MS, Pandey V, Nath S, Elangovan R. Maximum limit to the number of myosin II motors participating in processive sliding of actin. Nat Sci. Rep. (2016) 6:32043. doi:10.1038/srep32043

CrossRef Full Text | Google Scholar

70. Ciliberto S. Experiments in stochastic thermodynamics: Short history and perspectives. Phys Rev X (2017) 7:021051. doi:10.1103/PhysRevX.7.021051

CrossRef Full Text | Google Scholar

71. Reimann P. Brownian motors: noisy transport far from equilibrium. Phys Rep (2002) 461:57–265. doi:10.1016/S0370-1573(01)00081-3

CrossRef Full Text | Google Scholar

72. Chowdhury D. Stochastic mechano-chemical kinetics of molecular motors: A multidisciplinary enterprise from a physicist’s perspective. Phys Rep (2013) 529:1–197. doi:10.1016/j.physrep.2013.03.005

CrossRef Full Text | Google Scholar

73. Kolomeisky AB. Motor proteins and molecular motors: How to operate machines at the nanoscale. J Phys Condens Matter (2013) 25:463101. doi:10.1088/0953-8984/25/46/463101

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Brown AI, Sivak DA. Theory of nonequilibrium free energy transduction by molecular machines. Chem Rev (2020) 120:434–59. doi:10.1021/acs.chemrev.9b00254

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Chowdhury D. An exploration of how the thermodynamic efficiency of bioenergetic membrane systems varies with c-subunit stoichiometry of F1F0 ATP synthases. J Bioenerg Biomembr (2014) 46:229–41. doi:10.1007/s10863-014-9547-y

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Li CB, Toyabe S. Efficiencies of molecular motors: A comprehensible overview. Biophys Rev (2020) 12:419–23. doi:10.1007/s12551-020-00672-x

PubMed Abstract | CrossRef Full Text | Google Scholar

77. van Kampen NG. Stochastic processes in Physics and chemistry. 3rd ed. Amsterdam: Elsevier (2007).

Google Scholar

78. Gardiner CW. Handbook of stochastic methods. 3rd ed. Berlin Heidelberg: Springer (2004).

Google Scholar

79. Chétrite R, Rosinberg ML, Sagawa T, Tarjus G. Information thermodynamics for interacting stochastic systems without bipartite structure. J Stat Mech (2019) 2019:114002. doi:10.1088/1742-5468/ab47fe

CrossRef Full Text | Google Scholar

80. Ptaszyński K, Esposito M. Thermodynamics of quantum information flows. Phys Rev Lett (2019) 122:150603. doi:10.1103/PhysRevLett.122.150603

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Cover TM, Thomas JA. Elements of information theory. 2nd ed. Hoboken, NJ: Wiley-Interscience (2006).

Google Scholar

82. Risken H. The Fokker-Planck equation. 2nd ed. Berlin, Heidelberg, New York: Springer (1996).

Google Scholar

83. Seifert U. From stochastic thermodynamics to thermodynamic inference. Annu Rev Condens Matter (2019) 10:171–92. doi:10.1146/annurev-conmatphys-031218-013554

CrossRef Full Text | Google Scholar

84. Bergmann PG, Lebowitz JL. New approach to nonequilibrium processes. Phys Rev (1955) 99:578–87. doi:10.1103/PhysRev.99.578

CrossRef Full Text | Google Scholar

85. Maes C. Local detailed balance. Scipost Phys Lect Notes (2021) 32. doi:10.21468/SciPostPhysLectNotes.32

CrossRef Full Text | Google Scholar

86. Esposito M. Stochastic thermodynamics under coarse graining. Phys Rev E (2012) 85:041125. doi:10.1103/PhysRevE.85.041125

CrossRef Full Text | Google Scholar

87. Allahverdyan AE, Janzing D, Mahler G. Thermodynamic efficiency of information and heat flow. J Stat Mech (2009) 2009:P09011. doi:10.1088/1742-5468/2009/09/P09011

CrossRef Full Text | Google Scholar

88. Gaveau B, Schulman LS. A general framework for non-equilibrium phenomena: The master equation and its formal consequences. Phys Lett A (1997) 229:347–53. doi:10.1016/S0375-9601(97)00185-0

CrossRef Full Text | Google Scholar

89. Gaveau B, Moreau M, Schulman LS. Work and power production in non-equilibrium systems. Phys Lett A (2008) 372:3415–22. doi:10.1016/j.physleta.2008.01.081

CrossRef Full Text | Google Scholar

90. Esposito M, Van den Broeck C. Second law and Landauer principle far from equilibrium. Europhys Lett (2011) 95:40004. doi:10.1209/0295-5075/95/40004

CrossRef Full Text | Google Scholar

91. Sivak DA, Crooks GE. Near-equilibrium measurements of nonequilibrium free energy. Phys Rev Lett (2012) 108:150601. doi:10.1103/PhysRevLett.108.150601

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Zimmerman E, Seifert U. Effective rates from thermodynamically consistent coarse-graining of models for molecular motors with probe particles. Phys Rev E (2015) 91:022709. doi:10.1103/PhysRevE.91.022709

CrossRef Full Text | Google Scholar

93. Shiraishi N, Sagawa T. Fluctuation theorem for partially masked nonequilibrium dynamics. Phys Rev E (2015) 91:012130. doi:10.1103/physreve.91.012130

CrossRef Full Text | Google Scholar

94. Polettini M, Esposito M. Effective thermodynamics for a marginal observer. Phys Rev Lett (2017) 119:240601. doi:10.1103/physrevlett.119.240601

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Bisker G, Polettini M, Gingrich TR, Horowitz JM. Hierarchical bounds on entropy production inferred from partial information. J Stat Mech (2017) 2017:093210. doi:10.1088/1742-5468/aa8c0d

CrossRef Full Text | Google Scholar

96. Martínez IA, Bisker G, Horowitz JM, Parrondo JMR. Inferring broken detailed balance in the absence of observable currents. Nat Comm (2019) 10:3542. doi:10.1038/s41467-019-11051-w

CrossRef Full Text | Google Scholar

97. Skinner DJ, Dunkel J. Improved bounds on entropy production in living systems. Proc Nat Acad Sci (2021) 118:e2024300118. doi:10.1073/pnas.2024300118

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Ehrich J. Tightest bound on hidden entropy production from partially observed dynamics. J Stat Mech (2021) 2021:083214. doi:10.1088/1742-5468/ac150e

CrossRef Full Text | Google Scholar

99. Skinner DJ, Dunkel J. Estimating entropy production from waiting time distributions. Phys Rev Lett (2021) 127:198101. doi:10.1103/PhysRevLett.127.198101

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Hartich D, Godec A. Violation of local detailed balance despite a clear time-scale separation. arXiv:2111.14734 (2021).

Google Scholar

101. van der Meer J, Ertel B, Seifert U. Thermodynamic inference in partially accessible Markov networks: A unifying perspective from transition-based waiting time distributions. Phys Rev X (2022) 12:031025. doi:10.1103/PhysRevX.12.031025

CrossRef Full Text | Google Scholar

102. Harunari PE, Dutta A, Polettini M, Roldán E. What to learn from a few visible transitions’ statistics? Phys Rev (2022) X:041026. doi:10.1103/PhysRevX.12.041026

CrossRef Full Text | Google Scholar

103. Large SJ, Sivak DA. Hidden energy flows in strongly coupled nonequilibrium systems. Europhys Lett (2021) 133:10003. doi:10.1209/0295-5075/133/10003

CrossRef Full Text | Google Scholar

104. Mehl J, Lander B, Bechinger C, Blickle V, Seifert U. Role of hidden slow degrees of freedom in the fluctuation theorem. Phys Rev Lett (2012) 108:220601. doi:10.1103/PhysRevLett.108.220601

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Uhl M, Pietzonka P, Seifert U. Fluctuations of apparent entropy production in networks with hidden slow degrees of freedom. J Stat Mech (2018) 2018:023203. doi:10.1088/1742-5468/aaa78b

CrossRef Full Text | Google Scholar

106. Kahlen M, Ehrich J. Hidden slow degrees of freedom and fluctuation theorems: An analytically solvable model. J Stat Mech (2018) 2018:063204. doi:10.1088/1742-5468/aac2fd

CrossRef Full Text | Google Scholar

107. Barato AC, Seifert U. Thermodynamic uncertainty relation for biomolecular processes. Phys Rev Lett (2015) 114:158101. doi:10.1103/PhysRevLett.114.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Gingrich TR, Horowitz JM, Perunov N, England JL. Dissipation bounds all steady-state current fluctuations. Phys Rev Lett (2016) 116:120601. doi:10.1103/PhysRevLett.116.120601

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Li J, Horowitz JM, Gingrich TR, Fakhri N. Quantifying dissipation using fluctuating currents. Nat Comm (2019) 10:1666. doi:10.1038/s41467-019-09631-x

CrossRef Full Text | Google Scholar

110. Manikandan SK, Gupta D, Krishnamurthy S. Inferring entropy production from short experiments. Phys Rev Lett (2020) 124:120603. doi:10.1103/PhysRevLett.124.120603

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Vu TV, Vo VT, Hasegawa Y. Entropy production estimation with optimal current. Phys Rev E (2020) 101:042138. doi:10.1103/PhysRevE.101.042138

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Pietzonka P, Zimmermann E, Seifert U. Fine-structured large deviations and the fluctuation theorem: Molecular motors and beyond. Europhys Lett (2014) 107:20002. doi:10.1209/0295-5075/107/20002

CrossRef Full Text | Google Scholar

113. Kawaguchi K, Si S, Sagawa T. Nonequilibrium dissipation-free transport in F1-ATPase and the thermodynamic role of asymmetric allosterism. Biophys J (2014) 106:2450–7. doi:10.1016/j.bpj.2014.04.034

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Still S, Sivak DA, Bell AJ, Crooks GE. Thermodynamics of prediction. Phys Rev Lett (2012) 109:120604. doi:10.1103/PhysRevLett.109.120604

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Lahiri S, Rana S, Jayannavar AM. Fluctuation theorems in the presence of information gain and feedback. J Phys A: Math Theor (2012) 45:065002. doi:10.1088/1751-8113/45/6/065002

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Crooks GE, Still S. Marginal and conditional second laws of thermodynamics. Europhys Lett (2019) 125:40005. doi:10.1209/0295-5075/125/40005

CrossRef Full Text | Google Scholar

117. Strasberg P, Schaller G, Brandes T, Esposito M. Thermodynamics of a physical model implementing a Maxwell demon. Phys Rev Lett (2013) 110:040601. doi:10.1103/PhysRevLett.110.040601

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Ciliberto S. Autonomous out-of-equilibrium Maxwell's demon for controlling the energy fluxes produced by thermal fluctuations. Phys Rev E (2020) 102(R):050103. doi:10.1103/PhysRevE.102.050103

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Bialek W, Setayeshgar S. Physical limits to biochemical signaling. Proc Nat Acad Sci (2005) 102:10040–5. doi:10.1073/pnas.0504321102

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Tu Y. The nonequilibrium mechanism for ultrasensitivity in a biological switch: Sensing by Maxwell’s demons. Proc Nat Acad Sci (2007) 105:11737–41. doi:10.1073/pnas.0804641105

CrossRef Full Text | Google Scholar

121. Lan G, Tu Y. Information processing in bacteria: Memory, computation, and statistical physics: A key issues review. Rep Prog Phys (2016) 79:052601. doi:10.1088/0034-4885/79/5/052601

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Mattingly HH, Kamino K, Machta BB, Emonet T. Escherichia coli chemotaxis is information limited. Nat Phys (2021) 17:1426–31. doi:10.1038/s41567-021-01380-3

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Berg HC, Purcell EM. Physics of chemoreception. Phys chemoreception. Biophys. J. (1977) 20:193–219. doi:10.1016/S0006-3495(77)85544-6

CrossRef Full Text | Google Scholar

124. Endres RG, Wingreen NS. Maximum likelihood and the single receptor. Phys Rev Lett (2009) 103:158101. doi:10.1103/PhysRevLett.103.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Govern CC, ten Wolde PR. Fundamental limits on sensing chemical concentrations with linear biochemical networks. Phys Rev Lett (2012) 109:218103. doi:10.1103/PhysRevLett.109.218103

PubMed Abstract | CrossRef Full Text | Google Scholar

126. ten Wolde PR, Becker NB, Ouldridge TE, Mugler A. Fundamental limits to cellular sensing. J Stat Phys (2016) 162:1395–424. doi:10.1007/s10955-015-1440-5

CrossRef Full Text | Google Scholar

127. Lan G, Sartori P, Neumann S, Sourjik V, Tu Y. The energy–speed–accuracy trade-off in sensory adaptation. Nat Phys (2012) 8:422–8. doi:10.1038/nphys2276

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Govern CC, ten Wolde PR. Optimal resource allocation in cellular sensing systems. Proc Nat Acad Sci (2014) 111:17486–91. doi:10.1073/pnas.1411524111

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Sartori P, Granger L, Lee CF, Horowitz JM. Thermodynamic costs of information processing in sensory adaptation. Plos Comput Biol (2014) 10:e1003974. doi:10.1371/journal.pcbi.1003974

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Govern CC, ten Wolde PR. Energy dissipation and noise correlations in biochemical sensing. Phys Rev Lett (2014) 113:258102. doi:10.1103/PhysRevLett.113.258102

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Bo S, Del Giudice M, Celani A. Thermodynamic limits to information harvesting by sensory systems. J Stat Mech (2015) 2015:P01014. doi:10.1088/1742-5468/2015/01/P01014

CrossRef Full Text | Google Scholar

132. Ouldrudge TE, Govern CC, ten Wolde PR. Thermodynamics of computational copying in biochemical systems. Phys Rev X (2017) 7:021004. doi:10.1103/PhysRevX.7.021004

CrossRef Full Text | Google Scholar

133. Hartich D, Barato AC, Seifert U. Stochastic thermodynamics of bipartite systems: Transfer entropy inequalities and a Maxwell’s demon interpretation. J Stat Mech (2014) 2014:P02016. doi:10.1088/1742-5468/2014/02/P02016

CrossRef Full Text | Google Scholar

134. Tostevin F, ten Wolde PR. Mutual information between input and output trajectories of biochemical networks. Phys Rev Lett (2009) 102:218101. doi:10.1103/PhysRevLett.102.218101

PubMed Abstract | CrossRef Full Text | Google Scholar

135. Diana G, Esposito M. Mutual entropy production in bipartite systems. J Stat Mech (2014) 2014:P04010. doi:10.1088/1742-5468/2014/04/P04010

CrossRef Full Text | Google Scholar

136. Schreiber T. Measuring information transfer. Phys Rev Lett (2000) 85:461–4. doi:10.1103/PhysRevLett.85.461

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Marko H. The bidirectional communication theory - a generalization of information theory. IEEE Trans Comm (1973) 21:1345–51. doi:10.1109/TCOM.1973.1091610

CrossRef Full Text | Google Scholar

138. Massey JL. Causality, feedback and directed information. In: Proc. 1990 Intl. Symp. on Info. Th. and its Applications; Waikiki, Hawaii (1990). 1.

Google Scholar

139. Bechhoefer J. Control Theory for Physicists. New York: Cambridge University Press (2021).

Google Scholar

140. Hartich D, Barato AC, Seifert U. Sensory capacity: An information theoretical measure of the performance of a sensor. Phys Rev E (2016) 93:022116. doi:10.1103/physreve.93.022116

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Horowitz JM, Sandberg H. Second-law-like inequalities with information and their interpretations. New J Phys (2014) 16:125007. doi:10.1088/1367-2630/16/12/125007

CrossRef Full Text | Google Scholar

142. Särkkä S. Bayesian filtering and smoothing. New York: Cambridge University Press (2013). doi:10.1017/cbo9781139344203

CrossRef Full Text | Google Scholar

143. Brittain RA, Jones NS, Ouldridge TE. What we learn from the learning rate. J Stat Mech (2017) 2017:063502. doi:10.1088/1742-5468/aa71d4

CrossRef Full Text | Google Scholar

144. Bustamane CJ, Chemla YR, Liu S, Wang MD. Optical tweezers in single-molecule biophysics. Nat Rev Methods Primers (2021) 1:25. doi:10.1038/s43586-021-00021-6

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Megli A, Praly E, Ding F, Allemand JF, Bensimon D, Croquette V. Single DNA/protein studies with magnetic traps. Curr Op Struct Bio (2009) 19:615–22. doi:10.1016/j.sbi.2009.08.005

CrossRef Full Text | Google Scholar

146. Neumann K, Nagy A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat Methods (1008) 5:491–505. doi:10.1038/nmeth.1218

CrossRef Full Text | Google Scholar

147. Sekimoto K. Langevin equation and thermodynamics. Prog Theo Phys Suppl (1998) 130:17–27. doi:10.1143/PTPS.130.17

CrossRef Full Text | Google Scholar

148. Sekimoto K. Stochastic energetics. Lecture notes in phys. Berlin Heidelberg: Springer (2010).

Google Scholar

149. Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett (1997) 78:2690–3. doi:10.1103/PhysRevLett.78.2690

CrossRef Full Text | Google Scholar

150. Crooks GE. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys Rev E (1999) 60:2721–6. doi:10.1103/PhysRevE.60.2721

CrossRef Full Text | Google Scholar

151. Seifert U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys Rev Lett (2005) 95:040602. doi:10.1103/PhysRevLett.95.040602

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Schmiedl T, Seifert U. Optimal finite-time processes in stochastic thermodynamics. Phys Rev Lett (2007) 98:108301. doi:10.1103/PhysRevLett.98.108301

PubMed Abstract | CrossRef Full Text | Google Scholar

153. Then H, Engel A. Computing the optimal protocol for finite-time processes in stochastic thermodynamics. Phys Rev E (2008) 77:041105. doi:10.1103/PhysRevE.77.041105

CrossRef Full Text | Google Scholar

154. Sivak DA, Crooks GE. Thermodynamic metrics and optimal paths. Phys Rev Lett (2012) 108:190602. doi:10.1103/PhysRevLett.108.190602

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Zulkowski PR, Sivak DA, Crooks GE, DeWeese MR. Geometry of thermodynamic control. Phys Rev E (2012) 86:041148. doi:10.1103/PhysRevE.86.041148

CrossRef Full Text | Google Scholar

156. Martínez IA, Petrosyan A, Guéry-Odelin D, Trizac E, Ciliberto S. Engineered swift equilibration of a brownian particle. Nat Phys (2016) 12:843–6. doi:10.1038/nphys3758

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Tafoya S, Large SJ, Liu S, Bustamante C, Sivak DA. Using a system’s equilibrium behavior to reduce its energy dissipation in nonequilibrium processes. Proc Nat Acad Sci (2019) 116:5920–4. doi:10.1073/pnas.1817778116

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Solon AP, Horowitz JM. Phase transition in protocols minimizing work fluctuations. Phys Rev Lett (2018) 120:180605. doi:10.1103/PhysRevLett.120.180605

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Blaber S, Sivak DA. Skewed thermodynamic geometry and optimal free energy estimation. J Chem Phys (2020) 153:244119. doi:10.1063/5.0033405

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Boyer PD. The ATP synthase - a splendid molecular machine. Annu Rev Biochem (1997) 66:717–49. doi:10.1146/annurev.biochem.66.1.717

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Yoshida M, Muneyuki E, Hisabori T. ATP synthase a marvellous rotary engine of the cell. Nat Rev Mol Cel Biol. (2001) 2:669–77. doi:10.1038/35089509

CrossRef Full Text | Google Scholar

162. Xing J, Liao JC, Oster G. Making ATP. Proc Nat Acad Sci (2005) 102:16539–46. doi:10.1073/pnas.0507207102

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Golubeva N, Imparato A, Peliti L. Efficiency of molecular machines with continuous phase space. Europhys Lett (2012) 97:60005. doi:10.1209/0295-5075/97/60005

CrossRef Full Text | Google Scholar

164. Ai G, Liu P, Ge H. Torque-coupled thermodynamic model for FoF1-ATPase. Phys Rev E (2017) 95:052413. doi:10.1103/PhysRevE.95.052413

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Fogedby HC, Imparato A. A minimal model of an autonomous thermal motor. Europhys Lett (2017) 119:50007. doi:10.1209/0295-5075/119/50007

CrossRef Full Text | Google Scholar

166. Suñé M, Imparato A. Efficiency fluctuations in steady-state machines. J Phys A: Mathm Theor (2019) 52:045003. doi:10.1088/1751-8121/aaf2f8

CrossRef Full Text | Google Scholar

167. Encalada SE, Szpankowski L, Xia C, Goldstein L. Stable kinesin and dynein assemblies drive the axonal transport of mammalian prion protein vesicles. Cell (2011) 144:551–65. doi:10.1016/j.cell.2011.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Cooke R. Actomyosin interaction in striated muscle. Phys Rev (1997) 77:671–97. doi:10.1152/physrev.1997.77.3.671

CrossRef Full Text | Google Scholar

169. Klumpp S, Lipowsky R. Cooperative cargo transport by several molecular motors. Proc Nat Acad Sci USA (2005) 102:17284–9. doi:10.1073/pnas.0507363102

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Bhat D, Gopalakrishnan M. Transport of organelles by elastically coupled motor proteins. Eur Phus J E (2016) 39:71. doi:10.1140/epje/i2016-16071-0

CrossRef Full Text | Google Scholar

171. Bhat D, Gopalakrishnan M. Stall force of a cargo driven by n interacting motor proteins. Europhys Lett (2017) 117:28004. doi:10.1209/0295-5075/117/28004

CrossRef Full Text | Google Scholar

172. Wagoner JA, Dill KA. Evolution of mechanical cooperativity among myosin II motors. Proc Nat Acad Sci USA (2021) 118:e2101871118. doi:10.1073/pnas.2101871118

PubMed Abstract | CrossRef Full Text | Google Scholar

173. Leighton MP, Sivak DA. Performance scaling and trade-offs for collective motor-driven transport. New J Phys (2022) 24:013009. doi:10.1088/1367-2630/ac3db7

CrossRef Full Text | Google Scholar

174. Leighton MP, Sivak DA. Dynamic and thermodynamic bounds for collective motor-driven transport. Phys Rev Lett (2022) 129:118102. doi:10.1103/PhysRevLett.129.118102

PubMed Abstract | CrossRef Full Text | Google Scholar

175. Wachtel A, Rao R, Esposito M. Free-energy transduction in chemical reaction networks: From enzymes to metabolism. arXiv:2202.01316 (2022).

CrossRef Full Text | Google Scholar

176. Barato AC, Seifert U. Thermodynamic cost of external control. New J Phys (2017) 19:073021. doi:10.1088/1367-2630/aa77d0

CrossRef Full Text | Google Scholar

177. Yasuda R, Noji H, Yoshida M, Kinosita K, Itoh H. Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-Atpase. Nature (2001) 410:898–904. doi:10.1038/35073513

PubMed Abstract | CrossRef Full Text | Google Scholar

178. Toyabe S, Okamoto T, Watanabe-Nakayama T, Taketani H, Kudo S, Muneyuki E. Nonequilibrium energetics of a single F1-ATPase molecule. Phys Rev Lett (2010) 104:198103. doi:10.1103/PhysRevLett.104.198103

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Hayashi R, Sasaki K, Nakamura S, Kudo S, Inoue Y, Noji H, et al. Giant acceleration of diffusion observed in a single-molecule experiment on F1−ATPase. Phys Rev Lett (2015) 114:248101. doi:10.1103/PhysRevLett.114.248101

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Penocchio E, Avanzini F, Esposito M. Information thermodynamics for deterministic chemical reaction networks. J Chem Phys (2022) 157:034110. doi:10.1063/5.0094849

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Freitas N, Esposito M. Maxwell demon that can work at macroscopic scales. Phys Rev Lett (2022) 129:120602. doi:10.1103/PhysRevLett.129.120602

PubMed Abstract | CrossRef Full Text | Google Scholar

182. Freitas N, Esposito M. Information flows in macroscopic Maxwell’s demons. Phy Rev E (2023) 107:014136. doi:10.1103/PhysRevE.107.014136

CrossRef Full Text | Google Scholar