Reorientation processes of tilted skyrmion and spiral states in a bulk cubic helimagnet Cu2OSeO3

We present a systematic study of tilted spiral states obtained theoretically within the classical Dzyaloshinskii model for magnetic states in cubic non-centrosymmetric ferromagnets. Such tilted spirals are shown to stabilize under the competing effect of cubic and exchange anisotropies inherent to cubic helimagnets. By focusing on the internal structure of these spirals and their field-driven behaviour for different aspect ratios of the anisotropy coefficients, we are able to capture the main features of the experimental findings in a bulk cubic helimagnet Cu₂OSeO₃ and to make a step further towards a complete quantitative model of this chiral magnet. In particular, we show that for strong anisotropy values (which experimentally correspond to low temperatures near zero) there exist an angular separation between the conical and tilted spirals, i.e., the conical spiral flips into a tilted state and immediately composes some finite angle with respect to the field direction. As the anisotropy ratio decreases, such a transition between two spiral states becomes almost continuous and corresponds to higher temperatures at the experiments. In addition, we investigate the field-driven reorientation of metastable skyrmion lattices induced by the competing anisotropies, which may be responsible for some peculiarities at the experimental phase diagrams of Cu₂OSeO₃.

Introduction

Cu₂OSeO₃ represents a unique example in the family of B20 cubic helimagnets [1, 2] exhibiting two well-defined skyrmion pockets at the temperature-magnetic field phase diagram [3, 4] (Figure 1A). The “high-temperature” (HT) pocket is commonly referred to as the A-phase: it is located at the boundary with the paramagnetic state and is also intrinsic to other cubic helimagnets such as MnSi [8, 9] and/or FeGe [10, 11]. The “low-temperature” (LT) pocket, however, arises around zero temperature and only in this particular chiral magnet. It forms exclusively for magnetic fields applied along the easy crystallographic $⟨100⟩$ directions [6, 12].

FIGURE 1

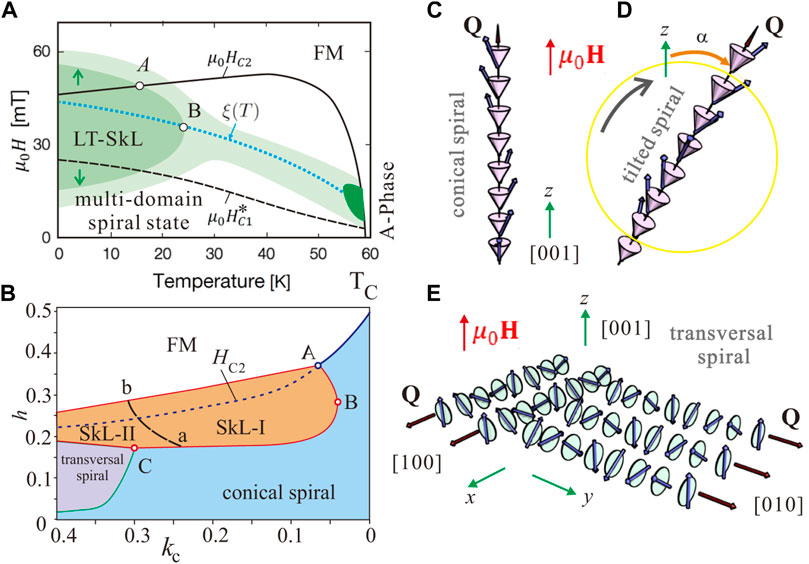
FIGURE 1. (color online) (A) Sketch of the experimental phase diagram indicating [3, 5] the extent and intensity of skyrmionic scattering after zero field cooling (ZFC) for H‖k_i‖[001]. The sample was brought to each selected target temperature after cooling it through T_C ≈ 59 K under zero magnetic field (i.e. under the residual magnetic field of the cryomagnet). Then, the measurements were performed upon increasing and decreasing the magnetic field and indicated hysteresis of LT-SkL formation [3, 6], i.e., skyrmionic scattering concentrates around the H_C2 line when the magnetic field increases from zero to above H_C2, and around the H_C1 line when the magnetic field subsequently decreases from above H_C2 to zero. Here, however, we superimpose both SkL stability regions, but indicate the described hysteresis by the green arrows. Deep dark green stands for the high-temperature A-phase; dark green—for the low-temperature SkL; and light green—for the weak scattering that surrounds both the LT and HT skyrmion pockets and connects them along the line ξ(T). Genuine experimental phase diagrams can be found in Refs. [3, 6], and [7]. (B) The theoretical phase diagram for k_c > 0 and b_ea = 0 for h‖[001]. The regions of the thermodynamical stability are colored orange (skyrmions), blue (cones), and pink (transversal spirals). Both phase diagrams contain the following characteristic points: point A is an intersection point between the curve H_C2 and an upper boundary of a LT-SkL pocket, which demarcates two temperature regimes and thus nucleation mechanisms of a SKL; point B is the outermost point of the LT-SkL pocket, which allows the direct ascription of the temperature from the experimental phase diagram (A) to the value of the cubic anisotropy at the theoretical phase diagram (B); point C signifies the appearance of the transversal spiral state, which was observed only in theory and thus constitutes the upper boundary for the constant of the cubic anisotropy. Both phase diagrams also contain the following characteristic lines: $H_{C1}^{*}$ is the field of transition between spiral and conical states, which due to the metastability of transversal spirals is observed only in the experiment (A); H_C2 is the field of the first-order phase transition from the conical into the homogeneous state; along the line ξ(T) the energy difference between the SkL and the conical state is negligible, which leads to the stabilization of LT-SkL and HT-SkL exactly along this line and their interconnection. The line a − b in (B) separates the regions of two skyrmion lattices rotated with respect to each other, which presumably lead to the ring-shaped scattering in (A). Careful comparison of different characteristic processes at both phase diagrams allows to construct the quantitative model of Cu₂OSeO₃ (see Sect. V for details). (C–E) Schematics of one-dimensional spiral states in non-centrosymmetric cubic magnets: (C) conical spiral with the propagation direction along the field; (D) the tilted spiral state with the wave vector canted with respect to the field; (E) coexisting domains of the transversal spiral states with the wave vectors Q_x‖[100] and Q_y‖[010] perpendicular to the field.

Within a small pocket of A-phase, skyrmion lattice (SkL) appears spontaneously and its stability is commonly attributed to the thermal fluctuations, which “work” at relatively high temperatures [9, 13]. Moreover, the temperature versus field regime of the HT-SkL is almost isotropic for different field directions with respect to the crystal lattice. The small angle neutron pattern has a sixfold intensity for a random orientation of a sample in the A-pocket [9]. At the same time, the boundaries of the A-phase can be drastically changed by applying pressure [14], electric fields [15–18], chemical doping [19] or uniaxial strains [20, 21].

The principle of HT-SkL stabilization rests on a specific field-driven evolution of the energetic difference to SkL’s main competitor, the conical spiral [22]. The difference between the energies of the hexagonal skyrmion lattice W_SkL and the conical spiral W_cone, ΔW_min = W_SkL − W_cone, has minima along a curve ξ(T) exactly for those magnetic fields that stabilize the A-phase [22–24] (Figure 1A). In the following, the conical spiral is defined as a solution of the isotropic Dzyaloshinskii model (1) with the propagation direction along the magnetic field in which the magnetization rotation retains single-harmonic character, but becomes additionally distorted by different anisotropic contributions (4) (Figure 1C).

Remarkably, the same stabilization principle holds for the LT-SkL [3]. The stabilization mechanism, however, is represented by a well-known cubic anisotropy with easy $⟨100⟩$ axes. Neutron diffraction measurements in Ref. [3] confirmed this mechanism and revealed the formation of skyrmion states in large areas of the magnetic phase diagram, from the lowest temperatures up to the A-phase along the line ξ(T) (Figure 1A). LT-skyrmionic scattering, however, shows a clear hysteretic behavior: it concentrates around the H_c2 line when the magnetic field increases from zero to above H_c2, and around the H_c1 line when the magnetic field subsequently decreases from above H_c2 to zero (as indicated by small green arrows at the sketch of the experimental phase diagram, Figure 1A). Moreover, the LT-skyrmion correlations underlie a ring-shaped scattering, which gains the strongest intensity in the LT-SkL region and the reduced radius as compared with the spiral peaks.

The role of cubic anisotropy in the LT-region is not limited only to the SkL stabilization, but is also manifested by many other remarkable phenomena:

(I) In particular, cubic anisotropy fixes the propagation directions of spiral states along easy anisotropy directions below the critical field H_c1 and underlies multidomain spiral states: for MnSi [8, 9] spirals propagate along the easy $⟨111⟩$ directions, for Cu₂OSeO₃ [1]—along $⟨100⟩$. If the propagation vector of a spiral state is perpendicular to an applied magnetic field, we will call such states transversal spirals (Figure 1E). If the wave vector composes some angle with respect to the field direction below the H_c1 line, such spirals will be called oblique spirals.

The multidomain spiral state of Cu₂OSeO₃ below H_c1 for H‖[001] consists of spiral domains with mutually perpendicular wave vectors: one domain represents the most energetically favorable conical state (Figure 1C), and the others—metastable transversal spirals (Figure 1E), which eventually flip along the field direction. According to the theoretical predictions, the domains of transversal spirals do not reappear with the lowering field, which is also indicated by the experimental results in Ref. [12]. Thus, the field H_c1 is not shown at the theoretical phase diagram (Figure 1B) for this field direction [22, 25].

Multidomain spiral state of MnSi for the magnetic field applied along the easy anisotropy direction, H‖[111], consists of energetically degenerate oblique spirals leaning towards the field and thus deflecting from their zero-field propagation directions along the $⟨111⟩$ axes. Since such spirals represent global minima of the system, the multidomain state will be repopulated even when lowering the magnetic field.

To discern the spiral behavior at the critical fields, we will use the notion $H_{c1}^{*}$ in the former case and H_c1 in the latter case.

(II) Interestingly, the spiral flips were theoretically predicted to occur also for higher fields (near H_c2) and relatively strong values of cubic anisotropy [22], but they have not been yet identified experimentally. Although the conical phase co-aligned with the field is considered to be the most favorable state above H_c1 that benefits from the Zeeman interaction, it may jump away from the field to be able to embrace a larger number of easy anisotropy axes.

For example, for $\mathbf{H}\Vert ⟨111⟩$ or $\mathbf{H}\Vert ⟨110⟩$ and easy cubic axes $⟨111⟩$, the wave vector jumps closer to the hard axes $⟨100⟩$ (see for details Refs. [22, 25]). Theoretically, if the spiral jumps from a conical into a tilted spiral (we will use this definition to distinguish such spirals from the mentioned oblique spiral states at low fields), the canting angle with respect to the field remains almost fixed by the strong cubic anisotropy [22, 25].

No tilted spiral states near H_c2, however, were identified theoretically for the easy cubic axes $⟨100⟩$ and the field along the high-symmetry directions $⟨111⟩$, $⟨110⟩$, and $⟨100⟩$.

(III) For moderate and small anisotropy values, cubic anisotropy defines the character of the phase transition between the conical and the homogeneous states at the critical field H_c2: first-order phase transition (FOPT) occurs when the magnetic field is applied along the easy anisotropy axes (in the case of Cu₂OSeO₃, for $\mathbf{H}\Vert ⟨100⟩$) whereas it retains its second-order character for the field along the hard anisotropy axes $⟨111⟩$. From the ascent of the critical line H_c2 from zero temperature and onwards to T_C, as indicated at the sketch of the experimental phase diagram (Figure 1A), we can deduce that in Cu₂OSeO₃ the cubic anisotropy exhibits a pronounced temperature dependence and gradually weakens as shown by the dashed blue line at the theoretical phase diagram (Figure 1B).

(IV) Additional deviation from the generic phase diagram of cubic chiral magnets [9] is manifested in Cu₂OSeO₃ by the tilted spiral state (TS), which appears for the same direction of the magnetic field $\mathbf{H}\Vert ⟨100⟩$ and coexists with the stability region of the LT-SkL [5]. As stated before in II, such a TS cannot be stabilized solely by the cubic anisotropy. In Ref. [5] it was found that the TS is presumably stabilized by the competing effect between cubic and exchange anisotropies. The exchange anisotropy in this case has easy $⟨111⟩$ axes and is sufficiently strong to deflect the wave vector of the conical state towards these crystallographic directions. With increasing temperature, apparently, the exchange anisotropy also fades away to keep the ratio of anisotropy constants below the threshold limit when spirals at zero field would flip along the easy $⟨111⟩$ directions of the exchange anisotropy. Besides, the tilted spiral state is hailed as a nucleation source of LT-skyrmions [6], which can form within domain boundaries between different TS-domains and thus leads to the aforementioned hysteretic behavior of the LT-SkL.

Such a pronounced temperature dependence of anisotropy coefficients alongside with their complex interplay constitutes the main obstacle on the way to construct the complete quantitative model of a bulk cubic helimagnet Cu₂OSeO₃. In previous reports, only separate assessments of anisotropy values have been undertaken without any regard to their temperature dependence and interplay [26].

In the present manuscript, we underline distinctive features of tilted spiral states that stem from the effect of the interplaying cubic and exchange anisotropies. We discuss these results in the frame of the phenomenological theory introduced by Dzyaloshinskii in an attempt to establish a quantitative comparison between the model and the experimental results for a bulk cubic helimagnet Cu₂OSeO₃. In particular, we find a crossover behavior of a tilted spiral state driven by the varying ratio of anisotropy constants: i) in the case of strong cubic and exchange anisotropies, the TS directly jumps into the homogeneous state and exhibits almost no rotation; ii) for weaker anisotropies, however, the TS can smoothly rotate towards the easy axes of exchange anisotropy and even shows a reverse rotation back to the easy axes of cubic anisotropy. We argue that experimentally these two regimes are defined with respect to the critical temperature T = 18K (point A at the phase diagram in Figure 1A), which introduces an important threshold. By a systematic study of the stability and ordering of the low temperature magnetic states in Cu₂OSeO₃ done in Refs. [3, 5, 7] we conclude that the former case of the TS behavior is inherent for low temperatures (T = 2K) whereas the latter case allows to explain the experimental observations in the vicinity of the point A.

Additionally, we show that skyrmion states may also become oblique with respect to an applied magnetic field, which, however, occurs for the field directions $⟨111⟩$ and $⟨110⟩$ making skyrmions metastable states. Their field-driven jump-like reorientation is accompanied by a gradual rotation perpendicular to the field and may come into a conflict with versatile oblique spiral states, which makes the experimental phase diagram rather complex.

Furthermore, by comparing the experimental and theoretical phase diagrams, we are able to delineate the ranges of anisotropy constants, which may subsequently serve as a guide for future experiments. Although such theoretical undertakings require some additional fine tuning, our approach and the reasoning behind it provide a viable strategy for an in-depth and quantitative understanding of chiral magnets in view of tailoring their properties for future applications.

Phenomenological model

Within the phenomenological theory introduced by Dzyaloshinskii [27] the magnetic energy density of a bulk non-centrosymmetric ferromagnet with spatially dependent magnetization M can be written as

$W_0\left(\mathbf{M}\right)=A\sum _{i,j}{\left(\frac{\partial m_j}{\partial x_i}\right)}^2+D{w}_D\left(\mathbf{M}\right)-\mathbf{M}\cdot \mathbf{H}(1)$

where A and D are coefficients of exchange and Dzyaloshinskii-Moriya interactions (DMI); H is an applied magnetic field; x_i are the Cartesian components of the spatial variable. w_D is composed of Lifshitz invariants

${\mathcal{L}}_{i,j}^{\left(k\right)}=M_i\partial M_j/\partial x_k-M_j\partial M_i/\partial x_k(2)$

that are energy terms involving first derivatives of the magnetization with respect to the spatial coordinates. In the following, all calculations will be done for cubic helimagnets with

$w_D=\mathbf{m}\cdot \nabla \times \mathbf{m}(3)$

although the results may be applied for magnets with other symmetry classes [28] including different combinations of Lifshitz invariants. $W(\mathbf{M})$ includes only basic interactions essential to stabilize skyrmion and spiral states and specifies their most general features attributed to all chiral ferromagnets.

In the forthcoming calculations, we use reduced values of the spatial variable, x = r/L_D, where L_D = A/D is the periodicity of the modulated states. $\mathbf{m}$ is the unity vector along the magnetization vector $\mathbf{M}=\mathbf{m}M$, and $\mathbf{h}=\mathbf{H}/H_D$ with μ₀H_D = D²/(AM) being the reduced value of the applied magnetic field.

For the cubic helimagnet Cu₂OSeO₃, we supplement the isotropic energy density (1) by the exchange and cubic anisotropic contributions [26, 29],

${\mathrm{\Phi }}_a=b_{ea}\left(T\right)\sum _i{\left(\partial m_i/\partial x_i\right)}^2+k_c\left(T\right)\sum _i{m}_i^4,(4)$

where b_ea = B_ea/A and k_c = K_cA/D² are reduced anisotropy constants, which are in general temperature-dependent. The constants k_c and b_ea are typically one order of magnitude smaller than the exchange stiffness A and are conventionally considered as a third level of hierarchy of energy scales following the exchange and DM interactions.

The theoretical explanation of SkL stability (Figure 1B) by the anisotropies (4) is mainly based on the effect imposed on one-dimensional spiral states. In fact, the ideal magnetization rotation in the conical state can be impaired by the easy and hard anisotropy axes for specific directions of the magnetic field. Through this mechanism, skyrmions, which are more resilient to anisotropy-induced deformations, due to their two-dimensional nature, gain stability [22].

In the following simulations, we restrict ourselves to k_c > 0 with easy $⟨100⟩$ axes and b_ea < 0 with easy $⟨111⟩$ axes, which is the presumable layout for the aforementioned Cu₂OSeO₃ [3]. The emphasis will be given to the results with H‖[001]. We also neglect the influence of dipole-dipole interactions due to the volume charges presumably formed within different oblique states. We assume that the DM interactions suppress demagnetization effects and are the main driving force leading to the magnetization rotation and to the equilibrium periodicity. The influence of dipole-dipole interactions on the effects found in the present manuscript will be considered elsewhere.

The Euler-Lagrange equations derived from the energy functional (1) are non-linear partial differential equations. These equations have been solved by numerical energy minimization procedure using finite-difference discretization on grids with adjustable grid spacings and periodic boundary conditions. Components of the magnetization vector $\mathbf{m}$ have been evaluated in the knots of the grid, and for the calculation of the energy density (1) we used finite-difference approximation of derivatives with different precision up to eight points as neighbors. To check the stability of the numerical routines we additionally refined and coarsened the grids. For axial fields, we used grid spacings Δ_y ≈ Δ_x so that grids are approximately square in the xy plane in order to reduce any artificial anisotropy incurred by the discretization. The final equilibrium structure for the modulated states was obtained according to the iterative procedure of the energy minimization using simulated annealing and a single-step Monte-Carlo dynamics with the Metropolis algorithm. In detail, numerical methods on energy minimization procedure are described in, e.g., Ref. [30] and hence will be omitted here.

To avoid an impediment introduced by the periodic boundary conditions, which would arise due to tilted/oblique spiral states in case of using a three-dimensional numerical grid, we perform two-dimensional simulations. For these, we write the energy density in a coordinate system $(\tilde{x},\tilde{y},\tilde{z})$ connected with the wave vector of a TS and a corresponding plane of rotation (Figure 2A). First, we rotate the coordinate system (CS) around z by an angle ψ. Then, we perform a subsequent CS rotation around $\tilde{y}$ in such a way that the wave vector of a spiral state, which points along $\tilde{x}$, makes an angle α with the z-axis. For a TS, we assign ψ = π/4 and thus can address the TS structure in the plane $(1\bar{1}0)$. The energy density is then minimized with respect to α and a tilted spiral with an optimal α is found. In a general case, we will also minimize the energy density of a spiral state with respect to ψ.

FIGURE 2

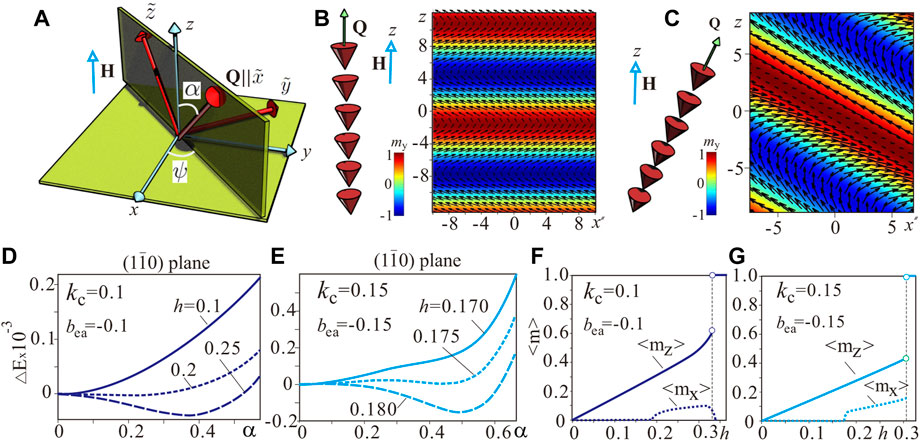
FIGURE 2. (color online) (A) Schematics of a coordinate system to address numerically two-dimensional tilted spiral states. The energy density is written in a new CS $(\tilde{x},\tilde{y},\tilde{z})$ and is minimized with respect to the angles ψ and α. (B), (C) Contour plots for the components m_y of the magnetization vector plotted in the CS (x, y, z) alongside with the sketches of the corresponding one-dimensional spiral states—cones (B) and tilted spirals (C). (D), (E) Energy density plotted as a function of the tilt angle α in the $(1\bar{1}0)$ plane for two representative sets of anisotropy coefficients and for several field values indicating the transition into the tilted spiral state: (D) k_c = 0.1, b_ea = −0.1; (E) k_c = 0.15, b_ea = −0.15. (F), (G) Magnetization curves, which imply the existence region of the tilted spiral by the non-zero magnetization component $⟨m_x⟩$.

Tilted spiral states due to the competing anisotropy interactions

For the present setup of easy $⟨100⟩$ anisotropy axes and h‖[001], the tilted spiral state was found by both theoretical and experimental means. Its behavior and occurrence at the phase diagram are pronouncedly temperature-dependent and exhibit well-distinguished “regimes”.

First of all, to stabilize TS in the vicinity of the critical field H_c2, the cubic anisotropy k_c must overcome some threshold value (the exact value will be computed elsewhere). A relatively weak cubic anisotropy k_c = 0.05 does not lead to any intermediate tilted spiral, although, according to the theoretical phase diagram in Refs. [3, 25], it is still able to stabilize a LT-SkL (Figure 1B). An increasing exchange anisotropy in this case would only switch the conical phase with α = 0 immediately into a $⟨111⟩$ oblique spiral even for zero field, which then aligns with the field at the H_c1 value, a situation, which was never observed experimentally in Cu₂OSeO₃. Higher values of cubic anisotropy, on the contrary, are found to be responsible not only for the stability of the tilted spiral state, but also for the crossover of its behavior.

In the following, as instructive and representative examples, we consider two cases with k_c = 0.1 (as becomes evident later, this value corresponds to higher temperatures in Cu₂OSeO₃) and k_c = 0.15 (lower temperature range, see Sect. V. for details). Further increase of k_c leads to a high-field jump from the conical into a transversal spiral, as featured by the theoretical phase diagram (see point C in Figure 1B and the pink-shaded region of the transversal spiral). Since such a limiting case was also not observed experimentally in bulk Cu₂OSeO₃, we may restrict ourselves to a finite range of anisotropy coefficients, which can be subsequently narrowed down for a better fitting with the experimental results.

Internal structure of a tilted spiral state for H‖[001]

Figures 2B,C show color plots of the m_y magnetization component for both conical and tilted spirals. The dependence of the spiral energy on the tilt angle α with Q varying in the (1$\bar{1}$0) plane is shown in Figures 2D,E for two sets of anisotropy constants and for several field values: d) k_c = 0.1, b_ea = −0.1; e) k_c = 0.15, b_ea = −0.15. In the first case (Figure 2D), the wave vector smoothly changes from the state along the field to a tilted state. For the higher cubic anisotropy (Figure 2E), however, one distinguishes a small energy barrier between the conical and the tilted spiral state (see dotted line corresponding to h = 0.175). Moreover, the field range of such a spiral evolution is also rather small in the second case. Indeed, for k_c = 0.1 the energy difference between the conical state (energy maximum) and the tilted spiral (energy minimum) is almost negligible, and the energy curve exhibits a plateau-like behaviour in the whole range of the TS existence (Figure 2D). For k_c = 0.15, on the other hand, the energy minimum corresponding to the tilted spiral becomes pronounced and develops for a small field range 0.17–0.18 (Figure 2E).

Additionally, we notice that the tilted spiral has a non-zero in-plane magnetization component, i.e., the magnetization projection onto the xy plane (Figures 2F,G), which could be discerned experimentally. However, due to the coexistence of four equivalent spiral domains canting towards four $⟨111⟩$ axes (Figure 3A), this in-plane magnetic contribution averages out. From the magnetization curves, it follows that oblique spirals transform into the homogeneous state by the first order phase transition, which is also the case for the conical phase with α = 0 (see Ref. [22] for details on the first-order phase transition between the conical and saturated states and on the strategy to choose an approprite field direction for both signs of the cubic anisotropy).

FIGURE 3

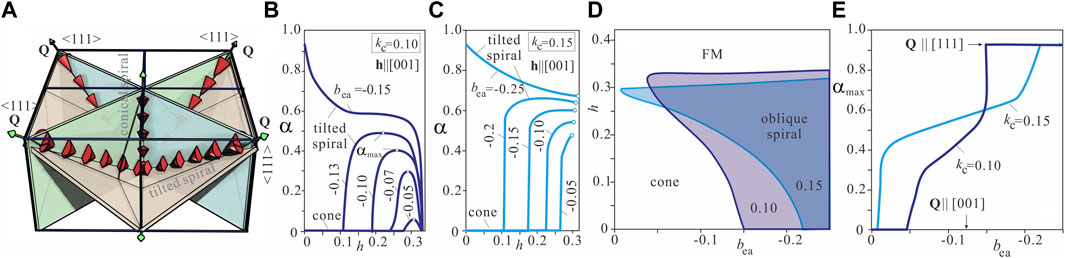
FIGURE 3. (color online) (A) Schematics showing coexisting conical and tilted spiral states. TS forms four energetically equivalent domains canting towards $⟨111⟩$ directions. Magnetic field dependence of the angle α for k_c = 0.1 (B) and k_c = 0.15 (C) with a varying value of the exchange anisotropy b_ea. In (B), the tilted spiral almost returns back to the direction of the field, whereas in (C), being deflected from the field by quite a large angle α, it undergoes the first-order phase transition with respect to the homogeneous state. (D) The diagram showing the regions where the conical and tilted spiral states possess the lowest energy density among all one-dimensional spiral modulations. The light-blue area stands for k_c = 0.15, and the dark-blue shaded area—for k_c = 0.10. (E) The dependence of the α_max defined in (B) on the exchange anisotropy value for the same two cubic anisotropy constants. For k_c = 0.15, this dependence exhibits a plateau with almost constant angle, which becomes smaller at k_c = 0.1 and steepens its slope. At some critical value of k_c (e.g., for k_c = 0.05), one would observe just a jump between two angle values corresponding to [001] and $⟨111⟩$ axes.

Interestingly, the conical state does not “feel” the exchange anisotropy (energy of the exchange anisotropy is zero for the conical phase, since the magnetization derivatives in (4) all vanish), which would enable and underpin the experimental situation when cones and tilted spirals coexist. This coexistence is additionally facilitated by the minor energy difference mentioned before for k_c = 0.1.

Remarkably, for a weaker cubic anisotropy (Figure 2F), the tilt angle α almost relaxes back to zero as for the conical phase, i.e., the value of $⟨m_z⟩$ tends to unity. For k_c = 0.15 (Figure 2G), on the contrary, the part of the curve with the reverse spiral rotation is far beyond the threshold field of the first-order phase transition into the homogeneous state (dashed vertical lines in Figures 2F,G). And even after, the tilt angle α may grow.

Field- and anisotropy-driven evolution of tilted spiral states for H‖[001]

The general behavior deduced from Figure 2 is as follows: above a critical field value, the conical spiral begins to tilt towards one of the four body diagonals, the ⟨111⟩ directions, as shown in Figure 3 and by a first-order phase transition transforms into the saturated state. Such a tilted spiral state appears when |b_ea| exceeds some critical value, which is slightly lower than 0.05 for k_c = 0.1 and almost vanishes for k_c = 0.15. For k_c = 0.1, as h increases, α grows (Figure 3B), reaches its maximal value α_max and then decreases back to zero (although the tilted spiral may jump into the homogeneous state slightly below this field value as shown in Figure 2F), corresponding to a return into the conical spiral state. The corresponding maximal tilt angle, α_max, which depends on the ratio of the competing fourth-order and exchange anisotropies, is plotted in Figure 3E. As the exchange anisotropy increases above the critical value, |b_ea| > 0.14, the oblique spiral state with Q‖⟨111⟩ is stabilized even at zero magnetic field.

For k_c = 0.15 (Figure 3C), the field-driven spiral rotation is slightly different. First of all, we notice that as h increases, the Q-vector abruptly accepts a rather high angle value (e.g., around 0.6 for b_ea = −0.15) and then stays almost unchanged forming a plateau up to the moment a tilted spiral undergoes the first-order phase transition with respect to the homogeneous state. Such a behaviour occurs even for small anisotropic exchange relative to the cubic anisotropy (e.g., b_ea = −0.05). An extended plateau is also observed on the curve α_max (b_ea) for the fixed k_c between two critical states—the conical phase for low b_ea values and the $⟨111⟩$ spiral for high b_ea (Figure 3E). Figure 3D shows corresponding stability areas of tilted and conical spirals for each value of the cubic anisotropy.

Tilted spiral state for H‖[110]

Two behavioural regimes of a tilted spiral are easily discernible for H‖[110]. Although no spiral canting towards ⟨111⟩ axes was found for k_c = 0.1 (which is also the case in the experiment), it becomes well apparent for k_c = 0.15 (has not been identified experimentally).

Figure 4A shows the three spiral domains with the wave vectors Q₁, Q₂ and Q₃ at low magnetic fields and k_c = 0.1. The zero-field degeneracy of the spiral states is lifted by the magnetic field, which favors the wave vectors Q₁ and Q₂ gradually rotating towards the field direction in the (001)-plane. Figures 4C–F show the energy density surface plots in the field range h = 0–0.07 as functions of α and ψ. The first-order phase transition between the oblique spiral states and the conical state with the wave vector Q₄‖H (Figure 4B) occurs at h ≈ 0.07. The transversal metastable spiral Q₃ jumps along the field at a higher field value $H_{c1}^{*}$. Thus, two critical lines of such spiral flips enter the experimental phase diagram of Cu₂OSeO₃ in Refs. [3, 5].

FIGURE 4

FIGURE 4. (color online) Spiral reorientation for H‖[110] and k_c = 0.1, b_ea = −0.13. (A) The three spiral states in low magnetic fields. Under an applied magnetic field, the oblique spiral states with Q₁ and Q₂ (along the [100] and [010] directions in zero field, respectively) undergo a first-order phase transition into the conical phase with Q₄‖H (B), whereas the metastable transversal spiral with the wave vector Q₃‖[001] persists up to a higher magnetic field. Such a spiral reorientation is characterized by the surface plots of the energy density (C–F) depending on the angles ψ and α as defined in Figure 2A.

In the same way, the degeneracy of the zero-field spiral states is lifted by an applied magnetic field for k_c = 0.15 (Figure 5). Oblique spirals with wave vectors Q₁ and Q₂ slowly approach the field direction (Figures 5A,C,D). At h = 0.065, however, a new energy minimum emerges, which corresponds to a tilted spiral state Q₅ (Figure 5E), which becomes the global minimum of the system at h = 0.07 (Figure 5F). Notice that the saddle point (Figure 5D) appears for both values of the cubic anisotropy but only for k_c = 0.15 it develops into a tilted spiral (Figure 5E). Eventually, this TS aligns with the field (Figures 5B,H).

FIGURE 5

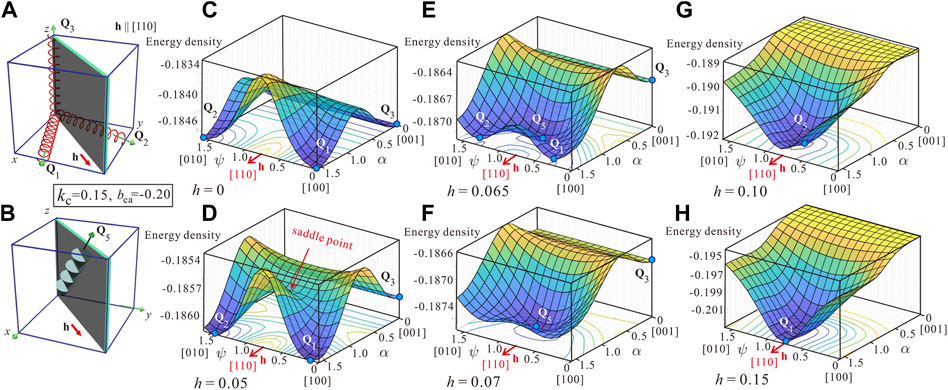
FIGURE 5. (color online) Spiral reorientation for H‖[110] and k_c = 0.15, b_ea = −0.20. (A) The three spiral states in low magnetic fields. Under an applied magnetic field, the oblique spiral states with Q₁ and Q₂ (along the [100] and [010] directions in zero field, respectively) undergo a first-order phase transition into the tilted spiral state with the wave vector Q₅ composing some angle with respect to the field (B), whereas the metastable transversal spiral with the wave vector Q₃‖[001] persists up to a higher magnetic field. With the increasing magnetic field, the tilted spiral aligns with the [110] direction. Such a spiral reorientation, which is different from the case considered in Figure 4, is characterized by the surface plots of the energy density (C–H) plotted for several field values and allowing to capture the subtleties of the described reorientation.

Tilted skyrmion states due to the competing anisotropy interactions

In the same way as it was implemented for tilted spirals, the spatial orientation of SkLs is specified by the competing effect of easy anisotropy axes and an applied magnetic field. For example in zero magnetic field and k_c > 0 (in the following, k_c = 0.1), SkLs are metastable states and occupy the crystallographic {001} planes with easy axes ⟨001⟩ of the cubic anisotropy (Figures 6, 7). For h‖[001], the equilibrium position of SkL was found to be codirectional with the applied magnetic field. Consequently SkL gains stability in the vast area of the theoretical phase diagram (Figure 1B). Two energetically close SkL minima were found to occur in the transversal (001) plane. The first minimum corresponds to the easy ⟨100⟩ cubic axes pointing along the diagonals of the hexagonal SkL and along their apothems. In the second minimum, the hexagonal lattice is rotated by the angle π/4. The cores of skyrmions in both states become square shaped with the tendency either to elongate or to shorten along particular directions (see for details Ref. [25]). In the experiment [3], one can discern 12 peaks originating from these two SkL domains within the ring of scattering. For larger anisotropy values, the easy cubic axes along the diagonals may induce an elliptical instability of the SkL similar to that of isolated skyrmions [31, 32] and trigger the phase transition into the helical state. Thus only the second SkL minimum is preserved. At the phase diagram of Figure 1B, the line a − b separates the two skyrmion lattice phases. For larger values of b_ea, SkLs may occupy {110} planes, which include the easy axes of the exchange anisotropy ⟨111⟩. However, even in a small magnetic field, SkL planes align perpendicular to the field.

FIGURE 6

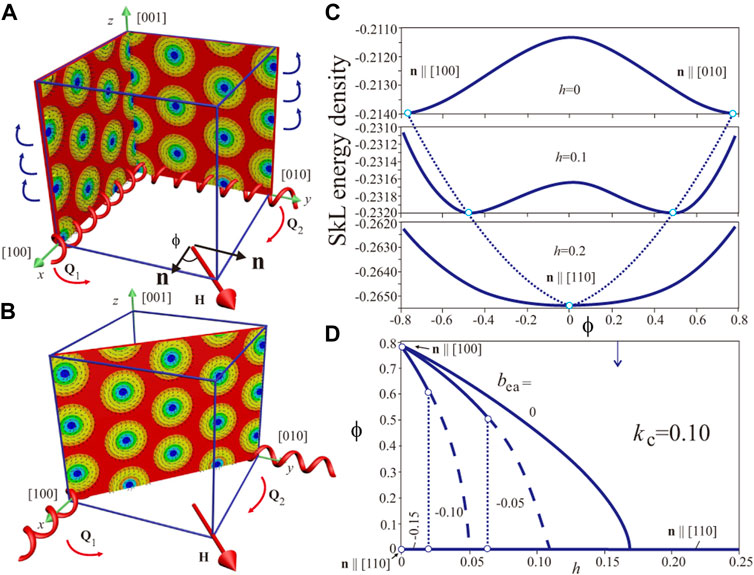
FIGURE 6. (color online) (A) Schematics of hexagonal skyrmion lattices occupying the {100} planes for the cubic anisotropy with easy ⟨001⟩ axes. In an applied magnetic field $\mathbf{h}$‖[110] the oblique SkLs orient perpendicular to the field (B), i.e., occupy the plane (110). The field dependence of the angle ϕ between the skyrmion axes and the field shown in (D) exhibits either a smooth rotation (for b_ea = 0) or a jump-like transition (for b_ea < 0). The SkL energy density, given in (C) for k_c = 0.1, b_ea = 0 in dependence on the field, is minimized with respect to the direction of $\mathbf{n}$.

FIGURE 7

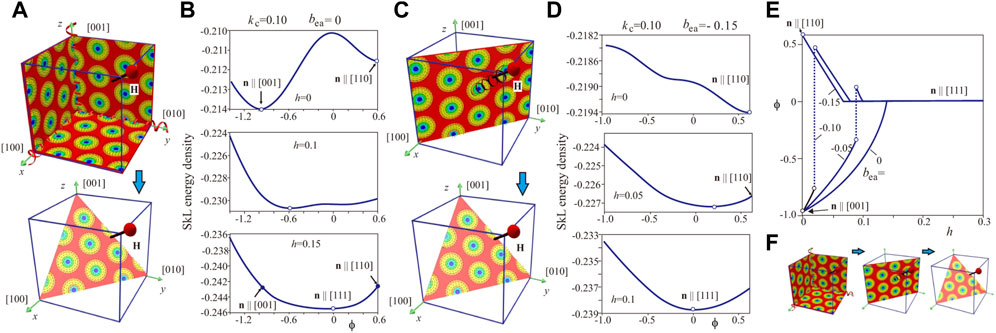
FIGURE 7. (color online) (A) Schematics of hexagonal skyrmion lattices occupying the {001} planes for the anisotropy set k_c = 0.1, b_ea = 0 at zero field. The metastable SkLs select these planes because of the easy ⟨100⟩ axes of the cubic anisotropy. In an applied magnetic field $\mathbf{h}$‖[111] the oblique SkLs orient perpendicular to the field, i.e., occupy the plane (111) [second panel in (A)]. Such a reorientation process is characterized by the energy density in (B) plotted in dependence on angle ϕ for different values of the field. The local minimum corresponding to the SkL in the {110} plane [first and second panel in (B)] disappears when the SkL reaches the plane {111} [third panel in (B)]. The field dependence of the angle ϕ corresponding to the global energy minimum in (B) is also shown in (E) depending on the field and exhibits smooth rotation in this case. (C) Schematics of hexagonal skyrmion lattices occupying the {110} planes for the anisotropy set k_c = 0, b_ea = −0.15. The metastable SkLs select these planes because of the easy ⟨111⟩ axes of the exchange anisotropy. In an applied magnetic field $\mathbf{h}$‖[111] the oblique SkLs also rotate towards the plane (111) [second panel in (C)] as also indicated by the field dependence ϕ(h) in (E). The SkL energy densities in (D) exhibit only one global minimum, which moves towards the value ϕ = 0 with the increasing field. For the set of competing anisotropies, the SkLs first jump into a (110) plane and then undergo rotation into the plane (111) as indicated by the dependencies ϕ(h) in (E) and by the schematics in (F).

For other directions of the field and k_c > 0, the SkL still remains a metastable solution. In an applied magnetic field h‖[110] (Figure 6A), the SkL rotates and orients perpendicular to the field, i.e., occupies the (110) plane. Whereas for b_ea = 0 such a rotation is smooth as shown by the energy density curves (Figure 6C), it becomes abrupt under the influence of exchange anisotropy. It is obvious that such SkLs’ jumps into the (110) plane are dictated by the easy axes ⟨111⟩ of the exchange anisotropy alongside with the Zeeman interaction. Figure 6D shows the angle ϕ between the field and the normal $\mathbf{n}$ to the SkL plane for different values of b_ea. The equilibrium angle ϕ is obtained by the energy minimization procedure, in which we smoothly rotate $\mathbf{n}$ in the plane (001). For b_ea = −0.15, the SkL is located in the plane (110) even for zero magnetic field, i.e., ϕ = 0 in the whole field range. Dashed lines indicate that the tilted SkLs exist as local energy minima even above the transition fields into the state perpendicular to the field.

For the magnetic field applied along [111] direction, the reorientation processes of LT-SkLs are more involved. Figures 7A,B show the details of SkL jumps for the “pure” effect of cubic anisotropy. SkLs, located in {001} planes, smoothly rotate towards {111} planes with increasing magnetic field. Interestingly, a SkL in the plane {110} represents a local energy minimum as shown by the first panel of Figure 7B. Two energy minima merge when the SkL aligns perpendicular to the field (third panel). For a dominating role of the exchange anisotropy (Figures 7C,D), SkLs occupy {110} planes and then gradually rotate towards {111} planes perpendicular to the field. For the chosen set of the anisotropy constants, the planes {100} do not even represent a local energy minimum (first panel in Figure 7D). For intermediate values of exchange anisotropy, however, SkLs undergo the following reorientation processes: first, they jump into a position close to {110} planes and then rotate towards {111} planes (Figure 7F). Such jumps become apparent at the field dependencies of ϕ(h) for fixed values of b_ea (Figure 7E).

Discussion: Quantitative model of Cu₂OSeO₃

To establish a quantitative phenomenological model of the bulk helimagnet Cu₂OSeO₃, one should determine all material constants entering Eqs. 1, 4. In this sense, hierarchically the most important Heisenberg exchange and Dzyaloshinskii-Moriya interactions may be evaluated at the atomic level, using, e.g., ab initio density functional theory (DFT) calculations. A multi-scale approach pursuing this goal is described in detail in Ref. [26] and Table 4 in the aforementioned paper gives the material constants A, D and K_c. Alternatively, the strength of the DMI together with the exchange interaction is known to govern the pitch of the spin spiral, the diameter of a single skyrmion, as well as the saturation field (H_c2) required to fully align the magnetic moments along the external field, and thus can be roughly evaluated. The obstacle to finalize the quantitative model, however, lies in the fact that anisotropic contributions with non-dimensional anisotropy coefficients k_c and b_ea usually appear together in the magnetization processes and moreover exhibit pronounced temperature dependence. In the following, we discuss qualitatively a strategy that could be utilized to complete a quantitative model for Cu₂OSeO₃. We will use some behavioral patterns drawn from previous theoretical results.

First of all, we notice that the point A at the experimental phase diagram—an intersection point between the curve H_c2 and an upper boundary of a LT-SkL pocket–demarcates two temperature regimes: for lower temperatures, SkL exists above H_c2 and its nucleation is believed to be directly related to the stability region of a tilted spiral [3, 4]; for higher temperatures, SkL dissolves before the cone saturation field H_c2; at the same time, identification of the tilted spiral in this temperature interval bumps into the accuracy of experimental procedures. According to the theoretical phase diagram constructed in Ref. [25], the point A corresponds to the value $k_c^{(A)}\approx 0.06$ (Figure 1B). The minimal anisotropy value k_c needed to stabilize skyrmions is computed theoretically, $k_c^{(B)}\approx 0.04$, which would correspond to the farthest temperature point of the LT-SkL pocket in Figure 1A. Such a cubic anisotropy, however, will not lead to a tilted spiral state, which sets in only for k_c > 0.05. At the same time, we argue that the value of k_c must be smaller than 0.15, since in the experiments no tilted spiral state was observed for H‖[110] (although it is predicted in Figure 5). The value of the exchange anisotropy b_ea can be then finely tuned by comparing different characteristics of the tilted spiral from the experiment and the theoretical modeling. An exhaustive analysis will be done elsewhere. Here, we just claim that the two regimes of the tilted spirals considered before roughly correspond to the experimental results for 2K and 18K, respectively.

A systematic study of the stability and ordering of the low temperature magnetic states was done in Refs. [3, 5, 7]. Analysis of experimental data for low temperatures (e.g., T = 2K) prompts the following conclusions: i) an experimental value of α_max = 0.61 cannot be explained by the theoretical data for k_c = 0.1, since theoretically only a smaller angle value can be achieved; on the other hand, for k_c = 0.15 such an angle value is readily reached on one of the plateau-like dependencies α(h) (Figure 3D) for b_ea < − 0.15; ii) comparing the experimental field interval of tilted spiral existence ΔH ≈ 0.59 with Figure 3F one may estimate b_ea ≈ − 0.18. In any case, theoretical results for k_c = 0.15 allow to qualitatively address the following experimentally observed phenomena in Ref; [7]: i) first-order phase transition with respect to the homogeneous state, which also becomes apparent in the coexistence of conical and tilted spiral states; ii) rather abrupt cone evolution into a tilted spiral state, which is identified as a blind zone, for which a tilted spiral angle does not exist (as seen in Figure 2E); iii) comparable angles and field intervals of spiral canting followed from the theory and the experiment.

Analysis of experimental data for temperatures close to the critical point A (e.g., T = 18K) can be summarized as follows: the first-order phase transition between a tilted and homogeneous states manifests itself in a rather unpronounced way; indeed, the spirals smoothly slant starting directly from the conical state and almost return back, which may be addressed by the anisotropy value k_c = 0.1; an experimental ratio of two fields H_c2 for the considered two temperatures is 1.0575, which theoretically results in k_c = 0.12 if one assumes k_c = 0.15 for T = 2.

The value k_c = 0.05 is located on the other side from the critical point A and thus corresponds to experimentally higher temperatures. The value of the exchange anisotropy must have an upper boundary, b_ea > − 0.08, since no oblique spirals in zero field were observed. One may remark that in this case other nucleation mechanisms should be considered to explain SkL stability [6]. Experimentally, the tilted spiral is found to persist up to above T = 35 K, which is not supported by the theoretical results with k_c < 0.04. Still, due to the “flat” energy minimum for the conical state, one observes experimentally some broadening of the conical peaks without a preferable tilt direction, an effect that spans the whole conical phase and persists up to above 35 K [7]. The subsequent endeavor to construct a quantitative model for a bulk helimagnet Cu₂OSeO₃ must take into account experimental data for other field directions. Moreover, non-hysteretic magnetization processes with high experimental accuracy must be given a fitting preference.

Conclusion

In order to narrow down the range of anisotropy coefficients in the phenomenological model of a bulk helimagnet Cu₂OSeO₃ and to build its complete quantitative model, we examined the low-temperature behavior of tilted skyrmion and spiral states. By comparing the results of numerical simulations with the plentiful experimental data from our previous publications [3, 5–7] we were able to ascribe the range of the cubic anisotropy, k_c = 0.15–0.10, to the temperature range T = 2–18K. The course of reasoning leading to a complete quantitative model for a bulk helimagnet Cu₂OSeO₃ is based on simultaneous examination of stable skyrmion and tilted-spiral states. One could not rely on the behavior of the tilted spiral alone, since it would result in some alternative parameter sets inconsistent with the behavior of LT-skyrmions. The complex reorientation processes of metastable skyrmions (Figure 6; Figure 7) are barely reflected at the experimental phase diagrams and are often hidden by the reorientation of spiral states. However, an experimental indication of tilted skyrmion states is presumably manifested by their abrupt disappearance above the $H_{c1}^{*}$ line for H‖[110] (see Figure 5B in Ref. [3]).

In the present manuscript, we used definitions of different modulated states (for example, transversal and conical spirals) conventional in the theoretical modeling. In the experiments, however, one would probably not specify different spiral states below the critical field H_c1 and would describe it as a multidomain spiral state. Moreover, the line H_c1 is not shown at the theoretical phase diagram in Figure 1B, since it is related to the reorientation processes of metastable transversal spirals, which, according to the theory, must not be reproduced with the decreasing magnetic field. Therefore, besides the further step to finalize the quantitative model of a bulk helimagnet Cu₂OSeO₃, we pursued the goal to make the terminology used in the theoretical and experimental aproaches consistent.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AL and CP conceived of the presented idea. AL developed the theory and performed the computations. AL wrote the manuscript. All authors discussed the results and contributed to the final manuscript.

Funding

JSPS Grant-in-Aid (C) No. 21K03406 the Vrije FOM-programma “Skyrmionics”.

Acknowledgments

The authors are grateful to Marta Crisanti for useful discussions. AL. thanks U. Nitzsche for technical assistance and acknowledges JSPS Grant-in-Aid (C) No. 21K03406. CP acknowledges financial support from the Vrije FOM-programma “Skyrmionics”.

Conflict of interest

The handling editor VU declared a past co-authorshipwith the author(s) AL.

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Seki S, Yu XZ, Ishiwata S, Tokura Y. Observation of skyrmions in a multiferroic material. Science (2012) 336:198–201. doi:10.1126/science.1214143

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Adams T, Chacon A, Wagner M, Bauer A, Brandl G, Pedersen B, et al. Long-wavelength helimagnetic order and skyrmion lattice phase inCu2OSeO3. Phys Rev Lett (2012) 108:237204. doi:10.1103/physrevlett.108.237204

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bannenberg LJ, Wilhelm H, Cubitt R, Labh A, Schmidt M, Lelievre-Berna E, et al. Multiple low-temperature skyrmionic states in a bulk chiral magnet. NPJ Quan Mater (2019) 4:11. doi:10.1038/s41535-019-0150-7

CrossRef Full Text | Google Scholar

4. Chacon A, Heinen L, Halder M, Bauer A, Simeth W, Muehlbauer S, et al. Observation of two independent skyrmion phases in a chiral magnetic material. Nat Phys (2018) 14:936–41. doi:10.1038/s41567-018-0184-y

CrossRef Full Text | Google Scholar

5. Qian F, Bannenberg LJ, Wilhelm H, Chaboussant G, DeBeer-Schmitt LM, Schmidt MP, et al. New magnetic phase of the chiral skyrmion material Cu2OSeO3. Sci Adv (2018) 4:eaat7323. doi:10.1126/sciadv.aat7323

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Leonov AO, Pappas C. Topological boundaries between helical domains as a nucleation source of skyrmions in a bulk cubic helimagnet Cu2OSeO3. Phys Rev Res (2022) 4:043137. doi:10.1103/PhysRevResearch.4.043137

CrossRef Full Text | Google Scholar

7. Crisanti M, Leonov AO, Cubitt R, Wilhelm H, Schmidt MP, Pappas C. Tilted spirals and low temperature skyrmions in Cu2OSeO3. Phys Rev Res (2023).

Google Scholar

8. Ishikawa Y, Arai M. Magnetic phase diagram of MnSi near critical temperature studied by neutron small angle scattering. J Phys Soc Jpn (1984) 53:2726–33. doi:10.1143/jpsj.53.2726

CrossRef Full Text | Google Scholar

9. Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, et al. Skyrmion lattice in a chiral magnet. Science (2009) 323:915–9. doi:10.1126/science.1166767

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Uchida M, Nagaosa N, He JP, Kaneko Y, Iguchi S, Matsui Y, et al. Topological spin textures in the helimagnet FeGe. Phys Rev B (2008) 77:184402. doi:10.1103/physrevb.77.184402

CrossRef Full Text | Google Scholar

11. Wilhelm H, Baenitz M, Schmidt M, Roessler UK, Leonov AA, Bogdanov AN. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys Rev Lett (2011) 107:127203. doi:10.1103/physrevlett.107.127203

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Halder M, Chacon A, Bauer A, Simeth W, Muehlbauer S, Berger H, et al. Thermodynamic evidence of a second skyrmion lattice phase and tilted conical phase inCu2OSeO3. Phys Rev B (2018) 98:144429. doi:10.1103/physrevb.98.144429

CrossRef Full Text | Google Scholar

13. Buhrandt S, Fritz L. Skyrmion lattice phase in three-dimensional chiral magnets from Monte Carlo simulations. Phys Rev B (2013) 88:195137. doi:10.1103/physrevb.88.195137

CrossRef Full Text | Google Scholar

14. Levatic I, Popcevic P, Surija V, Kruchkov A, Berger H, Magrez A, et al. Dramatic pressure-driven enhancement of bulk skyrmion stability. Sci Rep (2016) 6:21347. doi:10.1038/srep21347

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Okamura Y, Kagawa F, Seki S, Tokura Y. Transition to and from the skyrmion lattice phase by electric fields in a magnetoelectric compound. Nat Commun (2016) 7:12669. doi:10.1038/ncomms12669

PubMed Abstract | CrossRef Full Text | Google Scholar

16. White JS, Prsa K, Huang P, Omrani AA, Zivkovic I, Bartkowiak M, et al. Electric-field-induced skyrmion distortion and giant lattice rotation in the magnetoelectric InsulatorCu2OSeO3. Phys Rev Lett (2014) 113:107203. doi:10.1103/physrevlett.113.107203

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kruchkov AJ, White JS, Bartkowiak M, Zivkovic I, Magrez A, Ronnow HM. Direct electric field control of the skyrmion phase in a magnetoelectric insulator. Sci Rep (2018) 8:10466. doi:10.1038/s41598-018-27882-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. White JS, Zivkovic I, Kruchkov AJ, Bartkowiak M, Magrez A, Ronnow HM. Electric-field-driven topological phase switching and skyrmion-lattice metastability in magnetoelectric Cu2OSeO3. Phys Rev Appl (2018) 10:014021. doi:10.1103/physrevapplied.10.014021

CrossRef Full Text | Google Scholar

19. Wu HC, Wei TY, Chandrasekhar KD, Chen TY, Berger H, Yang HD. Unexpected observation of splitting of skyrmion phase in Zn doped Cu2OSeO3. Sci Rep (2015) 5:13579. doi:10.1038/srep13579

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Seki S, Okamura Y, Shibata K, Takagi R, Khanh ND, Kagawa F, et al. Stabilization of magnetic skyrmions by uniaxial tensile strain. Phys Rev B (2017) 96:220404. doi:10.1103/physrevb.96.220404

CrossRef Full Text | Google Scholar

21. Nakajima T, Ukleev V, Ohishi K, Oike H, Kagawa F, Seki S-i., et al. Uniaxial-stress effects on helimagnetic orders and skyrmion lattice in Cu2OSeO3. J Phys Soc Jpn (2018) 87:094709. doi:10.7566/jpsj.87.094709

CrossRef Full Text | Google Scholar

22. Leonov AO, Pappas C, Kezsmarki I. Field and anisotropy driven transformations of spin spirals in cubic skyrmion hosts. Phys Rev Res (2020) 2:043386. doi:10.1103/physrevresearch.2.043386

CrossRef Full Text | Google Scholar

23. Roessler UK, Leonov AA, Bogdanov AN. Skyrmionic textures in chiral magnets. J Phys Conf Ser (2010) 200:022029. doi:10.1088/1742-6596/200/2/022029

CrossRef Full Text | Google Scholar

24. Leonov AO, Bogdanov AN. Crossover of skyrmion and helical modulations in noncentrosymmetric ferromagnets. New J Phys (2018) 20:043017. doi:10.1088/1367-2630/aab702

CrossRef Full Text | Google Scholar

25. Leonov AO, Pappas C. Multiple skyrmionic states and oblique spirals in bulk cubic helimagnets. In: Magnetic Skyrmions and Their Applications. Editor G. Finocchio, and C. Panagopoulos (2021).

CrossRef Full Text | Google Scholar

26. Janson O, Rousochatzakis I, Tsirlin AA, Belesi M, Leonov AA, Roessler UK, et al. The quantum nature of skyrmions and half-skyrmions in Cu2OSeO3. Nat Commun (2014) 5:5376. doi:10.1038/ncomms6376

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Dzyaloshinskii IE. Theory of helicoidal structures in antiferromagnets. I. nonmetals. J Sov Phys Jetp-ussr (1964) 19:960.

Google Scholar

28. Bogdanov AN, Yablonsky DA. Theormodynamically stable vortices in magnetically ordered crystals. Mixed state of magnetics. Zh Eksp Teor Fiz (1989) 95:178.

Google Scholar

29. Bak P, Jensen MH. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J Phys C: Solid State Phys (1980) 13:L881–5. doi:10.1088/0022-3719/13/31/002

CrossRef Full Text | Google Scholar

30. Leonov AO, Pappas C, Smalyukh II. Field-driven metamorphoses of isolated skyrmions within the conical state of cubic helimagnets. Phys Rev B (2021) 104:064432. doi:10.1103/physrevb.104.064432

CrossRef Full Text | Google Scholar

31. Bogdanov A, Hubert A. The stability of vortex-like structures in uniaxial ferromagnets. J Magn Magn Mater (1994) 138195:255182–92. doi:10.1016/s0304-8853(98)01038-5

CrossRef Full Text | Google Scholar

32. Leonov AO, Monchesky TL, Romming N, Kubetzka A, Bogdanov AN, Wiesendanger R. The properties of isolated chiral skyrmions in thin magnetic films. New J Phys (2016) 18:065003. doi:10.1088/1367-2630/18/6/065003

CrossRef Full Text | Google Scholar