
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 07 February 2023
Sec. Quantum Engineering and Technology
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1101631
This article is part of the Research Topic Multiparty Quantum Communication and Quantum Cryptography View all 7 articles
 Xiao-Lei Jiang1,2
Xiao-Lei Jiang1,2 Yang Wang1,2,3*
Yang Wang1,2,3* Yi-Fei Lu1,2
Yi-Fei Lu1,2 Jia-Ji Li1,2
Jia-Ji Li1,2 Hai-Long Zhang1,2
Hai-Long Zhang1,2 Mu-Sheng Jiang1,2
Mu-Sheng Jiang1,2 Chun Zhou1,2
Chun Zhou1,2 Wan-Su Bao1,2*
Wan-Su Bao1,2*Quantum conference key agreement (QCKA) allows multiple users to distribute secret conference keys over long distances. Measurement-device-independent QCKA (MDI-QCKA) is an effective QCKA scheme, which closes all detection loopholes and greatly enhances QCKA’s security in practical application. However, an eavesdropper (Eve) may compromise the security of practical systems and acquire conference key information by taking advantage of the weak randomness from the imperfect quantum devices. In this article, we analyze the performance of the MDI-QCKA scheme based on the weak randomness model. Our simulation results show that even a small proportion of weak randomness may lead to a noticeable fluctuation in the conference key rate. For the case with finite-key size, we find that the weak randomness damages the performance of MDI-QCKA to different degrees according to the data size of total pulses transmitted. Furthermore, we infer that QCKA based on single-photon interference technology may perform better in resisting weak randomness vulnerabilities. Our work contributes to the practical security analysis of multiparty quantum communication and takes a further step in the development of quantum networks.
Quantum key distribution (QKD) has become the art of two legitimate parties (Alice and Bob) distributing secret information by virtue of the laws of physics [1]. It has information-theoretical security regardless of the unlimited computational power of an eavesdropper (Eve) [2, 3]. Over the past decades, QKD has developed rapidly and made remarkable progress in terms of theory and practice.
At present, the two-party scheme is the main direction of most theoretical and experimental works. In fact, multi-party quantum communication protocols have also been proposed and studied. The quantum conference key agreement (QCKA) [4–7] is one of the most promising applications that distributes the conference key among multiple parties over a long distance. Particularly, combing the MDI [8] technology via post-selected Greenberger–Horne–Zeilinger (GHZ) entangled states [9, 10], allows measurement-device-independent QCKA (MDI-QCKA) [11] to eliminate all side-channel attacks in detectors and plays a vital role in the construction and development of quantum networks. Furthermore, MDI-QCKA has been studied under different conditions consisting of finite-key size [12], continuous variables [13, 14], four users with the W state [15], and device independence [16, 17]. Recently, based on single-photon interference technology, some new QCKA protocols have also been proposed in which the conference key rate and transmission distance are improved greatly [18–23].
In terms of the practical quantum communication system, Eve may choose quantum devices of state preparation or measurement as the target of her (his) attack, which may result in bit encoding and basis selection being modulated not at random [24–27]. Li et al. proposed a weak randomness model [28–30] to analyze the quantum state preparation vulnerability in the BB84 protocol. Recently, this security analysis technology has been applied in the reference-frame-independent QKD (RFI-QKD) [31], MDI-QKD [32], and sending-or-not-sending twin-field QKD (SNS TF-QKD) [33]. Under the condition of weak randomness, the states prepared consisted of random and non-random parts [28]. States prepared from the non-random part may lead to the leakage of secret key information to Eve. In fact, the weak randomness model is also appropriate for the QCKA for two reasons. First, three communicators (Alice, Bob, and Charlie) are required in the QCKA to perform quantum state preparation operation, which has to be affected by imperfections of quantum devices. Eve may exploit the weak randomness of imperfect devices to intervene in bit encoding and the basis selection process. Second, based on the decoy-state method, signal states or decoy states emitted by Alice, Bob, and Charlie are transmitted in the optical channel. In this case, Eve may perform attenuation operation to maximize the leaked information. Consequently, it is necessary to consider QCKA protocols’ and the practical security of weak randomness.
In this article, we analyze the performance of the decoy-state MDI-QCKA [11] based on the weak randomness model. First, we analyze the potential influence of weak randomness on the conference key rate in the asymptotic case. Second, we analytically derive the formula of the length of the conference key with finite-key size by exploiting the Chernoff bound [34–36]. Utilizing the experimental parameters from Ref. [11], we numerically simulate the secret conference key rate under the condition of weak randomness. The results demonstrate that the performance of MDI-QCKA deteriorates rapidly, even with the fraction of weak randomness. For the case with finite-key size, we notice that weak randomness damages the performance of MDI-QCKA differently for different data sizes of total transmitted pulses, and the impact of weak randomness on the conference key rate may be greater than the data size of the total transmitted pulses. Moreover, we compare the results with our previous work and notice that utilizing single-photon interference technology in the QCKA may enhance resistance to vulnerabilities of weak randomness.
The remainder of the article is organized as follows: in Section 2, we describe a decoy-state MDI-QCKA protocol. In Section 3, we analyze the security of the decoy-state MDI-QCKA protocol based on the weak randomness model in both asymptotic and non-asymptotic cases. In Section 4, we present the numerical simulation results and a discussion. Finally, the conclusion is drawn in Section 5.
Here, let us review the three-intensity decoy-state MDI-QCKA protocol; the description of the protocol is as follows:
(1) State preparation. Alice, Bob, and Charlie randomly modulate the intensities
(2) Measurement. David performs a GHZ-state measurement of pulses sent by Alice, Bob, and Charlie and projects the received pulses into a GHZ state. Here, David only identifies two of the eight GHZ states:
(3) Sifting. Three legitimate members publish their basis and intensity choices via an authenticated channel. Once they choose the same basis with Alice’s intensity αa, Bob’s intensity βb, and Charlie’s intensity γc, David announces a successful measurement event, and three legitimate members record the number of detected pulses.
(4) Parameter estimation. First, Alice, Bob, and Charlie calculate the single-photon counting rate of successful measurement events on the Z or X basis. Second, they calculate the bit error rate on the X basis for the intensity combination αaβbγc (αa ∈ A, βb ∈ B, γc ∈ C). Finally, they verify the bit error rate of the X basis.
(5) Error correction. Here, we assume that the raw conference key of Alice refers to the reference raw key. Bob and Charlie perform an error correction step so that their raw keys match the raw key of Alice. This error correction operation consumes information at most LeakEC bits. In order to ensure that three legitimate members possess the same conference keys, they conduct an error verification operation.
(6) Private amplification. In order to decrease Eve’s information on three legitimate members’ conference keys, three legitimate members also use a random two-universal hash function to obtain the final conference key pairs (SA, SB, SC).
For the security analysis of decoy-state MDI-QCKA under the condition of weak randomness, hidden variables ξ, ζ, and ς from Eve are assumed to determine the states which are prepared by three legitimate members, and Eve should take responsibility for all abovementioned weak randomness imperfections. The probabilities of non-random part states prepared by three legitimate members are p1, p2, and p3. If p1(2,3) = 1, all conference key information may be leaked to Eve, that is, R = 0. If p1 = p2 = p3 = 0, Eve cannot obtain information theoretically. If 0 < p1(2,3) < 1, we can apply the weak randomness model to estimate the maximum quantity of information stolen by Eve.
Here, we suppose that the binary set of bits S, T, and G prepared by Alice, Bob, and Charlie, respectively, decide bit encoding and basis selection. |S|, |T|, and |G| represent the order of sets S, T, and G, respectively. Because of the weak randomness imperfection in the practical system, the random number cannot be perfectly prepared, which shows that partial bits belonging to sets S, T, and G are mastered by Eve. S is made up of a non-random part S1 and a random part S2. T is made up of a non-random part T1 and a random part T2. G is made up of a non-random part G1 and a random part G2. This is rational to assume by considering two scenarios. First, Eve may attack the random number generator and obtain partial random number information. Second, the state may be modulated by different laser diodes from three legitimate members, and Eve may distinguish them by observing characteristics such as the spectrum and timing sequence. Here, we define the weak randomness parameter
Under the condition of weak randomness, Eve attenuates the quantum states from random parts S2, T2, and G2 with a certain probability in the channel. For this case, the non-random part quantum states reach David without attenuation. Here, we assume that bit errors only come from random parts, and that the states of non-random part do not generate bit errors. If Eve performs attenuation and keeps the error rate within a rational range, her (his) presence cannot be detected by three legitimate members. Considering signal loss, the non-random probability in David’s side may be amplified. Consequently, the maximum transmission distance may compromise, the gain of single-photon on the Z basis may decrease, and the bit error rate may increase.
Based on the weak randomness model, Alice, Bob, and Charlie prepare quantum states as follows:
where Eve can obtain information about Alice’s (Bob’s and Charlie’s) system according to the auxiliary quantum state. For Alice’s (Bob’s and Charlie’s) system, if Eve’s auxiliary quantum state is
In the decoy-state MDI-QCKA protocol, three legitimate members may prepare signal and decoy states using the same laser diodes with the same random probabilities p1, p2, p3. Furthermore, signal and decoy states can also be prepared using different laser diodes. For this case, signal and decoy states prepared by three legitimate members can be distinguished with the probabilities p1, p2, p3. If signal states are distinguished, Eve can perform PNS attack [37] without being detected, and Eve performs an attenuate operation in the quantum channel when signal states are not distinguished.
Then, we may estimate the parameters under the condition of weak randomness. The final conference key rate of the decoy-state MDI-QCKA can be given by [11]:
where
The overall gain and bit error rate can be expressed as
where W = X, Z.
The gain of single-photon states on the Z basis can be given by
the gain when Alice sends the vacuum state while David gets a successful GHZ-state measurement event on the Z basis is given by
Considering the condition of weak randomness, the probability of Alice, Bob, and Charlie preparing non-random part quantum states are p1, p2, and p3, respectively. Eve not only attenuates the states in random parts to amplify the non-random proportion at David’s side but also controls the probability of attenuation to ensure that she (he) will not be detected by three members. We assume that Eve only attenuates the random portion of the single photon, and that multi-photons are not actually used to generate secret keys. The probability of signal loss from the random part is given by
The non-random proportion of quantum states reaching David’s side can be expressed as
The gain of the random part single-photon states which can generate conference keys on the Z basis can be expressed as
where
where
Considering the attenuation operation from Eve, the value of the bit error rate
With the method mentioned in [38, 39], we can calculate the value of
Here, we employ the weak randomness model to analyze the security of the decoy-state MDI-QCKA and derive formulas for the lower bound of the successful single-photon gain and the upper bound of the bit error rate. The final length of the conference keys on the Z basis can be given by [11, 12]:
where
Let
where
where
On the basis of Eq. 9, we can also derive the probability of random part signal loss in the case of finite-key size:
The non-random proportion of quantum states reaching David’s side can be expressed as
where N denotes the total data size of transmitted pulses, W = X, Z.
Taking independent events into account, we exploit the Chernoff bound [34–36] to calculate the number of practical measurement events, which can be expressed as
with the probability at least 1 − 2ɛ1, where
Furthermore,
where
where
For the case of finite sample sizes, the relation between the expected value and observed value of
with the probability at least 1 − 2ɛ2, where
The number of single-photon detections from a non-random set which cannot generate conference keys on the Z basis can be expressed as
The number of single-photon detections from a random set is supposed to satisfy
The number of detections from the non-random part when Alice sends a vacuum state while David gets a successful GHZ state measurement event on the Z basis can be expressed as
The secure single-photon detection from the random part when Alice sends a vacuum state while David gets a successful GHZ state measurement event on the Z basis is supposed to satisfy
The lower bound of the single-photon detection on the Z basis can be given by
where
The number of successful single-photon detection when Alice sends a vacuum state while David gets a successful GHZ state measurement event on the Z basis can be given by
where
Considering the attenuation operation from Eve, the value of the bit error rate
where
where
Furthermore, the number of bit errors on the X basis is related to the single-photon detection
where
where
Adopting the same calculation method of
Finally, combining Eqs. 24, 26, 31, we can derive the secret conference key length of the decoy-state MDI-QCKA under the condition of weak randomness.
In this section, based on the fiber-based channel model and the experimental parameters in Ref. [11], we simulate the performance of the decoy-state MDI-QCKA with the effect of weak randomness in both asymptotic and finite-key size cases.
Here, we define the fiber transmittance of Alice, Bob, and Charlie as

TABLE 1. List of experimental parameters applied in the numerical simulation. Here, α denotes the fiber loss coefficient (dB/km), pd is the dark count rate of David’s detectors, ηd is the detection efficiency of the David’s detectors, ed is the optical misalignment-error probability, f is the error correction inefficiency, and ɛ is the security bound when considering statistical fluctuation analysis.
In Figure 1, we simulate the performance of the decoy-state MDI-QCKA in the asymptotic case. Here, we assume that three legitimate members are symmetrical in the system. p1, p2, p3 = 0 means that randomness in the quantum-prepared operation is perfect, and p1, p2, p3 = 10−x(x = 10, 8, 6) means that Eve can master different randomness information. As shown in the results, we can deduce that the lack of randomness on either side will cause information leakage and affect the generation of the conference key. Although Eve only masters one party randomness information for p1 = 10−10 and p2, p3 = 0, the maximum transmission distance dropped evidently from 207 km to 149 km. Particularly, when the parameters of weak randomness p1, p2, p3 = 10−6, the achievable transmission distance decreases to 132 km.
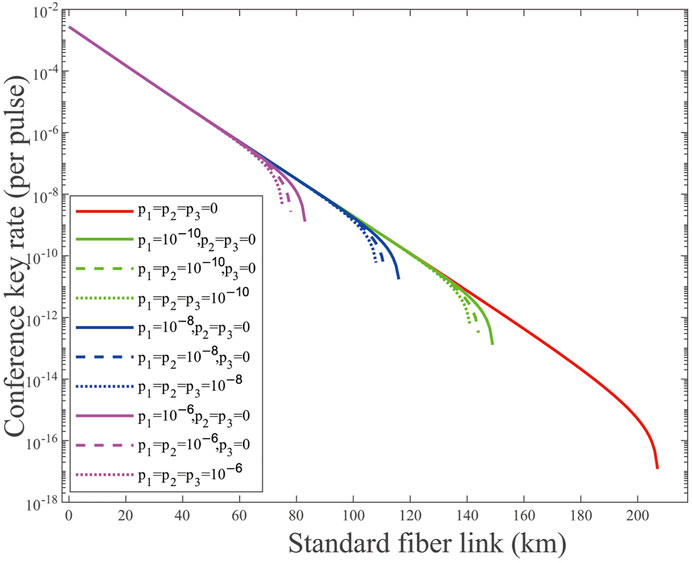
FIGURE 1. (Color online) Conference key rate (per pulse) on a logarithmic scale vs. transmission distance in the asymptotic case for p1,2,3 = 0, 10−x(x = 10, 8, 6). The solid lines are the results of weak randomness existing in one party, the dashed lines are the results of weak randomness existing in two parties, and the dotted lines are the results of weak randomness existing in three parties.
For the case with finite-key size, we simulate the conference key rate with the effects of weak randomness as shown in Figure 2. Here, we fixed the data size of the total transmitted signals N = 1014. The results show that weak randomness evidently limits the conference key rate and achievable transmission distance. Although Eve only masters one party randomness information for p1 = 10−6, 10−5, 10−4, and p2, p3 = 0, the achievable transmission distance decreases to 26, 42, and 49 km, respectively. When the weak randomness parameters p1, p2, p3 = 10−6, 10−5, 10−4, the achievable transmission distance decreases to 34, 50, and 66 km, respectively.
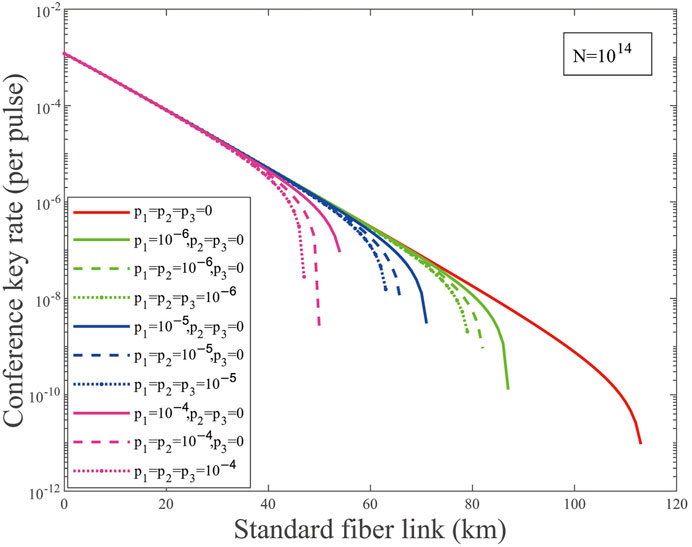
FIGURE 2. (Color online) Conference key rate (per pulse) on a logarithmic scale vs. transmission distance for p1,2,3 = 0, 10−x(x = 6, 5, 4) and the total number of transmitted signals N = 1014. The solid lines are the results of weak randomness existing in one party, the dashed lines are the results of weak randomness existing in two parties, and the dotted lines are the results of weak randomness existing in three parties.
As shown in Figure 3, the curves from right to left are acquired by the data size of transmitted pulses N = 10x(x = 15, 14, 13, 12). We can see that the greater the data size of the total transmitted pulses, the more obvious the effect of weak randomness. In detail, the achievable transmission distance decreases to 51.63%, 44.25%, 35.05%, and 23.75% when N = 1015, 1014, 1013, 1012, respectively. When the data size of the total transmitted signals increases, the number of quantum states attenuated increases. In the practical system, the leaked information may also increase because Eve can take advantage of the relationship between the expected values and observed values of different modulated states.
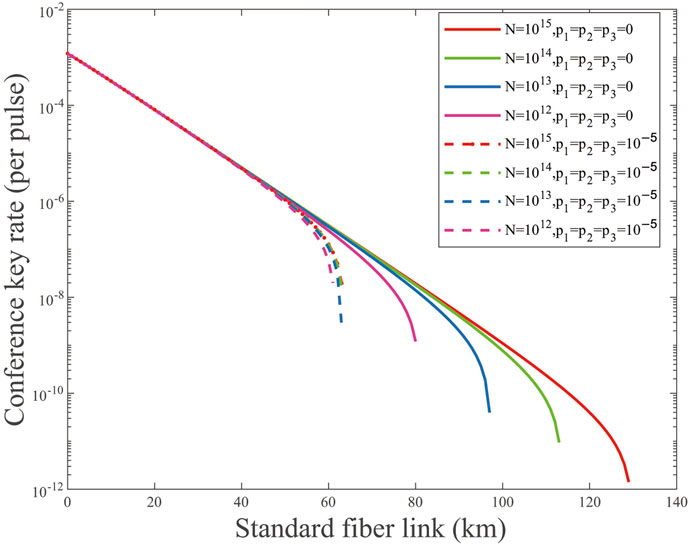
FIGURE 3. (Color online) Conference key rate (per pulse) on a logarithmic scale vs. transmission distance for p1,2,3 = 0, 10−5 and different total numbers of transmitted signals N = 10x(x = 15, 14, 13, 12). The solid lines are the results of p1,2,3 = 0, and the dashed lines are the results of p1,2,3 = 10−5.
In order to further analyze the impact of weak randomness in the case of finite-key size, we consider the conference key rate for N = 1014, 1013 with different weak randomness parameters p1, p2, p3 = 0, 10−x(x = 6, 5, 4). As shown in Figure 4, we can notice that the conference key rate lines for N = 1013 and N = 1014 overlap approximately when the weak randomness parameters are p1, p2, p3 ≥ 10−5. We also deduce that the impact of weak randomness on the conference key rate is stronger than the total data size of transmitted pulses when p1, p2, p3 ≥ 10−5.
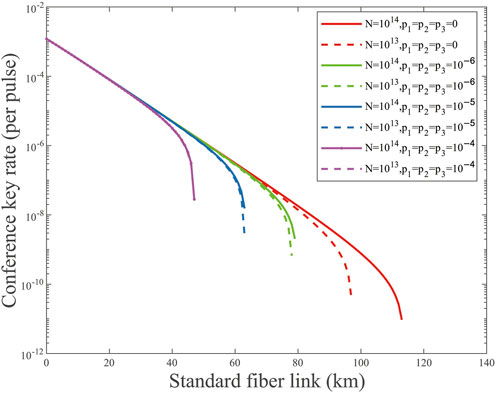
FIGURE 4. (Color online) Conference key rate (per pulse) on a logarithmic scale vs. transmission distance for p1,2,3 = 0, 10−x(x = 6, 5, 4) and different values of N = 1014, 1013. The solid lines are the results of N = 1014, and the dashed lines are the results of N = 1013.
Finally, let R(p) be the conference key rate with weak randomness and R(0) be the conference key rate without weak randomness. The relationship between R(p)/R(0) and transmission distance for p1, p2, p3 = 0, 10−6 and N = 1014 is shown in Figure 5. Compared with our previous studies on MDI-QKD [32] and SNS TF-QKD [33], we can find that MDI-QCKA is more susceptible to weak randomness. In fact, all three legitimate members need to prepare quantum states in the practical MDI-QCKA system, and it is more difficult to protect random information than the other two. In addition, we notice that SNS TF-QKD can better resist weak random imperfection and realize longer transmission distance; therefore, we suspect that QCKA based on single-photon interference technology may perform better in resisting weak randomness, which deserves further study.
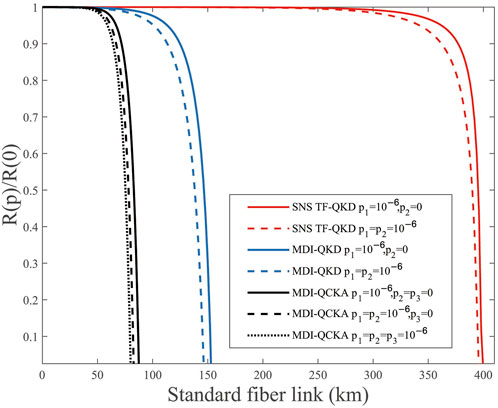
FIGURE 5. (Color online) R(p)/R(0) vs. transmission distance with p1, p2, p3 = 0, 10−6 and N = 1014. The red lines are the results of SNS TF-QKD, the blue lines are the results of MDI-QKD, and the black lines are the results of MDI-QCKA.
From the simulation results presented previously, we can find that the security of MDI-QCKA is sensitive to weak randomness in both asymptotic and finite-key size cases. Furthermore, we find that weak randomness damages the performance of MDI-QCKA to different degrees for different data sizes of the total transmitted signals. Finally, we conclude that QCKA based on the single-photon technology may be better resistant to weak random vulnerabilities.
In conclusion, we employ the weak randomness model to analyze the security of the decoy-state MDI-QCKA and study the performance of the decoy-state MDI-QCKA in both the asymptotic case and non-asymptotic case. The simulation results demonstrate that the weak randomness of the practical QCKA system is non-negligible. The conference key rate and achievable transmission distance will be significantly compromised due to the attenuation operation of Eve. Moreover, we find that weak randomness impacts the conference key rate differently for different data sizes of transmitted pulses and the impact may be greater than that of the data size of transmitted pulses in some cases. To avoid such a vulnerability risk in a QCKA system, two approaches can be considered. First, protecting randomness information from leakage. Second, the risk of the side channels at the source should be reduced and distinguishability of the quantum states in all degrees of freedom should be avoided. Compared with our previous work, we infer that QCKA based on single-photon interference technology may have more development prospects in resisting weak randomness, which is also our future research direction.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Methodology: X-LJ; software: X-LJ and YW; writing—original draft preparation: X-LJ; writing—review and editing: Y-FL, CZ, J-JL, H-LZ, and M-SJ; supervision: W-SB; funding acquisition: W-SB and YW.
This research was funded by the National Natural Science Foundation of China (Grant No. 62101597), the National Key Research and Development Program of China (Grant No. 2020YFA0309702), the China Postdoctoral Science Foundation (Grant No. 2021M691536), the Natural Science Foundation of Henan (Grant No. 202300410534), and the Anhui Initiative in Quantum Information Technologies.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Bennett C, Brassard G. Quantum cryptography: Public key distribution and coin tossing. In: Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing; 10-12 December 1984; Bangalore (1984). p. 175–9.
2. Xu F, Ma X, Zhang Q, Lo HK, Pan JW. Secure quantum key distribution with realistic devices. Rev Mod Phys (2020) 92:025002. doi:10.1103/revmodphys.92.025002
3. Pirandola S, Andersen UL, Banchi L, Berta M, Bunandar D, Colbeck R, et al. Advances in quantum cryptography. Adv Opt Photon (2020) 12:1012–236. doi:10.1364/aop.361502
4. Cabello A. Multiparty key distribution and secret sharing based on entanglement swapping (2000). arXiv preprint quant-ph/0009025.
5. Chen K, Lo HK. Multi-partite quantum cryptographic protocols with noisy ghz states. Qic (2007) 7:689–715. doi:10.26421/qic7.8-1
6. Matsumoto R. Multiparty quantum-key-distribution protocol without use of entanglement. Phys Rev A (2007) 76:062316. doi:10.1103/physreva.76.062316
7. Murta G, Grasselli F, Kampermann H, Bruß D. Quantum conference key agreement: A review. Adv Quan Tech (2020) 3:2000025. doi:10.1002/qute.202000025
8. Lo HK, Curty M, Qi B. Measurement-device-independent quantum key distribution. Phys Rev Lett (2012) 108:130503. doi:10.1103/physrevlett.108.130503
9. Lo HK, Chau HF. Unconditional security of quantum key distribution over arbitrarily long distances. Science (1999) 283:2050–6. doi:10.1126/science.283.5410.2050
10. Shor PW, Preskill J. Simple proof of security of the bb84 quantum key distribution protocol. Phys Rev Lett (2000) 85:441–4. doi:10.1103/physrevlett.85.441
11. Fu Y, Yin HL, Chen TY, Chen ZB. Long-distance measurement-device-independent multiparty quantum communication. Phys Rev Lett (2015) 114:090501. doi:10.1103/PhysRevLett.114.090501
12. Chen R, Bao W, Zhou C, Li H, Wang Y, Bao H. Biased decoy-state measurement-device-independent quantum cryptographic conferencing with finite resources. Opt Express (2016) 24:6594–605. doi:10.1364/oe.24.006594
13. Wu Y, Zhou J, Gong X, Guo Y, Zhang ZM, He G. Continuous-variable measurement-device-independent multipartite quantum communication. Phys Rev A (2016) 93:022325. doi:10.1103/physreva.93.022325
14. Ottaviani C, Lupo C, Laurenza R, Pirandola S. Modular network for high-rate quantum conferencing. Commun Phys (2019) 2:1–6. doi:10.1038/s42005-019-0209-6
15. Zhu C, Xu F, Pei C. W-state analyzer and multi-party measurement-device-independent quantum key distribution. Sci Rep (2015) 5:17449–10. doi:10.1038/srep17449
16. Ribeiro J, Murta G, Wehner S. Fully device-independent conference key agreement. Phys Rev A (2018) 97:022307. doi:10.1103/physreva.97.022307
17. Holz T, Kampermann H, Bruß D. Genuine multipartite bell inequality for device-independent conference key agreement. Phys Rev Res (2020) 2:023251. doi:10.1103/physrevresearch.2.023251
18. Grasselli F, Kampermann H, Bruß D. Conference key agreement with single-photon interference. New J Phys (2019) 21:123002. doi:10.1088/1367-2630/ab573e
19. Zhao S, Zeng P, Cao WF, Xu XY, Zhen YZ, Ma X, et al. Phase-matching quantum cryptographic conferencing. Phys Rev Appl (2020) 14:024010. doi:10.1103/physrevapplied.14.024010
20. Cao XY, Gu J, Lu YS, Yin HL, Chen ZB. Coherent one-way quantum conference key agreement based on twin field. New J Phys (2021) 23:043002. doi:10.1088/1367-2630/abef98
21. Cao XY, Lu YS, Li Z, Gu J, Yin HL, Chen ZB. High key rate quantum conference key agreement with unconditional security. IEEE Access (2021) 9:128870–6. doi:10.1109/access.2021.3113939
22. Li Z, Cao XY, Li CL, Weng CX, Gu J, Yin HL, et al. Finite-key analysis for quantum conference key agreement with asymmetric channels. Quan Sci. Technol. (2021) 6:045019. doi:10.1088/2058-9565/ac1e00
23. Bai JL, Xie YM, Li Z, Yin HL, Chen ZB. Post-matching quantum conference key agreement. Opt Express (2022) 30:28865–81. doi:10.1364/oe.460725
24. Yin ZQ, Fung CHF, Ma X, Zhang CM, Li HW, Chen W, et al. Measurement-device-independent quantum key distribution with uncharacterized qubit sources. Phys Rev A (2013) 88:062322. doi:10.1103/physreva.88.062322
25. Tamaki K, Curty M, Kato G, Lo HK, Azuma K. Loss-tolerant quantum cryptography with imperfect sources. Phys Rev A (2014) 90:052314. doi:10.1103/physreva.90.052314
26. Pereira M, Curty M, Tamaki K. Quantum key distribution with flawed and leaky sources. npj Quan Inf (2019) 5:1–12. doi:10.1038/s41534-019-0180-9
27. Pereira M, Kato G, Mizutani A, Curty M, Tamaki K. Quantum key distribution with correlated sources. Sci Adv (2020) 6:eaaz4487. doi:10.1126/sciadv.aaz4487
28. Li HW, Yin ZQ, Wang S, Qian YJ, Chen W, Guo GC, et al. Randomness determines practical security of bb84 quantum key distribution. Sci Rep (2015) 5:16200–8. doi:10.1038/srep16200
29. Li HW, Xu ZM, Cai QY. Small imperfect randomness restricts security of quantum key distribution. Phys Rev A (2018) 98:062325. doi:10.1103/physreva.98.062325
30. Sun SH, Tian ZY, Zhao MS, Ma Y. Security evaluation of quantum key distribution with weak basis-choice flaws. Sci Rep (2020) 10:18145–8. doi:10.1038/s41598-020-75159-6
31. Zhang CM, Wang WB, Li HW, Wang Q. Weak randomness impacts the security of reference-frame-independent quantum key distribution. Opt Lett (2019) 44:1226–9. doi:10.1364/ol.44.001226
32. Jiang XL, Deng XQ, Wang Y, Lu YF, Li JJ, Zhou C, et al. Weak randomness analysis of measurement-device-independent quantum key distribution with finite resources. Photonics (2022) 9:356. doi:10.3390/photonics9050356
33. Jiang XL, Wang Y, Lu YF, Li JJ, Zhou C, Bao WS. Security analysis of sending or not-sending twin-field quantum key distribution with weak randomness. Entropy (2022) 24:1339. doi:10.3390/e24101339
34. Chernoff H. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann Math Statist (1952) 23:493–507. doi:10.1214/aoms/1177729330
35. Curty M, Xu F, Cui W, Lim CCW, Tamaki K, Lo HK. Finite-key analysis for measurement-device-independent quantum key distribution. Nat Commun (2014) 5:3732–7. doi:10.1038/ncomms4732
36. Wang Y, Bao WS, Zhou C, Jiang MS, Li HW. Tight finite-key analysis of a practical decoy-state quantum key distribution with unstable sources. Phys Rev A (2016) 94:032335. doi:10.1103/physreva.94.032335
37. Lütkenhaus N, Jahma M. Quantum key distribution with realistic states: Photon-number statistics in the photon-number splitting attack. New J Phys (2002) 4:44. doi:10.1088/1367-2630/4/1/344
38. Xu F, Curty M, Qi B, Lo HK. Practical aspects of measurement-device-independent quantum key distribution. New J Phys (2013) 15:113007. doi:10.1088/1367-2630/15/11/113007
Keywords: measurement-device-independent, conference key agreement, weak randomness, finite-key, security analysis
Citation: Jiang X-L, Wang Y, Lu Y-F, Li J-J, Zhang H-L, Jiang M-S, Zhou C and Bao W-S (2023) Security analysis of measurement-device-independent quantum conference key agreement with weak randomness. Front. Phys. 11:1101631. doi: 10.3389/fphy.2023.1101631
Received: 18 November 2022; Accepted: 19 January 2023;
Published: 07 February 2023.
Edited by:
Goutam K. Samanta, Physical Research Laboratory, IndiaReviewed by:
Hongyi Zhou, Institute of Computing Technology (CAS), ChinaCopyright © 2023 Jiang, Wang, Lu, Li, Zhang, Jiang, Zhou and Bao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Wang, d3lAcWljbGFiLmNu; Wan-Su Bao, YndzQHFpY2xhYi5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.