Measuring the nuclear magnetic quadrupole moment in heavy polar molecules

Theories that extend the Standard Model of particle physics often introduce new interactions that violate charge-parity (CP) symmetry. Charge-parity-violating effects within an atomic nucleus can be probed by measuring its nuclear magnetic quadrupole moment (MQM). The sensitivity of such a measurement is enhanced when using a heavy polar molecule containing a nucleus with quadrupole deformation. We determine how the energy levels of a molecule are shifted by the magnetic quadrupole moment and how those shifts can be measured. The measurement scheme requires molecules in a superposition of magnetic sub-levels that differ by many units of angular momentum. We develop a generic scheme for preparing these states. Finally, we consider the sensitivity that can be reached, showing that this method can reduce the current uncertainties on several charge-parity-violating parameters.

1 Introduction

The observed baryon asymmetry in the Universe is one of the important unsolved problems in cosmology. Possible models that can lead to this asymmetry are discussed in Refs. [1, 2]. One such model is due to Sakharov, where the asymmetry can arise under conditions of baryon number violation, C and CP-violation, and thermal non-equilibrium [3]. The Standard Model cannot account for the observed asymmetry [4], motivating theories beyond the Standard Model to introduce new sources of CP-violation [5]. Equivalently, since these theories respect CPT symmetry [6], they introduce new sources of T-violation. An elementary particle with a permanent electric dipole moment (EDM) violates both P and T symmetries [7, 8], and measurements of these EDMs have been exceptionally fruitful in testing physics beyond the Standard Model. Paramagnetic molecules such as ¹⁷⁴YbF [9], ²³²ThO [10] and ¹⁸⁰HfF⁺ [11] are excellent probes of P,T-violating physics. These molecules are primarily sensitive to the electron EDM, d_e, and the scalar P,T-violating electron-nucleon interaction, C_S. The most precise measurement thus far, in ThO, constrains new CP-violating interactions to mass scales above 30 TeV in some models and above 3 TeV in most [10].

These electron EDM measurements use paramagnetic molecules with a heavy atom of zero nuclear spin, I = 0. As a result, they are not sensitive to P,T-violating nuclear moments¹. Instead, one can use isotopes with nuclear spin to probe CP-violating effects within the nucleus. The lowest-order P,T-violating nuclear moment is the EDM (which requires I ≥ 1/2), but that is effectively screened by the outer electrons [13]. The screening is incomplete due to the finite size of the nucleus [12], but in paramagnetic atoms and molecules the remaining effect (the nuclear Schiff moment) is negligible compared to the contribution from the electron EDM. Conversely, in diamagnetic atoms and molecules the contribution from the electron EDM is small and the Schiff moment can be probed. At present, the most stringent limits on the size of nucleon EDMs and P,T-violating nucleon-nucleon interactions come from a measurement of the nuclear Schiff moment of ¹⁹⁹Hg [14], a diamagnetic atom with I = 1/2. An experiment is being constructed that aims to improve on these constraints by measuring the Schiff moment of ²⁰⁵Tl in a beam of TlF molecules, taking advantage of the strong polarisation in an electric field due to the small splitting between opposite parity rotational states [15]. Since the Schiff moment is a screened effect, it is interesting to consider the effect of higher-order moments. The next-order nuclear moment of interest is the magnetic quadrupole moment (MQM) (requires I ≥ 1), which is not screened and can contribute significantly to the P,T-violating energy shifts of atoms and molecules.

A spherical nucleus can acquire an MQM from the EDM of its valence proton or neutron [16], or from P,T-odd nucleon-nucleon interactions involving the valence nucleon [17]. If we denote the total nuclear MQM as M and the contribution to the MQM from a single proton or neutron as $M_0^{p/n}$, then for these nuclei we have $M\sim M_0^{p/n}$. In nuclei with quadrupole deformation, there are many nucleons in open shells which collectively contribute to the nuclear MQM, which can increase M by an order of magnitude [18, 19]. Furthermore, the interaction of the nuclear MQM with the magnetic moment of the valence electron in the molecule is enhanced by relativistic effects due to the heavy atom [17]. Table 1 summarizes these effects for isotopologues of molecules currently used for electron EDM experiments.

TABLE 1

TABLE 1. Properties of certain molecules relevant for a nuclear MQM measurement. The selected molecules are ones currently being used or explored for electron EDM measurements. The P,T-violating energy shift due to a nuclear MQM, M, is proportional to W_MM, where W_M is the interaction strength. We list the nuclear spin, parity, quadrupole deformation (β₂), M, and W_M. The collective enhancement of M due to the deformation of the nucleus was calculated in [18, 19] using different nuclear orbitals, and expressed in terms of the single-nucleon contributions to the MQM, $M_0^{p/n}$.

In this paper, we consider how to make a measurement of nuclear MQMs using heavy, polar molecules. We first calculate the size of energy shifts in various states of a molecule due to the nuclear MQM. We then describe a procedure for preparing the molecules in the states most sensitive to the MQM. In particular, we introduce a generic state preparation and readout method which utilises the large tensor Stark shifts in molecules to induce a high-order coupling between the two states used for the measurement. Finally, we assess the sensitivity of such an experiment to CP-violating parameters in the hadronic sector, and compare this to other experiments such as Schiff moment or neutron EDM measurements. Our analysis applies to a wide range of molecules, though we will often use ¹⁷³YbF as a specific example. The nuclear spin of ¹⁷³Yb is 5/2, while that of ¹⁹F is 1/2. We note that the advantages of polyatomic molecules for measuring MQMs and other CP-violating effects are outlined in Ref. [26].

2 MQM energy shift in molecules

We consider a molecule in a ²Σ state with electron spin S and rotational angular momentum N. The nucleus of interest has spin I. The molecule is in an electric field $\mathcal{E}$ which is parallel to z. A suitable effective Hamiltonian is

$H=H_{\text{rot}}+H_{\text{Stark}}+H_{\text{hyp}}+H_{\text{M}},(1)$

where H_rot = BN² is the rotational energy, $H_{\text{Stark}}=-\mathit{\mu }\cdot \mathcal{E}$ describes the Stark shift, H_hyp describes the hyperfine interactions, and H_M describes the nuclear MQM interaction. Here, B is the rotational constant and $\mathit{\mu }$ is the electric dipole moment operator. The nuclear MQM interaction can be written as

$H_{\text{M}}=-\frac{W_{M}M}{2I\left(2I-1\right)}\mathbf{S}\widehat{\mathbf{T}}\mathbf{n},(2)$

where n is a unit vector along the internuclear axis and $\widehat{\mathbf{T}}$ is a second-rank tensor whose components are $T_{i,j}=I_i{I}_j+I_j{I}_i-\frac{2}{3}{\delta }_{i,j}I(I+1)$ [17, 18]. With the help of appendices 8.1 and 8.2 of Ref. [27], we can re-write this in spherical tensor notation as

$H_{\text{M}}=\frac{W_{M}M}{2I\left(2I-1\right)}\sqrt{\frac{20}{3}}{\mathrm{T}}^{(1)}(\mathbf{S},{\mathbf{I}}^{\left(2\right)})\cdot \mathbf{n}\equiv \mathbf{Q}\cdot \mathbf{n}=Q_{z^{\prime }},(3)$

where T⁽¹⁾(S, I⁽²⁾) is a rank-1 tensor constructed from S and I⁽²⁾; the latter is a rank-2 tensor constructed from the nuclear spin I. We see that the MQM interaction has been simplified to a vector Q that acts along the symmetry axis of the molecule, z′.

To keep the calculation simple, we first neglect H_hyp. Its effects are considered later. We find it advantageous to use a basis where the rotational and spin wavefunctions are separated, so we choose the basis set denoted by |G, M_G; N, M_N⟩, where G = S + I is the total spin and M_G and M_N are the projections of G and N on the laboratory z-axis. H_rot + H_Stark is diagonal in G, M_G and M_N, but the electric field mixes states of different N. After diagonalizing H_rot + H_Stark we obtain the eigenfunctions $|G,M_G;\tilde{N},M_N\rangle ={\sum }_N{a}_N|G,M_G;N,M_N\rangle$ and corresponding eigenvalues $E_{\tilde{N},M_N}$. Here, $\tilde{N}$ is a label which connects a state adiabatically to its field-free state.

The energy shift due to H_M is

$\mathrm{\Delta }{E}_{\text{M}}^{\prime }=\langle G,M_G;\tilde{N},M_N|Q_{z^{\prime }}|G,M_G;\tilde{N},M_N\rangle =W_{\text{M}}M\zeta \eta .(4)$

In this equation, ζ depends only on the electron and nuclear spins and is evaluated in Appendix A, whereas η is independent of the spins and expresses the degree of alignment between the internuclear axis of the molecule and the laboratory z-axis, often known as the polarization factor. It is given by

$\eta =-\frac{1}{{\mu }_{\text{mol}}}\frac{d{E}_{\tilde{N},M_N}}{d\mathcal{E}},(5)$

where μ_mol is the dipole moment along the internuclear axis. Figure 1 shows the evaluation of ζ for a few selected values of S and I. In all the examples given in Figure 1, the largest MQM energy shift is found for the states |G, M_G = ±G⟩, where G does not take its maximum possible value. It is interesting that the configuration where the electron and nuclear spins are parallel is not the one most sensitive to the nuclear MQM. We find this to be true for larger values of S and I as well.

FIGURE 1

FIGURE 1. Values of ζ in hyperfine states |G, M_G⟩, for (A) S = 1/2, I = 1; (B) S = 1/2, I = 3/2; (C) S = 1, I = 1. These are calculated using Eq. A6.

Now we consider the effect of H_hyp, which includes the spin-rotation interaction, the magnetic dipole hyperfine interaction and the electric quadrupole hyperfine interaction [28]. To handle this, we introduce the spin of the second nucleus I₂, an intermediate angular momentum F₁ = G + N and the total angular momentum F = F₁ + I₂. Using the field-free coupled basis, |N, G, F₁, F, M_F⟩, we diagonalize H_rot + H_Stark + H_hyp to find the new eigenstates $|\tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F\rangle$ which are adiabatically linked to the field-free states. Then, we calculate the MQM energy shift

$\mathrm{\Delta }{E}_M=\langle \tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F|H_{\text{M}}|\tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F\rangle .(6)$

The matrix elements needed to calculate ΔE_M are given in Appendix A.

Although Eq. 6 will be more accurate than Eq. 4, we expect the latter to work well for most ²Σ molecules since they have no spin-orbit coupling and the largest spin-rotation coupling is typically much smaller than the hyperfine and rotational energies. As a concrete example, for the ²Σ ground state of ¹⁷³YbF, the electron-spin-rotation coupling strength is γ = −13 MHz, the hyperfine Fermi contact strength between the electron and Yb nuclear spins is b_F(Yb) = −1.98 GHz, and the rotational constant is B = 7.24 GHz [28, 29]. The fluorine nucleus has spin I₂ = 1/2 but this gives rise to a much smaller hyperfine splitting than that of the Yb nucleus (b_F(F) = 0.17 GHz). Consequently, the decoupled basis $|N,M_N\rangle |G,M_G\rangle |I_2,M_{{\text{I˙}}_2}\rangle$ is a good first approximation to the exact eigenstates.

Table 2 lists the MQM energy shifts of all states that correlate to the lowest rotational level of ground state ¹⁷³YbF, in a static electric field of 18 kV/cm. At this field, the polarization factor is η = 0.676. We have given both ΔE_M calculated using Eq. 6 and the approximate result $\mathrm{\Delta }{E}_{\text{M}}^{\prime }$ calculated using Eq. 4. The two sets of results are similar, as we would expect from the arguments above. These states, together with the MQM energy shifts, are shown pictorially in Figure 2. The large splitting between the $\tilde{G}=2$ and $\tilde{G}=3$ states comes from the hyperfine interaction between the electron spin and the Yb nuclear spin. The much smaller splitting into states with $\tilde{F}=\tilde{G}\pm I_2$ is due to the interaction with the F nuclear spin. States of the same $\tilde{F}$ and $\tilde{G}$ but different |M_F| are split by the tensor part of the Stark interaction. This is small for the state with $\tilde{N}=0$, but much larger for all other states. In the absence of the MQM or other P, T-violating interactions, states of the same $\{\tilde{G},\tilde{F},|M_F|\}$ are degenerate. The MQM interaction lifts this degeneracy by the amounts indicated in the figure.

TABLE 2

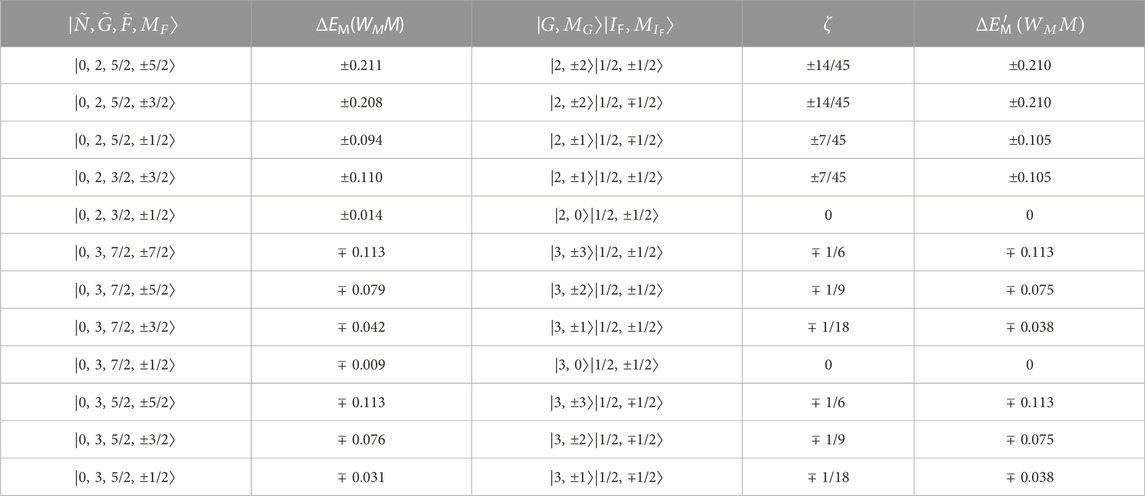
TABLE 2. MQM energy shifts for states correlating to the lowest rotational level of ¹⁷³YbF, in an electric field of 18 kV/cm. We have dropped ${\tilde{F}}_1$ from the state notation since ${\tilde{F}}_1=\tilde{G}$ for these states. The second column gives ΔE_M calculated using Eq. 6. The fourth column gives ζ calculated using Eq. A6 and the fifth column gives $\mathrm{\Delta }{E}_{\text{M}}^{\prime }$ calculated using Eq. 4.

FIGURE 2

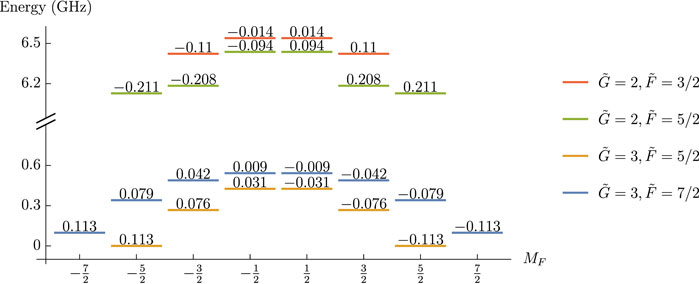
FIGURE 2. MQM energy shifts in the ground rotational state manifold of ¹⁷³YbF. The shifts are calculated at $\mathcal{E}$ = 18 kV/cm and given in units of W_MM. States labeled with $\tilde{G}$ and $\tilde{F}$ are adiabatically linked to field-free states with quantum numbers G and F.

3 Measurement scheme

An MQM measurement can be done in a similar way to measurements of the electron EDM or the nuclear Schiff moment [10, 15, 30]. Using the notation² |F, M_F⟩, let us define states |0⟩ = |F, F⟩ and $|\pm \rangle =\frac{1}{\sqrt{2}}\left(|F,+F\rangle \pm |F,-F\rangle \right)$. Molecules are first prepared in |0⟩, typically by optical pumping, and then transferred to | + ⟩. This state evolves for time τ in the presence of parallel electric and magnetic fields, becoming $|\psi \rangle =\frac{1}{\sqrt{2}}\left(e^{i\varphi }|F,+F\rangle +e^{-i\varphi }|F,-F\rangle \right)=\cos \varphi |+\rangle +i\sin \varphi |-\rangle$. Here, $\varphi ={\varphi }_{\text{M}}+{\varphi }_{\text{B}}=\left(\mathrm{\Delta }{E}_{\text{M}}+\mathrm{\Delta }{E}_{\text{B}}\right)\tau /\hslash$, where ΔE_B is the (absolute) Zeeman shift of the states. Finally, the populations in | + ⟩ and | − ⟩ are read out, typically by transferring the population in | + ⟩ to one state (e.g., back to |0⟩) and the population in | − ⟩ to a state of sufficiently different energy that the two are easily resolved (e.g., by laser-induced fluorescence detection).

A particular challenge in this measurement scheme, which does not typically arise in related experiments, is the preparation of a superposition of ±M_F states where M_F and −M_F differ by several units. For example, consider the levels of ¹⁷³YbF shown in Figure 2. The states most sensitive to the MQM have $\tilde{G}=2,\tilde{F}=5/2,M_F=\pm 5/2$. In that case, the measurement scheme calls for a superposition of a pair of states that differ in M_F by 5 units of angular momentum. Previously, optical pumping light modulated at a harmonic of the Larmor frequency has been used to prepare and study coherences within states of high angular momentum [31]. In the following, we describe a general method to prepare the states we need.

3.1 Optical pumping

We first describe how the molecules can be optically pumped into a single quantum state. This is done at zero electric field. We choose the state |0⟩ = |F, M_F = F⟩, where F is the target angular momentum for the MQM measurement. A small magnetic field defines the z-axis. It should be small enough that Zeeman splittings are small compared to the linewidth of the relevant optical transitions, but large enough to ensure that M_F is preserved. Then, using circularly polarized light with k-vector along z, we drive an optical transition where the excited state angular momentum is F′ = F. The light drives only σ⁺ transitions so the target state is a dark state and the population will be pumped into this state. There will be decay channels to other hyperfine and rotational states that are not resonant with the optical pumping light. Additional lasers need to be used to drive population out of these states. These extra lasers should have their polarizations modulated at a rate that is close to the Rabi frequency, to ensure that there are no other dark states in the system.

Figure 3 shows an example of this procedure for ¹⁷³YbF molecules. Within the ground state X²Σ⁺, each rotational manifold (labelled by N) is split into states G = 2 and G = 3 by the Yb hyperfine interaction. Each of these is then further split by spin-rotation and F hyperfine interactions. As an example, the inset shows the hyperfine structure of the N = 2, G = 3 manifold, spanning roughly 1 GHz. The figure also shows the lowest rotational manifold of the electronically excited state, A²Π_1/2 (J′ = 1/2). This is split into states of opposite parity by the Λ-doubling interaction, then by the Yb hyperfine interaction yielding states labelled by $F_1^{\prime }$, and finally by the fluorine hyperfine interaction, into states of total angular momenta F′. The latter splittings are smaller than the linewidth of the optical transition. The target state is |N = 0, G = 2, F = 5/2, M_F = 5/2⟩. To optically pump molecules into this state, σ⁺ transitions are driven from the N = 0, G = 2 levels of X to the F′ = 3/2, 5/2 levels of A. This state can decay to the G = 3 manifold of N = 0 and also to rotational state N = 2. Molecules decaying to those states are excited by additional polarization-modulated lasers in such a way that the target state is the only dark state. In addition, population in N = 1 can also be transferred to the target state by driving microwave transitions to N = 2 as shown. In this way, population distributed across many initial states is all driven to the target state. The efficiency of this process is limited by leaks to higher-lying vibrational states (not shown in the figure). We note that the number of spontaneous emission events needed to reach the stretched state can be substantially reduced by using a combination of coherent and incoherent processes, and that such schemes could improve the optical pumping efficiency in the case of substantial leaks to other states [32].

FIGURE 3

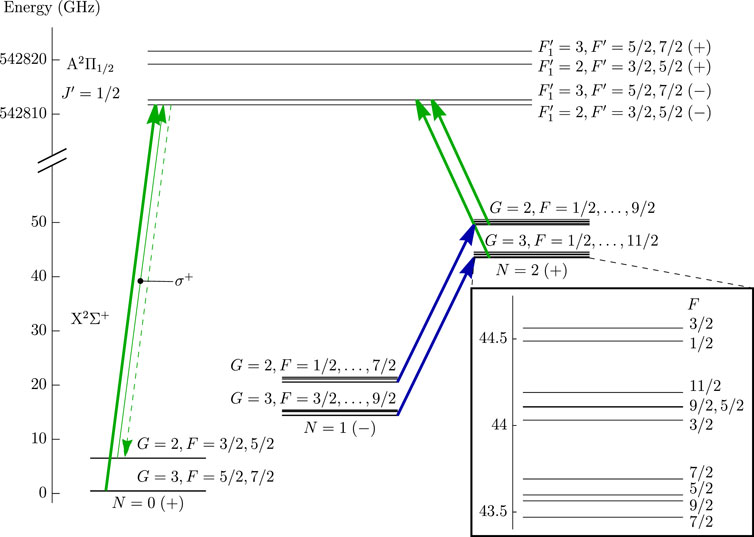
FIGURE 3. Optical pumping scheme for ¹⁷³YbF molecules. Thick green arrows denote transitions driven using polarization-modulated light. The thin green arrow denotes light that drives only σ⁺ transitions from the G = 2 manifold of N = 0. The target state, |N = 0, G = 2, F = 5/2, M_F = 5/2⟩, is the only dark state. Microwave transitions (blue arrows) can also be driven in order to bring population from N = 1 to the target state. The inset shows the hyperfine structure within N = 2, G = 3.

3.2 State preparation and readout

Next, we show how to drive effective Rabi oscillations between the initial state |F, M_F= F⟩ and the superposition state $|+\rangle =\frac{1}{\sqrt{2}}\left(|F,+F\rangle +|F,-F\rangle \right)$. We start by considering the F = 1 system illustrated in Figure 4. An electric field is applied along z so that there is a Stark shift Δ between the M_F = 0 and |M_F| = 1 states. We also allow a small splitting δ between the M_F = ±1 states due to a small magnetic field along z. There is a time-independent coupling, Ω, between the M_F = 0 and M_F = ±1 states. For example, this could be a magnetic field along the x-axis, B_x, which yields $\mathrm{\Omega }=-\mu B_x/\sqrt{2}$, where μ is the magnetic moment.

FIGURE 4

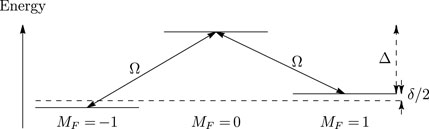
FIGURE 4. An F = 1 system with tensor Stark splitting Δ and couplings Ω between the M_F = 0 sublevel and M_F = ±1 sublevels. The M_F = ±1 states have a splitting δ between them.

The Hamiltonian describing this system, in the basis {M_F = −1, M_F = 0, M_F = 1}, is

$H=\left(\begin{array}{ccc}\hfill -\delta /2\hfill & \hfill \mathrm{\Omega }\hfill & \hfill 0\hfill \\ \hfill \mathrm{\Omega }\hfill & \hfill \mathrm{\Delta }\hfill & \hfill \mathrm{\Omega }\hfill \\ \hfill 0\hfill & \hfill \mathrm{\Omega }\hfill & \hfill \delta /2\hfill \end{array}\right).(7)$

This is the same Hamiltonian as for a two-photon Raman transition after transforming to the rotating frame. In that situation, Ω is the Rabi frequency, Δ is the one-photon detuning and δ is the two-photon or Raman detuning. Motivated by this, we consider the situation where Δ ≫Ω, δ and the initial state is one of the M_F = ±1 states. Then, adiabatic elimination of the M_F = 0 state reduces the dynamics to that of an effective two-level system:

$H_{\text{eff}}=\left(\begin{array}{cc}\hfill -\frac{\delta }{2}-\frac{{\mathrm{\Omega }}^2}{\mathrm{\Delta }}\hfill & \hfill -\frac{{\mathrm{\Omega }}^2}{\mathrm{\Delta }}\hfill \\ \hfill -\frac{{\mathrm{\Omega }}^2}{\mathrm{\Delta }}\hfill & \hfill \frac{\delta }{2}-\frac{{\mathrm{\Omega }}^2}{\mathrm{\Delta }}\hfill \end{array}\right).(8)$

This system undergoes Rabi oscillations between the M_F = ±1 states at the effective generalised Rabi frequency, $W_{\text{eff}}=\sqrt{{\delta }^2+{\mathrm{\Omega }}_{\text{eff}}^2}$, where the effective Rabi frequency is Ω_eff = 2Ω²/Δ. This effective coupling is mediated by the coupling of M_F = ±1 to M_F = 0.

This approach can be generalised to states of higher angular momentum. For example, consider the F = 5/2 system illustrated in Figure 5. Here we have two different tensor Stark splittings Δ_1,2, and three couplings between adjacent levels Ω_1,2,3. As before, these couplings can be generated by a magnetic field orthogonal to the electric field. For simplicity, we have made states of equal M_F degenerate. The Hamiltonian for this six-level system is

$H=\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill {\mathrm{\Omega }}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathrm{\Omega }}_1\hfill & \hfill {\mathrm{\Delta }}_1\hfill & \hfill {\mathrm{\Omega }}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Omega }}_2\hfill & \hfill {\mathrm{\Delta }}_2\hfill & \hfill {\mathrm{\Omega }}_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_3\hfill & \hfill {\mathrm{\Delta }}_2\hfill & \hfill {\mathrm{\Omega }}_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_2\hfill & \hfill {\mathrm{\Delta }}_1\hfill & \hfill {\mathrm{\Omega }}_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_1\hfill & \hfill 0\hfill \end{array}\right).(9)$

We adiabatically eliminate all states except for |M_F = ±5/2⟩ to derive the effective two-level Hamiltonian

$H_{\text{eff}}=\left(\begin{array}{cc}\hfill -\frac{{\mathrm{\Omega }}_1^2}{{\mathrm{\Delta }}_1}\hfill & \hfill \frac{{\mathrm{\Omega }}_1^2{\mathrm{\Omega }}_2^2{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_1^2{\mathrm{\Delta }}_2^2}\hfill \\ \hfill \frac{{\mathrm{\Omega }}_1^2{\mathrm{\Omega }}_2^2{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_1^2{\mathrm{\Delta }}_2^2}\hfill & \hfill -\frac{{\mathrm{\Omega }}_1^2}{{\mathrm{\Delta }}_1}\hfill \end{array}\right).(10)$

The derivation is given in Appendix B. We have assumed that the shifts Δ_1,2 are much greater than the couplings Ω_1,2,3. The effective Rabi frequency is

${\mathrm{\Omega }}_{\text{eff}}=\frac{2{\mathrm{\Omega }}_1^2{\mathrm{\Omega }}_2^2{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_1^2{\mathrm{\Delta }}_2^2}.(11)$

FIGURE 5

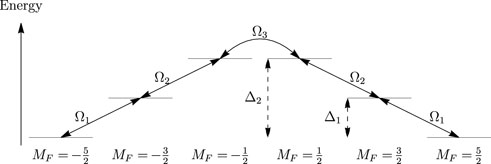
FIGURE 5. An F = 5/2 system with tensor Stark splittings Δ₁ and Δ₂, and couplings Ω₁, Ω₂, Ω₃ between states of adjacent M_F.

Figure 6A compares the numerical solution of the Schrödinger equation using Eq. 9 to the effective two-level dynamics described by Eq. 10. We see excellent agreement between the effective model and the complete solution. We also find that two-level Rabi flopping dynamics are obtained whenever Δ₁ ≫Ω₁, without needing to constrain Δ₂, Ω₂, Ω₃. The first condition ensures that the amplitudes of all intermediate states remain small, even when Ω₂ and Ω₃ are large. This greatly increases the effective Rabi frequency, producing a rapid coupling between the stretched states even though this is a high-order process mediated through many intermediate states. Note that in this case the effective Rabi frequency is no longer given by Eq. 11. Figure 6B compares the numerical solution to the two-level model in the case where the coupling between the states is similar to Δ₂. The numerical solution shows almost perfect Rabi oscillations between the stretched states, with negligible population in any of the other states. The Rabi frequency is larger than given by Eq. 11.

FIGURE 6

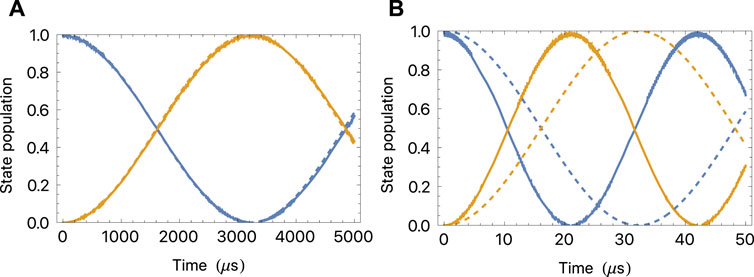
FIGURE 6. Dynamics of the six-level system shown in Figure 5. Populations of the states M_F = 5/2 (blue) and M_F = −5/2 (orange). Solid lines: solutions of the Schrödinger equation for the Hamiltonian given in Eq. 9. Dashed lines: effective two-level model, Eq. 10. Parameters are: (A) Ω₁ = Ω₂ = Ω₃ = 2π × 6 MHz, Δ₁ = Δ₂ = 2π × 100 MHz. (B) Same as (A) except Δ₂ = 2π × 10 MHz.

Let us consider again the specific example of the G = 2 manifold of ¹⁷³YbF. The upper half of Figure 2 shows the level structure of this manifold of 10 states in an electric field $\mathcal{E}$ = 18 kV/cm. We start with all population in the state |F, M_F⟩ = |5/2, 5/2⟩. We apply a magnetic field along x, B_x, such that Ω_ij = −μ_ijB_x where μ_ij is the magnetic dipole transition moment between states i and j. We ramp the field on for t_ramp = 20 µs, keep the field at its maximum value for t_on = 60 μs and then ramp the field down for t_ramp. The total time for the state evolution is therefore 100 µs. Figure 7 shows our numerical simulations for B_x = 5.9 mT, which is the value needed to apply an effective π/2 pulse. We find that when the initial state is |5/2, 5/2⟩ the final state is | + ⟩ as desired. The reverse process also works well, as is needed for the state readout. When the initial state is | + ⟩ the final state is |5/2, −5/2⟩, and when the initial state is | − ⟩ the final state is |5/2, 5/2⟩. Thus, despite the complexity of this system, a magnetic field pulse is sufficient to prepare the initial superposition state and to read out the final state.

FIGURE 7

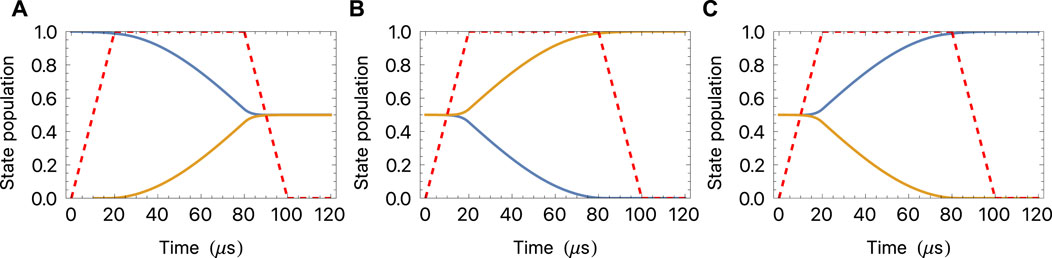
FIGURE 7. Dynamics within the G = 2 manifold of ¹⁷³YbF induced by a pulse of magnetic field orthogonal to the electric field, calculated by numerical solution of the Schrödinger equation for all 10 levels shown in the upper half of Figure 2. Populations of the states M_F = 5/2 (blue) and M_F = −5/2 (orange) as B_x is ramped on and off for a total time of 100 µs. The maximum value of the field is 5.9 mT and its amplitude relative to this maximum is shown by the dashed red line. (A) Initial state is |5/2, 5/2⟩; final state is | + ⟩. (B) Initial state is | + ⟩; final state is |5/2, −5/2⟩. (C) Initial state is | − ⟩; final state is |5/2, 5/2⟩.

4 Sensitivity to CP-violating parameters

Finally, we consider the sensitivity of a molecular MQM experiment to hadronic CP-violating parameters, and compare related experiments. Again, we use ¹⁷³YbF as a prototypical example. The parameters of the experiment are the coherence time τ and the number of molecules measured N. At the shot-noise limit, the statistical uncertainty of an ideal frequency measurement will be $\delta f=1/(2\pi \tau \sqrt{N})$. Recent experimental work and case studies [15, 33–35] suggest that measurements using the molecules considered here can reach a sensitivity of approximately 1 mHz/$\sqrt{\mathrm{H}\mathrm{z}}$. This could be achieved using a high flux focussed molecular beam from a cryogenic source, giving N ≈ 3 × 10⁸ molecules per second and τ ≈ 10 ms, or an ultracold molecular beam giving N ≈ 3 × 10⁶ molecules per second and τ ≈ 100 ms, or ultracold molecules in an optical lattice giving N ≈ 3 × 10⁴ molecules per second and τ ≈ 1 s. In this case, the uncertainty reaches δf = 1 μHz in about 300 h of measurement time.

If we assume that the CP-violating energy splitting in ¹⁷³YbF is due only to the MQM of the Yb nucleus, 2Δ_CP = 0.42W_MM, then the uncertainty is equivalent to a 2σ-sensitivity on the MQM of 4.5 × 10⁻¹³ e fm². From this, we can calculate the expected level to which we can measure various CP-violating parameters, using the parameter sensitivities compiled in Table 3. We compare these to the experimental constraints set by the Schiff moment measurement of ¹⁹⁹Hg [14] and the projected sensitivities of the proposed Schiff moment measurement of ²⁰⁵Tl from a TlF beam experiment [15]. The former is S (¹⁹⁹$\left.\mathrm{H}\mathrm{g}\right)<$3.1 × 10⁻¹³ e fm³, and the latter has an anticipated statistical sensitivity of δf = 45 nHz which corresponds to³ δS (²⁰⁵$\left.\mathrm{T}\mathrm{l}\right)$ = 9.1 × 10⁻¹⁴ e fm³.

TABLE 3

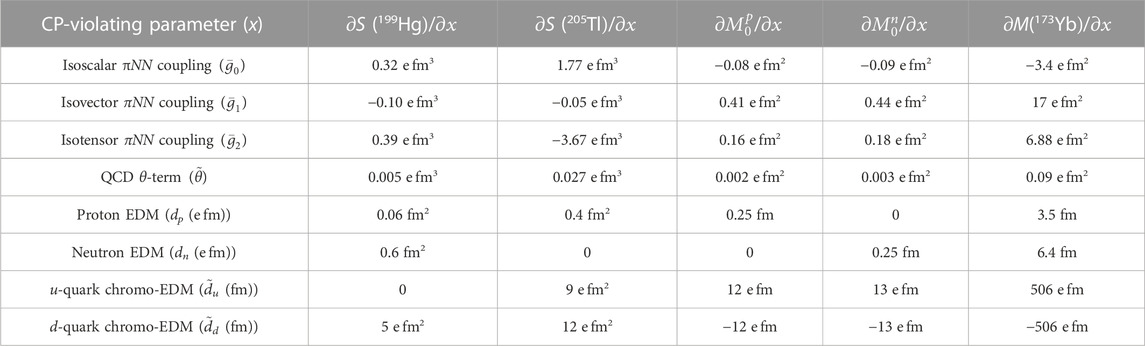
TABLE 3. The dependence of the Schiff moments of ¹⁹⁹Hg and ²⁰⁵Tl [36], nucleon MQMs and the MQM of ¹⁷³Yb [19] on CP-violating parameters. The dependence of M(¹⁷³Yb) is calculated from the enhancement of nucleon MQMs as given in Table 1. Throughout, we take the strong π-meson nucleon-nucleon interaction constant to be g = 13.6 [18].

Table 4 shows the 95% confidence limit constraints on CP-violating parameters set by the ¹⁹⁹Hg experiment, as well as projected 2σ-sensitivities for experiments using TlF and YbF, given the uncertainties quoted above. We find that a measurement of the MQM of ¹⁷³Yb using YbF molecules can make large improvements relative to the current limits on CP-violating parameters obtained from the Hg experiment. The measurement also gives greater sensitivities than obtainable from the proposed TlF experiment, even though the projected frequency uncertainty of the TlF experiment is 20 times smaller.

TABLE 4

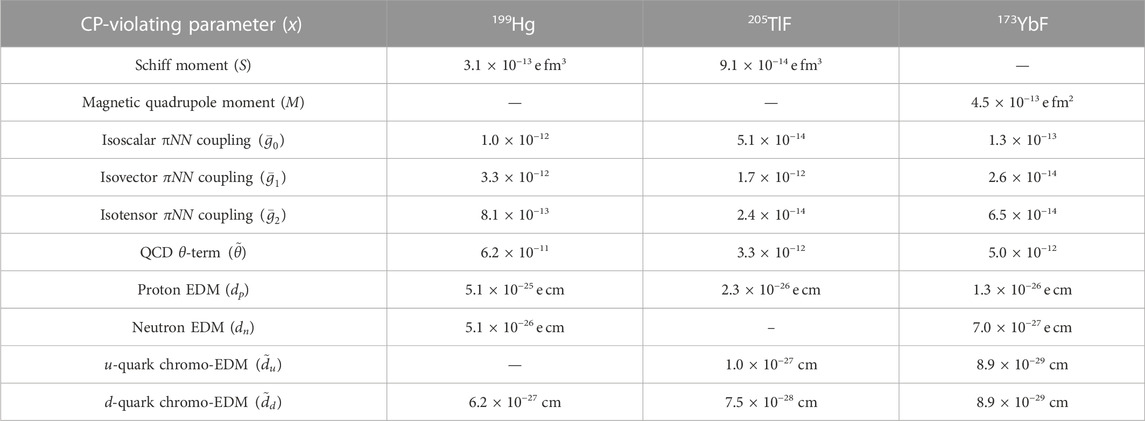
TABLE 4. Constraints (95% CL) on CP-violating parameters set experimentally by ¹⁹⁹Hg [14], and projected 2σ-sensitivities from proposals to measure these in ²⁰⁵TlF [15] and ¹⁷³YbF (this paper). For ¹⁹⁹Hg, the constraints given here differ from those given in [14] because we use the coefficients from [36].

5 Conclusion

Measurements of nuclear MQMs in isotopologues of heavy, paramagnetic molecules have the potential to probe hadronic CP-violating physics at a level well beyond current limits. We have calculated the molecular energy shifts to be expected, showing which states should be used. We find that measurements will require molecules prepared in a superposition of magnetic sub-levels that differ by many units of angular momentum, and we have described a general method for preparing these states. These experiments would benefit from the recent advances in laser cooling applied to molecules [38]. The nuclear spin of the heavy atom in the molecule leads to large hyperfine intervals and a more complex hyperfine structure which makes the laser cooling more difficult than for the isotopologues cooled so far. Nevertheless, a recent study [39] shows how cooling of the required molecules can be done with relatively small additions to existing experiments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CH performed the calculations and analyses and prepared the first draft of the manuscript. JL contributed to the concepts and ideas presented. BS conceived the study, contributed to the concepts and supervised the work. MT contributed to the state preparation method, checked the calculations, revised the manuscript and supervised the work. All authors discussed the work regularly, contributed to manuscript revision, read and approved the submitted version.

Funding

This work was supported by funding in part from the Science and Technology Facilities Council (grants ST/S000011/1 and ST/V00428X/1); the Sloan Foundation (grant G-2019-12505); and the Gordon and Betty Moore Foundation (grant 8864). The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of these funding bodies.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The light atom in the molecule often has nuclear spin but its contribution to any P,T-violating signal scales approximately as Z², where Z is the atomic number [12], so is much smaller than that of the heavy atom. For example, in YbF, the contribution from the F atom is about 60 times smaller than that of Yb.

²Here, for notational convenience, we have dropped the tildes and the other quantum numbers.

³This calculation comes from Δ_CP = ηW_SS, where the polarisation factor η = 0.547 and W_S = 40 539 au = 1.8 × 10⁶ Hz/(e fm³) [37].

References

1. Dolgov AD, Zeldovich YB. Cosmology and elementary particles. Rev Mod Phys (1981) 53:1–41. doi:10.1103/revmodphys.53.1

CrossRef Full Text | Google Scholar

2. Kolb EW, Turner MS. The early Universe. Boston: Addison-Wesley (1990).

Google Scholar

3. Sakharov AD. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. Sov Phys Usp (1991) 34:392–3. doi:10.1070/pu1991v034n05abeh002497

CrossRef Full Text | Google Scholar

4. Canetti L, Drewes M, Shaposhnikov M. Matter and antimatter in the universe. New J Phys (2012) 14:095012. doi:10.1088/1367-2630/14/9/095012

CrossRef Full Text | Google Scholar

5. Bödeker D, Buchmüller W. Baryogenesis from the weak scale to the grand unification scale. Rev Mod Phys (2021) 93:035004.

Google Scholar

6. Lüders G. Proof of the TCP theorem. Ann Phys (1957) 2:1. doi:10.1016/0003-4916(57)90032-5

CrossRef Full Text | Google Scholar

7. Purcell EM, Ramsey NF. On the possibility of electric dipole moments for elementary particles and nuclei. Phys Rev (1950) 78:807. doi:10.1103/physrev.78.807

CrossRef Full Text | Google Scholar

8. Landau L. On the conservation laws for weak interactions. Nucl Phys (1957) 3:127–31. doi:10.1016/0029-5582(57)90061-5

CrossRef Full Text | Google Scholar

9. Hudson JJ, Kara DM, Smallman IJ, Sauer BE, Tarbutt MR, Hinds EA. Improved measurement of the shape of the electron. Nature (2011) 473:493–6. doi:10.1038/nature10104

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Andreev V, Ang DG, DeMille D, Doyle JM, Gabrielse G, Haefner J, et al. Improved limit on the electric dipole moment of the electron. Nature (2018) 562:355. doi:10.1038/s41586-018-0599-8

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Cairncross WB, Gresh DN, Grau M, Cossel KC, Roussy TS, Ni Y, et al. Precision measurement of the electron's electric dipole moment using trapped molecular ions. Phys Rev Lett (2017) 119:153001. doi:10.1103/physrevlett.119.153001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hinds EA. Testing time reversal symmetry using molecules. Phys Scr (1997) T70:34–41. doi:10.1088/0031-8949/1997/t70/005

CrossRef Full Text | Google Scholar

13. Schiff LI. Measurability of nuclear electric dipole moments. Phys Rev (1963) 132:2194–200. doi:10.1103/physrev.132.2194

CrossRef Full Text | Google Scholar

14. Graner B, Chen Y, Lindahl EG, Heckel BR. Reduced limit on the permanent electric dipole moment of Hg199. Phys Rev Lett (2016) 116:161601. doi:10.1103/physrevlett.116.161601

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Grasdijk O, Timgren O, Kastelic J, Wright T, Lamoreaux S, DeMille D, et al. CeNTREX: A new search for time-reversal symmetry violation in the ²⁰⁵Tl nucleus. Quan Sci. Technol. (2021) 6:044007. doi:10.1088/2058-9565/abdca3

CrossRef Full Text | Google Scholar

16. Khriplovich IB. Zh Eksp Teor Fiz (1957) 71:51.

17. Sushkov OP, Flambaum VV, Khriplovich IB. Zh Eksp Teor Fiz (1984) 87:1521.

18. Flambaum VV, DeMille D, Kozlov MG. Time-Reversal symmetry violation in molecules induced by nuclear magnetic quadrupole moments. Phys Rev Lett (2014) 113:103003. doi:10.1103/physrevlett.113.103003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lackenby BGC, Flambaum VV. Time reversal violating magnetic quadrupole moment in heavy deformed nuclei. Phys Rev D (2018) 98:115019. doi:10.1103/physrevd.98.115019

CrossRef Full Text | Google Scholar

20. Möller P, Sierk AJ, Ichikawa T, Sagawa H. Nuclear ground-state masses and deformations: FRDM(2012). At Data Nucl Data Tables (2016) 109-110:1–204. doi:10.1016/j.adt.2015.10.002

CrossRef Full Text | Google Scholar

21. Denis M, Hao Y, Eliav E, Hutzler NR, Nayak MK, Timmermans RGE, et al. Enhanced P,T-violating nuclear magnetic quadrupole moment effects in laser-coolable molecules. J Chem Phys (2020) 152:084303. doi:10.1063/1.5141065

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Skripnikov LV, Petrov AN, Titov AV, Flambaum VV. CP-violating effect of the Th nuclear magnetic quadrupole moment: Accurate many-body study of ThO. Phys Rev Lett (2014) 113:263006. doi:10.1103/physrevlett.113.263006

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Skripnikov LV, Petrov AN, Titov AV, Flambaum VV. Erratum:CP-Violating effect of the Th nuclear magnetic quadrupole moment: Accurate many-body study of ThO [phys. Rev. Lett.113, 263006 (2014)]. Phys Rev Lett (2015) 115:259901. doi:10.1103/physrevlett.115.259901

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Skripnikov LV, Titov AV, Flambaum VV. Enhanced effect of CP-violating nuclear magnetic quadrupole moment in a HfF⁺ molecule. Phys Rev A (2017) 95:022512. doi:10.1103/physreva.95.022512

CrossRef Full Text | Google Scholar

25. Skripnikov LV, Titov AV. Theoretical study of ThF⁺ in the search for T, P-violation effects: Effective state of a Th atom in ThF⁺ and ThO compounds. Phys Rev A (2015) 91:042504. doi:10.1103/PhysRevA.91.042504

CrossRef Full Text | Google Scholar

26. Hutzler NR. Polyatomic molecules as quantum sensors for fundamental physics. Quan Sci. Technol. (2020) 5:044011. doi:10.1088/2058-9565/abb9c5

CrossRef Full Text | Google Scholar

27. Brown J, Carrington A. Rotational spectroscopy of diatomic molecules. Cambridge: Cambridge University Press (2003).

Google Scholar

28. Steimle TC, Ma T, Linton C. The hyperfine interaction in the AΠ1∕22 and XΣ+2 states of ytterbium monofluoride. J Chem Phys (2007) 127:234316. doi:10.1063/1.2820788

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang H, Le AT, Steimle TC, Koskelo EAC, Aufderheide G, Mawhorter R, et al. Fine and hyperfine interaction in ¹⁷³YbF. Phys Rev A (2019) 100:022516. doi:10.1103/physreva.100.022516

CrossRef Full Text | Google Scholar

30. Ho CJ, Devlin JA, Rabey IM, Yzombard P, Lim J, Wright SC, et al. New techniques for a measurement of the electron's electric dipole moment. New J Phys (2020) 22:043031. doi:10.1088/1367-2630/ab83d2

CrossRef Full Text | Google Scholar

31. Yashchuk VV, Budker D, Gawlik W, Kimball DF, Malakyan YP, Rochester SM. Selective addressing of high-rank atomic polarization moments. Phys Rev Lett (2003) 90:253001. doi:10.1103/physrevlett.90.253001

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Rochester SM, Szymanski K, Raizen M, Pustelny S, Auzinsh M, Budker D. Efficient polarization of high-angular-momentum systems. Phys Rev A (2016) 94:043416. doi:10.1103/physreva.94.043416

CrossRef Full Text | Google Scholar

33. Alauze X, Lim J, Trigatzis M, Swarbrick S, Collings FJ, Fitch NJ, et al. An ultracold molecular beam for testing fundamental physics. Quan Sci. Technol. (2021) 6:044005. doi:10.1088/2058-9565/ac107e

CrossRef Full Text | Google Scholar

34. Fitch NJ, Lim J, Hinds EA, Sauer BE, Tarbutt MR. Methods for measuring the electron's electric dipole moment using ultracold YbF molecules. Quan Sci. Technol. (2021) 6:014006. doi:10.1088/2058-9565/abc931

CrossRef Full Text | Google Scholar

35. Augenbraun BL, Lasner ZD, Frenett A, Sawaoka H, Miller C, Steimle TC, et al. Laser-cooled polyatomic molecules for improved electron electric dipole moment searches. New J Phys (2020) 22:022003. doi:10.1088/1367-2630/ab687b

CrossRef Full Text | Google Scholar

36. Flambaum VV, Dzuba VA. Electric dipole moments of atoms and molecules produced by enhanced nuclear Schiff moments. Phys Rev A (2020) 101:042504. doi:10.1103/physreva.101.042504

CrossRef Full Text | Google Scholar

37. Flambaum VV, Dzuba VA, Tran Tan HB. Time- and parity-violating effects of the nuclear Schiff moment in molecules and solids. Phys Rev A (2020) 101:042501. doi:10.1103/physreva.101.042501

CrossRef Full Text | Google Scholar

38. Fitch NJ, Tarbutt MR. Laser-cooled molecules. Adv Mol Opt Phys (2021) 70:157–262. doi:10.1016/bs.aamop.2021.04.003

CrossRef Full Text | Google Scholar

39. Kogel F, Rockenhäuser M, Albrecht R, Langen T. A laser cooling scheme for precision measurements using fermionic barium monofluoride (137Ba19F) molecules. New J Phys (2021) 23:095003. doi:10.1088/1367-2630/ac1df2

CrossRef Full Text | Google Scholar

Appendix A: Further details on the evaluation of the MQM energy shift

In Section 2, we considered the energy level shifts of a ²Σ molecule due to the nuclear MQM interaction. Here, we provide more details of the calculation. As described in Section 2, the Hamiltonian is

$H=H_{\text{rot}}+H_{\text{Stark}}+H_{\text{hyp}}+H_{\text{M}}.(\mathrm{A1})$

In the field-free basis, the matrix elements of H_rot are

$\langle N,M_N|H_{\text{rot}}|N^{\prime },M_N^{\prime }\rangle =BN\left(N+1\right){\delta }_{N,N^{\prime }}{\delta }_{M_N,M_N^{\prime }}.(\mathrm{A2})$

We can write $H_{\text{Stark}}=-{\mu }_{\text{mol}}\mathcal{E}{\mathcal{D}}_{00}$ where $\mathcal{D}$ is the rotation operator that transforms from the molecule frame to the laboratory frame. The matrix elements of H_Stark are

$\langle N,M_N|H_{\text{Stark}}|N^{\prime },M_N^{\prime }\rangle =-{\mu }_{\text{mol}}\mathcal{E}{\left(-1\right)}^{M_N}\sqrt{\left(2N+1\right)\left(2N^{\prime }+1\right)}\left(\begin{array}{ccc}\hfill N\hfill & \hfill 1\hfill & \hfill N^{\prime }\hfill \\ \hfill -M_N\hfill & \hfill 0\hfill & \hfill M_N^{\prime }\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill N\hfill & \hfill 1\hfill & \hfill N^{\prime }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).(\mathrm{A3})$

Neglecting the hyperfine interaction, the energy shift due to H_M is

$\mathrm{\Delta }{E}_{\text{M}}^{\prime }=\langle G,M_G;\tilde{N},M_N|Q_{z^{\prime }}|G,M_G;\tilde{N},M_N\rangle .(\mathrm{A4})$

This factorizes as

$\mathrm{\Delta }{E}_{\text{M}}^{\prime }=\langle G,M_G;\tilde{N},M_N|{\mathcal{D}}_{00}{Q}_z|G,M_G;\tilde{N},M_N\rangle =\langle G,M_G|Q_z|G,M_G\rangle \langle \tilde{N},M_N|{\mathcal{D}}_{00}|\tilde{N},M_N\rangle =\left(W_{\text{M}}M\zeta \right)\eta .(\mathrm{A5})$

The first factor depends only on electron and nuclear spins and evaluates to

$\begin{array}{ll}\hfill \langle G,M_G|Q_z|G,M_G\rangle & =W_{\text{M}}M\zeta =W_{\text{M}}M{\left(-1\right)}^{G-M_G}\sqrt{\frac{5}{6}}\left(2G+1\right)\sqrt{\frac{S\left(S+1\right)\left(2S+1\right)\left(2I+1\right)\left(2I+2\right)\left(2I+3\right)}{2I\left(2I-1\right)}}\hfill \\ \hfill & \times \left(\begin{array}{ccc}\hfill G\hfill & \hfill 1\hfill & \hfill G\hfill \\ \hfill -M_G\hfill & \hfill 0\hfill & \hfill M_G\hfill \end{array}\right)\left\{\begin{array}{ccc}\hfill G\hfill & \hfill G\hfill & \hfill 1\hfill \\ \hfill S\hfill & \hfill S\hfill & \hfill 1\hfill \\ \hfill I\hfill & \hfill I\hfill & \hfill 2\hfill \end{array}\right\}.\hfill \end{array}(\mathrm{A6})$

The second factor is $\eta =\langle \tilde{N},M_N|{\mathcal{D}}_{00}|\tilde{N},M_N\rangle$ and is known as the polarization factor. To evaluate η, we note that

$⟨H_{\text{Stark}}⟩=\langle \tilde{N},M_N|H_{\text{Stark}}|\tilde{N},M_N\rangle =-{\mu }_{\text{mol}}\mathcal{E}\langle \tilde{N},M_N|{\mathcal{D}}_{00}|\tilde{N},M_N\rangle =-\eta {\mu }_{\text{mol}}\mathcal{E},(\mathrm{A7})$

and that

$\rangle \frac{d{H}_{\text{Stark}}}{d\mathcal{E}}\rangle =\rangle \frac{dH}{d\mathcal{E}}\rangle =\frac{d⟨H⟩}{d\mathcal{E}}=\frac{d{E}_{\tilde{N},M_N}}{d\mathcal{E}}.(\mathrm{A8})$

Thus, we see that

$\eta =-\frac{1}{{\mu }_{\text{mol}}}\frac{d{E}_{\tilde{N},M_N}}{d\mathcal{E}},(\mathrm{A9})$

which is straightforward to calculate once the eigenvalues $E_{\tilde{N},M_N}$ have been found.

When we include the hyperfine interaction and the spin of the second nucleus, we use the field-free basis |N, G, F₁, F, M_F⟩ as discussed in Section 2. The matrix elements of H_hyp depend on the terms included in the hyperfine interaction and can all be found in [27]. The eigenstates of H_rot + H_Stark + H_hyp are denoted $|\tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F\rangle$ and the energy shift due to the MQM is

$\mathrm{\Delta }{E}_M=\langle \tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F|H_{\text{M}}|\tilde{N},\tilde{G},{\tilde{F}}_1,\tilde{F},M_F\rangle .(\mathrm{A10})$

This can be evaluated with the help of the matrix element

$\begin{array}{ll}\hfill \langle N^{\prime },G^{\prime },F_1,F,M_F|H_{\text{M}}|N,G,F_1,F,M_F\rangle & =W_{M}M{\left(-1\right)}^{F+2F_1+I_2+G}\sqrt{\frac{5}{6}}\hfill \\ \hfill & \times \sqrt{\left(2F+1\right)\left(2F_1+1\right)\left(2G+1\right)\left(2G^{\prime }+1\right)\left(2N+1\right)\left(2N^{\prime }+1\right)}\hfill \\ \hfill & \times \sqrt{\frac{S\left(S+1\right)\left(2S+1\right)\left(2I+1\right)\left(2I+2\right)\left(2I+3\right)}{2I\left(2I-1\right)}}\hfill \\ \hfill & \times \left\{\begin{array}{ccc}\hfill F_1\hfill & \hfill F\hfill & \hfill I_2\hfill \\ \hfill F\hfill & \hfill F_1\hfill & \hfill 0\hfill \end{array}\right\}\left\{\begin{array}{ccc}\hfill G\hfill & \hfill N\hfill & \hfill F_1\hfill \\ \hfill N^{\prime }\hfill & \hfill G^{\prime }\hfill & \hfill 1\hfill \end{array}\right\}\left(\begin{array}{ccc}\hfill N^{\prime }\hfill & \hfill 1\hfill & \hfill N\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left\{\begin{array}{ccc}\hfill G^{\prime }\hfill & \hfill G\hfill & \hfill 1\hfill \\ \hfill S\hfill & \hfill S\hfill & \hfill 1\hfill \\ \hfill I\hfill & \hfill I\hfill & \hfill 2\hfill \end{array}\right\}.\hfill \end{array}(\mathrm{A11})$

Appendix B: Derivation of effective two-level Hamiltonian for F = 5/2 system

The time-dependent Schrödinger equation for the Hamiltonian given in Eq. 9 can be written as (setting ℏ = 1):

$\begin{array}{ll}\hfill i\dot{a}\left(t\right)& ={\mathrm{\Omega }}_{1}b\left(t\right),\hfill \\ \hfill i\dot{b}\left(t\right)& ={\mathrm{\Omega }}_{1}a\left(t\right)+{\mathrm{\Delta }}_{1}b\left(t\right)+{\mathrm{\Omega }}_{2}c\left(t\right),\hfill \\ \hfill i\dot{c}\left(t\right)& ={\mathrm{\Omega }}_{2}b\left(t\right)+{\mathrm{\Delta }}_{2}c\left(t\right)+{\mathrm{\Omega }}_{3}d\left(t\right),\hfill \\ \hfill i\dot{d}\left(t\right)& ={\mathrm{\Omega }}_{3}c\left(t\right)+{\mathrm{\Delta }}_{2}d\left(t\right)+{\mathrm{\Omega }}_{2}e\left(t\right),\hfill \\ \hfill i\dot{e}\left(t\right)& ={\mathrm{\Omega }}_{2}d\left(t\right)+{\mathrm{\Delta }}_{1}e\left(t\right)+{\mathrm{\Omega }}_{1}f\left(t\right),\hfill \\ \hfill i\dot{f}\left(t\right)& ={\mathrm{\Omega }}_{1}e\left(t\right),\hfill \end{array}$

where the amplitudes {a(t), b(t), c(t), d(t), e(t), f(t)} correspond to those of M_F = −5/2, −3/2, −1/2, 1/2, 3/2, 5/2 respectively. Consider the initial condition where f (0) = 1 and all other amplitudes are zero at t = 0, and the assumption that Δ₁, Δ₂ ≫Ω₁, Ω₂, Ω₃. Then, we can approximate $\dot{b}(t)\approx \dot{c}(t)\approx \dot{d}(t)\approx \dot{e}(t)\approx 0$, which gives us

$\begin{array}{l}\hfill b\left(t\right)=-\frac{{\mathrm{\Omega }}_{1}a\left(t\right)+{\mathrm{\Omega }}_{2}c\left(t\right)}{{\mathrm{\Delta }}_1},\\ \hfill c\left(t\right)=-\frac{{\mathrm{\Omega }}_{2}b\left(t\right)+{\mathrm{\Omega }}_{3}d\left(t\right)}{{\mathrm{\Delta }}_2},\\ \hfill d\left(t\right)=-\frac{{\mathrm{\Omega }}_{3}c\left(t\right)+{\mathrm{\Omega }}_{2}e\left(t\right)}{{\mathrm{\Delta }}_2},\\ \hfill e\left(t\right)=-\frac{{\mathrm{\Omega }}_{2}d\left(t\right)+{\mathrm{\Omega }}_{1}f\left(t\right)}{{\mathrm{\Delta }}_1}.\end{array}$

We now substitute the expression for e(t) into d(t) to get

$\left(1-\frac{{\mathrm{\Omega }}_2^2}{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2}\right)d\left(t\right)=-\frac{{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_2}c\left(t\right)+\frac{{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2}{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2}f\left(t\right).$

Since the tensor shifts are much greater than the direct couplings between M_F states, the LHS is approximately d(t). Next, we substitute this expression into the equation for c(t) above and repeat the process. Eventually, we substitute an expression for b(t) into the first differential equation involving a(t) to get

$i\dot{a}\left(t\right)=-\frac{{\mathrm{\Omega }}_1^2}{{\mathrm{\Delta }}_1}a\left(t\right)+\frac{{\mathrm{\Omega }}_1^2{\mathrm{\Omega }}_2^2{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_1^2{\mathrm{\Delta }}_2^2}f\left(t\right).$

Similarly, we find for f(t),

$i\dot{f}\left(t\right)=\frac{{\mathrm{\Omega }}_1^2{\mathrm{\Omega }}_2^2{\mathrm{\Omega }}_3}{{\mathrm{\Delta }}_1^2{\mathrm{\Delta }}_2^2}a\left(t\right)-\frac{{\mathrm{\Omega }}_1^2}{{\mathrm{\Delta }}_1}f\left(t\right),$

which together give the effective two-level Hamiltonian in Eq. 10.