- 1Department of Mathematics, Islamia College Peshawar, Peshawar, Pakistan
- 2Department of Mathematics, City University of Science and Information Technology, Peshawar, Pakistan
- 3Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al Majma’ah, Saudi Arabia
- 4Center of Research, Faculty of Engineering, Future University in Egypt New Cairo, New Cairo, Egypt
Fractional calculus is a branch of mathematics that develops from the usual definitions of calculus integral and derivative operators, just as fractional exponents emerge from integer exponents. The fractional derivative has been successfully used to describe various fundamental processes, including coiling polymer, viscoelasticity, traffic construction, diffusive transport, fluid dynamics, electromagnetic theory and electrical networks. However, many researchers do not use fractional derivatives to understand the physical properties of a non-Newtonian fluid that flows over a moving plate. The present paper aims to consider the couple stress Casson fluid between the parallel plates under variable conditions. The flow regime is formulated in terms of partial differential equations. Unlike the published work, this model is fractionalized using Fick’s and Fourier’s Laws. The system of dimensionless fractional PDEs is solved by using the joint applications of Laplace and Fourier transforms. The influence of several physical parameters, such as the Grashof number, Casson parameter, couple stress parameter etc., on velocity, temperature, and concentration profiles are represented graphically and explained physically. Furthermore, skin friction, Sherwood and Nusselt numbers are numerically calculated and presented in tabular form. It is noted that the influence of physical parameters on skin fraction is opposite to the influence on velocity. Also, the Nusselt number decreases with increasing values of Pr and the Sherwood number increases for decreasing values of Sc. The results show that the velocity of the fluid is the decreasing function of the couple stress parameter and Casson parameter while the increasing function of the permeability parameter and Grashof numbers. It is also worth noting that, unlike the classical model, the present study provides various solutions in the range of an in-between (0, 1], shown in Figures 2, 7, 8) which might be useful for the experimental and numerical solver to compare their results.
1 Introduction
In recent times, fractional calculus has been used in different areas of science and engineering, including fractional control theory [1], tumor growth data, robotics manipulation, image processing, Cyber-physical systems (CPI) [2] and signal processing [3]. Rashid et al. [4] used a generalized fractional operator and Raina’s function to develop fractional integral equalities for convex functions. Huang et al. [5] studied linear fractional difference equations and developed exact solutions using Picard’s iteration method. The role of fractional calculus has been illustrated by tackling the hysteresis phenomenon found in biological sciences [6]. In addition, they also studied the SIR compartmental model, which is extensively used in epidemiology, to demonstrate the effectiveness of fractional calculus. Meng [7] analyzed the non-linear behavior of ferroelectric polymers from both perspectives, i.e. viscoelastic and dielectric, using the fractional calculus approach. In [8], Lima and Yang developed Hadamard-type integral inequalities and some related integral identities using fractional operators.
Porous materials are widely used in different fields of science and engineering. Some of the applications of porous medium include oil recovery, logic tissues, fuel cell [9], diffusion and heat transfer rate [10], groundwater flow, filtration and sedimentation operations [11]. A comprehensive review of previously published articles is made to highlight the porous media performances in the combustion systems [12]. Arif et al. [13] considered MHD Casson nanofluid flow through a porous medium, where engine oil (EO) is used as a base fluid. Two nanoparticles, Molybdenum disulfide (Mos2) and Graphene oxide (GO), are introduced to the base fluid to improve the heat transfer rate. The Laplace transform is used to find exact solutions. Jawad et al. [14] used couple stress hybrid nanoparticles as a medication carrier in a permeable media. The mathematical model is solved by using the HAM. Casson nanofluid model is studied in [15] used GO and TiO2 as nanoparticles and Ethylene glycol as base fluid through the porous medium. RKF-45 and adopting shooting methods are used to develop numerical solutions to the problem. Harshad and Snehal [16] studied micropolar fluid flow under the impact of a magnetic field through a porous medium, and the equations are solved using Homotopy Analysis Method.
Heat and mass transfer are concerned with determining the rate at which heat is transmitted across a medium due to the difference in temperature between the two mediums. It may be in the form of conduction, convection, or radiation. Heat and mass transfer utilisation include energy systems, automobiles, electronic device cooling, steam electric power generation and diagnosing diseases. Heat generation can be used in post-accident heat removal, fluids undergoing the exothermic process, and cooling of electronic components [17]. Considering the combined influences of heat and mass transfer rate, Ismail et al. [18] analysed the joint thermal effects of heat and mass distribution on unsteady flow with the Newtonian heating effect. Vajjha and Das [19] has studied the cumulative impact of heat and mass transport in the flow of nanofluids. Obalalu et al. [20] used OHAM to examine solar radiation’s effect on unsteady squeezing Casson fluid flow. Akolade et al. [21] studied the consequences of varying mass diffusivity and viscosity on free convective unsteady flow of Casson fluid. Zainab et al. [22] investigated heat transfer in Casson fluid flow in a closed channel using a finite difference approach. Kumam et al. [23] studied ternary hybrid nanofluid to enhance the heat transfer rate. They use Laplace, and finite Fourier sine transforms to find the exact solution. Furthermore, they discuss the different shapes of nanoparticles that are useful in enhancing heat transfer rate.
Casson fluid has an infinite viscosity at zero shear rates and a zero viscosity at infinite shear rates. e.g. concentrated fruit juices, jelly, tomato sauce, soup, etc. Casson fluid has many applications in engineering problems such as fluidisation, guided missiles, paint and aerosol spraying, rain erosion, atmospheric fallout, etc. [24]. Shahrim et al. [25] examined the analytic solutions of the Casson fluid flow generated by an accelerated plate using the Laplace transform method. Shahanaz et al. [26] modeled MHD boundary layer Casson flow and then solved it numerically using MATLAB bvp4c program. Renu et al. [27] examined the cumulative effect of inclined outer velocity and aligned magnetic field in a Casson fluid and used Runge-Kutta Fehlberg’s approach and shooting technique to solve the problem numerically. Gohar et al. [28] formulated the analytic solutions of the MHD Casson fluid flow with dust particles using Caputo fractional derivatives definition by using Laplace transform and finite Fourier sine transform. Anwar et al. [29] considered MHD Casson fluid flow over vertical infinite parallel plates through a porous medium and developed the analytic solutions of the flow of electrically conducted fluid with the help of Laplace transformation. Patel [30] studied MHD Casson fluid flow through a porous medium with heat generation and also developed the expression for Nusselt number, Sherwood number and Skin friction.
MHD has many applications such as MHD accelerator, power generator, and fusion research [31]. H. R. Patel [32] studied the MHD flow of Casson fluid through a porous medium with ramped wall temperature and analysed the impacts of Hall current, heat generation, thermal radiation, and chemical reaction on the flow. Patel [33] studied the impacts of thermal radiations on the micropolar fluid flow under a uniform magnetic field.
The fluids that contain randomly oriented and rigid particles are called couple stress fluids. Blood, liquid crystals, lubrication, etc., are couple stress fluids. The applications of couple stress fluids include pumping phenomenon, blood in the microcirculatory system, hydromagnetic, etc. [34]. Stoke [35] presented the concept of couple stress theory in fluids for the first time. Farooq et al. [36] considered the Reynolds viscosity model in which they studied non-isothermal couple stress fluid flow between two parallel heated plates. They analyzed four different types of flows depending on the plate’s relative motion and produced exact solutions using the perturbation technique. Ilyas et al. [37] utilized the Caputo-Fabrizio derivatives definition to determine the analytic solutions of a generalized Couette flow of couple stress fluid. They observed that the velocity behavior obtained from both definitions is the same for unit time. Ali et al. [38] considered couple stress nanofluid flow model and developed its exact solution via AB fractional derivative definition along with Laplace and finite Fourier sine transforms. Nagaraju and Mahesh [39] studied the impact of the magnetic field, Dufour and Soret, on the asymmetric couple stress fluid flow. The PDEs are converted into ODEs and then solved using the Homotopy analysis method. Farooq et al. [40] considered four separate flows, i.e., Plug, Poiseuille, Couette, and modified Couette flow of couple stress fluids having variable viscosity and then solved each with the help of the regular perturbation method. In another paper, Farooq et al. [41] investigated the generalized Couette couple stress fluid flow and used OHAM and NIM to solve the differential equations of the problem. The analytic solution of generalized Couette flow of couple stress fluid has been derived by Arif et al. [42] with the help of Caputo-Fabrizio derivatives. The same authors presented couple stress fluid solutions in a channel for heat transfer in another paper [43]. Arif et al. [44] developed the solutions of couple stress nanofluids flow in a channel using the newly defined definition, i.e. AB fractional derivatives. Ali et al. [45] considered the vicious free convective couple stress fluid flow in a channel. Engine oil is used as a base fluid and developed the analytic solutions with the help of the Laplace transform, and finite Fourier sine transforms.
Magnetohydrodynamics (MHD) is concerned with electrically conducting fluids. MHD has many applications such as MHD accelerator, power generator, and fusion research [31]. Harshad R. Patel [32] studied the MHD flow of micropolar fluid, and the governing equations are solved numerically. In addition, analytical solutions are also developed to validate numerical results.
In the above literature, Casson fluid flow passing through a porous medium has been discussed in detail. It has yet to examine couple stress Casson fluid flow through a porous medium in a channel. Unlike the published work like Arif et al. [45], the classical model is fractionalized using generalized Ficks and Fourier laws. Additionally, the variable conditions on the plate are considered. Exact solutions are obtained by using joint applications of Laplace and Fourier transforms. The obtained general solutions satisfy all the impose initial and boundary conditions. Furthermore, the obtained general solutions are reduced to the published work as a limiting case which agrees with the published work. This shows the validity of our obtained general solutions. The obtained results are also shown by different figures. The numerical skin fraction, Nusselt number, and Sherwood number are shown in the tables.
2 Problem formulation
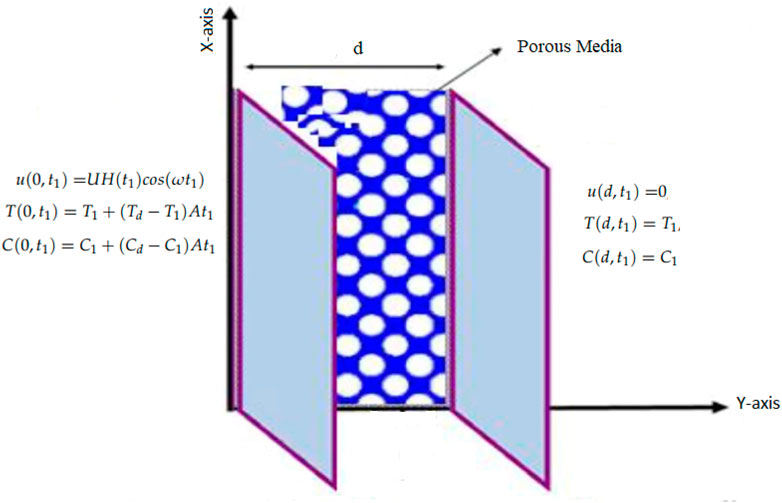
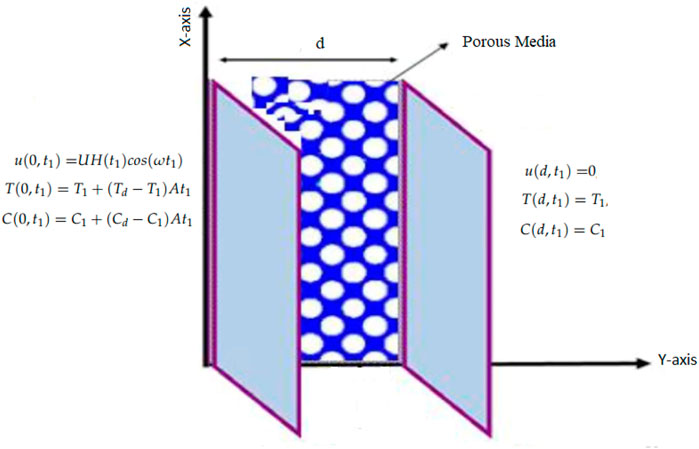
This article studied the unsteady incompressible flow of a couple stress Casson fluid through a porous material in a channel. The direction of the flow is considered along the x-axis. The distance between the plates is d. The length of both the plates is infinite. The fluid and both plates are at rest at time t1 = 0, with ambient temperature and concentration T1 and C1, respectively. After time t1 = 0+, the left plate at (y1 = 0) begins to oscillate with characteristic velocity U and frequency ω, while the right plate at y = d stays at rest. The temperature and concentration of the left plate are also raised to T -1 + (T -d − T -1)At1 and C1 + (Cd − C1)At1, respectively as displayed in Figure 1.
The equation of continuity is identically satisfied for the velocity
i.e.,
Governing equations for unsteady couple stress Casson fluid flow using Boussinesq’s approximation [46] are.The linear momentum equation with temperature and concentration terms is:
The thermal balance equation is:
The Fourier’s law:
The mass balance equation:
The Fick’s law:
The I.C and B.C for flow regime are [47]:
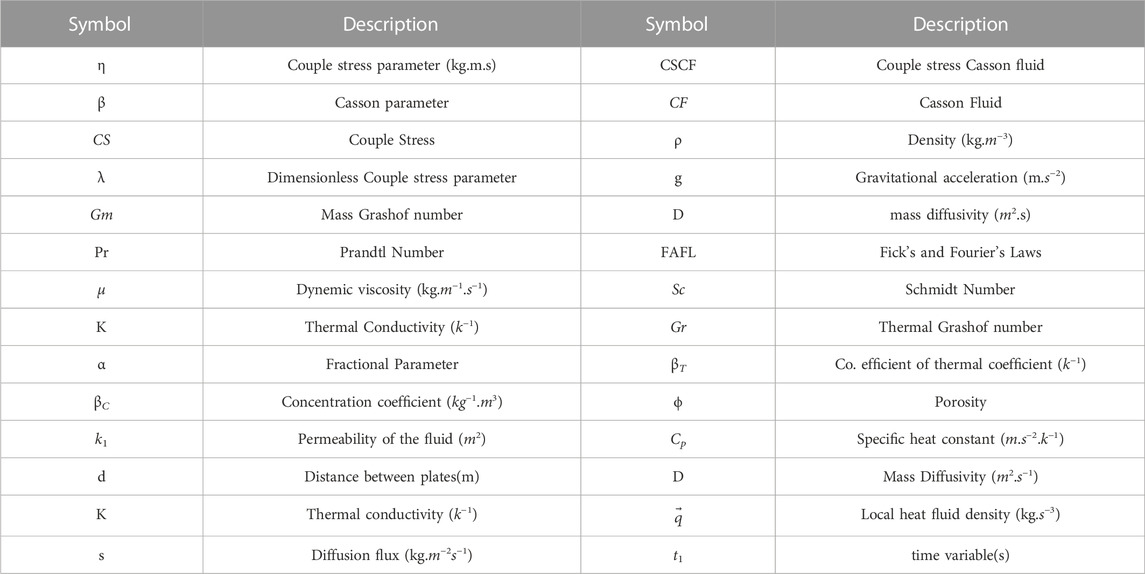
Here u, T -, and C are the symbols used to represent the velocity, temperature, and concentration of the fluid respectively. (ρCp), k1,
Using the above dimensionless variables in Eq. 9 and 3–8 reduce to (dropping ′′ *″ signs):
where,
3 Solution of the problem
This section contains the solutions of temperature, concentration, and velocity distributions.
3.1 Temperature distribution
Apply Laplace transform to Eq. 16; we have:
The transformed conditions for temperature distribution are stated below:
To find the solution of Eq. 18, applying finite Fourier sine transform and using Eq. 19, we have:
where the finite Fourier sine transform is defined as:
Also
where Ec,d(z) represent the Mittag- Leffler function and is given as:
Also
3.2 Concentration distribution
To find the solution of concentration distribution, apply Laplace transform to Eq. 17, we have:
The transformed conditions for concentration distribution are stated below:
To find the solution of Eq. 22, applying finite Fourier sine transform and using Eq. 23, we have:
where
3.3 Velocity distribution
To find the solution of velocity distribution, taking Laplace transform of Eq. 10; we have:
The transformed conditions for velocity distribution are stated below:
Now applying the finite Fourier sine transform to Eq. 26 and incorporating Eq. 27, we have:
Decomposing rational factors of Eq. 29 by partial fraction, we get:
Equivalent form of Eq. 30 is:
Taking Inverse Laplace transform, Eq. 31 can be written as:
Inverting finite Fourier sine transform of Eq. 32; we have:
where
4 Special cases
This section contain different special cases which are derived from the general solution developed in Eq. 33 by substituting different values to the parameters.
4.1 Couple stress casson fluid model without porous medium
By substituting
Applying finite Fourier sine transform to Eq. 34 and incorporating Eq. 27; we have:
Using Eqs. 20, 24, and after performing the steps as done in velocity distribution, the final solution is given by:
where R3 = KπR1
4.2 Couple stress model
In this section, we derived the solution only for couple stress fluid flow by taking β → ∞ or
Applying finite Fourier sine transform and incorporating the conditions defined in Eq. 27; we have:
Applying inverse transformations and after simplification, the final result is:
where R4 = (kπ) + λ(kπ)3 and
4.3 Casson fluid model
To obtain the Casson fluid model, put λ = 0 in Eq. 26; we have:
Applying finite Fourier sine transform and incorporating the conditions defined in Eq. 27; we have:
Using Eqs. 20, 24, and simplifying we get:
Applying inverse transformation; we have:
where R6 = R (kπ) and
5 Limiting cases
In this section, limiting cases are derived from general solutions and compared with already published work.
5.1 Classical couple stress casson fluid model
To obtain, the classical model for couple stress Casson fluid, taking α → 1, Gr → 0, and Gm → 0 in Eq. 33, we have:
By considering ω → 0,
The result obtained in Eq. 46 is similar to Eq. 62 derived by Arif et al. [45] for p = 0, that shows the correctness of the present study.
5.2 Couple stress casson fluid model without thermal and concentration
Considering Gr → 0 and Gm → 0 in general solutions given in Eq. 33; we have:
Again, By considering ω → 0,
Equation 48 is similar to Eq. 63 for p = 0 obtained by Arif et al. [45], that shows the validity of our general solutions.
5.3 Casson fluid model without concentration and porous medium
Considering λ → 0, Gm → 0 and
where
5.4 Skin friction
The Skin friction on the left plate for couple stress Casson fluid flow in dimensional form is:
In dimensionless form Eq. 51 is given as:
5.5 Nusselt number
The Nusselt number can be stated as:
5.6 Sherwood number
The Sherwood number can be stated as:
6 Results and discussion
In this article, we analyzed the impact of some physical parameters on the flow of a couple stress Casson fluid through a porous medium with Caputo time-fractional derivatives between parallel plates, such as thermal and mass Grashof number (Gr), and (Gm), Schmidt number (Sc), Prandtl number (Pr), Casson parameter (β), couple stress parameter (λ), and porosity parameter (k2). Generalized Fick’s and Fouier’s Laws are utilized to construct the fractional model and then Laplace and Fourier transforms are used to solve the model. In addition, the effects of the parameters mentioned above on Nusselt numbers, Sherwood numbers, and skin friction are evaluated and tabulated. The impact of physical parameters on velocity, temperature and concentration distributions are depicted in (Figure 2-Figure 8).
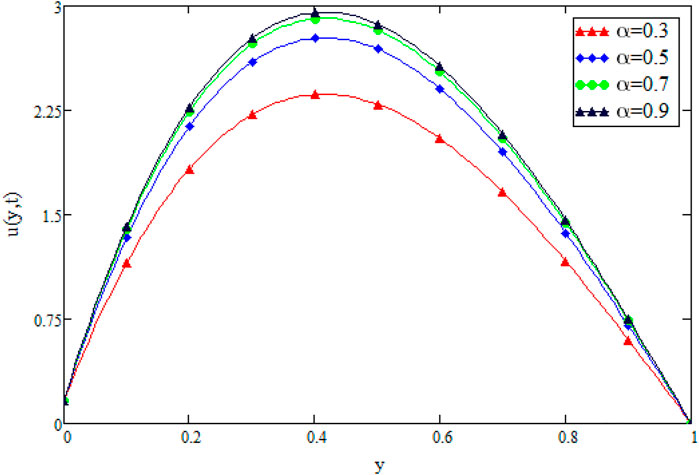
FIGURE 2. Variation in Velocity distribution against α when t1=1, Gr =30, Gm =10, Pr =15, Sc =0.3, λ =1000, β =0.2, k2=5, and ω =50.
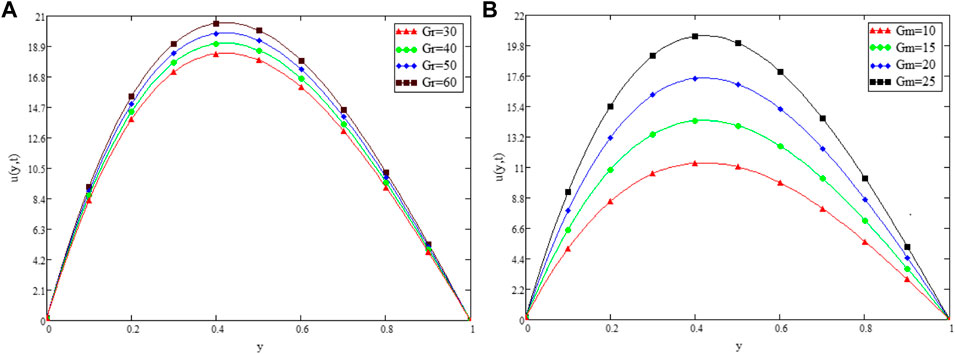
FIGURE 3. Variation in Velocity distribution against Gr (A) and Gm (B) when α =0.3 t1=1, Pr =15, Sc =0.3, λ =1000, β =0.2, k2=5, and ω =50.
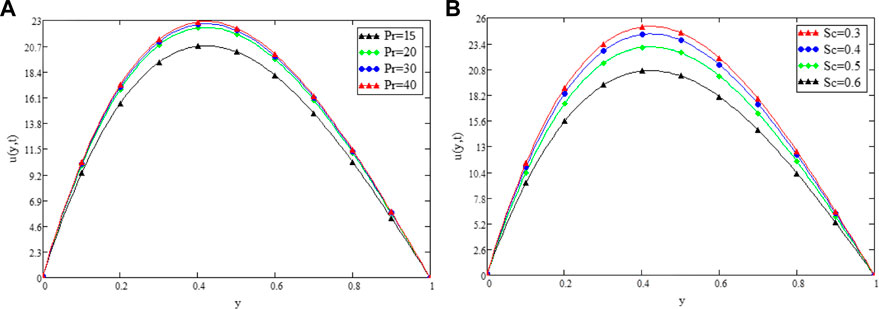
FIGURE 4. Variation in Velocity distribution against Pr (A) and Sc (B) when α =0.3 t1=1, Gr =30, Gm =10, λ =1000, β =0.2, k2=5, and ω =50.
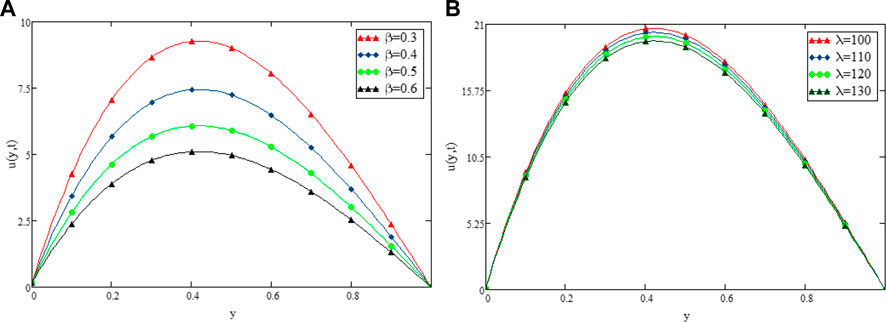
FIGURE 5. Variation in Velocity distribution against β (A) and λ (B) when α =0.3 t1=1, Gr =30, Gm =10, Pr =15, Sc =0.3, k2=5, and ω =50.
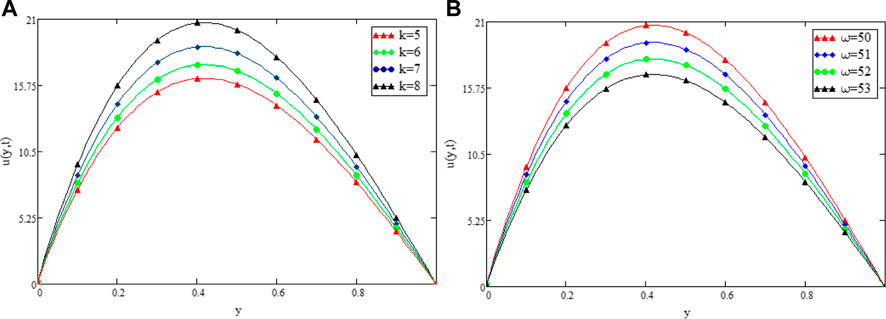
FIGURE 6. Variation in Velocity distribution against k2 (A) and ω (B) when α =0.3 t1=1, Gr =30, Gm =10, Pr =15, Sc =0.3, β =0.2, and λ =1.
Figure 9 shows the geometry of the problem. Figure 2 shows multiples solutions for different values of the (α) in the form of integral curves. This result is worth noting for the numerical solvers and experimentalists to best fit their results with one of the integral curves. Figure 3 illustrate the contribution of Gr and Gm on the flow of couple stressCasson fluid. Both Gr and Gm accelerate the flow as we increase the values of these parameters. The enhancement of thermal buoyancy force is the physical theory behind this. Because these parameters are directly proportional to buoyancy forces and inversely proportional to viscous forces, a rise in Gr and Gm indicates that buoyancy forces have subdued the viscous forces, decreasing the resistance offered, and thus, the velocity of the fluid increases. The only difference is that in Gr the buoyancy forces increase due to thermal volumetric expansion, whereas in Gm, buoyancy forces increase due to solutal volumetric expansion. The impact of the Pr on velocity is captured in Figure 4A. The velocity distribution decreases for increasing values of the Pr, which is physically true. As the Pr is directly proportional to kinematic viscosity and inversely proportional to thermal diffusivity, an increase in the Pr means kinematic viscosity dominates the thermal diffusivity, which causes more resistance to the flow and hence, the velocity of the fluid decreases. The influence of Sc on the velocity profile of couple stress Casson fluid is captured in Figure 4B. The figure clearly shows that the velocity distribution is a decreasing function of Sc, which is physically correct. Sc has a direct relationship with viscous forces and an inverse relationship with mass diffusion. By increasing the values of Sc means that viscous forces dominates the mass diffusion, which causes a decrease in velocity of fluid. Figure 5A displays the couple stress Casson fluid velocity with variation in the β. From the graph, it is clear that the velocity distribution is the decreasing function of β. Physically this behavior of β is true. As β is directly proportional to dynamic viscosity and inversely to yield stress, by increasing the β, the dynamic viscosity increases, generating resistance to the flow and the velocity of flow decreases. As λ has a direct relationship with inertial forces and inverse relation with viscous forces, increasing the values of λ means that inertial forces will dominate the viscous forces, which causes a decrease in the fluid’s velocity, which can be seen in Figure 5B. Figure 6A shows the influence of k2 on the velocity regime. From the figure, it is clear that the velocity distribution is the increasing function of k2. The physics behind this is that increasing the permeability means increasing the interconnectivity of the pores, consequently increasing the velocity flow rate. Figure 6B shows the impact of ω on velocity distribution. Form the figure, it is clear that the velocity is decreases for increasing values ω.
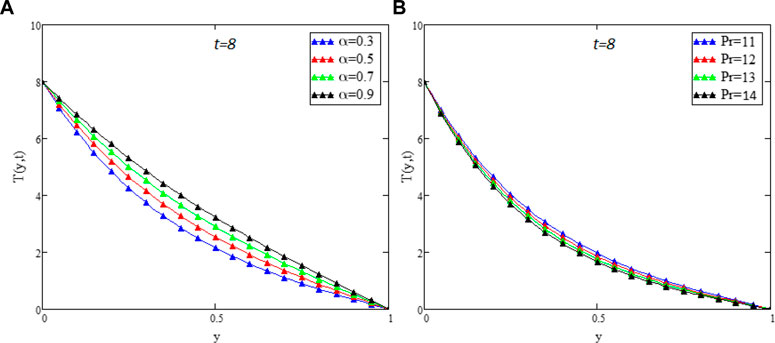
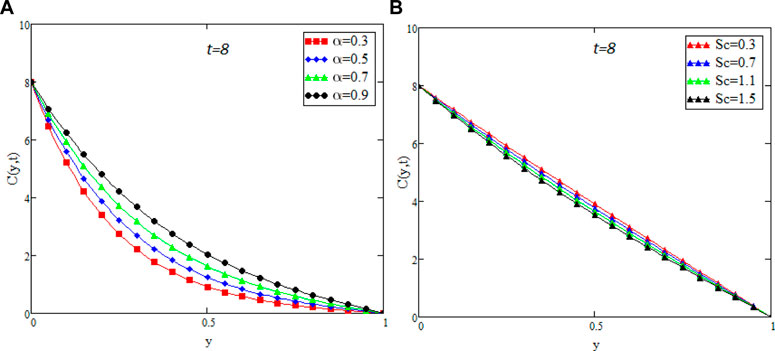
Figure 7A `describes the multiple solutions of the temperature profile as discussed in Figure 2. The impact of Pr on temperature distribution can be seen in Figure 7B. The figure shows that the temperature profile decreases as the value of Pr increases. Physically, this is valid since by increasing Pr the thermal forces become weaker and thus, a decrease in temperature occurs. Figure 8A shows the integral curves of concentration profile for different values of fractional parameter α. The impact of different values of α on the concentration profile is similar to that of the temperature and velocity profiles. Figure 8B depicts the concentration profile for various values of Sc, which illustrates that the concentration profile remains the same over time and a reduction for increasing values of Sc. As Sc has a direct relationship with viscous forces and an inverse relationship with mass diffusion. When the values of Sc rise, the viscous forces of the fluid rise, which cause to decrease in concentration profile. Figure 10 shows the comparison of the general solution with Arif et.al [45] graphically which confirm the accuracy of our solutions.
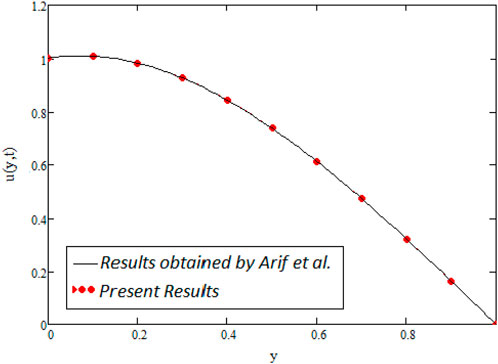
FIGURE 10. Comparison of obtained results with the results of Arif et al. [45] with Figure 3A for α =0.7 t1=2, Gr =1.5, Gm =1.5, Pr =1000, Sc =2, β →∞, k2→∞, ω =0 and λ =50.
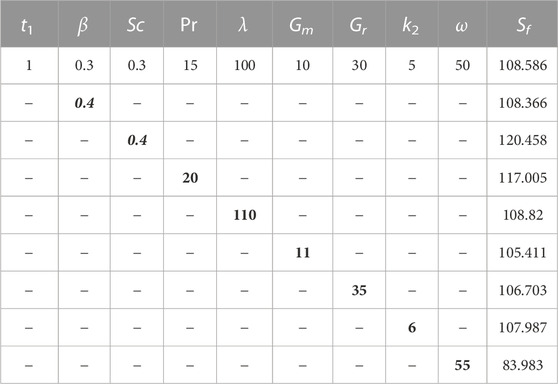
Table 1 consists of nomenclature box. Skin friction has so many applications in engineering, specifically civil engineering. Skin friction, Nusselt, and Sherwood numbers have many applications in engineering. Engineers can calculate an object’s overall frictional drag and the rate of convectional heat transfer over its surface by calculating skin friction. For instance, turbine blades are forced to operate in high-temperature gas, which might cause damage from the heat. Turbine blades must undergo a heat transfer study throughout the design phase. In this case, engineers estimate skin friction on the turbine blade’s surface to estimate heat transfer through the surface. Table 2 shows the effects of several physical parameters on skin friction. Table. 2 shows the influence of β on skin friction. As β is the ratio of dynamic viscosity to yield stress. Increasing values of β increases the dynamic viscosity enhancing the skin friction and this physical behavior is supported by the effect of β on the velocity. Similarly, Sc has a direct relationship to viscosity, so by increasing the value of Sc, viscous forces increases and thus the skin friction also rises. Again Pr depends on viscous forces, so the skin friction increases as we increase Pr. As λ is proportional to the fluid’s inertial forces, an increase in λ increases the inertial forces, which causes an increase in the skin friction, as illustrated in Table. 2. By raising Gr and Gm, the buoyancy forces rise, lowering the viscosity of the fluid, and, as a result, the skin friction is also reduced. The same phenomenon can be seen in the table. Finally, by increasing k2, skin friction reduces. The physics behind this is that resistive forces of the medium decrease which cause to decrease the skin friction.
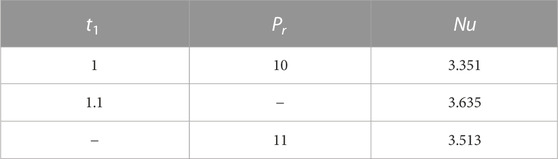
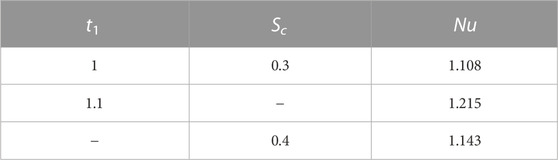
Table. 3 shows the variation in the values of the Nusselt number due to the variation in the values of different physical parameters. Nusselt number decreases for increasing values of Pr. The physics behind this is that by increasing Pr, the momentum diffusivity overcomes the thermal diffusivity, which causes to reduce the thermal boundary layer thickness and hence Nusselt number decreases. Values of Sherwood number are displayed in Table. 4. Sherwood number is the increasing function of Sc. As Sc has direct relationship with viscous forces and inverse relationship with the mass diffusion, increasing the Schmidt number generates a rise in viscous forces, hence the Sherwood number increases. Table. 5 and Table. 6 shows the comparison of solutions in terms of skin friction and Nusselt number. The skin friction and Nusselt numbers values are compared with Nadeem et al. [48].
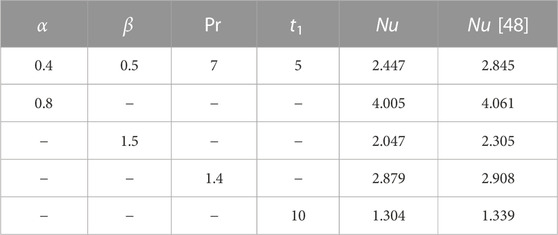
TABLE 5. Comparison of Skin friction with Nadeem et. al [48].
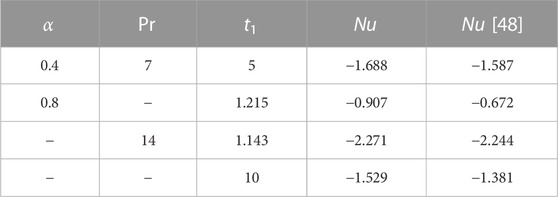
TABLE 6. Comparison of Nusselt number with Nadeem et. al [48].
7 Conclusion
In this article, we developed the exact solutions of couple stress Casson fluid flow through the porous medium using the modern approach of Fick’s and Fourier’s laws with the help of Caputo time-fractional derivatives definition and integral transformations. The effect of different physical parameters on temperature, concentration and velocity profile is depicted graphically and explained physically. The final remarks of the present study are given below.
1) Unlike the previous publish work, in this article the classical model are transformed to fractional model using generalized Ficks’s and Fourier’s Laws.
2) Unlike the classical model, the fractional model provides multiple solutions for different values of α, where α lies in between (0,1].
3) The Casson parameter β decreases the velocity for its increasing values.
4) The velocity of the couple stress Casson fluid increases for increasing values of k2, Gm and Gr, while the behavior of the velocity profile for increasing values of λ, Pr, Sc, and ω is opposite to that of k2, Gm and Gr.
5) The influence of different physical parameters on skin friction is quite the opposite of the influence on the velocity, which is a good agreement with the basic idea of skin friction.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SA first formulated the problem and then found the exact solution. SA and SH drew the graphs. SA and FA discussed all the graphs in detail and wrote the discussion and conclusion sections. IK performed the proofreading. SME did the comparison of physical quantities. All the authors reviewed the final draft of the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1031042/full#supplementary-material
References
2. Ostalczyk P. Discrete fractional calculus: Applications in control and image processing. Singapore: World Scientific (2015).
3. Assaleh K, Ahmad WM. Modeling of speech signals using fractional calculus. In: 2007 9th International Symposium on Signal Processing and Its Applications; 12-15 February 2007; Sharjah (2007).
4. Rashid S, Khalid A, Bazighifan O, Oros GI. New modifications of integral inequalities via ℘-Convexity pertaining to fractional calculus and their applications. Mathematics (2021) 9(15):1753. doi:10.3390/math9151753
5. Huang L-L, Wu G-C, Baleanu D, Wang H-Y. Discrete fractional calculus for interval–valued systems. Fuzzy Sets Syst (2021) 404:141–58. doi:10.1016/j.fss.2020.04.008
6. de Barros LC, Lopes MM, Santo Pedro F, Esmi E, dos Santos JPC, Sánchez DE. The memory effect on fractional calculus: An application in the spread of Covid-19. Comput Appl Math (2021) 40(3):72–21. doi:10.1007/s40314-021-01456-z
7. Meng R. Application of fractional calculus to modeling the non-linear behaviors of ferroelectric polymer composites: Viscoelasticity and dielectricity. Membranes (2021) 11(6):409. doi:10.3390/membranes11060409
8. Ma L, Yang G. Hadamard type inequalities via fractional calculus in the space of exp-convex functions and applications. Electron J Differential Equations (2021) 2021(33):1–18.
9. Anbari A, Chien H-T, Datta SS, Deng W, Weitz DA, Fan J. Microfluidic model porous media: Fabrication and applications. Small (2018) 14(18):1703575. doi:10.1002/smll.201703575
10. Mujeebu MA, Abdullah MZ, Bakar MA, Mohamad A, Abdullah M. Applications of porous media combustion technology–a review. Appl Energ (2009) 86(9):1365–75. doi:10.1016/j.apenergy.2009.01.017
11. Liu H, Kang Q, Leonardi CR, Schmieschek S, Narváez A, Jones BD, et al. Multiphase lattice Boltzmann simulations for porous media applications. Comput Geosciences (2016) 20(4):777–805. doi:10.1007/s10596-015-9542-3
12. Gharehghani A, Ghasemi K, Siavashi M, Mehranfar S. Applications of porous materials in combustion systems: A comprehensive and state-of-the-art review. Fuel (2021) 304:121411. doi:10.1016/j.fuel.2021.121411
13. Arif M, Kumam P, Kumam W, Khan I, Ramzan M. A fractional model of casson fluid with ramped wall temperature: Engineering applications of engine oil. Comput Math Methods (2021) 3:e1162. doi:10.1002/cmm4.1162
14. Jawad M, Khan A, Shah SAA. Examination of couple stress hybrid nanoparticles (cuo-cu/blood) as a targeted drug carrier with magnetic effects through porous sheet. Braz J Phys (2021) 1–12:1096–107. doi:10.1007/s13538-021-00930-7
15. Kumar RN, Gowda RJP, Gireesha BJ, Prasannakumara BC. Non-Newtonian hybrid nanofluid flow over vertically upward/downward moving rotating disk in a Darcy–forchheimer porous medium. Eur Phys Journal-special Top (2021) 230:1227–37. doi:10.1140/epjs/s11734-021-00054-8
16. Patel HR, Patel SD. Heat and mass transfer in mixed convection mhd micropolar fluid flow due to non-linear stretched sheet in porous medium with non-uniform heat generation and absorption. Waves in Random and Complex Media (2022) 32:1–31. doi:10.1080/17455030.2022.2044542
17. Patel HR. ′′Cross diffusion and heat generation effects on mixed convection stagnation point mhd carreau fluid flow in a porous medium. ′′ Int J Ambient Energ (2021) 43:4990–5005. doi:10.1080/01430750.2021.1931960
18. Hussanan A, Ismail Z, Khan I, Hussein AG, Shafie S. Unsteady boundary layer mhd free convection flow in a porous medium with constant mass diffusion and Newtonian heating. The Eur Phys J Plus (2014) 129:46–16. doi:10.1140/epjp/i2014-14046-x
19. Vajjha RS, Das D. A review and analysis on influence of temperature and concentration of nanofluids on thermophysical properties, heat transfer and pumping power. Int J Heat Mass Transfer (2012) 55:4063–78. doi:10.1016/j.ijheatmasstransfer.2012.03.048
20. Obalalu AM, Ajala AO, Akindele AO, Oladapo OA, Adepoju O, Jimoh MO. Unsteady squeezed flow and heat transfer of dissipative casson fluid using optimal homotopy analysis method: An application of solar radiation. Partial Differential Equations Appl Math (2021) 4:100146. doi:10.1016/j.padiff.2021.100146
21. Akolade MT, Adeosun TA, Olabode JO. Influence of thermophysical features on mhd squeezed flow of dissipative casson fluid with chemical and radiative effects. J Appl Comput Mech (2021) 7(4):1999–2009.
22. Bukhari Z, Ali A, Abbas Z, Farooq H. The pulsatile flow of thermally developed non-Newtonian casson fluid in a channel with constricted walls. AIP Adv (2021) 11(2):025324. doi:10.1063/5.0036738
23. Arif M, Kumam P, Kumam W, Mostafa Z. Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: A fractional model. Case Stud Therm Eng (2022) 31:101837. doi:10.1016/j.csite.2022.101837 2022.
24. Ramesh G, Kumar KG, Shehzad SA, Gireesha BJ. Enhancement of radiation on hydromagnetic casson fluid flow towards a stretched cylinder with suspension of liquid-particles. Can J Phys (2018) 96:18–24. doi:10.1139/cjp-2017-0307
25. Shahrim MN, Mohamad AQ, Jiann LY, Zakaria MN, Shafie S, Ismail Z, et al. Exact solution of fractional convective casson fluid through an accelerated plate. CFD Lett (2021) 13(6):15–25. doi:10.37934/cfdl.13.6.1525
26. Parvin S, Isa SSPM, Arifin NM, Ali FM. The magnetohydrodynamics casson fluid flow, heat and mass transfer due to the presence of assisting flow and buoyancy ratio parameters. Akademia Baru (2020) 12(8):64–75. doi:10.37934/cfdl.12.8.6475
27. Renu D, Poply V, Mani M. Effect of aligned magnetic field and inclined outer velocity in casson fluid flow over a stretching sheet with heat source. J Therm Eng (2021) 7(4):823–44. doi:10.18186/thermal.930347
28. Ali G, Ali F, Khan A, Ganie AH, Khan I. A generalized magnetohydrodynamic two-phase free convection flow of dusty casson fluid between parallel plates. Case Stud Therm Eng (2022) 29:101657–15. doi:10.1016/j.csite.2021.101657
29. Anwar T, Kumam P, Watthayu W. Unsteady mhd natural convection flow of casson fluid incorporating thermal radiative flux and heat injection/suction mechanism under variable wall conditions. Scientific Rep (2021) 11(1):4275–15. doi:10.1038/s41598-021-83691-2
30. Patel HR. Soret and heat generation effects on unsteady mhd casson fluid flow in porous medium. Waves in Random and Complex Media (2022) 32:1–24. doi:10.1080/17455030.2022.2030500
31. Patel HR. Effects of cross diffusion and heat generation on mixed convective mhd flow of casson fluid through porous medium with non-linear thermal radiation. Heliyon (2019) 5(4):e01555. doi:10.1016/j.heliyon.2019.e01555
32. Patel HR. Effects of heat generation, thermal radiation, and hall current on mhd casson fluid flow past an oscillating plate in porous medium. Multiphase Sci Tech (2019) 31(1):87–107. doi:10.1615/multscientechn.2019029514
33. Patel HR. Thermal radiation effects on mhd flow with heat and mass transfer of micropolar fluid between two vertical walls. Int J Ambient Energ (2021) 42(11):1281–96. doi:10.1080/01430750.2019.1594371
34. Tripathi D. Peristaltic flow of couple-stress conducting fluids through a porous channel: Applications to blood flow in the micro-circulatory system. J Biol Syst (2011) 19:461–77. doi:10.1142/s021833901100407x
35. Stokes VK. Couple stresses in fluids. In: Theories of fluids with microstructure. Germany: Springer (1984).
36. Farooq M, Islam S, Rahim M, Siddiqui A. Laminar flow of couple stress fluids for vogels model. Scientific Res Essays (2012) 7:2936–61.
37. Arif M, Ali F, Sheikh N, Khan I, Nisar K. Fractional model of couple stress fluid for generalized Couette flow: A comparative analysis of atangana–baleanu and caputo–fabrizio fractional derivatives. IEEE Access (2019) PP(99):1-. doi:10.1109/ACCESS.2019.2925699
38. Arif M, Ali F, Khan I, Nisar K. A time fractional model with non-singular kernel the generalized Couette flow of couple stress nanofluid. IEEE Access (2020) PP(99):1-. doi:10.1109/ACCESS.2020.2982028
39. Gajjela N, Garvandha M. The influence of magnetized couple stress heat, and mass transfer flow in a stretching cylinder with convective boundary condition, cross-diffusion, and chemical reaction. Therm Sci Eng Prog (2020) 18:100517. doi:10.1016/j.tsep.2020.100517
40. Farooq M, Islam S, Rahim M, Haroon T. Heat transfer flow of steady couple stress fluids between two parallel plates with variable viscosity. Heat Transfer Res (2011) 42(8):737–80. doi:10.1615/heattransres.2012000996
41. Farooq M, Khan A, Nawaz R, Islam S, Ayaz M, Chu Y-M. Comparative study of generalized Couette flow of couple stress fluid using optimal homotopy asymptotic method and new iterative method. Scientific Rep (2021) 11(1):3478–20. doi:10.1038/s41598-021-82746-8
42. Arif M, Ali F, Sheikh NA, Khan I, Nisar KS. Fractional model of couple stress fluid for generalized Couette flow: A comparative analysis of atangana baleanu and caputo fabrizio fractional derivatives. IEEE Access (2019) 7:88643–55. doi:10.1109/access.2019.2925699
43. Sheikh NA, Ali F, Khan I, Saqib M. A modern approach of caputo–fabrizio time-fractional derivative to mhd free convection flow of generalized second-grade fluid in a porous medium. Neural Comput Appl (2018) 30(6):1865–75. doi:10.1007/s00521-016-2815-5
44. Arif M, Ali F, Khan I, Nisar KS. A time fractional model with non-singular kernel the generalized Couette flow of couple stress nanofluid. IEEE Access (2020) 8:77378–95. doi:10.1109/access.2020.2982028
45. Ali F, Ahmad Z, Arif M, Khan I, Nisar KS. A time fractional model of generalized Couette flow of couple stress nanofluid with heat and mass transfer: Applications in engine oil. IEEE Access (2020) 8:146944–66. doi:10.1109/access.2020.3013701
46. Sheikh NA, Ching DLC, Khan I, Kumar D, Nisar KS. A new model of fractional casson fluid based on generalized fick’s and fourier’s laws together with heat and mass transfer. Alexandria Eng J (2020) 59(5):2865–76. doi:10.1016/j.aej.2019.12.023
47. Muthucumaraswamy R, Vijayalakshmi A. Effects of heat and mass transfer on flow past an oscillating vertical plate with variable temperature. Int J Appl Math Mech (2008) 4(1):59–65.
Keywords: fractional derivative, porous medium, variable temperature, variable concentration, laplace and fourier transforms
Citation: Ahmad S, Haq SU, Ali F, Khan I and Eldin SM (2023) Free convection channel flow of couple stress casson fluid: A fractional model using Fourier’s and Fick’s laws. Front. Phys. 11:1031042. doi: 10.3389/fphy.2023.1031042
Received: 29 August 2022; Accepted: 26 January 2023;
Published: 17 February 2023.
Edited by:
Fernando A. Oliveira, University of Brasilia, BrazilCopyright © 2023 Ahmad, Haq, Ali, Khan and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Farhad Ali, ZmFyaGFkYWxpQGN1c2l0LmVkdS5waw==
 Shafiq Ahmad
Shafiq Ahmad Sami Ul Haq1
Sami Ul Haq1 Farhad Ali
Farhad Ali Ilyas Khan
Ilyas Khan