Collimated terahertz radiation through a laser irradiating on a T-type target

A scheme, applying a linearly polarized laser irradiating on a T-type target which contains a longitudinal target followed by a transverse target, is proposed to collimate the terahertz radiation. The results show that the interaction between the laser and the longitudinal target can effectively reduce the electron transverse divergence while increasing the electron maximum cut-off energy. In this way, the terahertz radiation can be well collimated while enhancing its intensity. By using two-dimensional particle-in-cell simulations, we show that the pointing angle is about −13.6° and 17.5° when the length and thickness of the longitudianl target are 90.0 μm and 4.0 μm, respectively. In addition, the impact of the laser and target parameters on the collimation of terahertz radiation are also investigated separately. Such a scheme may pave a new way for enhancing and collimating the terahertz radiation via laser-solid interactions.

1 Introduction

With the rapid development of laser technology, the researches on the generation of terahertz (THz) waves based on the interaction between laser and plasma have attracted much attention in recent years [1–5]. THz radiation can be produced via the gas filamentation effect by a laser interacting directly with air or with different types of gases at different pressures [6–8]. For example, the two-color laser field ionization of gas is a commonly used scheme for enhancing THz radiation [6–12]. Besides, schemes like choosing different frequency ratios of two laser beams [13] or using a three-color laser field [14] have also been proposed and validated experimentally to enhance and modulate the generation of THz radiation. Although direct laser breakdown of the air or gas is a simple method to generate THz radiation, studies have shown that when the laser intensity reaches the order of 10¹⁵W/cm², the THz radiation generation will be saturated as the laser intensity increases [7].

High-intensity THz radiation has important applications in many research fields such as materials [11], attosecond science [15], and electron accelerators [16], etc. Theoretical simulations and experimental studies in recent years [17–20] point to a very promising approach to generate an intense THz radiation based on the interaction of an intense laser with a solid target via the coherent transition radiation (CTR) mechanism [21, 22]. And in recent experiments, the single-shot THz pulse energy has reached $\sim 50\mathrm{m}\mathrm{J}$ which is generated by the interaction of a picosecond laser with a solid target [23]. Meanwhile, many other novel schemes have also been proposed for efficient generation of THz radiation, such as the interaction of femtosecond lasers with aligned copper nanorod array targets [24], the microplasma waveguide (MPW) [25] via the coherent diffraction radiation (CDR) [26], and the laser interacting with a wire through the fast electrons’ helical motion [27] or the current-carrying line antenna [28], etc. In addition, the spectral modulation and angular characteristics of the THz radiation have also been studied in detail [29, 30]. In terms of the control of the THz radiation angle when a laser irradiate on a solid target, recently Cai et al. propose to collimate the THz radiation from an ultra-short intense laser and cone target [31]. Our previous study demonstrates that it is capable of effectively enhancing THz radiation, in which a linearly polarized laser irradiates on a T-type target (TTT) containing a longitudinal target followed by a transverse target [32]. While the control of this target on the THz radiation angle is still unclear.

In this work, the collimation of THz radiation by the interaction of a laser with the TTT is investigated by the particle-in-cell (PIC) simulations. The results present that under the promotion of TTT, not only the THz radiation is intensified, but also the poiniting angle is effectively reduced. This is mainly attributed to the higher cut-off energy and smaller transverse divergence angle of the electron beam generated in TTT. The paper is organized as follows. Section 2 outlines the target configurations, simulation parameters and results. Besides, the reasons for the well-collimated THz radiation are also analyzed in detail. Section 3 presents the effects of laser and target parameters on collimating the THz radiation. Lastly, a brief summary is given in Section 4.

2 Numerical simulations, results, and analysis

2.1 Target configurations and simulation parameters

In order to show the collimation of the THz radiation through the laser interacting with the TTT, we use the open PIC code EPOCH [33] to carry out a series of two-dimensional (2D) simulations. In the simulations, the box is located at the (x, y) plane, and the area is set as 200λ₀ × 100λ₀ with spatial grids 6000 × 2000, where λ₀ = 1.0 μm is the wavelength of the laser. The initial sketch of our proposed scheme is shown in Figure 1. Both targets I and II are composed of carbon ions, protons and electrons, which assumes that the ions are fully ionized since the laser intensity is much larger than the ionization potential of the carbon ions and protons [34, 35]. The number density of both them is n_e0 = 21.0n_c and n_p0 = n_C0 = 3.0n_c, where $n_c=m_e{\omega }_0^2/4\pi e^2$ is the electrons’ critical plasma number density, m_e is the electron mass, e is the electron charge, and ω₀ is the laser frequency. And the Target-I is uniformly distributed within 5λ₀ ≤ x ≤ 95λ₀ along the x-axis and −2λ₀ ≤ y ≤ 2λ₀ along the y-axis, while the Target-II is distributed within 95λ₀ ≤ x ≤ 100λ₀ along the x-axis and −50λ₀ ≤ x ≤ 50λ₀ along the y-axis. Besides, the macro-particle number of every cell is 50 for per kind of particle. Meanwhile, as a comparison, a flat target, which is located at 95λ₀ ≤ x ≤ 100λ₀ with the same plasma density as the TTT, is set in the simulations.

FIGURE 1

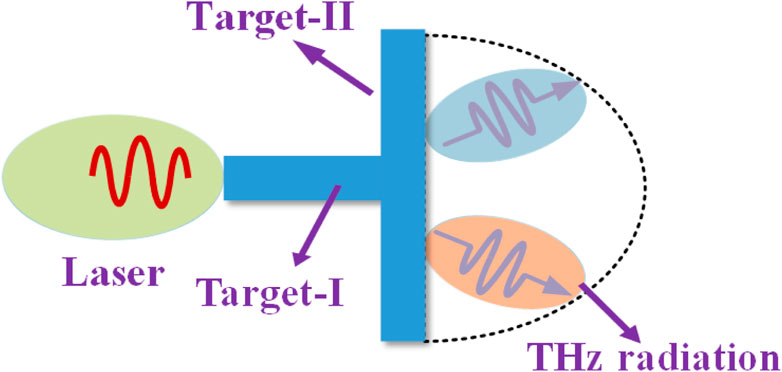
FIGURE 1. The initial sketch of the T-type target and the radiated electromagnetic field which is generated behind the target by the coherent transition radiation (CTR) mechanism. The black dashed line represents the semi-circle which is used to collect the radiated electromagnetic field.

The temporal and spatial profile of the laser is $I=I_0\exp [-{(t-t_0)}^2/{\tau }_0^2]\exp (-y^2/r_0^2)$ and it normally incident from the left boundary. We set r₀ = 6.0 μm and t₀ = τ₀ = 5T₀ in the simulations, where T₀ is the laser period. Besides, the peak intensity of the laser is I₀ = 6.0 × 10¹⁹ W/cm², corresponding to the normalized vector potential a₀ = eE₀/m_ecω₀ = 6.6 for λ₀ = 1.0 μm. The above laser parameters correspond to a compact laser system of about 70 TW, which is currently commonly used in the laboratory. Moreover, absorption boundary condition is applied to both particles and fields for all boundaries.

2.2 Simulation results and analysis

The radiated electromagnetic field (including the electric field E_y with units V/m and magnetic field B_z with units T) behind the target is collected by a semi-circle centered at (100λ₀, 0) in the (x, y) plane because it can be seen as a point source radiating outward over time [30, 31, 36]. We choose the radius of the detected semi-circle to be R₀ = 45.0 μm, which is enough to avoid the interference of the quasi-static fields formed behind the target and the noise caused by the expansion of the target [30, 36]. First, Figure 2 shows the collected electromagnetic field over time for both of the flat target and TTT. We can observe from Figure 2A that multiple pulses are radiated when the laser interacts with the flat target, which is consistent with the findings that have been reported previously [30]. The main reason for the above phenomenon is that a part of the electrons with lower energy after leaving the target will be dragged back to the inside of the target by the sheath field at the rear side of the target. The electrons can then radiate multiple electromagnetic pulses through such reciprocating motion [31, 37]. Therefore, after the fast Fourier transform (FFT), as shown in Figure 3A, the frequency has multiple peak structures under the action of the radiated electromagnetic field of the multiple peak structures in the time domain. While in the case of TTT, we have only detected a single pulse of the radiated electromagnetic field over the entire time series, and its intensity is significantly stronger than that of the flat target a lot, as shown in Figure 2B. Correspondingly, the angular distribution of the THz radiation in the frequency domain after FFT is shown in Figure 3B. On the one hand, one can observe that the radiated THz wave’s intensity is stronger at frequencies below 10 THz. On the other hand, as the frequency increases, the THz wave exhibits better collimation, becoming closer to the laser incident direction.

FIGURE 2

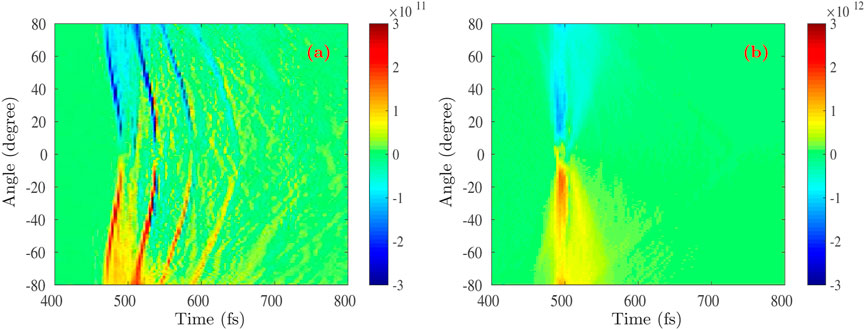
FIGURE 2. The collected electromagnetic field by a semi-circle over time for both of the flat target (A) and TTT (B).

FIGURE 3

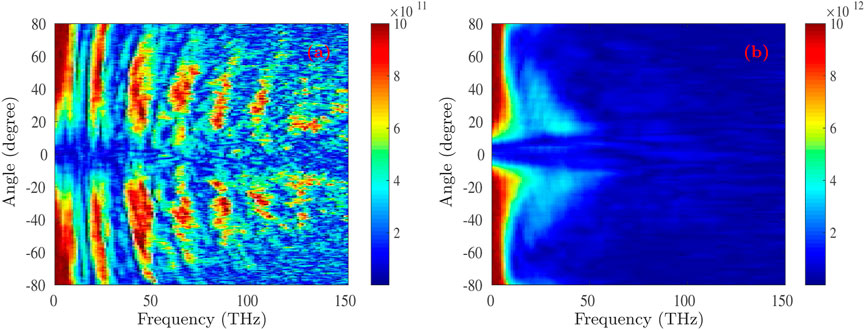
FIGURE 3. The angular-spectra distribution of the THz radiation for both of the flat target (A) and TTT (B).

To quantitatively illustrate the effect of TTT on the angular distribution and intensity of the THz radiation, we plot their intensity (accumulated and summed along the frequency axis in Figure 3) as a function of angle for both of the flat target and TTT, as shown in Figure 4. First, one can note that the intensity of the THz radiation can be significantly enhanced in the case of TTT at frequencies less than 150 THz, compared to that in the case of flat target. In addition, in terms of angular distribution modulation, the THz source points at about −36.7° and 40.6° in the case of flat target, respectively. However in the case of TTT, it is able to collimate the THz source significantly, which points at about −13.6° and 17.5°.

FIGURE 4

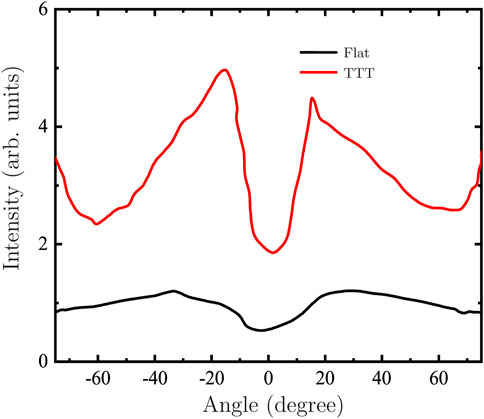
FIGURE 4. The angular-spectra distribution (accumulated and summed along the frequency axis in Figure 3) of THz radiation for both of the flat target and TTT.

When a single electron passes through the target-vacuum interface, the radiation energy spectrum distribution into the solid angle dΩ generated by the transit radiation mechanism can be expressed as [30, 38]

$\frac{d^2\epsilon }{d\omega d\mathrm{\Omega }}=\frac{e^2}{{\pi }^{2}c}\mid S\left(\beta ,\phi ,\varphi \right){\mid }^2,(1)$

where c is the light velocity in vacuum, β is the electron’s velocity normalized by c, φ is the injection direction of the electron, ϕ is the observation direction, and the S is expressed as

$S\left(\beta ,\phi ,\varphi \right)=\frac{\beta \cos \phi \left(\sin \varphi -\beta \sin \phi \right)}{{\left(1-\beta \sin \varphi \sin \phi \right)}^2-{\left(\beta \cos \varphi \cos \phi \right)}^2}.(2)$

From Eq. (1), one can get that the spatial angular distribution of the THz radiation is related to two factors for electrons: 1) The closer the injected electron beam’s direction φ is to the direction of the normal to the target, the better the collimation of the THz radiation. 2) The higher the electron beam’s velocity β, the better the collimation of the THz radiation. Since the THz radiation is generated by the CTR mechanism in this work, in order to clarify the reason why the TTT can collimate and enhance the THz radiation, we also plot the angular distribution of the electrons passing through the interface behind the target at time t = 110T₀, as shown in Figure 5. On the one hand, one can observe that the electrons coming from the Taeget-I are well collimated in the case of TTT with a divergence angle of only about 7.8° at the Full Width Half Maximum (FWHM), as shown in Figure 5A. This is mainly attributed to that the electrons pulled by the laser in the Target-I move forward along the surface of the target under the combined action of the electric field force and the magnetic field force, thereby obtaining good collimation [31, 37]. Yet in the case of flat target, the divergence angle of electrons passing through the target is significantly larger than that in the case of TTT. Meanwhile, it should be noted that the number of electrons behind the target is higher in the case of flat target than that in the case of TTT. We all know that the intensity of the radiated THz wave is positively related to both the number and energy of electrons, but the energy of electrons is more dominant [39]. Therefore, we also show that the electron energy spectral distribution after passing the target in both of cases at time t = 110T₀, as shown in Figure 5B. The maximum cut-off energy of electrons in the flat target is only less than 3 MeV, and the vast majority of electrons are in the energy range with energies less than 1 MeV. In contrast, thanks to the efficient energy conversion between the laser and Target-I, the maximum cut-off energy of electrons in the TTT can reach 60 MeV, which is 20 times higher than that in the flat target. Such high-energy electrons can not only enhance the intensity of the THz radiation field, but also effectively reduce its pointing angle, as shown in Figure 3B. Therefore, in the TTT scheme, the generated high-energy and well-collimated electrons result in high-intensity and well-collimated THz radiation.

FIGURE 5

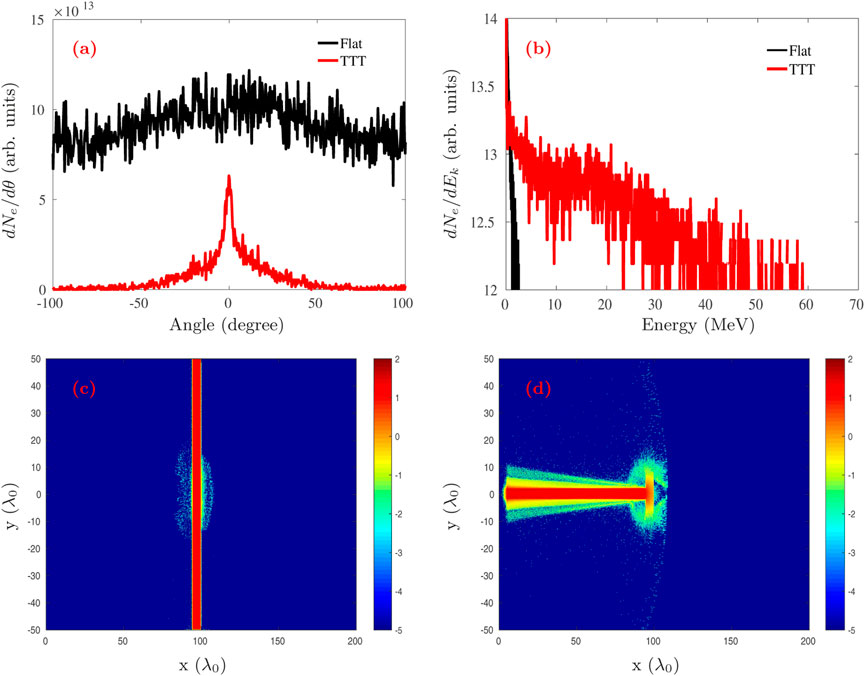
FIGURE 5. The angular distribution (A), energy spectrum distribution (B) and the spatial distributions (C), (D) of the electrons passing through the interface behind the target at time t = 110T₀ for both of the flat target and TTT.

3 Effects of laser and target parameters on collimating THz radiation

3.1 The laser’s pointing stability

The pointing stability of the laser plays a very important role in the actual experiments, which is because it may cause the misalignment between the focal spot center of the laser and the center of the target. Currently, it is achievable that the pointing deviation of the laser is less than 0.8r₀ [40–42]. Therefore, the effect of laser pointing deviation at y = ±4.8λ₀ off the x-axis on collimated THz radiation is demonstrated by the PIC simulations, as shown in Figures 6, 7. Compared with the result of Figure 3B without the incident deviation, we are surprised to find that the THz radiation is enhanced when the incidence is deviated, as shown in Figure 6. This indicates that proper laser incidence deviation can enhance the conversion efficiency between the laser and THz radiation. At the same time, it can also be observed from Figure 6 that the laser pointing stability affects the collimation of the THz radiation. Therefore, we also plot the THz radiations’ intensity as a function of angle, as shown in Figure 7. First, one can find that the distribution of the THz radiation exhibits more asymmetry on the left and right sides bounded by 0°, which is mainly caused by the asymmetry of the electrons after passing through the target. Besides, the better collimation of the THz radiation on the higher intensity side is accompanied by a pointing angle of about ±6.0°, probably due to the higher energy and smaller divergence angle of the electrons. With the above results, it is demonstrated that proper laser pointing deviation can enhance the THz radiation and better collimate its pointing direction.

FIGURE 6

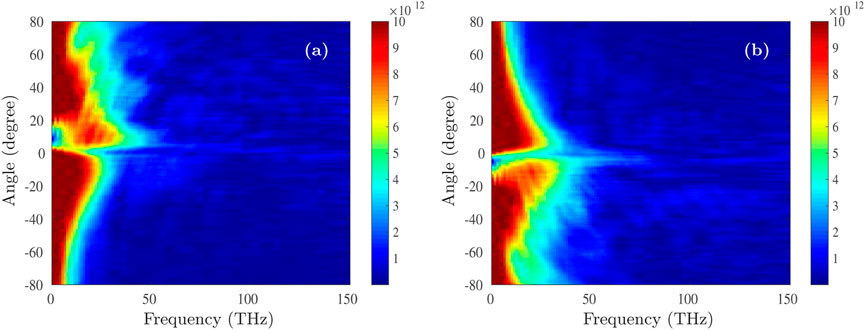
FIGURE 6. The angular-spectra distribution of the THz radiation for the y = 4.8λ₀ (A) and y = −4.8λ₀ (B).

FIGURE 7

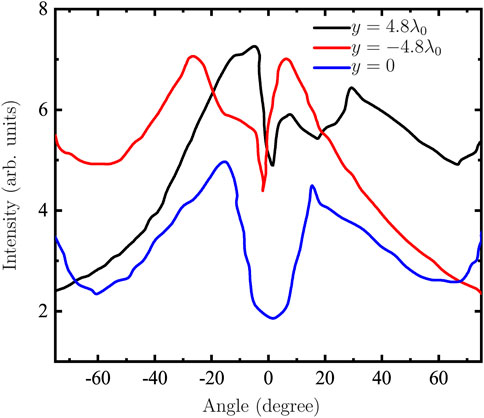
FIGURE 7. The cumulatively summed angular-spectra distribution of THz radiation for the y = 4.8λ₀, y = −4.8λ₀ and y = 0.

3.2 The length and thickness of the target

In this work, the enhancement of electron energy and the control of their divergence angle due to the interaction between laser and Target-I are the key factors to enhance THz radiation and reduce its pointing angle. So we also scan the thickness and length parameters of Target-I to verify the effect on THz radiation collimation through a series of PIC simulations. Figure 8 presents the effect of Target-I on the pointing angle of THz radiation at different thicknesses of d₀ = 2.0λ₀, d₀ = 1.0λ₀ and d₀ = 0.4λ₀ with the length of L₀ = 90λ₀ and no change in the laser parameters. We find that the THz radiation can be effectively enhanced and collimated when the thickness is changed, and the resulting pointing angles are -12.1° and 16.9° with d₀ = 2.0λ₀, −14.0° and 18.1° with d₀ = 1.0λ₀, and -9.2° and 16.9° with d₀ = 0.4λ₀. At the same time, it should be pointed out that no matter how the thickness changes (including d₀ = 4.0λ₀), the THz radiation intensity distributed on both sides of 0° shows asymmetry. This may be mainly due to the asymmetry of the electron distribution behind the target, resulting in an incompletely symmetric distribution. In addition, we also simulated the case that the laser focal spot radius (3.0λ₀) is less than the thickness of Target-I (4.0λ₀), and the results show that the THz radiation intensity will decrease. This is mainly because the laser cannot interact with Target-I sufficiently.

FIGURE 8

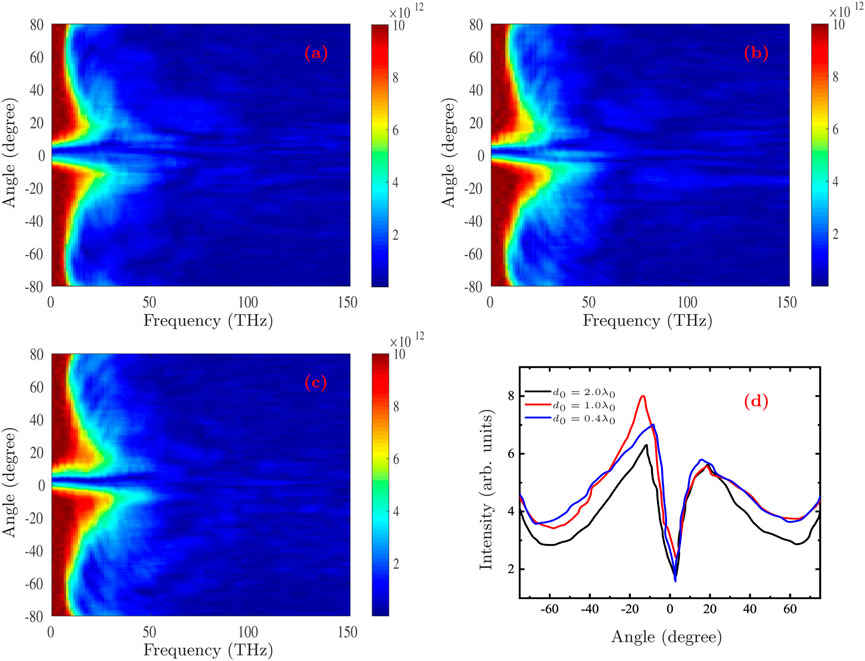
FIGURE 8. The angular-spectra distribution of the THz radiation for different thickness of the Target-I with d₀ = 2.0λ₀ (A), d₀ = 1.0λ₀ (B), and d₀ = 0.4λ₀ (C). (D) The corresponding cumulatively summed angular-spectra distribution of THz radiation.

Besides, also without changing the laser parameters, the effect of the length of Target-I on the pointing angle of the THz radiation is shown in Figure 9. One can notice that the effect of length is more sensitive than that of the thickness. When the length of Target-I is short, neither the intensity of THz radiation nor the pointing angle are significantly improved. However, as the Target-I length increases, both the intensity and the pointing angle of the THz radiation get better and then tend to saturate. This is mainly due to the fact that with the increase of length, the maximum cut-off energy of electrons generated by the interaction between the laser and Target-I will increase. Consequently, the resulting pointing angles are -35.6° and 37.3° with L₀ = 10λ₀, −22.9° and 27.6° with L₀ = 40λ₀, and −13.8° and 22.9° with L₀ = 70λ₀.

FIGURE 9

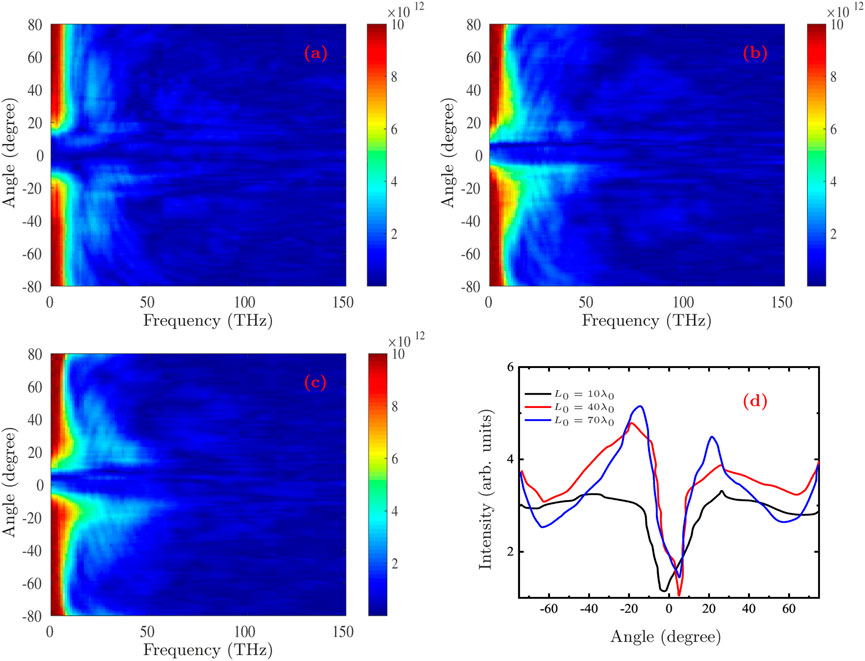
FIGURE 9. The angular-spectra distribution of the THz radiation for different length of the Target-I with L₀ = 10λ₀ (A), L₀ = 40λ₀ (B), and L₀ = 70λ₀ (C) when d₀ = 4.0λ₀. (D) The corresponding cumulatively summed angular-spectra distribution of THz radiation.

4 Summary

In summary, a novel scheme has been proposed for enhancement and collimation of THz radiation, which is that an ultra-intense laser irradiates on a T-type target. The processes and causes of enhancement and collimation are studied in detail through a series of PIC numerical simulations. The results show that a T-type target can effectively reduce THz radiation’s pointing angle while enhancing its intensity, which points at about −13.6° and 17.5° when the longitudinal target’s length is 90λ₀ and the thickness is 4.0λ₀. The reason for the above results is that the generated high-energy and well-collimated electrons in the case of the T-type target lead to the high-intensity and well-collimated THz radiation. Besides, the effects of laser pointing stability and target parameters on collimating the THz radiation are also studied, respectively. One can find that a proper laser pointing deviation can also enhance the THz radiation and better collimate its direction with a pointing angle about ±6.0°. The proposed scheme and simulation results may provide important support for enhancing and collimating the THz radiation by the laser interacting with a solid target.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

CL and FW proposed this study and led the simulations, data analysis, and the interpretation of the results. CL, WS, XB, and ZW carried out the PIC simulations. CL wrote the text. CL and FW led the discussion. All listed authors contributed to discussion and helped to improve the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 12005305, 11905169, and the Continue Basic Scientific Research Project under Grant Nos. WDJC-2019-02, and BJ20002501, and Foundation of China Institute of Atomic Energy under Grant Nos. YZ222402000401, and YC212212000301.

Acknowledgments

The PIC simulations were performed on the Beijing Super Cloud Computing Center (China). The authors are particularly grateful to CFSA at University of Warwick for allowing us to use the EPOCH. The EPOCH code was used under UK EPSRC contract (EP/G055165/1 and EP/G056803/1).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dai J, Liu J, Zhang XC. Terahertz wave air photonics: Terahertz wave generation and detection with laser-induced gas plasma. IEEE J Select Top Quan Electron (2010) 17:183–90. doi:10.1109/jstqe.2010.2047007

CrossRef Full Text | Google Scholar

2. Hafez H, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, et al. Intense terahertz radiation and their applications. J Opt (2016) 18:093004. doi:10.1088/2040-8978/18/9/093004

CrossRef Full Text | Google Scholar

3. Liao GQ, Li YT. Review of intense terahertz radiation from relativistic laser-produced plasmas. IEEE Trans Plasma Sci (2019) 47:3002–8. doi:10.1109/tps.2019.2915624

CrossRef Full Text | Google Scholar

4. Sheng ZM, Mima K, Zhang J, Sanuki H. Emission of electromagnetic pulses from laser wakefields through linear mode conversion. Phys Rev Lett (2005) 94:095003. doi:10.1103/physrevlett.94.095003

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Jin Z, Zhuo H, Nakazawa T, Shin J, Wakamatsu S, Yugami N, et al. Highly efficient terahertz radiation from a thin foil irradiated by a high-contrast laser pulse. Phys Rev E (2016) 94:033206. doi:10.1103/physreve.94.033206

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Cook D, Hochstrasser R. Intense terahertz pulses by four-wave rectification in air. Opt Lett (2000) 25:1210–2. doi:10.1364/ol.25.001210

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kim KY, Taylor A, Glownia J, Rodriguez G. Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions. Nat Photon (2008) 2:605–9. doi:10.1038/nphoton.2008.153

CrossRef Full Text | Google Scholar

8. Yoo YJ, Jang D, Kim KY. Highly enhanced terahertz conversion by two-color laser filamentation at low gas pressures. Opt Express (2019) 27:22663–73. doi:10.1364/oe.27.022663

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nazarov a, Mitrofanov AV, Sidorov-Biryukov DA, Chashin MV, Shcheglov PA, Zheltikov AM, et al. Enhancement of thz generation by two-color tw laser pulses in a low-pressure gas. J Infrared Milli Terahz Waves (2020) 41:1069–81. doi:10.1007/s10762-020-00689-z

CrossRef Full Text | Google Scholar

10. Wang WM, Gibbon P, Sheng ZM, Li YT. Tunable circularly polarized terahertz radiation from magnetized gas plasma. Phys Rev Lett (2015) 114:253901. doi:10.1103/physrevlett.114.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Koulouklidis AD, Gollner C, Shumakova V, Fedorov VY, Pugžlys A, Baltuška A, et al. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nat Commun (2020) 11:292–8. doi:10.1038/s41467-019-14206-x

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Vvedenskii N, Korytin A, Kostin V, Murzanev A, Silaev A, Stepanov A. Two-color laser-plasma generation of terahertz radiation using a frequency-tunable half harmonic of a femtosecond pulse. Phys Rev Lett (2014) 112:055004. doi:10.1103/physrevlett.112.055004

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhang LL, Wang WM, Wu T, Zhang R, Zhang SJ, Zhang CL, et al. Observation of terahertz radiation via the two-color laser scheme with uncommon frequency ratios. Phys Rev Lett (2017) 119:235001. doi:10.1103/physrevlett.119.235001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ma D, Dong L, Zhang M, Wu T, Zhao Y, Zhang L, et al. Enhancement of terahertz waves from two-color laser-field induced air plasma excited using a third-color femtosecond laser. Opt Express (2020) 28:20598. doi:10.1364/oe.395130

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Balogh E, Kovacs K, Dombi P, Fulop JA, Farkas G, Hebling J, et al. Single attosecond pulse from terahertz-assisted high-order harmonic generation. Phys Rev A (2011) 84:023806. doi:10.1103/physreva.84.023806

CrossRef Full Text | Google Scholar

16. Zhang D, Fallahi A, Hemmer M, Wu X, Fakhari M, Hua Y, et al. Segmented terahertz electron accelerator and manipulator (steam). Nat Photon (2018) 12:336–42. doi:10.1038/s41566-018-0138-z

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hamster H, Sullivan A, Gordon S, White W, Falcone R. Subpicosecond, electromagnetic pulses from intense laser-plasma interaction. Phys Rev Lett (1993) 71:2725–8. doi:10.1103/physrevlett.71.2725

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hamster H, Sullivan A, Gordon S, Falcone R. Short-pulse terahertz radiation from high-intensity-laser-produced plasmas. Phys Rev E (1994) 49:671–7. doi:10.1103/physreve.49.671

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ding W, Sheng Z, Koh W. High-field half-cycle terahertz radiation from relativistic laser interaction with thin solid targets. Appl Phys Lett (2013) 103:204107. doi:10.1063/1.4831684

CrossRef Full Text | Google Scholar

20. Gopal A, Singh P, Herzer S, Reinhard A, Schmidt A, Dillner U, et al. Characterization of 700 μj t rays generated during high-power laser solid interaction. Opt Lett (2013) 38:4705–7. doi:10.1364/ol.38.004705

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ginzburg V, Frank I. Radiation of a uniformly moving electron due to its transition from one medium into another. J Phys (Ussr) (1945) 9:353.

Google Scholar

22. Ginsburg V. Radiation of a uniformly moving electron due to its transition from one medium into another. Sov Phys (1946) 16:15.

Google Scholar

23. Liao G, Li Y, Liu H, Scott GG, Neely D, Zhang Y, et al. Multimillijoule coherent terahertz bursts from picosecond laser-irradiated metal foils. Proc Natl Acad Sci U S A (2019) 116:3994–9. doi:10.1073/pnas.1815256116

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mondal S, Wei Q, Ding W, Hafez HA, Fareed M, Laramée A, et al. Aligned copper nanorod arrays for highly efficient generation of intense ultra-broadband thz pulses. Sci Rep (2017) 7:40058–8. doi:10.1038/srep40058

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yi L, Fülöp T. Coherent diffraction radiation of relativistic terahertz pulses from a laser-driven microplasma waveguide. Phys Rev Lett (2019) 123:094801. doi:10.1103/physrevlett.123.094801

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Potylitsyn AP, Ryazanov MI, Strikhanov MN, Tishchenko AA. Radiation from relativistic particles. In: Diffraction radiation from relativistic particles. Springer (2010). p. 1

CrossRef Full Text | Google Scholar

27. Tian Y, Liu J, Bai Y, Zhou S, Sun H, Liu W, et al. Femtosecond-laser-driven wire-guided helical undulator for intense terahertz radiation. Nat Photon (2017) 11:242–6. doi:10.1038/nphoton.2017.16

CrossRef Full Text | Google Scholar

28. Zhuo H, Zhang S, Li X, Zhou H, Li X, Zou D, et al. Terahertz generation from laser-driven ultrafast current propagation along a wire target. Phys Rev E (2017) 95:013201. doi:10.1103/physreve.95.013201

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liao GQ, Liu H, Scott GG, Zhang YH, Zhu BJ, Zhang Z, et al. Towards terawatt-scale spectrally tunable terahertz pulses via relativistic laser-foil interactions. Phys Rev X (2020) 10:031062. doi:10.1103/physrevx.10.031062

CrossRef Full Text | Google Scholar

30. Ding W, Sheng Z, et al. Sub gv/cm terahertz radiation from relativistic laser-solid interactions via coherent transition radiation. Phys Rev E (2016) 93:063204. doi:10.1103/physreve.93.063204

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Cai J, Shou Y, Han L, Huang R, Wang Y, Song Z, et al. High efficiency and collimated terahertz pulse from ultra-short intense laser and cone target. Opt Lett (2022) 47:1658–61. doi:10.1364/ol.454811

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhang J, Ban X, Wan F, Lv C. Terahertz emission enhanced by a laser irradiating on a t-type target. Appl Sci (2022) 12:4464. doi:10.3390/app12094464

CrossRef Full Text | Google Scholar

33. Arber T, Bennett K, Brady C, Lawrence-Douglas A, Ramsay M, Sircombe N, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Control (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

34. Ammosov MV, Delone NB, Krainov VP. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Soviet J Exp Theor Phys (1986) 64:1191.

Google Scholar

35. Shen X, Qiao B, Zhang H, Xie Y, Kar S, Borghesi M, et al. Electrostatic capacitance-type acceleration of ions with an intense few-cycle laser pulse. Appl Phys Lett (2019) 114:144102. doi:10.1063/1.5088340

CrossRef Full Text | Google Scholar

36. Zhang S, Yu J, Shou Y, Gong Z, Li D, Geng Y, et al. Terahertz radiation enhanced by target ablation during the interaction of high intensity laser pulse and micron-thickness metal foil. Phys Plasmas (2020) 27:023101. doi:10.1063/1.5125611

CrossRef Full Text | Google Scholar

37. Li Y, Yuan X, Xu M, Zheng Z, Sheng Z, Chen M, et al. Observation of a fast electron beam emitted along the surface of a target irradiated by intense femtosecond laser pulses. Phys Rev Lett (2006) 96:165003. doi:10.1103/physrevlett.96.165003

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zheng J, Tanaka K, Miyakoshi T, Kitagawa Y, Kodama R, Kurahashi T, et al. Theoretical study of transition radiation from hot electrons generated in the laser–solid interaction. Phys Plasmas (2003) 10:2994–3003. doi:10.1063/1.1576388

CrossRef Full Text | Google Scholar

39. Herzer S, Woldegeorgis A, Polz J, Reinhard A, Almassarani M, Beleites B, et al. An investigation on thz yield from laser-produced solid density plasmas at relativistic laser intensities. New J Phys (2018) 20:063019. doi:10.1088/1367-2630/aaada0

CrossRef Full Text | Google Scholar

40. Shen X, Pukhov A, Qiao B. Monoenergetic high-energy ion source via femtosecond laser interacting with a microtape. Phys Rev X (2021) 11:041002. doi:10.1103/physrevx.11.041002

CrossRef Full Text | Google Scholar

41. Hilz P, Ostermayr T, Huebl A, Bagnoud V, Borm B, Bussmann M, et al. Isolated proton bunch acceleration by a petawatt laser pulse. Nat Commun (2018) 9:423–9. doi:10.1038/s41467-017-02663-1

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Danson CN, Haefner C, Bromage J, Butcher T, Chanteloup JCF, Chowdhury EA, et al. Petawatt and exawatt class lasers worldwide. High Pow Laser Sci Eng (2019) 7:e54. doi:10.1017/hpl.2019.36

CrossRef Full Text | Google Scholar