Abstract
Ethylene glycol with nanoparticles behaves as a non-Newtonian fluid and its rheology can be best predicted by the power-law rheological approach. Further nanoparticles (molybdenum disulfide and silicon dioxide) are responsible for anti-oxidation, anti-evaporation, and anti-aging. Therefore, their dispersion in ethylene glycol is considered as these properties make the nanofluid stable. This article examines the impact of molybdenum disulfide and silicon dioxide on the thermal enhancement of ethylene glycol as it is a worldwide used coolant. Moreover, simultaneous effects of temperature and concentration gradients, Joule heating, viscous dissipation, thermal radiations, and buoyancy forces are modeled and developed, and investigations are computed by the finite element method. An increase in temperature due to the composition gradient and an increase in concentration due to the temperature gradient are observed. A significant increase in the Ohmic phenomenon with an increase in the intensity of the magnetic field is observed. Numerical experiments are performed by considering single-type nanoparticles () and hybrid-type nanoparticles (simultaneous dispersion of andis considered). During the visualization of simulations, the effective thermal conductivity of --ethylene glycol is observed.
Introduction
Nanofluids can be created by dispersing colloidally dispersed single nanoparticles in a new base fluid. This fluid is suitable for various applications, including microelectronics, pharmaceuticals, thermal management, and temperature control. Finally, the base liquid contained nanoparticles of two different types, i.e., hybrid nanofluid. When nanofluids made of alumina are heated or cooled, their dynamic viscosity changes according to their composition. According to researchers, this is because of the shape of the nanoparticles. Nanoparticles and their base fluids are thought to have different surface charges, affecting how they interact with their base fluids. Nanoparticles [] have different surface charges, making them interact with each other in different ways, which makes them unique. Sahu and Sarkar [] wrote that the shape of nanoparticles affects how active and energetic nanoparticles are. Jiang et al. [] demonstrated the movement of nanofluids in an aqueous solution via convection caused by heat and water using a thermo-capillary convection chamber (spherical, cylinder, brick, and platelet). Spherical and platelet nanoparticles are the two nanoparticles with the most significant thermo-capillary convection. However, convection is not as strong as in a nanofluid containing platelet-shaped nanoparticles. The number of nanoparticles on the Nusselt blade has also gone up. It worked better for the people who used blade-shaped nanoparticles than those who used round nanoparticles. Nanoparticle shapes have been talked about by Arno et al. [] concerning this subject. This was the first time three different nanoparticles were mixed in a single primary fluid. Many studies have come up with good results and helpful information. Thermal analysis shows that high thermal diffusivity in supercritical solar power plants can be advantageous because of the plants’ high stability and the slight temperature fluctuations in their thermal diffusivity []. Mousavi et al. [] observed the movements of copper oxide, magnesium oxide, and titanium oxide in a laboratory. Because nanoparticle concentrations increased in all the nanofluids studied in this study, their viscosity increased. The viscosity of a liquid decreases as the temperature rises.
On the other hand, when it comes to the dynamics of ternary hybrid nanofluids, they behave just like Newtonian fluids. They did what they said they would and when they said they would. When the temperature rises, the density of ternary hybrid nanofluids gets less dense. Between 35 and 50°C, nanoparticles can be added to the base fluid to make it more heat-resistant to handle more heat. Sahoo and Kumar [] studied these nanoparticles in water to figure out how they work together and work with each other. They can move in three different ways at the same time. Dynamic viscosity can be used to determine how much volume a trinary hybrid nanofluid has. This then helps figure out its volume fraction. They have been talked about by Abbasi et al. [], Sahoo [], and other researchers. For a long time, fluids were moved by suction/injection and rotation, but this has been changed to stretching at the wall. As long as suction and stretching are used together, things can be moved in any direction. When there are low suction rates, the Reynolds number rises, which causes turbulence to form quickly. Gregory and Walker [] found this out. The findings of other scientists back up this claim. In terms of suction, there are two main ways to use it: to bring energy into the system and take it out. Another way to use it is to get energy. Suction can make blood pressure differences between arterial and venous vessels more significant []. Suction can be used to control shock and boundary layer separation and interaction, as shown by Krogmann et al. [], Animasaun [], and Zaydan []. A small medium can also be used to see how thermo-magneto-convection dynamics change. In addition, the work of Hashem Zadeh et al. and Alsabery et al. should also be talked about in these processes, and also Ghalambaz, Hashem Zadeh, and Alsabaery, you’ll also find the articles [, , , , and ] in this direction.
Reiner-model swirling water is used in the same way as Sahoo et al. [] studied the effects of suction and injection. This study found that injecting can exacerbate oscillation while changing the speed of transportation and using suction could lessen it. While the suction may not be strong enough to harm the brain, Rehman et al. [] claimed that the brain can still be damaged. The suction flux stays the same, but the suction speed changes depending on the situation. Several important contributions covering the transport of momentum and energy are covered in [,]. Moreover, studies regarding Hall impacts are mentioned in [,,,,]. Krishna et al. [] studied impacts based on ion slip and Hall in rotating flow considered magnetic field for unsteady flow in a porous surface. Krishna et al. [] investigated thermal features involving ion slip and Hall impacts in a vertical plate containing nanofluid considering the magnetic field. Bhandari and Tripathi [] discussed the mechanism of entropy generation and heat transfer in a microtube involving a membrane-based system. Akram et al. [] performed the phenomena of electro-osmotically modulated including peristaltic propulsion in the occurrence of nanoparticles in a curved channel. Bhandari et al. [] discussed the consequences of Newtonian fluid and thermal energy characteristics in a microchannel in the presence of buoyancy forces and pressure gradient. Studies related to thermal enhancement due to nanofluid are mentioned in [,,,,].
Formulation of the developed model
The assumptions are listed as follows.
➢ Steady and 2D flow are addressed;
➢ The rheology of the power law model is assumed;
➢ Hybrid nanoparticles are added;
➢ Aspects of the chemical reaction and heat source are accumulated;
➢ A vertical surface is taken out;
➢ Soret and Dufour impacts are implemented;
➢ Thermal radiation and Joule heating are included;
➢ Thermal properties for hybrid nanoparticles are shown in Table 1 while geometry is shown in Figure 1.
TABLE 1
| and | and | and | and |
Thermo-physical properties [] for and
FIGURE 1
The set of non-linear PDEs [, and ] in view of the 2D flow of heat and mass transfer is
Boundary conditions are based on the no-slip theory which states that the velocity of the fluid at the solid boundary is equal to the velocity of the solid boundary. Similarly, the temperature of fluid and concentration at the wall are equal to the temperature of the solid wall and the amount concentration of species at the solid wall, respectively. Hence, one gets the following boundary conditions [].
The following variables [] are used to convert governing equations into a dimensionless form:
ODEs in term of the dimensionless form [ and ] are
The following correlations [, and ] are used in numerical simulations:
The dimensionless parameters are listed as follows:
The skin friction coefficient [] is
The Nusselt number [] is expressed by
The Sherwood number [] is given as
Numerical procedure
The model problem along with boundary conditions is simulated by an efficient technique called the finite element method []. Numerous computational fluid dynamics problems are solved by the FEM. Basically, six steps of the FEM are discussed here and these steps are given in Figure 2.
FIGURE 2
Step IThe subdomains are obtained by dividing the problem domain into elements. The discretization of the elements gives an approximation solution over each element rather than over the whole domain and the approximation solution is considered as a linear polynomial. Weighted residuals are derived as
Step IIThe shape functions are the orthogonal nodal basis which possesses the property Kronecker delta. The approximation solution is obtained from the product of shape functions. The linear shape functions are used here.
Step IVassembly approach is implemented to obtain stiffness elements. Stiffness elements are
Step Vglobal stiffness matrix is obtained with the help of the assembly process.
Step VIFinally, algebraic equations are achieved using the Picard linearization method. The code is designed in MAPLE 18 and mesh free analysis is shown in Table 2. Validation of the current problem is shown in Table 2.
TABLE 2
| No. of elements | |||
|---|---|---|---|
| 30 | 0.02333985815 | 0.01983564166 | 0.01410914312 |
| 60 | 0.02102177491 | 0.01044906650 | 0.005291086151 |
| 90 | 0.1968636970 | 0.007226612780 | 0.002785750834 |
| 120 | 0.01834540620 | 0.005576056715 | 0.001700976130 |
| 150 | 0.01362936407 | 0.004579205769 | 0.001150379024 |
| 180 | 0.02562519759 | 0.003923974634 | 0.0008468378539 |
| 210 | 0.02205069404 | 0.003478348492 | 0.0006778816543 |
| 240 | 0.02118788022 | 0.003186664686 | 0.0006039711856 |
| 270 | 0.02045243579 | 0.003050970629 | 0.0006678049734 |
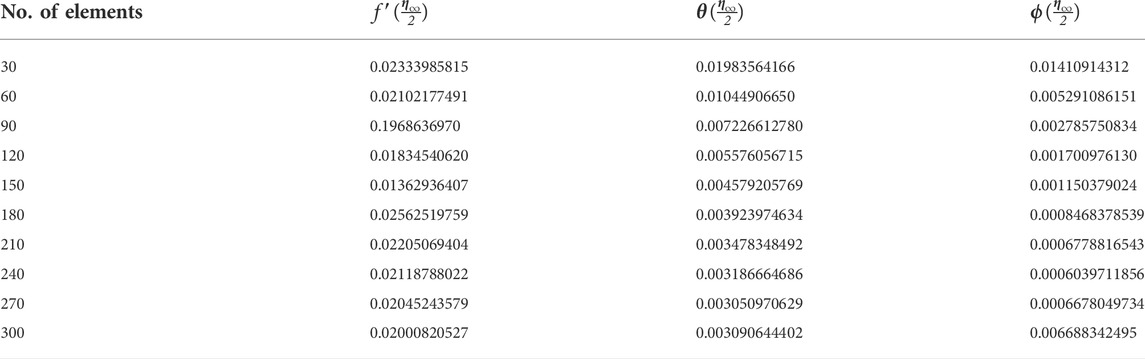
| 300 | 0.02000820527 | 0.003090644402 | 0.006688342495 |
Mesh-free study for concentration, velocity, and temperature fields predicted by 300 elements.
Mesh-free investigations
Maple 18 is utilized to design the programming of the finite element method. [0, 8] is assumed as the computational domain. Convergence analysis is shown in Table 2. The output numerical values of the velocity and temperature profiles are recorded against increasing elements via 300. It is estimated that the solution is converged at the mid of 300 elements. Table 2 shows the convergence analysis and mesh-free analysis for the velocity profile and temperature profile. It is investigated that grid sizes became independent via 300 elements.
Results and discussion
Theoretical assessment of the transfer of heat and mass in power-law fluid suspended with hybrid nanoparticles is carried out. The numerical tests are performed and results are noted. These outcomes are depicted as follows. Both --ethylene glycol and -ethylene glycol are electrically conducting fluids. In the present investigation, it is considered to visualize the influence of on the motion of fluid particles because the impact of the magnetic field directly impacts the velocity of fluid particles, and hence, has direct consequences on the tangential stresses. Therefore, graphical assessments related to the impact of the Hartmann number on the flow of nano and hybrid nanofluids are carried out. The related consequences are noted during numerical simulations. These simulations depict that the flow of both mono and hybrid nanofluids decelerates due to the increase in the intensity of the variable magnetic field. It is also referred that the influence of the magnetic field on the flow of mono nanofluid is higher than that on the flow of hybrid nanofluid. Thus, magnetic-fluid interaction in mono nanofluid is stronger than that in hybrid nanofluid. The comparison among the velocity profiles of -ethylene glycol and --ethylene glycol clearly depicts that -ethylene glycol experiences less drag due to Lorentz force than the drag experienced by --ethylene glycol. The viscous region for -ethylene glycol is wider than the viscous region for --ethylene glycol. The influence of buoyancy forces arise due to temperature and concentration differences (under Boussinesq approximation). The terms and in the momentum equations called buoyancy forces (see the dimensionless momentum equation) are and and here these are called mixed convection parameters. The values of mixed convection parameters and have negative values and the flow is under negative gravitational force. Alternatively, and are positive when the flow is in a vertical downward direction (such a flow is called an assisting flow) whereas and have negative values when the flow is in a vertically upward direction. Such flow is called opposing flow. Figures 3, 4 show the behavior of mixed convection parameters ( and ) on the velocity profiles of -ethylene glycol. Figures 3, 4 show the impact of buoyancy forces arising due to compositional and temperature gradients on the flow of the fluid. These figures show that for positive buoyancy forces, the flow is assisted and fluid particles are accelerated. However, an opposing flow is noticed in the case of negative values of mixed convection parameters and. Figures 5–7 show the transfer of heat in both mono and hybrid nanomaterials. The role of heat generation on temperature is graphically noted in Figure 6. It is shown that temperature increases due to enhancement in the values of . The simulations related to the variation of heat generation parameters are visualized and it is observed that heat generation effects on --ethylene glycol are stronger than those in ethylene glycol. Therefore, this is not encouraging behavior of --ethylene glycol as it affects thermal performance directly. This is a drawback of --ethylene glycol if it is used as a coolant. An increase in heat energy is found when heat generation is enhanced. This can be noted in Figure 8 It also studied that the temperature gradient effects on hybrid nanofluid (--ethylene glycol) are more significant those in ethylene glycol. The visualization of the chemical reaction number is shown in Figure 9. It has a tendency to decrease the concentration field while the chemical reaction (destructive) in the transport of mass specie is declined. Table 3 prepared to cover the comparitive investigation of performed research. Table 4 shows the numerical behavior flow rate, mass diffusion rate, and thermal rate.
FIGURE 3
FIGURE 4
FIGURE 5
FIGURE 6
FIGURE 7
FIGURE 8
FIGURE 9
TABLE 3
| M | n | Chen [] | Andersson et al[] | Present work |
|---|---|---|---|---|
| 0.0 | 0.4 | 1.27294 | 1.273 | 1.27291 |
| 0.5 | 0.4 | 1.81095 | 1.811 | 1.81230 |
| 1.0 | 0.4 | 2.28377 | 2.284 | 2.28291 |
| 1.5 | 0.4 | 2.71859 | 2.719 | 2.71970 |
| 2.0 | 0.4 | 3.12650 | 3.127 | 3.12692 |
| 0.0 | 0.8 | 1.02919 | 1.029 | 1.02899 |
| 0.5 | 0.8 | 1.30790 | 1.309 | 1.30899 |
Validation of the present work compared with published works in terms of considering
TABLE 4
| Nanofluid | Hybrid nanofluid | ||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.6143201 | 1.4313210 | 0.18132103 | 2.61234324 | 3.601143081 | 2.32100166 | |
| 0.3 | 0.6312020 | 1.4102103 | 0.17213132 | 2.41921431 | 3.410130384 | 2.23513013 | |
| 0.7 | 0.6503211 | 1.3810321 | 0.16096088 | 2.30288134 | 3.309141141 | 2.10112318 | |
| 0.0 | 0.7131062 | 1.40133072 | 1.72101032 | 2.72380340 | 2.871027101 | 2.51301075 | |
| 0.5 | 0.7131041 | 1.31330366 | 1.84313021 | 2.80321738 | 2.871026392 | 2.41434277 | |
| 0.7 | 0.7131032 | 1.30120128 | 1.62113830 | 2.51031738 | 2.871024313 | 3.33633311 | |
| -1.5 | 0.7321307 | 1.43192132 | 0.41381232 | 2.53084303 | 2.710528148 | 3.30202831 | |
| 0.0 | 0.6321332 | 1.30321703 | 0.71212103 | 2.41010324 | 2.619222028 | 3.53432738 | |
| 1.3 | 0.5310476 | 1.20133570 | 0.83601205 | 2.31080325 | 2.437842230 | 3.71305301 | |
| 0.0 | 0.3261313 | 1.60214321 | 1.41432029 | 2.63218308 | 2.301582235 | 3.52310255 | |
| 0.3 | 0.3317219 | 1.83225323 | 1.63073590 | 2.83207133 | 2.731351055 | 3.72293301 | |
| 0.7 | 0.3730205 | 1.90133208 | 1.81380493 | 2.90113208 | 2.820323283 | 3.92303135 | |
| 0.0 | 0.7320972 | 1.41240320 | 2.71353132 | 2.32102820 | 2.503308303 | 3.52103425 | |
| 1.3 | 0.8310235 | 1.83213535 | 2.53280713 | 2.52127033 | 2.733214343 | 3.80352125 | |
| 1.5 | 0.9312303 | 1.63232706 | 2.32122054 | 2.83038323 | 2.802352150 | 3.90320323 | |
Numerical behavior of flow rate, Sherwood number, and Nusselt number against , and
Conclusion
Thermal enhancement and mass transport in ethylene glycol (non-Newtonian-power law fluid) in the presence of hybrid nanoparticles (
and
) are studied numerically via the finite element method. The simulations for the impact of viscous and Joule heating, buoyancy and Lorentz forces, heat generation, temperature gradients, and concentration difference are investigated through several parameters.
➢Due to the dispersion of nanoparticles and diffusion of solute in fluid (ethylene glycol), the compositional gradient becomes significant, and the aroused buoyancy force due to the compositional gradient has considerable magnitude. Thus, it leads to erroneous results if this force is not considered, especially for the flow’s vertical surface. Similar observations are also noted for density differences caused by the temperature gradient;
➢Significant effects of the temperature gradient on mass transport and concentration gradient on heat transfer are noticed from numerical experiments. Therefore, it is advised to consider such effects for the simultaneous transfer of heat and mass in fluid regimes. Without consideration of such effects, it may lead to results that will not match the results obtained on an experimental basis;
➢Numerical experiments are performed by considering single-type nanoparticles () and hybrid nanoparticles (simultaneous dispersion of and ). During the visualization of simulations, it is observed that the effective thermal conductivity of --ethylene glycol is greater than that of -ethylene glycol. Hence, it is observed that --ethylene glycol is a better coolant than -ethylene glycol.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
UN: conceptualization, investigation, software, validation, writing—review and editing. MS: data curation, writing—original draft, writing—review and editing, visualization, methodalogy. AS: formal analysis, funding acquisition, software. SM: methodology, project administration. AG: project administration, formal analysis. ET: visualization, supervision, funding acquisition. SH: visualization, supervision, funding acquisition.
Acknowledgments
Authors are grateful to the Deanship of Scientific Research, Islamic University of Madinah, Ministry of Education, KSA, for supporting this research work through the research project grant under Research Group Program/1/804.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
Velocity components
Fluidic dynamic viscosity
Electrical conductivity
Coefficients of concentrations
Thermal conductivity
Temperature and ambient fluidic temperature
Specific heat capacitance
Heat source number
Magnetic induction
Stretching rate along the x-axis
Reynolds number
Dimensionless velocity
Volume fractions
Magnetic number
Prandtl number
Eckert number
Dufour number
Schmidt number
Wall shear stress
Mass flux
Space coordinates
Power-law index number
Gravitational acceleration
Concentration and ambient concentration
Stefan–Boltzmann constant
Fluidic density
Mean absorption coefficient
Diffusion coefficient
Thermal diffusion
Chemical reaction
Wall velocity
Characteristic length
Stream function
Dimensionless temperature
Thermal radiation number
Buoyancy parameters
- Heat source number
- Magnetic number
Chemical reaction number
Soret number
Skin friction number
Nusselt number
Sherwood number
References
1.
TimofeevaE.V.RoutbortJ.L.SinghD.Particle shape effects on thermophysical properties of alumina nanofluids. lAppldPhycs (2009) 106(1):014304. 10.1063/1.3155999
2.
SahuM.SarkarJ.Steady-state energetic and exergetic performances of single-phase natural circulation loop with hybrid nanofluids. l Heat Transfer (2019) 141(8). 10.1115/1.4043819
3.
JiangY.ZhouX.WangY.. Effects of nanoparticle shapes on heat and mass transfer of nanofluid thermocapillary convection around a gas bubble. Microgravity Sci Technol (2020) 32(2):167–77. 10.1007/s12217-019-09757-z
4.
ArnoM.C.InamM.WeemsA.C.LiZ.BinchA.L.PlattC.I.et alExploiting the role of nanoparticle shape in enhancing hydrogel adhesive and mechanical properties. Nat Commun (2020) 11(1):1420–9. 10.1038/s41467-020-15206-y
5.
SangL.AiW.WuY.MaC.. Enhanced specific heat and thermal conductivity of ternary carbonate nanofluids with carbon nanotubes for solar power applications. Int JEnergy Res (2020) 44(1):334–43. 10.1002/er.4923
6.
MousaviS.M.EsmaeilzadehF.WangX.P.. Effects of temperature and particles volume concentration on the thermophysical properties and the rheological behavior of CuO/MgO/TiO2 aqueous ternary hybrid nanofluid. J Therm Anal Calorim (2019) 137(3):879–901. 10.1007/s10973-019-08006-0
7.
SahooR.R.KumarV.. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Inl Commus Heat Mass Transfer (2020) 111:104451. 10.1016/j.icheatmasstransfer.2019.104451
8.
AbbasiM.HeyhatM.M.RajabpourA.. Study of the effects of particle shape and base fluid type on density of nanofluids using ternary mixture formula: A molecular dynamics simulation. l Mor Liquids (2020) 305:112831. 10.1016/j.molliq.2020.112831
9.
SahooR.R.. Thermo-hydraulic characteristics of radiator with various shape nanoparticle-based ternary hybrid nanofluid. PowderTechnoly (2020) 370:19–28. 10.1016/j.powtec.2020.05.013
10.
GregoryN.WalkerW.S.. Experiments on the effect of suction on the flow due to a rotating disk. J Fluid Mech (1960) 9(2):225–34. 10.1017/s0022112060001067
11.
SmythC.N.. Effect of suction on blood-flow in ischæmic limbs. The Lancet (1969) 294(7622):657–9. 10.1016/s0140-6736(69)90373-0
12.
KrogmannP.StanewskyE.ThiedeP.. Effects of suction on shock/boundary-layer interaction and shock-induced separation. l aircraft (1985) 22(1):37–42. 10.2514/3.45077
13.
AnimasaunI.L.AdebileE.A.FagbadeA.I.. Casson fluid flow with variable thermo-physical property along exponentially stretching sheet with suction and exponentially decaying internal heat generation using the homotopy analysis method. l Nigen Matl Soy (2016) 35(1):1–17. 10.1016/j.jnnms.2015.02.001
14.
ZaydanM.WakifA.AnimasaunI.L.KhanU.BaleanuD.SehaquiR.. Significances of blowing and suction processes on the occurrence of thermo-magneto-convection phenomenon in a narrow nanofluidic medium: A revised buongiorno's nanofluid model. Case Stus Therl Eng (2020) 22:100726. 10.1016/j.csite.2020.100726
15.
WakifA.ChamkhaA.AnimasaunI.L.ZaydanM.WaqasH.SehaquiR.. Novel physical insights into the thermodynamic irreversibilities within dissipative EMHD fluid flows past over a moving horizontal riga plate in the coexistence of wall suction and joule heating effects: A comprehensive numerical investigation. Arab J Sci Eng (2020) 45(11):9423–38. 10.1007/s13369-020-04757-3
16.
GhalambazM.MehryanS.A.M.MashoofiN.HajjarA.ChamkhaA.J.SheremetM.et alFree convective melting-solidification heat transfer of nano-encapsulated phase change particles suspensions inside a coaxial pipe. Add PowderTechy (2020) 31(11):4470–81. 10.1016/j.apt.2020.09.022
17.
GhalambazM.MehryanS.A.M.ZahmatkeshI.ChamkhaA.. Free convection heat transfer analysis of a suspension of nano–encapsulated phase change materials (NEPCMs) in an inclined porous cavity. Inl l Therl Scs (2020) 157:106503. 10.1016/j.ijthermalsci.2020.106503
18.
ZadehS.M.H.MehryanS.A.M.SheremetM.GhodratM.GhalambazM.. Thermo-hydrodynamic and entropy generation analysis of a dilute aqueous suspension enhanced with nano-encapsulated phase change material. Inl l Mecl Scs (2020) 178:105609. 10.1016/j.ijmecsci.2020.105609
19.
AlsaberyA.I.HashimI.HajjarA.GhalambazM.NadeemS.Saffari PourM.. Entropy generation and natural convection flow of hybrid nanofluids in a partially divided wavy cavity including solid blocks. Energies (2020) 13(11):2942. 10.3390/en13112942
20.
SahooB.PoncetS.LabropuluF.. Suction/injection effects on the swirling flow of a Reiner-Rivlin fluid near a rough surface. l Fluids (2015) 2015:1–5. 10.1155/2015/253504
21.
RehmanS.IdreesM.ShahR.A.KhanZ.. Suction/injection effects on an unsteady MHD Casson thin film flow with slip and uniform thickness over a stretching sheet along variable flow properties. Bound Value Probl (2019) 2019(1):26–4. 10.1186/s13661-019-1133-0
22.
SohailM.NazirU.El-ZaharE.R.AlrabaiahH.KumamP.MousaA.A.A.et alA study of triple-mass diffusion species and energy transfer in Carreau–Yasuda material influenced by activation energy and heat source. Sci Rep (2022) 12(1):10219–7. 10.1038/s41598-022-13890-y
23.
ShahzadF.JamshedW.SafdarR.HussainS.M.NasirN.A.A.M.DhangeM.et alThermal analysis characterisation of solar-powered ship using Oldroyd hybrid nanofluids in parabolic trough solar collector: An optimal thermal application. Nanotechnology Res (2022) 11(1):2015–37. 10.1515/ntrev-2022-0108
24.
ShahZ.UllahA.BonyahE.AyazM.IslamS.KhanI.. Hall effect on Titania nanofluids thin film flow and radiative thermal behavior with different base fluids on an inclined rotating surface. AIP Ads (2019) 9(5):055113. 10.1063/1.5099435
25.
DamsehR.A.Al-OdatM.Q.ChamkhaA.J.ShannakB.A.. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Inl l Therl Scs (2009) 48(8):1658–63. 10.1016/j.ijthermalsci.2008.12.018
26.
ShaZ.DawarA.AlzahraniE.O.KumamP.KhanA.J.IslamS.. Hall effect on couple stress 3D nanofluid flow over an exponentially stretched surface with Cattaneo Christov heat flux model. IEEE Access (2019) 7:64844–55. 10.1109/access.2019.2916162
27.
LiP.AbbasiA.El-ZaharE.R.FarooqW.HussainZ.KhanS.U.et alHall effects and viscous dissipation applications in peristaltic transport of Jeffrey nanofluid due to wave frame. Colloid Intere Sce Commus (2022) 47:100593. 10.1016/j.colcom.2022.100593
28.
ChamkhaA.J.Ben-NakhiA.. MHD mixed convection–radiation interaction along a permeable surface immersed in a porous medium in the presence of Soret and Dufour’s effects. Heat Mass Transfer (2008) 44(7):845–56. 10.1007/s00231-007-0296-x
29.
KrishnaM.V.AhamadN.A.ChamkhaA.J.. Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alexandria Eng l (2020) 59(2):565–77. 10.1016/j.aej.2020.01.043
30.
KrishnaM.V.AhamadN.A.ChamkhaA.J.. Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alexandria Eng l (2021) 60(1):845–58. 10.1016/j.aej.2020.10.013
31.
BhandariD.S.TripathiD.. Study of entropy generation and heat flow through a microtube induced by the membrane-based thermofluidics systems. Therl Sce Eng Pros (2022) 34:101395. 10.1016/j.tsep.2022.101395
32.
AkramJ.AkbarN.S.AlansariM.TripathiD.. Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Inl Commus Heat Mass Transfer (2022) 136:106208. 10.1016/j.icheatmasstransfer.2022.106208
33.
BhandariD.S.TripathiD.PrakashJ.. Insight into Newtonian fluid flow and heat transfer in vertical microchannel subject to rhythmic membrane contraction due to pressure gradient and buoyancy forces. Inl l Heat Mass Transfer (2022) 184:122249. 10.1016/j.ijheatmasstransfer.2021.122249
34.
LiX.KhanA.U.KhanM.R.NadeemS.KhanS.U.. Oblique stagnation point flow of nanofluids over stretching/shrinking sheet with cattaneo–christov heat flux model: Existence of dual solution. Symmetry (2019) 11(9):1070. 10.3390/sym11091070
35.
RasoolG.ShafiqA.KhaliqueC.M.ZhangT.. Magnetohydrodynamic Darcy–Forchheimer nanofluid flow over a nonlinear stretching sheet. Phys Scr (2019) 94(10):105221. 10.1088/1402-4896/ab18c8
36.
AliB.RasoolG.HussainS.BaleanuD.BanoS.. Finite element study of magnetohydrodynamics (MHD) and activation energy in Darcy–Forchheimer rotating flow of Casson Carreau nanofluid. Processes (2020) 8(9):1185. 10.3390/pr8091185
37.
ChabaniI.Mebarek-OudinaF.IsmailA.A.I.. MHD flow of a hybrid nano-fluid in a triangular enclosure with zigzags and an elliptic obstacle. Micromachines (2022) 13(2):224. 10.3390/mi13020224
38.
ZaydanM.RiahiM.Mebarek-OudinaF.SehaquiR.. Mixed convection in a two-sided lid-driven square cavity filled with different types of nanoparticles: A comparative study assuming nanoparticles with different shapes. Fluid Dys Mates Procesg (2021) 17(4):789–819. 10.32604/fdmp.2021.015422
39.
ChenC.H.. Effects of magnetic field and suction/injection on convection heat transfer of non-Newtonian power-law fluids past a power-law stretched sheet with surface heat flux. Inl l Therl Scs (2008) 47(7):954–61. 10.1016/j.ijthermalsci.2007.06.003
40.
AnderssonH.I.BechK.H.DandapatB.S.. Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. Inl l Non-Linear Mecs (1992) 27(6):929–36. 10.1016/0020-7462(92)90045-9
41.
NawazM.NazirU.AlharbiS.O.AlaouiM.K.. Thermal and solutal analysis in power law fluid under non-Fourier's diffusion conditions. Inl Commus Heat Mass Transfer (2021) 126:105331. 10.1016/j.icheatmasstransfer.2021.105331
42.
NazirU.NawazM.AlharbiS.O.. Thermal performance of magnetohydrodynamic complex fluid using nano and hybrid nanoparticles. Physica A: Stal Mecs its Apps (2020) 553:124345. 10.1016/j.physa.2020.124345
Summary
Keywords
solute particles, thermal properties, heat source/sink, heat transfer, hybrid nanoparticle
Citation
Nazir U, Sohail M, Singh A, Muhsen S, Galal AM, Tag El Din ESM and Hussain SM (2022) Finite element analysis for thermal enhancement in power law hybrid nanofluid. Front. Phys. 10:996174. doi: 10.3389/fphy.2022.996174
Received
17 July 2022
Accepted
18 August 2022
Published
28 September 2022
Volume
10 - 2022
Edited by
Muhammad Mubashir Bhatti, Shandong University of Science and Technology, China
Reviewed by
Ali Chamkha, Kuwait College of Science and Technology, Kuwait
Dharmendra Tripathi, National Institute of Technology Uttarakhand, India
Updates
Copyright
© 2022 Nazir, Sohail, Singh, Muhsen, Galal, Tag El Din and Hussain.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Sohail, muhammad_sohail111@yahoo.com
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.