Lasers for the observation of multiple order nuclear reactions

Nuclear reaction rates become nonlinear with respect to flux (cm⁻²s⁻¹) in extreme environments such as those found during stellar nucleosynthesis and terrestrial nuclear detonations. To observe these effects directly in the laboratory, extremely high particle fluences (cm⁻²) are necessary but not sufficient. Reactor-based neutron sources, such as the Institut Laue-Langevin’s high-flux neutron reactor, were previously the closest to meeting this challenge, albeit over ∼hour time scales. In ultra-high flux environments, where multiple reactions occur on picosecond time scales, nuclei are unable to return to their ground states between reactions; consequently, reactions take place on excited nuclei. To accurately model high-flux environments, data on the cross-sections of excited nuclear states are required, which differ significantly from those of ground states due to spin/parity effects. In order to replicate these effects in the laboratory, short high-fluence pulses on the order of the lifetime of a typical nuclear excited state (generally ≲1 ns) are required. Particle beams generated by high-intensity lasers are uniquely positioned to meet this need with the potential to produce fluences of 10¹⁷ protons/cm² and 10²² neutrons/cm² over a few pico-seconds or less. In addition to providing a quantitative analysis of the rates of multiple rapid reactions in general, the present work examines a number of laser-based experiments that could be conducted in the near future to observe multiple rapid reactions for laboratory-based astrophysics and the measurement of exotic cross-sections.

1 Introduction

The rates of certain nuclear reactions in extremely hot and dense environments are determined not only by the nuclear cross-sections of the ground state, but also by the nuclear cross-sections of isomeric states since a significant population of them can be maintained by constant bombardment from high particle flux and electromagnetic processes. While the term “isomer” typically refers to nuclear excited states with half-lives greater than 1 ns, an isomer in the present context is a nuclear excited state with a half-life greater than 1 ps. Most nuclear isomers have an energy range of a few keV to a few MeV and a half-life of less than a few hundred nanoseconds, making sample preparation in sufficient quantity for cross-section measurements extremely difficult for traditional experiments. However, due to its exceptionally low excitation energy of 76 eV coupled with a long half-life of 26 min, the first excited state of ${}^{235}\mathrm{U}$ is among the few cases where measurement, while very difficult, has been possible up to now. Measurements of cross-sections on ${}^{235m}\mathrm{U}$ appear to be up to a factor of 2.5 greater than that of the ground state for thermal neutron induced fission [1]. Deviations of a similar magnitude are expected to exist in the numerous short-lived isomers too and will have a large influence on reaction rates in certain extreme environments.

In plasmas with temperatures less than 10 keV, calculations have suggested that isomeric states are strongly populated by energetic neutrons and/or protons as opposed to other electromagnetic processes [2]. Nevertheless, complex processes such as nuclear excitation by electron capture (NEEC) and nuclear excitation by electron transition (NEET) may also contribute significantly despite the fact that previous observations have ranged from inconclusive to controversial [3–5]. The NEEC and NEET processes require the overlap of an atomic and (extremely narrow) nuclear transition. Thus, accurate predictions require very precise knowledge of atomic transitions in a plasma, which is challenging due to density effects, charge screening, and other phenomena. Definitive observation of NEEC and NEET, especially in the plasma environment, will be of great importance to the question of how a population of nuclear isomers is maintained in a plasma.

As the use of high intensity short-pulsed lasers to generate ultra-high flux particle beams has increased in popularity, so has the desire to study isomers and other short-lived nuclei using such beams. It has been proposed that short, high-flux laser-accelerated particle pulses could be used to excite a population of isomers (via both nuclear plasma interactions and other nuclear reactions) while also inducing a nuclear reaction in the excited target population [6]. The astrophysical implications of the maintenance of a thermal population of nuclear excited states by various mechanisms in extreme environments is covered elsewhere, for example see [7]. The present work focuses on the generation and probing of short-lived nuclei by rapid repeat nuclear reactions using energetic particles produced by lasers, as well as the potential for novel cross-section measurements relevant to the astrophysics community as higher fluxes become available. Two nuclear reactions occur on the “same” nucleus during this process, with the first reaction producing the nucleus to be studied, which is then subjected to a second nuclear reaction. The term double reaction is used herein to refer to such a reaction.

In the past, reactor-based neutron sources have utilized double reactions to make cross-section measurements on nuclei as short-lived as ${}^{233}\mathrm{T}\mathrm{h}$ (t_1/2 = 22 min) [8]. In contrast, many more excited states are accessible at high intensity laser facilities with pulse lengths between 10^–15 to 10^–11 s and time integrated particle fluxes that are comparable to those produced by the most powerful reactor-based sources in an hour. Following a nuclear reaction, such as neutron capture or inelastic scattering, the nucleus is nearly always left in a short-lived excited state. Because laser pulse lengths are shorter than the lifetimes of many of these excited states, if two nuclear reactions occur on the same nucleus, the second reaction will sometimes occur on an excited nucleus. Section 2 provides several examples of possible measurements on radioactive nuclei and nuclear isomers that may be of interest to the community, as well as a quantitative analysis of the rates of multiple reactions on a single nucleus. Section 3 provides a quantitative assessment of the prospects for studying double reactions at existing facilities.

2 Multiple rapid reactions

2.1 Precise definition and significance

During the r-process, many successive nuclear reactions occur on short time scales. Even during terrestrial nuclear detonations, up to 16 rapid neutron captures have been observed [9]. Detailed quantitative analysis of large leaps in nuclear mass up to the neutron drip lines requires the modeling of a large number of reaction channels and is a complex task best left to codes. The observation of more than a few consecutive reactions in sufficient quantities would demand a flux well beyond the capabilities of current facilities. For these reasons, the present work is primarily concerned with double successive reactions of the general form

$I+n\to J(1)$

followed by

$J+n\to K(2)$

where a flux of particle n is incident on a sample of some initial target nucleus, I, producing an intermediate residue nucleus, J, which undergoes a further reaction to produce the final nucleus, K. For example consider double neutron capture on ${}^{56}\mathrm{F}\mathrm{e}$

$\begin{array}{cc}\hfill {}^{56}\mathrm{F}\mathrm{e}+\text{n}& \to {}^{57}\mathrm{F}\mathrm{e}^{\ast }\hfill \\ \hfill {}^{57}\mathrm{F}\mathrm{e}^{\ast }+\text{n}& \to {}^{58}\mathrm{F}\mathrm{e}\hfill \end{array}(3)$

where * indicates that ${}^{57}\mathrm{F}\mathrm{e}$ is in an excited state, which will be the case at the time of the second neutron capture if it occurs on a short time scale due to the presence of several long-lived isomeric levels encountered during the de-excitation of ${}^{57}\mathrm{F}\mathrm{e}$. Thus, double neutron capture on ${}^{56}\mathrm{F}\mathrm{e}$ is a candidate for measurements of cross-sections on a short-lived isomer. Another application is cross-sections measurements on nuclei whose preparation in sufficient quantities is prohibitively difficult due to their short half lives. Consider, for instance, double neutron capture on ${}^{50}\mathrm{T}\mathrm{i}$, which, in contrast to double capture on ${}^{56}\mathrm{F}\mathrm{e}$, results in the ${}^{51}\mathrm{T}\mathrm{i}$ nucleus returning to its ground state almost instantly after the first capture. At the National Ignition Facility (NIF), the required neutron yields for the observation of such double reactions are already attainable.

Astrophysics is interested in double proton/neutron absorption reactions as a possible pathway to measuring cross-sections on unstable proton/neutron-rich nuclei that are needed to constrain models. Neutron capture cross-sections on unstable nuclei are important to the rapid neutron capture process (r-process), which produces approximately half of the atomic nuclei heavier than iron. Proton absorption cross-sections on unstable nuclei are important to the rapid-proton process (rp–process), which may explain the abundances of a few nuclei that are bypassed by the other known processes. Double capture/absorption reactions are more straightforward to observe experimentally. To see why, consider the following reaction where the incoming proton is not absorbed,

$\begin{array}{cc}\hfill {}^{62}\mathrm{N}\mathrm{i}+\text{p}& \to {}^{61}\mathrm{N}\mathrm{i}+\text{np}\left(460\text{\hspace{0.17em}mb}\right)\hfill \\ \hfill {}^{61}\mathrm{N}\mathrm{i}+\text{p}& \to {}^{60}\mathrm{C}\mathrm{u}+2\text{n}\left(44\text{\hspace{0.17em}mb}\right)\hfill \end{array}(4)$

where the cross-sections are taken from the ENDF library and integrated over a typical laser accelerated proton energy spectrum (see Figure 1). The double reaction pathway for the production of ${}^{60}\mathrm{C}\mathrm{u}$ from Eq. (4) is in competition with the following ordinary reaction pathway

${}^{62}\mathrm{N}\mathrm{i}+\text{p}\to {}^{60}\mathrm{C}\mathrm{u}+3\text{n}\left(2\text{\hspace{0.17em}mb}\right).(5)$

Because the cross-sections of the double reaction pathway are larger than those of the ordinary reaction pathway, it may be tempting to predict that the double reaction pathway will contribute significantly to ${}^{60}\mathrm{C}\mathrm{u}$ production in high flux environments. However, due to the statistics of double reactions, the ordinary reaction pathway will continue to predominate over the double reaction pathway even at the highest proton fluence that is currently achievable in the laboratory. The same problem exists for any double reactions involving fission, which is exemplified in section 3.1.2 using neutrons produced at NIF. In contrast, double capture/absorption reactions, in which Z increases by two for incident protons (or A for neutrons), avoid this problem because the final product can only be produced via the double reaction pathway.This problem is also avoided in circumstances where the maximum energy of the incident particles is below the cut-off for the competing single-order reaction. For example, consider the following reaction induced using 14 MeV energy of neutrons from D-T fusion

$\begin{array}{cc}\hfill {}^{208}\mathrm{P}\mathrm{b}+\text{n}& \to {}^{207}\mathrm{P}\mathrm{b}+2\text{n}\hfill \\ \hfill {}^{207}\mathrm{P}\mathrm{b}+\text{n}& \to {}^{206}\mathrm{P}\mathrm{b}+2\text{n}.\hfill \end{array}(6)$

The cross-section for the production of ${}^{206}\mathrm{P}\mathrm{b}$ from ${}^{208}\mathrm{P}\mathrm{b}$ in a single reaction, or ${}^{208}\mathrm{P}\mathrm{b}+n\to {}^{206}\mathrm{P}\mathrm{b}+3\text{n}$, is vanishingly small because the two-neutron separation energy of ${}^{208}\mathrm{P}\mathrm{b}$ is 14.1 MeV. Therefore, like double absorption reactions, the detection of ${}^{206}\mathrm{P}\mathrm{b}$ is unambiguously linked to the double reaction in Eq. (6).

FIGURE 1

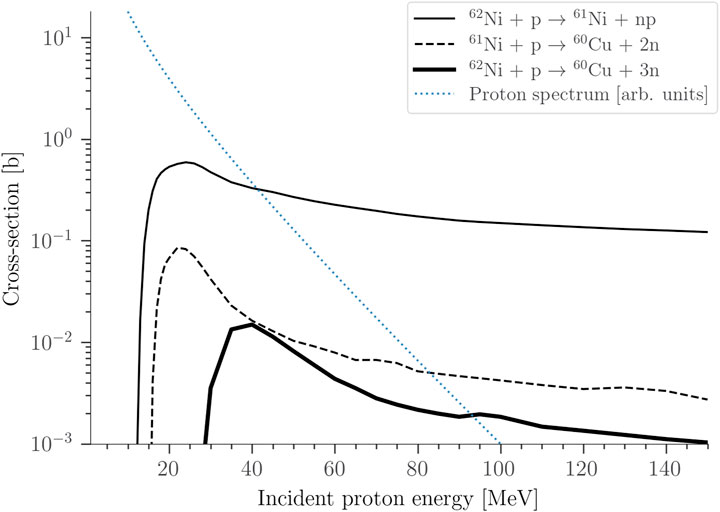
FIGURE 1. Cross-sections for the reactions in Eqs 4 and 5. Taken from the ENDF library. For reference, a typical distribution of laser accelerated proton energies is shown.

2.2 Quantitative analysis of double reaction rates

2.2.1 Simplified mathematical forms

The following assumptions are useful in order to analyze double reaction rates in laboratory conditions:

1. All reactions occur virtually instantaneously (zero pulse width), and

2. Multiple order reaction rates are low relative to ordinary reactions.

Assumption (I) is true if nuclides J and K have a long half-life relative to the pulse width; and hence, species decay is irrelevant. This assumption highlights a benefit of short pulsed lasers: shorter pulse widths make more intermediate states available as short-lived isomers that would otherwise decay to the ground state before a second reaction occurs. Assumption (II) is mathematically true if the inverse of the fluence is much less than the relevant cross-sections, which in practice amounts to a fluence of at least $\sim 10^{22}$ particles per cm² in most cases of interest. A consequence of assumption (II) is that “burn-up” of the initial target atoms can be ignored. While the neutron fluence from recent high yield NIF shots approach this limit, none of the other laboratory sources currently available come close. Establishing a differential equation accounting for the rate of production and loss, such as through decay or nuclear reactions (if applicable), of each nucleus is the standard procedure for calculating the amounts of a species of nuclei over time while subject to flux. Other examples of this procedure can be seen in [8–10]. Under the assumptions (I) and (II), the relevant rate equations are

$\frac{\partial }{{\partial }_t}\left[\begin{array}{c}\hfill I\left(t\right)\hfill \\ \hfill J\left(t\right)\hfill \\ \hfill K\left(t\right)\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \varphi {\sigma }_J\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \varphi {\sigma }_K\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill I\left(t\right)\hfill \\ \hfill J\left(t\right)\hfill \\ \hfill K\left(t\right)\hfill \end{array}\right]\text{such\hspace{0.17em}that}\left[\begin{array}{c}\hfill I\left(0\right)\hfill \\ \hfill J\left(0\right)\hfill \\ \hfill K\left(0\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill N_I\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right](7)$

where I(t), J(t), and K(t) are the time dependent number of the initial target nucleus, the intermediate residue nucleus, and the final nucleus following the double reaction, respectively. ϕ is the flux (cm⁻²s⁻¹) and N_I is the number of target nuclei. σ_J is the cross-section for the reaction that produces J from I and σ_K is the cross-section for the reaction that produces K from J. The diagonal terms of the matrix in Eq. (7) vanish due to the simplifying assumptions described above. Otherwise, the solutions become unwieldy but can be handled using mathematical software if needed. Assumption (II) makes a difference of less than 5% for all figures given in the present work. The solutions of interest to Eq. (7) are

$\begin{array}{cc}\hfill J\left(t\right)& =N_I\left(\varphi t\right){\sigma }_J\hfill \\ \hfill K\left(t\right)& =\frac{1}{2}{N}_I{\left(\varphi t\right)}^2{\sigma }_K{\sigma }_J\hfill \end{array}(8)$

K(t) in Eq. (8) is the total number of double reactions. A lower bound on the fluence (ϕt) in order to observe double reactions is then determined by setting K(t) = 1, giving

${\left(\varphi t\right)}_{\text{min}}\sim \sqrt{\frac{2}{N_I{\sigma }_K{\sigma }_J}}.(9)$

2.2.2 General mathematical forms

Eq. (8) is easily generalized to higher order reactions (e.g. triple neutron capture) giving

$\left(\text{yield\hspace{0.17em}of}{\text{n}}^{\text{th}}\text{order\hspace{0.17em}reaction}\right)=\frac{N_I}{n!}{\left(\varphi t\right)}^n\prod _{i=1}^n{\sigma }_i(10)$

where n is the number of successive reactions and σ_i is the cross-section for the ith reaction.

Relaxing assumption (I) by allowing the intermediate nucleus, J, to undergo decay at a rate of λ_J per second, the following multiplicative correction factor can be applied to Eq. (8) to get double reaction yield

$\left(\text{multiplicative\hspace{0.17em}decay\hspace{0.17em}correction}\right)=\frac{2\left(t{\lambda }_j+e^{-t{\lambda }_j}-1\right)}{t^2{\lambda }_j^2}.(11)$

Since the rate of double-reactions is not linear with respect to the fluence, the following generalization of Eq. (8) must be used in the case of spatially non-uniform fluence

$K\left(t\right)=\frac{1}{2}\int F^2\langle {\sigma }_K\left(E\right)\rangle \langle {\sigma }_J\left(E\right)\rangle \rho dV(12)$

where the angle brackets around σ_K(E) and σ_J(E) represent flux-weighted average cross-sections, F is the fluence, and ρ is the atom density. Because Eq. (12) depends on the square of the fluence, the rates for diverging sources break from the intuition one may have for ordinary reaction rates. Consider the following example. An isotropic point source is embedded in a spherical vacuum of radius r₀ and surrounded by material with atom density ρ extending from r₀ < r < ∞. The total double reaction yield is, assuming zero attenuation

$\left(\text{yield}\right)=\frac{1}{2}{\sigma }_K{\sigma }_J\rho \int F^{2}dV=\frac{1}{2}{\sigma }_K{\sigma }_J\rho {\int }_{r_0}^{\infty }{\left(\frac{s}{4\pi r^2}\right)}^{2}4\pi r^{2}dr=\frac{s^2{\sigma }_K{\sigma }_J\rho }{8\pi r_0}(13)$

where a total of s particles are emitted by the point source. Interestingly, the yield of the double reaction is finite despite particles traversing an infinite amount of material, whereas the yield of single, ordinary reactions diverges to infinity.

2.3 Cross-section determination

Because most cross-sections for the population of isomers by inelastic nuclear reactions have not been experimentally measured, the present work uses the TALYS [11] code to estimate cross-sections as needed. The ${}^{235}U(\text{n},{\text{n}}^{\prime }){}^{235\text{m}}U$ cross-section has been measured experimentally with results agreeing very well with TALYS [12]. While such success is not universal, errors greater than a factor of two are expected to be uncommon. TAYLS can calculate the cross-section for the production of any isomer given that the corresponding discrete nuclear level is documented and assigned a half-life in the Evaluated Nuclear Data Structure File (ENDSF) library. If the discrete state is not assigned a half-life then it cannot be treated as an isomer by TALYS. In TALYS, isomers are produced by both direct inelastic scattering and a time-dependent cascade of decays from higher levels. Fortunately, the code can account for isomer production via feeding from decay of higher excited states, which in many cases is the dominant mechanism as opposed to direct inelastic excitation to a given level. This feature is crucial for isomer production calculations in laser environments where isomeric states with lifetimes as short as a few hundred ps may be effectively stable on the time-scale of the laser’s pulse width. The algorithm in TALYS will allow an excited nucleus to decay to any available lower lying discrete levels until a level is reached with a half-life greater than or equal to a user-specified threshold, at which point further decays stop. The effects of this setting are demonstrated in Figure 2 where large differences are seen in the calculated cross-sections for the excitation of the 70 eV isomer of ${}^{235}U$ by neutrons. Setting the minimum half-life threshold to 100 ps results in a lower calculated cross-section because higher, shorter-lived levels are now considered stable by the code and no longer decay to the 70 eV excited state. As a result, perhaps surprisingly, the first excited state of ${}^{235}U$ is not a great candidate for studying isomers on laser time scales. According to TALYS, the isomer ${}^{235\text{m}}\mathrm{U}$ is maintained in the largest quantities on ps scales when ${}^{235}\mathrm{U}$ target nuclei are irradiated by 14 MeV neutrons, as discussed in greater detail in section 3.1.2.

FIGURE 2

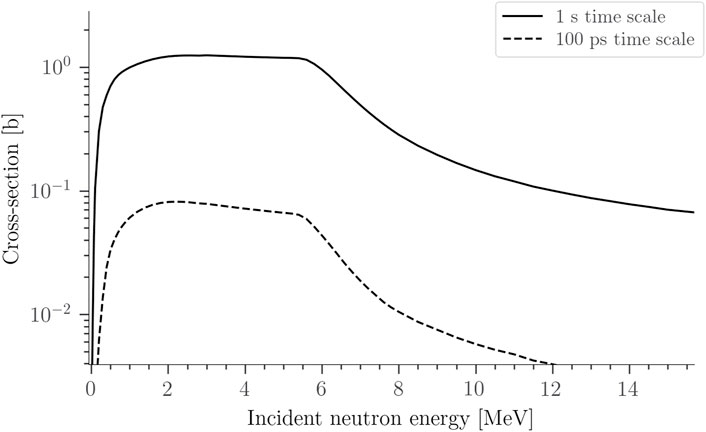
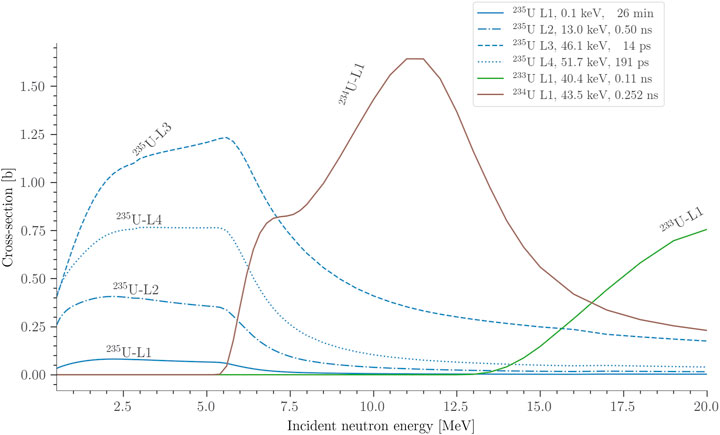
FIGURE 2. Two different TALYS calculations of the cross-sections for the production of the first excited state in ${}^{235}U$ by neutron inelastic scattering. The time-scale can be adjusted by setting the minimum half-life to be treated as an isomer. The effective cross-section for the production of the first excited state is smaller on short time scales because higher excited states do not have enough time to feed the first excited state.

3 Running the numbers

3.1 Neutrons at NIF

3.1.1 Estimated yields

The National Ignition Facility (NIF) currently holds the record for highest neutron flux produced in a lab. Implosion experiments on the NIF vary in their complexity and the neutron yield, thus fluence, that is achievable. Simple gas-filled capsules can produce DT neutron yields of 10¹⁴–10¹⁵ and are straightforward to execute. More complex “layered” experiments, in which a layer of DT ice is grown against the inner surface of the capsule, are significantly more complex but enable higher yield. Experiments in the “burning plasma” regime have produced neutron yields up to $\sim 5\times 10^{16}$ [13] and more recent experiments have generated much higher yields, up to $\sim 4\times 10^{17}$ [14]. Based on these results, near-term experiments using yields above 10¹⁷ are possible and even higher yields, for example up to 10¹⁸, may be plausible within the next several years. In these experiments, the neutron flux lasts $\sim 100$ ps and is contained within a $\sim 50\mu$m radius. For a neutron yield of 10¹⁷, this corresponds to neutron fluence of 4 × 10²¹ neutrons per cm². The next most intense neutron source in terms of run-integrated fluence is found in research reactors, which are capable of producing $\sim 10^{19}$ thermal neutrons per cm² per day.

In the following examples, it is assumed that 10¹⁵ target atoms are seeded in the NIF capsule and exposed to a neutron yield of 10¹⁷ (fluence = 10²¹ neutrons/cm²). For a given pair of cross-sections, these conditions give a double reaction yield of

$\left(\text{yield\hspace{0.17em}of\hspace{0.17em}double\hspace{0.17em}reaction}\right)\approx 5\times 10^8{\sigma }_J{\sigma }_K\left[b^{-2}\right].(14)$

where σ_J and σ_K are the cross-sections for the first and second reactions in units of barns.

3.1.2 Fission on an excited nuclear state ${}^{235m}U$

According to cross-sections provided by TALYS, the most numerous fissionable isomer created by neutron interactions on ${}^{235}\mathrm{U}$ nuclei under the conditions of a high yield NIF implosion is the 43.5 keV, 252 ps isomer of ${}^{234}U$ produced by the ${}^{235}U(\text{n},2\text{n}){}^{234m}U$ reaction, with a calculated cross-section of about 0.7 b for the relevant neutrons. See Figure 3 for a few other relevent cross-sections output by TALYS. Using this value and a fission cross-section of 2 b, Eq. (14) gives 7 × 10⁸ fissions on ${}^{234m}U$. This is small in comparison to the number of ordinary fission on the ${}^{235}\mathrm{U}$ target nuclei, which calculated using standard methods gives 2 × 10¹². Since fission of ${}^{235}\mathrm{U}$ dominates over ${}^{234m}\mathrm{U}$ by a factor of ∼3,000 under these conditions, it is unlikely that there will be a measurable difference in overall fission rate or fission product yields due to the presence of isomers created by neutrons. Figure 4 shows the time averaged ratio between the number of ${}^{234}U$ isomers and initial ${}^{235}\mathrm{U}$ nuclei as a function of neutron fluence. A ratio that would potentially lead to a measurable difference in fission observables is ≈1/10. The flux required to achieve this at NIF, all else equal, would be $\approx 2\times 10^{23}\text{\hspace{0.17em}n}/({\text{cm}}^2)$, or a factor of $\sim 50$ increase over current capabilities. Coincidentally, this value is about what is expected for igniting capsules at NIF [15]; page 92). NIF appears to be the most promising high flux source of any particle type currently available for this type of measurement. In the near future, however, completely different approaches, such as using surrogate reactions with reverse kinematics in storage rings are also promising [16].

FIGURE 3

FIGURE 3. Cross-sections for the production of several isomers from neutron bombardment of ${}^{235}\mathrm{U}$.

FIGURE 4

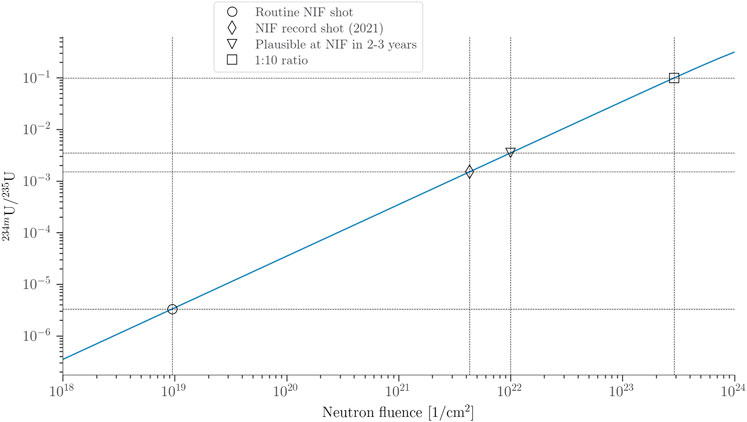
FIGURE 4. Time averaged ratio of ${}^{235m}\mathrm{U}$ to ${}^{235}\mathrm{U}$ maintained by the ${}^{235}\mathrm{U}$(n, 2n)${}^{234m}\mathrm{U}$ reaction during high flux bombardment of ${}^{235}\mathrm{U}$ by 14 MeV neutrons. ${}^{234m}\mathrm{U}$ refers to the 43.5 keV, 252 ps half-life isomer of ${}^{234}\mathrm{U}$. This isomer of ${}^{234}\mathrm{U}$ is chosen here because it has the highest production cross-section from NIF neutrons on ²³⁵U according to TALYS calculations. At a ratio of 1:10, it likely becomes possible to observe changes in fission rates and yields due to multiple reactions.

3.1.3 Double neutron capture

In contrast to fission, where the observability of double reaction effects are determined by the ratio of ordinary fission to fission following a secondary reaction, double neutron capture can be observed unambiguously by the detection of (Z, A+ 2) nuclei. While the neutron capture cross-sections for 14 MeV D-T neutrons are quite low, a significant fraction of neutrons at NIF are down scattered to lower energies. Figure 5 depicts the energy spectrum down to 1 MeV; the rates of neutrons with energies less than approximately 1 MeV are poorly understood due to the difficulty of measuring them at NIF [15]; page 76. Even though only a minute fraction of neutron flux is in the thermal energy range, because the cross-sections for neutron capture at thermal energies can be over 100,000 times larger than for MeV neutrons, the low energy neutron component can have a significant effect on capture yields. Note that the calculations below do not include neutron energies below 1 MeV and therefore represent lower bounds on expected yields.

FIGURE 5

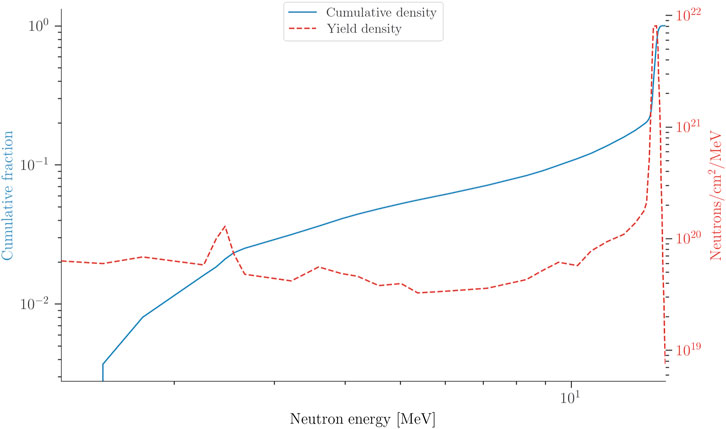
FIGURE 5. Energy distribution of neutrons during a NIF implosion. Data taken from [15]; page 7). The cumulative fraction is also given for the reader’s convenience so that the fraction of neutrons in a given energy range can be quickly estimated by taking the difference between the values at two energies.

Consider double neutron capture on ${}^{40}\mathrm{A}\mathrm{r}$, yielding ${}^{42}\mathrm{A}\mathrm{r}$. The cross-sections for this reaction, integrated over the NIF spectrum in Figure 5, are 1.2 × 10^–4 b, and 1.4 × 10^–3 b for ${}^{40}\mathrm{A}\mathrm{r}+n\to {}^{41}\mathrm{A}\mathrm{r}$ and ${}^{41}\mathrm{A}\mathrm{r}+n\to {}^{42}\mathrm{A}\mathrm{r}$, respectively, according to the ENDF library. This gives an expected yield according to Eq. (14) of $1.5\times 10^3{}^{42}\mathrm{A}\mathrm{r}$ nuclei given that 10¹⁵ initial ${}^{40}\mathrm{A}\mathrm{r}$ nuclei are seeded into the capsule. With a half-life of over 30 years, these rates are not high enough to perform gamma spectroscopy. Efforts are currently underway to test the viability of using the RAGS system to collect and store ${}^{42}\mathrm{A}\mathrm{r}$ for transport to Argonne National Laboratory where accelerator mass spectrometry will be performed (per personal communication with Micheal Paul of Argonne National Laboratory). Much higher double neutron capture yields are possible, with the highest achievable at NIF being around $\sim 5\times 10^6$ if a nucleus with a high neutron capture cross-section like ${}^{158}\mathrm{D}\mathrm{y}$ is used. Using a nucleus with a more typical neutron capture cross-section like ${}^{235}\mathrm{U}$ gives an estimated yield of $\sim 6\times 10^5$ radioactive ${}^{237}\mathrm{U}$ nuclei from double neutron capture. As a final example, consider double capture on ${}^{56}\mathrm{F}\mathrm{e}$ as denoted in Eq. (3), a possible scheme to measure neutron capture cross-section on excited ${}^{57}\mathrm{F}\mathrm{e}$ as compared to the ground state. This reaction gives a calculated yield of $\sim 10^4{}^{58}\mathrm{F}\mathrm{e}$ nuclei, easily measurable by techniques such as accelerator mass spectroscopy.

3.1.4 Other reactions

The production of ${}^{232}\mathrm{U}$ from ${}^{235}\mathrm{U}$ via double reactions cannot occur via a single reaction from neutrons at NIF because the threshold for the (n, 4n) reaction is approximately 19 MeV, avoiding the previously described problem of dominance by an ordinary reaction channel. There are two pathways to produce ${}^{232}\mathrm{U}$ from ${}^{235}\mathrm{U}$ via double reactions

$\begin{array}{cc}\hfill {}^{235}\mathrm{U}+\text{n}& \to {}^{234}\mathrm{U}+2\text{n}\left(\text{.}56\text{\hspace{0.17em}b}\right)\hfill \\ \hfill {}^{234}\mathrm{U}+\text{n}& \to {}^{232}\mathrm{U}+3\text{n}\left(3.2\times 10^{-3}\text{\hspace{0.17em}b}\right)\hfill \end{array}(15)$

and

$\begin{array}{cc}\hfill {}^{235}\mathrm{U}+\text{n}& \to {}^{233}\mathrm{U}+3\text{n}\left(3.0\times 10^{-2}\text{\hspace{0.17em}b}\right)\hfill \\ \hfill {}^{233}\mathrm{U}+\text{n}& \to {}^{232}\mathrm{U}+2\text{n}\left(0.18\text{\hspace{0.17em}b}\right)\hfill \end{array}(16)$

where the cross-sections, taken from ENDF, are energy-weighted. The usefulness of this example is the high yields. Compared to the example of double neutron capture reaction on ${}^{235}\mathrm{U}$, the calculated yield of ${}^{232}\mathrm{U}$ in this example is 3,000x greater, at 2 × 10⁹, owing to the higher cross-sections.

3.2 Protons from TNSA

3.2.1 Estimated yields

Irradiating thin foils with short-pulse, ultrahigh intensity lasers to generate energetic protons is emerging as a promising method for achieving fluxes high enough to be relevant for multiple reactions. In particular, the well-known Target Normal Sheath Acceleration (TNSA) method is distinguished from conventional ion accelerators by its ability to send high count particle bunches into very small areas with a very short pulse length. The best set of conditions within reach of current systems is $\sim 10^{13}$ protons [17] produced over a 50 μm radius with a 15° diverging angle. The following yield calculation assumes that the protons traverse through a target material of typical solid densities (5 × 10²³ atoms/cm³) and a thickness of a few mm, beyond which the double reaction rate is virtually zero due to beam divergence (this can be seen by using Eq. (12), following the same pattern of the example of Eq. (13)). Taking into account these (generous) assumptions, the maximum achievable rate of a double proton reaction using protons from TNSA at existing facilities is about

$\left(\text{max.\hspace{0.17em}tot.\hspace{0.17em}yield\hspace{0.17em}of\hspace{0.17em}double\hspace{0.17em}reaction}\right)\approx 6\times 10^2{\sigma }_J{\sigma }_K\left[b^{-2}\right](17)$

where σ_J and σ_K and the cross-sections for the two reactions in barns. Thus, to be readily detectable, the product of the cross-sections of the two reactions must be such that σ_Jσ_K ≳ 0.001 b².

3.2.2 Double proton absorption

For example, consider the following double proton absorption reaction on ${}^{206}\mathrm{P}\mathrm{b}$

$\begin{array}{cc}\hfill {}^{206}\mathrm{P}\mathrm{b}+p& \to {}^{205}\mathrm{B}\mathrm{i}+2n\hfill \\ \hfill {}^{205}\mathrm{B}\mathrm{i}+p& \to {}^{204}\mathrm{P}\mathrm{o}+2n.\hfill \end{array}(18)$

Using data from ENDF and TALYS for Pb and Bi, respectively, and averaging the cross-sections over a typical TNSA spectrum gives a value of 0.5 b for both reactions. From Eq. (17) this gives a yield of 150 ${}^{204}\mathrm{P}\mathrm{o}$ per laser shot. Since the conditions leading to Eq. (17) were generous, experimental observation of double reactions using TNSA is possible in the relative near-term with some improvements. Upcoming laser facilities with a higher repetition rate will be particularly useful; newer lasers are expected to shoot once per minute or at Hz to 10 Hz rates, making “rare event” searches feasible with routine proton yields as low as 10¹¹.

3.2.3 Initial steps at PHELIX facility

In the vicinity of high intensity laser interactions with matter, the majority of conventional nuclear measurement techniques will fail due in part to high peak current, strong electromagnetic pulse (colloquially EMP), and the presence of plasmas. This has motivated the development of a gas transport and collection system in which nuclear reactions occur within a small, hermetically sealed chamber through which inert gas flows, carrying reaction products to a filter where gamma spectroscopy is performed (see Figure 6). A successful proof-of-principle demonstration was conducted at the peta-watt PHELIX laser facility in 2020 [18] using 500 fs, $\approx 200$ J laser pulses to accelerate bunches of protons via TNSA. The maximum proton fluence tested using this method at PHELIX is 2 × 10¹¹ protons/cm², incident on ${}^{238}\mathrm{U}$ targets. An optimistic estimate of the rate of double reactions under these circumstances predicts only one occurrence every ∼10,000 laser shots, which would require years of daily operation at the maximum repetition rate. The distance between the ${}^{238}\mathrm{U}$ target and the gold TNSA foil (5 cm, see Figure 6) was the primary factor limiting the amount of usable fluence in these experiments. This distance, ideally, would be on the order of a few microns, effectively bringing the laser-matter interaction inside the chamber–a significant overhaul over the current design. Nonetheless, this is the initial step toward radchem-type experiments at peta-watt laser facilities, whereas similar capabilities known as RAGS have existed at NIF for about a decade. The development of this platform is ongoing, and additional work by the present authors and collaborators will be published elsewhere in the coming months by the present authors in collaboration with others.

FIGURE 6

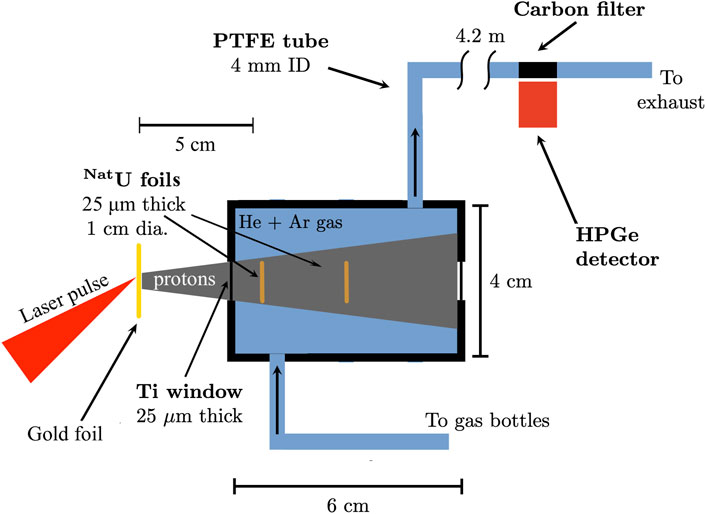
FIGURE 6. Schematic of a gas transport system for the collection of nuclear reaction products that was tested at the PHELIX laser facility.

4 Summary and outlook

The possibility of inducing multiple nuclear reactions in rapid succession has been considered in order to study nuclear reactions on short-lived isomers and exotic nuclei. A set of practical equations with varying degrees of generality for estimating double reaction rates has been developed. Double neutron-capture reactions have been performed using reactors capable of producing 10¹⁹ neutrons/cm²/day, but the slow accumulation of fluence precludes studies on short-lived nuclear isomers, which are required to conduct studies relevant to ultra high-flux environments such as those that occur during the r-process. High intensity lasers, while posing new measurement challenges, have the potential to outperform the highest fluence achievable with conventional methods by orders of magnitude, and have pulse lengths down to a few ps to ns.

For reactions where an isotopic signature can be uniquely linked to the double reaction, such as double neutron capture, the necessary fluence is currently readily attainable at NIF using D-T fusion neutrons. Upcoming facilities such as ELI-NP will also meet this threshold with sources of neutrons and protons. For double reactions that do not produce an unambiguous isotopic signature, such as neutron capture followed by neutron induced fission, the experimental fluence required to observe them is much higher, generally greater than $\sim 10^{23}$ particles per cm². This is because this class of double reactions will only manifest experimentally if double reaction rates are on the same order as ordinary reaction rates. At this point, nonlinearities in reaction rates with respect to flux become apparent; such an observation in a laboratory would be monumental in the study of extreme environments. NIF is currently the most promising facility for achieving the necessary fluence, but further increases of ∼50x are still required.

Owing to their ability to squeeze a large number of particles into a very small area in a very short duration, next-generation lasers will be at the forefront of the study of nuclear reactions in extreme environments. A major challenge in the near term will be the adaptation of current measurement methods and instruments to the hostile environment of the high intensity laser, as well as the development of new measurement methods. The present authors hope that this work will serve as a catalyst for additional research and discussions in this emerging field.

Author contributions

JB conceived and drafted the document, while AZ contributed insight and editing.

Funding

This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE‐AC52‐07NA27344 and was supported by the LLNL‐LDRD Program under Project No. 20-ERD‐031.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. D’Eer A, Wagemans C, Nève de Mévergnies M, Gönnenwein F, Geltenbort P, Moore MS, et al. Neutron-induced fission of the 26 min isomer. Phys Rev C (1988) 38:1270–6. doi:10.1103/PhysRevC.38.1270

CrossRef Full Text | Google Scholar

2. Luu TC, Friar JL, Hayes AC. Electromagnetic excitation rates for nuclear isomers in a hot dense plasma. Nucl Sci Eng (2006) 152:98–105. doi:10.13182/NSE06-A2567

CrossRef Full Text | Google Scholar

3. Guo S, Fang Y, Zhou X, Petrache CM. Possible overestimation of isomer depletion due to contamination. Nature (2021) 594:E1–2. doi:10.1038/s41586-021-03333-5

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chiara CJ, Carroll JJ, Carpenter MP, Greene JP, Hartley DJ, Janssens RVF, et al. Reply to: Possible overestimation of isomer depletion due to contamination. Nature (2021) 594:E3–E4. doi:10.1038/s41586-021-03334-4

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rzadkiewicz J, Polasik M, Słabkowska K, Syrocki L, Carroll JJ, Chiara CJ. Novel approach to isomer depletion: Nuclear excitation by electron capture in resonant transfer process. Phys Rev Lett (2021) 127:042501. doi:10.1103/PhysRevLett.127.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chen SN, Negoita F, Spohr K, d’Humières E, Pomerantz I, Fuchs J. Extreme brightness laser-based neutron pulses as a pathway for investigating nucleosynthesis in the laboratory. Matter Radiat Extremes (2019) 4:054402. doi:10.1063/1.5081666

CrossRef Full Text | Google Scholar

7. Rauscher T. Revision of the derivation of stellar rates from experiment and impact on eu s-process contributions. J Phys : Conf Ser (2016) 665:012024. doi:10.1088/1742-6596/665/1/012024

CrossRef Full Text | Google Scholar

8. Chatani H. Measurement of effective cross section of Th-233(n, γ)Th-234 reaction using the KUR. AIP Conf Proc (2005) 769. doi:10.1063/1.1945097

CrossRef Full Text | Google Scholar

9. Lutostansky YS, Lyashuk VI. Production of transuranium nuclides in pulsed neutron fluxes from thermonuclear explosions. Jetp Lett (2018) 107:79–85. doi:10.1134/S0021364018020108

CrossRef Full Text | Google Scholar

10. Zagrebaev VI, Karpov AV, Mishustin IN, Greiner W. Production of heavy and superheavy neutron-rich nuclei in neutron capture processes. Phys Rev C (2011) 84:044617. doi:10.1103/PhysRevC.84.044617

CrossRef Full Text | Google Scholar

11. Koning AJ, Hilaire S, Duijvestijn MC. Talys-1.0. In: International conference on nuclear data for science and technology. EDP Sciences (2007). p. 211

Google Scholar

12. Bélier G, Bond EM, Vieira DJ, Authier N, Becker JA, Hyneck D, et al. Integral cross section measurement of the reaction in a pulsed reactor. Phys Rev C (2015) 91:044605. doi:10.1103/PhysRevC.91.044605

CrossRef Full Text | Google Scholar

13. Zylstra A, Hurricane O, Callahan D, Kritcher A, Ralph J, Robey H, et al. Burning plasma achieved in inertial fusion. Nature (2022) 601:542–8. doi:10.1038/s41586-021-04281-w

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Herrmann M. Building to a solution: The elements of a fusion breakthrough (2021). Available from: https://lasers.llnl.gov/news/building-to-a-solution-elements-of-a-fusion-breakthrough (accessed July, 2022).

Google Scholar

15. Cerjan CJ, Bernstein L, Hopkins LB, Bionta RM, Bleuel DL, Caggiano JA, et al. Dynamic high energy density plasma environments at the national ignition facility for nuclear science research. J Phys G: Nucl Part Phys (2018) 45:033003–2. doi:10.1088/1361-6471/aa8693

CrossRef Full Text | Google Scholar

16. Henriques A, Jurado B, Denis-Petit D, Chiron T, Gaudefroy L, Glorius J, et al. Future perspectives for surrogate-reaction studies at storage rings. In: J Escher, Y Alhassid, LA Bernstein, D Brown, C Fröhlich, P Talouet al. editorsCompound-nuclear reactions. Cham: Springer International Publishing (2021). p. 209

CrossRef Full Text | Google Scholar

17. Borghesi M. Laser-driven ion acceleration: State of the art and emerging mechanisms. In: Nuclear instruments and methods in Physics research section A: Accelerators, spectrometers, detectors and associated equipment, 740. Proceedings of the first European Advanced Accelerator Concepts Workshop 2013 (2014). p. 6–9. doi:10.1016/j.nima.2013.11.098

CrossRef Full Text | Google Scholar

18. Boller P, Zylstra A, Neumayer P, Bernstein L, Brabetz C, Despotopulos J, et al. First on-line detection of radioactive fission isotopes produced by laser-accelerated protons. Sci Rep (2020) 10:17183. doi:10.1038/s41598-020-74045-5

PubMed Abstract | CrossRef Full Text | Google Scholar