- 1National Institute for Laser, Plasma and Radiation Physics, Magurele-Bucharest, Bucharest, Romania
- 2Consorzio RFX (CNR, ENEA, INFN, Universita’ di Padova, Acciaierie Venete SpA), Padua, Italy
- 3University of Rome “Tor Vergata”, Rome, Italy
- 4Max-Planck-Insitut für Plasmaphysik, Garching, Germany
- 5Institute of Applied Physics, TU Wien, Fusion@ÖAW, Vienna, Austria
The control of macroscopic instabilities, such as Edge Localised Modes (ELMs) and sawteeth, is becoming an essential ingredient in the optimisation of scenarios in preparation for the next generation of tokamaks and the demonstrative reactor. Various pacing experiments have been indeed successfully carried out in many devices but various details of their interactions with the plasma remain poorly understood, in particular the assessment of the relative contribution of driver phase and amplitude to frequency synchronization. In this paper, a data analysis methodology for investigating the details of pacing experiments is proposed. The approach is based on the wavelet decomposition of the signals and the following implementation of information theoretic indicators, to determine the basic form of the interactions. The main analysis tool deployed is the conditional mutual information, equivalent to the informational transfer entropy, which can detect actual causal influences and not only statistical correlations between signals. The most flexible type of ELM pacing, the vertical kicks, permits to clearly confirm the potential of the analysis tools developed. In the dedicated experiments to optimise the ELMs pacing with pellets and sawteeth synchronization with ICRH modulation, the main effect is due to the influence of the amplitude of the external perturbations. Some evidence of phase synchronization has been found, in both JET and AUG, which indicates the direction of possible future optimization of the interventions. Indeed, adjusting the phase of the pacing schemes would free density and ICRH power to give more leeway to other feedback loops, an important aspect, particularly for the integrated control of the next generation of devices. The long-term objective of this line of research is therefore twofold. On the one hand, it is expected to contribute to better physical interpretation of the pacing experiments and possibly also of their target instabilities. From an operational perspective, hopefully these insights will help in the development of reactor relevant scenarios, as exemplified by examples of ELM a pacing with pellets carried out in preparation for the DT campaign on JET.
Synchronization and pacing experiments in tokamaks
Synchronization has become an important subject of research in various fields of science. It can be defined as the organization in time of events, in such a way that they operate in a coordinated way, forming a sort of unique system. Historically, the practical importance of synchronization became evident first in the organization of human activities and the control of man-made systems [1]. In the times before radio and satellite-based navigation, accurate time keeping was necessary to determine the longitude (how far east or west a position was) with the help of astronomical observations. Indeed, the development of accurate chronometers dramatically changed marine navigation. In the 19th-century, the railways further promoted the investigation of synchronization, which was important for their timetables, since trains moved so fast to be affected by excessive differences in local mean time between nearby towns. The requirement of strict timekeeping induced the major companies to settle on one standard and this railway time was then adopted by the civil authorities, eventually abandoning local mean time. Another technological sector, with increasingly more strict demands in terms of synchronization, is certainly electrical engineering, particularly for data transfer. Synchronous circuits and transmission need indeed a clock signal, indicating the start and/or end of some time period, which normally has an arbitrary relationship to sidereal, solar, or lunar time. Laser beams are also the outcome of perfect synchronization of trillions of atoms.
More recently, it has become evident that synchronization plays an important role also in many natural systems and even pervades our daily lives [2]. For example, many animals and plants physiological functions are synchronized to the day-night cycle (circadian rhythm). In various countries, myriads of fireflies convene at night, mostly along riverbanks, and synchronize their flashes. In human bodies, thousands of pacemaker cells in the sinoatrial node have to fire at unison to maintain the regular rhythm of the heart.
As is apparent from these examples, and many others reported in the literature, synchronization is an emergent property that occurs in a broad range of dynamical systems [3]. The most common and widely investigated case is the synchronization between self-sustained oscillators, through some kind of coupling between them. Quite surprisingly, given the exponential divergence of the nearby trajectories of chaotic systems, synchronization of coupled or driven chaotic oscillators is a phenomenon well established as well [4].
Tokamak plasmas are the site of many instabilities, whose quasi-periodic nature suggests that they can be modelled as oscillators. Two of the macroscopic more important are the Edge Localised Modes (ELMs) in the edge and the sawteeth in the core.
ELMs are periodic and very short bursts of energy and particles emitted by tokamak plasmas in H-mode, the main reference scenario for ITER. The ELMs are due to a deterioration of the confinement properties of the plasma edge and the consequent heat and particles fluxes are deposited on the plasma facing components and in particular on the divertor. The loads due the ELMs will have to be well controlled and reduced in size in the next generation of devices and possibly in the future fusion reactor. Indeed type I ELMs, typical of performing scenarios in present devices, are not compatible with DEMO, because they would excessively reduce the lifetime of its divertor. In ITER, the size of ELMs will have to be limited and the frequency kept sufficiently high for impurity control. Some form of active control of ELMs will probably be necessary and indeed it is already foreseen in ITER. An overview of the ELMs dynamics and the requirements to alleviate their consequences in ITER is provided in [5, 6].
Sawteeth are another important class of instabilities with a complex role in tokamaks. If their crash is not too large, they do not have a significantly detrimental effect on confinement. However, their reconnections can provoke such large changes in the plasma core that can trigger other instabilities, particularly Neoclassical Tearing Modes (NTMs), whose effects are not compatible with high performance scenarios. Moreover, in their turn NTMS can result in disruptions, a situation to be avoided as much as possible in large devices. On the other hand, complete suppression of sawteeth is not necessarily the best long term strategy, because they can prove crucial to expel helium ash and impurities from the very plasma core, essential particle transport issues for the reactor [7, 8]. Consequently, also sawteeth are a type of instabilities, which will probably have to be carefully controlled in DEMO.
Due to the complex effects of ELMs and sawteeth, in the last decades various experimental techniques have been developed to influence their dynamics. In the cases of interest for the present discussion, the approach is the same and takes advantage of the natural evolution of these instabilities, which present a charge-and-fire nature. They grow on a slower time scale and then they collapse very rapidly. External perturbations are therefore periodically applied to trigger their crash sufficiently often, to avoid plasma conditions leading to excessively large perturbations of the plasma. ELMs pacing, with vertical kicks and pellets, and sawteeth triggering, with ICRH modulation, are typical examples tested on various devices. Other techniques have also been tried but are not the main subject of the present work [9–13]. In any case, with suitable adjustments, the tools presented in this work could be used also in the investigation of the other pacing schemes.
The quasi periodic nature of ELMs and sawteeth renders somewhat problematic the interpretation of the experiments, relying on periodic external perturbation of the plasma. Determining which crashes have actually been triggered by the external intervention is no simple matter and relatively sophisticated analysis methods have been deployed to solve this conundrum [14–19]. Another delicate aspect is the quantification of the relative importance of phase and amplitude synchronization. This issue is particularly relevant for the optimisation of the pacing schemes in the next generation of devices. Indeed ITER, and even more DEMO, will have to be much more feedback controlled than present day tokamaks. A more efficient use of phase synchronization would therefore allow to reduce the amplitude of the vertical kicks and size of the pellets for the ELM pacing. Smaller vertical kicks would be less stressful for the vacuum vessels of the devices and smaller pellets would give more margins of manoeuvring to other density control strategies (see Subsection 2.2). Analogous considerations apply to ICRH modulation; tiding down less power for sawteeth pacing would give more freedom to other requirements on this additional power system, which is nowadays in great demand for various purposes (see Subsection 2.3).
In the paper, a new data analysis approach, to disentangle the effects of phase and amplitude in pacing experiments, is proposed. The main innovative aspect of the developed technique is its capability of detecting not only statistical correlations but actual causal interactions. This aspect is essential for the case of pacing schemes, whose objective consists of intervening on and therefore modifying the behaviour of the plasmas and not simply describing it. The techniques are applied to ELM pacing via vertical kicks and with pellets and to sawteeth synchronization with ICRH modulation (see next section). The methodology for analysing causal interactions across time scales, deployed to investigate the experimental data recorded in JET and AUG, is described in Section 3. Some representative results of a battery of numerical tests, performed to assess the accuracy of the developed technology, are reported in Section 4, together with a discussion about the reasons why more traditional approaches, such as bicoherence, cannot cope with the transient nonlinear interactions typical of the experiments analysed in the present work. Section 4 includes also a validation experimental example, to prove the proposed numerical tools potential in handling real life signals. The outcomes, of applying the techniques to optimise experiments of ELM pacing with pellets in AUG and JET, are described in detail in Section 5, which covers also sawteeth triggering with ICRH modulation in JET. More advanced applications are the subject of Section 6, aimed at explicitly exemplifying the potential contribution of the proposed technique to the optimisation of scenarios, including examples of the high current campaign in JET to prepare for DT operation. Some conclusions are drawn in the last section of the paper, where also future lines of investigation are discussed.
Amplitude and phase synchronization in ELMs pacing via vertical kicks and with pellets, and sawteeth triggering with ICRH modulation
The synchronization between systems and phenomena has become a rich field of research. Subsection 2.1 provides a short overview of the topic, with particular attention to the aspects more related to the rest of the work. Subsection 2.2 describes the basics of ELMs pacing via vertical kicks and with pellets and the following Subsection 2.3 summarises the rationale of sawteeth triggering with ICRH.
Types of synchronization
Several types of synchronization have been identified in the behaviour of various dynamical systems, ranging from physics and engineering to environmental sciences and economics [1]. Identical synchronization, which is also called complete synchronization, refers to the situation, in which identical systems are completely synchronized. For identical initial conditions, these systems therefore eventually evolve identically in time. Generalised synchronization relates to different systems, whose dynamical variables are (x1,x2, ...,xn) and (y1,y2, ...,ym), and is achieved when there is a functional, Φ, such that, after a transition depending on the initial conditions, the evolution of the two systems obeys the equation [y1(t), y2(t),...,ym(t)] = Φ[x1(t), x2(t),...,xn(t)]. Consequently, the dynamic evolution of one system can be uniquely determined by observing the other. In the case of phase synchronization, the evolution of the coupled oscillators is characterised by an asymptotic bounded phase difference, while their amplitudes remain uncorrelated [20–23]. All the previous classes can be affected by a time delay, giving rise to anticipated and lag synchronization, whose main characteristic is a time interval τ, such that the dynamical state variables of the oscillators are related by yi(t) = xi (t+τ) or yi(t) = Φ[xi (t+τ)]. Basically, in these situations, the evolution of one oscillator follows, or anticipates, the evolution of the other. The synchronisation may be sometimes intermittent or limited, when a finite difference, between certain subsets of the variables in the two systems, is asymptotically reached.
The pacing experiments analysed in the following subsections are a form of generalised synchronisation and are characterised by significant interactions between processes operating at different time scales. This is a characteristic of non-linear interactions between dynamical systems, exhibiting not just one but several correlations, varying in time. The response induced by the driver system across time scales can be analysed by means of wavelet decomposition. From a practical point of view, this approach has the advantage of expressing the problem in terms of a few tens of wavelet coefficients, instead of using the measured time series, which can comprise thousands of data points.
As discussed in detail in the following subsections, the target oscillators (ELMs, sawteeth) are charge-and-fire ones. The main aim consists of influencing these complex instabilities, so that their crash occurs at a predefined frequency, sufficiently high so that the perturbations that they induce are acceptably small. Therefore, in practical terms, the main objective resides in the attempt to limit the amplitude of the crashes. The drivers (vertical kicks, pellets, ICRH modulations) are pulsed external interventions. The nature of high temperature plasmas and the characteristics of the instabilities, particularly their quasi periodic nature, pose various challenges and constraints to the possible pacing techniques and to the understanding of their action, as discussed in detail in the rest of this section.
ELM pacing via vertical kicks and with pellets
The edge of H mode plasmas almost always presents a class of instabilities called ELMs [24]. In addition to causing a reduction of the energy confinement, by deteriorating the edge transport barrier, they are unacceptable in reactor grade devices, because they would damage the divertor. On JET, the pressure at the pedestal grows for periods of tens of ms but then the transport barrier collapses on millisecond time scales. The resulting expulsion of energy and matter from the region within the last closed magnetic surface would result in unacceptable erosion of the plasma facing components in the divertor of large devices, such as ITER and DEMO.
Given their potential harmful nature, in the last decades a lot of efforts have been devoted to the investigation of ELMs, with mixed results. Basic modelling of their stability, in particular the peeling-ballooning theory, is accepted in the community [25, 26]. On the other hand, no satisfactory understanding of their dynamics has emerged yet. Even their general statistical properties are controversial, since in some studies ELMs seem to show a quasi-periodic behaviour, in other their dynamic is more chaotic and recently evidence of quasi chaotic behaviour has also emerged [27].
In the last years, even if the details of the ELMs dynamics are not fully understood, a lot of attention has been devoted to developing ELM-free plasma scenarios such as the QH-mode [28] and the I-mode [29]. Unfortunately no robust solution has been identified yet. Therefore there is a general consensus that it is important to keep developing some form of ELMs control, as a fall-back solution for ITER and DEMO. Consequently, in various machines.
ELM pacing techniques have been implemented and tested. Particular attention deserve the experiments on JET, not only because it is the only device with the same plasma facing components as ITER but also because of the just completed DT campaign [30, 31].
The rationale of pacing consists of triggering ELMs with external perturbations, whose frequency is set in such a way that the gradients at the edge do not increase excessively, between two subsequent crashes [5, 32, 33]. Of course such pacing experiments constitute a form of synchronization.
Among the various techniques of ELM control proposed, one extensively tested on JET is based on the vertical stabilisation (VS.) control system [34]. The VS. system, which is implemented in all tokamaks to guarantee stable operation, can be adapted to apply voltage pulses, which are called vertical kicks in common jargon, because they cause sudden displacements of the plasma vertical position. Experimental evidence in various devices has confirmed that ELMs can be triggered by vertical displacements of the order of a few percent of the plasma minor radius. The VS. of the devices can apply pulses with somewhat short periods of a few milliseconds. In Figure 1 the main quantities of a representative experiment, implementing the vertical kicks pacing scheme on JET, are reported. . The approach, originally pioneered on TCV [35] has been also applied successfully on other devices [36–38]. Several simulations indicate that it could be considered a backup system also in ITER [6]. Even if the application of vertical kicks to the reactor is very doubtful, because of the unavoidable stresses on the mechanical structures and the requirements on the electromagnetic circuits, they are the most flexible scheme in present day devices, therefore allowing particularly interesting tests of the tools developed in the present work.
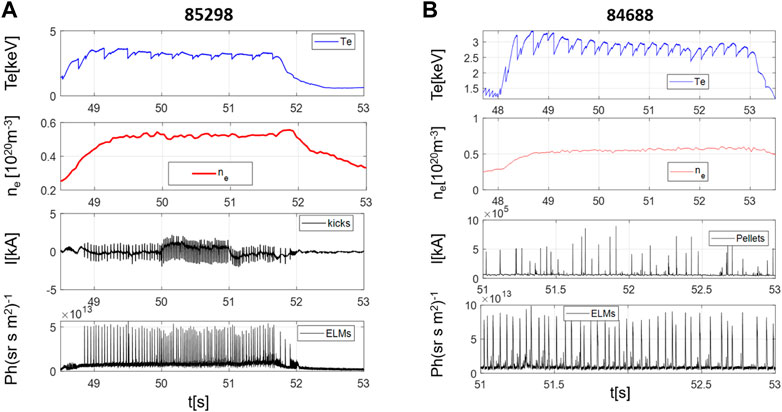
FIGURE 1. (A) example of ELM pacing via vertical kicks on JET. From top to bottom: central electron temperature, central electron density, currents in the ERFA amplifiers, Dα to detect the ELMs (see Section 4.2). (B) example of ELM pacing with pellets in JET. From top to bottom: central electron temperature, central electron density, microwave cavity signal to detect the arrival times of the pellets in the plasma, Dα to detect the ELMs (see Section 5.1).
A second very important alternative for controlling ELMs consists of pacing with pellets, mm sized bodies composed from frozen hydrogen fuel [5]. Given the fact that the reliability of pellet injectors is improving very fast, the approach is gaining favour. On the other hand, the details of the interactions of the pellets with the plasma remain difficult to model in detail. Indeed, the quasi periodic nature of the ELMs renders the assessment of their actual efficacy problematic because, after any pellet, an ELM is always bound to occur, if enough time is allowed to elapse. This problem is more severe than in the case of the kicks, which, as already mentioned, are much more flexible and allow verifying their effects much more easily, for example by scanning the amplitude or the frequency of the modulation in the same discharge. In any case, the issue of pellet efficiency has already been addressed on JET with a series of really sophisticated causality detection tools for time series [16–19]. The obtained results proved clearly that simple analysis tools, such as banal measures of correlations, can be significantly misleading. Indeed in many experiments, the triggering efficiency of pacing pellets turned out to be much higher than originally claimed.
One of the main remaining issues, to optimise ELM triggering, either via vertical kicks or with pellets, is the determination of the relative importance of phase and amplitude contributions to synchronization. Clarifying this aspect could also improve the understanding of the ELM dynamics. In any case, it would allow better tuning of kicks amplitude and the pellets mass and timing, which could be important in the next generation of devices. Better phasing of the vertical kicks would permit to operate them at lower amplitude with the same level of efficiency, reducing the plasma displacements to a minimum, with a consequent reduction of the repercussion of the scheme on the vacuum vessel, control coils and power supplies, which would render the approach more palatable. With regard to the pellet pacing, in machines of ITER class, a very accurate control of the density is expected to be crucial. The radiated fraction, detachment and disruptivity can be strongly affected by even relatively minor differences in density. Good understanding of the relative importance of amplitude and phase of the pellets, with respect to the ELM cycle, could therefore allow reducing the fuel expenditure, giving more leeway to other forms of control. However, the difficulty of discriminating the effects of amplitude and phasing of pellets for triggering ELMs can be easily appreciated from the plots of Figure 1, showing a representative JET discharge. In addition to the involved character of the diagnostic signals, it should also be considered that present day pellet injectors allow for limited tuning during experiments. In most discharges, the frequency has to be set in advance and remains constant during the discharge. Recently on JET, feed forward dual frequency injections of pellets have been extensively used for scenario development (see section 6.1). Pellet mass is even more complex to modify, requiring the change of barrels, which can normally be implemented only between experimental sessions. Information theoretic indicators for causality detection (see Section 3) become therefore very useful to investigate the details of synchronization with pellet injectors.
Sawteeth triggering with ICRH modulation
The centre of tokamak plasmas very often exhibits macroscopic oscillations of the main quantities under a wide range of conditions but typically when the safety factor on axis falls below 1. Also these oscillations have the character of non-linear charge and fire instabilities, whose essential feature is the presence of two time scales. The resulting effects of the dynamics, in the central plasma parameters, present a slower phase, in which the confinement improves and the temperature and density in the core tend to increase. This phase is then followed by a much faster reconnection, with consequent expulsion of material from the centre and a fast drop of the kinetic quantities particularly of the on axis temperature. The time evolution of these oscillations resembles a sequence of sawteeth, from which they derive their name.
In the phase immediately following the crash, the energy, ejected from the plasma core, typically induces an increase of the temperature in the outer plasma regions. The radial coordinate, separating the regions of drop and increase of the temperature, is called the sawtooth inversion radius. In the vast majority of cases, the sawtooth cycle occurs only when the plasma safety factor (q) is smaller than one in the plasma central region. Since the inversion radius is typically located close to the q = 1 flux surface, it is believed that the sawtooth instability is triggered by the growth of an (n,m)=(1,1) kink mode [39]. More sophisticated models of the instability are available in the literature but are not necessary for the comprehension of the present work [40–42].
In the perspective of scenario development for ITER and DEMO, the effects of sawteeth have to be evaluated carefully. On the one hand, if they are not too large, they normally cause only a moderate degradation in energy confinement. On the other hand, they can be beneficial in terms of particle confinement, because they are expected to contribute to the expulsion of heavy impurities and helium ash from the plasma core of the reactor. The critical aspect is the amplitude of their crash, which, if too large, can constitute a seeding for more deleterious instabilities, namely neo-classical tearing modes (NTM’s), particularly those associated with outer flux surfaces, where the safety factor q assumes a rational value (typically q = 2 or q = 3/2). In their turn, NTMs can degrade the confinement properties and even affect the plasma global stability, triggering the chain of events leading to disruptions. It is therefore essential to limit the amplitude of sawteeth and this can be achieved by influencing their period. In analogy with the ELMs, again the principle consists of triggering sawteeth sufficiently often to avoid their excessive growth.
Since an essential element of sawteeth are magnetic reconnections, taking place close to the q = 1 surface, the evolution of these instabilities can be altered by modifying the local current profile with actuators, particularly Electron Cyclotron Resonance Heating and Current Drive (ECRH) systems [10–14].
An alternative approach to sawtooth pacing is based on modulating ICRH power, which is believed to act not on the local current profile but on the distribution function of energetic ions. In their turn, the fast ions are known to have the potential to influence the sawtooth cycle through their effect on the pressure profile. The details of the fast ions orbits, circulating near the q = 1 surface, may also play a role on the stabilisation of sawteeth [42].
Leaving aside higher order effects, according the basic understanding of these instabilities, a sawtooth crash occurs when two conditions are simultaneously met: 1) the magnetic shear s at the q = 1 surface crosses a certain threshold
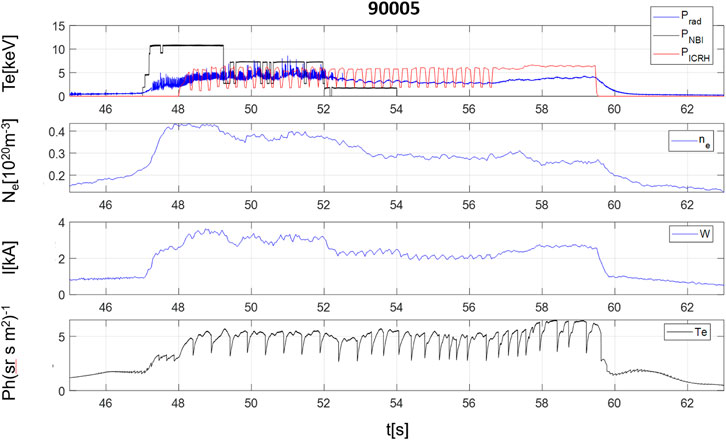
FIGURE 2. Typical experiment of sawteeth modulation with ICRH in a JET H mode plasma. From top to bottom: additional heating powers, central electron density, plasma internal energy W, central electron temperature (see Sections 5.2 and 6.2).
Analogously to the ELM case, disentangling the amplitude and phase component of the pacing would be beneficial. It would help not only to shed light on the physical mechanisms leading to the pacing but could also allow optimising the ICRH power required. Since, particularly in metallic devices, ICRH is used nowadays for many different purposes, from the investigation of fast particle physics to the control of impurities, being able to achieve good sawteeth synchronization with a minimum of power would be valuable, since it would free RF power for other tasks.
Analysis of causal interactions across time scales
This section is devoted to the description of the analysis tools implemented to investigate the interactions between drivers and targets in synchronization experiments. As already mentioned, the main goal consists of discriminating the different causal effects of the drivers’ phase and amplitude in pacing schemes. Subsection 3.1 is an overview of the techniques implemented to decompose the signals and extract their phase and amplitude components for the subsequent analysis. In Subsection 3.2, the information theoretic indicators adopted for causality detection are described in detail. The issue of determining the statistical relevance of the results is addressed in Subsection 3.3.
Signal decomposition
A scale-wise decomposition of the signals into (quasi) oscillatory components is necessary for the study of the interactions across time scales [43, 44]. A convenient way to decompose the time series is the continuous complex wavelet transform (CCWT) [45]. This is not the first time that wavelets have been applied to the investigation of edge-localized modes. An example of wavelet deployment to investigate ELM precursors, including the Morlet wavelet implemented in this work, is given in [46]. Wavelets have also been used to study turbulence in fusion plasmas [47]; however, in the present paper, the technique is applied for the first time to the concept of correlation between pacing techniques, specifically vertical kicks and pellet ELM pacing and ICRH sawtooth pacing.
CCWT converts the time series
A common choice is the Morlet wavelet [48]:
where
The complex wavelet coefficients
where e
A set of instantaneous phases and amplitudes can be derived for the vertical kicks/pellets and ELM time series:
Mutual information, its conditional version and transfer entropy
A wide variety of methods, for measuring the degree of synchronization in coupled dynamical systems, have been proposed. They all share Reichenbach’s common cause principle, which states that, if variables are dependent, then they are in a causal relation or they depend on a common driver [49]. A vast majority of the techniques use the additional stronger hypothesis that causality can be assessed by predictability. This assumption promoted by Granger [50] states that if a signal helps predicting another one, it can be considered to causally influence it. For reviews on this subject the reader is referred to [51, 52].
For the analysis of causal interactions across time scales, the mutual information (MI) concept has proved to be a reliable tool [53]. In this interpretation, causality is equated to information transfer.
The mutual information (MI) is an information-theoretic functional of probability distribution functions. It constitutes a measure of the general statistical dependence of two random variables, of the mutual relation between them. In particular, it quantifies the amount of information about one random variable, which can be derived by the knowledge of another one. In this perspective MI is also known as the Information Gain [54].
For discrete variables, the MI can be explicitly written as:
Where Px,y is the joint distribution of the two random variables X and Y, and Px, Py their marginal distributions. To interpret Equation 6, it should be remembered that the mutual information is always non-negative and reduces to zero only when the joint distribution Pxy is exactly equal to the product of the marginals, i.e. when the variables X and Y are independent [54]. Of course, if the two random variables are independent, no information about one can be derived by the knowledge of the other. The mutual information is also monotonic, in the sense that it keeps increasing when the difference between the two pdfs becomes larger.
A process
In general
Explicitly, based on Takens theorem, the conditional mutual information can be expressed in time series representation by the relation:
As noticed in [57], exactly the same formulation can be used for Markov processes of finite orders m and n. Indeed, the idea of the transfer entropy, introduced by Schreiber [58], is based on the use of finite-order Markov processes, aiming to provide a measure quantifying the causal information transfer between systems. It can be proved that transfer entropy is in fact an equivalent expression of CMI (see [57] for details).
In the present approach, the conditional mutual information has been estimated using the k-nearest neighbour (kNN) algorithm [59]. This method is able to quantify the mutual information from a finite data set, without requiring specific assumptions about the distribution of the variables. The calculation is based on expressing data points in neighbourhood volumes in terms of distances between each data point and the other data points in the neighbourhood. The method provides accurate estimates, but at the price of a non-negligible computational time.
The assessment of statistical significance
The set of instantaneous phases and amplitudes derived for the vertical kicks/pellets and ELM time series,
-the influence of kicks/pellets phase on the ELM phase (phase-phase map)
-the influence of kicks/pellets amplitude on the ELM amplitude (amplitude-amplitude map)
-the influence of kicks/pellets phase on the ELM amplitude (phase-amplitude map)
-the influence of kicks/pellets amplitude on the ELM phase (amplitude-phase map)
Each element of these maps is calculated for a certain value of the central period
In principle, due to physical reasons, the causal interaction is expected to be a nonlinear process. On the other hand, this nonlinearity could be not necessarily reflected in the measured signals and therefore the existence of nonlinear components should be proved. Also, spurious correlations between signals may emerge from linear stochastic processes. These components are not relevant for the physical interaction between the two dynamical systems and should be filtered. An efficient method to cope with these problems is the surrogate data testing [60].
The main idea behind surrogate data analysis is to compare the maps derived from the available experimental time series with the maps obtained from a large number of time series satisfying a certain null hypothesis. The null-hypothesis is that the data were generated by a stationary linear Gaussian process, or equivalently, that the data does not contain any nonlinear structure. In the present study, surrogate time series have been obtained by taking the Fourier transform of the original time series, randomising the phases (of the Fourier components) and transforming back into the temporal domain. The surrogate time series have the same spectrum but no interactions between processes at different time scales. A number of 50 surrogates have been calculated for each phase or amplitude time series and the conditional mutual information analysis has been repeated for each realization. In order to invalidate false causalities, the mean and the standard deviation of the results provided by the set of 50 surrogates have been computed. Then the mean plus three times the standard deviation has been defined as the threshold (99% significance level): only CMI values of the original time series above this level are considered statistically significant.
Testing the techniques with synthetic data and experimental signals
This section is devoted to building confidence in the capability of the proposed technique to handle properly data of the type collected in the pacing experiments characteristic of tokamak devices. To this end, Subsection 4.1 reports some numerical tests, with challenging examples of synthetic data, considered a benchmark in the literature on pacing of nonlinear quasi periodic systems. In Section 4.2 the analysis tools are benchmarked with dedicated JET experiments, which exploit the flexibility of the VS. system to obtain consolidated and easily interpretable results about the pacing of ELMs via vertical kicks.
Numerical tests with synthetic data
Synthetic data has been used to test the capability of the above described method to correctly identify the causality patterns. Numerical simulations, of the type widely used in the literature for testing this kind of tools, have been performed. The results for a numerical case related to the cross-frequency coupling (CFC), very relevant to the following real life applications, are presented first. CFC is an intensively studied phenomenon in neuroscience due to the increased evidence related to its fundamental role in the execution of cognitive functions like memory and learning [61–64]. Particular attention has been devoted to the modulation of the amplitude of high-frequency oscillations by the phase of low-frequency oscillations. A widely used synthetic signal has been designed by Tort et al. [61]. The time series are obtained as the sum of two sinusoids and an additive noise component:
where the amplitude of the high frequency component
The amplitude of the sinusoidal components
Simulations have been performed using the following parameters:
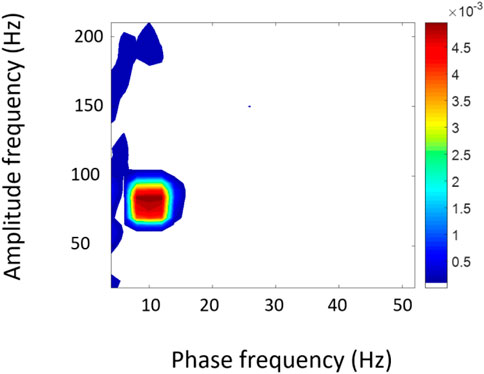
FIGURE 3. Causal map revealing the phase-amplitude coupling for the signal generated by Eqs 9, 10. The colour code represents the level of coupling derived with the conditional mutual information CMI. The position of the central spot in the CMI map indicates the coupling between the slow oscillation phase (10 Hz) with the amplitude of the faster rhythm (80 Hz).
As an additional reference test, a simulated signal for cross-frequency amplitude-amplitude coupling, provided in [64], has been analysed. The synthetic signal comprises oscillations of 10-Hz and 40-Hz, whose amplitudes are simultaneously modulated by a 2-Hz sinusoidal wave. The signal, generated for 100 s with a sampling rate of 300 Hz, is available from the repository [65]. A 10% Gaussian noise has been superimposed on the signal (Figure 4 - left). CMI correctly displays a spot around the plane point 10 Hz × 40 Hz (Figure 4 - right).
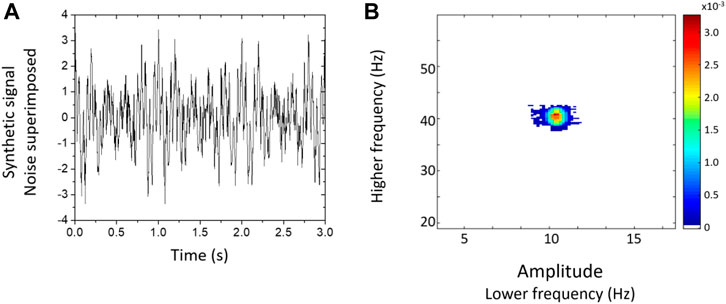
FIGURE 4. (A) the first 3 s (out of 100 s) of the synthetic signal with 10-Hz and 40-Hz oscillations, whose amplitudes are simultaneously modulated by a 2-Hz sinusoidal wave. (B) the position of the central spot in the CMI map corresponds to the coupling the 10 Hz and 40 Hz oscillations.
It is worth mentioning that the investigation of the numerical cases just reported, and other similar, has confirmed the potential of the proposed methodology compared to more standard techniques such as bicoherence [66]. Bicoherence or bispectral coherency is a squared normalised version of the bispectrum, which takes values between 0 and one and is therefore often used to quantify the phase coupling between signals and to search for nonlinear interactions. The Fourier transform third-order cumulant is called bispectrum or bispectral density. Unfortunately, it cannot take properly into account nonlinearity in non-stationary conditions [67, 68]. This can be easily understood considering that it is based on the Fourier transform. Nonlinear oscillations with non-stationary amplitude may produce spurious amplitude-amplitude coupling when Fourier analysed. Even a slight nonlinearity in the waveform alone can induce strong spurious amplitude coupling over a wide range of frequencies. The main reason for this problem is that the Fourier transform assumes sinusoidal oscillations with constant amplitudes. Even for oscillations or waves at a fixed frequency, the power will spread into a close spectral region. Moreover, since the Fourier transform decomposes a nonlinear waveform with sinusoids, it must utilise not only the fundamental frequency but also its harmonics. Consequently, although the original does not contain high-frequency oscillations, the Fourier spectrum can have significant powers at high (harmonic) frequencies [69]. Therefore, amplitude coupling can be spuriously detected due to even minor nonlinear non stationary amplitude oscillations. It has also been proven that the similar limitations of the Fourier analysis can also lead to spuriously detect phase synchronization [70].
Analysis of dedicated experiments devoted to understanding the ELM pacing with vertical kicks
A few years ago, a series of dedicated experiments were conducted on JET, to study the dependence of the vertical kicks performance on the basic parameters influencing their efficiency. In particular, the vertical kicks efficacy with varying amplitude of their amplitude was investigated in great detail [34]. JET elongated plasmas are highly vertical unstable and therefore their position must be carefully controlled. To this end the vertical stabilisation system generates a radial field, variable at high frequency, to counteract the possible disturbances due to either plasma instabilities or external sources. The radial field is generated by four poloidal field coils, located outside the vacuum vessel and driven by a high speed voltage amplifier. In the experiments with the ITER Like Wall (see Section 5.1) described in the following, these coils were energised by the Enhanced Radial Field Amplifier (ERFA), the new power supply of the vertical stabilisation system installed in 2009–2010 [71, 72]. The ERFA has the capability of delivering ±12 kV and a maximum output current of ±5kA, a significant improvement with respect to the previous FRFA system.
The experimental approach consisted of applying vertical kicks of different amplitude to discharges with fixed current, field and plasma shape. The perturbation was varied by increasing the voltage excursion of the ERFA. The reference plasma for these ELM control experiments is a low triangularity shape (average δAV = 0.22) with the strike point position in the best pumping location to optimise the density control [34]. The experiments described were deuterium plasmas with IP = 2 MA, BT = 2.2 T with mainly neutral beam heating and low gas dosing, to avoid impurity accumulation and achieve a stable Type I ELM regime. The main properties of one of these discharges are shown in Figure 5.
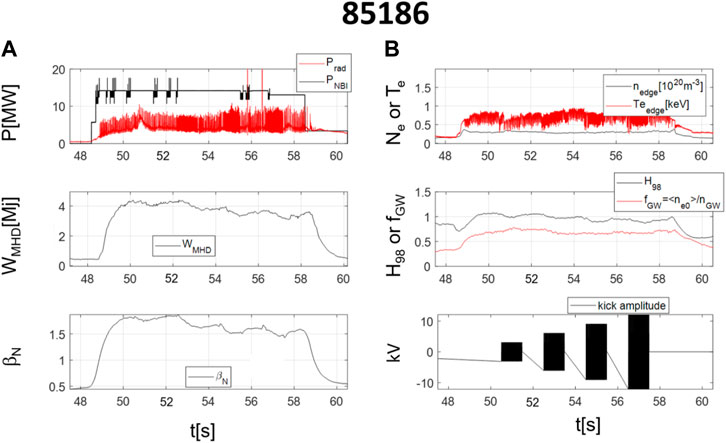
FIGURE 5. Main plasma parameters of discharge 85,186. From top to bottom (A) additional heating powers, plasma internal energy, normalised plasma beta. From top to bottom (B) central electron temperature and density, global improved confinement factor and Greenwald density fraction. The vertical black rectangles in the bottom left plot indicate the interval of the kicks, in increasing order of amplitude. The triggering efficiency was estimated in [34] to be low, about 40%, in the first interval and almost 100% in the following three intervals.
The good stability for about 10 s, achieved in the previously described scenario, allowed performing a scan of the amplitude of the vertical kicks in the same discharge. Four sequences of kicks at a frequency of 45 Hz were applied to the discharge, with increasing amplitude AK of the perturbation: AK = 8, 15, 22, 28 Wb. On the contrary, the duration of the kicks was kept constant at 2.5 ms.
On the basis of the delay between the kicks and the following ELM, in [34] it was assessed that the efficiency of the scheme was only 40% for the 8 Wb amplitude interval. The delay regularised almost perfectly already at the following level of kick amplitude, 15 Wb. For this interval, and the following two, it was therefore estimated that the efficiency of the kicks was practically 100%. Therefore, the experimental evidence is that for Ak ≥ 15 Wb, the ELM frequency is synchronised with the externally imposed kick frequency. Above this threshold it was therefore considered that every kick practically triggered an ELM.
The previously reported interpretation of the experimental evidence is confirmed by the analysis performed with the technique proposed in the present work. Figure 6 reports the various couplings estimated with the method of combing the wavelet decomposition with the conditional mutual information. As can be derived by simple inspection of the plots, all the forms of causality are very low for the interval with Ak = 8 Wb. They increase significantly, and remain basically constant for all the other three intervals. It is also interesting to notice that the main increase in the CMI is detected for the Amplitude-Amplitude and Amplitude-Phase relations. This is perfect agreement with the implementation and the results of the experiment. The amplitude of the perturbation was increased and, above 15 Wb, the kicks practically have an efficiency of 100% in triggering ELMs. The higher CMI for the Amplitude-Amplitude interaction and its almost constant value above this threshold are therefore perfectly justified and fully in harmony with the previous analysis [34]. The CMI shows a similar trend also for the Amplitude-Phase influence; this can be interpreted considering that, as reported in [34], for the three intervals with equal or above 15 Wb, not only the triggering efficiency is 100% but the delay between the kicks and the ELM crashes is practically constant. The CMI has therefore detected also this effect of the increased driver amplitude on the phase of the target.
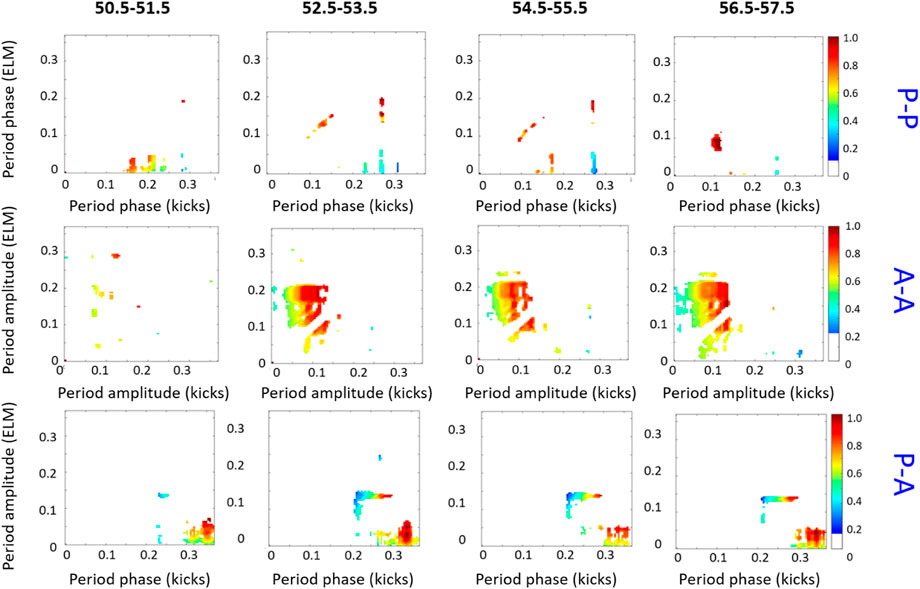
FIGURE 6. Values of CMI for the experiment of ELM pacing with vertical kicks, whose main characteristics are shown graphically in Figure 5. The axes report the various types of interaction (amplitude-amplitude, phase-amplitude etc.). The colour code represents the level of coupling derived with the conditional mutual information CMI. The CMI plots corresponding to phase-phase (P-P, first row), amplitude-amplitude (A-A, second row) and phase-amplitude (P-A, third row) are shown for four time intervals, from left to right column [50.5–51.5]s, [52.5–53.5]s [54.5–55.5]s, [56.5–57.5]s. CMI plots are shown with the period of the driver time series (kicks evolution) on the x-axis and driven time series (ELMs) on the y-axis. Periods are measured in seconds. Shown are the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
This example is rather important, because it reveals how the proposed methodology manages to deal quite effectively with signals of the same type and form of those encountered in the actual experiments.
Application to the optimisation of pacing experiments in JET with the ILW and AUG
In this section the conditional mutual information is applied to the investigation of the coupling in phase and amplitude between the drivers (pellets, ICRH) and the targets (ELMs, sawteeth). The results obtained for the pellets pacing experiments in AUG and JET are covered in Subsection 5.1. The triggering of sawteeth with ICRH is discussed in Subsection 5.2, presenting data of JET, since the experiments have been historically performed on this machine only. On both devices, the discharges were dedicated experiments, devoted to studying and optimising the respective synchronization schemes. They implement constant frequency pacing, in which the externally driven perturbation are applied with a strictly fix period and amplitude.
ELMs pacing with pellets in AUG and JET
The causal interactions across time scales between pellets and ELMs have been investigated for some JET and AUG discharges. The main properties of two representative pulses are reported in Figure 7. All the analysed discharges of this type have always shown similar behaviour, from the perspective of the synchronization properties, and therefore only some representative cases are reported in detail. In JET the diagnostic used consists of Dα emission (Balmer alpha, n = 3 - > n = 2) measured with diodes seeing the divertor and the entrance the pellet injector, a quite reliable technique for the studies reported in this work [73]. In AUG the ELMs are detected with shunts in the divertor tiles [5].
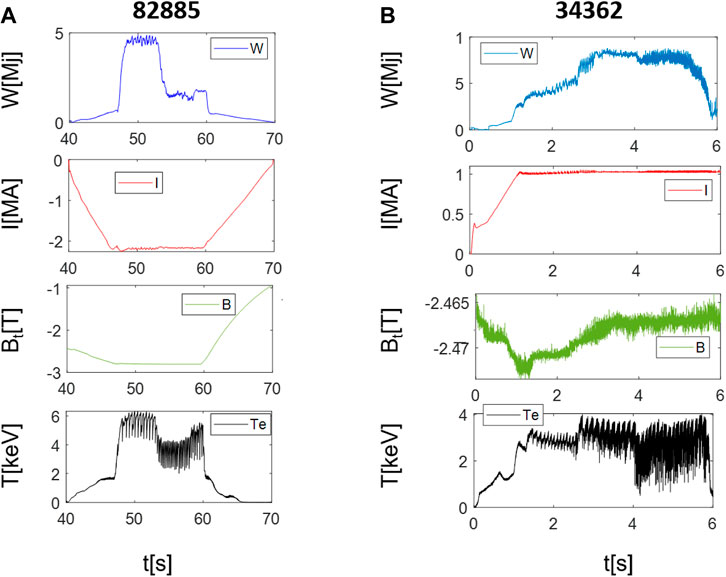
FIGURE 7. Typical examples of experiments devoted to ELM pacing with pellets. (A) JET and AUG (B). From top to bottom: plasma internal energy, plasma current, toroidal field, central electron temperature.
For JET, the discharges analysed in the following belong to campaigns performed during the first year of operation of JET with the new ITER-like wall, which was installed during a major shutdown in 2009–2011 [30, 31]. In this major JET upgrade, the graphite plasma-facing components were replaced with a combination of beryllium (Be) in the main chamber and tungsten (W) in the divertor, to mimic as much as possible ITER mix of first wall materials. The modification of the plasma facing components resulted in an order magnitude reduction of the fuel retention [74], while the plasma C content was reduced on average, by a factor of 20. Oxygen levels were also reduced by roughly one order of magnitude and the Zeff dropped from 1.9 to 1.2 (again on average) [75]. To re-establish the performance of high confinement scenarios it was necessary to carefully control the metallic impurity sources and the heat loads. As expected, JET with the ILW confirmed that the ELM frequency is the main factor for the control of metallic impurity influxes.
A baseline scenario with low triangularity (IP = 2.0 MA, Bt = 2.1T, q95 = 3.3; lower and upper triangularities δl = 0.36 and δu = 0.19, respectively) was chosen as the scenario for the dedicated pacing experiments discussed in this work. This configuration proved to be sufficiently robust against impurity accumulation and radiation induced confinement degradation even at low heating power (10 MW NI heating) and gas flux (0.5 × 022 Ds−1) at low ELM frequencies of 6–8 Hz. Small pacing pellets were injected from the Low Field Side (LFS) at a nominal size and speed of 2.1 × 1020 D, 170 ms−1 respectively. Unfortunately, the installed transfer system causes a reduction of performance [42]. Whereas almost all the fuelling pellets arrived in the plasma when injected from the outboard (LFS), only 30–50% of the smaller pacing pellets make it through the same flight line and only with significant mass scatter and with reduced speed between 60 and 110 ms−1. In any case, in the best performance cases, a maximum frequency of 32 Hz is observed, albeit transiently, corresponding to a 4.5 times enhancement of the initial pellet frequency of 7 Hz.
The signals, identifying the occurrence of ELMs and indicating the arrival of the pellets into the plasma, have been decomposed with the continuous wavelet transform, using the Morlet wavelet, as described in Subsection 3.1. An example of these decomposition is presented in Figure 8 for JET pulse #82885. Then conditional mutual information analysis has been applied for deriving causality maps.
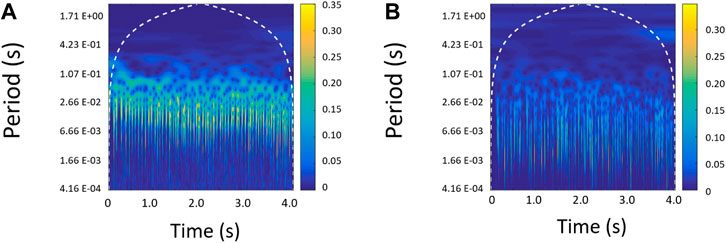
FIGURE 8. Representation of the absolute value of the complex wavelet transform coefficients for the signals identifying the occurrence of ELMs (A) and the arrival of the pellets into the plasma (B). Each line in the images represents the evolution (a time-series) corresponding to a fixed temporal scale. The period is plotted in logarithmic scale. The time series of the instantaneous phases and amplitudes are used for the CMI calculation.
Figure 9 presents two causal maps for JET pulses #82854 and #82855. Only the amplitude-amplitude CMI assumes meaningful levels. All the other forms of coupling are not statistically significant. The main conclusion is therefore that it is possible to identify patterns of causality only in the case of amplitude-amplitude synchronisation. This is in agreement with the setup of the experiments. As reported in [42], the triggering efficiency was found to depend strongly on the pellet mass and speed. Moreover analysis with the code ELITE indicate that, before the pellet arrival, the plasma edge was well inside the stability boundary [76]. These observation support the interpretation that the amplitude of the perturbation is the main pacing effect. When the mas and speed of the pellet are high enough, they tend to make the plasma cross the stability boundary. When the external driver is not strong enough, the edge of the plasma remains stable and the ELM dynamics is not significantly altered. Consequently, the CMI detects no effect of the pellets phase on the instability.
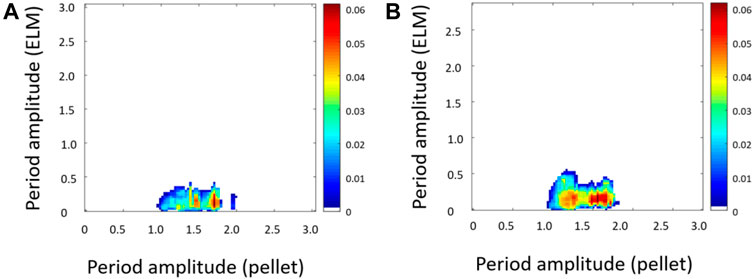
FIGURE 9. Amplitude (pellet)–amplitude (ELM) causality for the JET pulses #82885 (A) and #82854 (B). The colour code represents the level of coupling derived with the conditional mutual information CMI. For both pulses only the amplitude-amplitude component of the coupling is reported, because the others are within the uncertainties range of the method. CMI plots are shown with the period of the driver time series (pellets) on the x-axis and driven time series (ELMs) on the y-axis. Periods are measured in seconds. Shown are the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
For AUG the investigation has been focussed on high density small ELMs regime pulses. Indeed an attractive alternative, to reduce the peak thermal loads on the plasma facing components, is the confinement regimes with small ELMs such as type-II or grassy ELMs [77–80]. In these regimes the plasma is in the H-mode, with good confinement compared to the type-I ELM regime, but with much lower energy fluxes on the divertor tiles. Within EUROfusion programme, a series of experiments have been conducted on AUG and TCV to investigate the conditions leading to the onset of small ELM regimes. On both machines, two conditions have to be fulfilled at the same time to achieve these regimes with high confinement. First, the plasma density at the separatrix must be sufficiently high, typically above about 30% of the Greenwald limit. This leads to flattening of the pressure profile around the separatrix; consequently, the pedestal width is shrunk which in turn increases the stability of type-I ELMs. The second facilitating condition involves the magnetic configuration, which has to be close to a Double Null (DN) configuration. This topology of the fields results in a lower magnetic shear in the vicinity of the separatrix. Numerical simulations indicate that ballooning modes, with high toroidal mode numbers, are driven by the local pressure gradient and are stabilized by a higher magnetic shear [81, 82]. Therefore, it is believed that small ELMs are ballooning modes driven unstable in the vicinity of the separatrix. This explanation fits both the evidence and the background knowledge on these modes, which indeed have a high toroidal mode number and are therefore radially narrow [83]. They are known for being driven by the local pressure gradient and stabilized by the magnetic shear.
An overview of a typical discharge of this type of experiments is shown in the right column of Figure 7. The deployment of the wavelet decomposition and the conditional mutual information reveals that amplitude-amplitude causal interaction is again the dominant effect but the phase-phase interaction is of the same order of magnitude. Phase-amplitude and amplitude-phase interactions are one order of magnitude lower. This is illustrated in Figure 10 for AUG pulse #34462.
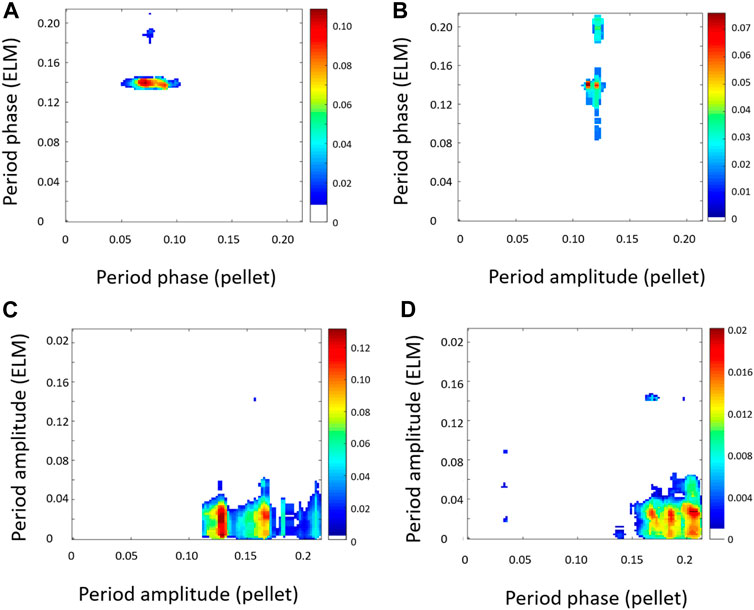
FIGURE 10. CMI plots patterns showing causal interactions between pellets and ELMs time series for AUG pulse #34462, for the time interval 5.2–5.5s: phase-phase (A), amplitude-phase (B), amplitude-amplitude (C) and phase-amplitude (D). Amplitude-amplitude causal interactions are the dominant effect but the phase-phase interactions are of the same order of magnitude. The colour code represents the level of coupling derived with the conditional mutual information CMI. Periods are measured in seconds. The figures display the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
A possible interpretation of this evidence is based on the observation that these discharges have high edge density. The additional density deposited by the pellets is therefore conjectured to have a smaller perturbation effect on the plasma stability. The ELMs are therefore not destabilised systematically by the simple increase of the local density but the timing of the pellets’ arrival plays a more important role. This effect shows in the appreciable values of the phase-phase component of the causal interaction detected by the CMI. Of course specific experiments should be designed to test this hypothesis but the proposed methodology seems to have a rather good potential for shedding light on this phenomenology of ELMs.
Sawteeth triggering with ICRH modulation in JET
The same kind of analysis has been performed also for sawteeth pacing by means of ICRH modulation on JET. Modulations in both L and H mode scenarios have been considered. Since the results are very similar, only the case of an H mode discharge is shown in the following for JET pulse #90005. The main quantities of a typical discharge of this series of experiments is reported in Figure 2.
In both cases (L and H mode), the main interaction is between amplitudes, as shown in Figure 11. Also, very localized phase (ICRH)-phase (sawtooth) and amplitude (ICRH)–phase (sawtooth) interactions are pretty evident. Signs of phase (ICRH) -amplitude (sawtooth) are clearly detectable but with lower amplitude. As already mentioned, the localization of the distinctive features on the maps is relatively similar for L-mode and H-mode phases of the pulses. This result is quite encouraging because in these discharges not attention was paid to synchronise the ICRH notches with the sawteeth phase. Consequently, there seem to be margins for improving this aspect of the coupling, a subject to be investigated in detail in future experiments.
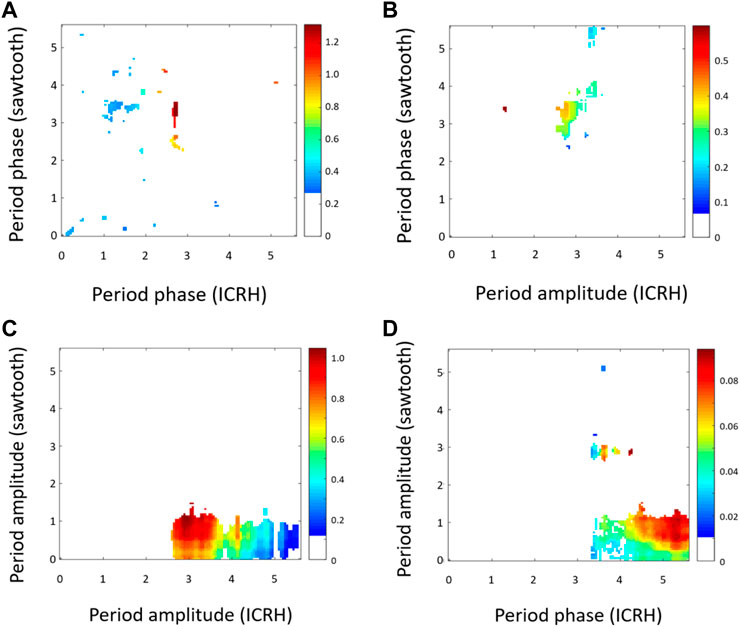
FIGURE 11. CMI plots patterns showing causal interactions between ICRH modulation and sawteeth time series for JET pulse #90005, for the time interval 48.5–55.5s: phase-phase (A), amplitude-phase (B), amplitude-amplitude (C) and phase-amplitude (D). Amplitude-amplitude and amplitude-phase causal interactions are dominant but phase-amplitude coupling is also detectable. The distinctive features on the maps are relatively similar for L-mode and H-mode phases of the pulses. The colour code represents the level of coupling derived with the conditional mutual information CMI. Periods are measured in seconds. The figures display the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
CMI plots patterns showing causal interactions between ICRH modulation and sawteeth time series for JET pulse #90005, for the time interval 48.5–55.5s: phase-phase (top-left), amplitude-phase (top-right), amplitude-amplitude (bottom-left) and phase-amplitude (bottom-left). Amplitude-amplitude and amplitude-phase causal interactions are dominant but phase-amplitude coupling is also detectable. The distinctive features on the maps are relatively similar for L-mode and H-mode phases of the pulses. The colour code represents the level of coupling derived with the conditional mutual information CMI. Periods are measured in seconds. The figures display the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
Examples of contribution to scenario optimisation and phase coupling
This section is devoted to the discussion of a couple of examples, which describe the potential of the develop tools to contribute to the understanding and the optimisation of pacing schemes. The first case concerns the issue of ELM pacing with pellets in experiments devoted to scenario development in preparation of the DT campaign. This example is important because the pellet pacing scheme is not the main objective of the experiment, but tries to fulfil its main intended role of controlling ELMs in support to scenario development. The second synchronisation experiment is meant to illustrate the importance of advanced data analysis tools to optimise phase synchronisation, in situations for which this is indispensable such as sawteeth triggering with ICRH modulation.
ELMs pacing for scenario optimisation on JET
During the scenario development in preparation for the DT campaign on JET, the use of pellet pacing has been increasingly used. Indeed, the injector has been recently upgraded and has reached a high level of reliability [73]. Consequently, it has proved a good tool to avoid ELM free phases, which are typically followed by giant ELMs having a not negligible detrimental effects on the influxes of impurities inside the last closed magnetic surface [84]. One of the more widely used schemes consists of programming two different pellet frequencies in feedforward, one for the ramp up of the plasma current and one, at lower frequency, for the steady state phase of the discharge. A typical example is reported in Figure 12, for a baseline scenario in deuterium at 3.5 MA and 3.35 T. The size and velocity of the pellets are of course the same because JET does not have the capability to vary these parameters during the discharges. Unfortunately, the efficiency of the pellets is much slower during the steady state part of the discharge, as can be appreciated also visually by simple inspection of the plots of Figure 12. In this so called Low Frequency (LF) various pellets are ineffective and the nature of the ELM they trigger is different, some of them having a compound nature.

FIGURE 12. Typical set up of the pellet frequency in the discharges of the baseline scenario for the operation at high current. (A) from top to bottom: neutral beam power and total emitted radiation, BeII to detect the ELMs, microwave cavity to determine the pellets timing, total plasma internal energy, neutron of emission, central electron temperature. On the (B) an expanded view of BeII and the microwave cavity signal.
Applying the technique proposed in the paper to these cases reveals a candidate interpretation of the difference in the efficiency and effects of the pellets. As shown in Figure 13, during the ramp up of the plasma current, the most important effect of the pacing is attributable to amplitude-amplitude synchronization. At the flat top, the phase amplitude becomes much more relevant.
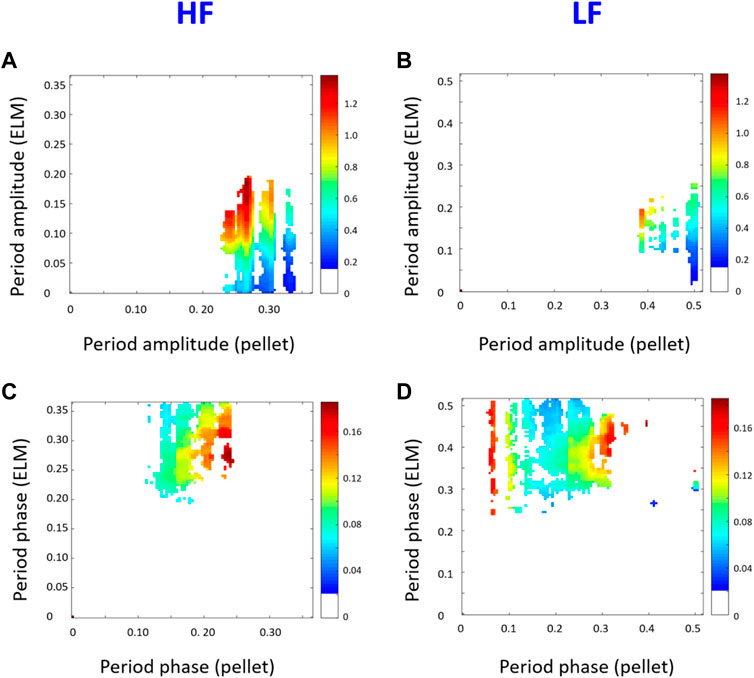
FIGURE 13. CMI plots patterns showing causal interactions between pellets and ELMs time series for AUG pulse #34462, for the time interval 5.2-5.5s: phase-phase (A), amplitude-phase (B), amplitude-amplitude (C) and phase-amplitude (D). Amplitude-amplitude causal interactions are the dominant effect but the phase-phase interactions are of the same order of magnitude. The colour code represents the level of coupling derived with the conditional mutual information CMI. Periods are measured in seconds. The figures display the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
A possible explanation of this experimental evidence consists of considering that the pellet size, remaining unchanged in the two phase LF and HF, is probably more effective during the ramp up of the plasma current, when the density of the plasma is lower. At the flat top, pellets of higher size would be required to produce the same effect in plasmas of much significantly higher density and input power. On the other hand, those pellets arriving just before the time of natural ELM crashes remain effective and this produce the increase in the phase amplitude component of the conditional mutual information. Experiments to verify this hypothesis could be planned on JET for the phase after the end of the deuterium tritium campaign.
Sawteeth pacing: Frequency optimisation
The optimisation of the sawtooth pacing with the ICRH modulation is a quite delicate matter. Both amplitude and frequency of the RF power must be set to the right values at the same time. Practically, the amplitude of the notches is typically easier to adjust, because it is always possible to err on the safe side by implementing a modulation larger than strictly necessary. Even if such a choice would induce an excessive perturbation of the plasma, the modulation would be effective in pacing the sawteeth. The amplitude of the notches can then be easily reduced to determine the optimal level. The effect of the frequency is more subtle. The effective operational window is typically quire narrow; too large or too low frequencies compromise significantly the efficiency of the pacing scheme.
CMI plots patterns showing causal interactions between pellets and ELMs time series for AUG pulse #34462, for the time interval 5.2–5.5s: phase-phase (top-left), amplitude-phase (top-right), amplitude-amplitude (bottom-left) and phase-amplitude (bottom-left). Amplitude-amplitude causal interactions are the dominant effect but the phase-phase interactions are of the same order of magnitude. The colour code represents the level of coupling derived with the conditional mutual information CMI. Periods are measured in seconds. The figures display the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
The tools developed in the context of this work can be very helpful in understanding the effects of the changes in amplitude and frequency of the modulation. A typical example is constituted by the couple of discharges 94,088 and 94,089 at JET. These were baseline shots at 2.2. MA/2.8 T. The neutral beam power was kept at about 20 MW.
In these two experiments, everything was kept basically constant except the frequency of the ICRH modulation, which was reduced from three to 2.5 Hz in the H mode phase of the discharges. The relation between the notches and the sawteeth is shown in Figure 14 for this confinement regime. It is worth noting that in these discharges, without the pacing, the natural period of the sawteeth would be about 0.8 s.

FIGURE 14. ICRH notches (blue) and sawteeth/electron temperature (red): discharge # 90,488 with ICRH notches at 3 Hz (A); bottom discharge # 90,489 with ICRH notches at 2.5 Hz. (B).
Simple inspection of Figure 14 reveals that the pacing of discharge 90,488 is less effective. Indeed, with the ICRH notches at 3 Hz, the sawteeth are more irregular. The situation is much better in discharge 90,489, in which the frequency of the modulation was reduced to 2.5 Hz. Indeed in this shot the synchronization between the ICRH modulation and the sawteeth crashes is almost perfect and the delay compatible with the slowing down time of the ions.
The pacing frequency being the dominant factor in determining the efficiency of the modulation is confirmed by the results of the analysis with the conditional mutual information. The CMI values for the most important forms of coupling are reported in Figure 15, for the interval between 48.5 and 52 s, when the plasma is in the H mode regime of confinement.
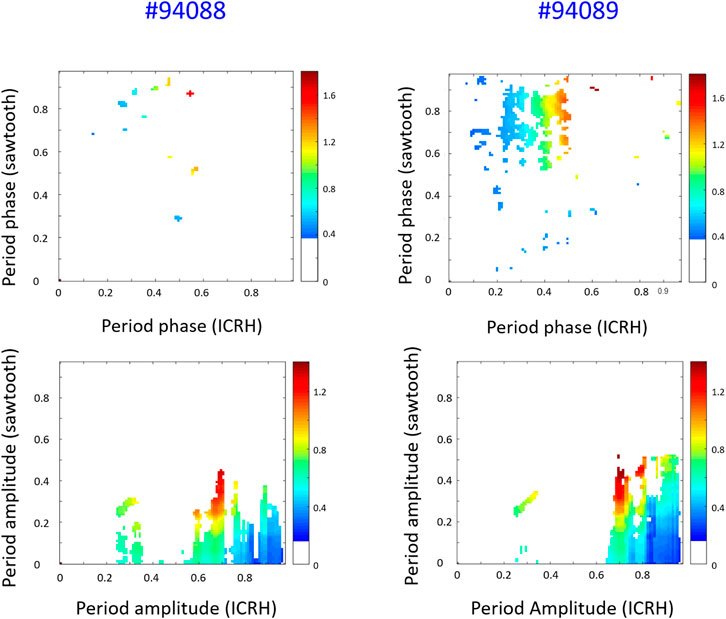
FIGURE 15. Comparison of the CMI for the phase-phase (top row) and amplitude-amplitude (bottom row) synchronisation of the discharges 90,488 (A) and 90,489 (B). The colour code represents the level of coupling derived with the conditional mutual information CMI. CMI plots are shown with the period of the driver time series (ICRH) on the x-axis and driven time series (sawtooth) on the y-axis. Periods are measured in seconds. Shown are the positive significance-level deviations from the 99th percentile of the average CMI calculated using 50 Fourier transform surrogates.
Inspection of the plots in Figure 15 reveals that the main difference in the two discharges is the phase-phase coupling, while the amplitude-amplitude remains basically the same. Since the amplitude of the notches is the same in the two cases, this evidence is coherent with the interpretation that the modulation at 2.5 Hz is more effective, because it improves the phase coupling between the RF and the plasma sawteeth instabilities. The modulation at 3 Hz was indeed too fast for the plasma dynamics to get in synchrony with the external modulation.
Discussion and conclusion
In this paper, a novel analysis approach is deployed for the first time to study fusion data, namely the investigation of synchronization experiments in tokamaks The combination of wavelet decomposition and information theoretic tools is aimed at understanding the nature of pacing techniques. Extensive numerical tests have proved the power and competitive advantages of the analysis tools developed. Their deployment for some dedicated and well understood experiments, implementing ELM pacing with vertical kicks, has confirmed the potential of the methodology to deal with experimental data of the type typical of tokamak signals.
Application to ELM pacing with pellets experiments in AUG and JET has shown the similarity between the two devices, particularly the prevalence of amplitude synchronization. In both machines, the amplitude-amplitude effect is the dominant one. For AUG small ELMs, the phase-phase synchronisation is also an important effect, while signs of synchronization between phases and amplitudes have been detected, but are one order of magnitude lower. The investigation of sawteeth triggering with ICRH modulation has also provided rather solid and coherent results. On JET, this pacing scheme shows some signs of phase modulation but much smaller than the amplitude-amplitude effect. In any case, even if dedicated experiments should be planned to confirm this aspect, the studied implementations of the synchronisation schemes would suggest that there are ample margins for improving the phase-amplitude driving, by better timing of the external perturbations with respect to the natural cycle of both instabilities.
The investigation of delicate experiments has confirmed that the developed tools could provide valuable help for the improvement of the pacing schemes. The analysis of the dual frequency pacing of the ELMs with pellets has revealed that the technique would benefit from varying also the mass of the pellets during the discharge. Indeed, the amplitude modulation due to the pellets is enough during the ramp up of the plasma current but is too small in the flat top, when the density has stabilised around its steady state value. Pellets of larger size would be more effective in the flat top but they would increase the density excessively in the ramp up of the plasma current. In some sawteeth triggering experiments with ICRH modulation a complementary situation arises. The amplitude of the notches remains sufficiently high but even a relatively minor increase in the frequency affects significantly the efficiency of the modulation, because the plasma dynamics does not manage to keep up with the speed of the modulation.
Of course, as powerfully argued in [85], all the intricacies of causality cannot be resolved only with observational techniques. The final answer can often come only from specifically designed experiments. These considerations apply also to the results reported in the present work, which describes the first pioneering applications of a newly developed analysis tools. Some of the tentative conclusions drawn with the proposed methodology will have to be confirmed or falsified experimentally.
Notwithstanding the cautionary remarks and limitations mentioned in the previous paragraph, the approach seems to have a good potential, to help in dealing with the practical problems, encountered in adjusting the pacing schemes of these instabilities in the perspective of the next generation of devices. In future machines, indeed, the plasma will have to be much more systematically controlled in real time. The feedback needs are not necessarily easy to integrate, since the various operational objectives can even translate into contradictory requirements to the control systems. Better understanding the relative importance of phase and amplitude coupling could therefore provide important margins of manoeuvring to the operators. Another aspect of the reactor operation, which is not always fully appreciated, is that any fine tuning of the scenarios will have to be much more efficient than in present day machines. These larger devices will not have the luxury of a lot of margins for trial and error adjustments for various reasons. First, the experiment time will be extremely expensive. Second, even relatively minor suboptimal regimes of operation could damage their structures. For example, loss of control of the ELMS can quickly shorten the life of the divertor. Interpretative tools, which can effectively guide the optimisation of pacing schemes, can be therefore very valuable.
In terms of future developments of the technique, one of the important steps involves the speeding up of the codes, which are computationally demanding. Once properly accelerated, the algorithms could be applied systematically to many discharges, to obtain more general conclusions. More generally and from a physics perspective, with suitable modifications the developed tools could be applied also to various ambitious forms of feedback, for example to the control of impurities or of distributed quantities [86]. Fine tuning of the current profile, for example, has become an important ingredient in ITER relevant scenarios such as the hybrid, and the mathematical techniques developed could provide support to the optimisation of feedback schemes of the type described in [87].
Data availability statement
The data analyzed in this study is subject to the following licenses/restrictions: and Euratom copyright and. Requests to access these datasets should be directed to and Kinga Gal, Kinga.Gal@euro-fusion.org.
Author contributions
TC and AM contributed to conception and design of the study. MG, EP, LS, PL, and GH organized the database. And performed the statistical analysis. AM and TC wrote the first draft of the manuscript. Data validation performed by MG, EP, LP, PL, and GH. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014-2018 and 2019-2020 under grant agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 — EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A universal concept in nonlinear sciences. In: Cambridge nonlinear science series book (2001). Cambridge, United Kingdom. p. 12.
2. Stone L, Olinky R, Blasius B, Huppert A, Cazelles B. Complex synchronization phenomena in ecological systems. AIP Conf Proc (2002) 622:476. doi:10.1063/1.1487695
3. Nolte D. Introduction to modern dynamics: Chaos, networks, space and time. Oxford, United Kingdom: Oxford Univerity Press (2015).
4. Eroglu D, W Lamb JS, Pereira T. Synchronisation of chaos and its applications. Contemp Phys (2017) 58(3):207–43. doi:10.1080/00107514.2017.1345844
5. Lang PT, Loarte A, Saibene G, Baylor LR, Becoulet M, Cavinato M, et al. ELM control strategies and tools: Status and potential for ITER. Nucl Fusion (2013) 53:043004. doi:10.1088/0029-5515/53/4/043004
6. Loarte A, Huijsmans G, Futatani S, Baylor LR, Evans TE, Orlov DM, et al. Progress on the application of ELM control schemes to ITER scenarios from the non-active phase to DT operation. Nucl Fusion (2014) 54:033007. doi:10.1088/0029-5515/54/3/033007
7. Graves JP, Lennholm M, Chapman IT, Lerche E, Reich M, Alper B, et al. Sawtooth control in JET with ITER relevant low field side resonance ion cyclotron resonance heating and ITER-like Wall. Plasma Phys Control Fusion (2015) 57:014033. doi:10.1088/0741-3335/57/1/014033
8. Chapman IT, Buttery RJ, Coda S, Gerhardt S, Graves JP, Howell DF, et al. Empirical scaling of sawtooth period for onset of neoclassical tearing modes. Nucl Fusion (2010) 50:102001. doi:10.1088/0029-5515/50/10/102001
9. Lennholm M, Eriksson L-G, Turco F, Bouquey F, Darbos C, Dumont R, et al. Demonstration of effective control of fast-ion-stabilized sawteeth by electron-cyclotron current drive. Phys Rev Lett (2009) 102:115004. doi:10.1103/physrevlett.102.115004
10. Lennholm M, Eriksson L-G, Turco F, Bouquey F, Darbos C, Dumont R, et al. Closed loop sawtooth period control using variable ECCD injection angles on tore supra. Fusion Sci Tech (2009) 55:45–55. doi:10.13182/fst09-a4052
11. Paley JI, Felici F, Coda S, Goodman TPF, Piras F. Real time control of the sawtooth period using EC launchers. Plasma Phys Control Fusion (2009) 51:055010. doi:10.1088/0741-3335/51/5/055010
12. Goodman TP, Felici F, Sauter O, Graves JP. Sawtooth pacing by real-time auxiliary power control in a tokamak plasma. Phys Rev Lett (2001) 106:245002. doi:10.1103/physrevlett.106.245002
13. Lauret M, Felici F, Witvoet G, Goodman TP, Vandersteen G, Sauter O, et al. Demonstration of sawtooth period locking with power modulation in TCV plasmas. Nucl Fusion (2012) 52:062002. doi:10.1088/0029-5515/52/6/062002
14. Frigione D, Garzotti L, Lennholm M, Alper B, Artaserse G, Bennett P, et al. Divertor load footprint of ELMs in pellet triggering and pacing experiments at JET. J Nucl Mater (2015) 463:714–7. doi:10.1016/j.jnucmat.2015.01.048
15. Garzotti L, Lang PT, Alonso A, Alper B, Belonohy E, Boboc A, et al. Investigating pellet ELM triggering physics using the new small size pellet launcher at JET. In: Plasma Physics (Proc. 37th EPS Conf. Dublin, 2010), 34A. New York: European Physical Society (2010). P2.131.
16. Murari A, Craciunescu T, Peluso E, Gelfusa M, Lungaroni M, Garzotti L, et al. How to assess the efficiency of synchronization experiments in tokamaks. Nucl Fusion (2016) 56(7):076008. doi:10.1088/0029-5515/56/7/076008
17. Murari A, Craciunescu T, Peluso E, Gelfusa M. Detection of causal relations in time series affected by noise in tokamaks using geodesic distance on Gaussian manifolds. Entropy (Basel) (2017) 19(10):569. doi:10.3390/e19100569
18. Craciunescu T, Murari A, Lerche E, Gelfusa M. Image-based methods to investigate synchronization between time series relevant for plasma fusion diagnostics. Entropy (2020) 22(7):775. doi:10.3390/e22070775
19. Murari A, Craciunescu T, Peluso E, Lerche E, Gelfusa M. On efficiency and interpretation of sawteeth pacing with on-axis ICRH modulation in JET. Nucl Fusion (2017) 57(12):126057. art. 126057. doi:10.1088/1741-4326/aa87e7
20. Meucci R, Gadomski W, Ciofini M, Arecchi FT. Experimental control of chaos by means of weak parametric perturbations. Phys Rev E (1994) 49(4):R2528–31. doi:10.1103/physreve.49.r2528
21. Meucci R, Ginoux J-M, Mehrabbeik M, Jafari S, Sprott JC. Generalized multistability and its control in a laser. Chaos (2022) 32:083111. doi:10.1063/5.0093727
22. Meucci R, Euzzor S, Ciofini M, A Lapucci S. Demonstrating filtered feedback control near a boundary crisis. IEEE Trans Circuits Syst (2021) 68(7):3023–30. doi:10.1109/tcsi.2021.3077656
23. Euzzor S, Di Garbo A, Ginoux JM, Zambrano S, Arecchi FT, Meucci R. On the destabilization of a periodically driven three-dimensional torus. Nonlinear Dyn (2021) 103(2):1969–77. doi:10.1007/s11071-020-06174-5
25. Wesson JA, Gill RD, Hugon M, Schüller FC, Snipes JA, Ward DJ, et al. Disruptions in JET. Nucl Fusion (1989) 29(4):641–66. doi:10.1088/0029-5515/29/4/009
26. Snyder PB, Wilson HR, Ferron JR, Lao LL, Leonard AW, Mossessian D, et al. ELMs and constraints on the H-mode pedestal: Peeling–ballooning stability calculation and comparison with experiment. Nucl Fusion (2004) 44:320–8. doi:10.1088/0029-5515/44/2/014
27. Cannas B, Fanni A, Murari A, Pisano F. Nonlinear dynamic analysis of Dαsignals for type I edge localized modes characterization on JET with a carbon wall. Plasma Phys Control Fusion (2018) 60:025010. doi:10.1088/1361-6587/aa96cd
28. Burrell KH, Garofalo AM, Solomon WM, Fenstermacher ME, Osborne TH, Park J-K, et al. Reactor-relevant quiescent H-mode operation using torque from nonaxisymmetric, non-resonant magnetic fields. Phys Plasmas (2012) 19:056117. doi:10.1063/1.3695119
29. Whyte DG, Hubbard AE, Hughes JW, Lipschultz B, Rice JE, Marmar ES, et al. I-Mode: An H-mode energy confinement regime with L-mode particle transport in ALCATOR C-mod 2010 Nucl. Fusion (2010) 50:105005. doi:10.1088/0029-5515/50/10/105005
30. Paméla J, Romanelli F, Watkins ML, Lioure A, Matthews G, Philipps V, et al. The JET programme in support of ITER. Fusion Eng Des (2007) 82:590–602. doi:10.1016/j.fusengdes.2007.03.003
31. Romanelli M, Corrigan G, Parail V, Wiesen S, Ambrosino R, Da Silva Aresta Belo P, et al. Jintrac: A system of codes for integrated simulation of tokamak scenarios. Plasma Fusion Res (2014) 9:3403023. doi:10.1585/pfr.9.3403023
32. Baylor LR, Commaux N, Jernigan TC, Brooks NH, Combs SK, Evans TE, et al. Reduction of edge-localized mode intensity using high-repetition-rate pellet injection in TokamakH-mode plasmas. Phys Rev Lett (2013) 110:245001. doi:10.1103/physrevlett.110.245001
33. Bortolon A, Maingi R, Mansfield DK, Nagy A, Roquemore AL, Baylor LR, et al. High frequency pacing of edge localized modes by injection of lithium granules in DIII-D H-mode discharges. Nucl Fusion (2016) 56:056008. doi:10.1088/0029-5515/56/5/056008
34. de la Luna E, Chapman IT, Rimini F, Lomas PJ, Saibene G, Koechl F, et al. Understanding the physics of ELM pacing via vertical kicks in JET in view of ITER. Nucl Fusion (2016) 56:026001. doi:10.1088/0029-5515/56/2/026001
35. Degeling AW, Martin YR, Lister JB, Villard L, Dokouka VN, Lukash VE, et al. Magnetic triggering of ELMs in TCV. Plasma Phys Control Fusion (2003) 45:1637–55. doi:10.1088/0741-3335/45/9/306
36. Lang PT, Degeling AW, Lister JB, Martin YR, Mc Carthy PJ, Sips ACC, et al. Frequency control of type-I ELMs by magnetic triggering in ASDEX Upgrade. Plasma Phys Control Fusion (2004) 46:L31–9. doi:10.1088/0741-3335/46/11/l02
37. Gerhardt SP, Ahn J-W, Canik JM, Maingi R, Bell R, Gates D, et al. First observation of ELM pacing with vertical jogs in a spherical torus. Nucl Fusion (2010) 50:064015. doi:10.1088/0029-5515/50/6/064015
38. Kim J, Jeon Y-M, Xiao WW, Yoon S-W, Park J-K, Yun GS, et al. ELM control experiments in the KSTAR device. Nucl Fusion (2012) 52:114011. doi:10.1088/0029-5515/52/11/114011
39. Jardin SC, Krebs I, Ferraro N. A new explanation of the sawtooth phenomena in tokamaks. Phys Plasmas (2020) 27:032509. doi:10.1063/1.5140968
40. Porcelli F, Boucher D, Rosenbluth MN. Model for the sawtooth period and amplitude. Plasma Phys Control Fusion (1996) 38:2163–86. doi:10.1088/0741-3335/38/12/010
41. Lazarus EA, Luce TC, Austin ME, Brennan DP, Burrell KH, Chu MS, et al. Sawtooth oscillations in shaped plasmas. Phys Plasmas (2007) 14:055701. doi:10.1063/1.2436849
42. Lerche E, Lennholm M, Carvalho IS, Dumortier P, Durodie F, Van Eester D, et al. Sawtooth pacing with on-axis ICRH modulation in JET-ILW. Nucl Fusion (2021) 61:036027. doi:10.1088/1741-4326/aa53b6
43. Jajcay N, Kravtsov S, Sugihara G, Tsonis AA, Palus M. Synchronization and causality across time scales in el niño southern oscillation. Npj Clim Atmos Sci (2018) 1:33. doi:10.1038/s41612-018-0043-7
44. Palus M. Cross-scale interactions and information transfer. Entropy (Basel) (2014) 16(10):5263–89. doi:10.3390/e16105263
45. Heil C, Walnut D. Continuous and discrete wavelet transforms. SIAM Rev (1989) 31:628–66. doi:10.1137/1031129
46. Lê A, Roytershteyn V, Karimabadi H, Stanier A, Chacon L, Schneider K. Wavelet methods for studying the onset of strong plasma turbulence. Phys Plasmas (2018) 25:122310. doi:10.1063/1.5062853
47. Poli FM, Sharapov SE, Chapan SC. Study of the spectral properties of ELM precursors by means of wavelets Plasma. Phys Control Fusion (2008) 50:095009. doi:10.1088/0741-3335/50/9/095009
48. Torrence C, Compo GP. A practical guide to wavelet analysis. Bull Am Meteorol Soc (1998) 79:61–78. doi:10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2
49. Reichenbach H. The direction of time. Berkeley and Los Angeles, CA, USA: University of California Press (1956).
50. Granger C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica (1969) 37:424. doi:10.2307/1912791
51. Kreuz T, Mormann F, Andrzejak RG, Kraskov A, Lehnertz K, Grassberger P. Measuring synchronization in coupled model systems: A comparison of different approaches. Physica D: Nonlinear Phenomena (2007) 225:29–42. doi:10.1016/j.physd.2006.09.039
52. Runge J, Bathiany S, Bollt E, Camps-Valls G, Coumou D, Deyle E, et al. Inferring causation from time series in Earth system sciences. Nat Commun (2019) 10:2553. doi:10.1038/s41467-019-10105-3
53. Palus M. Coupling in complex systems as information transfer across time scales. Phil Trans R Soc A (2019) 377:20190094. doi:10.1098/rsta.2019.0094
55. Takens F. Detecting strange attractors in turbulence. In: DA Rand, and L-S Young, editors. Dynamical systems and turbulence, lecture notes in mathematics, 898 (1981). Cham, Switzerland. p. 366–81.
56. Kennel M, Brown R, Abarbanel H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys Rev A (Coll Park) (1992) 45(6):3403–11. doi:10.1103/physreva.45.3403
57. Hlavácková-Schindler K, Palus M, Vejmelka M, Bhattacharya J. Causality detection based on information-theoretic approaches in time series analysis. Phys Rep (2007) 441:1–46. doi:10.1016/j.physrep.2006.12.004
58. Schreiber T. Measuring information transfer. Phys Rev Lett (2000) 85(2):461–4. doi:10.1103/physrevlett.85.461
59. Lord WM, Sun J, Bollt EM. Geometric k-nearest neighbor estimation of entropy and mutual information. Chaos (2018) 28:033114. doi:10.1063/1.5011683
60. Schreiber T, Schmitz A. Surrogate time series. Physica D: Nonlinear Phenomena (2000) 142:346–82. doi:10.1016/s0167-2789(00)00043-9
61. Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, et al. High gamma power is phase-locked to theta oscillations in human neocortex. Science (2006) 313(5793):1626–8. doi:10.1126/science.1128115
62. Tort ABL, Komorowski R, Eichenbaum H, Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J Neurophysiol (2010) 104:1195–210. doi:10.1152/jn.00106.2010
63. Aru J, Aru J, Priesemann V, Wibral M, Lana L, Pipa G, et al. Untangling cross-frequency coupling in neuroscience. Curr Opin Neurobiol (2015) 31:51–61. doi:10.1016/j.conb.2014.08.002
64. Yeha C-H, Lo M-T, Hu K. Spurious cross-frequency amplitude-amplitude coupling in nonstationary, nonlinear signals. Physica A: Stat Mech its Appl (2016) 454:143–50. doi:10.1016/j.physa.2016.02.012
65. Lo M-T IMAAC (2022). Available at: http://in.ncu.edu.tw/mzlo/index_files/IMAAC.rar (Accessed May 18, 2022).
66. Maccarone TJ, Schnittman JD. The bicoherence as a diagnostic for models of high-frequency quasi-periodic oscillations. Mon Not R Astron Soc (2004) 357:12–6. doi:10.1111/j.1365-2966.2004.08615.x
67. Hagihira S, Takashina M, Mori T, Mashimo T, Yoshiya I. Practical issues in bispectral analysis of electroencephalographic signals. Anesth Analg (2001) 93(4):966–70. doi:10.1097/00000539-200110000-00032
68. Nagashima Y, Itoh K, Itoh SI, Hoshino K, Fujisawa A, Ejiri A, et al. Observation of coherent bicoherence and biphase in potential fluctuations around geodesic acoustic mode frequency on JFT-2M. Plasma Phys Control Fusion (2006) 48(5A):A377–86. doi:10.1088/0741-3335/48/5a/s38
69. Schiff SJ, Colella D, Jacyna GM, Hughes E, Creekmore JW, Marshall A, et al. Brain chirps: Spectrographic signatures of epileptic seizures. Clin Neurophysiol (2000) 111:953–8. doi:10.1016/s1388-2457(00)00259-5
70. Xu L, Chen Z, Hu K, Eugene Stanley H, Ivanov PC. Spurious detection of phase synchronization in coupled nonlinear oscillators. Phys Rev E (2006) 73:065201. doi:10.1103/physreve.73.065201
71. Sartori F, Lomas P, Piccolo F, Zedda MK. Synchronous ELM pacing at JET using the vertical stabilization controller 35th EPS Conf. on Plasma Physics. Greece: Hersonissos, Crete (2010).
72. Toigo V, Zanotto L, Bigi M, Gaio E, Hay JH, Piovan R, et al. Conceptual design of the enhanced radial field amplifier for plasma vertical stabilisation in JET. Fusion Eng Des (2007) 82:1599–606. doi:10.1016/j.fusengdes.2007.03.036
73. Lennholm M, McKean R, Mooney R, Tvalashvili G, Artaserse G, Baruzzo M, et al. Statistical assessment of ELM triggering by pellets on JET. Nucl Fusion (2021) 61:036035. doi:10.1088/1741-4326/abd861
74. Brezinsek S, Jachmich S, Stamp MF, Meigs AG, Coenen JW, Krieger K, et al. Residual carbon content in the initial ITER-Like Wall experiments at JET. J Nucl Mater (2013) 438:S303–8. doi:10.1016/j.jnucmat.2013.01.122
75. Neu R, Arnoux G, Beurskens M, Bobkov V, Brezinsek S, Bucalossi J, et al. First operation with the JET international thermonuclear experimental reactor-like wall. Phys Plasmas (2013) 20:056111. doi:10.1063/1.4804411
76. Chapman IT, de la Luna E, Lang PT, Liang Y, Alper B, Denner P, et al. Advances in understanding and utilising ELM control in JET. Plasma Phys Control Fusion (2016) 58(1):014017. doi:10.1088/0741-3335/58/1/014017
77. Stober J, Maraschek M, Conway G, Gruber O, Herrmann A, Sips A, et al. Type II ELMy H modes on ASDEX Upgrade with good confinement at high density. Nucl Fusion (2001) 41(9):1123–34. doi:10.1088/0029-5515/41/9/301
78. Oyama N, Gohil P, Horton LD, Hubbard AE, Hughes JW, Kamada Y, et al. Pedestal conditions for small ELM regimes in tokamaks. Plasma Phys Control Fusion (2006) 48(5A):A171–A181. doi:10.1088/0741-3335/48/5a/s16
79. Wolfrum E, Bernert M, Boom JE, Burckhart A, Classen IGJ, Conway GD, et al. Characterization of edge profiles and fluctuations in discharges with type-II and nitrogen-mitigated edge localized modes in ASDEX Upgrade. Plasma Phys Control Fusion (2011) 53(8):085026. doi:10.1088/0741-3335/53/8/085026
80. Viezzer E. Access and sustainment of naturally ELM-free and small-ELM regimes Nucl. Fusion (2018) 58(11):115002. doi:10.1088/1741-4326/aac222
81. Harrer GF, Wolfrum E, Dunne MG, Manz P, Cavedon M, Lang PT, et al. Parameter dependences of small edge localized modes (ELMs). Nucl Fusion (2018) 58(11):112001. doi:10.1088/1741-4326/aad757
82. Kirk A, Muller HW, Wolfrum E, Meyer H, Herrmann A, Lunt T, et al. Comparison of the filament behaviour observed during type I ELMs in ASDEX upgrade and MAST. J Phys : Conf Ser (2008) 123(1):012012. doi:10.1088/1742-6596/123/1/012012
83. Labit B, Eich T, Harrer GF, Wolfrum E, Bernert M, Dunne MG, et al. Dependence on plasma shape and plasma fueling for small edge-localized mode regimes in TCV and ASDEX Upgrade, Nucl. Fusion (2019) 59:086020. doi:10.1088/1741-4326/ab2211
84. Garzotti L, Challis C, Dumont R, Frigione D, Graves j., Lerche E, et al. Scenario development for D–T operation at JET. Nucl Fusion (2019) 59:076037. doi:10.1088/1741-4326/ab1cca
85. Pearl J, Mackenzie D. The book of why: The new science of cause and effect. London, United Kingdom: Penguin Books (2019).
86. Puiatti ME, Mattioli M, Telesca G, Valisa M, Coffey I, Dumortier P, et al. Radiation pattern and impurity transport in argon seeded ELMy H-mode discharges in JET. Plasma Phys Control Fusion (2002) 44:1863–78. doi:10.1088/0741-3335/44/9/305
Keywords: ELMs, sawteeth, pacing, pellets, ICRH modulation, vertical kicks, synchronization
Citation: Craciunescu T, Murari A, Peluso E, Lang PT, Harrer G, Spolladore L, Gelfusa M, JET Contributors and the ASDEX Upgrade Team (2022) A methodology for discriminating phase and amplitude effects on synchronization in tokamak pacing experiments. Front. Phys. 10:985422. doi: 10.3389/fphy.2022.985422
Received: 03 July 2022; Accepted: 27 September 2022;
Published: 18 October 2022.
Edited by:
Ricardo Luiz Viana, Federal University of Paraná, BrazilReviewed by:
Iberê Caldas, University of São Paulo, BrazilRiccardo Meucci, National Research Council (CNR), Italy
Copyright © 2022 Craciunescu, Murari, Peluso, Lang, Harrer, Spolladore, Gelfusa, JET Contributors and the ASDEX Upgrade Team. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Gelfusa, Z2VsZnVzYUBpbmcudW5pcm9tYTIuaXQ=
†These two authors have contributed equally to this work
‡See the author list of ‘Overview of JET results for optimising ITER operation’ by J.Mailloux et al. to be published in Nuclear Fusion Special issue: Overview and Summary Papers from the 28th Fusion Energy Conference (Nice, France, 10-15 May 2021)
§See author list of H. Meyer et al. 2019 Nucl. Fusion 59 112014.
 T. Craciunescu
T. Craciunescu A. Murari2†
A. Murari2† M. Gelfusa
M. Gelfusa