Quantum dot scanning tunneling microscopy for Majorana bound states in continuum

We propose a device composed of a quantum dot (QD) connected to a normal metal lead to detect Majorana bound states (MBSs), which are formed at the ends of a topological superconductor nanowire (TSNW) and coupled to the lead with spin-dependent hybridization strengths. The information of the MBSs leaked into the lead is inferred from the spectral function of the QD serving as the tip of a scanning tunneling microscope (STM). It is found that lead–MBSs interaction induces a bound state characterized by an infinitely high peak in the dot’s zero-energy spectral function. The overlap between the two modes of the MBSs turns this bound state into a resonant one, and thus the zero-energy peak is split into three with the height of the central one equaling that in the absence of lead–MBSs coupling. We also find that the MBSs have lower impacts on the additional peak in the dot’s spectral function induced by intradot Coulomb interaction.

1 Introduction

In submicro- and nano-scale systems, the quantum interference effect resulting from electrons transporting through multiple paths or states induces various interesting phenomena that are important in both fundamental and applied subjects [1, 2]. Recently, to enrich physical phenomena, quantum dots (QDs) with well-separated and adjustable energy levels were embedded in the tunneling channels of multiply connected or T-shaped geometries [3–7]. Such energy levels couple to the states with a continuum energy spectrum in the leads that is connected to the central region and thus form exotic bound states in the continuum (BICs). This kind of platform enables the emergence of Fano and Dick effects that originally solely occurred in molecular systems [3, 6]. These two effects are characterized by the asymmetric line shape of the conductance varying with respective to the Fermi energy or dot level, as well as by zero-width resonant peaks in local density of states (LDOS). According to the uncertainty principle, a state with zero-width peak means that its lifetime is infinity and thus is important in applications such as quantum information or quantum storage. A recent experimental work demonstrated that Fano resonances are closely related to quasi-BICs [8]. These effects are also crucial for either fundamental or technological applications. For example, BICs have been successfully used in designing new kinds of lasers that may be applicable in various fields including photoelectric devices, detection instruments, and quantum information [9]. The quantum interference effects induced by the presence of BICs have also been extensively studied in low-dimensional phononic systems [10]. Experimentally, BICs have been observed in systems beyond electronic ones, for example in optical waveguides arranged in a series [11], dielectric slabs [12], cylinders [13], and nano-scale resonators [9].

Issues related to BICs were also studied in the scope of topological phases of matter [12, 14]. In particular, recent theoretical and experimental work has demonstrated that exotic Majorana bound states (MBSs) can be formed at the ends of p-wave topological superconductor nanowires [15]. The MBSs are quasi-particles of Majorana fermions and of their own antiparticle excitations with zero energy. They are coherent superpositions of electrons and holes and resemble the properties of electron–hole pairs in superconductors. Accordingly, researchers have been seeking Majorana fermions in superconductors since they were predicted as early as in 1937 [16]. In 2008, Fu and Kane first demonstrated the possibility of realizing MBSs in a vortex core in a p-wave superconductor [17]. Subsequently, researchers proved that MBSs may be formed at opposite ends of a one-dimensional p-wave superconductor realized from a semiconductor nanowire with Rashba spin-orbit interaction subjected to both a strong external magnetic field and proximity-induced s-wave superconductor [17]. Until now, MBSs have been successfully prepared in various solid-state platforms, such as topological insulators connected to superconductors [17], defects in topological superconductors [18], semiconductor [19], or ferromagnetic [20] nanowires having strong spin-orbit interaction proximitized to conventional s-wave superconductors, Josephson junctions [21], single monolayer systems [22], and chains of magnetic adatoms [23]. The detection of MBSs remains a challenge. In the past 2 decades, zero-bias conductance peaks [24, 25] were believed to be the most reliable evidence of the existence of MBSs. But some theoretical and experimental works have proved that such an effect can also arise from trivial Andreev bound states and Yu–Shiba–Rusinov states, as well as from the Kondo effect in experimental platforms having a proximitized nanowire connected to a quantum dot (QD) [26, 27]. Due to the controversy regarding to the zero-bias abnormal peak related to MBSs, some other means to detect MBSs were subsequently proposed. For example, the presence of MBSs may induce a sign reversion or abnormal enhancement of themopower in a hybridized Majorana nanowire/QD system, and can efficiently detect the existence of the MBSs [28–31]. Impacts of MBSs on the properties of tunnel magnetoresistance [32], photo-assisted transport [33–36], and Fano resonance [37–40] were also demonstrated to be promising in the detection of MBSs.

Recently, the generation of BICs by the presence of MBSs was investigated in systems composed of QD and Majorana nanowires, an interesting phenomenon termed MBCIs [41–43]. In a departure from earlier work, Vernek et al. proposed to generate and manipulate the MBICs under the condition that both the MBSs and the QD be coupled to an external lead with continuum energy spectrum [44], except when the MBSs and QD are directly connected. The researchers focused on the spectral and transport properties of the hybridized system in both the noninteracting and strong-interacting regimes of the QD [44]. Their numerical results show that there is bound state in the spectral function of the QD, as long as the MBS is coupled to the lead, regardless of the coupling strength. Such a result remains unchanged in the presence of intradot Coulomb interaction and variation of the system temperatures. They explained the physical mechanism of the MBICs by examining the properties of the dot–lead coupling strength under the influence of the MBSs. These results are useful for reading and writing information through veiling and unveiling these states, and they are promising in applications for quantum computing. In the present work, we revisit this system by considering both the MBS–MBS overlap and spin-dependent coupling between the MBSs and the lead, which were neglected in previous work. Experimentally, the two modes of the MBSs formed at opposite ends of the TSNW will interact with each and change the transport properties significantly [21, 24]. Moreover, the MBSs can couple to both spin-up and spin-down electrons, even with different coupling strengths [45, 46]. Our results show that the direct overlap between the two modes of the MBSs may destruct the MBICs under particular conditions, and the spin-dependent coupling between the MBSs and the lead enables the interaction between electrons of opposite spin directions, even in the noninteracting regime. The information of the MBSs at the ends of the TSNW will change the properties of the lead and then leak into the QD when the lead and QD are close enough. By investigating the behavior of the spectral function of the QD, one can infer the existence of the MBSs or the MBICs. The QD thus functions as the tip of an STM to detect the above two phenomena.

2 Model and methods

The system we study here is similar to that in Ref. [44], except that the two modes of the MBSs overlap, and one mode of the MBSs interacts with electrons in a lead with spin-dependent hybridization strength. The lead–dot coupling strength is sensitive to the properties of MBSs and thus to changing the spectral function of the QD. The Hamiltonian of this system can be written in the following form [25, 44]:

$H=\sum _{k\sigma }{\epsilon }_{k\sigma }{c}_{k\sigma }^{†}{c}_{k\sigma }+\sum _{\sigma }{\epsilon }_d{d}_{\sigma }^{†}{d}_{\sigma }+U{d}_{\uparrow }^{†}{d}_{\uparrow }{d}_{\downarrow }^{†}{d}_{\downarrow }+\sum _{k\sigma }\left(t_k{c}_{k\sigma }^{†}{d}_{\sigma }+H.c\right)+H_{\mathit{MBSs}},(1)$

where $c_{k\sigma }^{†}(c_{k\sigma })$ creates (annihilates) an electron of momentum k and energy ɛ_kσ, which depends on electron spin σ = ↑, ↓ in the lead serving as the tip of an STM. The operator $d_{\sigma }^{†}(d_{\sigma })$ is the creation (annihilation) operator of an electron with gate voltage tunable energy level ɛ_d, spin-σ, and intradot Coulomb interaction U. The MBSs couple to spinless electrons in the QD because of the chirality properties, which has been studied in previous papers. Experimentally, this happens when the system holding MBSs is subjected to strong magnetic fields that enable only one spin-component electron to dwell on the systems due to the Zeeman splitting effect [25]. When the external magnetic field is not too strong, and both the spin-up and spin-down energy levels of the systems are in the transport window, the MBSs interact with both spin-up and spin-down electrons [24]. The Coulomb repulsion between the electrons is crucial and should be considered. The coupling strength between the QD and the lead is described by t_k. The last term, H_MBSs, in Eq. 1 is for the MBSs prepared at opposite ends of a TSNW. Here we consider the case in which only one mode of the MBS is coupled to the electrons on the lead with spin-dependent hybridization strength λ_σ [45, 46]:

$H_{\mathit{MBSs}}=i{\delta }_M{\eta }_1{\eta }_2+\sum _{\sigma }{\lambda }_{\sigma }\left(d_{\sigma }-d_{\sigma }^{†}\right){\eta }_1,(2)$

in which δ_M is the interaction strength between the MBSs whose operators satisfy ${\eta }_j={\eta }_j^{†}(j=\mathrm{1,2})$ and {η_i, η_j} = δ_i,j. The coupling strength between the MBSs and electrons on the lead is λ_σ. The information of the MBSs leaked into the lead can be detected non-invasively by investigating the local density of the states (LDOS) ρ_σ of the QD attached to the lead [44]. It can be obtained from the imaginary part of the retarded Green’s function as ${\rho }_{\sigma }=-\mathrm{I}\mathrm{m}[\ll d_{\sigma }|d_{\sigma }^{†}{\gg }^r]/\pi$. By adopting the equation-of-motion technique, the Green’s function can be expressed in the following matrix form [24, 25, 44]

$\left[\begin{array}{cccc}\hfill G_{d,\uparrow }^{r-1}+K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\uparrow }\hfill & \hfill K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\uparrow }\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill \\ \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill {\tilde{G}}_{d,\uparrow }^{r-1}+K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\uparrow }\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill \\ \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill G_{d,\downarrow }^{r-1}+K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\downarrow }\hfill & \hfill K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\downarrow }\hfill \\ \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill K\mathrm{\Gamma }\sqrt{{\mathrm{\Lambda }}_{\uparrow }{\mathrm{\Lambda }}_{\downarrow }}\hfill & \hfill K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\downarrow }\hfill & \hfill {\tilde{G}}_{d,\downarrow }^{r-1}+K\mathrm{\Gamma }{\mathrm{\Lambda }}_{\downarrow }\hfill \end{array}\right]\left[\begin{array}{c}\hfill \ll d_{\uparrow }|d_{\sigma }^{†}{\gg }^r\hfill \\ \hfill \ll d_{\uparrow }^{†}|d_{\sigma }^{†}{\gg }^r\hfill \\ \hfill \ll d_{\downarrow }|d_{\sigma }^{†}{\gg }^r\hfill \\ \hfill \ll d_{\downarrow }^{†}|d_{\sigma }^{†}{\gg }^r\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\delta }_{\uparrow ,\sigma }\hfill \\ \hfill 0\hfill \\ \hfill {\delta }_{\downarrow ,\sigma }\hfill \\ \hfill 0\hfill \end{array}\right],(3)$

in which the inverse of the QD Green’s function is

$G_{d,\sigma }^{r-1}=\frac{\left(\epsilon -{\epsilon }_d\right)\left(\epsilon -{\epsilon }_d-U\right)}{\epsilon -{\epsilon }_d-U\left(1-n_{\bar{\sigma }}\right)}+i\mathrm{\Gamma },(4)$

and the Green’s function of holes is

${\tilde{G}}_{d,\sigma }^{r-1}=\frac{\left(\epsilon +{\epsilon }_d\right)\left(\epsilon +{\epsilon }_d+U\right)}{\epsilon +{\epsilon }_d+U\left(1-n_{\bar{\sigma }}\right)}+i\mathrm{\Gamma },(5)$

where ${\sum }_k\frac{|t_k{|}^2}{\epsilon \pm {\epsilon }_{k\sigma }}=-i\mathrm{\Gamma }$, ${\sum }_k\frac{|{\lambda }_{\sigma }{|}^2}{\epsilon \pm {\epsilon }_{k\sigma }}=-i{\mathrm{\Lambda }}_{\sigma }$, and $K={[\epsilon +2i\sum {\mathrm{\Lambda }}_{\sigma }-{\delta }_M^2/(\epsilon +i{0}^{+})]}^{-1}$. The occupation number n_σ must be calculated from the self-consistent equation of $n_{\sigma }=-\int \mathrm{I}\mathrm{m}\ll d_{\sigma }|d_{\sigma }^{†}{\gg }^{r}f(\epsilon )d\epsilon /\pi$ , with f(ɛ) being the Fermi distribution function in the equilibrium state.

3 Results and discussion

In the following numerical calculations, we choose half-band width of the lead D ≡ 40 [25] as the energy unit and fix the value of dot-lead coupling strength at Γ = 0.1. Figure 1 presents the spin-up (a) and spin-down (b) spectral functions and (c) their spin-polarization P = (ρ_↑ − ρ_↓)/(ρ_↑ + ρ_↓) for different values of spin-down lead–MBS hybridization strength λ_↓ with fixed λ_↑ = 0.1. For λ_↓ = 0, the zero-energy spin-up spectral function is πΓρ_↑(ɛ = 0) → ∞ (black solid line in Figure 1A), whereas πΓρ_↓(ɛ = 0) = 1 is shown by the solid black line in Figure 1B. This indicates that the MBSs leaked into the lead, inducing a bound state in the QD at zero electron energy. Turning on the coupling between spin-down electrons on the QD and the MBSs in the lead (λ_↓ ≠ 0), the bound state in spin-up spectral function is stable, which is characterized by πΓρ_↑(ɛ = 0) → ∞. Now the zero-energy spectral function of the QD for spin-down electrons also becomes a bound state (πΓρ_↓(ɛ = 0) → ∞). Note that the bound state emerges as long as the dot-lead coupling is turned on and is independent in its magnitude. Shifting the QD energy level by gate voltage away from zero energy, it is found that the magnitude of spin-up (spin-down) spectral function is monotonously enhanced (suppressed) by increasing λ_↓. The reason is that the MBSs leaked into the QD change the dot level, and then the electron transport probability in each channel (electron state) is lowered. This result is in consistent with earlier works [25, 44].

FIGURE 1

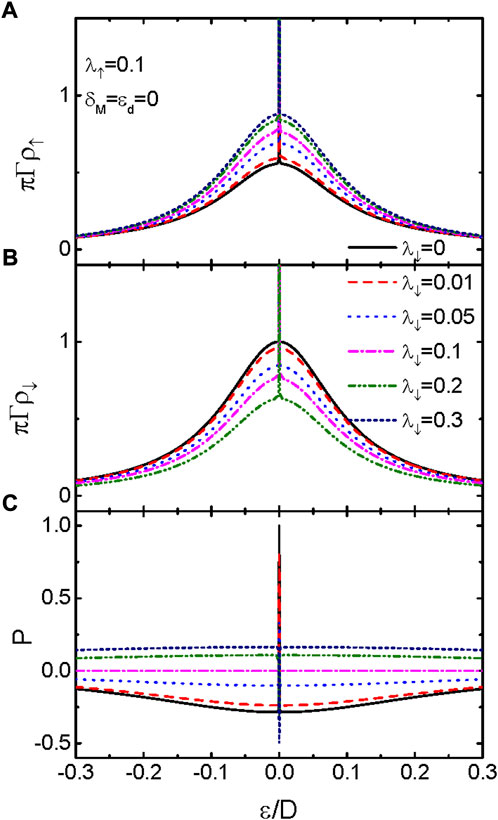
FIGURE 1. (Color online) Spin-up (A) and spin-down (B) LDOS varying as functions of electron energy for different values of λ_↓. (C) is for the spin polarization of the LDOS. Other parameters are U = 0, λ_↑ = 0.1, dot level ɛ_d = 0, and MBS–MBS interaction strength δ_M = 0. With increasing λ_↓, the magnitude of ρ_↑ (A) and ρ_↓ (B) is individually enhanced and suppressed. As a result, the spin polarization of the LDOS (C) first decreases, changing its sign, and then increases.

The bound state induced by the MBSs can be understood by examining the properties of the hybridization between the QD and the lead KΛ_σ. As is known from the Green’s function, the position of the peaks in the spectral function is determined by the dot level as well as by the real part of the self-energy, and the width (lifetime of the state) of the peaks is related to the value of the imaginary part of the self-energy. A larger (smaller) value of the imaginary part of the self-energy corresponds to wider (narrower) peaks, and hence a longer (shorter) electron life on the energy state. The real part of KΓΛ_σ will shift the dot level, and its imaginary part determines the broadening of peaks in the spectral function πΓρ_σ(ɛ). As shown in Ref. [44], − Im[KΓΛ_σ] is the effective coupling between the QD and the lead with continuum spectrum. Under the conditions of λ_σ = 0 and ɛ_d = 0, − Im[KΓΛ_σ] reduces to Γ of the usual case with πΓρ_σ(ɛ = 0) = 1. In the presence of coupling between the QD and the continuum (λ_σ ≠ 0), − Im[KΓΛ_σ] ≡ 0 at ɛ = 0 indicates the emergence of a bound state with infinite long-electron dwell time due to the uncertainty relation of Δt ∼ ℏ/2Γ. The real part of KΓΛ_σ, however, is zero at ɛ = 0, and the position of the peak in spectral function is unchanged. Note that the value of KΓΛ_σ also depends on the dot level ɛ_d, which is out of the scope of the present work because the MBSs exert significant impacts on the electron transport at zero energy. The spin-polarization of the spectral functions P is shown in Figure 1C. It is found that the value of P depends on both λ_σ and electron energy ɛ. At ɛ = 0, the spin-polarization is 1 for λ_↓ = 0. This means now only spin-up electrons can enter the QD, an ideal case for spintronic devices. With increasing λ_↓, the magnitude of the spin-polarization is reduced. Now both spin-up and spin-down electrons can occupy the states on the QD. Interestingly, at sufficiently large λ_↓, the value of the spin-polarization is changed from a positive value to a negative one. Now the majority spin in the QD is changed from spin-up to spin-down, and the system can be used as a spin-conversion device by changing the hybridization between the QD and the lead.

In real cases, the two modes of the MBSs prepared at opposite ends of the nanowire overlap with each other with strength δ_M ∼ exp(−l/ζ), where l is the length of the nanowire and ζ is directly proportional to the magnetic field applied on the nanowire. The overlap between the MBSs changes their properties significantly, but this fact has been neglected in previous work concerning MBSs coupled to continuum [44]. Figure 2A shows the behavior of πΓρ_↑(ɛ) for different values of δ_M with fixed λ_↑ = 0.1 and λ_↓ = 0. As is shown by the black solid line in Figure 2A, a bound state is formed at ɛ = 0 characterized by infinite large πΓρ_↑ for δ_M, which is just the case shown in Figure 1. Turning on the hybridization between the two modes of the MBSs (δ_M ≠ 0), the zero-energy peak of the spin-up spectral function is split into two. Meanwhile, the two peaks are broadened and lowered. Importantly, the height of the central peak in the spin-up spectral function reduces from infinity to one as long as δ_M ≠ 0. For δ_M = 0.3, as is shown by the green dash-dot-dot line, the central peak in πΓρ_↑ evolves into a broad resonant one. The spin-down spectral function in Figure 2B is unchanged regardless of the value of δ_M, as the spin-down electrons are decoupled from the MBSs (λ_↓ = 0). The results shown in Figure 2 indicate that the imaginary part of the effective self-energy − Im[KΓΛ_σ] no longer equals zero at ɛ = 0, and the overlap between the two modes of the MBSs destroy the bound state induced by them.

FIGURE 2

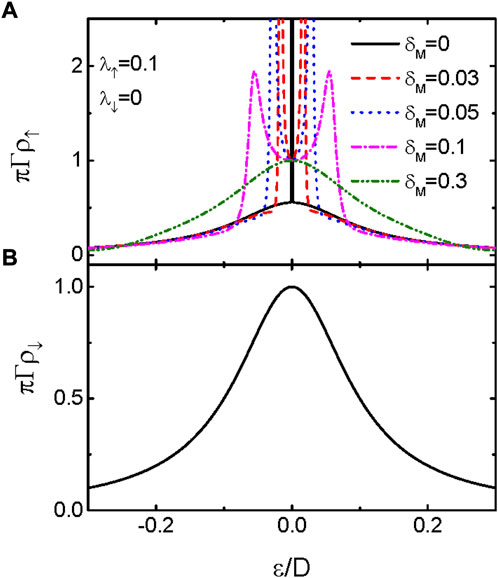
FIGURE 2. (Color online) (A)Spin-up and (B) spin-down LDOS as functions of the electron energy for fixed λ_↑ = 0.1, λ_↓ = 0, and different values of δ_M. The other parameters are as in Figure 1.

We now study the case in which both spin-up and spin-down electrons are coupled to the MBSs with different hybridization strengths in Figure 3. Similar to the results in Figure 2, in which only spin-up electrons on the QD interact with the MBSs, the single-peak in the spectral functions of the two spin components is split into a broadened and lowered double-peak configuration, indicating the destruction of the bound states by direct hybridization between the two modes of the MBSs. With increasing δ_M, the central peaks in both spin-up and spin-down spectral functions evolve into resonant ones with a fixed value of πΓρ_σ(ɛ = 0) = 1. Comparing Figure 3A,C and Figure 3B,D, one finds that the width of the central peak in the spectral function is changed to be non-monotonous by both λ_σ and δ_M. Apart from the Fermi energy ɛ = 0, the magnitude of the spectral function is enhanced by increasing δ_M, indicating that the impacts of the MBSs on electron transport are weakened by their direct hybridization.

FIGURE 3

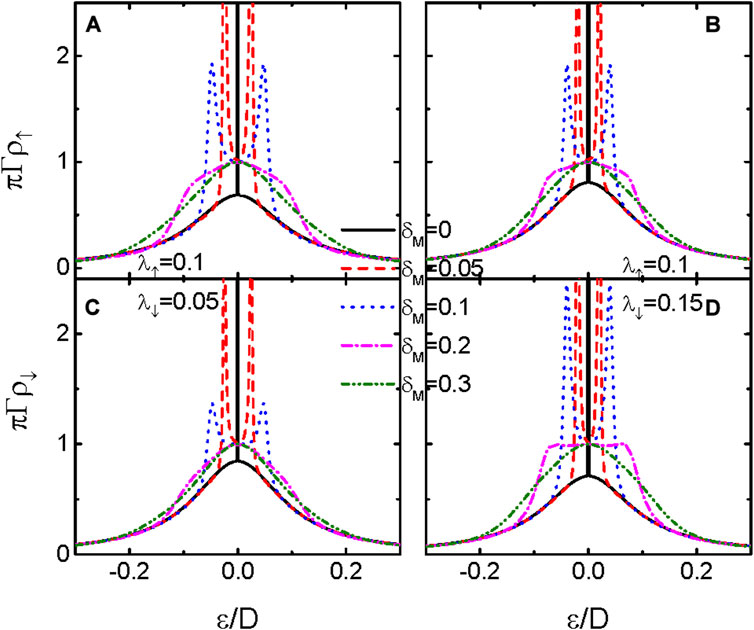
FIGURE 3. (Color online) Spin-resolved LDOS varying with respect to the electron energy for fixed λ_↑ = 0.1 and different values of δ_M. The value of λ_↑ in (A,C) is 0.05, and is fixed at 0.15 in (B,D). The other parameters are as in Figure 1.

In submicro-nano structures including QD, electron–electron Coulomb interaction can generate some interesting phenomena, such as Coulomb blockade and Kondo effects, that exert significant influences on transport processes. We next show the impacts of intradot Coulomb interaction on the spectral function πΓρ_σ(ɛ) for fixed λ_↑ and different values of λ_↓ in Figure 4A,B and different δ_M in Figure 4C,D. It is found that the spectral functions in the presence of intradot Coulomb interaction resemble those in Figures 2, 3, except that an additional peak arises at ɛ = U. A bound state is also induced by hybridization between the electrons on the QD and the MBSs formed at the ends of the nanowire. As was shown in Ref. [44], even with the effective self-energy − Im[KΓΛ_σ] = 0 at both ɛ = 0 and U, the state at ɛ = U is still a resonant one. The values of λ_σ and δ_M mainly change the spectral functions at ɛ = 0 and have less impact on those at ɛ = U. Moreover, their functions are similar to the non-interacting cases given in Figures 1–3.

FIGURE 4

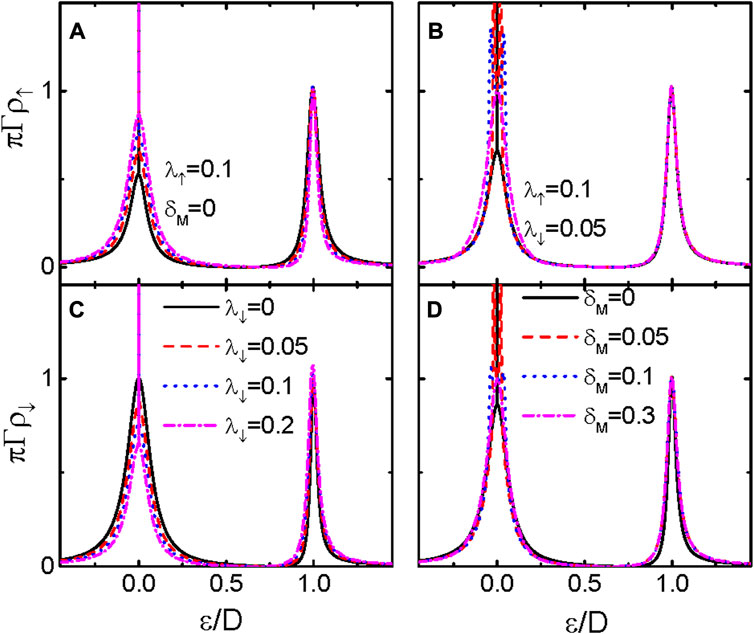
FIGURE 4. (Color online) Spin-up and spin-down LDOS in the presence of intradot Coulomb interaction U = 1 as functions of the electron energy for different values of λ_↓ and δ_M = 0 in (A,D), and λ_↓ = 0.05 and different δ_M in (B,C). The value of λ_↑ is fixed at 0.1. The other parameters are as in Figure 1.

4 Summary

In conclusion, we have studied the properties of a QD coupled to a lead with a continuum energy spectrum, which interacts with one mode of the MBSs formed at the ends of a TSNW. Our results show that the spectral function, which is detectable experimentally in terms of techniques of transport spectroscopy, develops a sharp peak with infinite height at zero energy, indicating a bound state induced by the MBSs leaked into the QD. This bound state is destroyed as long as the two modes of the MBSs are overlapped, and the height of the central peak in the spectral function is suppressed from infinity to unit. Moreover, the central peak is split into a double-peak configuration by direct MBS–MBS hybridization. This bound state induced by the MBSs is robust against the presence of the intradot Coulomb interaction, although it generates another peak in the spectral function due to the Coulomb blockade effect. The present device can be used as an STM for the non-invasive detection of MBSs.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

H-RZ derived the formulas, performed the numerical calculations, and wrote the original manuscript. Y-PS helped polish the manuscript and discussed the physical mechanisms of the results.

Funding

This study was supported by the Program for 2020 Key Research Items of Hohhot Minzu College (Grant No. HMZD-202004).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Miroshnichenko AE, Flach S, Kivshar YS. Fano resonances in nanoscale structures. Rev Mod Phys (2010) 82:2257–98. doi:10.1103/RevModPhys.82.2257

CrossRef Full Text | Google Scholar

2. Hsu CW, Zhen B, Stone AD, Joannopoulos JD, Soljačić M. Bound states in the continuum. Nat Rev Mater (2016) 1:16048. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

3. Hofstetter W, König J, Schoeller H. Kondo correlations and the fano effect in closed aharonov-bohm interferometers. Phys Rev Lett (2001) 87:156803. doi:10.1103/PhysRevLett.87.156803

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yacoby A, Heiblum M, Mahalu D, Shtrikman H. Coherence and phase sensitive measurements in a quantum dot. Phys Rev Lett.Phys Rev Lett (1995) 74:4047–50. doi:10.1103/PhysRevLett.74.4047

CrossRef Full Text | Google Scholar

5. Kubala B, König J. Flux-dependent level attraction in double-dot aharonov-bohm interferometers. Phys Rev B (2002) 65:245301. doi:10.1103/PhysRevB.65.245301

CrossRef Full Text | Google Scholar

6. Guevara MLL, Claro F, Orellana PA. Ghost fano resonance in a double quantum dot molecule attached to leads. Phys Rev B (2003) 67:195335. doi:10.1103/PhysRevB.67.195335

CrossRef Full Text | Google Scholar

7. Ueda A, Eto M. Resonant tunneling and fano resonance in quantum dots with electron-phonon interaction. Phys Rev B (2006) 73:235353. doi:10.1103/PhysRevB.73.235353

CrossRef Full Text | Google Scholar

8. Melik-Gaykazyan EM, Koshelev K, Choi JH, Kruk SS, Bogdanov A, Park Y, et al. From fano to quasi-bic resonances in individual dielectric nanoantennas. Nano Lett (2021) 21:1765–71. doi:10.1021/acs.nanolett.0c04660

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kodigala A, Lepetit T, Gu Q, Bahari B, Fainman Y, Kanté B. Lasing action from photonic bound states in continuum. Nature 541 (2017) 196, 9. doi:10.1038/nature20799

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Huang SB, Liu T, Zhou ZL, Wang X, Zhu J, Li Y. Extreme sound confinement from quasibound states in the continuum. Phys Rev Appl (2020) 14:021001. doi:10.1103/PhysRevApplied.14.021001

CrossRef Full Text | Google Scholar

11. Doeleman H, Monticone F, den Hollander W, Alù A, Koenderink AF. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat Photon (2018) 12:397–401. doi:10.1038/s41566-018-0177-5

CrossRef Full Text | Google Scholar

12. Bulgakov EN, Maksimov DN. Topological bound states in the continuum in arrays of dielectric spheres. Phys Rev Lett (2017) 118:267401. doi:10.1103/PhysRevLett.118.267401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Marinica DC, Borisov AG, Shabanov SV. Bound states in the continuum in photonics. Phys Rev Lett (2008) 100:183902. doi:10.1103/PhysRevLett.100.183902

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Benalcazar WA, Cerjan A. Bound states in the continuum of higher-order topological insulators. Phys Rev B (2020) 101:161116. doi:10.1103/PhysRevB.101.161116

CrossRef Full Text | Google Scholar

15. Wang R, Su W, Zhu J, Ting CS, Li H, Chen C, et al. Kondo signatures of a quantum magnetic impurity in topological superconductors. Phys Rev Lett (2019) 122:087001. doi:10.1103/PhysRevLett.122.087001

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Volovik GE. Fermion zero modes on vortices in chiral superconductors. Jetp Lett 70 (1999) 609, 14. doi:10.1134/1.568223

CrossRef Full Text | Google Scholar

17. Mourik V, Zuo K, Frolov SM, Plissard SR, Bakkers EPAM, Kouwenhoven LP. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science (2012) 336:1003–7. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wimmer M, Akhmerov AR, Medvedyeva MV, Tworzydło J, Beenakker CWJ. Majorana bound states without vortices in topological superconductors with electrostatic defects. Phys Rev Lett (2010) 105:046803. doi:10.1103/PhysRevLett.105.046803

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lutchyn RM, Sau JD, Das Sarma SD. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys Rev Lett (2010) 105:077001. doi:10.1103/PhysRevLett.105.077001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Choy TP, Edge JM, Akhmerov AR, Beenakker CWJ. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys Rev B (2011) 84:195442. doi:10.1103/PhysRevB.84.195442

CrossRef Full Text | Google Scholar

21. San-Jose P, Prada E, Aguado R. Ac josephson effect in finite-length nanowire junctions with majorana modes. Phys Rev Lett (2012) 108:257001. doi:10.1103/PhysRevLett.108.257001

PubMed Abstract | CrossRef Full Text | Google Scholar

22. San-Jose P, Lado JL, Aguado R, Guinea F, Fernández-Rossier J. Majorana zero modes in graphene. Phys Rev X (2015) 5:041042. doi:10.1103/PhysRevX.5.041042

CrossRef Full Text | Google Scholar

23. Nadj-Perge S, Drozdov I, Bernevig BA, Yazdani A. Proposal for realizing majorana fermions in chains of magnetic atoms on a superconductor. Phys Rev B (2013) 88:020407. doi:10.1103/PhysRevB.88.020407

CrossRef Full Text | Google Scholar

24. Ricco LS, de Souza M, Figueira MS, Shelykh IA, Seridonio AC. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: Distinguishing isolated majorana fermions from andreev bound states. Phys Rev B (2019) 99:155159. doi:10.1103/physrevb.99.155159

CrossRef Full Text | Google Scholar

25. Liu DE, Baranger HU. Detecting a majorana-fermion zero mode using a quantum dot. Phys Rev B (2011) 84:201308R1–4. doi:10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

26. He JB, Pan D, Yang G, Liu ML, Ying JH, Lyu ZZ, et al. Nonequilibrium interplay between andreev bound states and kondo effect. Phys Rev B (2020) 102:075121. doi:10.1103/PhysRevB.102.075121

CrossRef Full Text | Google Scholar

27. Liu DH, Cao Z, Liu X, Zhang H, Liu DE. Topological kondo device for distinguishing quasi-majorana and majorana signatures. Phys Rev B (2021) 104:205125. doi:10.1103/PhysRevB.104.205125

CrossRef Full Text | Google Scholar

28. López R, Lee M, Serra L, Lim J. Thermoelectrical detection of majorana states. Phys Rev B 89 (2014) 205418. doi:10.1103/PhysRevB.89.205418

CrossRef Full Text | Google Scholar

29. Hong L, Chi F, Fu ZG, HouWang YKML Z, Wang Z, Li K-M, et al. Large enhancement of thermoelectric effect by majorana bound states coupled to a quantum dot. J Appl Phys 127 (2020) 124302. doi:10.1063/1.5125971

CrossRef Full Text | Google Scholar

30. Chi F, Fu ZG, Liu J, Li K, Wang Z, Zhang P. Thermoelectric effect in a correlated quantum dot side-coupled to majorana bound states. Nanoscale Res Lett 15 (2020) 79. doi:10.1186/s11671-020-03307-y

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sun LL, Fu ZG. Spin seebeck effect in a hybridized quantum-dot/majorana-nanowire with spin heat accumulation. Front Phys 9 (2021) 750102. doi:10.3389/fphy.2021.750102

CrossRef Full Text | Google Scholar

32. Tang LW, Mao WG. Detection of majorana bound states by sign change of the tunnel magnetoresistance in a quantum dot coupled to ferromagnetic electrodes. Front Phys 8 (2020) 147. doi:10.3389/fphy.2020.001471

CrossRef Full Text | Google Scholar

33. Tang HZ, Zhang JJ, Liu J-J Photon-assisted tunneling through a topological superconductor with majorana bound states. AIP ADVANCES 5 (2015) 127129. doi:10.1063/1.4939096

CrossRef Full Text | Google Scholar

34. Chen H, Zhu K. All-optical scheme for detecting the possible majorana signature based on qd and nanomechanical resonator systems. Sci China Phys Mech Astron 58 (2015) 1, 14. doi:10.1007/s11433-014-5637-4

CrossRef Full Text | Google Scholar

35. Väyrynen JI, Rastelli G, Belzig LI, Glazman LI Microwave signatures of majorana states in a topological josephson junction. Phys Rev B 92 (2015) 134508. doi:10.1103/PhysRevB.92.134508

CrossRef Full Text | Google Scholar

36. Chi F, He TY, Wang J, Fu ZG, Liu LM, Liu P, et al. Photon-assisted transport through a quantum dot side-coupled to majorana bound states. Front Phys 8 (2020) 2541. doi:10.3389/fphy.2020.00254

CrossRef Full Text | Google Scholar

37. Ueda A, Yokoyama T. Anomalous interference in aharonov-bohm rings with two majorana bound states. Phys Rev B (2014) 90:081405. doi:10.1103/PhysRevB.90.081405

CrossRef Full Text | Google Scholar

38. Jiang C, Zheng YS. Fano effect in the Andreev reflection of the Aharonov-Bohm-Fano ring with Majorana bound states. Solid State Commun (2015) 212:14–8. doi:10.1016/j.ssc.2015.04.001

CrossRef Full Text | Google Scholar

39. Zeng QB, Chen S, Lü R. Fano effect in an ab interferometer with a quantum dot side-coupled to a single majorana bound state. Phys Lett A (2016) 380:951–7. doi:10.1016/j.physleta.2015.12.026

CrossRef Full Text | Google Scholar

40. Chi F, Wang J, He TY, Fu ZG, Zhang P, Zhang XW, et al. Quantum interference effects in quantum dot molecular with majorana bound states. Front Phys 8 (2021) 631031. doi:10.3389/fphy.2020.631031

CrossRef Full Text | Google Scholar

41. Ricco LS, Marques Y, Dessotti FA, Machado RS, de Souza M, Seridonio AC. Decay of bound states in the continuum of majorana fermions induced by vacuum fluctuations: Proposal of qubit technology. Phys Rev B (2016) 93:165116. doi:10.1103/PhysRevB.93.165116

CrossRef Full Text | Google Scholar

42. Guessi LH, Dessotti FA, Marques Y, Ricco LS, Pereira GM, Menegasso P, et al. Encrypting majorana fermion qubits as bound states in the continuum. Phys Rev B (2017) 96:041114. doi:10.1103/PhysRevB.96.041114

CrossRef Full Text | Google Scholar

43. Zambrano D, Ramos-Andrade JP, Orellana PA. Bound states in the continuum poisoned by majorana fermions. J Phys Condens Matter (2018) 30:375301. doi:10.1088/1361-648X/aad7ca

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Ramos-Andrade JP, Orellana PA, Vernek E. Majorana bound state in the continuum: Coupling between a majorana bound state and a quantum dot mediated by a continuum energy spectrum. Phys Rev B 101 (2020) 115403. doi:10.1103/PhysRevB.101.115403

CrossRef Full Text | Google Scholar

45. Hoffman S, Chevallier D, Loss D, Klinovaja J. Spin-dependent coupling between quantum dots and topological quantum wires. Phys Rev B (2017) 96:045440. doi:10.1103/PhysRevB.96.045440

CrossRef Full Text | Google Scholar

46. Górski G, Kucab K. The spin-dependent coupling in the hybrid quantum dot-majorana wire system. Phys Status Solidi B (2019) 256:1800492. doi:10.1002/pssb.201800492

CrossRef Full Text | Google Scholar