- School of Mathematics and Big Date, Chaohu University, Chaohu, China
Developable surface is a simple and common surface in surface modeling. Geodesic, line of curvature, asymptotic curve, and D-type curve are important characteristic curves on the surfaces. This study gives a unified method for constructing developable surface pencils interpolating these four kinds of characteristic curves. Given a regular space curve R(r), we derive a new condition that a surface pencil P (r, t) interpolating R(r) is developable. The result shows that the condition completely depends on a univalent function λ and an angle θ. By choosing different λ and θ, we can not only control the shape of P (r, t), but also make R(r) become any kind of characteristic curve on P (r, t). Furthermore, we take natural and conjugate curve pairs as those characteristic curves to construct developable surface pairs. Finally, an example of a slant helix shows that the proposed unified method is more general than other methods, and has good interactivity and convenience.
1 Introduction
A developable surface can unfold into a flat without scaling, folding, or tearing, which is widely used in the manufacture of many products, such as the design of leather, paper, and metal plates [1–6]. With the in-depth research of many scholars on the developable surface, its construction theory has gradually become a system. At present, there are three main construction methods: the point geometry method [7, 8], the dual method [9, 10], and the construction method with certain geometric constraints [11–13]. In addition, there are also scholars who focused on its related research, such as [14–19].
Geodesic, line of curvature, and asymptotic curve are crucial characteristic curves on the surfaces, which determine the properties and shapes of the surfaces. The third method mentioned earlier, namely, the surface construction method with certain geometric constraints, is the method of constructing a surface pencil interpolating a given geodesic, line of curvature, or asymptotic curve. This method was first proposed by Wang and Tang [20], which constructed a surface pencil interpolating a given geodesic, then Zhao and Wang [11] extended the method to the developable surface. Li and Wang [21] proved the constraint conditions that need to be satisfied when a given curve is a common line of curvature on a surface pencil. Later, they [12] also proposed a brand new method of constructing a developable surface pencil interpolating a given line of curvature. Bayram and Güler [22] explored the construction of a surface pencil with a given asymptotic curve, and Liu and Wang [13] extended the results of [22] to the developable surface. In recent years, it has become popular to use special curve pairs to construct surface pairs. Atalay [23, 24], constructed surface pencil pairs interpolating Mannheim curve pairs as common asymptotic curves and geodesics, and extended the surface pairs to the ruled surface pairs. Wang and Jiang [25] took natural and conjugate curve pairs as common asymptotic curves to construct developable surface pencil pairs. Jiang [26] took the Bertrand curve pair as asymptotic curves to construct surface pencil pair in Galilean space, and the result is extended to the ruled surface pair.
Kaya and Önder [27] introduced a new characteristic curve called D-type curve, which satisfies W0 ⋅n = constant, where W0 is the unit Darboux vector of a surface curve, n is the unit surface normal vector along the surface curve, and W0 ⋅n denotes the dot product of W0 and n. The conditions required for a surface pencil interpolating a common D-type curve are proposed in [27]. The D-type curve is more general because it contains the geodesic and the asymptotic curve. However, it does not contain the line of curvature, and the study on it is not extended to the developable surface. This study discusses whether a unified method can be proposed to construct developable surfaces interpolating geodesic, line of curvature, asymptotic curve, and D-type curve.
In addition, Wang and Jiang [25] only proposed developable surface pencil pairs interpolating natural and conjugate curve pairs as asymptotic curves. To complete the results, we put forward developable surface pencil pairs interpolating these two kinds of curve pairs as common geodesics, lines of curvature, and D-type curves, respectively.
In Section 2, we introduce the judgment methods of four kinds of characteristic curves on the surfaces. In Section 3, the unified method for constructing developable surface pencils interpolating four kinds of characteristic curves is given. In Section 4, we give the specific expressions for developable surface pencil pairs interpolating natural and conjugate curve pairs as common geodesics, lines of curvature, and D-type curves, respectively. In Section 5, an example of a slant helix is given to verify the efficiency and convenience of this unified method.
2 Preliminaries
Let R(r), L1 ≤ r ≤ L2 be a regular curve in
where κ, τ, R, T, N, and B denote the shorthand of κ(r), τ(r), R(r), T(r), N(r), and B(r), respectively, “×”denotes the cross product, and (⋅, ⋅, ⋅) denotes the mixed product. T, N, and B form the Frenet frame of R, which follows [28].
Suppose [20].
is a surface pencil interpolating R(r), and P (r, t0) = R(r), where α(r, t), β(r, t), and γ(r, t) are called the marching-scale functions, T1, T2 are two real numbers, and t0 ∈ [T1, T2].
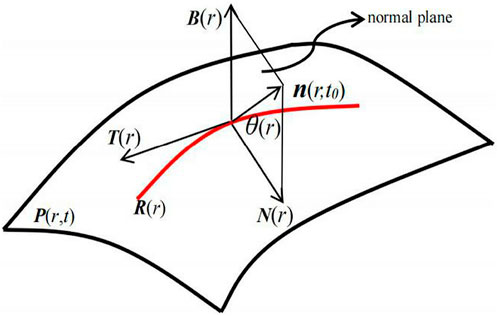
Let the angle between the principal normal vector N(r) of R(r) and the surface normal vector n (r, t0) along R(r) be θ(r) (Figure 1). Because the surface normal vector n (r, t0) is in the normal plane, and the normal plane is made up of the principal normal vector N(r) and the binormal vector B(r), the surface normal vector n (r, t0) can be represented as a linear combination of N(r) and B(r), that is.
where λ(r) is a univalent function.
If θ(r) satisfies a specific condition, then the curve R(r) will become the corresponding characteristic curve of P (r, t). That is
Lemma 2.1 [29]. R(r) is a geodesic of P (r, t) as θ = 0 or π.
Lemma 2.2 [13]. R(r) is an asymptotic curve of P (r, t) as
Lemma 2.3 [21]. R(r) is a line of curvature of P (r, t) as θ′ = −τ|R′|.
Lemma 2.4. R(r) is a D-type curve of P (r, t) as
In Lemmas 2.1–2.4, θ denotes the shorthand of θ(r).
Proof. According to Eq. 3, suppose the unit surface normal vector along R(r) is
and the unit Darboux vector of R(r) is [27].
if R(r) is a D-type curve of P(r, t), then [27].
then we get
3 Unified necessary and sufficient conditions for developable surface pencils interpolating characteristic curves
The results of developable surface pencils interpolating a common geodesic, a common line of curvature, and a common asymptotic curve can be found in [11–13], respectively, but there is no unified method for constructing developable surface pencils interpolating these characteristic curves. In this section, we make up for this shortcoming. First, we recall a known lemma.
Lemma 3.1 [13]. P(r, t) (Eq. (2)) is developable if and only if
and
where α(r), β(r), and γ(r) are marching-scale functions.
By Eq. 3, Lemma 3.1 can be rewritten as Theorem 3.1.
Theorem 3.1. P(r, t) (Eq. (2)) is developable if and only if the functions α, β, γ, λ, and θ satisfy Eq. (7) and the following conditions
where α, β, γ, λ, and θ represent the shorthand of α(r), β(r), γ(r), λ(r), and θ(r), respectively.
Proof. According to Eqs 2, 7, P(r, t) can be represented as
By taking the partial derivative of Eq. 10 and using Eq. 1, we obtain that
then, according to Eq. 11, the surface normal vector is
substituting Eq. 13 into Eq.8, we obtain
Hence, the theorem is proved.
Obviously, if λ = 0, P(r, t) is the tangent surface pencil of R(r), that is, it is always developable, so next, we consider only the case λ ≠ 0.
By Lemmas 2.1–2.4, if θ further satisfies a particular condition, the curve R(r) can become the corresponding characteristic curve on the developable surface, so we get Theorem 3.2.
Theorem 3.2. P(r, t) (Eq. (2)) is a developable surface pencil interpolating R(r) as a common characteristic curve if and only if the functions α, β, γ, λ, and θ satisfy Eqs. (7), (9), and the following conditions:
1. If this characteristic curve is a geodesic, then θ = 0 or π.
2. If this characteristic curve is an asymptotic curve, then
3. If this characteristic curve is a line of curvature, then θ′ = −τ|R′|.
4. If this characteristic curve is a D-type curve, then
Theorem 3.2 unifies the conditions for interpolating four kinds of characteristic curves to construct developable surface pencils, it not only contains the results of [11–13], but also puts forward interpolating a D-type curve to construct developable surface pencil, simultaneously, which is not involved in all current studies.
According to Theorems 3.1 and 3.2, the functions α, β, and γ of the developable surface are only related to a function λ and an angle θ, we can change the shape of the developable surface by choosing different λ, and make the given curve become any kind of characteristic curve on the developable surface by choosing different θ. Therefore, the method in this study has better interactivity than other methods. Now we continue to use this method to complete the study of developable surface pairs interpolating natural and conjugate curve pairs.
4 Developable surface pencil pairs interpolating natural and conjugate curve pairs as common characteristic curves
Developable surface pencil pairs interpolating natural and conjugate curve pairs as asymptotic curves have been proposed in [25]. To make this result complete, we continue to give developable surface pencil pairs interpolating these two kinds of curve pairs as the other three kinds of characteristic curves.
Definition 4.1 [25]. Given a unit speed curve R0(s), L1 ≤ s ≤ L2. R1(s) = ∫N0(s)ds and R2(s) = ∫B0(s)ds are called the natural mate curve and the conjugate mate curve of R0(s), respectively, where N0(s) and B0(s) are the principal normal vector and binormal vector of R0(s), respectively. {R0(s), R1(s)} and {R0(s), R2(s)} are called the natural curve pair and the conjugate curve pair, respectively.
Definition 4.2 [25]. Let the developable surface pencils Pi(s, t) interpolate Ri(s), i = 0, 1, 2, {P0(s, t), P1(s, t)} and {P0(s, t), P2(s, t)} are called the natural developable surface pencil pair and the conjugate developable surface pencil pair, respectively.
Let{Ti, Ni, Bi}, κi, and τi denote the Frenet frame, curvature, and torsion of Ri(s), i = 0, 1, 2, respectively.
According to Theorem 3.1, if t0 = 0 and
where θi are the angles between the surface normal vectors ni(s, t0) along Ri(s) and the principal normal vectors Ni of Ri(s), λi are functions that control the shapes of Pi(s, t).
According to Theorem 3.2, substituting θi = 0 or π,
Theorem 4.1. Ri(s) are common geodesics of Pi(s, t) (see Eq. (14)) if and only if
Theorem 4.2. Ri(s) are common lines of curvature of Pi(s, t) (Eq. (14)) if and only if
where
Theorem 4.3. Ri(s) are common D-type curves of Pi(s, t) (see Eq. (14)) if and only if
where
5 Example
Given a unit speed slant helix [25].
The Frenet frame, curvature, and torsion of R0(s) are
According to Definition 4.1, the natural mate curve is
and the conjugate mate curve is
By [30], the Frenet frame, curvature, and torsion of R1(s) are
Also, the Frenet frame, curvature, and torsion of R2(s) are
where ɛ = sgn τ0.
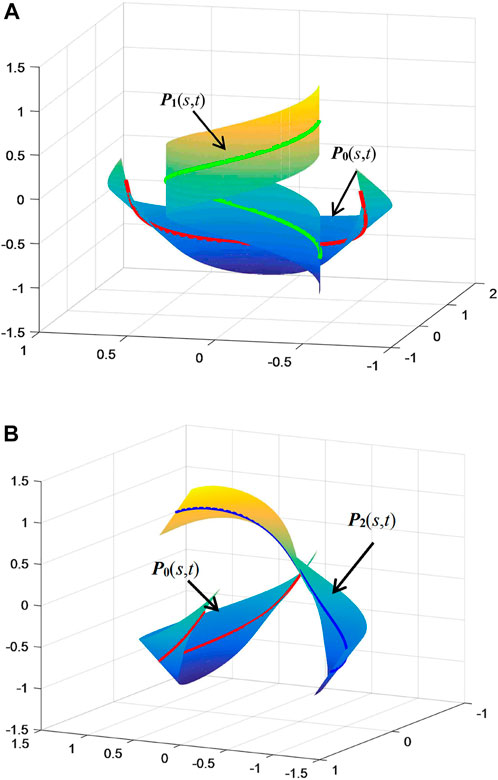
Case 1. By taking λi = −κi in Eq. 15, {P0(s, t), Pi(s, t)} interpolating {R0(s), Ri(s)}, (i = 1, 2) as common geodesics are shown in Figure 2, and
Case 2. By taking
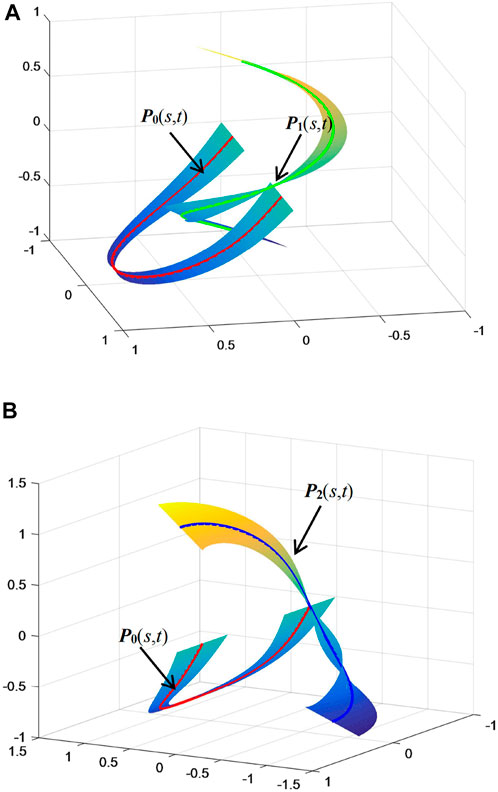
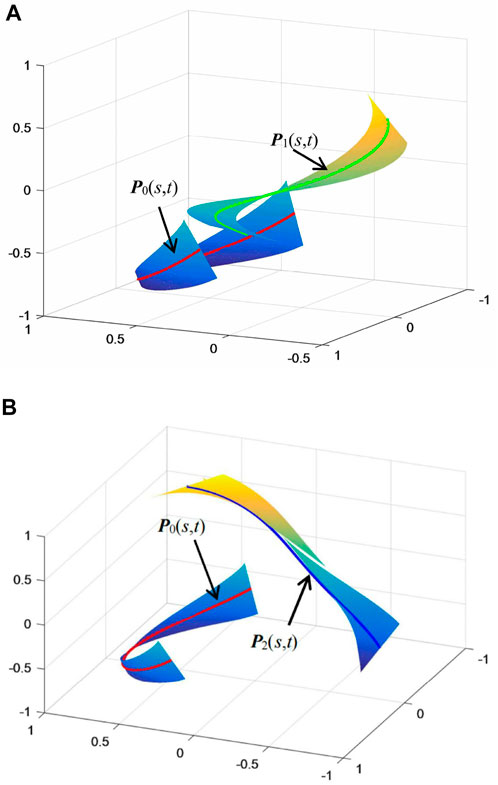
FIGURE 3. {P0(s, t), Pi(s, t)} interpolating {R0(s), Ri(s)}, (i = 1, 2) as common lines of curvature.
Case 3. By taking
In Eq. 17, {P0(s, t), Pi(s, t)} interpolating {R0(s), Ri(s)}, (i = 1, 2), as common D-type curves are shown in Figure 4, and
where − 0.2 ≤ t ≤ 0.2, and if i = 0, 1, then
In Figures 2–4, the red curve, the green curve, and the blue curve represent R0(s), R1(s), and R2(s), respectively.
6 Conclusion
We give a unified method for constructing developable surface pencils interpolating four kinds of characteristic curves. This method not only contains the results of [11–13], but also includes the method for constructing a developable surface pencil interpolating a common D-type curve. We find that the marching-scale functions are completely determined by a univalent function λ and an angle θ, where λ controls the shape of the developable surface and θ determines which kind of characteristic curve the given curve is. Therefore, the method in this study is more general and interactive than other methods. Furthermore, we obtain specific expressions of developable surface pencil pairs interpolating natural and conjugate curve pairs as common geodesics, lines of curvature, and D-type curves, respectively, which complete the results of [25].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
JW, MC, and DW contributed to the conception and design of the study. DW collected methods for constructing developable surfaces. JW and MC provided the theoretical derivation of the method and implemented the method through examples. JW wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation (grant number 12171459), Domestic Visiting Scholar Project for Outstanding Young University Teachers of Anhui Province (grant number gxgnfx2022060), University Natural Science Research Project of Anhui Province (grant number KJ2018A0455), and Scientific Research Foundation of Chaohu University (grant number KYQD-201707).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Boersma J, Molenaar J. Geometry of the shoulder of a packaging machine. SIAM Rev Soc Ind Appl Math (1995) 37:406–22. doi:10.1137/1037084
2. Kergosien YL, Gotoda H, Kunii TL. Bending and creasing virtual paper. IEEE Comput Graph Appl (1994) 14:40–8. doi:10.1109/38.250917
3. Aono M, Breen DE, Wozny MJ. Fitting a woven-cloth model to a curved surface: Mapping algorithms. Computer-Aided Des (1994) 26:278–92. doi:10.1016/0010-4485(94)90074-4
4. Bercu G, Crasmareanu M. Classes of harmonic functions in 2d generalized poincaré geometry. Filomat (2021) 35:287–97. doi:10.2298/FIL2101287B
5. Gala S, Ragusa MA. Logarithmically improved regularity criteria for supercritical quasi-geostrophic equations in orlicz-morrey spaces. Electron J Differential Equations (2016) 2016:1–7.
6. Guan J, Liu H. The sub-riemannian limit of curvatures for curves and surfaces and a gauss-bonnet theorem in the group of rigid motions of minkowski plane with general left-invariant metric. J Funct Spaces (2021) 2021:1–14. doi:10.1155/2021/1431082
7. Lang J, Roschel O. Developable (1, n) - Bézier surfaces. Computer Aided Geometric Des (1992) 9:291–8. doi:10.1016/0167-8396(92)90036-O
8. Chu C-H, Séquin CH. Developable bézier patches: Properties and design. Computer-Aided Des (2002) 34:511–27. doi:10.1016/S0010-4485(01)00122-1
9. Bodduluri R, Ravani B. Design of developable surfaces using duality between plane and point geometries. Computer-aided Des (1993) 25:621–32. doi:10.1016/0010-4485(93)90017-I
10. Pottmann H, Farin G. Developable rational bézier and b-spline surfaces. Computer Aided Geometric Des (1995) 12:513–31. doi:10.1016/0167-8396(94)00031-M
11. Zhao H, Wang G. A new method for designing a developable surface utilizing the surface pencil through a given curve. Prog Nat Sci (2008) 18:105–10. doi:10.1016/j.pnsc.2007.09.001
12. Li C, Wang R, Zhu C. An approach for designing a developable surface through a given line of curvature. Computer-Aided Des (2013) 45:621–7. doi:10.1016/j.cad.2012.11.001
13. Liu Y, Wang G. Designing developable surface pencil through given curve as its common asymptotic curve. J Zhejiang Univ (Engineering Science) (2013) 47:1246–52. doi:10.3785/j.issn.1008-973X.2013.07.017
14. Zhang W, Wang G. Constructiong quasi-developable meshes through a given discrete line of curvature. J Computer-Aided Des Computer Graphics (2015) 27:1950–5.
15. Li C, Xiang X, Zhu C. Design of ruled developable surface through the line of curvature. J image graphics (2016) 21:527–31. doi:10.11834/jig.20160415
16. Hu G, Wu J, Li H, Hu X. Shape optimization of generalized developable h-bézier surfaces using adaptive cuckoo search algorithm. Adv Eng Softw (2020) 149:102889. doi:10.1016/j.advengsoft.2020.102889
17. Lian H, Ge W. Calculus of variations for a boundary value problem of differential system on the half line. Comput Mathematics Appl (2009) 58:58–64. doi:10.1016/j.camwa.2009.03.088
18. Yang L, Su H, Zhong C, Meng Z, Luo H, Li X, et al. Hyperspectral image classification using wavelet transform-based smooth ordering. Int J Wavelets Multiresolut Inf Process (2019) 17:1950050. doi:10.1142/S0219691319500504
19. Zheng X, Tang YY, Zhou J. A framework of adaptive multiscale wavelet decomposition for signals on undirected graphs. IEEE Trans Signal Process (2019) 67:1696–711. doi:10.1109/TSP.2019.2896246
20. Wang G, Tang K, Tai C-L. Parametric representation of a surface pencil with a common spatial geodesic. Computer-Aided Des (2004) 36:447–59. doi:10.1016/S0010-4485(03)00117-9
21. Li C, Wang R, Zhu C. Parametric representation of a surface pencil with a common line of curvature. Computer-Aided Des (2011) 43:1110–7. doi:10.1016/j.cad.2011.05.001
22. Bayram E, Güler F, Kasap E. Parametric representation of a surface pencil with a common asymptotic curve. Computer-Aided Des (2012) 44:637–43. doi:10.1016/j.cad.2012.02.007
23. Atalay GŞ. Surfaces family with a common mannheim asymptotic curve. J Appl Mathematics Comput (2018) 2:143–54. doi:10.26855/jamc.2018.04.004
24. Atalay GŞ. Surfaces family with a common mannheim geodesic curve. J Appl Mathematics Comput (2018) 2:155–65. doi:10.26855/jamc.2018.04.005
25. Wang J, Jiang P, Guo Y, Meng J. Developable surface pencil pairs with special pairs as common asymptotes. Appl Mathematics Comput (2019) 362:124583. doi:10.1016/j.amc.2019.124583
26. Jiang X, Jiang P, Meng J, Wang K. Surface pencil pair interpolating bertrand pair as common asymptotic curves in galilean space g3. Int J Geom Methods Mod Phys (2021) 18:2150114. doi:10.1142/S0219887821501140
27. Kaya O, Önder M. Construction of a surface pencil with a common special surface curve. J mahani Math Res Cent (2017) 6:57–72. doi:10.22103/JMMRC.2017.10079.1038
28. Farin G. Curves and surfaces for computer-aided geometric design. New York: Academic Press (1990).
Keywords: geodesic, line of curvature, asymptotic curve, D-type curve, natural pair, conjugate pair, developable surface pencils, simple and common surfaces
Citation: Wang J, Chen M and Wang D (2022) A unified method for constructing developable surface pencils interpolating characteristic curves. Front. Phys. 10:979094. doi: 10.3389/fphy.2022.979094
Received: 29 June 2022; Accepted: 12 August 2022;
Published: 19 September 2022.
Edited by:
Emanuel Guariglia, São Paulo State University, BrazilReviewed by:
Maria Alessandra Ragusa, University of Catania, ItalyAnouar Ben Mabrouk, University of Kairouan, Tunisia
Copyright © 2022 Wang, Chen and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Wang, MDU4MDMyQGNodS5lZHUuY24=
 Jun Wang
Jun Wang Miaochao Chen
Miaochao Chen