The model for non-Abelian field topology for the multilayer fractional quantum anomalous Hall device

From the recent empirical discovery of the quantum anomalous Hall effect (QAHE), the interaction of the particle with spin–orbit coupling (SOC) plays an essential role in the cause of the QAHE, which includes three terms: external, internal, and chiral symmetric terms. Then, the non-Abelian quantum field theory was adopted to analyze and prove the conjecture on the causes that can lead to the fractional quantum Hall effect (FQHE). The spontaneously topological chiral symmetry breaking is the main contribution to the FQHE, which also includes two terms: the hopping of sublattice and Coulomb energy by the interaction of many-body particles. More generally, this exciton possesses an intermediate characteristic between the Wannier regimes and displays a peculiar two-dimensional wavefunction in the three-dimensional FQHE states. Finally, a bilayer three-dimensional model is proposed to implement the FQHE on the lattice by incorporating ferromagnetic dopants into three-dimensional topological insulative thin films. This study theoretically predicts the FQHE on the basis of other reports that have experimentally verified the rationality of the proposed model in magnetic topological insulators.

1 Introduction

The quantum anomalous Hall effect (QAHE) has a totally different physical nature, with a semi-integer quantum Hall effect and a perfect quantum tunneling effect. It allows for resistance quantization and dissipationless edge states without the presence of any applied magnetic field. The materials and structures of the QAHE, where quantum effects are responsible for novel physical properties, reveal the important roles of symmetry, topology, and dimensionality. In 1988, according to Haldane, there might be no need to apply any external magnetic field for the quantum Hall effect, but it seemed impossible to implement such a particular material system of quantum effects in physical ways. In 2010, physicists achieved a breakthrough in the theory and design of materials, such that Cr/Fe magnetic ions could be doped into Bi₂Te₃ and Bi₂Se₃ and Sb₂Te₃ topological insulators. There are special V-Vleck ferromagnetic exchange mechanisms to ensure stability of ferromagnetic insulators, creating the best system to achieve the quantum anomalous Hall effect [1, 2]. The calculations show that the multilayer magnetic exchange of magnetic topological insulators takes place at a certain thickness and strength, that is, in the “QAHE” state. The breakthrough in theories and material design has given rise to the idea of looking for the QAHE.

The topological flat-band model is an extended version of the famous Haldane model. At least one energy band has non-trivial topological properties, that is, it has a non-zero Chern number, and the bandwidth of this energy band is very narrow. There is a wide energy gap between these energy bands. Recently, through the systematic numerical study of fermions and boson lattice systems with strong correlative interactions with topological flat bands, a novel class of Abelian and non-Abelian FQHEs has been discovered. The newly discovered FQHE is distinct from the continuous FQHE on the traditional Landau energy level. Without requiring any external magnetic field, it has a relatively wide characteristic energy gap and can exist at higher temperatures without requiring a single-particle Landau. The energy level cannot be described by conventional Laughlin wavefunctions. These fractional phenomena with no external magnetic field and no Landau energy levels define a new class of fractional topological phases, which are also called fractional insulators. The FQHE is also called the fractional quantum anomalous Hall effect (FQAHE) [3].

This paper is organized into five sections: Section 1 discusses the spin–orbit coupling theory for the QAHE in Section 2. Section 3 shifts the attention to an explanation of the intrinsic non-Abelian gauge field for properties of QHE and the cause of the QAHE. The next two sections expand the circumstance to the three-dimensional topology insulator and a conjecture on the existence of the FQAHE. Conclusions are drawn in Section 6.

2 Mathematical theory foundation of the quantum anomalous Hall effect

The difference between the QAHE and QAH lies in the absence of an external magnetic field, with homogeneous magnetization M. Their measurements in the magnetic field can be presented as follows:

${\rho }_{xy}=R_{0}B+4\pi R_{s}M.(1)$

There are three causes for QHE: The first, the extrinsic mechanism, views QHE as related to material impurities and spin–orbit (SO) interaction, such as skew scattering and side-jump of the lattice; the second, the intrinsic mechanism, points out that crystal potential is periodic and SO is interactive; the third, the chirality mechanism, suggests in noncollinear ferromagnets the spin–orbit interaction causes the effect [4]. The spin–orbit interaction can be expressed as follows:

$H_{SO,vac}={\lambda }_{\mathit{vac}}\cdot \sigma \cdot \left(k\times \nabla \tilde{V}\right),(2)$

where subscripts SO and vac signify the spin–orbit interaction and vacuum holes, respectively; the random Rashba coupling parameter λ has the zero mean and a Gaussian correlator; the other parameters are k for the wave vector, V for the voltage, and σ for the current conductivity.

Also, in a 2D high-symmetry system, anomalous Hall effect Hamiltonian has three forms:

$\begin{array}{ll}\hfill H_{\mathit{eff}}& ={\epsilon }_k+V+H_{\text{int}}+H_{\mathit{ext}}\hfill \\ \hfill H_{\mathit{int}}& =\frac{1}{2}\mathbf{b}\left(\mathbf{k}\right)\cdot \sigma \hfill \\ \hfill H_{\mathit{ext}}& =\lambda \cdot \sigma \cdot \left(\mathrm{k}\times \nabla V\right).\hfill \end{array}(3)$

The QAHE has the following characteristics: magnetization, spin-polarized and transverse carriers, Hall voltage on spin current, and spin accumulation. On the other hand, the pure spin Hall effect (SHE) is different, without applying any external magnetic field. The spin–orbit interaction causes electrons to carry opposite spins to move in opposite directions at the 2D insulator boundary with metal boundaries. The electric field provided generates a spin current that fails to create a charge flow.

The linear response of non-conserved spin current to the applied electric field can be calculated by the Kubo formula.

$\sigma =\frac{e^2}{{\omega }^2}\mathit{Tr}\int \frac{d\epsilon }{2\pi }⟨{\widehat{v}}_i\widehat{G}\left(\epsilon +\omega \right){\widehat{v}}_j\widehat{G}\left(\epsilon \right)⟩.(4)$

Taking the static limit, we get the Streda formula as follows:

$\begin{array}{cc}\hfill {\sigma }_{ij}^I& =\frac{e^2}{2}\mathit{Tr}\int \frac{d\epsilon }{2\pi }\left(-\frac{\partial f\left(\epsilon \right)}{\partial \epsilon }\right)⟨{\widehat{v}}_i\left[{\widehat{G}}^R\left(\epsilon \right)-{\widehat{G}}^A\left(\epsilon \right)\right]\hfill \\ \hfill & v_j{\widehat{G}}^A\left(\epsilon \right)-{\widehat{v}}_i{\widehat{G}}^R\left(\epsilon \right){\widehat{v}}_j\left[{\widehat{G}}^R\left(\epsilon \right)-{\widehat{G}}^A\left(\epsilon \right)\right]⟩\hfill \end{array};$

$\begin{array}{cc}\hfill {\sigma }_{ij}^{II}& =\frac{e^2}{2}\mathit{Tr}\int \frac{d\epsilon }{2\pi }f\left(\epsilon \right)⟨{\widehat{v}}_i\frac{\partial {\widehat{G}}^A\left(\epsilon \right)}{\partial \epsilon }{\widehat{v}}_j{\widehat{G}}^A\left(\epsilon \right)-{\widehat{v}}_i{\widehat{G}}^A\left(\epsilon \right){\widehat{v}}_j\hfill \\ \hfill & \frac{\partial {\widehat{G}}^A\left(\epsilon \right)}{\partial \epsilon }+{\widehat{v}}_i{\widehat{G}}^R\left(\epsilon \right){\widehat{v}}_j\frac{\partial {\widehat{G}}^R\left(\epsilon \right)}{\partial \epsilon }-{\widehat{v}}_i\frac{\partial {\widehat{G}}^R\left(\epsilon \right)}{\partial \epsilon }{\widehat{v}}_j{\widehat{G}}^R\left(\epsilon \right)⟩\hfill \end{array},(5)$

where ${\widehat{G}}^A$ and ${\widehat{G}}^R$ are the advanced and retarded Green functions, respectively. The off-diagonal conductivity presents the contribution from all occupied states. The limit as ω → 0 implies ω → ℏ/τ.

The difference in cleanliness of the current and the possible disappearance of Gaussian disorder can be explained by asymmetric dispersion. Impurities have no effect on the side view current [5].

The single-particle energy band system is dispersive and does not support fractional excitation and cannot implement the FQHE. A series of topological flat-band lattice models are expected to overcome the abovementioned difficulties and implement the FQHE. The tight-binding model of the two-dimensional triangular lattice model is expressed in the Hamiltonian. Hall conductivity is calculated by the Kubo formula:

$\begin{array}{ccc}\hfill & {\sigma }_{xy}\left(\omega \right)=\frac{{\text{e}}^2}{\omega }{\int }_{-\infty }^{\infty }\frac{\text{d}\epsilon }{2\pi }\sum _{mm}\sum _k{\left(v_x\right)}_{nm}\hfill & \hfill \\ \hfill & G_{\mathit{kam}}\left(\epsilon +w\right){\left(v_y\right)}_{mm}{G}_{\mathit{knn}}\left(\epsilon \right)\hfill & ,\hfill \end{array}(6)$

where the velocity operator v = ∂H/∂k.

Hence, we have

${\sigma }_{xy}=e^2\sum _n\sum _{\mathbf{k}}\tilde{f}\left(E_{\mathbf{k}n}\right)\left(\frac{\partial A_y\left(\mathbf{k}n\right)}{\partial k_x}-\frac{\partial A_x\left(\mathbf{k}n\right)}{\partial k_y}\right),$

where $\tilde{f}$ is the Femi statistic function with gauge potential

$A_{\alpha }\left(\mathbf{k}n\right)=-i⟨\mathbf{k}n\left|\frac{\partial }{\partial k_{\alpha }}\right|\mathbf{k}n⟩.$

Based on the 2D Rashba model, we obtain the magnetization Rashba Hamiltonian:

$H={\epsilon }_k+\alpha \left(k_y{\sigma }_x-k_x{\sigma }_y\right)-M{\sigma }_z,$

where ɛ_k = k²/2m. Then, the Hall conductivity is

${\sigma }_{xy}\left(\omega \right)=\frac{e^2}{\omega }\mathit{Tr}{\int }_{-\infty }^{\infty }\frac{d\epsilon }{2\pi }\frac{d^2\mathbf{k}}{{\left(2\pi \right)}^2}{v}_x{G}_{\mathbf{k}}\left(\epsilon +\omega \right)v_y{G}_{\mathbf{k}}\left(\epsilon \right),(7)$

with $v_x=\frac{k_m}{m}-\alpha {\sigma }_y,v_y=\frac{k_m}{m}-\alpha {\sigma }_x$, and the energy spectrum is

$E_{k\uparrow ,\downarrow }=\epsilon \mp \lambda \left(k\right),\lambda \left(k\right)\sqrt{M^2+{\alpha }^2{k}^2},$

where M corresponds to a uniform magnetization along the z-axis, which is uncorrelated with the macroscopic magnetic field, whose value is half of the spin splitting. The second of the two contribution terms contributes to the states below the Fermi energy.

${\sigma }_{xy}^{II}=-4e^{2}M{\alpha }^2\int \frac{d^{2}k}{{\left(2\pi \right)}^2}\frac{f\left(E_{k\uparrow }\right)-f\left(E_{k\downarrow }\right)}{\left(E_{k\uparrow }-E_{k\downarrow }\right)}.(8)$

Then, we have

${\sigma }_{xy}^{II}=\frac{e^{2}M}{4\pi }\left(\frac{1}{\lambda \left(k_{F\downarrow }\right)}-\frac{1}{\lambda \left(k_{F\uparrow }\right)}\right).(9)$

The symmetric breaking of topological material structure affects the Berry phase and causes the QAHE, while the Hamiltonian

$H={\epsilon }_k+\lambda \left(k\right)\sigma \cdot \mathbf{n}\left(k\right),(10)$

where the unit normal vector to the sphere gives

$\mathbf{n}\left(\mathbf{k}\right)=\left(\frac{\alpha {\mathbf{k}}_{\mathbf{y}}}{\lambda \left(\mathbf{k}\right)},-\frac{\alpha {\mathbf{k}}_{\mathbf{x}}}{\lambda \left(\mathbf{k}\right)},\frac{\mathbf{M}}{\lambda \left(\mathbf{k}\right)}\right),$

so the conductivity can be expressed in terms of $\mathbf{n}\left(\mathbf{k}\right)$.

${\sigma }_{xy}^{II}=-\frac{e^2}{2}\int \frac{d^2\mathbf{k}}{{\left(2\pi \right)}^2}f\left(E_{\mathbf{k}\uparrow }\right){\epsilon }_{\alpha \beta \gamma }{n}_{\alpha }\frac{\partial n_{\beta }}{\partial k_x}\frac{\partial n_{\gamma }}{\partial k_y}.(11)$

Spin current density in the wire can be defined as follows:

$J_{\alpha }^i\left(\mathbf{r},t\right)=\frac{\delta L}{\delta A_{\alpha }^i\left(\mathbf{r},t\right)}.(12)$

The aforementioned formula defines a non-conserved equilibrium spin current, and it is related to real motion. The redefinition of spin current in Lagrangian allows for the equilibrium spin current.

$\begin{array}{cc}\hfill L& =\int {\text{d}}^{3}r\left\{{\mathrm{\Psi }}^{†}\left(r,t\right)\left(\text{i}\frac{\partial }{\partial t}-H\right)\mathrm{\Psi }\left(r,t\right)\right.\hfill \\ \hfill L& =\int {\text{d}}^3\mathbf{r}{\mathrm{\Psi }}^{+}\left(\mathbf{r},t\right)\left(\text{i}\frac{\partial }{\partial t}+\frac{{\nabla }^2}{2m}-V\left(r\right)\right)\mathrm{\Psi }\left(\mathbf{r},t\right)\hfill \end{array}.$

In rotation space, the local transformation is

$\mathrm{\Psi }\left(\mathbf{r},t\right)\to \exp \left[-ig\mathbf{n}\left(\mathbf{r},t\right)\cdot \sigma \right]\psi \left(\mathbf{r},t\right).$

Adopting the Lagrangian transformation, we obtain

$\begin{array}{cc}\hfill L& =\int {\text{d}}^3\mathbf{r}{\psi }^{†}\left(\text{r,}t\right)\left[\text{i}\left(\frac{\partial }{\partial t}-\text{i}{A}_0^i\left(\mathbf{r},t\right){\sigma }^i\right)+\right.\hfill \\ \hfill & \left.\frac{1}{2m}{\left(\frac{\partial }{\partial r_{\alpha }}-\text{i}{A}_{\alpha }^i\left(\text{r,}t\right){\sigma }^i\right)}^2-V\left(\mathbf{r}\right)\right]\psi \left(\mathbf{r},t\right)\hfill \end{array}.(13)$

The gauge vectors in the fields are

$A_0^i\left(\mathbf{r},t\right)=g\frac{\partial n^{\text{i}}\left(\mathbf{r},t\right)}{\partial t},A_{\alpha }^i\left(\mathbf{r},t\right)=g\frac{\partial n^{\text{i}}\left(\mathbf{r},t\right)}{\partial r_{\alpha }}.$

Thus, the spin density and spin current density can be expressed as follows:

$S^i\left(r,t\right)=\frac{\delta L}{\delta A_0^i\left(r,t\right)},J_{\alpha }^i\left(r,t\right)=\frac{\delta L}{\delta A_{\alpha }^i\left(r,t\right)}.(14)$

For equilibrium spin currents, we consider the simplest model with two interactive spins in local fields, where Hamiltonian is given by

$H=-{\mathbf{J}\mathbf{S}}_1\cdot {\mathbf{S}}_2-{\mathbf{B}}_1\cdot {\mathbf{B}}_2-{\mathbf{B}}_2\cdot {\mathbf{B}}_2.$

The equation of motion for spin S₁ is expressed as follows:

${\dot{\mathbf{S}}}_1=\left(i/\hslash \right)\left[H,S_1\right];$

${\dot{S}}_1=\left(J/\hslash \right){\mathbf{S}}_1\times {\mathbf{S}}_2+\left(1/\hslash \right){\mathbf{S}}_1\times {\mathbf{B}}_1.$

The spin current density is expressed as follows:

$J_{2\to 1}\equiv \frac{J}{\hslash }{\mathbf{S}}_1\times {\mathbf{S}}_2=-J_{1\to 2}.$

The two-point Hubbard model can be used to represent the interaction between present electrons s.t.

$H=-t\left(c_{1\alpha }^{†}{c}_{2\alpha }+c_{2\alpha }^{†}{c}_{1\alpha }\right)+\sum _{i=\mathrm{1,2}}\left(U{n}_i^{\uparrow }{n}_i^{\downarrow }-{\mathbf{B}}_{\mathbf{i}}\cdot {\mathbf{S}}_{\mathbf{i}}\right).$

The motion equation is expressed as follows:

$\begin{array}{cc}\hfill {\dot{\mathbf{S}}}_1& =\left(i/\hslash \right)\left[H,S_1\right]\hfill \\ \hfill {\dot{\mathbf{S}}}_1& =\frac{it}{2\hslash }\left(c_{1\alpha }^{†}{c}_{2\beta }+c_{2\alpha }^{†}{c}_{1\beta }\right){\sigma }_{\alpha \beta }+\frac{1}{\hslash }{\mathbf{S}}_1\times {\mathbf{B}}_1\hfill \end{array}.(15)$

The spin current density is expressed as follows:

$j_{2\to 1}^i\equiv =\frac{it}{2\hslash }\left(c_{1\alpha }^{†}{c}_{2\beta }+c_{2\alpha }^{†}{c}_{1\beta }\right){\sigma }_{\alpha \beta }=-j_{1\to 2}.(16)$

Therefore, the equilibrium spin current is related to the jump across different positions. Where − J ≡ 4t²/U. Thus, spin current density is given by: Therefore, the equilibrium spin current is re-lated to the jump across different positions.

Applying the six functions based on ground states, we have the strong e–e interaction such that t/U ≪ 1, and effective Hamiltonian is expressed as follows:

$\tilde{H}=-J\left(S_1\cdot S_2-1/4\right)-{\mathbf{B}}_1\cdot {\mathbf{S}}_2-{\mathbf{B}}_2\cdot {\mathbf{S}}_2,(17)$

where − J ≡ 4t²/U. Thus, the spin current density is given by

${\tilde{j}}_{2\to 1}\equiv \frac{J}{\hslash }{\mathbf{S}}_1\times {\mathbf{S}}_2.(18)$

The anomalous Hall effect (AHE) can lead to the rotating Hall effect; that is, by studying the anomalous Hall voltage, the spin Hall voltage and the spin current are generated by rotating electrons. The relationship between them is derived.

$\begin{array}{ccc}\hfill & V_H=4R_{s}L{j}_x{n}_{\uparrow }{\mu }_B\hfill & \hfill \\ \hfill & V_{SH}=2\pi R_{s}L{j}_{x}n{\mu }_B\hfill & ,\hfill \end{array}(19)$

$\begin{array}{ccc}\hfill & j_{\sigma }=V_{SH}\rho L\hfill & \hfill \\ \hfill & V_{sc}=8{\pi }^2{R}_s^{2}l\frac{{\left(n{\mu }_B\right)}^2}{\rho }{j}_x\hfill & .\hfill \end{array}(20)$

The intrinsic contribution to the spin Hall effect is given as follows:

${\sigma }_{xy}^{SH}=\frac{e}{8\pi }.$

Considering impurities and as N_imp → 0,

${\sigma }_{xy}^{SH}=0.$

This cancellation is special for the Rashba model. Next, AHE and SHE are quantized with the 2D Dirac model on graphene.

$H=v\left(k_x{\sigma }_x+k_y{\sigma }_y\right)+\mathrm{\Delta }{\sigma }_z.(21)$

The energy spectrum is expressed as follows:

$\epsilon =\pm E_k,E_k=\sqrt{{\mathrm{\Delta }}^2+{\nu }^2{k}^2}.$

Also, the intrinsic Hall conductivity is expressed as follows:

${\sigma }_{xy}=-\frac{e^2}{4\pi }\frac{\mathrm{\Delta }}{E_F},E_F>\mathrm{\Delta }.$

With E_F as the gap, the abovementioned expression becomes

${\sigma }_{xy}=-\frac{e^2}{4\pi },{\sigma }_{xy}^{SH}=\frac{2}{e}{\sigma }_{xy}.$

In the 2D case, the effective conductivity is expressed as follows:

${\sigma }_{xy}^{II}=\frac{e^2}{2}\sum _n\sum _{\mathbf{k}}f\left(E_{\mathbf{k}n}\right){\epsilon }_{ij}{F}_{ij},(22)$

where “gauge field tensor” is

$F_{ij}=\frac{\partial A_j}{\partial k_i}-\frac{\partial A_i}{\partial k_j}.$

Also, the eigenvector gives

$|\mathbf{k}\uparrow ⟩=\sqrt{\frac{M+\lambda \left(k\right)}{2\lambda \left(k\right)}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \frac{i\alpha \left(k_x+i{k}_y\right)}{M+\lambda \left(k\right)}\hfill \end{array}\right),(23)$

$\mathbf{A}\left(\mathbf{k}\right)=\left(-\frac{{\alpha }^2{k}_y}{2\lambda \left(k\right)\left[M+\lambda \left(k\right)\right]},\frac{{\alpha }^2{k}_x}{2\lambda \left(k\right)\left[M+\lambda \left(k\right)\right]}\right).(24)$

The sub-number Hall anomaly effect is to be implemented on the lattice model. The key to the fractional topological state is to realize the near-flat-band structure with a non-mean topology. Given that the strict flat band (the zero bandwidth) is non-physical in practical materials, the limit can be relaxed by only requiring the bandwidth to be much narrower than the band gap width. The topological flat-band lattice model is expected to overcome the abovementioned difficulties and implement the FQHE. In these lattice models, by adjusting the short-range transition parameters, the SOC strength, or the staggered magnetic flux, the bandwidth can be made narrower than or even close to the flat band. Based on the similarity between the energy band close to the flat band and the Landau level [6], it can be reckoned that in these flat-band models, the FQHE (or the fractional topological insulator) can exist stably considering the repulsive interaction.

In this paper, we will study in detail the 2D triangular lattice model ignoring the interaction and determine the inhomogeneous flat-band structure by adjusting the sub-nearest neighbor transition strength and the staggered magnetic flux to implement the integer quantum Hall effect (IQHE). In this model, the IQHE can exist stably due to a non-uniform magnetic field being applied with a zero net magnetic field, with the Hall conductivity equal to a topological constant. In addition, in the continuous model under the effect of the normal magnetic field, the number of the Landau levels is typically 1, while in this system, a high number, that is, a C ≥ 2 topological flat band can be implemented.

3 Non-Abelian gauge theory for the fractional quantum Hall effect

These fractional phenomena of non-Landau energy levels define a new class of fractional topological phases or fractional Chern insulators (FCI). This work studied two situations with Chern number = 1 and 2, respectively.

At the semiconductor heterojunction interface and under the measurement condition below the temperature and above the magnetic field strength, it has been found that $\nu ={\sigma }_H/\left(e^2/h\right)=1/\mathrm{2,1}/3\dots$ appears on the platform and that simultaneous longitudinal resistance is close to zero, that is, the FQHE. When C = 1, ν = 1/2, 1/4, and 1/3, corresponding to the boson case. When C = 2, ν = 1/3 and 1/5. In the latter case, Laughlin’s fermion fractional quantum Hall state abides by the generalized Pauli exclusion principle.

L. Susskind has given a non-communicative geometric explanation about the FHE [7, 8]. Through the study into the Abelian non-exchangeability of the system values of the fermion and boson lattice systems with strong correlative interactions on topological flat bands, the Franklin theory based on Chern’s theory and the filling fraction 1/n are exactly the same at every level. Similar to the D₀-branes described in the string theory, this theory can also be considered as the quantum theory of mapping between two non-commutative spaces Q_x and Q_y. In the toroidal structure, the FQH state has an odd or even number of quasi-degenerate ground states. There is a wide energy gap between these ground states and the high-energy excited states. The FQHE of the lattice type of the boson system is found to be different from that of the fermion system of conventional electrons, and the corresponding FQH state can be regarded as the chiral spin state in the equivalent spin model. The non-commutative theory exactly reproduces the quantitative connection between the filling fraction (level in the Chern–Simons description) and statistics required by Laughlin’s theory.

The phase transition between quantum Hall fluid behavior and the Wigner crystal that occurs at a low filling fraction is a phase transition in the non-commutative Chern–Simons theory. The transition would be associated with the spontaneous breaking of the symmetry under area-preserving diffeomorphisms of real space Q_x. The variation of the gauge field vector is expressed as follows:

$\begin{array}{cc}\hfill \delta A_i& =2\pi {\rho }_0\frac{\partial \mathrm{\Lambda }}{\partial Q{y}_i}+\frac{\partial A_i}{\partial Q{y}_j}\frac{\mathrm{\Lambda }}{\partial Q{y}_k}\hfill \\ \hfill & =2\pi {\rho }_0\left(\frac{\partial \mathrm{\Lambda }}{\partial Q{y}_i}+\theta \left\{A_i,\mathrm{\Lambda }\right\}\right)\hfill \end{array},(25)$

where the carriers have a density of rho₀; each particle occupies the non-communicative area θ = 1/2πρ₀; Λ is a parameter related to gauge transformation. For quantum phase space Q_x, its conjugate momentum is proportional to its coordination; hence, it is also non-communicative.

The non-exchangeable parameter 1/eB (${\mathcal{B}}_A$ is a substitute for $\mathcal{B}$ in anomalous situation) indicates a single flux subspace. The NC-CS theory describes the mapping between these two non-commutative spaces. It should be noted that the space Q_y is incompressible and that the function $f\left(Q_y\right)$ defined on the space Q_y is non-gauge invariant observables. In the space Q_x, we define

$\rho \left(Qx\right)={\rho }_0-\frac{1}{2\pi }\nabla \times A.(26)$

As the layers are adiabatically brought together so that the electrons are easily shared between them, the state must approach the fractional quantum Hall state with ν = p/n. Experience with D-branes suggests that the resulting theory should be a non-Abelian version of the gauge theory. A natural guess is that it may be the non-commutative Chern–Simons $U\left(p\right)$ theory at level n. The non-communicative geometrical theory means both the phase and energy band are (quasi) flat, with certain interaction between different layers. This causes the symmetry breaking; hence, Chern number C₁ > 1, that is, the FQHE.

The non-dissipative quantum spin current, by the Kubo formula, in the case of the SOC of the Luttinger Hamiltonian for p-type semiconductors, it is possible to define a precisely conserved spin current, that is, the non-dissipative quantum spin current [9]. For the 1/3 filled boson fractional quantum anomalous Hall state, when the boundary phase angle is adjusted, the ground state group maintains its quasi-degeneracy and a wide energy gap in the low-energy excited state, indicating that the topological phase is stable. Under the effect of $SU\left(2\right)$, the non-Abelian gauge field, its curvature tensor results in the non-dissipative spin Hall effect.

The quasi-hole excitation spectrum shows a characteristic energy gap between the excited and high-energy excited states, and there are multiple low-energy quasi-hole excited states touching at the Γ-point in each momentum partition below the characteristic energy gap. In a hole-doped semiconductor with four valence bands of spin–orbit interaction, each hole contains three quasi-cavities, and the generalized Pauli exclusion principle is incompatible with the Laughlin 1/3 fermion fractional quantum Hall state. The spin current of the two-dimensional subspace of the band can be expressed in terms of the operator P.

$J_i=\frac{\partial H}{k_j},J_i^{ab}=\frac{1}{2}\left\{P^l{\mathrm{\Gamma }}^{ab}{P}^l+P^h{\mathrm{\Gamma }}^{ab}{P}^h\right\}.(27)$

Luttinger Hamiltonian can be presented with valence bands by giving $SO\left(5\right)$ Clifford algebra. Under a certain amount of momentum, the SOC is in a fixed direction of the five-dimensional space, and the symmetry breaking can be decomposed into $SO\left(4\right)=SU\left(2\right)\times SU\left(2\right)$. This symmetry can be expressed as a conservative spin current in the light and heavy cavity bands, and its quantum response can be accurately calculated by the Kubo formula.

The Berry curvature and the multi-body number can explain the non-Abelian unipolar field, equivalent to a vector—or technically defined as momentum and true Yang-monopole—in the five-dimensional vector space. The correctness of quantum mechanical results is determined due to the entanglement of spin and velocity, a phenomenon that can be traced back to the non-commutative entanglement between the current spin operators. In physical systems, the entangled state driven by the decoherence mechanism may achieve semi-classical results. Notwithstanding the traditional definition of spin current, the semi-classical results, using the non-zero correlation between spin and velocity, combined with the terms “spin dipole” and “torque moment” in the wave packet form, can be obtained. The Kubo formula has achieved the same results.

Using a theoretical model of non-dissipative spin current, the finite longitudinal charge conductance and dissipation values associated with charge transport can be calculated [9]. The SOC system with a gap in the electron excitation spectrum results in the quantized spin Hall effect. The facts show that the integral of σ_xy is expressed as the gauge curvature in the occupied state and that the Fermi surface of the particle cavity excitation may not occur. The transition of spin-polarized electrons, usually described by an unbalanced Green function, can be derived from the first-principle calculation. The density function is used to calculate the steady-state electronic structure. The effect of the semi-infinite electrode is described by the self-energy function.

The spin $SU\left(2\right)$ symmetry type of the SOC model includes two types of models: Rashba and Dresselhauss. Based on this symmetry, there may exist a persistent spin helix [10], though other relaxation mechanisms may lead to its eventual decline. From the coupling of Rashba and Dresselhauss, the transition equations for arbitrary strength are provided to explain the chiral helix states. Will the chiral symmetry be preserved under anomalous circumstances?

From the analysis in the previous section, the cause of the anomalous Hall effect falls into three parts: the internal, external, and chiral effects. Since a non-Abelian gauge field is present around the Hall device with non-local features, there exits the chiral symmetry breaking in bilayer graphene, as described in the γ⁵ breaking in the non-Abelian field theory, which will cause FQAH.

The gauge theory implements the basic laws of physics through local symmetry constraints. Literature [48] reported a quantum simulation of the extended U(1) lattice gauge theory and experimentally quantified the gauge invariance in a multi-body system containing matters and gauge fields. These fields are realized in an array of boron atoms in a 71-site optical superlattice. The model parameters are fully tunable, and the object–gauge interaction is calibrated by sweeping the quantum phase transition. The degree of violation of Gauss’s law is measured by extracting the probability of the local gauge invariant state from related atomic experiments. As such, a method has been provided for exploring the gauge symmetry breaking in basic FQAHE particle interaction.

The research in [11] shows that the Coulomb interaction is strong enough for the sublattice symmetry breaking to take place in undoped graphene and for the formation of a strong coupling extension in the Coulomb Hamiltonian ground state by jumping kinetic perturbation.

In a two-dimensional graphene with a hexagonal array of carbon atoms, the Coulomb interaction has the intrinsic property of interacting the relativistic Fermi subsystem with $U\left(4\right)$ symmetry. The dynamics of the continuous field theory can be described by its low-energy ($<1ev$) action.

$\begin{array}{cc}\hfill S& =\int d^{3}x\sum _{k=1}^4{\bar{\psi }}_k\left[{\partial }^t\left(i{\partial }_t-A_t\right)+v_F\vec{\gamma }\cdot \left(i\vec{\nabla }-\vec{A}\right)\right]{\psi }_k\hfill \\ \hfill & -\frac{ϵ}{4e^2}\int d^{3}x{F}_{ab}\frac{1}{2\sqrt{-{\partial }^2}}{F}^{ab}\hfill \end{array},(28)$

where the integral is taken over the Q_x plane; v_F is the velocity of the massless electron in graphene; γ is a Dirac matrix in quantum field theory (for the band matrix using Γ and γ_B to present); the superscript t means a hopping term; F_ab is the gauge field term. Herein, non-dimensional parameters can be used to perform extensions that can be renormalized with a parameter $\frac{1}{N}$.

Further generalizing the previous expression to a strong coupling field, we have two terms of Hamilton: a hopping term and a Coulomb interaction term. The generation and annihilation operators of an electron are denoted by ${\psi }_{\sigma ,n}^{†}$ and ψ_σ,n, respectively. The state has two rotation states, identified by ↑ or ↓ for a rotating spin label as σ, on either A or B sublattice. The parameter u₀ is the on-site self-energy of the electron and the hole [11].

$\begin{array}{cc}\hfill H& =H_t+H_e\hfill \\ \hfill H_t& =t\sum _{A,i,\sigma }\left({\psi }_{\sigma ,A+s_i}^{†}{\psi }_{\sigma ,A}+{\psi }_{\sigma ,A}^{†}{\psi }_{\sigma ,A+s_i}\right)\hfill \\ \hfill H_e& =\frac{e^2}{8\pi ϵa}\sum _n{u}_0{\rho }_n^2+\frac{e^2}{8\pi ϵa}\sum _{n\ne n^{\prime }}{\rho }_n\frac{1}{\left|n-n^{\prime }\right|}\hfill \end{array}.(29)$

The lattice translation symmetry breaking is spontaneously related to some sort of gap generation. The symmetry breaking parameter can be expressed as the following operator’s mathematical expectation:

$H_m=\left(\sum _{n\in A}-\sum _{n\in B}\right)\left[{\mu }_0{\psi }_{\sigma ,n}^{†}+\vec{\mu }\cdot {\psi }_{\sigma ,n}^{†}{\vec{\sigma }}_{\sigma {\sigma }^{\prime }}{\psi }_{{\sigma }^{\prime },n}\right].(30)$

This mass term is constant at time reversal and flat valence, but the $U\left(4\right)$ pattern of symmetry breaking is formed by the fermion surface state and the chiral Landau level of the magnetic field Weyl semimetal film. If the parameters of μ are non-zero, the symmetry breaking forms $U\left(4\right)\to U\left(1\right)$ pattern, only one of which is zero, hence, the $U\left(4\right)\to U\left(2\right)\times U\left(2\right)$ pattern.

Within a fairly wide range of resonant potentials, changing the strength of the binding potential makes no difference to the edge excitation sequence, which also shows the topological stability of the quantum Hall state. The ground state approximation to the complete Hamiltonian has been found, with the Coulomb energy usually greater than the kinetic energy of the electron. By integrating over the Brillouin region, the charge density of the diagonal energy is obtained.

$\begin{array}{cc}\hfill H_e& =\frac{e^2}{4\pi ϵa}\int d^{2}k|\widehat{\rho }\left(k\right){|}^2\left(\frac{u_0}{2}+\right.\hfill \\ \hfill & \left.\sum _{n\ne 0,n\in A}{e}^{ik\cdot n}\left[\frac{1}{|n|}+\frac{\cos k}{\left|n+s_1\right|}\right]\right)\hfill \end{array}.(31)$

The perturbation theory is applied to calculate Hamilton’s effect, with the finding that the lower energy state is an antiferromagnetic state. While Hamiltonian for the degenerate ground states proves effective as

$\begin{array}{cc}\hfill H_{\mathit{eff}}& =-H_t\frac{1}{H_e}{H}_t\hfill \\ \hfill & =\frac{-t^2}{\frac{e^2}{4\pi ϵa}\left(u_0-1\right)}\sum _{A,s_i,\sigma }\left({\psi }_{\sigma ,A+s_i}^{†}{\psi }_{\sigma ,A}{\psi }_{\sigma ,A}^{†}{\psi }_{\sigma ,A+s_i}\right.\hfill \\ \hfill & \left.+{\psi }_{\sigma ,A}^{†}{\psi }_{\sigma ,A+s_i}{\psi }_{\sigma ,A+s_i}^{†}{\psi }_{\sigma ,A}\right)\hfill \end{array}.(32)$

The abovementioned equation can be simplified through the Pauli matrix. The Haldane–Bose–Hubbard model is used to describe the ground state and its low-energy dynamics. The topological flat-band model is an extended version of the Haldane model. At least one band has a non-mean topology, that is, a non-zero Chern number C = 1; each band has a narrow bandwidth; and there is a wide gap between the bands. For the cellular lattice Haldane model, if only the nearest neighbor and the next nearest neighbor are allowed to jump, the flatness ratio is only 7; if the next nearest neighbor jump is allowed, a large class of parameter space can be found by numerical search in the non-zero number of topological flat bands.

Each location corresponds to the basic excited state of an electronic lattice, whose energy is expressed as U and is approximately 10 ev.

The Hubbard model interaction discloses many properties of graphene, especially its sublattice symmetry breaking ground state is an antiferromagnetic Mott insulator. Illustrations are provided on both the quantum phase diagram of the top half of the top-filled fill and also on the quantum phase transition from the FQAH state to other symmetrically fractured phases. Derived from the strong correlative effect of hard bosons (unlike the Coulomb interaction between conventional electron or fermion systems), the lattice type of the FQHE of the boson system can be regarded as a chiral symmetry in an equivalent spin model.Meanwhile, most theories and experience predict the fractional quantum anomalous Hall effect (FQAHE) on lattice structures, such as the honeycomb or quantum flux state, which is also known as the topological nematic state. In the topological flat-band model, considering the short-range interaction between the hard boson systems, a large number of numerical calculations and systematic theoretical analysis have provided strong evidence for lattice FQHE [12]. In the toroidal structure, the fractional quantum anomalous Hall state has an even number of quasi-degenerate ground states that share a quantized number, with wide energy gaps between the excited states.

The quantum Hall effect is a dissipation-free quantum transport property caused by the quantization of the Landau level under an externally enhanced magnetic field. At present, the quantum anomalous Hall effect that has been proposed or realized is concentrated in the small Chern number system with a Chern number of 1 (based on magnetic topological insulator films) or 2 (based on single-layer graphene), and the size of the Chern number directly corresponds to the quantum. The number of channels and the status of the low Chen number also significantly affect the working efficiency of quantum anomalous Hall devices.

The first Chern number is defined as $C_1=\int d^2\mathbf{k}{f}_{xy}\left(\mathbf{k}\right)$ with$f_{xy}\left(\mathbf{k}\right)={\partial }_{\mathbf{x}}{\mathbf{A}}_{\mathbf{y}}-\partial {\mathbf{A}}_{\mathbf{x}}$ and $A_i\left(\mathbf{k}\right)=-\mathbf{i}\sum _{\mathbf{En}<\mathbf{E}\mathbf{f}}\left.⟨n,\mathbf{k}\right|{\partial }_{\mathbf{i}}\left|\mathbf{n},\mathbf{k}\right.⟩$, and the QAHE is described in terms of the nontrivial Chern number.

By calculating the Berry curvature distribution, the quantized five Chern numbers are found to be C₁ = −1, 2, 1, 1, and 2, respectively, with the Fermi level lying in these five gaps. In a general quantum anomalous Hall system, a honeycombed Kagome lattice structure can be obtained, where there exists a near-flat band with C₁ = 1. The FQAHE may be implemented. The zigzag star-like lattice has chiral edge states, which endow the system with topological properties.

With respect to the hopping of

$\begin{array}{cc}\hfill H& =t\sum _{A,i}\left({\psi }_{A+s_i}^{†}{\psi }_A+{\psi }_A^{†}{\psi }_{A+s_i}\right)\hfill \\ \hfill & +\frac{U}{2}\sum _{n\in A,B}{\left(\sum _{\sigma =\uparrow \downarrow }{\psi }_{\sigma n}^{†}{\psi }_{\sigma n}-1\right)}^2\hfill \end{array},(33)$

there are two terms in Figure 1. Assuming that the magnitude of the jump between adjacent points takes the same value within each of the triangles t₁ and t₂ as between them, with $t_2<\frac{3}{2}{t}_1$, the probability that the electrons jump out of each of the triangles is less than the probability of jumping between the triangles. This assumption means that the three points can be strongly combined into one single point. The result in this case is similar to that in the case of graphene in the low-energy band, which is similar to the Kagome lattice in the opposite case with $t_2<\frac{3}{2}{t}_1$. At this point, t₂ = t₁ will cause the gap to shrink. In the absence of Rashba SOC and exchange fields, the six-site cells form six bands with double degradation.

FIGURE 1

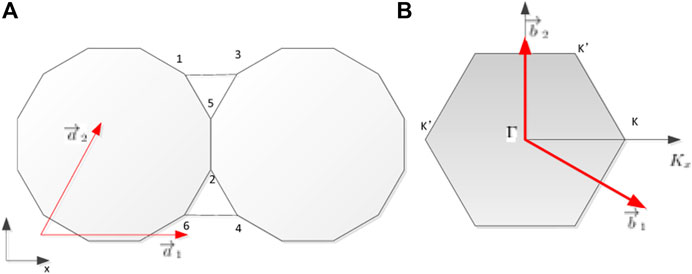
FIGURE 1. (A) Star-like lattice with primitive vectors of the Bravais lattice and (B) reciprocal vectors.

For the Berry curvature and multi-body calculations, the boundary phases θ₁ and θ₂ are introduced in two directions of periodic boundary conditions, and the number of quantum multi-body states (the corresponding Berry phase 2πC) is obtained by integrating throughout the boundary phase space.

$C=\frac{1}{2\pi }\iint d{\theta }_{1}d{\theta }_{2}F\left({\theta }_1,{\theta }_2\right)$, Berry curvature. $F\left({\theta }_1,{\theta }_2\right)=\text{Im}\left(⟨\frac{\partial \Psi }{\partial {\theta }_2}\mid \frac{\partial \Psi }{\partial {\theta }_1}⟩-⟨\frac{\partial \Psi }{\partial {\theta }_1}\mid \frac{\partial \Psi }{\partial {\theta }_2}⟩\right).$

For N_s = 24, 36, and 40 lattices, the two ground states in the quasi-degenerate ground state group are in separate momentum partitions. As the boundary phase is adjusted, the two ground states evolve and cross the energy levels, but there remains a wide characteristic energy gap between these ground states with the low-energy excited states. For N_s = 32 lattices, the two ground states in the quasi-degenerate ground state group are at momentum partitions; as the boundary phase is adjusted, each ground state evolves to itself and avoids crossing energy levels. In the case where the two ground states are in separate momentum partitions, numerical calculations show that each ground state contributes almost equally to the Berry phase of π, that is, provided the total number of turns C = 1, each ground state corresponds to a fractional number of 1/2. In the case where the two ground states are in the same momentum partition, numerical calculations show that one of the ground states contributes a Berry phase of 2π, while the other contributes a Berry phase of zero; still, provided the total number of turns C = 1, each ground state is the average of Chern number, 1/2.

Generally, the filling factor and the Chern number can be related by $\nu =k/\left(C_1+1\right)$ [20], where k is the wave number. From recent research reports [13–22], it can be known that the FQAHE exists with fill numbers 1/2, 1/3, 2/5, 4/5, 5/2, and 7/2.

4 Wannier’s function of the fractional quantum Hall effect

For the extended Haldane model with topological flat bands, the three-body hardcore bosons filled with strong correlative interactions were studied, with the discovery of the non-Abelian type (non-Abelian) quantum Hall effect. The non-Abelian quantum Hall effect of this lattice type has characteristic triplet ground state topological degeneracy, a quantized Chern number, a wider characteristic energy gap, a characteristic quasi-hole excitation spectrum, and a number of particles with topological degeneracy parity effect. The non-Abelian quantum Hall effect of bosons discovered by the author has similar topological properties to the Moore-Read state filled with Landau level 5/2. In contrast, the image of the Fermi-type and Moore-Read states in the two-dimensional electron gas has not been fully created so far. There remain some differences and disputes between numerical calculation and theoretical analysis.

For quasi-hole fraction statistics, since the Laughlin wave single-particle and the many-body function for FQH states are not directly connected with FQAH states, the quasi-hole states in non-Abelian quantum anomalous Hall phases can be counted by the generalized Pauli exclusion principle. Using the Wannier representation of the topological flat band, a N_orb = N_s/2 periodic single-particle orbit is formed. Now, take N_orb = 12 as an example. The number of bosons occupied in two consecutive orbits does not exceed two, and the generalized Pauli exclusion principle gives the following three configurations of ground state distribution $\left|n_{{\lambda }_1},n_{{\lambda }_2},\dots ,n_{{\lambda }_{N_{\mathit{orb}}}}\right.⟩:\left(02\right)\equiv \left|02020202\right.⟩$,$\left(20\right)\equiv \left|202020202020\right.⟩$ and $\left(11\right)\equiv \left|11111111\right.⟩$. Now, count the number of bosons from the three ground state configurations (02), (20), and (11). The occupancy configuration of the double quasi-hole state of the boson should be a mixture of two ground-state configurations that forms two domain walls, each of which represents a fractional charge of 1/2. A simple analysis gives six configurations with an odd number of 1 s: $|\dots 20|1\left|020\dots \right.⟩$,$|\dots 20|111\left|020\dots \right.⟩$,$|\dots 020|11111\left|020\dots \right.⟩$,…, and $|0\left|11111111111\right.⟩$. Two of the domain walls (quasi-holes) are represented by two vertical lines (‖). Considering the 12 translations of the abovementioned six configurations, there are finally 72 (generally N_orb = N_s/2) double quasi-cavity states in total. This count is completely consistent with the numerical calculation results. In the band calculated by DFT, the construction of a tightly bound Hamiltonian is implemented with the help of the largest localized Wannier function (ML-WF).

Through the Brillouin zone, the wavefunction cannot be regarded as single valued; then, unidimensional Wannier functions are maximally localized in the y direction by taking the eigenstates of k_y on y. Let the occupied band of a QAH system be $\left|k_x,k_y\right.⟩$, with the Berry phase gauge field vector A_i, A_y = 0, the Wannier function with local maximization has explicit form [23].

$\begin{array}{cc}\hfill \left|W\left(k_y,x\right)\right.⟩& =\frac{1}{\sqrt{L_x}}\sum _{k_x}{e}^{-i{\int }_0^{k_x}{A}_x\left(p_x,k_y\right)d{p}_x}\hfill \\ \hfill & \cdot e^{-i{k}_x\left(x-\frac{\theta \left(k_y\right)}{2\pi }\right)}\left|k_x,k_y\right.⟩\hfill \end{array},(34)$

where p_x , p_y are the branches of the projection operator on each coordinate. For lattice sites’ labels,

$\theta \left(k_y\right)={\int }_0^{2\pi }{A}_x\left(p_z,y_k\right)d{p}_x,x\in \mathbf{Z},$

the phase factor $e^{i\theta \left(k_y\right)k_x/2\pi }$ of the Bloch function is periodically guaranteed with k_x → k_x + 2π. Hence, the Wannier function satisfies the following warp boundary condition:

$\left|W\left(k_y+2\pi ,x\right)\right.⟩=\left|W\left(k_y,x+C_1\right)\right.⟩.(35)$

This method can be easily extended to more general FQAH states such as the Moore-Read state of non-Abelian quasiparticles, thus determining the various topological properties of the fractional quantum anomalous Hall (FCI/FQAH) state. Considering that the fractional quantum anomalous Hall (FCI/FQAH) state is first realized in the optical lattice cold atomic system, a feasible experimental detection method can also be devised for edge excitation. The edge space excitation spectrum in dish geometry is found in the real space strict diagonalization (ED) calculation, and similar results are obtained based on the study of the quantum entanglement spectrum [23]. In the hard boson-filled Haldane dish model and the Kagome lattice dish model, a series of characteristic edge excitation spectra have been found consistent with the chiral Luttinger liquid theory. By inserting and adjusting the magnetic flux in the center of the dish structure, it is further verified that the compressibility of the excited state is indeed the chiral edge state of the carrying current. Within the particular lattice structure of this system, the intrinsic and additional Rashba SOCs compete with each other, allowing one to adjust the number and position of Dirac cones. When the time inversion invariance is no longer preserved, the energy band structure of the system will exhibit various QAHEs with distinct Chern numbers (C₁ > 1).

It is also predicted that a large number of turns can be achieved in a magnetic three-dimensional topological insulator film, in which case the film system needs to jump out of two-dimensional limitations. Under two-dimensional constraints, the number of QAHEs derived from the direct coupling of the upper and lower surface states of the sample is the minimum. When the film is thicker, the conduction band energy band and the valence band energy band, which are constrained in two directions, will cause multiple band inversions under the influence of the coupling between the Zeeman field and the spin–orbit, with the state $\left|FTI\right.⟩=\left|1/m,\uparrow \right.⟩\otimes \left|-1/m,\downarrow \right.⟩$. Therefore, the number of QAHEs strongly depends on the relative size between the Zeeman field and the sample thickness, which determines the spacing between the sub-bands. For samples of different thicknesses, increasing the Zeeman field strength can increase the number of turns to a larger integer, which is contrary to the fact that the Hall conductivity of the general quantum Hall effect decreases as the magnetic field strength increases.

Another way to build a local Wannier function is to use the largest localization method proposed by Marzari and Vanderbilt. In this method, they introduce a local function to strictly define the locality of the Wannier function and transform the matrix $U\left(N\right)$ by optimizing the specification so that the local function reaches a minimum. Then, generalize the expression of the maximally localized Wannier function with N occupied bands [23]:

$\begin{array}{cc}\hfill \left|W^i\left(k_y,x\right)\right.⟩& =\frac{1}{\sqrt{L_x}}\sum _{k_x,m,n}{e}^{-i{k}_x\left(x-\frac{{\theta }_i\left(k_y\right)}{2\pi }\right)}{u}_m^i\hfill \\ \hfill & \cdot {\left[P{e}^{-i{\int }_0^{k_x}{A}_x\left(p_x,k_y\right)d{p}_x}\right]}_{mn}\left|n,k_x,k_y\right.⟩\hfill \end{array}.(36)$

With $e^{i{\theta }_n\left(k_y\right)},i=\mathrm{1,2},\dots ,N$, they are the eigenvalues of Wilson’s loop operator (inside []) and $u_m^i$ the corresponding eigenstates. Here, $A_x{\left(p_x,k_x\right)}^{mn}$ is the gauge field vector of the Berry curvature.

For the multilayer FQAH system with C₁ = 2, $\left|W\left(k_y+2\pi ,n\right)\right.⟩=\left|W\left(k_y,n+2\right)\right.⟩$. We will see that all components of the stretch function can be represented by overlapping matrices. In practical calculations, each overlap matrix needs to be given from the first-principle calculation.

$\begin{array}{cc}\hfill \left|W_{K=k_y+2\pi n}^1\right.⟩& =\left|W\left(K_y,2n-1\right)\right.⟩\hfill \\ \hfill \left|W_{K=k_y+2\pi n}^2\right.⟩& =\left|W\left(k_y,2n\right)\right.⟩\hfill \end{array}(37)$

such that both the parameters K and $\left|W_K^{\mathrm{1,2}}\right.⟩$ are continuous and that the contributions of all components of the broadening function in the x direction are interrelated.

Multilayer FQH states can exhibit a great diversity of topological states. The wavefunction of Laughlin states at states $\left(mnl\right)$ can be expressed as follows [24]:

$\begin{array}{ccc}\hfill & \mathrm{\Psi }\left(\left\{z_i\right\},\left\{w_i\right\}\right)=\prod _{i<j}{\left(z_i-z_j\right)}^m{\left(w_i-w_j\right)}^n\hfill & \hfill \\ \hfill & \prod _{i,j}{\left(z_i-z_j\right)}^l\cdot \left[-\sum _i\left(|z_i{|}^2+|w_i{|}^2\right)/4l_B^2\right]\hfill & ,\hfill \end{array}(38)$

where l_B is the magnetic length in each layer; z_i and w_i are the ith particle’s complex coordinates, which are intrinsically in the non-Abelian states for multilayer.

In the actual calculation process of two-layer FQAH, the Bloch wavefunction is usually projected onto some appropriate local orbits and used as the initial value of the maximum localization process. T_x and T_y, in the Wannier states, are given by [25]

$\begin{array}{ccc}\hfill & T_x\left|W_K^1\right.⟩=\left|W_K^2\right.⟩,T_x\left|W_K^2\right.⟩=\left|W_{K+2\pi }^1\right.⟩\hfill & \hfill \\ \hfill & T_y\left|W_K^a\right.⟩=e^{iK}\left|W_K^a\right.⟩\hfill & .\hfill \end{array}(39)$

We calculated the electronic structure of the interfacial region and its evolution with the interface coupling scale factor. For the two subsystems that are not coupled, we found that the QSH insulator had a one-dimensional Dirac edge state, while the edge of the QAH insulator, with a number C = 2, had two edge states with chiral edge states. The valence band of the energy valley position (K and K′) and the energy gap state of the conduction band construct the two QAH edge states. They have the same spin polarization but are localized in the K or K′ energy valley. The torus with the misaligned layer can be connected by the “wormhole” of the branch cutting, and it has a nontrivial topological degeneracy [26].

The topological degeneracy from the edge state can also be explained by chiral symmetry breaking, since hardcore bosons have been filled into the Haldane dish model and the Kagome lattice dish model, and a series of characteristic edge excitation spectra have been found, which is consistent with the chiral Luttinger liquid theory. By inserting and adjusting the magnetic flux in the center of the dish structure, it is further verified that the compressibility of these excited states is indeed the chiral edge state of the carrying current. Let N₀ be the number of all possible states, $\left(mnl\right)$ are the Laughlin states in Eq. 39. Then, the topological degeneracy of pairs of dislocations is as follows [27]:

$N=\frac{N_0}{{\left(m+1\right)}^{2n-1}}=\left|\left(m^2-l^2\right){\left(m-l\right)}^{n-1}\right|.(40)$

The two oppositely polarized interfacial states are localized in two energy valleys that are far apart in the momentum space. That is to say, the formation of the QSH/HQAH interface makes the spin polarization of the interfacial state dependent on the energy valley, with $d=\sqrt{m}$ as the quantum dimension. The coupling of spin and energy physics for the interface makes it possible to distinguish the energy of the valley by controlling the degree of spin freedom [28].

The effective Hamiltonian of the interface system is constructed directly from the Wannier Hamiltonian of two individual materials using the effect term $U\left(2\right)$. Finally, we use the Green function method for interfaces to calculate the local state density of the interfacial region. It is noteworthy that when the Wannier function is generated to handle interface problems, Wannier-based functions in two systems should be selected as consistently as possible. Only in this way can the coupling matrix of the material passing through the interface be well defined as $U\left(1\right)\times U\left(1\right)$ by Chern–Simons theory [29]. Therefore, we used the projected atomic orbital Wannier function and rejected the maximum localization process. Using the vacuum level as a reference, we aligned the valence bands of two bulk materials in the interface system to a uniform Fermi energy [30].

As a new topological quantum state, quantum anomalous Hall insulators (Chern insulators) have attracted wide attention due to their unique edge state characteristics. Combining the first-principle calculation method and the tight-binding model based on the Wannier function, we prove that SOC can transform a typical semi-Dirac system, namely, TiO2/VO2 composite structure, into a quantum anomalous Hall insulator, with the further discovery that there is only one special type[31].

This transformation can only be implemented in the semi-Dirac system. Unlike the usual semi-Dirac spectrum, temporarily called the second type of semi-Dirac spectrum, that system can actually be regarded as a combination of three common Dirac cones. Our results reveal the non-mean topological properties of this type of semi-Dirac system and provide new ideas and approaches for implementing QAHEs in real systems [32]. In addition, we have proposed other composite systems that can implement Chern insulation. These solutions are expected to not only to create new possibilities for developing more accessible, higher temperature Chern insulators but also to lay a necessary material basis for designing topological quantum devices [33].

Due to the unique Dirac cone surface state that not only has topological insulators become a research hotspot in condensed matter physics and material science, but they also promise potential application prospects in low-energy electronic devices. Therefore, once the topological insulator phase can be realized in the traditional III–V semiconductor, it will be of great significance to spintronic applications and quantum computing methods. We propose a universal strategy for implementing topological insulators in III–V semiconductors by means of helium atom doping and applied stress. Using the first-principle method based on the maximum localized Wannier function to directly calculate the Z₂ topological invariants and surface states of the system, we find that under applied stress, AlBi (GaBi and InBi) can serve as topological insulators (semimetals). We further demonstrate that erbium doping can induce topological phase transitions in traditional III–V semiconductors such as GaAs semiconductors. In view of the maturity of modern technology in the semiconductor industry and the wide application of III–V semiconductors in electronic devices, our proposed method provides new design ideas for the preparation of large-scale topological insulator electronic devices that are easy to integrate and control [34].

By studying the interface between quantum spins and quantum anomalous Hall insulators and analyzing the effective model, we find that there are stable and specific chiral topological interfacial states at the interface between the two. Using the tight-binding model and the first-principle calculation based on the maximum localized Wannier function, we move on to systematically analyze the unique properties of the interfacial state between quantum spin Hall insulators and different quantum anomalous Hall insulators, including single-energy valley QAH [14], the multi-energy valley high number QAH, and valley-polarized QAH insulators. Despite the existence of topological interfaces on these interfaces, they have different specific behaviors. Since the interface exists between two materials, its state is naturally protected from the effects of edge defects, chemical modifications, and the like. Therefore, the interfacial state should be more stable and less sensitive to external disturbances than the surface state. Our results have not only gained an important understanding of the topological properties of materials but also provided a possible way to enhance the performance and stability of topological electronic devices in real-world environments [35–40].

5 Multilayer fractional quantum Hall effect model

We propose an approach to implement the multilayer FQAH model. The top and bottom sides are connected to two external charge reservoirs. The quantum devices have two TI layers with different chiral properties and FQAHE at their edge. The wave vector is fixed somewhere in the y direction, with periodic phases in the x direction, which can be expanded by the Wannier function to create a band gap due to the intrinsic topological invariant, hence, the FQAH nematic state. Now, the device can be divided into two parts, as shown in Figure 2, the one on the left side g < 0 and the other on the right side g > 0 (g is the Landau factor). The two sides are connected by a quantum wire matrix (the blue block) to change Majorana fermions.In the case of bilayer graphene, expand the Hamiltonian, considering the effects of Rashba SOC α, intrinsic exchange field M, and imbalance U(τ) means the Pauli matrix of the layer degrees of freedom [28].

$\begin{array}{cc}\hfill H& =\left[v\sigma \cdot \mathbf{k}{\psi }_{\mathbf{s}}+\mathbf{M}{\psi }_{\sigma +\text{sz}}+\left(\frac{{\alpha }_1+{\alpha }_{\mathbf{h}}}{2}\right){\left(\sigma \times \mathbf{s}\right)}_{\mathbf{z}}\right]{\psi }_{\tau }\hfill \\ \hfill & +\left[\left({\alpha }_l-{\alpha }_h\right){\left(\sigma \times \mathbf{s}\right)}_{\mathbf{z}}+\mathbf{U}{\psi }_{\sigma +\mathbf{s}}\right]{\tau }_z\hfill \\ \hfill & +\frac{1}{2}{t}_{\perp }{\psi }_s\left({}_x\tau _x+{\sigma }_y{\tau }_y\right)\hfill \end{array}.(41)$

FIGURE 2

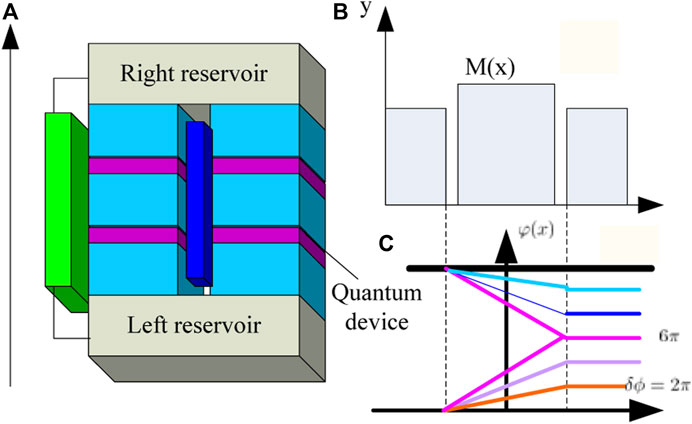
FIGURE 2. (A) Schematic of the three-dimensional quantum device interface with two-layer localized system evolution with a coupling scale factor. (B) Pairing spatial profile for amplitude and tunneling strength M(x) induced by the superconductors and insulator. (C) Energy band and band gap diagram along the high-symmetry line.

Subject to the boundary condition $\psi \left(y=0,L\right)=0$ and according to the calculation from [28–34], l is the energy dispersion in terms of λ.

$\begin{array}{cc}\hfill ϵ& =\mu \left\{M^2+v^2\left(k_x^2-\lambda \right)+2{\alpha }^2\right.\hfill \\ \hfill & {\left.+2s\sqrt{{\alpha }^4+v^2\left(k_x^2-{\lambda }^2\right)\left(M^2+{\alpha }^2\right)}\right\}}^{1/2}\hfill \end{array}.(42)$

The magnetic heterostructures in which two sub-monolayers of transition metals embedded in the semiconductor TI host form the ferromagnetic delta (δ)-layers within which there may appear two distinct types of in-gap bound states: the symmetric and antisymmetric states. The symmetric state is a one-to-one correspondence to the origin of the convenient confinement states of carriers at interface insertions in traditional semiconductor-layered structures, while the antisymmetric state is a close analogy to the topological surface states attributed to the Z₂ invariant for TI [41–45]. The latter emerges near the δ layer, where the topological invariance is locally destroyed, and the antisymmetric state represents the anomalous topological properties of the host material [46–50].

Therefore, it is feasible to design a control gate for quantum spin transport on the clean surface holding the helical electrons. The essential advantage of this mechanism is that the time reversal symmetry breaking and the helical state gapping are achieved on the surface [51, 52].

6 Conclusion and discussion

In this paper, we have discussed the cause of FQAH with a non-Abelian quantum field theory. We have also investigated the physical reliability of a FQAH device. The spontaneously topological chiral symmetry breaking of fermions hopping on a honeycomb lattice in the presence of a synthetic non-Abelian gauge potential has been identified as the cause of FQAH. The topological quantum Berry phase transition indicates the hopping of sublattice and the Coulomb energy through interaction between many-body particles causes a pre-formed band inversion in the band structure. With the integration on continuous breaking, the non-locality symmetry breaking of the Higgs field will affect the band topological phase property and the gap amplitude in a way that will engender different energy level platforms with distinct phase shifting.

A novel type of the FQHE is found on the topological flat belt. The VASP simulation and experiment have shown the following items: the topologically quasi-degenerate ground state group, topologically stable characteristic energy gap, the characteristic momentum correlation of the ground state group, the topological evolution of the ground state group, the smooth Berry curvature, fractional Hall conductivity (or fractional aging number), quasi-hole excited fractional charge statistics, and chiral edge excitation. This effect is distinct from the continuous FQHE on the traditional Landau level. Without requiring any external magnetic field, it has a large characteristic energy gap and can exist at higher temperatures. It does not require a single-particle Landau level and cannot be used in conventional ways. The Laughlin wave function describes these fractional phenomena with no external magnetic field and no Landau energy levels and defines a new class of fractional topological phases, also known as fractional insulators. The fractional quantum Hall effect is also called the fractional quantum anomalous Hall effect.

Some possible theoretical research directions are outlined as follows: proposal of other topological flat belt models, including a better topological flat-belt model with high Chern numbers and a lattice model with multiple topological flat belts at the same time; exploration into the abnormal edges of fractional topological phases on topological flat belts excitation; exploration into Abelian and non-Abelian fractional statistics on topological flat belts; exploration into singular fraction statistics and edge excitations on topological flat belts with high Chern numbers; exploration into possible fractional superconducting phases and superfluid phases; a qualitative and quantitative comparative study on the numerical wavefunction and analytical wavefunction of the FQHE on the topological flat belt; exploration into the topological order and the superfluid phase, the solid phase, and the topological quantum phase change characteristics. Experimental research in this field is in more urgent need of working out how to realize topological flat bands in condensed matter materials and in cold atom optical lattices, how to realize fractional quantum anomalous Hall states in both types of systems, how to detect the exact topological order, and how to detect the fractionalization.

A recent systematic experiment found that the quantum anomalous Hall effect with different Chern numbers can be achieved by regulating the magnetization direction of a single-layer transition metal oxide material by applying a weak magnetic field. At the Fermi level, both materials have six spin-polarized Dirac points. After introducing spin–orbit coupling, each Dirac point contributes half a quantized Hall conductance, but in different directions. When the magnetization direction is in-plane and the vertical mirror symmetry is broken, four Dirac points have the same Berry curvature, and the remaining two Dirac points have opposite Berry curvatures; at this time, the system has a Chern number of 1. This constitutes an integer order quantum anomalous Hall effect. When the magnetization direction deviates from the system plane, the six Dirac points contribute to the same direction of the Berry curvature. At this time, the system has a quantum anomalous Hall effect with a Chen number of 3. This experiment not only provides a new material platform to study the quantum anomalous Hall effect but more importantly reveals the existence of the quantum anomalous Hall effect with tunable Chen number (i.e., fractional order) and its physical causes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

JS, WD, XS, JW, YW, and HL were employed by State Grid Wind and Solar Energy Storage and Transportation New Energy Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bernevig BA, Hughes TL, Zhang S-C. Quantum spin Hall ef-fect and topological phase transition in HgTe quantum wells. Science (2006) 314(5806):1757–61. [2010-03-25]. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

2.Quantized Anomalous Hall Effect inMag-netic Topological Insulators Rui Yu Zhang HJ, Zhang SC, Dai X, Fang Z. Quantized anomalous Hall effect in magnetic topological insulators. Science (2010) 329:61–4. doi:10.1126/science.1187485

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhang J, Chang CZ, Tang P, Zhang Z, Feng X, Li K, et al. Topology-driven magnetic quantum phase transition in topological insulators. Science (2013) 339:1582–6. doi:10.1126/science.1230905

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Stagraczynski S, Chotorlishvili L, Dugaev VK, Jia CL, Ernst A, Komnik A, et al. Topological insulator in a helicoidal magnetization field. Phys Rev B (2016) 94(1-17):174436. doi:10.1103/physrevb.94.174436

CrossRef Full Text | Google Scholar

5. Sinitsyn NA. Anomalous Hall effect in 2D Dirac band: Link between kubo-streda formula and semiclassical Boltzmann equa-tion approach (2011). arXiv: cond-mat/0608682v3.

Google Scholar

6. Dugaev VK. Nonlinear anomalous Hall effect and negative magnetoresistance in a system with random Rashba field (2011). arXiv:1211.5304v1.

Google Scholar

7. Hou BY. Differential geometry for physics. Beijing: Science press (2004). p. 689–703.

Google Scholar

8. Susskind L. The quantum Hall fluid and non-commutative chern simons theory (2001). arXiv:hep-th/0101029v3.

Google Scholar

9. Murakami S, Nagaosa N, Zhang SC. SU(2) non-abelian holonomy and dissi-pationless spin current in semiconductors (2011). arXiv:cond-mat/0310005.

Google Scholar

10. Bernevig BA, Zhang SC. An exact SU(2) symmetry and persistent spin helix in a spin-orbit coupled system” phys. Rev Lett (2006) 97:236601.

CrossRef Full Text | Google Scholar

11. Semenoff GW. Chiral symmetry breaking in graphene (2011). arXiv:1108.2945v2.

Google Scholar

12. Chen M, Wan S. Quantum anomalous Hall effect on star lattice with spin-orbit coupling and exchange field (2012). arXiv:1203.2855v2 [cond-mat.str-el].

Google Scholar

13. Goerbig MO. From fractional chern insu-lators to a fractional quantum spin Hall effect (2011). arXiv: 1107. 1986 v3.

Google Scholar

14. Clarke DJ, Alicea J, Shtengel K. Exotic non-Abelian anyons from conventional fractional quantum Hall states zero (2011). arXiv:1204.5479v1.

Google Scholar

15. Liu X, Wang Z, Xie XC, Yu Y. Abelian and non-abelian anyons in integer quantum anomalous Hall effect and topological phase transitions via superconducting proximity effect (2011). arXiv:1011.3885v4.

Google Scholar

16. Ryu S, Moore JE, Ludwig AWW. Elec-tromagnetic and gravitational responses and anomalies in topological insulators and su-perconductors (2011). arXiv:1010.0936v2.

Google Scholar

17. Carrega M, Ferraro D, Braggio A, Magnoli N, Sassetti M. Anomalous charge tunneling in the fractional quantum Hall edge states at filling factor = 5/2 (2011). arXiv:1102.5666v2.

Google Scholar

18. Liu Y, Kamburov D, Shayegan M, Pfeier LN, West KW, Baldwin KW. Anomalous robustness of the = 5/2 frac-tional quantum Hall state near a sharp phase boundary (2011). arXiv:1106.0089v3.

Google Scholar

19. Luo W-W, Chen W-C, Wang Y-F. Chang-de gong ”edge excitations in frac-tional chern insulators (2011). arXiv:1304.4338v1.

Google Scholar

20. Sterdyniak A, Repellin1 C, Andrei Bernevig B, Regnault N. Series of abelian and non-abelian states in C > 1 fractional chern insulators (2011). arXiv:1207.6385v1.

Google Scholar

21. Zhao L, Emil J. Bergholtz ”From fractional Chern insulators to Abelian and non-Abelian fractional quantum Hall states: Adiabatic continuity and orbital entanglement spec-trum (2011). arXiv:1209.5310v2.

Google Scholar

22. Gabriel D, Lima LS, Dias SA. Edge modes in the fractional quantum Hall effect without extra edge fermions (2011). arXiv:0910.3661v7.

Google Scholar

23. Qi XL. Generic wavefunction description of fractional quantum anomalous Hall states and fractional topological insulators. Phys Rev Let (2011). arXiv:1105.4298v1.

CrossRef Full Text | Google Scholar

24. Barkeshli M, Qi XL. Topological nematic states and non-Abelian lattice dislocations (2011). arXiv:1112.3311v2.

Google Scholar

25. Hinarejos M, Perez1 A, Banuls MC. Wig-ner function for a particle in an infinite lat-tice (2011). doi:10.1088/1367-2630/14/10/103009

CrossRef Full Text | Google Scholar

26. Vetsigian K. Chern-simons theory of fractional quantum Hall effect (2011).

Google Scholar

27. Steuernagel O, Kakofengitis D, Ritter G. Wigner flow reveals topological order in quantum phase space dynamics (2011). arXiv:1208.2970v2.

Google Scholar

28. Tse GWK, Qiao ZH, Yao YG, MacDonaldNiu AHQ. Quantum anom-alous Hall effect in single-layer and bilayer (2011). arXiv:1101.2042v2.

Google Scholar

29. Qi X-L, Hughes TL, Zhang S-C. Chiral topological superconductor from the quantum Hall state (2011). arXiv:1003.5448v1.

Google Scholar

30. Sacramento PD, Arajo MAN, Vieira1 VR, Dugaev VK, Barnas J. Anoma-lous Hall effect in superconductors with spin-orbit interaction (2011). arXiv:1111.6748v1.

Google Scholar

31. Liu S, Yu-Zhen Y, Hu L-B. Characteristics of anomalous Hall effect in spin-polarized two-dimensional electron gases in the presence of both intrinsic, ex-trinsic, and external electric-field induced spin orbit couplings” Chin. Phys B (2012) 21:027201.

CrossRef Full Text | Google Scholar

32. Li T. Spontaneous quantum Hall effect in quarter doped Hubbard model on honey-comb lattice and its possible realization in quarter doped graphene system (2011). arXiv:1103.2420v1.

Google Scholar

33. Qi X-L, Zhang S-C. Topological insulators and superconductors (2011). arXiv:1008.2026v1.

Google Scholar

34. Yang Y-f. Anomalous Hall effect in heavy electron materials (2011). arXiv:1207.0646v1.

Google Scholar

35. men”shov VN, Tugushev VV, Chulkov EV. Bound states induced by a ferromagnetic delta-layer inserted into a three-dimensional topological insulator. Jetp Lett (2012) 96(7):445–51. doi:10.1134/s0021364012190113

CrossRef Full Text | Google Scholar

36. Zhang C, Zhang Y, Xiang Y, Lu S, Zhang J, Narayan A, et al. Quantum Hall effect based on Weyl or-bits in Cd3As2. Nature (2018) 565:331–6. doi:10.1038/s41586-018-0798-3

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Qi XL. Generic wave-function description of fractional quantum anomalous Hall states and fractional topological insulators. Phys Rev Lett (2011) 107(12):126803. doi:10.1103/physrevlett.107.126803

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Vshivtsev AS, Magnitskii BV, Klimenko KG. A gluon condensate and the three-dimensional (bar ””) 2 field theory[J]. Phys At Nuclei (1994) 57(12):2171–5.

Google Scholar

39. Bangrong Z. Proof of chiral symmetry breaking and persistent mass condition in vector-like gauge theory. Commun Theor Phys (1991) 15(3):319–30. doi:10.1088/0253-6102/15/3/319

CrossRef Full Text | Google Scholar

40. Clark TE, Nitta M, Ter Veldhuis T. Non-BPS brane dynamics and dual tensor gauge theory. Phys Rev D (2004) 70(12):125011. doi:10.1103/physrevd.70.125011

CrossRef Full Text | Google Scholar

41. Zhang YH, Mao D, Cao Y, Jarillo-Herrero P, Senthil T. Nearly flat Chern bands in moiré superlattices superlattices[J]. Phys Rev B (2019) 99(7):075127. doi:10.1103/physrevb.99.075127

CrossRef Full Text | Google Scholar

42. Deng Y, Yu Y, Shi MZ, Wang J, Chen XH, Zhang Y. Quantum Anomalous Hall Effect in Intrinsic Magnetic Topological Insulator MnBi2Te4[C]// APS March Meeting 2020 (2020). Denver, United States: American Physical Society.

Google Scholar

43. Zhao L, Bergholtz EJ. Heng Fan,Fractional chern insulators in topolog-ical flat bands with higher chern number (2012). arXiv:1206.3759v3 [cond-mat.str-el].

Google Scholar

44. Jacak J, Jacak L. Unconventional fractional quantum Hall effect in monolayer and bilayer graphene. Sci Technol Adv Mater (2016) 17(1):149–65. doi:10.1080/14686996.2016.1145531

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Milz S, Sakuldee F, Pollock FA. Kolmogorov extension theorem for (quan-tum) causal modelling and general probabil-istic theories[J] (2017). arXiv.

Google Scholar

46. Sheng DN, Gu ZC, Sun K, Sheng L. Fractional quantum Hall effect in the absence of Landau levels. Nat Commun (2011) 2(1):389. doi:10.1038/ncomms1380

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Simon M, Pollock FA, Kavan M. Reconstructing non-Markovian quantum dynamics with limited control. Phys Rev A (Coll Park) (2018) 98(1):012108. doi:10.1103/physreva.98.012108

CrossRef Full Text | Google Scholar

48. Yang B, Sun H, Ott R. Observation of gauge invariance in a 71-site Bose-Hubbard quantum simulator[J] (2020).

Google Scholar

49. Zhang XL, Liu LF, Liu WM. Quantum anomalous Hall effect and tunable topological states in 3d transition metals doped silicene. Sci Rep (2013) 3:2908. doi:10.1038/srep02908

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Song ZG, Zhang YY, Song JT, Li SS. Route towards localization for quantum anoma-lous Hall systems with chern number 2. Sci Rep (2016) 6:19018. doi:10.1038/srep19018

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Wang Y, Gong C. Fractional quantum anomalous Hall effect on topolog-ical flat bands (1)[J]. J Zhejiang Normal University:Natural Sci Edition (2013)(04) 361–71.

Google Scholar

52. Wang Y, Gong C. Fractional quantum anomalous Hall effect on topolog-ical flat bands (2)[J]. J Zhejiang Normal Univ (2014)(01) 42–9. Natural Science Edition.

Google Scholar