Dynamics of topological defects in the noisy Kuramoto model in two dimensions

We consider the two-dimensional (2D) noisy Kuramoto model of synchronization with short-range coupling and a Gaussian distribution of intrinsic frequencies, and investigate its ordering dynamics following a quench. We consider both underdamped (inertial) and over-damped dynamics, and show that the long-term properties of this intrinsically out-of-equilibrium system do not depend on the inertia of individual oscillators. The model does not exhibit any phase transition as its correlation length remains finite, scaling as the inverse of the standard deviation of the distribution of intrinsic frequencies. The quench dynamics proceeds via domain growth, with a characteristic length that initially follows the growth law of the 2D XY model, although is not given by the mean separation between defects. Topological defects are generically free, breaking the Berezinskii-Kosterlitz-Thouless scenario of the 2D XY model. Vortices perform a random walk reminiscent of the self-avoiding random walk, advected by the dynamic network of boundaries between synchronised domains; featuring long-time super-diffusion, with the anomalous exponent α = 3/2.

1 Introduction

Back in the XVII-th century, Huygens realised that two pendulum clocks, when sitting on the same board, start, after some transient time, to beat at the same frequency in phase or in anti-phase [1]. Such spontaneous temporal coordination of coupled oscillatory objects is referred to as synchronization. Since then, the study of synchronization in large populations of oscillators has remained a recurrent problem across different sciences, ranging from physics to biology, computational social sciences or engineering [2, 3].

Much progress in the understanding of synchronisation has been achieved through the detailed analysis of simplified model systems. In this context, the Kuramoto model of phase coupled oscillators has (and still does) played a central role [4, 5]. The original version of the model [4], considering only all-to-all interactions, shows that global phase synchronisation can be achieved for large enough coupling, relative to the dispersion of the oscillators’ intrinsic frequencies.

Persistent oscillations, obviously need a constant energy supply, which at the microscopic scale is dissipated into the environment, which also provides a source of noise. Thus, to describe oscillator systems at the micro-scale, such as genetic oscillators [6], noise should be taken into account, as well as shorter-range interactions, leading to finite-dimensional noisy extensions of the Kuramoto model [7]. The situation in this case, which is the object of the present study, is quite more involved than the original Kuramoto model and the literature far more scarce [8–10].

The problem of synchronisation in physical sciences has more recently experienced a resurge of interest in the context of active matter. Active matter stands for a class of soft matter systems, composed of coupled interacting agents that convert energy from their surrounding into some kind of persistent motion [11], such as biological units oscillating at a given rate. Such injection of energy at the level of each single constituent, drives active systems out-of-equilibrium. At the collective level, interactions between active agents result in the emergence of a variety of collective states. In particular, a broad class of active systems can spontaneously self-organise into synchronised states characterised by the coherent motion of self-propelled individuals, a phenomenon called flocking (a term borrowed from the spectacular example of the murmuration of starling birds) [12]. The interpretation of flocking in terms of synchronisation of active oscillators has been pointed out in a number of recent works [13–15].

Closer to the standard synchronisation set-up of oscillators lying on a static substrate, synchronised states have been studied in numerous active matter systems in the absence of self-propulsion. A salient example are active filament carpets, such as cilia or flagella attached on a surface. Cilia, for instance, perform a beating cycle (usually modelled as a phase oscillator) generating a net hydrodynamic flow (at low Reynolds number) that affects the motion of their neighbours [16–18]. Such filaments, thought as coupled oscillators, might then synchronise, to optimise a biological function such as propelling microorganisms. Chiral colloidal fluids composed of spinning colloidal magnets constitute another promising novel venue to investigate synchronisation at the micro-scale [19–22]. In these systems, an external oscillatory field drives the colloidal magnets, making them rotate around their body axis at a given frequency imposed by the field.

Here we investigate the collective dynamics of Kuramoto oscillators, with short range coupling, in two dimensions (2D), in contact with a thermal bath and with a Gaussian distribution of intrinsic frequencies. In the absence of driving, or intrinsic oscillations, the system is equivalent to the 2D XY model, which exhibits a topological Berezinskii-Kosterlitz-Thouless (BKT) transition driven by the unbinding of topological defects [23–25]. As such, it provides a natural playground to study the role played by topological defects in systems of coupled oscillators. The dynamics of topological defects in out-of-equilibrium systems has been extensively investigated over the last decade in soft active systems [11], where it has been found that, in many instances, defects self-propel, or super-diffuse [10, 21, 26, 27]. A recent study of this model shows that defects become free upon self-spinning, although two regimes remain clearly distinct, a vortex-rich and a vortex-poor one [10]. Here we focus our attention on the dynamics of the system following a quench, from a random initial state, where many defects proliferate, to the low temperature (noise) regime where defects are scarce. The coarsening dynamics following an infinitely rapid quench has been extensively studied in model statistical physics systems [28], but has received little attention in the context of synchronisation [29]. Of particular interest for us, the study of the coarsening dynamics of the 2D XY model has shown that topological defects, here vortices, diffuse, interact and annihilate, in a way that sheds light on the mechanisms underlying the non-equilibrium relaxation of the system [30–34]. In this contribution, we aim at characterising the dynamics of the noisy Kuramoto model in 2D, to examine the random motion of vortices and discuss the fundamental differences displayed by the system as compared to its equilibrium limit.

We first introduce the model and its governing Langevin equation in Section 2. The main results are presented in Section 3: in section 3.1, we first focus on the overdamped regime and study the coarsening dynamics of the system following different quench protocols, focusing our analysis on the evolution of different correlation lengths and density of topological defects. We then study the relaxation dynamics in the underdamped regime in section 3.2 to show that the inertia of individual spins (or oscillators) does not influence the overall large-scale dynamics of the system. Section 4 is devoted to the defects’s dynamics. We first discuss the breakdown of the Berezenskii-Kosterlitz-Thouless scenario in section 4.1, by investigating the effective interactions between defects. In section 4.2, we then describe the spontaneous creation process of vortices and the complex dynamics they exhibit. We argue that even though the trajectories of defects are very much reminiscent of genuine self-avoiding random walks, the full displacement statistics indicate that they are not strictly equivalent.

2 The model

We consider a set of N phase oscillators sitting on the nodes of a L × L square lattice with periodic boundary conditions (PBC). The evolution of their phase θ_i is described by the Kuramoto model. The governing equations of motion are given by the following set of coupled Langevin equations

$m{\ddot{\theta }}_i+\gamma {\dot{\theta }}_i=\sigma {\omega }_i+J\sum _{j\in {\partial }_i}\sin \left({\theta }_j-{\theta }_i\right)+\sqrt{2\gamma k_{B}T}{\nu }_i(1)$

where the sum runs over the four nearest-neighbours of spin i, denoted by ∂_i, ν_i is a Gaussian white noise of unit variance and zero mean and γ the damping coefficient. The system is thus in contact with a thermal bath at temperature T. The driving amplitude ω_i is drawn from a Gaussian distribution with zero mean and unit variance. [Since Eq. 1 is invariant under the transformation θ → θ − Ωt, one can choose a distribution of frequencies with zero-mean without loss of generality. ]. The amplitude σ quantifies the dispersion of the intrinsic frequencies.

In the absence of intrinsic persistent oscillations, i.e. σ = 0, the model Eq. 1 is equivalent to the 2D XY model with non-conserved order parameter dynamics [35]. Indeed, Eq. 1 can be rewritten as

$m{\ddot{\theta }}_i=-\gamma {\dot{\theta }}_i+\sigma {\omega }_i-\frac{\partial H}{\partial {\theta }_i}+\sqrt{2\gamma k_{B}T}{\nu }_i(2)$

where

$H=-J\sum _{⟨i,j⟩}{\mathbf{S}}_i\cdot {\mathbf{S}}_j,{\mathbf{S}}_i=\left(\cos {\theta }_i,\sin {\theta }_i\right)(3)$

is just the classical XY Hamiltonian (here the sum runs over all the links of the lattice, or, equivalently, all nearest neighbours pairs). This system exhibits a BKT transition at a critical temperature T_KT ≈ 0.89 [36, 37]. The distribution of natural frequencies introduces quench disorder in the XY model. The way it is introduced though, is fundamentally different to what is typically done in disordered systems, namely, adding disorder in the interactions or an external random field [38–40]. The distribution of intrinsic frequencies drives the system out-of-equilibrium. Adding a term σ∑_iθ_iω_i in the Hamiltonian H → H′ = H + σ∑_iθ_iω_i, would provide the same equation of motion Eq. 1 when writing: $m{\ddot{\theta }}_i+\gamma {\dot{\theta }}_i=-\frac{\partial H^{\prime }}{\partial {\theta }_i}+\sqrt{2\gamma k_{B}T}{\nu }_i$. However, H′ is now unbounded, as a result of the constant injection of energy into the system needed in order to sustain the intrinsic oscillations. Thus, the system is intrinsically out-of-equilibrium and cannot be mapped to random field or random bond XY models.

In equilibrium conditions (σ = 0), the nature of the dynamics does not affect the steady-properties of the system, as long as it fulfills detailed balance. Most studies on the dynamics of the 2D XY model have been performed in the overdamped limit, namely

$\gamma {\dot{\theta }}_i=\sigma {\omega }_i-\frac{\partial H}{\partial {\theta }_i}+\sqrt{2\gamma k_{B}T}{\nu }_i,(4)$

in its Langevin version, or, equivalently, using single-spin flip Monte Carlo dynamics [33, 34, 36, 37, 40].

However, in non-equilibrium conditions, the specific features of the dynamics might affect the resulting large scale behavior at long times. The dynamics of the model introduced by Kuramoto was also originally overdamped. Later on, the model was extended to include inertia [41–43]. Here we study both the model with underdamped and overdamped dynamics following Eqs 2, 4, respectively.

To identify the key control parameters of the present model, we rewrite the equations of motion in their dimensionless form (see Supplementary Material (SM) [44]), expressing time in units of γ/J. This leads to the following set of quantities: 1) the reduced temperature $\tilde{T}=k_{B}T/J$, 2) the reduced frequency dispersion $\tilde{\sigma }=\sigma /J$ and, for inertial dynamics, 3) the reduced inertia $\tilde{m}=mJ/{\gamma }^2$. From now on, we shall make use of these reduced parameters and drop the tilde $\tilde{T},\tilde{\sigma },\tilde{m}\to T,\sigma ,m$.

We integrate numerically Eqs 2, 4 using a modified velocity Verlet algorithm as in [41] and standard Euler-Mayurama scheme (details provided in the SM [44]). The typical system size used is L = 200, if not stated otherwise.

3 Results

3.1 Overdamped dynamics

We first study in this section the dynamics of the model in the overdamped limit, i.e., Eq. 4, following a infinitely rapid quench from an initially disordered state where all the phases are picked from a homogeneous distribution between 0 and 2π.

In order to illustrate the nature of the low temperature state, we show in Figure 1 representative steady state snapshots for (A) T = 0.2 and σ² = 0 (B) T = 0.2 and σ² = 0.1. Both snapshots contain the same number of defects: four vortices (circles) and four antivortices (triangles), visually identified as the points where black, red, yellow, green and blue regions meet. This correspond to plaquettes with a winding number q = ±1, defined by the discrete circulation of the phase differences along a plaquette, namely ∑_□Δθ_ij = 2πq.

FIGURE 1

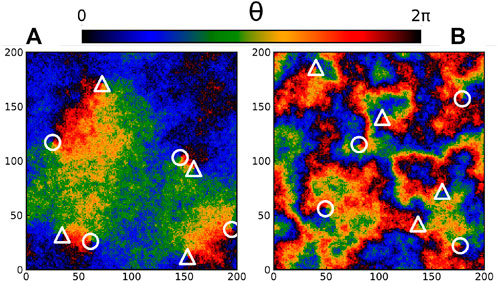
FIGURE 1. Snapshots for T = 0.2, (A) σ² = 0 and (B) σ² = 0.1. The phase of each oscillator is represented by a color scale. Vortices (antivortices) are represented by circles (triangles).

At equilibrium, when spins are not forced, one recovers the classical XY model picture, with large regions of spins sharing the same color, ending at topological defects of opposite charge. As the Kosterlitz-Thouless theory [23, 24] predicts, those defects visually come in pairs. From the snapshots one already observes a clear connection between the typical size of correlated domains of mostly parallel spins, and the typical distance between defects. We will come back to this point later on.

On the contrary, upon self-spinning, the first impression is qualitatively different, even though the number of defects is identical in both panels (here 8). The phase field pattern emanating from the vortices does not extend over large distances, and the typical size of oriented domains seem decoupled from the defects’ locations, as seen in Figure 1B. Ordered regions are in this case rather localized, and one can no longer pair vortices by visual inspection of the snapshots.

3.1.1 Coarsening dynamics

To gain quantitative insight, we compute the spin-spin correlation function

$C\left(r,t\right)=⟨\cos \left(\theta \left(r,t\right)-\theta \left(0,t\right)\right)⟩,(5)$

where the angular brackets denote the average over spins and independent realisations of both thermal noise and quenched frequencies and r is the lattice distance between two oscillators, or spins. For σ = 0 equilibrium correlations in the low-T regime, T < T_KT, decay algebraically in space:

$C_0\left(r\right)\sim r^{-\eta \left(T\right)},\eta \left(T\right)=T/2\pi ,(6)$

a signature of quasi-long-range order. For σ > 0, it has been shown that steady state correlations decay exponentially in space [10].

$C_{\sigma }\left(r\right)\sim e^{-r/{\xi }_{\infty }},(7)$

at any finite temperature, signalling the absence of quasi-long-range order in the system.

We show in Figure 2A the spatial decay of C (r, t) at different times following a quench to T = 0.4, for σ² = 0 (in purple) and for σ² = 0.1 (in green). The data is shown in a log-log scale to easily discriminate between algebraic and geometric decays. As time goes on, spatial correlations build up in the system, indicating the growth of ordered structures, to finally collapse on the before mentioned long-time behaviour. To study the coarsening, or phase ordering, dynamics, we define a correlation length ξ(t), extracted from C (ξ(t), t) = 1/e and plot its time evolution in Figure 3A for different values of σ. For σ = 0, we recover without surprise the well-known scaling $\xi (t)\sim \sqrt{t/\log t}$ [30, 31, 34]. The logarithmic correction takes root in the logarithmic dependence of a defect mobility on its size; note that it is only relevant for large t. Such logarithmic correction to the usual $\sim \sqrt{t}$ growth law in systems with non-conserved order parameter dynamics also appears in all related quantities such as the evolution of the number of vortices n or the mean square displacement (MSD) of a single vortex, as we shall discuss in more detail later on. As shown in Figure 2B the dynamic scaling hypothesis [45] is consistently fulfilled for σ = 0, as all the curves C(r, t) collapse into a single master curve in the scaling regime, once the space variable has been rescaled by the characteristic growing length.

FIGURE 2

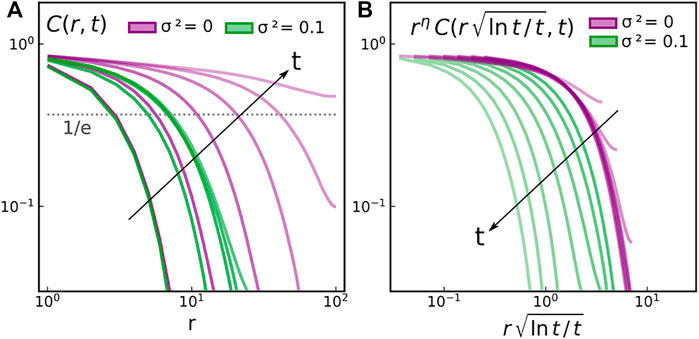
FIGURE 2. Time evolution of (A) the space correlation function C (r, t) at different times t ≈ 4, 20, 100, 400, 2000, 10000 (B) the rescaled correlation function (η = T/2π from the spin-wave theory) against the rescaled time. In both panels, the purple curves correspond to the XY model at T = 0.4 and the green curves correspond to a forced system at T = 0.4 and σ² = 0.1. Longer times are represented by lighter colors, as the arrows indicate.

FIGURE 3

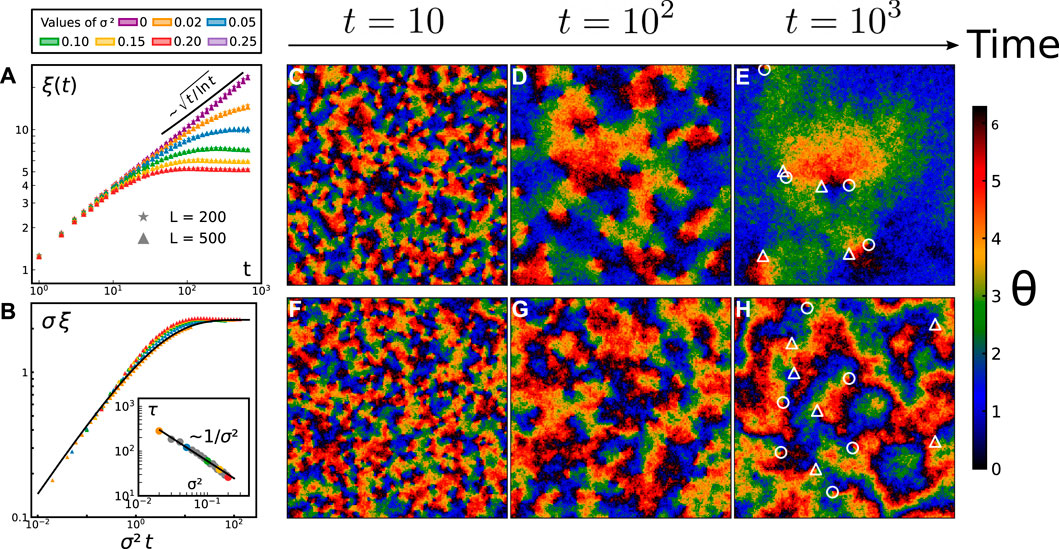
FIGURE 3. Time evolution of the characteristic length scale (A–B) illustrated by typical snapshots of a 200 × 200 system (C–H). (A) Growth of the typical length scale ξ(t) for T = 0.4 and several σ, as indicated in the legend above (same colors as in Figures 2, 4); (B) the same data where ξ and t have been rescaled by σ and σ², respectively. All curves collapse onto a single master curve $f(x)=a(1-\exp (-b\sqrt{x}))$ with a = 2.3 and b = 0.65. Inset: variation of the transients time τ defined in Eq. 9 against the self-spinning intensity. (C–D–E) Representative configurations at different times showing the evolution of the system after a quench (for T = 0.2 and σ² = 0). The phase of each oscillator is represented by a cyclic color scale. In the last panel only, vortices (anti-vortices) are represented by circles (triangles). (F–G–H) Representative configurations at different times now for T = 0.2 and σ² = 0.1.

For σ > 0, the results qualitatively differ: independently of the system size L, the growing length ξ(t) saturates at a finite value ξ_∞ at long times. Such steady value decreases as σ increases. This is consistent with the limit case σ → ∞, corresponding to a system of decoupled oscillators. Interestingly, Figure 3B shows that all curves for σ > 0 collapse into a single master curve if both distances and time are rescaled. This master curve follows $f(x)=a(1-\exp (-b\sqrt{x}))$, from which we conclude that

$\xi \left(t\right)=\frac{a}{\sigma }\left(1-e^{-b\sqrt{{\sigma }^{2}t}}\right),(8)$

with a = 2.3, a constant related to the long time limit of ξ, and b = 0.65.

Eq. 8 contains information about both short time and long time dynamics. At short times, one recovers the short-time dynamics of the XY model. Indeed, by expanding ξ(t) to first order in t, one gets $\sigma \xi (t)\approx ab\sqrt{t}$; ab = 1.5 thus represent the slope of the initial $\sim \sqrt{t}$ coarsening. At long times, in the steady state, the characteristic length boils down to lim_t→∞ξ(t) = ξ_∞∼ 1/σ, as found in [10] using a simplified 1D argument, which we sum up hereafter. Let’s consider, for the sake of clarity, two neighbouring spins i and j at T = 0 sitting on the nodes of a 1D chain. One can easily show that their steady-state angle difference is no longer Δθ = 0 as in equilibrium, but instead Δθ = arcsin (Δω/2), where Δθ = |θ_i − θ_j| and Δω = |ω_i − ω_j|. If we now consider the phase difference accumulated along n links in the chain, and replace the phase difference between each pair of nearest-neighbour oscillators by its expectation value $\overline{|\mathrm{\Delta }\theta |}$, one gets a characteristic length $\propto 1/\overline{|\mathrm{\Delta }\theta |}\sim {\sigma }^{-1}$. Note that in addition to this argument, the same scaling can be tackled and understood from a different angle, involving topological defects; we will come back to this point later on.

At intermediate times, the system crosses over from its short-time dynamics, following the passive XY scaling, to its steady state. We define this transient time τ(σ) as the time for which the equilibrium correlation length is equal to the steady state out-of-equilibrium one:

$\xi \left(\sigma =0,\tau \right)=\xi \left(\sigma ,t\to \infty \right).(9)$

We plot it in the inset of Figure 3B and obtain τ ∼ 1/σ²: the wider the frequency distribution is, the faster is the relaxation process. This intuitive tendency is easily captured by a trivial scaling argument: the logarithmic correction is a long term effect, so we drop it and assume for the sake of simplicity that ξ first follows an equilibrium growth $\sqrt{t}$. As it eventually saturates at a steady state value ξ_∞∼ 1/σ, the crossover between both regimes thus occurs when

$\sqrt{\tau }\sim {\xi }_{\infty }\sim 1/\sigma \Rightarrow \tau \sim 1/{\sigma }^2,(10)$

confirming the scaling naturally contained in Eq. 8.

We complete the picture by reporting the total number of defects n(t) for different driving strengths σ in Figure 4A. At equilibrium (purple), one obtains n(t) ∼ log  t/t. The similarity of the equilibrium long-term scaling for ξ(t) and for n(t) is not a coincidence. The correlation length ξ is intimately related to the total number of defects n in the equilibrium XY model. Indeed, as a first approximation, ξ is given by the average distance between defects; the system being homogeneous, it follows that $\xi \sim 1/\sqrt{n}$. We indeed recover that at equilibrium, $\xi \sqrt{n}$ is constant over time, cf. Figure 4B. For σ > 0, n(t) eventually saturates at a finite steady state value, as the number of defects at a given temperature increases with σ. This departure from the XY equilibrium behavior is also clearly reflected by the fact that ξ is no longer given by the typical distance between defects, as shown in Figure 4B. The steady state of the Kuramoto model is characterized by both a finite number of defects and a finite correlation length which are, a priori, unrelated. As such, the quench dynamics of the system is no longer fully governed by a single growing length, as its equilibrium counterpart, and the dynamics of the vortices have to be considered in more detail.

FIGURE 4

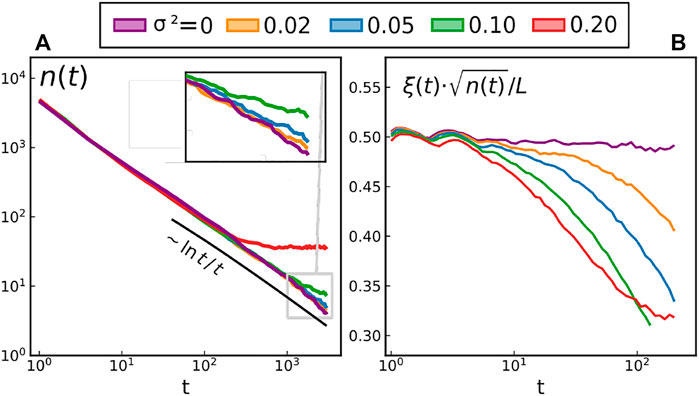
FIGURE 4. Time evolution of (A) the total number of defects n for different forcing intensities and T = 0.4 (B) the quantity $\xi \sqrt{\rho }$ where ρ = n/L² is the defect density. Note that because the defects are homogeneously distributed, $1/\sqrt{\rho }$ is the average distance between two of them.

3.1.2 Topological defects

As a useful reference for our analysis, we first report a map of the total number of vortices in the steady state over the σ² − T plane in Figure 5. As T and σ² decrease, the dynamics gets slower and slower, up to the T = 0 limit case where the self-spinning alone cannot help annihilating pairs of defects: the system initially disordered remains stuck in a metastable state with a lot more vortices than the number of vortices it would exhibit if relaxed from an initially ordered state.

FIGURE 5

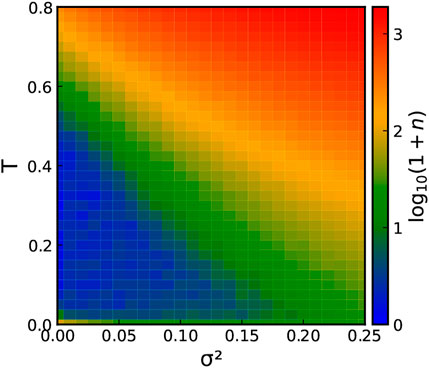
FIGURE 5. Color map of the number of the number of defects n (in log-scale, log₁₀ (1 + n)) over the parameter space σ² − T in the steady state. In the blue region defects are scarce in the system, while in the red one the system is populated by lots of defects (the number growing exponentially fast as one leaves the blue region).

We state once again that the crossover from the defect-rare (blue region) to the defect-rich (red region) regime does not result from an actual phase transition: there is no qualitative change in the correlation length as one moves across the phase space (the system only exhibits short-range order at any σ ≠ 0 for all T ≥ 0). At contrast with the standard literature of the XY model [23, 46], we do not classify vortices into free and bounded here. Indeed, as mentioned above and discussed in more detail below, the core mechanism responsible for the BKT phase transition, namely the defects’ unbinding at a finite temperature, breaks down upon self-spinning. In the driven model, topological defects are found to be genuinely free at any temperature T > 0. In other words, there exists no finite temperature at which vortices are bounded into pairs. While two XY defects of opposite charge attract each other with a logarithmic potential, we find that the defects, upon self-spinning, generically unbind at any T ≥ 0 and σ > 0. We prove it by tracking vortices in time, and considering the average distance between two defects. To do so, we initialize the system in a configuration with a vortex-antivortex pair at a distance R₀, enforcing PBC (cf. SM [44] for details). We then let the system evolve at low-T and low-σ such that there is no (or very few) spontaneous creation of vortices. We monitor the distance R(t) between our two defects and present the results in Figure 6A.

FIGURE 6

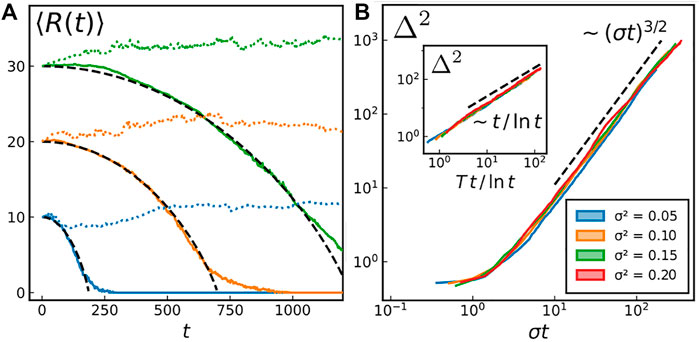
FIGURE 6. (A) Vortex-antivortex separation, averaged over 120 independent runs, for three different initial vortex-antivortex distances R₀ (blue: R₀ = 10, orange: R₀ = 20 and green: R₀ = 30). Full colored lines correspond to T = 0.1 and σ² = 0. Dotted colored lines correspond to T = 0.1 and σ² = 0.1. Black dashed lines are the predictions for an overdamped dynamics with a Coulomb interaction potential Eq. 11. (B) Mean square displacement (MSD) Δ²(t) = ⟨(r(t) −r (0))²⟩ against time, at T = 0.05 for different σ. Inset: MSD for the XY model (σ = 0) for different temperatures (T = 0.2, 0.3, 0.4, 0.5 from blue [left] to red [right]).

As shown in Figure 6A, the XY model data is in perfect agreement with the overdamped description

$\dot{R}\log R=V^{\prime }\left(R\right)(11)$

where V(R) ∝ log  R, a Coulomb 2D potential [30]. For the Kuramoto model, the vortex-antivortex distance R(t) remains in average equal to their initial distance R₀, proving that there is no distinct effective potential between them. One could naively attribute this feature solely to the non-equilibrium nature of the system. However, deciphering the impact of a non-equilibrium drive on the long-range properties of a system on general grounds is a challenging task and one is usually constrained to rely on specific examples where this question has been addressed. For instance, it has been shown that the general BKT scenario remains valid (at least not so far from equilibrium) for an XY model with exponentially correlated thermal noise [47] and for the 2D solid-hexatic transition of self-propelled disks [48, 49]. In the present model system though, the BKT scenario breaks down.

Another remarkable property of topological defects upon self-spinning is found in the statistics of their displacement: they feature anomalous diffusion, their mean-square displacement Δ²(t) ∼ t^α, with α = 3/2 (i.e., super-diffusion). Once again we investigate the dynamics of vortices by tracking them. Since, as discussed earlier, defects are free, we can now focus on the motion a single defect. To do so, we prepare an initial configuration hosting a single +1 defect at the center of the simulation box. One can exclusively focus on + 1 vortices without loss of generality because the equation of motion 1) is statistically invariant under a change of variable θ → −θ (as long as the distribution of the {ω_i} is centered) and such a transformation transforms a +1 vortex into a −1 anti-vortex. The dynamics of ±1 defects are thus statistically identical. We then let the system evolve at low-T and low-σ ensuring that 1) new defects are not spontaneously created and 2) the simulation box is large enough such that boundary effects are negligible. The mean square displacement (MSD) thus obtained is shown in Figure 6B. For the XY model (inset of 6B) and at long times, it follows

${\mathrm{\Delta }}^2\left(t\right)=⟨{\left(\mathbf{r}\left(t\right)-\mathbf{r}\left(0\right)\right)}^2⟩\sim t/\log t,(12)$

showing the expected correction to the normal diffusion scaling, due to the logarithmic dependence of the defect mobility on its size [30] [r(t) being the position of the vortex in the lattice at time t.].

Upon self-spinning, the defects become super-diffusive and the MSD (cf. Figure 6B) instead follows

${\mathrm{\Delta }}^2\left(t\right)\sim {\left(\sigma t\right)}^{3/2}.(13)$

The σ-dependence of the vortex dynamics enters through a rescaling of time: the typical time associated with its motion along a domain is proportional to its typical size ξ ∼ 1/σ. A careful characterisation of the stochastic motion of the defects will be presented in Section 4.2.

3.2 Underdamped dynamics

The nature of the dynamics, being overdamped or underdamped, does not have any impact on the long-time, large-scale properties of a system as long as its dynamics fulfil detailed balance. If this defining feature of equilibrium is satisfied, the steady-states obey Boltzmann statistics. For the Kuramoto model, being out-of-equilibrium, different ways of exploring the configuration space might lead to different steady large scale behaviour [41–43]. We are thus interested in putting into test the robustness of our results to the presence of inertial effects.

We first explore the steady states produced by letting the model Eq. 2, with inertia, relax from an initially disordered state with many vortices, to a state with only a few of them (i.e. the low temperature regime). If we look at typical snapshots of the steady state, Figure 7 (for the same parameter values in Figure 1 but m = 1), we observe basically the same features as in the overdamped case: for σ = 0 we find oppositely charged defects pairs visually connected by a phase field reminiscent of the magnetic field lines generated by a planar magnet, while for σ > 0 vortices are surrounded by a phase texture that makes difficult pairing them by eye, featuring synchronised domains of different shapes and sizes.

FIGURE 7

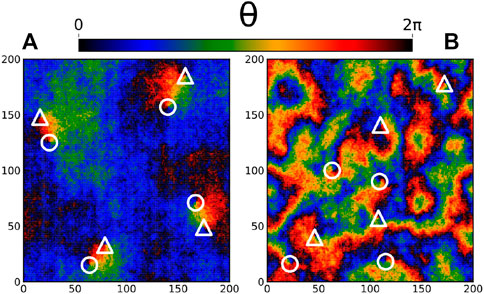
FIGURE 7. Snapshots for m = 1, T = 0.2, (A) σ² = 0 and (B) σ² = 0.1. The phase of each oscillator is represented by a color scale. Vortices (antivortices) are represented by circles (triangles).

3.2.1 Coarsening dynamics

We now turn into the relaxation dynamics of the model with inertia following a quench from an initially disordered state. We investigate the same dynamical quantities as for the overdamped regime (cf. Figures 2–4), varying the inertia from m = 10^–2 to 10 and comparing them to their overdamped counterparts (in blue, m = 0). The results are reported in Figure 8.

FIGURE 8

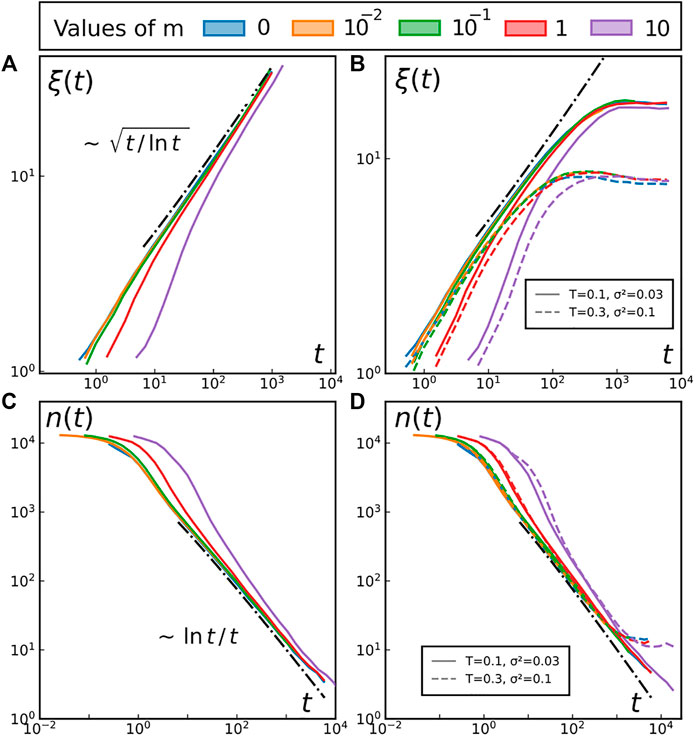
FIGURE 8. Relaxation from an initially disordered state. Different colours represent different inertia m for all four panels, as indicated at the top of the figure. Top row: Time evolution of the correlation length ξ(t) for (A) the XY model at T = 0.2 and for (B) the driven system at the different values of T and σ. Bottom row: Time evolution of the total number of defects n(t) for (C) the XY model at T = 0.2 and for (D) the driven system at the different values of T and σ. We only display two sets of parameters for readability but we have reached the same conclusions for all the other tested parameters (distributed across the entire phase space). Left column: At equilibrium. Right column: out-of-equilibrium.

At equilibrium, the results confirm that we do recover the same long term values for ξ and n independently from the inertia m, cf. Figures 8A,C. The results also indicate that, even in the presence of self-spinning, the inertia does not affect significantly the long-time behavior as one recover the same steady state values for values of m covering three orders of magnitude (see Figures 8B,D). The short-time dynamics is however affected by the inertia of individual rotors.

3.2.2 Topological defects

We now turn back to topological defects and shall see that, surprisingly, their MSD is not affected by the inertia of individual oscillators. We resort to the same protocol (track a single defect over time in a big system with free boundaries) and plot the result in Figure 9.

FIGURE 9

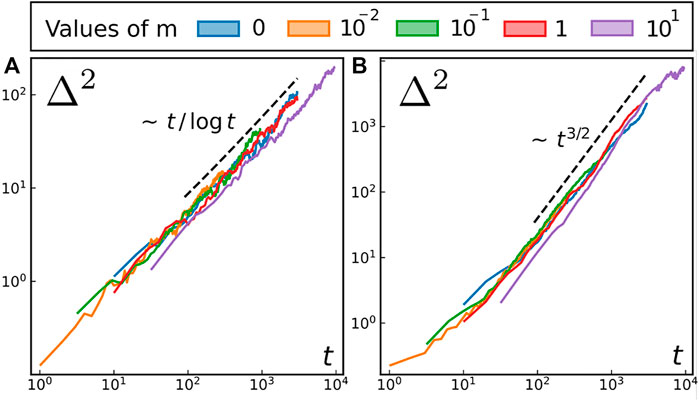
FIGURE 9. Mean Square Displacement (MSD) of individual defects for (A) XY model at T = 0.2 (B) forced model at T = 0.2 and σ² = 0.03.

We recover the same (sub)diffusive motion for the XY model and the super-diffusion with the same exponent in the presence of self-spinning.

Overall, our results are robust as they indicate that the long-term properties of the system are not affected by the inertia of the underlying individual oscillators. We emphasis that this result is new and somehow surprising as, beyond the fact that there are no general guidelines for out-of-equilibrium systems, including inertia in a model of coupled oscillators can yield dramatic changes. For instance, in the globally coupled Kuramoto model inertia changes the order of the disordered/synchronised transition from second to first order [41–43, 50]. It is therefore remarkable that this does not happen in a model of locally coupled oscillators.

And finally, we have seen that a non-equilibrium forcing σ > 0 dramatically changes the MSD regime from sub-diffusive to super-diffusive.

4 Discussion

4.1 The fate of the BKT transition

The BKT transition scenario usually occurs when topological defects interact with a long-ranged $\sim 1/r$ force, in 2D, establishing quasi-long range order at low temperatures. After a quench across such a phase transition, due to the collective behaviour of topological defects, the typical length scale grows as $\xi \sim \sqrt{t/\log t}$. Such behaviour is driven by the diffusion and annihilation of defects, whose number decreases as n ∼ 1/ξ².

In contrast, in the presence of intrinsic spinning, the field disturbances generated by the defects only expand over relatively short length scales, at any temperature. Consider the equation of motion Eq. 1 defining the model, at T = 0, for a test spin at distance r from a topological defect. The defect generates a field θ(x, y) = arctan (y/x) around itself. As a first approximation, we replace the influence of the spin’s neighbourhood (∂) by the Coulomb force generated by the defect, namely:

$\sum _{\partial }\sin \left(\mathrm{\Delta }\theta \right)\approx \sum _{\partial }|\nabla \theta \left(x,y\right)|=c/r.$

The constant c, homogeneous to a length, depends on various parameters, in particular the defect’s charge. One thus gets $\dot{{\theta }_i}=\sigma {\omega }_i+c/r$. It now becomes clear that for r > c/(σω), $\dot{\theta }$ is dominated by the forcing term. As ω is a random variable with zero mean and unit variance, averaging over the whole system proves that beyond a typical distance ξ ∼ 1/σ, the spins’ dynamics is no longer primarily governed by the topological defects’ influence but rather by the intrinsic driving frequency. Importantly, this second argument explains the same scaling without resorting to the crude 1D approximation of the first argument.

Indeed, the behaviour of a pair of vortices shows a clear absence of any relevant defect-defect interacting potential: topological defects are genuinely free in the driven system. Once the phase patterns have formed, they screen the expected ∼ log  r potential of the XY model, key prerequisite to belong to the BKT universality class.

The measurements of the correlation length ξ ∼ 1/σ and the absence of relation between ξ and n upon self-spinning strengthen that claim. In our model, it only took an energy injection at the smallest scale, independent from spin to spin, for the BKT scenario of the XY model to collapse. As it shows that long-range influence is lost as soon as the model is made active, the present work conceptually supports the conclusions of Pearce et al. [51], where they report the absence of long-range ordering of defects in active nematics. Following up on the recent work of Pokawanvit et al. [52], we underline that our system features an incompressible, dense and immobile ensemble of particles, which, based on their work, will not give rise to any collective motion of topological defects.

However, this out-of-equilibrium system still inherits some of the coarsening dynamics of the 2D Xy model physics: Figure 3 (and Figures 8B,D for m ≪ 1) show that the short-time dynamics do follow $\xi \sim \sqrt{t/\log t}$, n(t) ∼ log  t/t and Δ² ∼ t/log  t. As the establishment of the domain boundaries (on which defects will then surf) take some transient time, the underlying equilibrium XY mechanisms prevail at short times. For example, consider an initially disordered system, at first crowded with defects: the vortex mean free time (time before collision/annihilation) is so small that

They rapidly end up colliding and annihilating, as bounded vortices would have done. We have shown that such transient time τ from equilibrium to active dynamics scales as 1/σ².

4.2 Defects’ dynamics

This section aims at shedding some light on the underlying mechanisms responsible for the spontaneous creation of domain boundaries and topological defects, and their super-diffusive random motion.

4.2.1 Creation of domain boundaries and defects

Interested by the emergence of the patterns such as those in Figures 1B, 7B, we look at the short time dynamics of the fields θ ≡ θ(x, y) and $\dot{\theta }\equiv \dot{\theta }(x,y)$ (x, y being the spatial coordinates of a point in the lattice). We do so by following the evolution of the system from an ordered initial condition (all sites with identical phase). We proceed in such a way in order to isolate the underlying mechanisms at stake and avoid being blurred by the numerous defects inherent to a disordered initial condition. As the time series of θ is noisy for T > 0, one has to average in time to obtain a meaningful signal $\dot{\theta }$. Details about the exponential moving average used in that preliminary signal processing step can be found in the SM [44].

After very few time-steps, a clear picture appears: locally synchronised regions develop in the $\dot{\theta }$ field. We recall that since d = 2 is the lower critical dimension for frequency locking in the noiseless short range Kuramoto model, we do not expect more than local frequency synchronization. Since the average instantaneous frequency (over the N spins at a given time t) scales as $1/\sqrt{N}$ —as one should expect from a zero-mean distribution of intrinsic frequencies, reciprocal interactions and Gaussian white noise—, some regions rotate clockwise and some others counterclockwise; look for instance at the dark and bright regions of Figure 10A. Naturally, these locally synchronized regions in $\dot{\theta }$ translate into locally aligned domains in the phase field. This is illustrated in Figure 10: the dark region by the left of panel 10A generates a phase synchronised domain of same shape and at the same position in panel 10D, now in red.

FIGURE 10

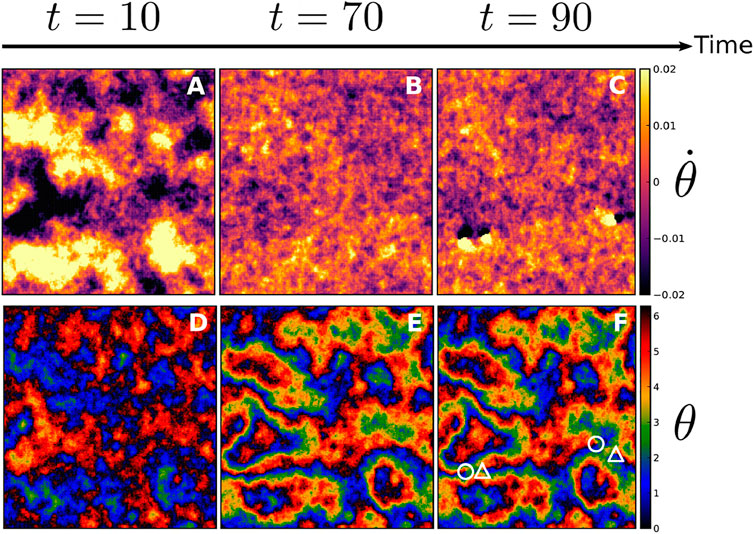
FIGURE 10. Three snapshots over time of the fields $\dot{\theta }(x,y)$ (A–C) and θ(x, y) (D–F) for a system initially ordered with T = 0.05 and σ² = 0.2. In panel (C), defects are clearly identified thanks to the localized and intense amplitude of the instantaneous frequencies. In panel (F), +1 defects are highlighted by a circle, − 1 defects are highlighted by a triangle.

Progressively, as time goes on, the different domains grow, (cf. Panel 10E), defining a network of domain boundaries. As they correspond to regions where |∇θ| is large, they can be visually identified by looking for thin elongated regions across which colours change rapidly (though in a smooth way in contrast to, for instance, domain boundaries in the Ising model).

At this stage, the domains are locally ordered, their boundaries concentrate most of the energy of the system and the instantaneous frequencies $\dot{\theta }$ gradually decrease in amplitude (compare panels 10A and 10B). The system finally reaches its steady state characterised by synchronised domains resulting from the competition between the elastic energy and the driving frequencies σω_i.

These domain boundaries play a crucial role in the formation of defects. There, the important gradients |∇θ| provide most of the energy needed to create and sustain topological defects. The remaining energy contribution eventually comes from thermal fluctuations, explaining why the temperature threshold necessary to spontaneously generate defects decreases as the forcing increases, see Figure 5. It also explains why one observes defects creation primarily at the domain boundaries, as exemplified in Figure 10F. This creation mechanism contrasts with that of the equilibrium case, entirely due to thermal fluctuations and hence homogeneously distributed in space.

Yet, the creation mechanism is not the only difference between the active and the passive case: a major difference lies in the motion of these topological defects, as we detail in the last part of this article.

4.2.2 Defects super-diffusion

The MSD of individual defects is shown in Figures 6B, 9. As soon as σ ≠ 0, in the time window allowed by our simulations (spanning over 4 decades) the MSD of the defects has an anomalous exponent α = 3/2 without any sign of a crossover to a diffusive regime at longer times. We depict in Figure 11A typical vortex trajectories. Since super-diffusion is a frequent phenomenon in active matter (e.g., topological defects in active nematics [11, 53–55] or cells in biophysics experiments [56]), it naturally led to a plethora of random walk models exhibiting transient [57, 58] or long term super-diffusion [59–61].

FIGURE 11

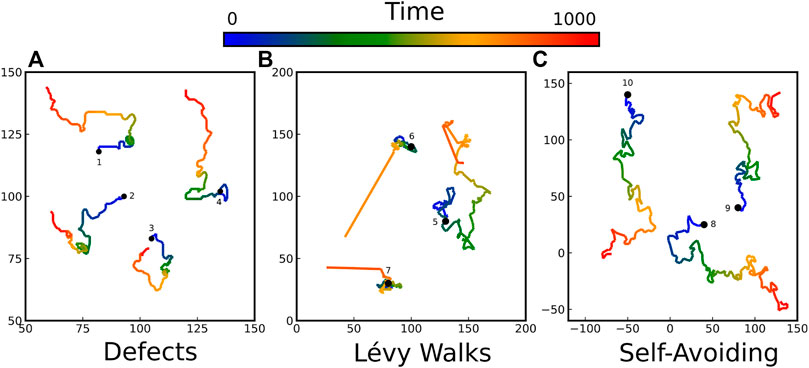
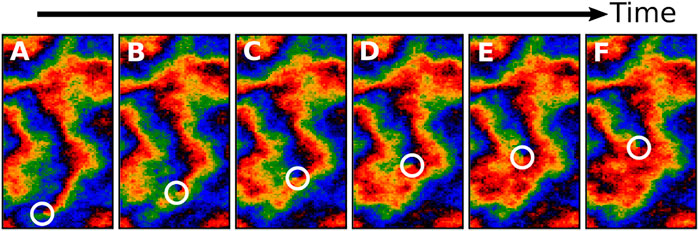
FIGURE 11. Sample trajectories of (A) topological defects in the actual spin model (B) Lévy walks with exponent γ = 3/2 (C) self-avoiding random walks (SAW). Each path departs from a black circle and lasts for Δt = 10³, indicated by the color code.

Among models featuring long-term super-diffusion, the family of Lévy processes is a popular choice, in particular in biology [56, 62]. In Lévy walks (respectively Lévy flights, their discontinuous counterpart), the duration τ of each walk (respectively the size of each jump) is usually sampled from a fat-tailed distribution f(τ) ∼ τ^−(1+γ), where 1 < γ < 2 is a common choice for super-diffusing Lévy walks. The resulting MSD follows ∼ t^3−γ (see [63] and references therein for a complete review). The super-diffusion stems from the infinite variance of this distribution, explaining why the resulting trajectories sometimes feature a dramatic jump (as trajectories six and seven depict in Figure 11B. As such jumps cannot occur in our system, Lévy processes do not provide a faithful description of the random motion of vortices in the Kuramoto model. In addition, there is no physical argument to support the specific choice of the exponent γ = 3/2 (the only one reproducing the anomalous exponent α = 3/2 of the vortices).

An important feature of the system to grasp the dynamics of the vortices is the domain structure of the system. Indeed, there is a feedback between the spatio-temporal patterns dynamics and the defects’ motion. On one hand, defects have a strong preference to move along domain boundaries, where elastic energy is the largest [10, 64]. As a domain boundary separates two neighbouring synchronised regions, it is characterised by an excess elastic energy. They thus provide a preferential direction for the motion of the topological defects, in contrast with the isotropic random motion of a single defect in the equilibrium XY model, for instance. This phenomenon has been observed recently in experimental systems by Kumar et al. [65], where they report that defects are ‘catapulted’ along these boundaries. On the other hand, such excess energy is released during the motion of the defects along domain boundaries. Indeed, the local θ field is strongly and quickly rearranged upon the passage of a topological defect. The field becomes smoother as the domain boundary is removed by the passage of a vortex, dissipating elastic energy. As shown in the successive snapshots of Figure 12, defects act like a zip, bringing together the two domains on each side of the boundary (e.g., in Figure 12A, these are the two red regions, separated by the thin black line), leaving a synchronized region behind (big red region in Figure 12F). This area is no longer favorable to the future passage of a defect (be it itself or another one), as the elastic energy it previously contained has been dissipated. As such, the phase pattern has a strong impact on the motion of the defects and conversely, defects significantly alter the structure of the system as they move.

FIGURE 12

FIGURE 12. Times are T = (A) 260 (B) 270 (C) 280 (D) 290 (E) 300 (F) 308.

As vortices remove the domain boundaries as they move, they perform a random walk with memory: it is more likely for a vortex to keep moving along the domain boundary than retrace its steps. The classical framework to treat this kind of motion is the self-avoiding random walk (SAW), which might be at the origin of the anomalous exponent 3/2. In order to explore whether SAW could provide a useful description of our defects motion, we simulate a few of SAW and visually compare the generated trajectories with the ones we recorded for vortices. As shown in Figure 11C, they look qualitatively similar. To be more quantitative, we also computed the MSD and the distribution of displacements G (x, t), defined as the probability that a walker initially at x = 0 at t = 0 is at position x at time t > 0. SAW feature a super-diffusion with Δ²(t) ∼ t^ν with $\nu =\frac{6}{d+2}$ [66], hence providing an explanation of the 3/2 exponent we found for the defects’ MSD (here d = 2, the number of spatial dimensions). Yet, the description provided by SAW is not complete, as the full distribution of displacements differ significantly. As shown in Figure 13A, for defects,

$G\left(x,t\right)\sim \exp \left(-x^2/t^{3/2}\right)(14)$

while for SAW, one obtains (cf. Inset of Figure 13B)

$G\left(x,t\right)\sim \exp \left(-x^4/t^3\right).(15)$

FIGURE 13

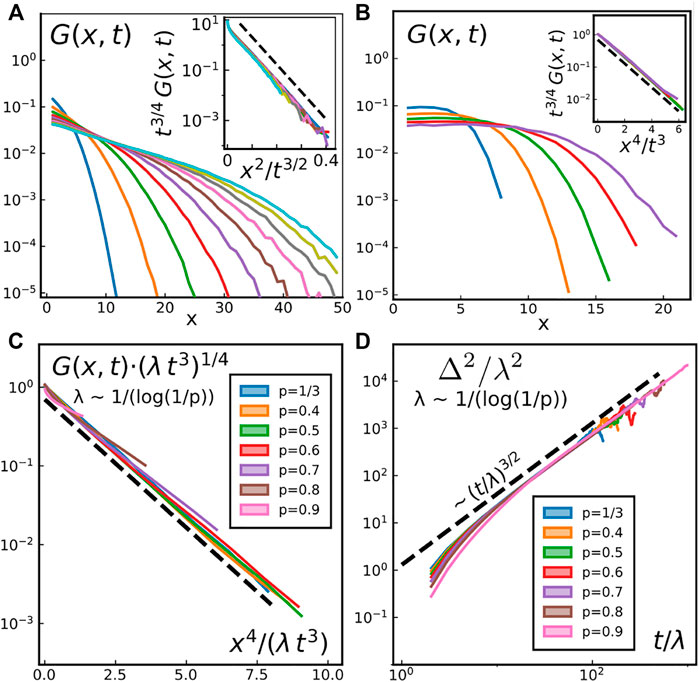
FIGURE 13. Probability densities of displacement G (x, t) (see main text for definition) for different cases. Both insets represent rescaled data in order to highlight the functional form of (G). We considered (A) topological defects with σ² = 0.025 and T = 0.2, at times (from left to right) t = 50, 100, 150, … , 500. Inset: the dashed line follows f(x) ∼ exp ( − 60x) (B) SAW (Δt = 1) at times (from left to right) t = 10, 15, 20, 25, 30. Inset: the dashed line follows f(x) ∼ exp ( − 0.85x) (C) Persistent SAW (see main text for definition) with different persistence probabilities on rescaled axes to highlight that the functional form is identical for all 1/3 ≤ p < 1. The dashed line follows f(x) ∼ exp ( − 3x/4). (D) MSD resulting from G (x, t) of panel (C), for different persistence probabilities p.

We also investigated the effect of including self-propulsion to mimic the behaviour of vortices on domain boundaries. To do so, we add persistence to the walk, on top of the self-avoiding condition. Instead of continuing straight, turning left or turning right with equal probability 1/3, we set the probability to continue straight to 1/3 ≤ p < 1, and thus turning left or right with probability (1 − p)/2. This process introduces a typical length λ ∼ 1/log (1/p), as pⁿ = e^−n/λ. The typical timescale before the trajectory has changed orientation with probability 1/3 also scales as λ. In other words, a persistent SAW, when expressed in terms of the rescaled space x/λ and rescaled time t/λ, is indistinguishable from a non persistent SAW expressed in terms of x and t. This explains why, for all 1/3 ≤ p < 1, the probability density of displacement for a persistent SAW with probability p is given by

$G\left(x,t\right)=\frac{1}{2\mathrm{\Gamma }\left(5/4\right){\left(\lambda t^3\right)}^{1/4}}\exp \left(-\frac{x^4}{\lambda t^3}\right),(16)$

where Γ(x) is the usual Gamma function. Note that the slope of the curves in Figure 13C determines the exact value of the rescaling factor: λ = 4/(3 log (1/p)).

Overall, a complete, faithful microscopic description of the topological defects’ motion in the short-range Kuramoto model remains to be found. Despite the simplicity of their displacements’ functional form G (x, t) ∼ exp (−x²/t^3/2), it is likely that collective effects drive the defects’ motion in a way simple random walk models cannot capture. While vortex superdiffusion and the value of the anoumalous exponent can be reproduced by a self-avoiding walk picture (considering only a single vortex and omitting the dynamics of the domain boundaries), the particular form of G (x, t) seems to require a more involved treatment, calling for a full many-body description which takes into account the two-way coupling between the domain boundaries’ dynamics and the vortex motion.

5 Conclusion

In this article we have studied the dynamics of the short-range noisy Kuramoto model, constructed as a non-equilibrium extension of the 2D XY model, where spins rotate with an intrinsic frequency, taken from a (quenched) Gaussian distribution. Exploiting the connection between the emergence of synchronisation and the topological Berezenskii-Kosterlitz-Thouless phase transition in the 2D XY model, we investigate the dynamics of vortices in detail, contributing to our current understanding of the dynamics of topological defects in non-equilibrium soft condensed matter.

In 2D, the short range noisy Kuramoto does not exhibit any kind of phase transition at any finite temperature, its correlation length is always finite and scales as ξ ∼ σ⁻¹. Instead, there is a crossover between a high temperature region with many topological defects, and a low temperature region with a few, as the number of vortices decreases exponentially fast close to such crossover temperature. We have showed that the relaxation towards the low temperature regime from a disordered initial state proceeds via the growth of a characteristic length scale, setting the typical size of synchronised domains Such growth does not proceed indefinitely, as the correlation length of the system is finite. The number of defects decays in time following the expected behaviour from the 2D XY model, although the mean separation between defects is not given by growing length extracted from the correlation function, meaning that the dynamics cannot be fully described by a single length scale, as for the coarsening of the 2D XY model. Indeed, vortices are free in the non-equilibrium model, advected by the domain boundaries of phase synchronised regions, resulting in super-diffusion with a long-time mean-square displacement Δ²(t) ∼ t^3/2. Thus, the mean distance between topological defects does not bare any information regarding the large-scale structure of the system. Interestingly, similar defect’s dynamics has been observed in different experimental systems: in active nematics [65], monolayers of self-propelled colloids [64] and spinning colloidal magnets [21].

We have found that our results remain valid both for inertial and over-damped Kuramoto dynamics, showing the robustness of the before-mentioned scenario and the breakdown of BKT physics. We have provided a detailed characterisation of the random walks performed by vortices, and have found that, although their stochastic dynamics shares several similarities to self-avoiding walks, in particular the scaling Δ²(t) ∼ t^3/2, their full statistics of displacements are not equivalent. A faithful description of the dynamics of the dynamics of vortices would require a theory capturing the two-way dynamical feedback between the phase field and the vortices, a challenging endeavour that we leave for future work.

Data availability statement

The Julia code used to conduct the research and produce the figures is available on GitHub at https://github.com/yrouzaire/forced_xy.

Author contributions

YR and DL designed research: YR performed the research and analysed the data; YR and DL wrote the paper.

Funding

YR thanks the CECAM (Centre Européen de Calcul Atomique et Moléculaire; Head-director: I. Pagonabarraga) for financial support. DL acknowledges Ministerio de Ciencia, Innovación y Universidades MCIU/AEI/FEDER for financial support under grant agreement RTI2018-099032-J-I00.

Acknowledgments

We warmly thank Elisabeth Agoritsas for helpful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.976515/full#supplementary-material.

References

1. Huygens C. Letters to de sluse, (letters; no. 1333 of 24 february 1665, no. 1335 of 26 february 1665, no. 1345 of 6 march 1665). La Haye: Societe Hollandaise Des Sciences, Martinus Nijhoff (1895).

Google Scholar

2. Strogatz SH. Sync: How order emerges from chaos in the universe, nature, and daily life. Hachette UK) (2012).

Google Scholar

3. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A universal concept in nonlinear sciences, 12. Cambridge University Press (2003).

Google Scholar

4. Sakaguchi H, Shinomoto S, Kuramoto Y. Local and global self-entrainments in oscillator lattices. Prog Theor Phys (1897).

Google Scholar

5. Acebrón JA, Bonilla LL, Perez-Vicente CJ, Ritort F, Spigler R. The kuramoto model: A simple paradigm for synchronization phenomena. Rev Mod Phys (2005) 77:137–85. doi:10.1103/revmodphys.77.137

CrossRef Full Text | Google Scholar

6. Mondragón-Palomino O, Danino T, Selimkhanov J, Tsimring L, Hasty J. Entrainment of a population of synthetic genetic oscillators. Science (2011) 333:1315–9. doi:10.1126/science.1205369

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou C. Synchronization in complex networks. Phys Rep (2008) 469:93–153. doi:10.1016/j.physrep.2008.09.002

CrossRef Full Text | Google Scholar

8. Hong H, Chaté H, Tang LH, Park H. Finite-size scaling, dynamic fluctuations, and hyperscaling relation in the kuramoto model. Phys Rev E (2015) 92:022122. doi:10.1103/physreve.92.022122

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lee TE, Tam H, Refael G, Rogers JL, Cross M. Vortices and the entrainment transition in the two-dimensional kuramoto model. Phys Rev E (2010) 82:036202. doi:10.1103/physreve.82.036202

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Rouzaire Y, Levis D. Defect superdiffusion and unbinding in a 2D XY model of self-driven rotors. Phys Rev Lett (2021) 127:088004. doi:10.1103/physrevlett.127.088004

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Shankar S, Souslov A, Bowick MJ, Marchetti MC, Vitelli V. Topological active matter. Nat Rev Phys (2022) 4:380–98. doi:10.1038/s42254-022-00445-3

CrossRef Full Text | Google Scholar

12. Ginelli F. The physics of the vicsek model. Eur Phys J Spec Top (2016) 225:2099–117. doi:10.1140/epjst/e2016-60066-8

CrossRef Full Text | Google Scholar

13. Chepizhko A, Kulinskii V. On the relation between vicsek and kuramoto models of spontaneous synchronization. Physica A: Stat Mech its Appl (2010) 389:5347–52. doi:10.1016/j.physa.2010.08.016

CrossRef Full Text | Google Scholar

14. Chepizhko O, Saintillan D, Peruani F. Revisiting the emergence of order in active matter. Soft Matter (2021) 17:3113–20. doi:10.1039/d0sm01220c

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Levis D, Pagonabarraga I, Liebchen B. Activity induced synchronization: Mutual flocking and chiral self-sorting. Phys Rev Res (2019) 1:023026. doi:10.1103/physrevresearch.1.023026

CrossRef Full Text | Google Scholar

16. Golestanian R, Yeomans JM, Uchida N. Hydrodynamic synchronization at low Reynolds number. Soft Matter (2011) 7:3074–82. doi:10.1039/c0sm01121e

CrossRef Full Text | Google Scholar

17. Solovev A, Friedrich BM. Synchronization in cilia carpets: Multiple metachronal waves are stable, but one wave dominates. New J Phys (2022) 24:013015. doi:10.1088/1367-2630/ac2ae4

CrossRef Full Text | Google Scholar

18. Solovev A, Friedrich BM. Synchronization in cilia carpets and the kuramoto model with local coupling: Breakup of global synchronization in the presence of noise. Chaos (2022) 32:013124. doi:10.1063/5.0075095

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Soni V, Bililign ES, Magkiriadou S, Sacanna S, Bartolo D, Shelley MJ, et al. The odd free surface flows of a colloidal chiral fluid. Nat Phys (2019) 15:1188–94. doi:10.1038/s41567-019-0603-8

CrossRef Full Text | Google Scholar

20. Massana-Cid H, Levis D, Hernández RJH, Pagonabarraga I, Tierno P. Arrested phase separation in chiral fluids of colloidal spinners. Phys Rev Res (2021) 3:L042021. doi:10.1103/physrevresearch.3.l042021

CrossRef Full Text | Google Scholar

21. Bililign ES, Usabiaga FB, Ganan YA, Soni V, Magkiriadou S, Shelley MJ, et al. Chiral crystals self-knead into whorls. arXiv preprint arXiv:2102.03263 (2021).

Google Scholar

22. Liebchen B, Levis D. Chiral active matter (2022). arXiv e-printsarXiv–2207.

Google Scholar

23. Kosterlitz JM, Thouless DJ. Ordering, metastability and phase transitions in two-dimensional systems. J Phys C: Solid State Phys (1973) 6:1181–203. doi:10.1088/0022-3719/6/7/010

CrossRef Full Text | Google Scholar

24. Kosterlitz JM. The critical properties of the two-dimensional xy model. J Phys C: Solid State Phys (1974) 7:1046–60. doi:10.1088/0022-3719/7/6/005

CrossRef Full Text | Google Scholar

25. Berezinskii V. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group i. classical systems. Sov Phys JETP (1971) 32:493–500.

Google Scholar

26. You Z, Pearce DJ, Sengupta A, Giomi L. Geometry and mechanics of microdomains in growing bacterial colonies. Phys Rev X (2018) 8:031065. doi:10.1103/physrevx.8.031065

CrossRef Full Text | Google Scholar

27. Bowick MJ, Fakhri N, Marchetti MC, Ramaswamy S. Symmetry, thermodynamics, and topology in active matter. Phys Rev X (2022) 12:010501. doi:10.1103/physrevx.12.010501

CrossRef Full Text | Google Scholar

28. Bray AJ. Theory of phase-ordering kinetics. Adv Phys X (2002) 51:481–587. doi:10.1080/00018730110117433

CrossRef Full Text | Google Scholar

29. Levis D, Pagonabarraga I, Diaz-Guilera A. Synchronization in dynamical networks of locally coupled self-propelled oscillators. Phys Rev X (2017) 7:011028. doi:10.1103/physrevx.7.011028

CrossRef Full Text | Google Scholar

30. Yurke B, Pargellis A, Kovacs T, Huse D. Coarsening dynamics of the xy model. Phys Rev E (1993) 47:1525–30. doi:10.1103/physreve.47.1525

CrossRef Full Text | Google Scholar

31. Rojas F, Rutenberg A. Dynamical scaling: The two-dimensionalXYmodel following a quench. Phys Rev E (1999) 60:212–21. doi:10.1103/physreve.60.212

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bray A, Briant A, Jervis D. Breakdown of scaling in the nonequilibrium critical dynamics of the two-DimensionalXYModel. Phys Rev Lett (2000) 84:1503–6. doi:10.1103/physrevlett.84.1503

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Berthier L, Holdsworth PC, Sellitto M. Nonequilibrium critical dynamics of the two-dimensional xy model. J Phys A: Math Gen (2001) 34:1805–24. doi:10.1088/0305-4470/34/9/301

CrossRef Full Text | Google Scholar

34. Jelic A, Cugliandolo L. Quench dynamics of the 2d xy model. J Stat Mech (2018) 2011:P02032. doi:10.1088/1742-5468/2011/02/p02032

CrossRef Full Text | Google Scholar

35. Hohenberg PC, Halperin BI. Theory of dynamic critical phenomena. Rev Mod Phys (1977) 49:435–79. doi:10.1103/revmodphys.49.435

CrossRef Full Text | Google Scholar

36. Weber H, Minnhagen P. Monte Carlo determination of the critical temperature for the two-dimensionalXYmodel. Phys Rev B (1988) 37:5986–9. doi:10.1103/physrevb.37.5986

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Hasenbusch M. The two-dimensional xy model at the transition temperature: A high-precision Monte Carlo study. J Phys A: Math Gen (2005) 38:5869–83. doi:10.1088/0305-4470/38/26/003

CrossRef Full Text | Google Scholar

38. Cardy JL, Ostlund S. Random symmetry-breaking fields and theXYmodel. Phys Rev B (1982) 25:6899–909. doi:10.1103/physrevb.25.6899

CrossRef Full Text | Google Scholar

39. Le Doussal P, Giamarchi T. Replica symmetry breaking instability in the 2DXYModel in a random field. Phys Rev Lett (1995) 74:606–9. doi:10.1103/physrevlett.74.606

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Agrawal R, Kumar M, Puri S. Domain growth and aging in the random field xy model: A Monte Carlo study. Phys Rev E (2021) 104:044123. doi:10.1103/physreve.104.044123

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Komarov M, Gupta S, Pikovsky A. Synchronization transitions in globally coupled rotors in the presence of noise and inertia: Exact results. EPL (2014) 106:40003. doi:10.1209/0295-5075/106/40003

CrossRef Full Text | Google Scholar

42. Gupta S, Campa A, Ruffo S. Kuramoto model of synchronization: Equilibrium and nonequilibrium aspects. J Stat Mech (2014) 2014:R08001. doi:10.1088/1742-5468/14/08/R08001

CrossRef Full Text | Google Scholar

43. Olmi S, Navas A, Boccaletti S, Torcini A. Hysteretic transitions in the kuramoto model with inertia. Phys Rev E (2014) 90:042905. doi:10.1103/PhysRevE.90.042905

PubMed Abstract | CrossRef Full Text | Google Scholar

44.

45. Bray A. Random walks in logarithmic and power-law potentials, nonuniversal persistence, and vortex dynamics in the two-dimensionalXYmodel. Phys Rev E (2000) 62:103–12. doi:10.1103/physreve.62.103

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Cugliandolo L. Advanced statistical physics: Phase transitions (2018).

Google Scholar

47. Paoluzzi M, Marconi UMB, Maggi C. Effective equilibrium picture in the xy model with exponentially correlated noise. Phys Rev E (2018) 97:022605. doi:10.1103/physreve.97.022605

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Digregorio P, Levis D, Suma A, Cugliandolo LF, Gonnella G, Pagonabarraga I. Full phase diagram of active brownian disks: From melting to motility-induced phase separation. Phys Rev Lett (2018) 121:098003. doi:10.1103/physrevlett.121.098003

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Digregorio P, Levis D, Cugliandolo LF, Gonnella G, Pagonabarraga I. Unified analysis of topological defects in 2d systems of active and passive disks. Soft Matter (2022) 18:566–91. doi:10.1039/d1sm01411k

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Tanaka HA, Lichtenberg AJ, Oishi S. First order phase transition resulting from finite inertia in coupled oscillator systems. Phys Rev Lett (1997) 78:2104–7. doi:10.1103/PhysRevLett.78.2104

CrossRef Full Text | Google Scholar

51. Pearce D, Nambisan J, Ellis P, Fernandez-Nieves A, Giomi L. Orientational correlations in active and passive nematic defects. Phys Rev Lett (2021) 127:197801. doi:10.1103/PhysRevLett.127.197801

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Pokawanvit S, Chen Z, You Z, Angheluta L, Marchetti MC, Bowick MJ. Active nematic defects in compressible and incompressible flows (2022). arXiv preprint arXiv:2206.13598.

Google Scholar

53. Doostmohammadi A, Ignés-Mullol J, Yeomans JM, Sagués F. Active Nematics Nat Commun (2018) 9:1–13.

CrossRef Full Text

54. Giomi L, Bowick MJ, Mishra P, Sknepnek R, Marchetti MC. Defect dynamics in active nematics. Phil Trans R Soc A (2014) 372:20130365. doi:10.1098/rsta.2013.0365

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Vliegenthart GA, Ravichandran A, Ripoll M, Auth T, Gompper G. Filamentous active matter: Band formation, bending, buckling, and defects. Sci Adv (2020) 6:eaaw9975. doi:10.1126/sciadv.aaw9975

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Huda S, Weigelin B, Wolf K, Tretiakov KV, Polev K, Wilk G, et al. Lévy-like movement patterns of metastatic cancer cells revealed in microfabricated systems and implicated in vivo. Nat Commun (2018) 9:4539. doi:10.1038/s41467-018-06563-w

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Caprini L, Marconi UMB, Wittmann R, Löwen H. Dynamics of active particles with space-dependent swim velocity. Soft Matter (2022) 18:1412–22. doi:10.1039/d1sm01648b

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Villa-Torrealba A, Chávez-Raby C, de Castro P, Soto R. Run-and-tumble bacteria slowly approaching the diffusive regime. Phys Rev E (2020) 101:062607. doi:10.1103/PhysRevE.101.062607

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Fedotov S, Korabel N. Emergence of Lévy walks in systems of interacting individuals. Phys Rev E (2017) 95:030107. doi:10.1103/PhysRevE.95.030107

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Han D, da Silva MAA, Korabel N, Fedotov S. Self-reinforcing directionality generates truncated lévy walks without the power-law assumption. Phys Rev E (2021) 103:022132. doi:10.1103/PhysRevE.103.022132

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Bertoin J. Lévy processes, 121. Cambridge university press Cambridge (1996).

Google Scholar

62. Ariel G, Beér A, Reynolds A. Chaotic model for lévy walks in swarming bacteria. Phys Rev Lett (2017) 118:228102. doi:10.1103/physrevlett.118.228102

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Zaburdaev V, Denisov S, Klafter J. Lévy walks. Lévy Walks Rev Mod Phys (2015) 87:483–530. doi:10.1103/RevModPhys.87.483

CrossRef Full Text | Google Scholar

64. Chardac A, Hoffmann LA, Poupart Y, Giomi L, Bartolo D. Topology-driven ordering of flocking matter. Phys Rev X (2021) 11:031069. doi:10.1103/physrevx.11.031069

CrossRef Full Text | Google Scholar

65. Kumar N, Zhang R, Redford S, de Pablo JJ, Gardel M. Catapulting of topological defects through elasticity bands in active nematics. Soft Matter (2022) 18:5271–81. doi:10.1039/d2sm00414c

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Barat K, Chakrabarti BK. Statistics of self-avoiding walks on random lattices. Phys Rep (1995) 258:377–411. doi:10.1016/0370-1573(95)00009-6

CrossRef Full Text | Google Scholar