
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 19 August 2022
Sec. Interdisciplinary Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.976379
This article is part of the Research Topic Multiphase Flow Behavior in the Deep-Stratum and Deep-Water Wellbores View all 13 articles
MPD is one of the effective means to solve the drilling problems in deep-water and deep-stratum complex formations such as narrow pressure window. To reduce the cost, it is mostly implemented only in complex and narrow pressure window strata. However, at present, there is no scientific method to determine the MPD matching stratum interval under the “conventional + MPD” composite drilling mode. Aiming at this problem, by introducing the methods of risk quantitative evaluation and taking the principle of “avoiding risk and reducing MPD cost”, combined with the accurate ECD calculation method considering multiphase flow, this paper puts forward the accurate determination method of matching the stratum interval of MPD, which can reduce the section of MPD construction as much as possible and optimize the casing level on the premise of ensuring safety. Based on the artificial bee colony algorithm, the intelligent determination method of casing level and setting depth under the condition of pressure control is established, which can quickly and accurately obtain the maximum casing setting depth and its corresponding optimal pressure control parameters in the open-hole section. The case analysis shows that, compared with the conventional drilling mode, the “upper conventional + lower MPD” drilling method can save one layer of casing while ensuring safety. The proposed method can provide theoretical and scientific basis for the accurate calculation of MPD matching stratum interval under the “conventional + MPD” compound drilling mode and the scientific and efficient design of casing levels and setting depth under the condition of pressure control.
Managed pressure drilling (MPD) is one of the powerful methods to improve the safety and efficiency of drilling in deep water and deep strata with narrow safe density window [1, 2]. With the deepening of oil and gas exploration and development into deep water and complex strata, the number of applications of the MPD technique in the world is increasing year by year [3–5]. The feasibility and applicability of the MPD technique in deep water gas fields in the south China sea are also being studied [6, 7]. In recent years, the research on MPD technique mainly focuses on key equipment and pressure control technology, and gradually forms a variety of MPD techniques with different pressure control principles, such as double gradient and wellhead back pressure. The field practice has also changed from the objective restriction of “feasible or not” to the subjective choice of “use or not” [8–9]. Preliminary research and practice show [1014] that by virtue of its advantages of accurately regulating wellbore ECD under different drilling conditions, the MPD technique can broaden the safe density window, reduce complex downhole risks, and have the certain potential of optimizing well structure. On the other hand, due to the high cost of the MPD technique, to save cost, in the operation of the same well, the MPD technique is only applied in part of the well section. For other uncomplicated strata, the conventional drilling method is still adopted. However, the coordination mechanism between cost investment and risk avoidance of the MPD technique is not clear at present. In the field implementation process, only the stratum interval of MPD can be qualitatively evaluated based on the characteristics of the formation pressure profile and the experience of engineers and technicians. It is difficult to comprehensively consider many factors such as “cost-saving (reducing unnecessary pressure control formation interval)”, “reducing complex risks” and “optimizing well structure”, and to quantitatively determine the reasonable construction interval of MPD. At the same time, the trial calculation method is still used for casing layer and setting depth design under pressure control, and the efficiency and accuracy need to be further improved.
Given the above problems, quantitative risk evaluation methods are introduced in this paper. Under the principle of “avoiding risks and reducing pressure control costs”, a method for determining the matching strata interval of controlled pressure drilling under the “conventional + MPD” compound drilling mode is proposed, as well as an intelligent method for determining casing level and setting depth under controlled pressure conditions. It provides the scientific basis and technical support for the optimal design and safe and efficient implementation of the MPD technique in deep water and complex formations.
For a well, the upper strata tend to have a normal pressure trend and a wide safe density window that allows the conventional drilling method to be adopted. While the complex and narrow density windows are usually in the deeper strata. Therefore, to save pressure control costs, it is necessary to reduce the pressure control section as much as possible on the premise of ensuring the safety of drilling in the whole well section. So, when determining the pressure-controlled matching formation interval, is the conventional drilling method limited to the normal pressure formation. Are there some wellbore sections suitable for conventional drilling in deep complex/narrow density window formations? Do all narrow density window formations require the MPD technique? The essence of many problems is the formation adaptability of the MPD technique and its risk avoidance. It is necessary to introduce quantitative risk assessment methods to compare and analyze the potential engineering risks of conventional drilling and managed pressure drilling in different wellbore sections. In terms of “saving cost”, “reducing complex risks”, and “optimizing well structure”, MPD is preferred to match the formation interval.
Because of the strong uncertainty of deep well complex formation information and the limitations and incompleteness of the existing seismic and logging interpretation model, the author team proposed a quantitative description method of drilling geomechanical parameters under the condition of uncertain information [15–18]. According to the constraint conditions of pressure balance in the open-hole section, a safe drilling fluid density window with credibility is constructed. Combined with the well structure and construction scheme, the underground risk intensity profiles are calculated (as shown in Figure 1), which realizes the quantitative assessment of downhole engineering risk before drilling. The basic principle of this method is shown in Figure 2, the probability distribution of geological characteristic parameters is obtained through probability statistics and Monte Carlo simulation methods, and then combined with the drilling construction methods, based on the stress-strength interference theory, the quantitative risk assessment of the whole well section is realized. The specific method is in literature [15–18], which will not be described here. Since the quantitative risk assessment method is based on the formation pressure profile with credibility, well structure, and construction (drilling fluid density/ECD) scheme, it can satisfy the needs of this paper to compare and analyze the potential engineering risks of conventional drilling and MPD in different wellbore sections.
This method can select two technical routes: Horizontal stratification statistics of regional wells (HSSRW) and vertical rolling statistics of single well (VRSSW) according to the abundance of regional drilled data. Among them, HSSRW refers to the statistical analysis of rock mechanics parameters and tectonic stress coefficient distribution in the region by using the well logging data given the abundant drilling data in the region. In combination with the Monte Carlo simulation method, four pressure profiles with credibility are established. VRSSW refers to the preliminary exploration blocks with few wells or only seismic data in the region, using the normal diffusion estimation method to fully excavate the seismic data response characteristics in the depth direction (longitudinal) of the well, to construct a four pressure profiles with credibility. Either technical route is based on the existing data and interpretation model, quantitatively describing the error (uncertainty) of formation pressure prediction results in the form of probability. The formation pressure profile is no longer a single determined value but is transformed into an interval, which considers the influence of parameter uncertainty in the prediction model, as shown in Figure 3. This method can evaluate the design scheme of the wellbore structure to be drilled, predict the potential drilling risks before drilling, and then optimize the scheme based on the prediction results, and finally realize risk avoidance.
To accurately calculate the matching formation interval of MPD, the conventional drilling method is adopted in the upper normal pressure formation. And the risk assessment method in chapter 2.1 is used in the lower abnormal pressure formation. Based on the principles of risk avoidance, optimization of well structure, and reduction of pressure control cost, the potential risks and casing levels of conventional drilling and MPD in different wellbore sections are compared and analyzed. The specific process is shown in Figure 4 and described as follows:
1. According to the characteristics of the formation pressure profile, it can be divided into normal pressure region and abnormal pressure region. Generally, the upper part is the normal pressure area, assuming that the well depth at the cut-off point is H1.
2. Using chapter 2.1, the safe drilling fluid density window with credibility is established. For the upper normal pressure formation, the conventional drilling technique is used to design from top to bottom in the safe drilling fluid density window with credibility. Assume that the maximum safe setting depth of the last spud casing is H0 (H0 can be greater than, equal to, or less than H1).
3. Starting from H0, the conventional drilling technique and MPD technique are used to design casing layers and setting depth respectively, and chapter 2.1 is used to evaluate potential risks.
4. It is assumed that the maximum safe setting depth of conventional drilling is H2 (If H2 equals to the target well depth, which means that there is no risk of conventional drilling in the whole well. Otherwise, it is risky to use conventional drilling technique for H > H2 intervals). Taking H0 as the starting point, H2 as the ending point, and △H as the step length, calculate the number of casing layers Ci of the whole well when the MPD technique is used from
5. Then, the well depth Hj corresponding to Cj = min (Ci) is the peak of formation matching interval of MPD.
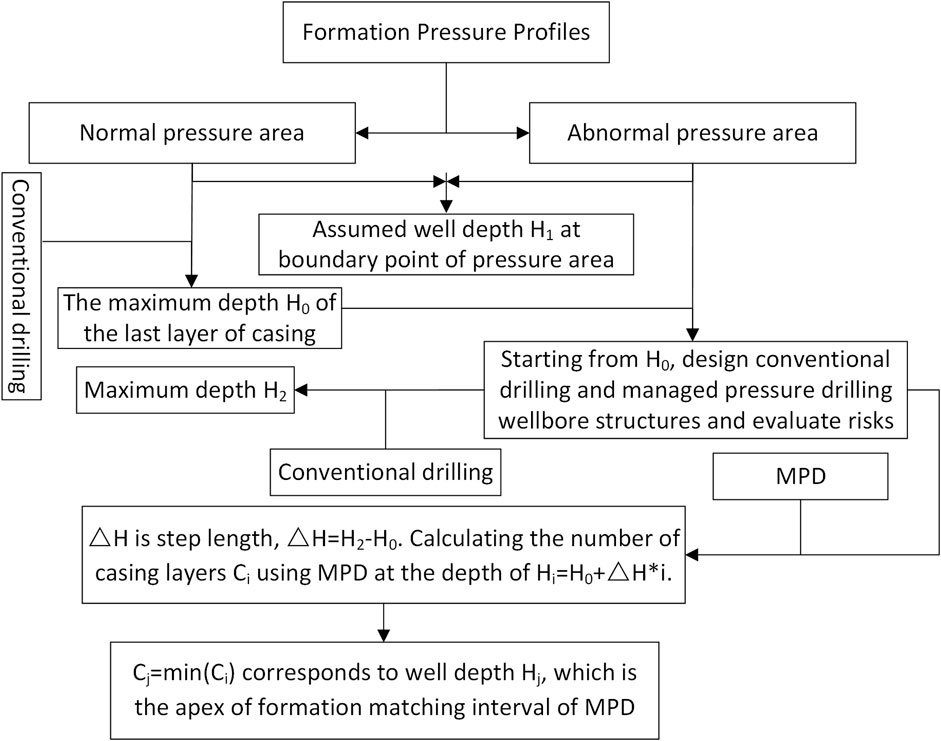
FIGURE 4. Flow chart of well structure optimization design of MPD based on artificial bee colony algorithm.
The basic principle of the casing level and setting depth design in the MPD mode mentioned in chapter 2.2 is to calculate the wellbore ECD profile by adjusting the controlled pressure parameters to match or balance the formation pressure. This is significantly different from the conventional drilling technique using the static equivalent density of drilling fluid. Aiming at the complex conditions of high temperature, high pressure and deep-water drilling, this paper adopts the accurate calculation method of wellbore ECD considering temperature pressure coupling, drill pipe eccentricity and drilling fluid fluidity [19–22]. Selecting appropriate MPD parameters for the open-hole section and obtaining the optimal wellbore ECD profile is one of the keys to the design of casing level and setting depth in MPD.
However, in current practice, it is necessary to rely on manual experience to determine “reasonable” pressure control parameters and “optimal” wellbore ECD profile, which is not only a heavy workload but also largely depends on human factors and the number of samples of different pressure control parameters calculated, lacking scientific and efficiency [11–13, 23]. In recent years, the rise of intelligent bionic algorithms such as particle swarm algorithm, genetic algorithm, annealing algorithm, ant colony algorithm, and artificial bee colony algorithm has brought opportunities for scientific and efficient solutions to optimization problems in engineering practice [24–30].
Therefore, according to the characteristics of MPD and the actual needs of well structure optimization design, it is necessary to put forward the method of optimizing pressure control parameters and wellbore ECD profile in the open-hole section based on the intelligent algorithm, and the method of determining casing layer and setting depth under pressure control conditions based on this, to improve the design efficiency and the accuracy of design results.
By analyzing the principle of pressure control and the design principle of casing layer and casing depth, the artificial bee colony algorithm can be applied to the intelligent optimization of wellbore ECD and casing setting depth under pressure control.
The basic principle of the artificial bee colony algorithm is that the solution of the problem to be solved is regarded as the nectar source, and the more abundant the honey source and the better the quality, the better the solution quality. Through a group of artificial bees randomly searching the rich source, exchanging information, and switching roles, the optimal solution is finally obtained efficiently.
The application of the artificial bee colony algorithm should satisfy the following basic conditions [13, 17, 23]: 1) The problem to be solved is a multi-parameter optimization problem; 2) the objective function should be a continuous function or approximately a continuous function; 3) the variable has a certain value range.
In the well structure design of MPD, for the open-hole section determined by formation pressure window: 1) There is an optimal value of ECD profile under controlled pressure, and the corresponding pressure control parameters are the optimal pressure control parameters; 2) if the maximum casing depth in the open-hole section is taken as the objective function, the function is a continuous function of each control pressure parameter; 3) the variables of the objective function are different pressure control parameters, such as wellhead back pressure and drilling fluid density, which all have a certain value range. It can be seen that the optimization of pressure control parameters satisfies the basic conditions of applying the artificial bee colony algorithm.
On the other hand, there are generally more than 2 pressure control parameters for MPD. There are many combinations of various pressure control parameters within the adjustable range, and the wellbore ECD profiles under different pressure control parameter combinations are also quite different, which belongs to a typical multivariable optimization problem. If we rely on manual calculation, not only the workload is heavy, but also the calculation accuracy can not be guaranteed. If we use the artificial bee colony algorithm and rely on its efficient and stable intelligent optimization mechanism, it is expected to efficiently and accurately obtain the optimal wellbore ECD and its corresponding pressure control parameters in the open-hole section under the condition of multiple pressure control parameters.
The basic calculation steps of casing setting depth and optimal pressure control parameters in the open-hole section of MPD are as follows:
1) Geological must seal point determination:
According to the geological data, determine the necessary sealing stratum.
2) Safe pressure window determination:
The safety pressure window is determined according to the prediction results of formation pore pressure, formation fracture pressure, and formation collapse pressure before drilling and the design coefficient of the regional well bore structure. The lower limit of the safe pressure window at well depth H is ρlower (H) and the upper limit is ρupper (H).
3) Determination of adjustable range of pressure control parameters:
Controlled pressure parameters have a direct influence on the ECD profile of the wellbore. The pressure control parameters Ki (i = 1,2,……) are determined according to the pressure control characteristics and actual working conditions of different pressure control drilling methods. The adjustable range of each pressure control parameter is:
(4) Wellbore ECD calculation under different pressure control conditions:
Within the adjustable range of each controlled pressure parameter involved in Step (3), the wellbore ECD calculation model was used to calculate the wellbore ECD profile under different controlled pressure conditions.
Wellbore ECD under the condition of controlled pressure parameter combination scheme j is a function of well depth H:
5) Determination of optimal pressure control parameters and casing setting depth in open-hole section:
Within the safe pressure window [ρlower(H), ρupper(H)] determined in Step (2), the maximum safe well depth of wellbore ECD profile H1, j can be expressed as:
For a certain pressure control parameter combination scheme j, the wellbore ECD profile at depth Hi in the open-hole section satisfies the following requirements:
Then, the maximum casing setting depth H1 of the open-hole section is:
Then, the maximum casing setting depth of the open-hole section is H1, and the corresponding pressure control parameter scheme is j0.
The above is the basic calculation method of casing setting depth and optimal pressure control parameters in the open-hole section of MPD. The schematic diagram of the design result is shown in Figure 5. As the pressure control parameters of MPD are often more than two (for example, the pressure control parameters of CML controlled pressure drilling mainly include: displacement, mud pump position, mud slurry level depth; the pressure control parameters of bottom hole constant pressure MPD are as follows: Drilling fluid density, wellhead back pressure). There are many combination schemes of various pressure control parameters within the adjustable range (the higher the accuracy requirements, the more calculation samples of various pressure control parameters, the number of combination schemes increases exponentially), and the wellbore ECD profile under different parameter combination schemes also varies greatly. Therefore, the conventional method requires a lot of calculation, which greatly reduces the design efficiency and cannot guarantee the optimization of design results.
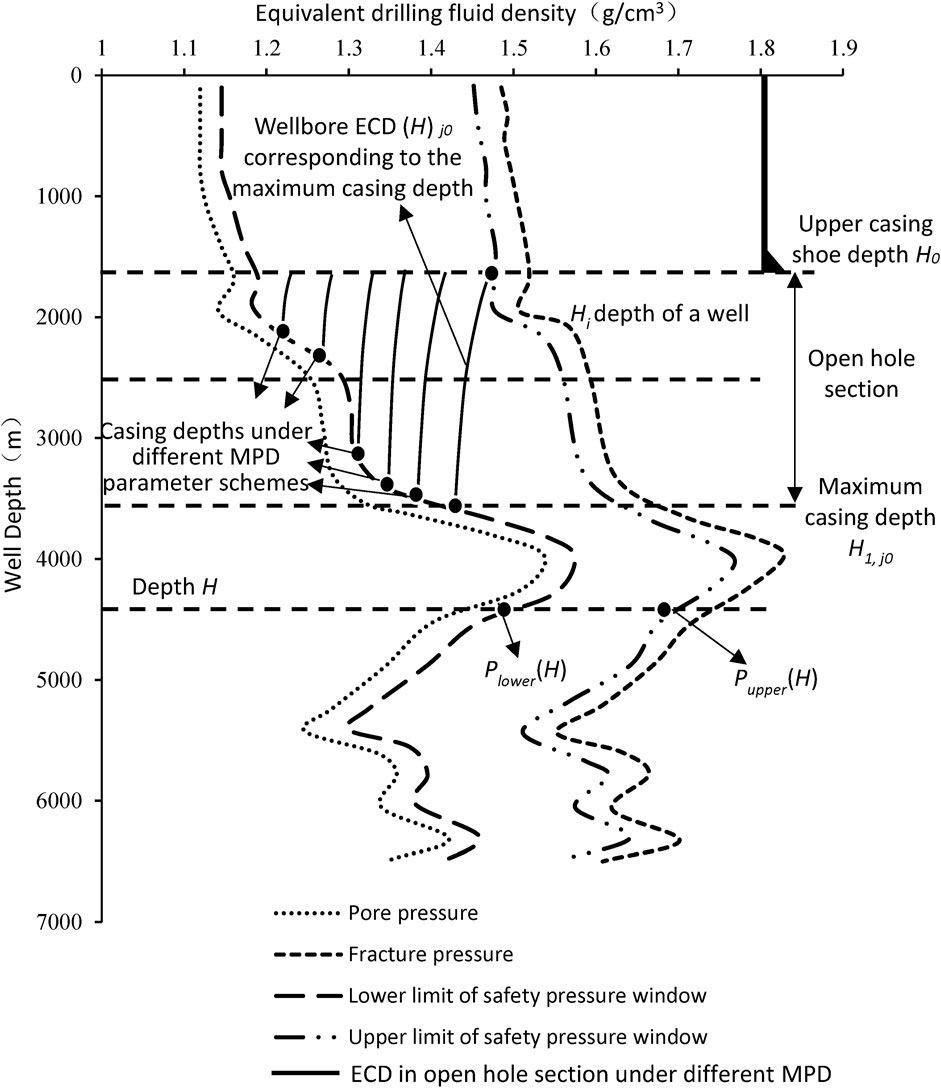
FIGURE 5. A well with reliable formation pressure profile and design results of casing layers and running depth under different drilling methods.
Since conventional calculation methods cannot satisfy the actual requirements of the optimization design of the well structure of MPD, the artificial bee colony algorithm is introduced to intelligently and efficiently optimize the casing setting depth H1 and its corresponding optimal pressure control parameters in the open-hole section under the condition of pressure control. The basic process is shown in Figure 6, and the specific steps are as follows:
1) Initialize population: total number of bees SN; the number of leading bees and following bees is the number of pressure control parameter combination schemes, generally SN/2; maximum iteration times MCN (generally 1000) and control parameter Limit (generally 20); objective function
2) Calculate and evaluate the fitness of each initial solution. Fitness function fitness is the objective function itself, that is,
3) The lead-bee uses the Eq. 4 to randomly search the neighborhood to get a new location (refer to each buzzer search to control pressure parameters combination scheme), under the principle of greedy choice, if the fitness of the new position (i.e., the maximum casing setting depth) is greater than that of the original position, the original position shall be updated with the new position; otherwise, the original position shall remain unchanged. When all lead-bees completed the neighborhood search, the probability Pi was calculated according to Eq. 5.
Where, j∈{1, 2, …, D}, k∈{1, 2, …, SN} and k≠i.
4) Follow-bees use the calculated probability Pi to select the lead-bees based on the roulette principle. After the follow-bees complete the selection of the lead-bees, Eq. 4 is used to search the neighborhood and also select the position with high fitness according to the greedy selection principle.
5) Determine whether there is a solution to be abandoned. If the result of a lead-bee does not change after the Limit iteration, it will change from the lead-bee to the scout-bee and randomly generate a new position to replace the original position according to Eq. 6.
6) Record the optimal solution of the bee colony so far.
7) If the current iteration number is greater than the maximum number MCN, the iteration ends and the algorithm ends. Otherwise, return step (2), the overall number of iterations Cycle = Cycle+1.
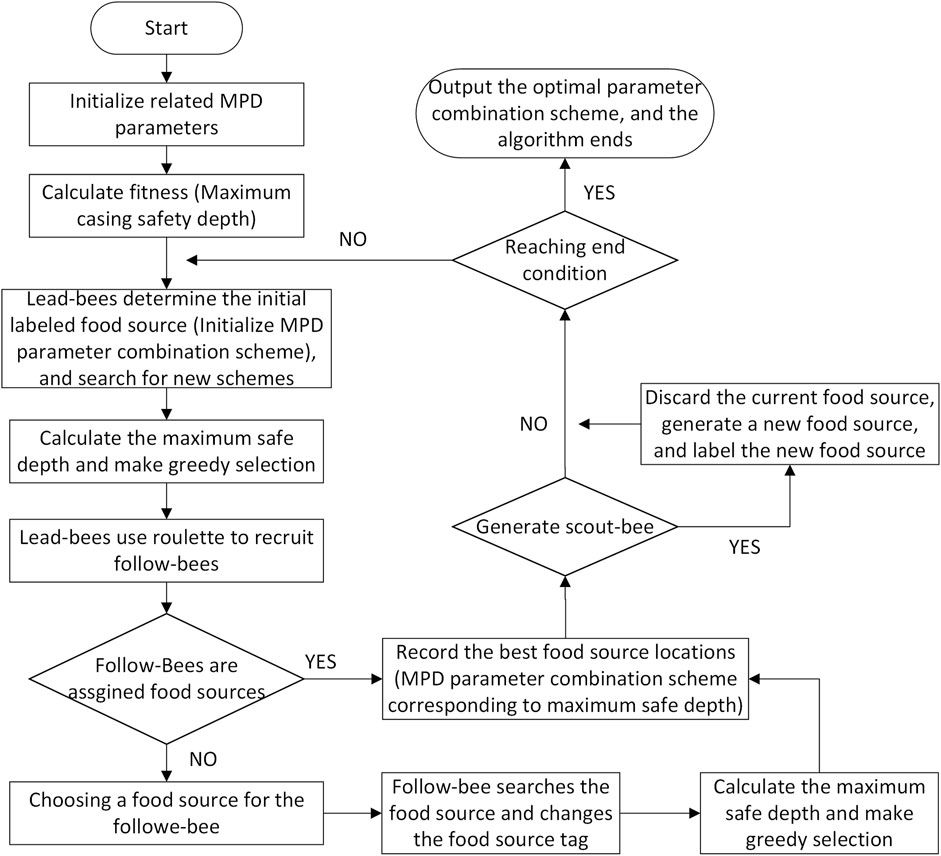
FIGURE 6. Schematic diagram of wellbore ECD distribution and determination of maximum casing depth under different pressure control parameters in open hole section.
The basic information of well A is as follows:
The target depth of the well is 6600 m, and the geological sealing points in this area are mainly 200 m loose gravel layer and 1700 m easy-loss formation. The well structure design coefficients are as follows: the suction pressure coefficient is 0.036 g/cm3; the surge pressure coefficient is 0.036 g/cm3; the fracture pressure safety factor is 0.024 g/cm3; the kick allowance is 0.06 g/cm3; the differential pressure sticking factor is 22 MPa. The formation pore pressure and fracture pressure profile with credibility established by chapter 2.1 and the upper and lower limits of the safe drilling fluid density window are shown in Figure 7. This well is planned to use conventional drilling and bottom hole constant pressure MPD. The pressure control parameters are mainly drilling fluid density and wellhead back pressure. Among them, the maximum controlled pressure value of wellhead controlled pressure equipment in well A is 5 MPa.
According to the process shown in chapter 2.2 and Figure 4, by analyzing the pressure profile of the well, the depth at the cut-off point of the normal pressure area is 3350 m. Conventional drilling was designed from top to bottom within the safe drilling fluid density window, and the maximum safe setting depth of the last casing is H0 = 3780 m. Starting from 3750 m, the conventional drilling and MPD techniques are used to design casing layers and setting depth respectively. And chapter 2.1 is used to evaluate potential risks. Among them, the conventional drilling technique can safely drill to the target well depth, and 2 casing layers are needed below H0, that is, 5 casing layers are needed in the whole well.
Under the condition of MPD (with H0 = 3780 m as the starting point, H2 = 6600 m as the endpoint, 10 m as the step length) chapter 3.3 is used to design the casing layers and depth and optimize the controlled pressure parameters. The number of casing layers Ci in the whole well is calculated from Hi=(3,780 + 10 × i)m when the MPD technique is used. The results showed that: except for C0 = 4 (that is, one layer of casing can be safely drilled to the target well depth by using MPD from H0), Ci = 5 (i ≥ 1) under other conditions, which is the same as the casing layer times under conventional drilling methods. Therefore, the well depth H0 = 3780 m corresponding to C0 = min (Ci) = 4 is the peak of the formation matching interval of MPD, and the controlled pressure interval is 3780–6600 m.
The design results of casing layers and setting depth under different drilling methods as well as the optimal pressure control parameters in controlled pressure formation intervals are shown in Table 1.
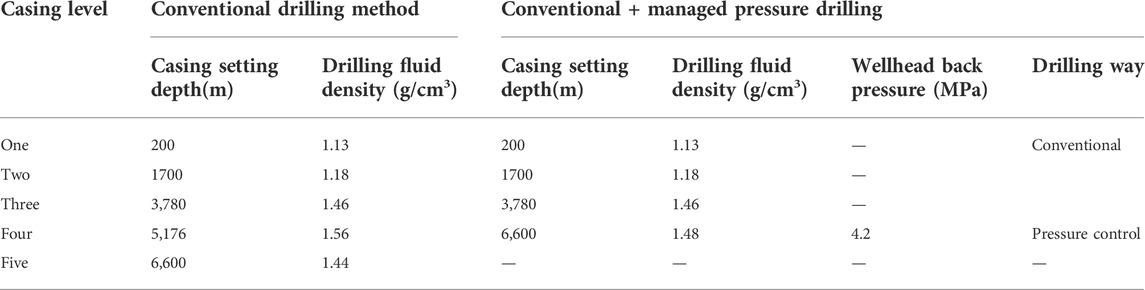
TABLE 1. A Well design results of casing level and depth under different drilling methods and optimization results of pressure control parameters.
1) By introducing the quantitative evaluation method of drilling engineering risk, and based on the principle of “avoiding risks and reducing the cost of pressure control”, a method for determining the matching formation interval for MPD under the “conventional + MPD” composite drilling method is proposed. On the premise of ensuring safety, it can reduce the well section of pressure control construction as much as possible, and optimize the casing layer, which provides a scientific basis for the accurate calculation of pressure control formation interval and the optimization design of well structure under the “conventional + MPD” composite drilling method.
2) By introducing the artificial bee colony algorithm, the intelligent determination method of casing layer and setting depth under MPD is established, which can quickly and accurately obtain the maximum casing setting depth and its corresponding optimal pressure control parameters of the open-hole section, and improve the scientificity, accuracy and efficiency of casing layer and depth under MPD.
3) The example calculation shows that if the conventional drilling method is adopted for well A, it can be safely drilled to the target layer, but the whole well needs five spuds. If the “upper conventional + lower MPD” drilling method is adopted, one layer of casing can be saved while ensuring safety. Through the analysis of the method established in this paper, the discrimination basis is provided for the selection of the MPD technique in complex formations, and theoretical support is provided for the determination of the applicable formation interval.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
All authors have contributed to the creation of this manuscript for important intellectual content and read and approved the final manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Jiang Z, Zhou Y, Wang Q. Managed pressure drilling system used in narrow density window drilling scenarios. Nat Gas Industry (2011) 31(08):76–9.
2. Krivolapov DS, Magda AV, Soroka TB, Dobrokhleb PY, Evdokimo SA, Gagloyev GG, et al. Managed pressure drilling as an advanced solution for deep hthp wells and long intervals with narrow safe pressure limits. In: SPE Annual Caspian Technical Conference; October 21–22, 2020 (2020).
3. Zein J, Irawan F, Hidayat AM, Amin RA, Norani B, Redzuan M, et al. Case study-constant bottom hole pressure of managed-pressure drilling utilization to maintain wellbore instability in east java drilling operation, Indonesia. In: SPE Asia Pacific Oil & Gas Conference and Exhibition; October 25–27, 2016; Perth, Australia (2016).
4. Siddiqi FA, Riskiawan A, Al-Yami A, Jain B, Louati I, Martanto R, et al. Successful managed pressure cementing with hydraulic simulations verification in a narrow pore-frac pressure window using managed pressure drilling in Saudi Arabia. In: SPE Annual Technical Conference and Exhibition; September 26–28, 2016; Dubai, UAE (2016).
5. Kazakbayeva Z, Kaidarov A, Magda A, Aliyev F, Patil H, Cook I, et al. Successful implementation of managed pressure drilling and managed pressure cementing techniques in fractured carbonate formation prone to total lost circulation in far north region. In: SPE Eastern Europe Subsurface Conference; November 23–24, 2021; Kyiv, Ukraine (2021).
6. Wang J, Li J, Liu G, Huang T, Yang H. Parameters optimization in deepwater dual-gradient drilling based on downhole separation. Pet Exploration Develop (2019) 46(4):819–25. doi:10.1016/s1876-3804(19)60240-5
7. Yan L, Wu H, Yan Y. Application of precise MPD in kick & loss well. Nat Gas Industry (2015) 35(2):59–63. doi:10.3787/j.issn.1000-0976.2015.02.009
8. Wang G. MPD wellbore pressure control method based on linear throttle Valve. Oil Drilling Prod Tech (2021) 43(2):197–202.
9. Huang Y, Yang J, Shi S. Application of MPD technology in offshore ultra-HTHP wells. Oil Drilling Prod Tech (2018) 40(6):699–705.
10. Mashaal MA, Fuller T, Brown CJ, Paterson R. Managed pressure drilling, casing and cementing enables success in conventionally undrillable wells in the harding field. In: SPE Annual Technical Conference and Exhibition; September 30–October 2, 2013; New Orleans, Louisiana, USA (2013).
11. Wang G, Liu J, Ding C, Fan H. Casing program optimization with the managed pressure drilling technique. Acta Petrolei Sinica (2013) 34(03):545–9. doi:10.7623/syxb201303019
12. Nguyen TC, de Oliveira R, Al-Safran E, Saasen A. Casing-design optimization with CAML technique and drilling-fluid performance. SPE Drilling & Completion (2017) 32(03):208–12. doi:10.2118/185951-pa
13. Xu Y. Design method of controlled pressure drilling body structure. East China: China University of Petroleum (2012).
14. Yan L, Wu H, Yan Y. Application of fine managed pressure drilling technique in complex wells with both blowout and lost circulation risks. Nat Gas Industry B (2015) 2(2-3):192–7. doi:10.1016/j.ngib.2015.07.010
15. Ke K, Guan Z, Zhou X. An approach to determining pre-drilling formation pore pressure with credibility for deep water exploration wells. J China Univ Pet (Edition Nat Sciences) (2009) 33(5):61–7.
16. Sheng YN, Guan ZC, Xu YQ. Quantitative description method for uncertainty of formation pore pressure. Arab J Sci Eng (2018) 43(5):2605–13. doi:10.1007/s13369-017-2863-x
17. Guan Z, Ke K, Lu B. An approach to casing program design with formation pressure uncertainties. J China Univ Pet (Edition Nat Sciences) (2009) 33(4):71–5.
18. Han C, Guan Z, Xu C, Lai F, Li P. Study on method of determining the safe operation window of drilling fluid density with credibility in deep igneous rock strata. Math Probl Eng (2021) 2021:11. doi:10.1155/2021/5514427
19. Ataga E, Ogbonna J. Accurate estimation of equivalent circulating density during high pressure high temperature (HPHT) drilling operations. In: Nigeria Annual International Conference and Exhibition; August 6–8, 2012; Lagos, Nigeria (2012).
20. Ashena R, Bahreini H, Ghalambor A, Sahraei E, Darab MAL. Investigation of parameters controlling equivalent circulating density ECD in managed pressure drilling MPD. In: SPE International Conference and Exhibition on Formation Damage Control; February 23–24, 2022; Lafayette, Louisiana, USA (2022).
21. Dokhani V, Ma Y, Yu M. Determination of equivalent circulating density of drilling fluids in deepwater drilling. J Nat Gas Sci Eng (2016) 34:1096–105. doi:10.1016/j.jngse.2016.08.009
22. Zhang B, Lu N, Guo Y, Wang Q, Cai M, Lou E. Modeling and analysis of sustained annular pressure and gas accumulation caused by tubing integrity failure in the production process of deep natural gas wells. J Energ Resour Tech (2022) 144(6). doi:10.1115/1.4051944
23. Yin Z, Chen G, Xu L, Jiang S. Optimization of casing program of deepwater well by dual-gradient drilling. Nat Gas Industry (2006) 26(12):112–4.
24. Liang H, Zou J, Zuo K, Khan MJ. An improved genetic algorithm optimization fuzzy controller applied to the wellhead back pressure control system. Mech Syst Signal Process (2020) 142:106708. doi:10.1016/j.ymssp.2020.106708
25. Jia D, Liu H, Zhang J, Gong B, Pei X, Wang Q, et al. Data-driven optimization for fine water injection in a mature oil field. Pet Exploration Develop (2020) 47(03):674–82. doi:10.1016/s1876-3804(20)60084-2
26. Karaboga D, Akay B. A comparative study of Artificial Bee Colony algorithm. Appl Math Comput (2009) 214(1):108–32. doi:10.1016/j.amc.2009.03.090
27. Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J Glob Optim (2007) 39(3):459–71. doi:10.1007/s10898-007-9149-x
28. Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm. Appl soft Comput (2008) 8(1):687–97. doi:10.1016/j.asoc.2007.05.007
29. Irani R, Nasimi R. Application of artificial bee colony-based neural network in bottom hole pressure prediction in underbalanced drilling. J Pet Sci Eng (2011) 78(1):6–12. doi:10.1016/j.petrol.2011.05.006
30. Liao Q, Zhang D. Probabilistic collocation method for strongly nonlinear problems: 3. Transform by time. Water Resour Res (2016) 52(3):2366–75. doi:10.1002/2015wr017724
Ki is the control pressure parameter is each controlled pressure parameter under a combined scheme
KL is the lower limit of pressure control parameters
KH is the upper limit of controlled pressure parameters
ECD (H) j is the wellbore ECD under the condition of the jth combination scheme of control pressure parameters is the wellbore ECD under the condition of the jth combination of controlled pressure parameters, which is the function of well depth H
j is the order number of the combined scheme of control pressure parameters, j = 1,2,…
Ki is the control pressure parameter is each controlled pressure parameter under a combined scheme
D is the dimension of the problem
Xmaxj and Xminj represent the upper and lower top bounds of the jth dimension parameters respectively
ECD (H) j is the wellbore ECD under the condition of the jth combination scheme of control pressure parameters is the wellbore ECD under the condition of the jth combination of controlled pressure parameters, which is the function of well depth H
j0 is the order number of the pressure control parameter scheme corresponding to the maximum casing setting depth
Xij refers to the jth dimension parameter of the ith individual bee, that is, the jth parameter value of the ith combination scheme of the pressure control parameter
Xkj refers to the jth dimension parameter of the kth individual bee, that is, the jth parameter value of the kth combination scheme of the pressure control parameters
Vij is a new position generated near Xij
φij is the random number between [−1,1]
fitnessi is the fitness value of the ith solution
Pi is the probability of follow-bees choosing lead-bees
ρd is static drilling fluid density, g/cm3
Pwellhead is the wellhead back pressure, MPa
Keywords: managed pressure drilling, risk aversion, formation matching interval, artificial bee colony algorithm, optimization of pressure control parameters
Citation: Xu Y, Han C, Sun J, He B, Guan Z and Zhao Y (2022) Formation interval determination method of MPD based on risk aversion and casing level optimization. Front. Phys. 10:976379. doi: 10.3389/fphy.2022.976379
Received: 23 June 2022; Accepted: 18 July 2022;
Published: 19 August 2022.
Edited by:
Weiqi Fu, China University of Mining and Technology, ChinaReviewed by:
Die Hu, University of Calgary, CanadaCopyright © 2022 Xu, Han, Sun, He, Guan and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chao Han, hansuper713@hotmail.com
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.