Abstract
Following improvements in devices used in biomedical engineering, cancer treatments, and thermal extrusion systems, this report explores the dynamics of Ree-Eyring nanofluid when subject to free convection, bioconvection, heat source, and thermal radiation over a convection-heated Riga plate. Bioconvection is assessed in light of the movement of the motile microorganisms that stabilize the dispersion of nanoparticles in the fluid. The impact of thermophoresis and Brownian motion, critical in the flow of heat and mass is also considered, together with the convective boundary condition. In many manufacturing sectors, non-Newtonian nanofluid flow is a crucial cooling component. Based on these factors, partial differential equations—the governing equations that model the transportation phenomena—are converted into nonlinear ordinary differential equations using the relevant relations. Finally, the nonlinear differential equations are solved using the homotopy analysis method (HAM), and the solutions are displayed in graphs representing distinct fluid flow parameters. It is conclusively found that the skin friction coefficient increases as the mixed convection parameter value rises, while the opposite effect is seen as the bioconvection Rayleigh number grows.
Introduction
The term “nano liquid” was coined by Choi [1] and refers to the suspension of nanoparticles in standard fluid-like ethylene glycol, oil, and water. Nanomaterials have various consequences for heat transfer, such as in hybrid energy engines, microprocessors, energy engines, and in temperature diminution. Buongiorno [2] introduced two new features to the mathematical formulation, namely Brownian motion and thermophoretic force. Then Islam et al. [3], deliberated on the MHD flow of micropolar nanofluids using a thermal mechanism between two surfaces. Alempour et al. [4] described an elliptical cross-section of spinning wall tubes to explain the behavior of a nano liquid. Entropy analysis of the Darcy-Forchheimer flow of a nanoliquid past the nonlinear sheet was conducted by Rasool et al. [5]. Numerical investigation of the slip effect of Ree-Eyring nanofluid under peristaltic flow over a curved surface was conducted by Tanvir and Malik [6]. The heat transfer enhancement accompanying nano liquid flow was scrutinized by Wang et al. [7]. Many researchers have described nano liquid flow in terms of thermal conductivity and heat transfer [8–12]. The Hall effect and impact of a chemical reaction on the physical properties of a hybrid nanofluid were discussed by Mkhatshwaet et al. [13]. Tlili et al. [14] explained the 3-D flow of Eyring-Powell nano liquid in the Darcy-Forchheimer [15] over a porous medium. The effect of Lorentz force on Ree-Eyring nanoliquid past a paraboloid surface was studied by Khan and co-workers [7]. Khan et al. [16] explored the thermal slip in the magnetized axi-symmetric flow of Oldroyd-B fluid configured by infinite stretchable disks.
Non-Newtonian flows are more efficient, due to their practical application in industrial, physiological, and technological processes. The properties of all non-Newtonian fluids are diverse, and the behaviors of all types of such fluids are depicted by a single relation. Hence different flows are given the significance of non-Newtonian liquids. Ree-Eyring fluids elucidate such behaviors with more advantages than other fluids. While the power-law model is the prominent flow model, demonstrating the shear-thinning as well as the thickening behaviors of fluids, the Ree-Eyring liquid flow is more effective in that it can be decreased to a Newtonian fluid flow [17–20]. Shao et al. [21] thus represented the thermal analysis of hydrodynamic lubrication on the Ree-Eyring fluid model, while Hayat et al. [22] scrutinized the influence of Ree-Erying flow on peristaltic transport past a rotating disk, and Ijaz et al. [23] explored the MHD flow of Ree-Eyring peristaltic propulsion. Hayat et al. [24] explained the homogenous-heterogeneous influence on the peristaltic MHD flow of Ree-Eyring fluid under chemical reactions, while the influence of a chemical reaction through Dacy-Forchheimer flow on Ree-Eyring fluid over an inclined surface was assessed by Rao et al. [25]. Some of the latest literature related to non-Newtonian models is given in References [20, 26–31].
Bioconvection is the phenomenon that occurs when up-swimming microorganisms form a smaller area denser than water. The higher portion of the surface is suspended and becomes denser due to the collection of the microorganisms. The behavior of the microorganisms in the dispersion of nanoparticles explains their remarkable applications in microsystems, biodiesel fuels, biosensors, biotechnology, and microsystems. The work of bioconvection was initiated by Wager [32] and Platt [33]. Self-thrusting microorganisms are denser than cell fluids and are inherently destabilizing, either inducing or enhancing bioconvection. The Gyrotactic microorganism has the strength of viscosity and the gravitational capacity of bottom-heavy microorganisms to move away from the vertical. The premier contribution related to bio-convention with nanoparticles under motile microorganisms is an investigation by Kuznetsov [34]. Uddin and co-workers [35] inspected the mixed convection flow of thermal slip nano liquid with microorganisms over a permeable medium. The flow of Sisko nanoparticles under microorganisms with mixed convection was then examined by Farooq et al. [36]. Exploration of the unsteady flow of nanoparticles, along with microorganisms in conjunction with nanoparticles, was carried out by Waqas et al. [37]. A study of the bioconvection flow of nanoparticles around a cone was conducted by Khan et al. [38]. The significance of Stefan flow on the bioconvection flow of nanofluids was studied by [39, 40], while the effect of viscous dissipation with the thermal radiative bioconvection flow of Casson nanofluids past a suction/injection is discussed by Kiari et al. [41]. The influence of oxytactic microorganisms in a porous medium is presented by Shaw et al [42].
The ever-increasing population expansion and the industrial revolution of the twenty-first century have led to a growing energy demand in the modern world, which is a source of concern. Traditional energy sources are to be largely replaced with clean and sustainable renewable sources, such as solar, wind, hydropower, and biogas, to meet current and future global energy needs without causing harmful environmental impacts such as pollution. Because of its affordability, its non-conventional character, and environmental friendliness, solar energy is the most pleasing renewable energy source (non-polluting). Solar energy can be transformed into heat, water, and electricity when it is acquired from nature in the form of solar radiation. Because the size of nanoparticles is less than the de Broglie wavelength, they allow deep absorption in the base fluid by scattering incident solar light. By adjusting nanoparticle size and shape to the needs of a given application, absorption efficiency can be improved. As a result, nanoparticles improve a fluid’s radiative characteristics, increasing the heat transfer rate and direct absorption efficiency of solar collectors (which may be employed in commercial and household water heating applications). Furthermore, the nanofluid’s solar energy absorption capability is aided by nonlinear thermal radiation. As a result, using nanofluids and including nonlinear thermal radiation increases solar energy absorption, while also increasing heat transfer rates. Furthermore, entropy reduction increases the heat transfer rate, resulting in heat transfer intensification. Combining these processes results in an increase in heat transfer rate from the sheet, and hence significantly more cooling, thereby meeting the various requirements of today’s industrial world, where the quality/properties of the end products are highly dependent on the rate of cooling used in the manufacturing process (for example, the drawing of continuous filaments through quiescent fluids, the annealing and tinning of copper wires, etc.).
While the aforementioned literature review reveals numerous articles in the area of bioconvection, bioconvection using Ree-Eyring nanofluid is rarely researched. This gap led to the present thorough analysis of the way gyrotactic microorganisms affect the flow of Ree-Eyring fluid across a Riga plate, as well as how the heat convective condition of the surface is controlled. On surfaces like stretching plates, Riga plates, and surfaces with variable thickness, nanofluids have better wetting, dispersion, and separation capabilities. The addition of the right nanoparticles to the working fluid has a significant impact on improving the thermal conductivity of the base working fluid. Such studies are important for medical, aerospace, microelectronic, and cancer thermal treatment applications. The current study concentrates on the thermal properties of Ree-Eyring nanofluid based on a mathematical model created using partial differential equations stemming from these applications. These equations are converted to ordinary differential equations by performing the proper similarity transformations, and the resulting system of equations is then solved using HAM.
Flow analysis
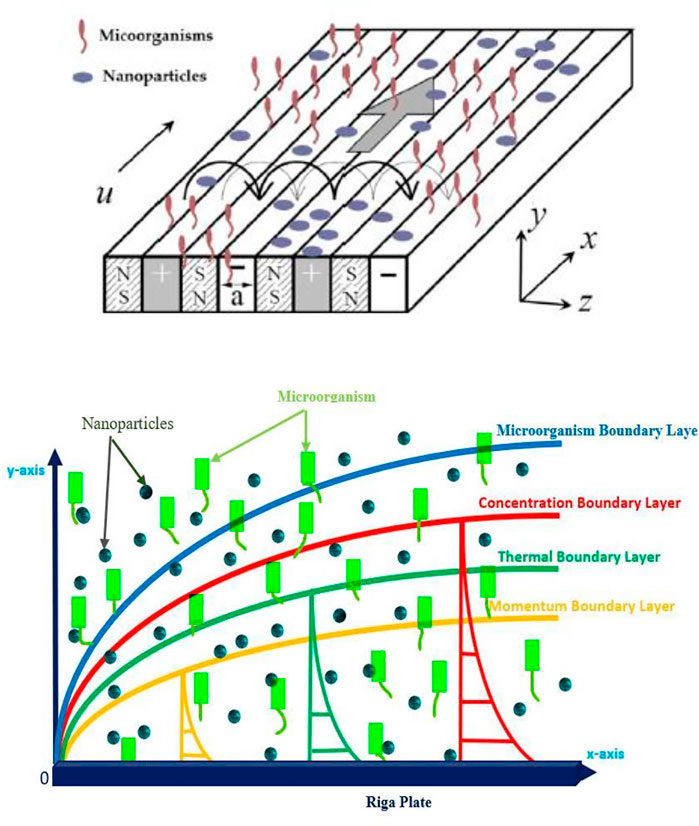
A steady 2-D incompressible mixed convective Ree-Eyring liquid flow along a Riga plate is considered. The flow pattern is depicted in Figure 1. The significance of the heat transportation is explored using the heat generation/absorption and convective boundary condition. The flow produced considers surface heat, wall concentration, and wall motile density as respectively, with respective ambient temperature , ambient concentration , and ambient microorganisms .The stress tensor for the Ree-Eyring nanofluid model is defined aswhere A. The governing equations assume the following form when these assumptions and the boundary layer approximation are included in the mathematical model:
FIGURE 1
When a non-destructive layer is on a Riga plate, the dynamics of such a layer are affected, due to its movement at a specified stretching rate. Since the wall is convectively heated, the suitable boundary conditions are
If one introduces the following transformations,
Eqs 2–5, under transformation (7), take the following form:
The subject to the boundary condition is as follows:
The non-dimensional variables:
, , , and are given by
Shear stress, heat, mass, and motile density microorganism are given by and are changed as follows:
Solution methodology
Numerous numerical methods are appropriate for addressing nonlinearity difficulties. However, the most effective semi-analytical strategy for making use of these very nonlinear equations is the HAM technique. Liao [43, 44] designed the HAM technique and later changed the auxiliary parameter to have a non-zero value. The approximation rate of this solution is calculated using these variables. Additionally, the user may choose the initial premises of the solution.
By applying this function, we can write , , and in the subsequent forms:where , and are the magnitude. The linear operators, including initial guesses, are
The above auxiliary linear operators and initial guesses arewhere are coefficient constants.
The non-zero auxiliary parameters , , and are
Considering the Taylor series expansion, one has
We ensure that , ,and are chosen correctly, such that Eq. 25 converges at . Then we have
The general solutions can be explained aswhere , , and are the special solutions.
Convergence of homotopy solution
The study of auxiliary variables , , and depends on adjusting and controlling convergence. The acceptable range of convergence values are used to draw the h-graphs. Figures 2A–D show that the appropriate values of , , and are Table 1 evaluates the convergence of the series solution when ,
FIGURE 2
TABLE 1
| Order of m | ||||
|---|---|---|---|---|
| 1 | 0.431973 | 0.241666 | 1.219230 | 0.885050 |
| 5 | 0.433558 | 0.248552 | 1.400270 | 0.919057 |
| 10 | 0.434237 | 0.248180 | 1.400350 | 0.948990 |
| 15 | 0.434296 | 0.248154 | 1.400160 | 0.944370 |
| 20 | 0.434257 | 0.248152 | 1.400173 | 0.944358 |
| 25 | 0.434250 | 0.248154 | 1.400172 | 0.944355 |
| 30 | 0.434250 | 0.248154 | 1.400172 | 0.944355 |
| 35 | 0.434250 | 0.248154 | 1.400172 | 0.944355 |
| 40 | 0.434250 | 0.248154 | 1.400172 | 0.944355 |
Convergence table for HAM.
Result and discussion
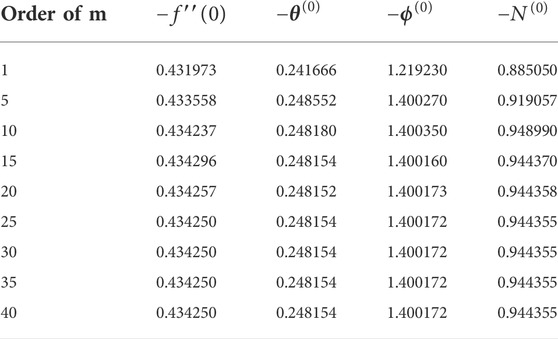
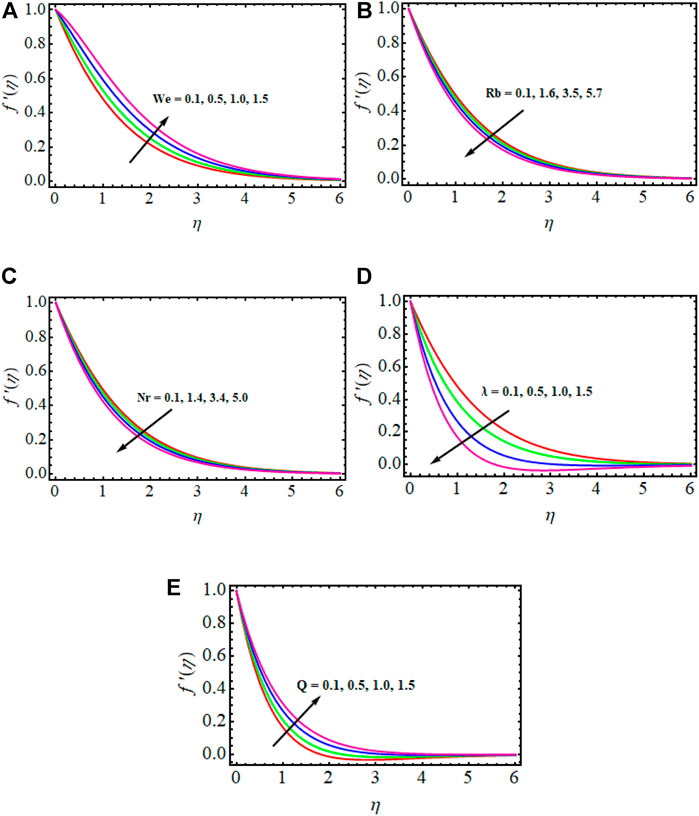
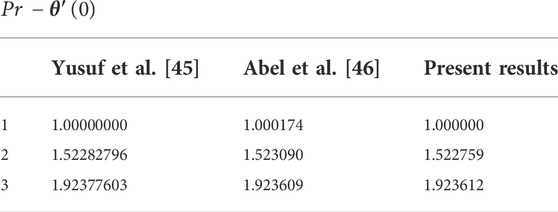
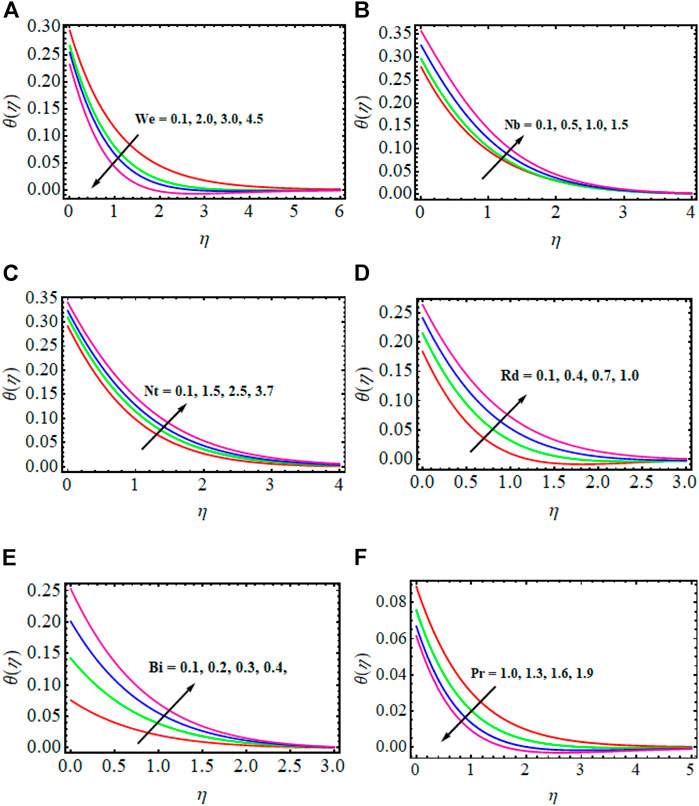
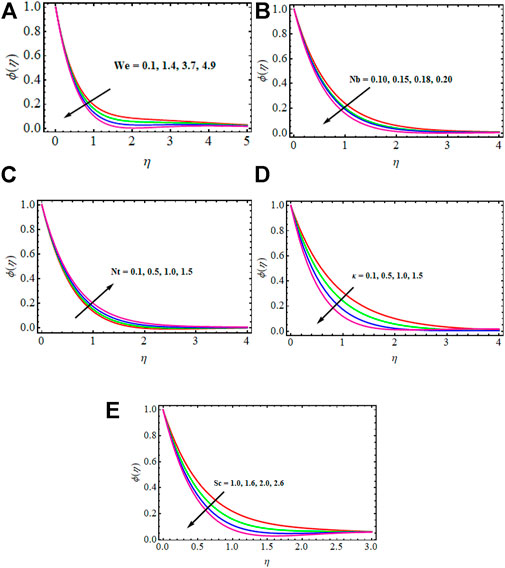
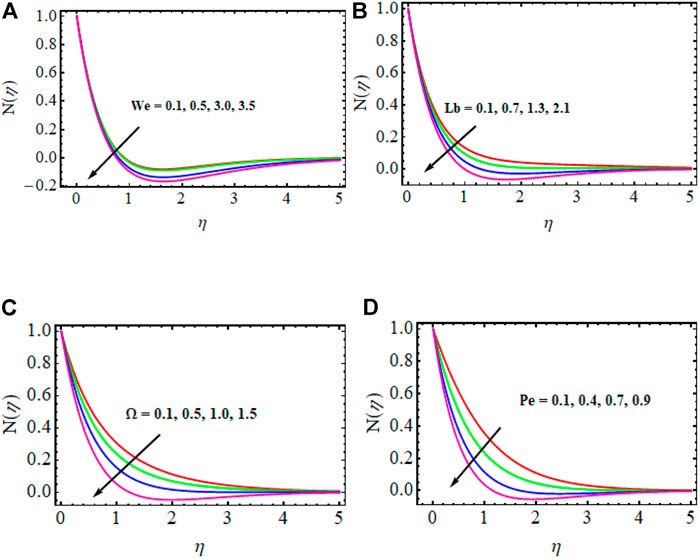
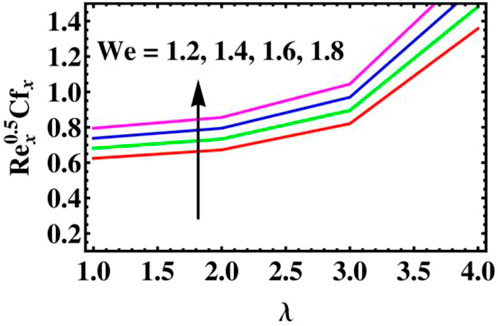
The significance of numerous physical variables is elucidated in Figures 3–11. These physical parameters are sketched for velocity, temperature, concentration, and microorganism profiles for several magnitudes of variables. Table 2 compares present findings with past outcomes under certain conditions. We noted a good agreement.
FIGURE 3
TABLE 2
| Yusuf et al. [45] | Abel et al. [46] | Present results | |
|---|---|---|---|
| 1 | 1.00000000 | 1.000174 | 1.000000 |
| 2 | 1.52282796 | 1.523090 | 1.522759 |
| 3 | 1.92377603 | 1.923609 | 1.923612 |
Comparison of current findings with earlier results for under special cases.
Figures 3A–E show the impact of the parameters ,and on the velocity field . Enhancement in We results and momentum layer thickness is also enhanced. Physically, a greater velocity minimizes the viscous force, due to this velocity shows increment. Figure 3B shows there is no development when exceeding the value of the bioconvection Rayleigh number. Figure 3C exhibits the impact of the buoyancy ratio parameter , leading to reduction in the velocity profile. The varied effect of the mixed convection variable on the velocity profile is shown in Figure 3D. From the figure, it is clear that the augmented magnitude of depreciates the velocity profile. Physically, an uplift in obtains a higher thermal bounce force, due to the increment in the velocity of the fluid. The impact of the modified Hartman number on velocity distribution is illustrated in Figure 3E. Velocity distribution displays behavior of increased magnitude. With additional momentum, boundary layer thickness is also enhanced.
The performance of the thermal layer against the values of the variables is shown in Figures 4A–F. From Figure 4B, it can be observed that temperature profiles increase the function of The temperature profile improves when the Brownian motion is increased, as shown in Figure 4B. The value of grows as the thermal layer and boundary layer thickness increases. As the value of rises, the intensity of this hectic movement increases, increasing the kinetic energy of the nanoparticles and therefore improving the temperature field. Figure 4C reveals that when the thermophoresis parameter increases, the concentration field and solutal boundary layer thickness accelerate. For greater levels, both the temperature and the thickness of the thermal boundary layer display distinct behaviors. Thermophoresis is a process by which heated particles are drawn away from a hot surface into a cool area. C thermal radiation is shown in Figure 4D. The raising values of uplifts the thermal layer. The escalated value of obtains inside heat that is the reason for the acceleration. The estimation of the effect on is revealed in Figure 4E. An increment in the value of causes enhancement of the thermal layer and boundary layer thickness. The Biot is described as the proportion of conductive resistance inside the surface over the conductive resistance outside the surface. The impact of the Prandtl number on the temperature profile is shown in Figure 4F. The temperature profile and the thickness of the thermal boundary layer are both reduced as the Prandtl number is increased. Thermal diffusivity reduces when the Prandtl number rises, resulting in a drop in temperature profile.
FIGURE 4
A view of the impact of against the fluctuation of and is given in Figures 5A–E. The concentration profile decays with larger values, as shown in Figure 5A. For modest levels of the Brownian motion parameter, the leading behavior of the concentration profile is shown in Figure 5B. The collision of the fluid particles increases, and the concentration profile falls when the Brownian motion parameter is increased. Figure 5C illustrates the effect of the thermophoresis parameter on the concentration field. It is discovered that when the thermophoresis parameter increases, the concentration field and solutal boundary layer thickness accelerate. For larger levels, both the temperature and the thickness of the thermal boundary layer have distinct behaviors. Thermophoresis is a process by which heated particles are drawn away from a hot surface and into a cool area. The impact of and on has been plotted in Figures 5D,E. Increasing value of and reduces the concentration profile . A large value for the parameter reduces the mass transfer rate due to this concentration profile reduction. It is clear from the figure that the magnitude of affects the proportion of thermal diffusivity vis-a-vis mass diffusivity.
FIGURE 5
Figures 6A–D are plotted to display and against the microorganism density profiles. The larger microorganism density profile reductions can be seen in Figure 6A. From Figure 6B, we notice the impact of on microorganism density profile . The Peclet number has dominant influence when examining the swimming strength of microorganisms in the diffusion of microorganisms. Diffusion is the phenomenon that accelerates movement from a larger concentration to a lower concentration. It is noticed that diffusion of microorganism density reduces in face of the mounting value of Increased depreciation in the motile density can be seen in Figure 6B. Figure 6C elucidates the consequences of the Bioconvection Schmidt number on the motile microorganisms . From Figure 6D, it can be seen that an augmentation in causes a depreciation in the diffusivity of microorganisms due to this reduction in the motile microorganism profile.
FIGURE 6
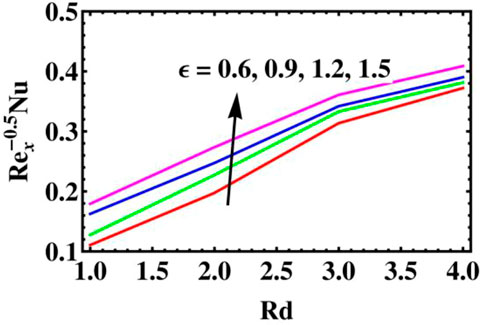
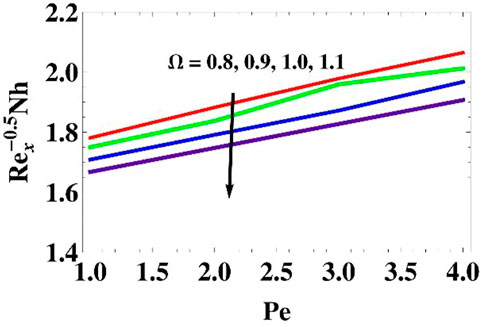
Figures 7–10 exhibit variations of and on . From Figure 7it is noted that larger values of We and are maximized in . Figure 8 studies the influence of on against The larger values of and reduce the Nusselt number. Figure 9 gives the impact of and on . It is observed that the rate of mass transport is enhanced by increasing the value of and Sc. The impact of and on can be viewed in Figure 10, where it is seen that the surges for the given value of and .
FIGURE 7
FIGURE 8
FIGURE 9
FIGURE 10
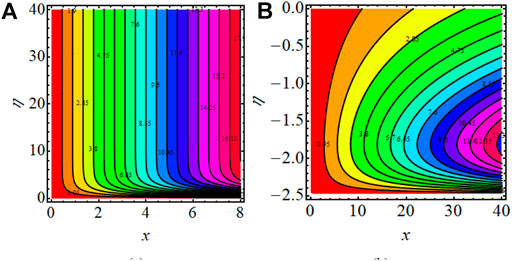
The streamlines are tangent curves to the local instantaneous velocity field. The formation of an inner mixing bolus within a fluid surrounded by streamlines is referred to as trapping. Finally, Figures 11A,B present the streamlines and isotherm pattern. It is noted that the lines increase when The streamlined patterns are simple curves and close to the surface. Figure 11B shows that isotherm line for a value of .
FIGURE 11
Conclusion
This study explored the dynamics of Ree-Eyring nanofluid subject to free convection, bioconvection, heat source, and thermal radiation over a convectively heated Riga plate, with emphasis on the attributes of heat and mass transfer. The interesting significance of thermal radiative and chemical reactions are also studied in terms of temperature and concentration profiles. The homotopy analysis method (HAM) is used to obtain the series solution of the transport phenomenon.
➢ Fluid velocity accelerates when elevating the values of the Weissenberg number, and it deteriorates when strengthening the mixed convection parameter.
➢ Fluid temperature surges upward when enhancing the radiation parameter and Biot number, while the opposite impact is found for higher Brownian moment and the thermophoretic parameters.
➢ Brownian moment and the thermophoretic parameters lead to decrepitude in the nanoparticle concentration
➢ The motile microorganisms fall downwards when the Weissenberg number and Peclet number rise.
➢ The skin friction coefficient improves when enhancing the values of mixed convection parameters, and the opposite occurs when increasing the bioconvection Rayleigh number.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R59), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
Weissenberg number, Dimensionless
Mixed convection parameter, Dimensionless
Brownian motion parameter, Dimensionless
Thermophoresis parameter, Dimensionless
Buoncy ratio parameter, Dimensionless
Prandtl number, Dimensionless
Radiation parameter, Dimensionless
Bioconvection Rayleigh number, Dimensionless
Schmidt number, Dimensionless
Bioconvection Schmidt number, Dimensionless
Bioconvection Peclet number, Dimensionless
Chemical reaction parameter, Dimensionless
Heat source/sink parameter, Dimensionless
Skin friction coefficient, Dimensionless
Nusselt number, Dimensionless
Sherwood number, Dimensionless
Microorganism density number, Dimensionless
Dimensionless velocity profile, Dimensionless
Dimensionless temperature profile, Dimensionless
Dimensionless concentration profile, Dimensionless
Dimensionless microorganism profile, Dimensionless
Microorganism concentration difference parameter, Dimensionless
Similarity variable, Dimensionless
Components of velocity along direction
Ratio of the effective heat capacity, Dimensionless
Kinematic viscosity,
Stretching rate,
Density,
Density of nanofluid,
Density of nanoparticles,
Density of microorganism’s particles,
Specific heat,
Brownian diffusion coefficient,
Thermophoretic diffusion coefficient,
Microorganism’s diffusion coefficient,
Concentration,
Ambient concentration,
Surface concentration of nanoparticles,
Thermal conductivity,
Temperature,
Ambient temperature,
Surface heat,
Coefficient of heat transfer W,
Microorganism’s profile, Dimensionless
Surface concentration of microorganisms,
Ambient concentration of microorganisms,
Maximum cell swimming speed,
Cartesian coordinates,
Velocity of the sheet,
References
1.
ChoiSUSEastmanJA, Enhancing thermal conductivity of fluids with nanoparticles. In: 1995 International mechanical engineering congress and exhibition; San Francisco, CA, 12-17 November 1995; ASME Publications-Fed (1995). p. 99–106.
2.
BuongiornJ. Convective transport in nanofluids. J Heat Transfer (2006) 28:240–50. 10.1115/1.2150834
3.
IslamSKhanADeebaniWBonyahEAlreshidiNAShahZ. Influences of Hall current and radiation on MHD micropolar non-Newtonian hybrid nanofluid flow between two surfaces. AIP Adv (2020) 10(5):055015. 10.1063/1.5145298)
4.
AlempourSMAraniAAANajafizadehMM. Numerical investigation of nanofluid flow characteristics and heat transfer inside a twisted tube with elliptic cross section. J Therm Anal Calorim (2020) 140:1237–57. 10.1007/s10973-020-09337-z
5.
RasoolGShafiqAKhanIBaleanuDNisarKSShahzadiG. Entropy generation and consequences of MHD in Darcy-Forchheimer nanofluid flow bounded by non-linearly stretching surface. Symmetry (2020) 12(4):652. 10.3390/sym12040652
6.
TanveerAMalikMY. Slip and porosity effects on peristalsis of MHD Ree-Eyring nanofluid in curved geometry. Ain Shams Eng J (2021) 12(1):955–68. 10.1016/j.asej.2020.04.008
7.
IjazKhanMKadrySChuYMKhanWAKumarA. Exploration of Lorentz force on a paraboloid stretched surface in flow of Ree-Eyring nanomaterial. J Mater Res Technol (2020) 9(5):10265–75. 10.1016/j.jmrt.2020.07.017
8.
NadeemSKhanMNAbbasN. Transportation of slip effects on nanomaterial micropolar fluid flow over exponentially stretching. Alexandria Eng J (2020) 59:3443–50. 10.1016/j.aej.2020.05.024
9.
WaqasHImranMKhanSUShehzadSAMerajMA. Slip flow of maxwell viscoelasticity-based micropolar nanoparticles with porous medium: A numerical study. Appl Math Mech (2019) 40(9):1255–68. 10.1007/s10483-019-2518-9
10.
NadeemSAbbasNMalikMY. Heat transport in CNTs based nanomaterial flow of non-Newtonian fluid having electro magnetize plate. Alexandria Eng J (2020) 59:3431–42. 10.1016/j.aej.2020.05.022
11.
HayatTYaqoobRQayyumSAlsaediA. Entropy generation optimization in nanofluid flow by variable thicked sheet. Physica A: Stat Mech its Appl (2020) 551:124022. 10.1016/j.physa.2019.124022
12.
AlicF. Entransy dissipation analysis and new irreversibility dimension ratio of nanofluid flow through adaptive heating elements. Energies (2020) 13(1):114. 10.3390/en13010114
13.
MkhatshwaMPMotsaSSAyanoMSSibandaP. MHD mixed convective nanofluid flow about a vertical slender cylinder using overlapping multi-domain spectral collocation approach. Case Stud Therm Eng (2020) 18:100598. 10.1016/j.csite.2020.100598)
14.
TliliIShahmirNRamzanMKadrySKimJYNamYet alA novel model to analyze Darcy Forchheimer nanofluid flow in a permeable medium with Entropy generation analysis. J Taibah Univ Sci (2020) 14(1):916–30. 10.1080/16583655.2020.1790171
15.
AmjadMZehraINadeemSAbbasN. Thermal analysis of Casson micropolar nanofluid flow over a permeable curved stretching surface under the stagnation region. J Therm Anal Calorim (2020) 143:2485–97. 10.1007/s10973-020-10127-w
16.
KhanIUllahKSChuYMNisarKSAl-KhaledK. Oldroyd-B nanofluid-flow between stretching disks with thermal slip and multiple flow features. Therm Sci (2020) 24(1):83–94. 10.2298/tsci20s1083k
17.
BhattiMMAli AbbasMRashidiMM. Combine effects of Magnetohydrodynamics (MHD) and partial slip on peristaltic Blood flow of Ree-Eyring fluid with wall properties. Eng Sci Tech Int J (2016) 19:1497–502. 10.1016/j.jestch.2016.05.004
18.
YoonHKGhajarAJ. A note on the Powell-Eyring fluid model. Int Commun Heat Mass Transfer (1987) 14:381–90. 10.1016/0735-1933(87)90059-5
19.
AkbarNSNadeemS. Characteristics of heating scheme and mass transfer on the peristaltic flow for an Eyring -Powell fluid in an endoscope. Int J Heat Mass Transf (2012) 55:375–83. 10.1016/j.ijheatmasstransfer.2011.09.029
20.
LoganathanKMohanaKMohanrajMSakthivelPRajanS. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: An approach to entropy optimization. J Therm Anal Calorim (2020) 144(5):1935–47. 10.1007/s10973-020-09751-3
21.
WangSCusanoCCConryTF. Thermal analysis of elastohydrodynamic lubrication of line contacts using the Ree-Eyring fluid model. J Tribol (1991) 113:232–42. 10.1115/1.2920611
22.
HayatTZahirHAlsaediAAhmadB. Heat transfer analysis on peristaltictransport of Ree-Eyring fluid in rotating frame. Chin J Phys (2018) 55:1894–907. 10.1016/j.cjph.2017.08.016
23.
IjazNZeeshanABhattiMM. Peristaltic propulsion of particulate non Newtonian Ree-Eyring fluid in a duct through constant magnetic field. Alexandria Eng J (2017) 57(2):1055–60. 10.1016/j.aej.2017.02.009
24.
HayatTAkramJAlsaediAZahirH. Endoscopy and homogeneous heterogeneous reactions in MHD radiative peristaltic activity of Ree-Eyring fluid. Results Phys (2018) 8:481–8. 10.1016/j.rinp.2017.12.056
25.
Purna Chandar RaoDThiagarajanSSrinivasa KumarV. Darcy–Forchheimer flow of ree–eyring fluid over an inclined plate with chemical reaction: A statistical approach. Heat Transf (2021) 50:7120–38. 10.1002/htj.22220
26.
ShawkyHM. Pulsatile flow with heat transfer of dusty magnetohydrodynamic Ree Eyring fluid through a channel. Heat Mass Transfer (2009) 45:1261–9. 10.1007/s00231-009-0502-0
27.
HsiaoKL. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy (2017) 130:486–99. 10.1016/j.energy.2017.05.004
28.
LoganathanKRajanS. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J Therm Anal Calorim (2020) 141:2599–612. 10.1007/s10973-020-09414-3
29.
B-ChakraEC-BarriozJMazuyerDJarniasFBouffetA. A non-Newtonian model based on Ree–Eyring theory and surface effect to predict friction in elastohydrodynamic lubrication. Tribol Int (2010) 43:1674–82. 10.1016/j.triboint.2010.03.016
30.
LoganathanKSivasankaranSBhuvaneshwariMRajanS. Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of Oldroyd-B liquid using Cattaneo–Christov heat flux with convective heating. J Therm Anal Calorim (2019) 136:401–9. 10.1007/s10973-018-7912-5
31.
HsiaoKL. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl Therm Eng (2017) 112:1281–8. 10.1016/j.applthermaleng.2016.08.208
32.
WagerH. On the effect of gravity upon the movements and aggregation of euglena viridis, ehrb., and other micro-organisms. Philos Trans R Soc B (1911) 201:333–90. 10.1098/rstb.1911.0007
33.
PlattJR. Bioconvection patterns in cultures of free-swimming organisms. Science (New York, N.Y.) (1961) 133:1766–7. 10.1126/science.133.3466.1766
34.
KuznetsovAV. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int Commun Heat Mass Transfer (2010) 37(10):1421–5. 10.1016/j.icheatmasstransfer.2010.08.015
35.
UddinMJAlginahiYBégOKabirMN. Numerical solutions for gyrotactic bioconvection in nanofluid-saturated porous media with Stefan blowing and multiple slip effects. Comput Math Appl (2016) 72(10):2562–81. 10.1016/j.camwa.2016.09.018
36.
FarooqSHayatTAlsaediAAhmadB. Numerically framing the features of second order velocity slip in mixed convective flow of Sisko nanomaterial considering gyrotactic microorganisms. Int J Heat Mass Transf (2017) 112:521–32. 10.1016/j.ijheatmasstransfer.2017.05.005
37.
WaqasHKhanSUImranMBhattiMM. Thermally developed Falkner–Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys Scr (2019) 94(11):115304. 10.1088/1402-4896/ab2ddc
38.
KhanWARashadAMAbdouMMMTliliI. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur J Mech - B/Fluids (2019) 75:133–42. 10.1016/j.euromechflu.2019.01.002
39.
AmirsomNAUddinMJIsmailAI. MHD boundary layer bionanoconvective non-Newtonian flow past a needle with Stefan blowing. Heat Transfer-asian Res (2019) 48(2):727–43. 10.1002/htj.21403
40.
DeroSUddinMJRohniAM. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Trans Asian Res (2019) 48(4):2047–66. 10.1002/htj.21470
41.
KairiRRShawSRoySRautS. Thermo-solutalmarangoni impact on bioconvection in suspension of gyrotactic microorganisms over an inclined stretching sheet. J Heat Transfer (2020) 143(3). 10.1115/1.4048946
42.
ShawSKameswaranPKNarayanaMSibandaP. Bioconvection in a non-Darcy porous medium saturated with a nanofluid and oxytactic micro-organisms. Int J Biomath (2014) 7(01):1450005. 10.1142/s1793524514500053
43.
LiaoS. Homotopy analysis method in nonlinear differential equations. Germany: Higher Education Press: Berlin/Heidelberg (2012). p. 153–65.
44.
ZhaoYLiaoS. On the HAM-based mathematica package BVPh for coupled nonlinear ODEs. In: AIP Conference Proceedings; College Park, MD, USA, 26 September 2012; American Institute of Physics (2012). p. 1842–4. 10.1063/1.4756540
45.
YusufTAGbadeyanJA. Entropy generation on maxwell fluid flow past an inclined stretching plate with slip and convective surface conditon: Darcy-forchheimer model. Nano Hybrids and Composites (2019) 26:62–83. 10.4028/www.scientific.net/nhc.26.62
46.
AbelMSTawadeJVNandeppanavarMM. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica (2012) 47(2):385–93. 10.1007/s11012-011-9448-7
Summary
Keywords
Ree-Eyring nanomaterial, Riga plate, bioconvection, thermal radiation, homotopy analysis method
Citation
Loganathan K, Alessa N, Jain R, Ali F and Zaib A (2022) Dynamics of heat and mass transfer: Ree-Eyring nanofluid flow over a Riga plate with bioconvention and thermal radiation. Front. Phys. 10:974562. doi: 10.3389/fphy.2022.974562
Received
21 June 2022
Accepted
21 September 2022
Published
13 October 2022
Volume
10 - 2022
Edited by
Animasaun I. L., Federal University of Technology, Nigeria
Reviewed by
Prasannakumara B. C., Davangere University, India
Oluwole Daniel Makinde, Stellenbosch University, South Africa
S. Eswaramoorthi, Dr.N.G.P. Arts and Science College, India
Khadija Maqbool, International Islamic University, Pakistan
Anwar Shahid, Zhejiang University of Science and Technology, China
Updates
Copyright
© 2022 Loganathan, Alessa, Jain, Ali and Zaib.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: K. Loganathan, loganathankaruppusamy304@gmail.com
†These authors have contributed equally to this work
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.