- 1College of Pharmacy, Guangxi University of Chinese Medicine, Nanning, China
- 2Guangxi Key Laboratory of Nuclear Physics and Nuclear Technology, Guangxi Normal University, Guilin, China
The transverse momentum distributions of deuterons and anti-deuterons in Au + Au collisions at
1 Introduction
A great opportunity to explore the properties of strongly interacting substances at extreme densities and temperatures was provided by heavy-ion collisions (HICs) at ultra-relativistic energies [1–5]. More investigation is warranted about the generation mechanism of the particles and fragments in the ultra-relativistic HICs, as it may provide important information on the quantum chromodynamics (QCD) phase transition from quark-gluon plasma (QGP) to hadron gas (HG) [6, 7]. In the past 2 decades, many experiments have been carried out at the Relativistic Heavy Ion Collider (RHIC) near the critical energy for the transition from hadronic matter to QGP [8]. The theoretical studies on the production of particles and anti-particles are been going on for years, for example, the coalescence model, thermal model and transport models [9–21]. In particular, the study of transport phenomena is very important for understanding many fundamental properties [22, 23]. The transverse momentum spectrum of particles produced in high-energy collisions is of great research value because it can provide us with key information about the dynamic freezing state of the interacting system [24]. In the dynamic freezing stage, the effective temperature is not the actual temperature, which describes the sum of the excitation degree of the interacting system and the influence of the lateral flow [25].
The underlying mechanism for the generation of light (anti-) nuclei in relativistic heavy ion collisions is still under investigation. The traditional phase space polymerization method can be widely applied to HICs in large beam energy range [26]. It is of great significance to study deuteron generation at RHIC energy using the traditional coalescence model. In addition, there is a strong correlation between the particle’s coordinates and momentum, and this correlation varies over time. Therefore, the time evolution of the parameter set (R0, P0) needs to be scanned within a reasonable range so that the coalescence process produces the same yield [26]. From these experiments, the effect of coalescent parameters on the (anti-)deuteron and its transverse momentum distribution can be observed. The inverse law correlation between R0 and P0 should be described in detail in the third section.
In this paper, the Ultra-relativistic Quantum Molecular Dynamics (UrQMD) transport model is adopted to produce the transverse momentum distributions of (anti-)deuterons in Au + Au collisions at
2 Ultra-relativistic quantum molecular dynamics transport model and the coalescence model
2.1 The UrQMD model
The UrQMD model is a microscopic multi-body transport method that can be used to study proton-proton (pp), proton-nucleus (pA) and nucleon-nucleus (AA) interactions in the energy range from SIS to LHC. The transport model is based on covariant propagation of color strings, constituent quarks, and double quarks (as string ends) with meson and baryon degrees of freedom [28]. It can combine different reaction mechanisms and give theoretical simulation results of various experimental observations. In this model, by introducing the formation time of hadrons produced by string fragments, the degree of freedom of subhadrons is entered [29–31]. They predominate in the early stages of heavy ion collisions (HICs) with high SPS and RHIC energies.
The UrQMD model and quantum molecular dynamics (QMD) model are based on the parallel principle: hadrons are represented by Gaussian wave packets in phase space, and the phase space of hadrons propagates according to Hamiltonian equations of motion [32],
Here,
This microscopic transport approach simulates multiple interactions of in-going and newly produced particles, the excitation and fragmentation of color strings and the formation and decay of hadronic resonances. For higher energies, the treatment of subhadronic degrees of freedom is very important. In the current model, these degrees of freedom enter by introducing the formation time of hadrons produced by string fragments. The phase transition to the quark-gluon state is not explicitly incorporated into the model dynamics. However, a detailed analysis of the model in equilibrium state gives an effective Hagedorn type equation of state [33].
In this paper, we mainly study the effect of the correlations between coordinate and momentum spaces on the yields and the transverse momentum distribution of deuteron and anti-deuteron with the cascade mode in the RHIC energy region. In the nextwork, we will focus on the influence of potential on production of light particles in this energy region.
2.2 The coalescence model
The coalescence model describes the formation of hadronic clusters in the kinetic freeze-out stage of a heavy-ion collision. A pair of final (anti-) nucleons with similar momentum can merge to form a deuteron or anti-deuteron with total momentum P [34]. In the calculation, we use a conventional phase space clustering model [35] to construct clusters, in which hadrons with relative distances less than R0 and relative momentum less than P0 are considered to belong to a cluster. As a rule of thumb, the parameter set (R0, P0) can be selected in the range of (3-4 fm, 0.25–0.35 GeV/c) to describe the experimental data of HICs [26]. In this article, we will investigate the effects of different set of R0 and P0 on the yield of (anti-)deuteron over the evolutional time.
3 Time evolution and transverse momentum distributions of the production of (Anti-)deuterons
3.1 The time evolution of (anti-)deuterons
The time dependence of the production of (anti-)deuterons in the mid-rapidity (|y| < 0.3) for 0, −,10% centrality should be considered since they might be produced by different mechanisms. The time evolution of the yield of (anti-)deuterons at
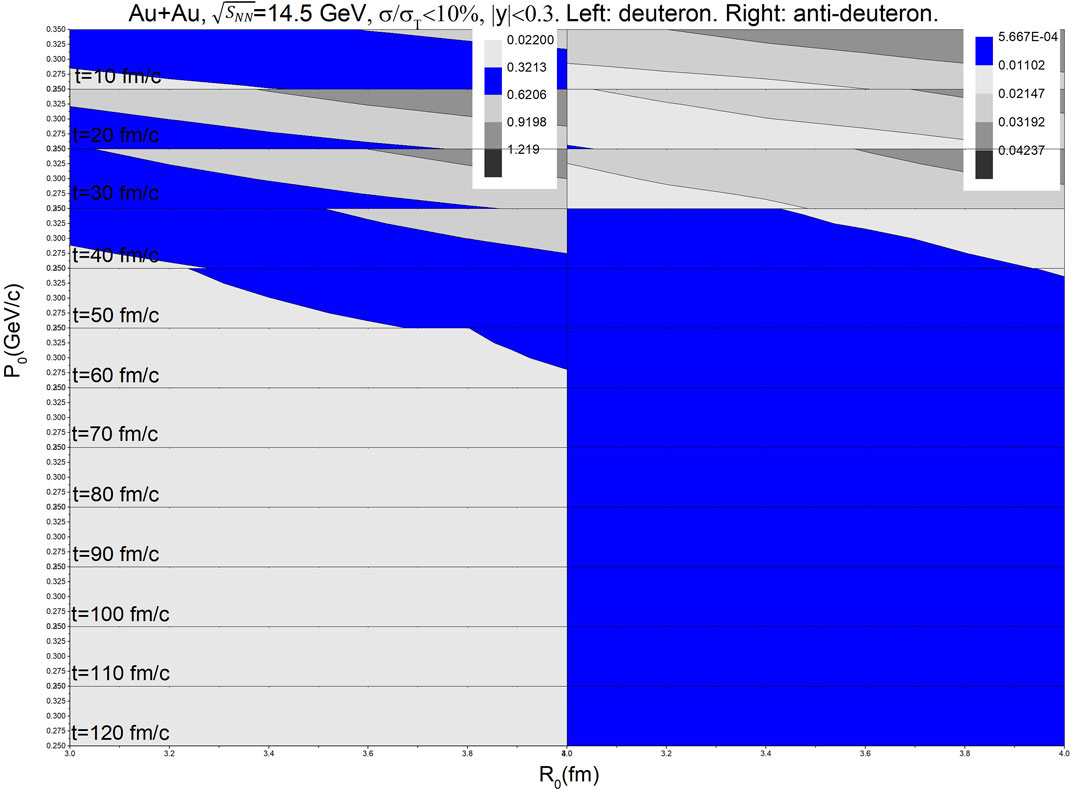
FIGURE 1. Time evolution of R0-P0 contour plots of (anti-)deuteron from the central Au + Au collisions at
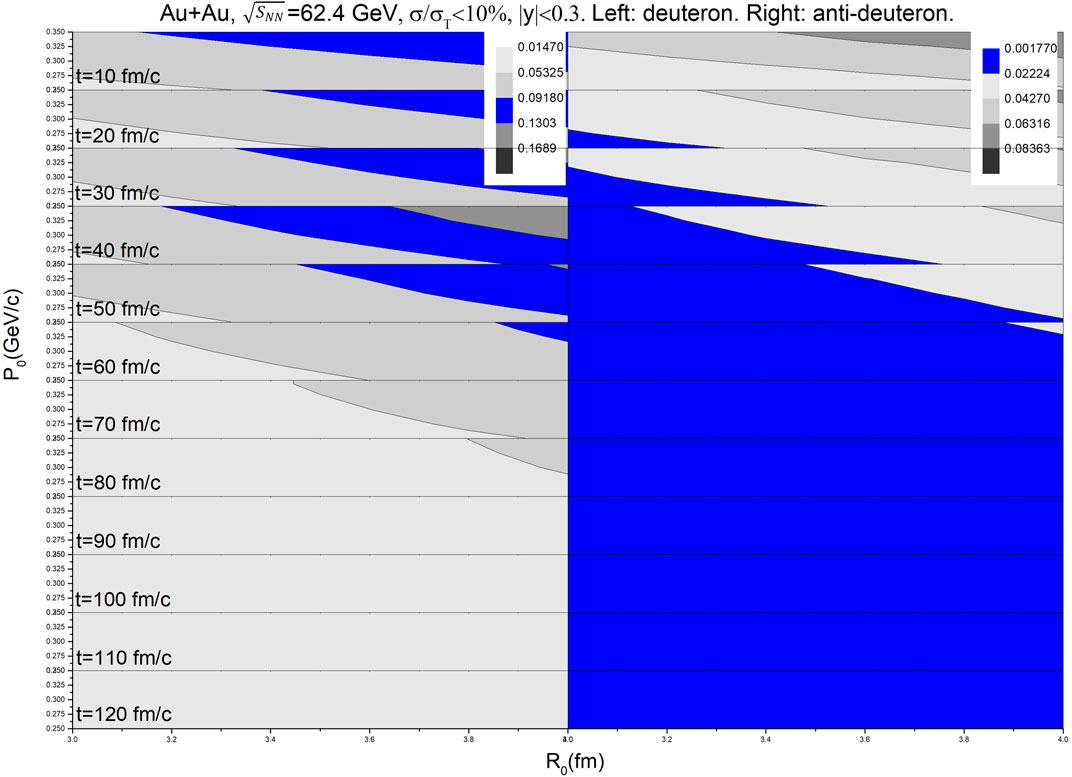
FIGURE 2. Time evolution of R0-P0 contour plots of (anti-)deuteron from the central Au + Au collisions at
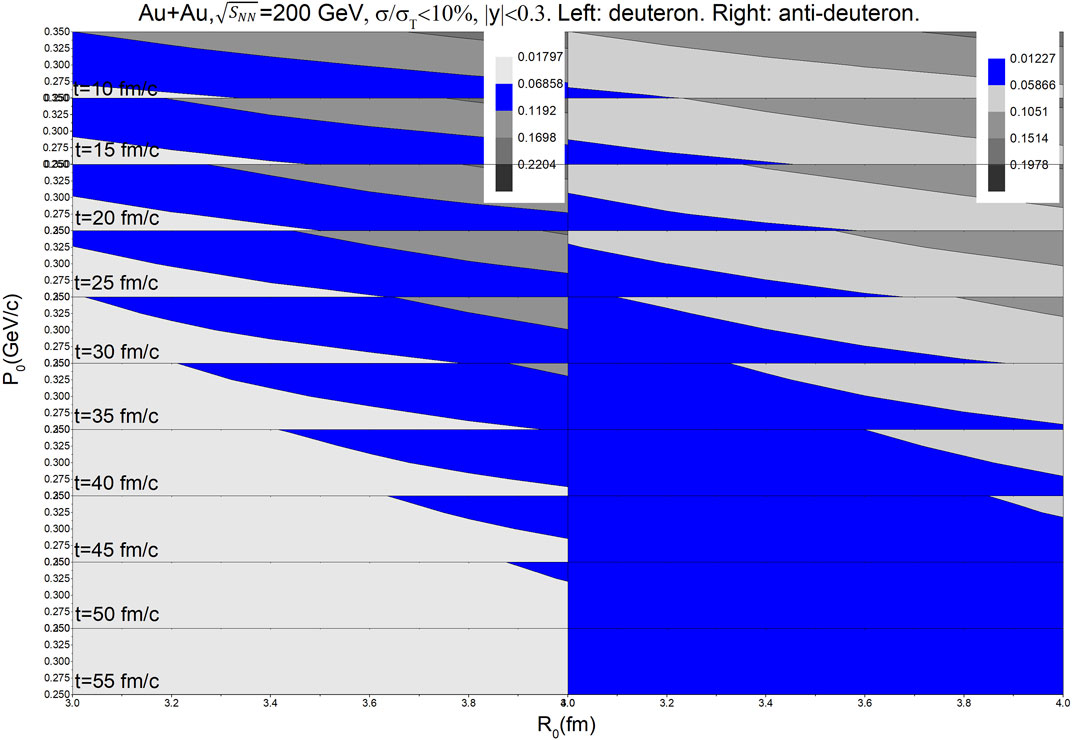
FIGURE 3. Time evolution of R0-P0 contour plots of (anti-)deuteron from the central Au + Au collisions at
Figure 4 show the yields of (anti-)deuterons as the time evolution in the 0, −,10% centrality Au + Au collisions at
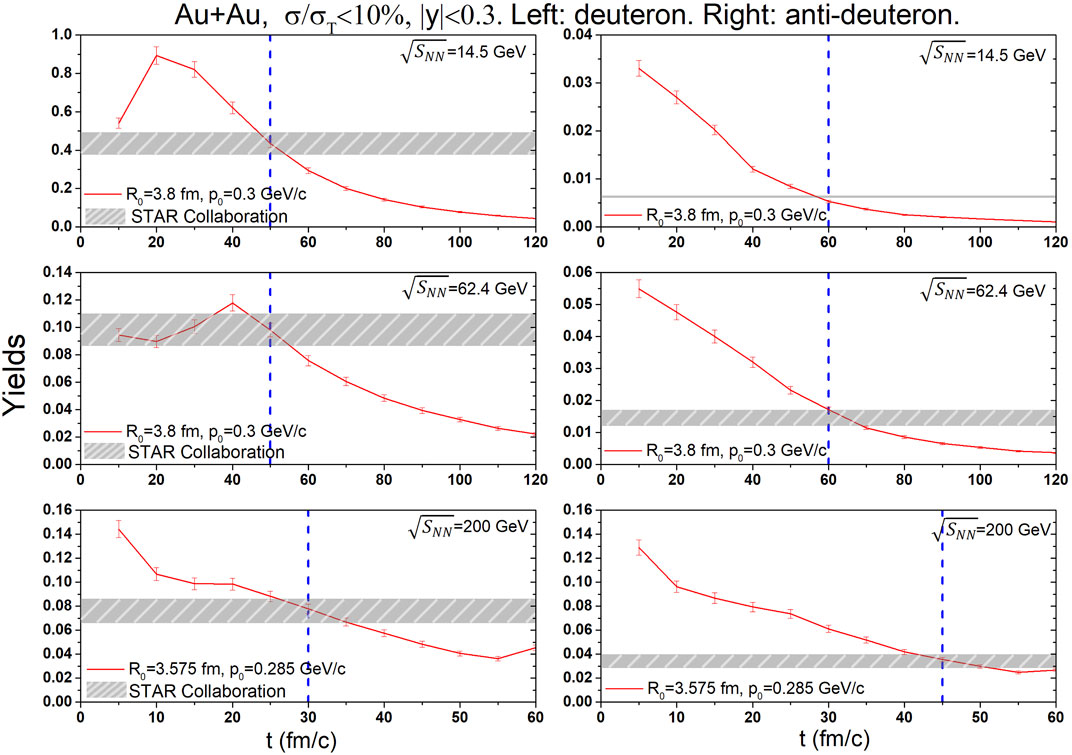
FIGURE 4. The yields of (anti-)deuterons as the time evolution in Au + Au collisions at
The scanning of R0 and P0 located in the colored regions of Figure 1, Figure 2 and Figure 3 is useful because they are reliable in the (anti-) deuteron data description of the mid-rapidity region. It is clear that the (anti-)deuteron production rate of RHIC can be well described by the cooperative method of UrQMD + coalescence if the UrQMD stop times are properly combined and the parameter set of (R0, P0) in the coalescence is chosen.
3.2 Transverse momentum distributions of (anti-)deuterons
Figures 5–7 show the transverse momentum spectra for deuterons at mid-rapidity (|y| < 0.3) in Au + Au collisions at
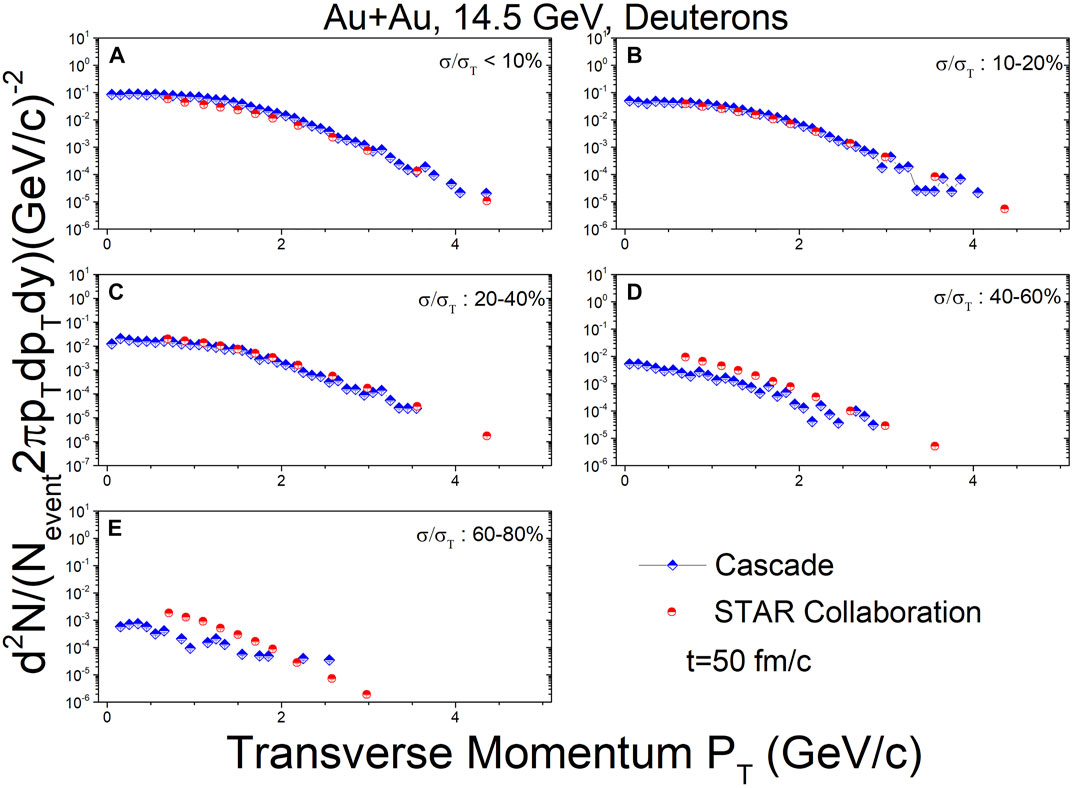
FIGURE 5. In the
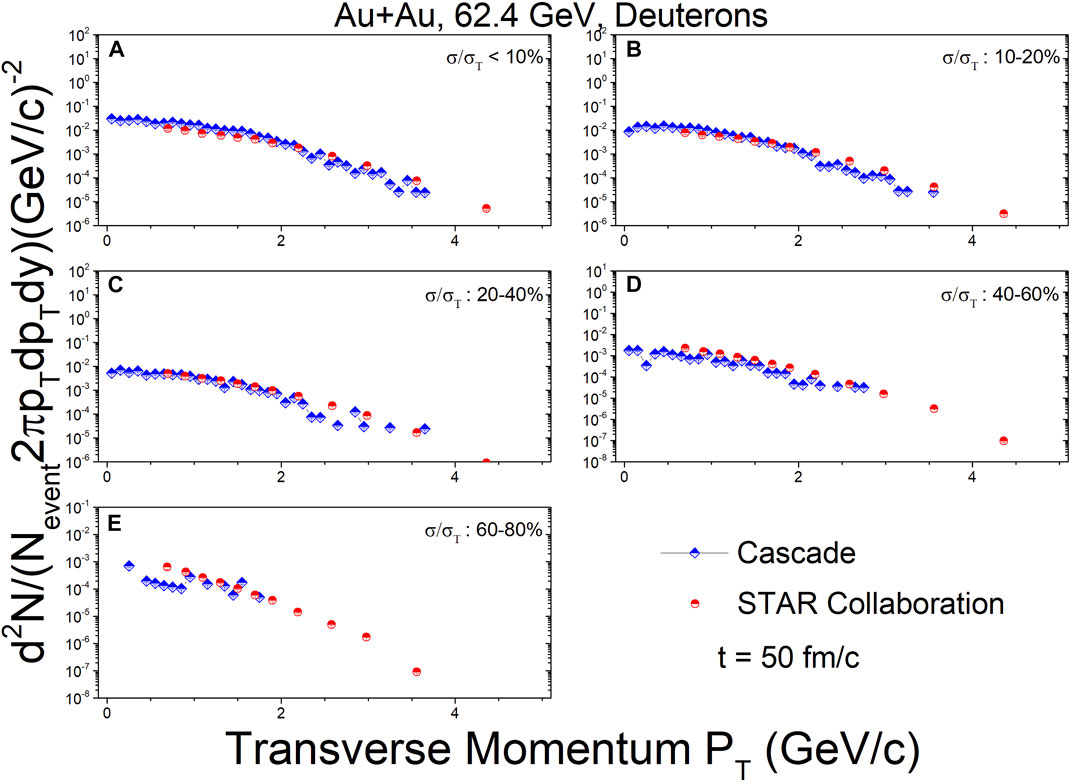
FIGURE 6. In the
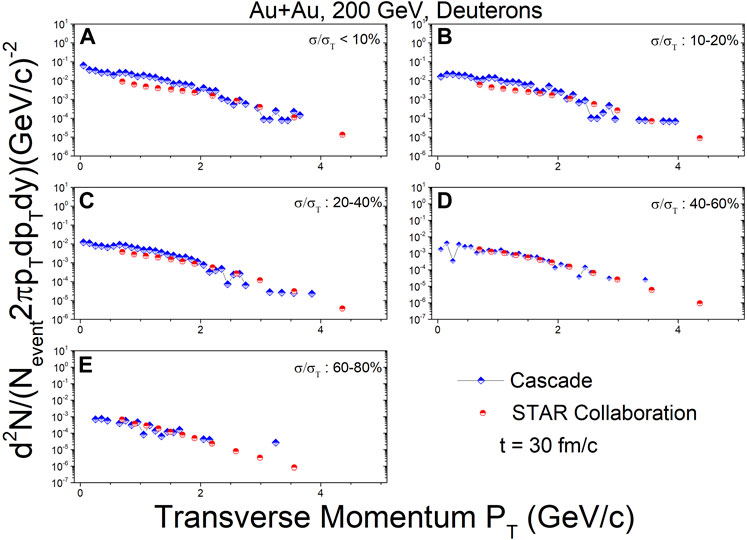
FIGURE 7. In the
Figures 8–10 show the transverse momentum spectra for anti-deuterons at mid-rapidity (|y| < 0.3) in Au + Au collisions at
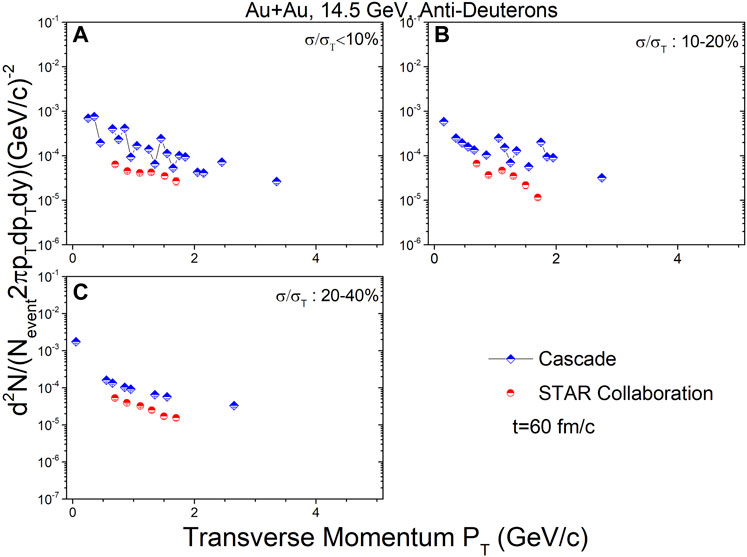
FIGURE 8. In the
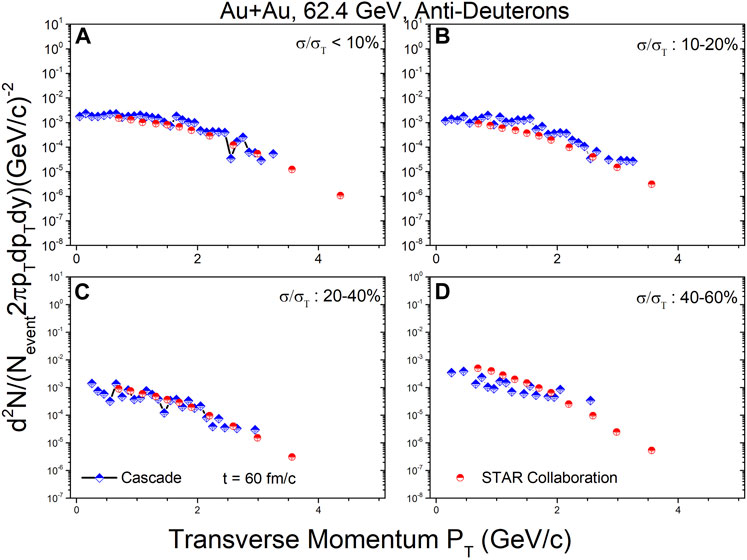
FIGURE 9. In the
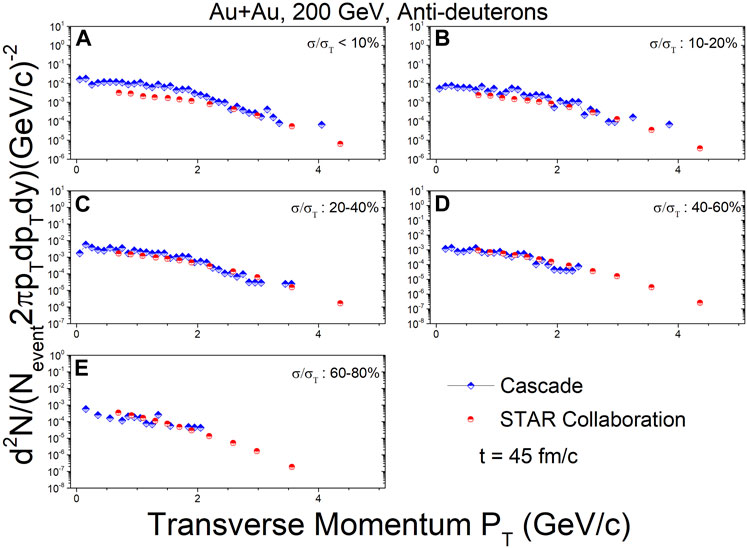
FIGURE 10. In the
4 Summary and outlook
In conclusion, we give the time evolution of the (anti-) deuteron in 0, −,10% center Au + Au collisions at
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
Conceptualization, XZ; formal analysis, ZH; writing—original draft, YY; writing—review editing, XW.
Funding
This work was supported by the Natural Science Foundation of Guangxi Zhuangzu Autonomous Region of China under Grant Nos. 2021GXNSFAA196052, the Introduction of Doctoral Starting Funds of Scientific Research of Guangxi University of Chinese Medicine under Grant Nos. 2018BS024, and the Open Project of Guangxi Key Laboratory of Nuclear Physics and Nuclear Technology, No. NLK2020-03.
Acknowledgments
We are grateful to the C3S2 computing center in Huzhou University for calculation support. We thank Qingfeng Li and Pengcheng Li for valuable suggestions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Alt C. Energy dependence of Λ and Ξ production in central Pb+Pb collisions at 20A, 30A, 40A, 80A, and 158A GeV measured at the CERN Super Proton Synchrotron. Phys Rev C (2008) 78(3):034918. doi:10.1103/PhysRevC.78.034918
2. Sun JX, Liu FH, Wang EQ. Pseudorapidity distributions of charged particles and contributions of leading nucleons in Cu-Cu collisions at high energies. Chin Phys Lett (2010) 27(3):032503. doi:10.1088/0256-307x/27/3/032503
3. Wang EQ, Liu FH, Rahim MA, Fakhraddin S, Sun JX. Singly and doubly charged projectile fragments in nucleus-emulsion collisions at dubna energy in the framework of the multi-source model. Chin Phys Lett (2011) 28(8):082501. doi:10.1088/0256-307X/28/8/082501
4. Li BC, Huang M. Strongly coupled matter near phase transition. J Phys G: Nucl Part Phys (2009) 36:064062. doi:10.1088/0954-3899/36/6/064062
5. Liu FH. Anisotropic emission of charged mesons and structure characteristic of emission source in heavy ion collisions at 1–2A GeV. Chin Phys B (2008) 17(3):883–95. doi:10.1088/1674-1056/17/3/025
6. Arsenescu R, Baglin C, Beck HP, Borer K, Bussiere A, Elsener K, et al. An investigation of the antinuclei and nuclei production mechanism in Pb + Pb collisions at 158 A GeV. New J Phys (2003) 5:150. doi:10.1088/1367-2630/5/1/150
7. Li QF, Wang YJ, Wang XB, Shen CW. Helium-3 production from Pb+Pb collisions at SPS energies with the UrQMD model and the traditional coalescence afterburner. Sci China Phys Mech Astron (2016) 59(3):632002. doi:10.1007/s11433-015-5775-3
8. Lao HL, Wei HR, Liu FH, Lacey RA. An evidence of mass-dependent differential kinetic freeze-out scenario observed in Pb-Pb collisions at 2.76 TeV. Eur Phys J A (2016) 52:203. doi:10.1140/epja/i2016-16203-2
9. Mrowczynski S, Slon P. Hadron-deuteron correlations and production of light nuclei in relativistic heavy-ion collisions (2016) Available from: http://arxiv.org/abs/nucl-th/1904.08320v2. (Accessed Jun 24, 2019).
10. Mrowczynski S. Production of light nuclei in the thermal and coalescence models. Acta Phys Pol B (2017) 48:707. doi:10.5506/aphyspolb.48.707
11. Mrowczynski S. 4He versus 4Li and production of light nuclei in relativistic heavy-ion collisions. Mod Phys Lett A (2018) 33:1850142. doi:10.1142/s0217732318501420
12. Liu P, Chen JH, Ma YG, Zhang S. Production of light nuclei and hypernuclei at High Intensity Accelerator Facility energy region. Nucl Sci Tech (2017) 28:55. doi:10.1007/s41365-017-0207-x
13. Liu FX, Chen G, Zhe ZL, Zhou DM, Xie YL. Light (anti)nuclei production in Cu+Cu collisions at $\sqrt{s_{NN}}$=200 GeV. Eur Phys J A (2019) 55:160. doi:10.1140/epja/i2019-12851-x
14. Yuan Y, Li Q, Li Z, Liu F-H. Transport model study of nuclear stopping in heavy-ion collisions over the energy range from0.09Ato160A GeV. Phys Rev C (2010) 81:034913. doi:10.1103/physrevc.81.034913
15. Yuan Y. Study of Production of (Anti-)deuteron Observed in Au+Au Collisions at $\sqrt{s_{NN}}$= 14.5, 62.4, and 200 GeV. Advances in high energy Physics (2021) 2021:9305605. doi:10.1155/2021/9305605
16. Li P, Wang Y, Li Q. Hongfei Zhang “Accessing the in-medium effects on nucleon-nucleon elastic cross section with collective flows and nuclear stopping. Phys Lett B (2022) 828:2022. doi:10.1016/j.physletb.2022.137019
17. Oliinychenko D, Pang L-G, Elfner H, Koch V. Microscopic study of deuteron production in PbPb collisions at $\sqrt{s_{NN}}$2.76 TeV via hydrodynamics and a hadronic afterburner. Phys Rev C (2019) 99:044907. doi:10.1103/PhysRevC.99.044907
18. Aichelin J, Bratkovskaya E, Le Fèvre A, Kireyeu V, Kolesnikov V, Leifels Y, et al. Parton-hadron-quantum-molecular dynamics: A novel microscopic n-body transport approach for heavy-ion collisions, dynamical cluster formation, and hypernuclei production. Phys Rev C (2020) 101:044905. doi:10.1103/physrevc.101.044905
19. Kireyeu V. Cluster dynamics studied with the phase-space minimum spanning tree approach. Phys Rev C (2021) 103:054905. doi:10.1103/physrevc.103.054905
20. Staudenmaier J, Oliinychenko D, Torres-Rincon JM, Elfner H. Deuteron production in relativistic heavy ion collisions via stochastic multiparticle reactions. Phys Rev C (2021) 104:034908. Aticle ID 034908. doi:10.1103/physrevc.104.034908
21. Gläßel S, Kireyeu V, Voronyuk V, Aichelin J, Blume C, Bratkovskaya E, et al. Cluster and hypercluster production in relativistic heavy-ion collisions within the parton-hadron-quantum-molecular-dynamics approach. Phys Rev C (2022) 105:014908. doi:10.1103/PhysRevC.105.014908
22. Li BC, Fu YY, Wang LL, Liu FH. Dependence of elliptic flows on transverse momentum and number of participants in Au+Au collisions at $\sqrt{\mathrm{\it s_{NN}}}$ = 200 GeV. J Phys G: Nucl Part Phys (2013) 40:025104. doi:10.1088/0954-3899/40/2/025104
23. Sombun S, Tomuang K, Limphirat A, Hillmann P, Herold C, Jan S, et al. Deuteron production from phase-space coalescence in the UrQMD approach. Phys Rev C (2019) 99:014901. doi:10.1103/physrevc.99.014901
24. Chen YH, Liu FH, Sarkisyan-Grinbaum EK. Event patterns from negative pion spectra in proton-proton and nucleus-nucleus collisions at SPS. Chin Phys C (2018) 42(10):104102. doi:10.1088/1674-1137/42/10/104102
25. Waqas M, Liu FH, Li LL, Alfanda HM. Analysis of effective temperature and kinetic freeze-out volume in high energy nucleus-nucleus and proton-proton collisions. Nucl Sci Tech (2020) 31:109. doi:10.1007/s41365-020-00821-7
26. Li QF, Wang YJ, Wang XB, Shen CW. Influence of coalescence parameters on the production of protons and Helium-3 fragments. Sci China Phys Mech Astron (2016) 59:672013. doi:10.1007/s11433-016-0120-3
27. Adam J. Beam energy dependengce of (anti-)deuteron production in Au+Au collisions at RHIC. Phys Rev C (2019) 99. 064905. doi:10.1103/PhysRevC.99.064905
28. Petersen H, Bleicher M, Bass SA, Stocker H. UrQMD-2.3 - changes and comparisons (2022) Available from: http://arxiv.org/abs/0805.0567. (Accessed May 5, 2008).
29. Andersson B, Gustafson G, Nilsson-Almqvist B. A model for low P(T) hadronic reactions, with generalizations to hadron-nucleus and nucleus-nucleus collisions. Nucl Phys B (1987) 281(1-2):289–309. doi:10.1016/0550-3213(87)90257-4
30. Nilsson-Almqvist B, Stenlund E. Interactions between hadrons and nuclei: The lund Monte Carlo, fritiof version 1.6. Computer Phys Commun (1987) 43(3):387–97. doi:10.1016/0010-4655(87)90056-7
31. Sjostrand T. High-energy physics event generation with PYTHIA 5.7 and JETSET 7.4. Computer Phys Commun (1994) 82(1):74–89. doi:10.1016/0010-4655(94)90132-5
32. Bleicher M, Zabrodin E, Spieles C, Bass SA, Ernst C, Soff S, et al. Relativistic hadron hadron collisions in the ultra-relativistic quantum molecular dynamics model. J Phys G: Nucl Part Phys (1999) 25(9):1859–96. doi:10.1088/0954-3899/25/9/308
33. Petersen H, Li Q, Zhu X, Bleicher M. Directed and elliptic flow in heavy-ion collisions from Ebeam = 90 MeV/nucleon to Ec.m. = 200 GeV/nucleon. Phys Rev C (2006) 74:064908. doi:10.1103/physrevc.74.064908
34. Kittiratpattana A, Wondrak MF, Hamzic M, Bleicher M, Herold C, Limphirat A. Deuteron and antideuteron coalescence in heavy-iom collisions: Energy dependence of the formation geometry. Eur Phys J A (2020) 56:274. doi:10.1140/epja/s10050-020-00269-8
35. Kruse H, Jacak BV, Molitoris JJ, Westfall GD, Stoecker H. Vlasov-uehling-uhlenbeck theory of medium-energy heavy ion reactions: Role of mean field dynamics and two-body collisions. Phys Rev C (1985) 31:1770–4. doi:10.1103/physrevc.31.1770
Keywords: transverse momentum distributions, UrQMD model, coalescence, heavy-ion collisions, Au+Au collisions
Citation: Yuan Y, Huang Z, Zhang X and Wei X (2022) Transport model study of transverse momentum distributions of (anti-)deuterons production in Au+Au collisions at
Received: 17 June 2022; Accepted: 08 August 2022;
Published: 15 September 2022.
Edited by:
Fu-Hu Liu, Shanxi University, ChinaReviewed by:
Waqas Muhammad, University of Chinese Academy of Sciences, ChinaHua-Rong Wei, Lishui University, China
Junsheng Li, Shanxi Normal University, China
Copyright © 2022 Yuan, Huang, Zhang and Wei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Yuan, eXVhbnlAZ3h0Y211LmVkdS5jbg==; Xiangzhong Wei, d294b3pAMTYzLmNvbQ==
 Ying Yuan
Ying Yuan Ziqian Huang1
Ziqian Huang1