Characterization of avoided crossings in acoustic superlattices: The Shannon entropy in acoustics

We show that Shannon’s information entropy provides a correct physical insight of localization effects taking place in structured fields fashioned by eigenmodes upon substrate. In particular, we find that the localization exchange among levels when an avoided crossing occurs is explainable in terms of an informational trade among those levels. We use it to characterize the resonant Zener-like effect in two types of ultrasonic superlattices, one made of metamaterial slabs and the other made of Plexiglas and water cavities. When the gradient of the layer cavities is varied along the narrow region where the avoided crossing appears, it is found that Shannon’s entropy of both levels maximizes at the critical gradient showing the levels’ anti-crossing.

1 Introduction

Information theory [1] boosted an increasing number of interdisciplinary applications in the last 3 decades. The entropy functional is becoming significant to characterize complexity in stochastic thermodynamics, where the formal equivalence between the Gibbs and Shannon expressions is merging the once distant concepts of order and information [2–6]. In the quantum realm, novel and counter-intuitive ways of processing and transmitting information are transforming technologies from conceptual roots [7–10]. Shannon entropy opened new avenues of interpretation of well known physical phenomena in crystallography [11, 12] and atomic physics [13–16]. In molecular biology, Turing-like proteins process nucleic acid molecules, which are genetic information carriers, by coupling chemical energy to entropy reduction, hence embodying information as another manifestation of entropy, like heat to energy [17, 18].

When a physical field is multiply scattered at material interfaces, it forms eigenmodes, which are strong field enhancements spatially localized due to the boundary conditions. These modes are actually the result of the non-Markovian interaction between the interfaces through the impinging field. They can be found in particles [19, 20], including plasmonic devices [21, 22], with current applications such as optical binding [23, 24], nano-antennas [25–27] and biological sensing [28–31].

Here, we introduce Shannon entropy in situations where localization plays a fundamental role. There are several indicators of the spatial spreading of an eigenmode, among others the inverse participation ratio [32, 33]. However, we propose Shannon entropy because it is a global concept, coupling information and complexity from wave phenomena to virtually any discipline in science. Particularly, it will be employed to study the dynamics of the acoustical analogue [34] of the electronic Zener effect [35], a phenomenon that was previously observed in semiconductor superlattices [36, 37]. This will be done by analyzing the avoided crossing occurring between acoustic levels belonging to different minibands in ultrasonic superlattices. We next introduce the Shannon functional for a general field and report an in-depth analysis for the acoustic case of a multilayer of a fluid-like metamaterial. Results for an array of water cavities and methyl-metacrylate (Plexiglas) layers, which is the structure studied in [34], will be also presented to address significance in real systems.

2 Shannon entropy in acoustics

Shannon entropy has been defined in atomic physics as $S_{\rho }=-\int \rho \left(\mathbf{r}\right)\ln \rho \left(\mathbf{r}\right)d\mathbf{r}$, where $\rho \left(\mathbf{r}\right)={\left|\psi (\mathbf{r})\right|}^2$ is the probability density distribution of a given electronic pure state. For classical fields, however, there is not an equivalent magnitude having an interpretation of a probability distribution. To overcome this issue we have exploited the analogy between electronic states in quantum mechanics and electromagnetic or acoustic levels in material structures. Optical fields can excite so-called Mie resonances on nanoparticles, whether whispering-gallery modes or plasmons depending on the absorptive nature of the nanoparticle [38, 39]; likewise, slabs of a solid material in air sustain acoustic vibrations that are quasibound. The resonant behavior of these fields are eigenmodes in their associated wave equations, with the boundary conditions imposed by the material interfaces, thus considered the quantum counterparts of the atomic levels.

From the analogy with atomic systems, we introduce the following probability distribution function:

$P\left(\mathbf{r}\right)\equiv {\left|u\left(\mathbf{r}\right)\right|}^2/\int {\left|u\left(\mathbf{r}\right)\right|}^{2}d\mathbf{r},(1)$

where ${\left|u\left(\mathbf{r}\right)\right|}^2$ is the square norm of the field. In optics, this quantity is the dot product of the electric (magnetic) field and its complex conjugate. In acoustics, the probability of Eq. 1 is obtained similarly by normalizing the square of the displacement field, $u\left(\mathbf{r}\right)$. These square norms are proportional to respective field intensities. Therefore, a probability density so defined is proportional to a field intensity, a relation that adds physical meaning to P(r). It will play in a classical field the same role as the electronic density distribution in quantum mechanics. The Shannon’s information entropy is defined by:

$S_u=-\int P\left(\mathbf{r}\right)\ln P\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}.(2)$

This quantity is an information measure of the spatial delocalization of the field level in the corresponding material system, hence yielding the uncertainty in the field localization. Like the Shannon entropy [1], S_u increases with increasing uncertainty (i.e., spreading of the field state). We should point out that the velocity or the pressure can be equally employed in the definition of P(r) since they are related quantities in linear acoustics. We don’t expect any change in the conclusions of this work when using any of them.

The main purpose of this work lies beneath Eqs 1, 2. They can be applied to any classical system containing interacting modes yielding the characterization of their spreading in terms of informational exchange. It is important to stress that the Shannon entropy, as it is here introduced, is more general than the inverse participation ratio since it can be applied not only to disordered systems. It, indeed, serves as a measure of localization of vibrating states. However, we do not think that it carries information about the group or phase velocity of a given mode or its density of states. Therefore, it is not a criterion for the rate of information transfer along a channel or a waveguide. Moreover, for a running (propagating) mode the integral (1) becomes singular since the normalization integral diverges.

3 Results and discussion

In what follows, we use S_u to get physical insight in the dynamics of an acoustic system in which two interacting acoustic levels present an avoided crossing region. The repulsion of the acoustic modes (as the external field adiabatically changes) illustrates how the avoided crossing effect is a mechanism for sound localization reordering with frequency.

Let us consider structures like the one schematically depicted in Figure 1A, consisting on a multilayer made of m coupled cavities, W_m, enclosed by m + 1 metamaterial slabs, A_m. For an easy realization, we also consider that the metamaterial slabs A_m are made of a finite sonic crystal (SC) defined by a two-dimensional (2D) periodic distribution of solid cylinders embedded in a fluid background. These type of structures are feasible and have been employed to observe acoustic Bloch oscillations and Zener tunneling (ZT) using water as the background fluid [40, 41]. They are studied here because, in the homogenization limit, the SC-based metamaterial slabs A_m behave as fluid-like materials whose effective parameters (density and sound velocity) can be tailored with practically no limitation by changing the filling fraction of the underlying lattice and/or the solid material employed in its construction [42–44]. Therefore, the structure shown in Figure 1A is simplified to that depicted in Figure 1B, where the clusters of cylinders are replaced by homogeneous fluid-like layers and the transmission coefficient can be easily obtained by applying the transfer matrix (TM) method [45].

FIGURE 1

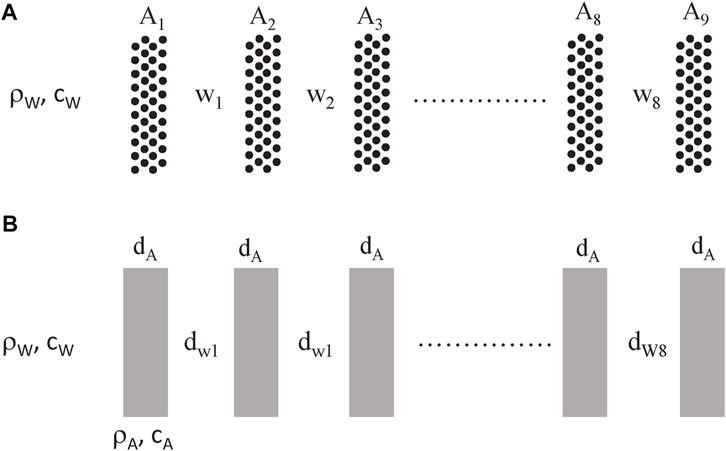
FIGURE 1. (A) Scheme of the multilayered structures considered in this study, consisting of eight cavities W_m separated by nine sonic-crystal (SC) metamaterial slabs A_m embedded in a inviscid fluid with acoustic parameters ρ_W and c_W. (B) The resulting structure after the homogenization of the SC slabs, which are replaced by homogeneous fluid-like layers with effective parameters ρ_Aand c_A. Structures have been studied in which layers A_m have equal thicknesses, d_A, while the cavities W_Wi have different thicknesses, d_Wi.

The TM calculations are performed using the system described in Figure 1B made of eight (m = 8) water cavities and using the following inputs: ρ_A = 5ρ_W and c_A = 0.78c_W, where ρ_W (= 1 g/cm³) and c_W (= 1.48 × 10⁵ cm/s) are the density and sound velocity in water, respectively. The values ρ_A and c_A represent the effective parameters obtained from the homogenization algorithm [43] applied to rectangular clusters made of rigid cylinders embedded in an inviscid fluid background and arranged in a hexagonal distribution whose filling fraction is 0.68. The case of the perfect superlattice is studied with layer thicknesses d_A = 0.08 cm and d_W = 2d_A, respectively.

The displacement field amplitude, $\log {\left|u(z)\right|}^2$, inside the perfect superlattice made of eight water cavities and the corresponding transmission spectrum through the complete structure are shown in Figures 2A,B, respectively. Two minibands, MB1 and MB2, are clearly observed in the transmission; miniband MB1 is approximately centered at the frequency corresponding to the first Fabry-Perot resonance of a water cavity with thickness d_W (i.e., at c_W/2d_W = 462 kHz). The modes in MB1 are strongly localized in the water cavities but those in MB2 are mixed and their spatial localization is not sharply defined.

FIGURE 2

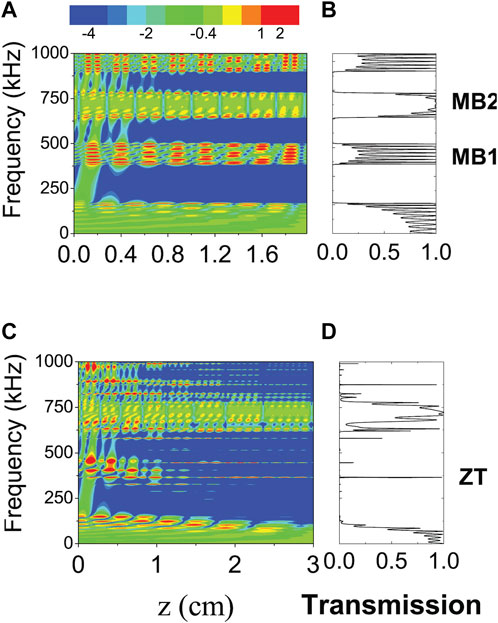
FIGURE 2. (A) Transfer-matrix calculation of the square displacement of the sound field $(\log {\left|u(z)\right|}^2)$ inside a perfect acoustic superlattice, corresponding to the structure depicted in Figure 1B with d_A = 0.08 cm and d_W = 2d_A. (B) The calculated transmission coefficient, where MB1 and MB2 stand for minibands 1 and 2, respectively. (C) $\log {\left|u(z)\right|}^2$ calculated for the multilayered structure shown in Figure 1B, with d_A = 0.08 cm and d_Wm take the values defined by the critical gradient thickness (10.04%). (D) The corresponding transmission coefficient, where ZT stands for Zener tunneling effect.

To observe the resonant Zener-tunneling (ZT) effect, we break the translational symmetry by introducing a thickness gradient in the thicknesses, d_W, of the water cavities. Such a gradient plays the role of a driven force producing effects similar to those of the electric field in an electronic superlattice [34]. The magnitude of the gradient is given by the dimensionless parameter

$\mathrm{\Delta }\left(1/d_W\right)=\left[\left(1/d_{W_{\ell }}\right)-\left(1/d_{W_{\ell -1}}\right)\right]/\left(1/d_{W_1}\right),(3)$

where $d_{W_1}=0.08$ cm is the thickness of the first (ℓ = 1) cavity. Figure 2C displays the amplitude $\log {\left|u(z)\right|}^2$ and Figure 2D represents the total transmission through a structure with the critical gradient $\mathrm{\Delta }{\left(1/d_W\right)}_c=10.04\%$, for which the acoustic ZT effect appears. The interaction between the upper resonant mode in MB1, here denominated as u₁, and the bottom mode in MB2, here denominated as u₂, is the strongest for this gradient, hence making maximum the total transmission through the structure.

Figure 3 shows an in-depth analysis of the result described above, presenting the transmission coefficient as a function of frequency for several values of the gradient. It is observed that the peaks in the transmission profiles are strongly reduced when the gradient is slightly smaller or larger than the critical. In addition, the transmission profile at the critical gradient (black line) clearly shows a double peak, indicating the anticrossing effect between the two interacting modes u₁ and u₂ with frequencies below and above, respectively, the central frequency ω₀.

FIGURE 3

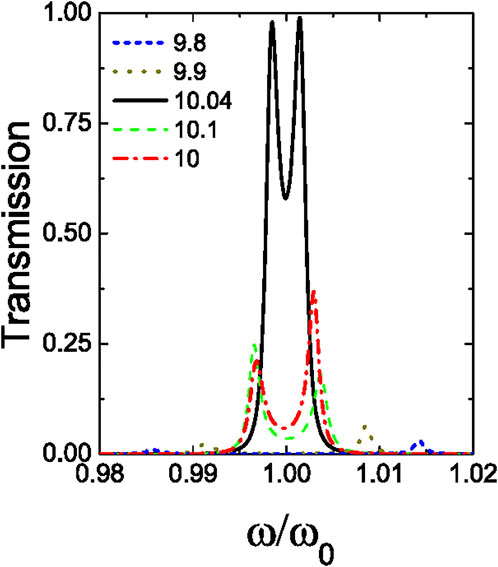
FIGURE 3. Transmission spectra around the thickness gradient for which the Zener-like resonant effect occurs (same acoustic multilayer as in Figure 1). The transmission is plotted for several gradients (in %) as a function of the reduced frequency, ω/ω₀, with ω₀ the central frequency at each gradient.

Figures 4A,B display, respectively, the frequency and Shannon entropy of the levels involved in the avoided crossing. It is observed in Figure 4A that the frequency of u₂ (red dashed line) is always higher than that of u₁ (blue continuous line), although both frequencies approach each other near the critical thickness gradient. With regards to the entropy of the modes, Figure 4B shows different behaviors, strongly correlated with the gradient values. For small gradients (i.e., for values much lower than the critical) the entropy S_u2 (red-dashed line) is smaller than S_u1 (blue continuous line). This behavior indicates that the sound in the mode with frequency u₂ is more localized than in u₁. The entropy difference ΔS = S_u2 − S_u1 is, thus, negative for small gradients. For increasing values of the gradient, both modes shows a similar trend, increasing their entropy up to the region between 10.02% and 10.06%, where the modes strongly mix up and the slope of their entropy abruptly changes from positive to negative at the critical gradient value (10.04%). At this critical gradient, both modes reach their maximum entropy and the entropy difference is not exactly zero but very small; i.e., ΔS(10.04%) = 0.022 (arb. units). Given the numerical uncertainty of the calculations, we consider that the critical gradient represents the value at which ΔS reverses sign. Finally, for gradients above the critical value, namely, for $\mathrm{\Delta }\left(1/d_W\right)>\mathrm{\Delta }{\left(1/d_W\right)}_c$, the entropy of the levels monotonically decreases, approaching the values corresponding to the case of non-interacting levels. In this region, the entropy difference is always positive; i.e., S_u2 > S_u1, indicating that sound in mode u₁ is more localized than in mode u₂. From an information theory perspective, it can be concluded that the information contained in the two interacting levels, u₁ and u₂, has been exchanged when passing through the avoided crossing region. In other words, the spreading of the corresponding modes has been exchanged, thus the information, when the driven force $\mathrm{\Delta }\left(1/d_W\right)$ has been adiabatically tuned from 9.95% to 10.06%.

FIGURE 4

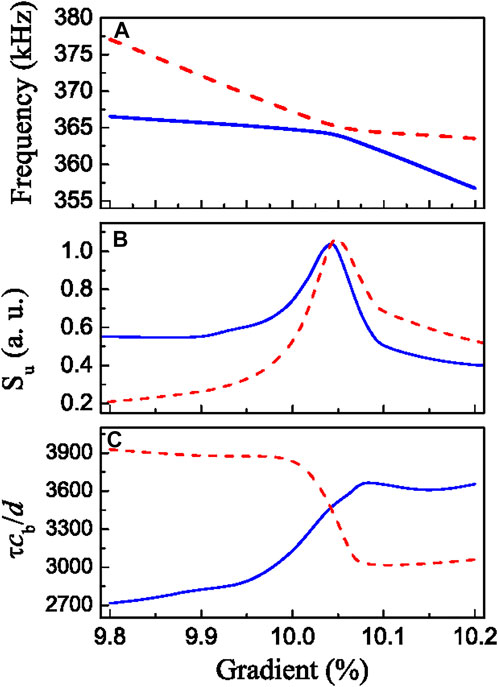
FIGURE 4. (A) Frequency, (B) Shannon entropy, and (C) lifetime of the two interacting acoustic modes, u₁ and u₂, near the avoided crossing region for the acoustic structure described in Figure 1A. The blue continuous (red dashed) lines represent the corresponding magnitudes associated to mode u₁ (u₂). The lifetime, τ, is given in reduced units.

To further support this interpretation, we have calculated the lifetime of the acoustic modes involved in the resonant effect. The complex frequency of a mode, ν_i = Re(ν_i) + iIm(ν_i), is obtained by following the procedure in [46]. The real part represents the frequencies already plotted in Figure 4A. The resonance lifetime, τ_i, of a given eigenmode, u_i, is associated to the imaginary part of its frequency, being represented in Figure 4C in units of d/c_b, with d and c_b the total thickness of the structure and the sound speed in the background fluid, respectively. Below the critical thickness gradient, the lifetime τ₂ (red dashed line) of the acoustic mode u₂ is longer, which implies a lower radiative damping—hence, a reduced mode spreading and a stronger spatial localization—. Let us point out that viscothermal dissipation effects are not taken into account in our calculation since they are considered very small in these type of acoustic structures. Around the critical gradient, the lifetimes of both levels abruptly change their trends and intersect each other. After the avoided crossing region, the lifetime τ₁ (blue continuous line) of mode u₁ becomes longer than τ₂, which spreads spatially as discussed below.

Additional physical insight of the information exchange, as a consequence of the localization dynamics taking place across the critical gradient is shown in Figure 5. The amplitudes of both acoustic modes are plotted for three different gradients, the central panel corresponding to the critical gradient. It is observed that the greater the Shannon entropy, the larger the acoustic mode spreading. Moreover, at the critical gradient (10.04%), the modes resulting from the interaction are the bonding and antibonding combinations of the non-interacting modes, which explain the similar spreading shown by both wavefunctions (displacement fields) in Figure 5, middle panel.

FIGURE 5

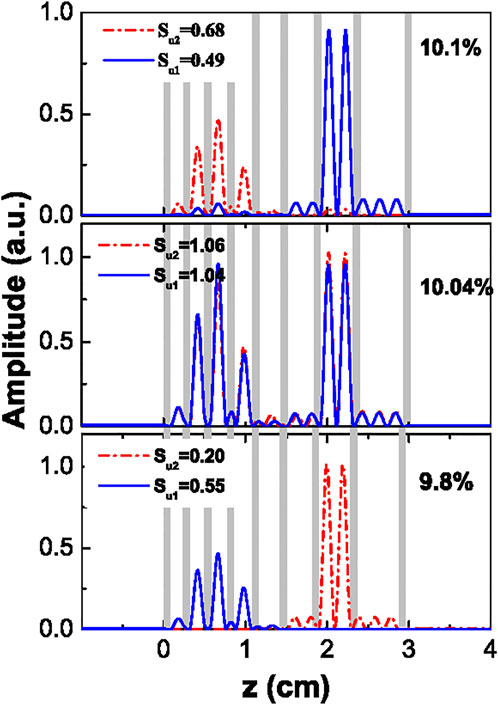
FIGURE 5. Amplitude (in arbitrary units) of the acoustic modes u₁ (blue continuous line) and u₂ (red dashed line) calculated for three values of the thickness gradient. The value 10.04% corresponds to the critical gradient where the avoided crossing occurs. The values of the Shannon entropy are extracted from Figure 4B. The vertical gray bars are guides for eye providing the location of the metamaterial layers (their height is physically meaningless).

Finally, for the sake of easy implementation, we have studied the Zener-like effect experimentally characterized in a superlattice made of Plexiglas and water cavities [34]. The frequency, Shannon entropy and lifetime of the two involved levels, u₁ and u₂, are shown in Figures 6A–C, respectively. The calculations are performed using structures having the same set of parameters than those employed in the measurements [34]. The frequencies, though smoother, follow similar trends as those displayed theoretically in the previous figure. With regards to the entropy, we observe once again that the critical gradient (this time 9.93%) maximizes the entropy of both levels and minimizes the entropy difference, which reverses sign near (slightly below) the critical gradient. The corresponding lifetimes of the non-crossing levels (bonding and antibonding) intersect at the critical gradient, as shown in Figure 6C, where the maximum interaction between levels is achieved.

FIGURE 6

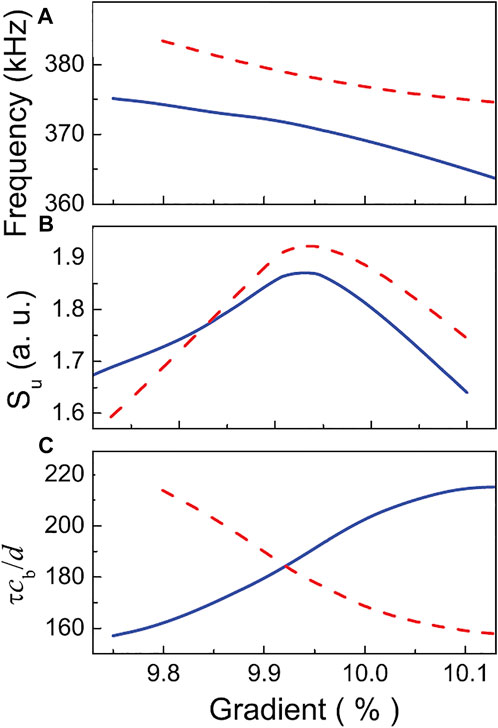
FIGURE 6. (A) The frequency of the two interacting modes near the avoided crossing region for the system experimentally characterized in [34]. (B) The Shannon entropy, S_u, in arbitrary units. (C) The lifetime, τ, (in reduced units) of modes involved in the interacting process. The blue continuous (red dashed) lines represent magnitudes associated to mode u₁ (u₂).

4 Conclusion

We have introduced the Shannon entropy in acoustics as a characterization tool revealing the spatial spreading of acoustic eingenmodes. The Shannon entropy is a global concept in science and is here proposed as an alternative to other indicators employed to measuring the localization of eigenmodes. The Shannon entropy, as it is introduced here, is more general feature than, for example, the inverse participation ratio since it can be applied not only to disordered systems. We show that it represents fairly well localization effects taking place in phenomena associated with physical fields, like the resonant Zener-like effect. The information exchange between levels is a translation into acoustics of the crossing previously pointed out by von Neumann and Wigner [47], who studied interacting levels in quantum mechanics. The Shannon entropy is therefore an appropriate magnitude to quantitatively estimate information exchange among field eigenmodes. Let us stress that Shannon entropy can be experimentally determined in any acoustical system, where direct measurements of displacement fields can be performed, as in the structures described in [48]. The application of information theory in studying electromagnetic confinement produced by photonic crystals is in order, since localization still remains an open problem. Moreover, field eigenmodes involves localization and strong enhancements, which are useful to engineering metasurfaces, enhancing field emission, controlling light at the nanoscale, sensing and spectroscopy at the single-molecule level or non-linear and ultrafast optics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JS-D conceived the idea and developed the theoretical model. JRA-G performed numerical simulations. Both authors discussed the results and wrote the manuscript.

Funding

JRA-G acknowledges the financial support by the Spanish Ministerio de Ciencia e Innovación through the grant with Ref. PID2019-107391RB-I00. The work of JS-D is part of the RDI grant PID2020-112759GB-I00 funded by MCIN/AEI/10.13039/501100011033.”

Acknowledgments

Both authors thank H. Sanchis-Alepuz for his help in the numerical simulations. JS-D acknowledges R. Gonzaléz-Férez and J. S. Dehesa for useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shannon CE. A mathematical theory of communication. Bell Syst Tech J (1948) 27:379–656.

CrossRef Full Text | Google Scholar

2. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys (2012) 75:126001. doi:10.1088/0034-4885/75/12/126001

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Parrondo JMR, Horowitz JM, Sagawa T. Thermodynamics of information. Nat Phys (2015) 11:131–9. doi:10.1038/nphys3230

CrossRef Full Text | Google Scholar

4. Arias-Gonzalez JR. Thermodynamic framework for information in nanoscale systems with memory. J Chem Phys (2017) 147:205101. doi:10.1063/1.5004793

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Gavrilov M, Chétrite R, Bechhoefer J. Direct measurement of weakly nonequilibrium system entropy is consistent with Gibbs–Shannon form. Proc Natl Acad Sci U S A (2017) 114:11097–102. doi:10.1073/pnas.1708689114

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gaudenzi R, Burzurí E, Maegawa S, van der Zant HSJ, Luis F. Quantum Landauer erasure with a molecular nanomagnet. Nat Phys (2018) 14:565–8. doi:10.1038/s41567-018-0070-7

CrossRef Full Text | Google Scholar

7. Lewis-Swan RJ, Safavi-Naini A, Kaufman AM, Rey AM. Dynamics of quantum information. Nat Rev Phys (2019) 1:627–34. doi:10.1038/s42254-019-0090-y

CrossRef Full Text | Google Scholar

8. Bruss D, Leuchs G. Quantum information: from foundations to quantum Technology. Weinheim, Germany: Wiley VCH (2019).

Google Scholar

9. Nielsen M, Chuang I. Quantum computation and information. Cambridge: Cambridge University Press (2000).

Google Scholar

10. Head-Marsden K, Flick J, Ciccarino CJ, Narang P. Quantum information and algorithms for correlated quantum matter. Chem Rev (2021) 121:3061–120. doi:10.1021/acs.chemrev.0c00620

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Diamond R. Fourth and higher order inequalities. Acta Cryst (1963) 16:627–39. doi:10.1107/s0365110x63001675

CrossRef Full Text | Google Scholar

12. Menendez-Velazquez A, Garcia-Granda S. Informational entropy of Fourier maps. Acta Crystallogr A (2006) 62:129–35. doi:10.1107/s010876730503713x

PubMed Abstract | CrossRef Full Text | Google Scholar

13. González-Férez R, Dehesa JS. Shannon entropy as an indicator of atomic avoided crossings in strong parallel magnetic and electric fields. Phys Rev Lett (2003) 91:113001. doi:10.1103/physrevlett.91.113001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. González-Férez R, Dehesa JS. Diamagnetic informational exchange in hydrogenic avoided crossings. Chem Phys Lett (2003) 373:615–9. doi:10.1016/s0009-2614(03)00669-9

CrossRef Full Text | Google Scholar

15. Sen KD. Characteristic features of Shannon information entropy of confined atoms. J Chem Phys (2005) 123:074110. doi:10.1063/1.2008212

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Thompson DC, JamesAnderson SM, Sen KD. Information theory and wigner crystallization: a model perspective. Int J Quan Chem (2021) 121:e26549. doi:10.1002/qua.26549

CrossRef Full Text | Google Scholar

17. Ribezzi-Crivellari M, Ritort F. Large work extraction and the Landauer limit in a continuous Maxwell demon. Nat Phys (2019) 15:660–4. doi:10.1038/s41567-019-0481-0

CrossRef Full Text | Google Scholar

18. Bérut A, Arakelyan A, Petrosyan A, Ciliberto S, Dillenschneider R, Lutz E, et al. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature (2012) 483:187–9. doi:10.1038/nature10872

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Arias-Gonzalez JR, Nieto-Vesperinas M, Madrazo A. Morphology-dependent resonances in the scattering of electromagnetic waves from an object buried beneath a plane or a random rough surface. J Opt Soc Am A (1999) 16:2928–34. doi:10.1364/josaa.16.002928

CrossRef Full Text | Google Scholar

20. Arias-Gonzalez JR, Nieto-Vesperinas M. Radiation pressure over dielectric and metallic nanocylinders on surfaces: polarization dependence and plasmon resonance conditions. Opt Lett (2002) 27:2149–51. doi:10.1364/ol.27.002149

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Stockman MI. Nanoplasmonic sensing and detection. Science (2015) 348:287–8. doi:10.1126/science.aaa6805

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jiang N, Zhuo X, Wang J. Active plasmonics: principles, structures, and applications. Chem Rev (2018) 118:3054–99. doi:10.1021/acs.chemrev.7b00252

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Burns MA, Fournier JM, Golovchenco JA. Optical binding. Phys Rev Lett (1989) 63:1233–6. doi:10.1103/physrevlett.63.1233

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Forbes KA, Bradshaw DS, Andrews DL. Optical binding of nanoparticles. Nanophotonics (2020) 9:1–17. doi:10.1515/nanoph-2019-0361

CrossRef Full Text | Google Scholar

25. Metzger B, Hentschel M, Giessen H. Ultrafast nonlinear plasmonic spectroscopy: from dipole nanoantennas to complex hybrid plasmonic structures. ACS Photon (2016) 3:1336–50. doi:10.1021/acsphotonics.5b00587

CrossRef Full Text | Google Scholar

26. Chen PY, Monticone F, Argyropoulos C, Alù A. Chapter 4 - Plasmonic Optical Nanoantennas. In: NV Richardson, and S Holloway, editors Modern Plasmonics. Handbook of Surface Science, Vol. 4. North-Holland (2014). p. 109–36. doi:10.1016/B978-0-444-59526-3.00004-5

CrossRef Full Text | Google Scholar

27. Juan ML, Righini M, Quidant R. Plasmon nano-optical tweezers. Nat Photon (2011) 4:349–56. doi:10.1038/nphoton.2011.56

CrossRef Full Text | Google Scholar

28. Piatkowski L, Accanto N, van Hulst NF. Ultrafast meets ultrasmall: controlling nanoantennas and molecules. ACS Photon (2016) 3:1401–14. doi:10.1021/acsphotonics.6b00124

CrossRef Full Text | Google Scholar

29. Taylor AB, Zijlstra P. Single-molecule plasmon sensing: current status and future prospects. ACS Sens (2017) 2:1103–22. doi:10.1021/acssensors.7b00382

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Verschueren DV, Pud S, Shi X, De Angelis L, Kuipers L, Dekker C, et al. Label-free optical detection of DNA translocations through plasmonic nanopores. ACS Nano (2018) 13:61–70. doi:10.1021/acsnano.8b06758

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Urban AS, Fedoruk M, Horton MR, Rädler JO, Stefani FD, Feldmann J, et al. Controlled nanometric phase transitions of phospholipid membranes by plasmonic heating of single gold nanoparticles. Nano Lett (2009) 9:2903–8. doi:10.1021/nl901201h

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bell RJ, Dean P. Atomic vibrations in vitreous silica. Discuss Faraday Soc (1970) 50:55. doi:10.1039/df9705000055

CrossRef Full Text | Google Scholar

33. Thouless DJ. Electrons in disordered systems and the theory of localization. Phys Rep (1974) 13:93–142. doi:10.1016/0370-1573(74)90029-5

CrossRef Full Text | Google Scholar

34. Sanchis-Alepuz H, Kosevich YA, Sánchez-Dehesa J. Acoustic analogue of electronic Bloch oscillations and resonant zener tunneling in ultrasonic superlattices. Phys Rev Lett (2007) 98:134301. doi:10.1103/physrevlett.98.134301

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zener C. A theory of the electrical breakdown of solid dielectrics. Proc R Soc Lond A (1934) 145:523–9.

Google Scholar

36. Schneider H, Grahn HT, Klitzing Kv., Ploog K. Resonance-induced delocalization of electrons in GaAs-AlAs superlattices. Phys Rev Lett (1990) 65:2720–3. doi:10.1103/physrevlett.65.2720

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Rosam B, Leo K, Glück M, Keck F, Korsch HJ, Zimmer F, et al. Lifetime of Wannier-Stark states in semiconductor superlattices under strong Zener tunneling to above-barrier bands. Phys Rev B (2003) 68:125301. doi:10.1103/physrevb.68.125301

CrossRef Full Text | Google Scholar

38. Knight JC, Dubreuil N, Sandoghdar V, Hare J, Lefèvre-Seguin V, Raimond JM, et al. Mapping whispering-gallery modes in microspheres with a near-field probe. Opt Lett (1995) 20:1515. doi:10.1364/ol.20.001515

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Arias-Gonzalez JR, Nieto-Vesperinas M. Resonant near-field eigenmodes of nanocylinders on flat surfaces under both homogeneous and inhomogeneous lightwave excitation. J Opt Soc Am A (2001) 18:657–65. doi:10.1364/josaa.18.000657

CrossRef Full Text | Google Scholar

40. Sanchez-Dehesa J, Sanchis-Alepuz H, Kosevich YA, Torrent D. Acoustic analog of electronic Bloch oscillations and Zener tunneling. J Acoust Soc Am (2006) 120:3283. doi:10.1121/1.4777512

CrossRef Full Text | Google Scholar

41. He Z, Peng S, Cai F, Ke M, Liu Z. Acoustic Bloch oscillations in a two-dimensional phononic crystal. Phys Rev E (2007) 76:056605. doi:10.1103/physreve.76.056605

CrossRef Full Text | Google Scholar

42. Torrent D, Håkansson A, Cervera F, Sánchez-Dehesa J. Homogenization of two-dimensional clusters of rigid rods in air. Phys Rev Lett (2006) 94:204302. doi:10.1103/physrevlett.96.204302

CrossRef Full Text | Google Scholar

43. Torrent D, Sánchez-Dehesa J. Effective parameters of clusters of cylinders embedded in a nonviscous fluid or gas. Phys Rev B (2006) 74:224305. doi:10.1103/physrevb.74.224305

CrossRef Full Text | Google Scholar

44. Torrent D, Sánchez-Dehesa J. Acoustic metamaterials for new two-dimensional sonic devices. New J Phys (2007) 9:323. doi:10.1088/1367-2630/9/9/323

CrossRef Full Text | Google Scholar

45. Brekhovskikh LM. Waves in layered media. New York: Academic Press (1980).

Google Scholar

46. Sanchis L, Håkansson A, Cervera F, Sánchez-Dehesa J. Acoustic interferometers based on two-dimensional arrays of rigid cylinders in air. Phys Rev B (2003) 67:035422. doi:10.1103/physrevb.67.035422

CrossRef Full Text | Google Scholar

47. von Neumann J, Wigner E, Phys Z. English translation. In: RS Knox, and A Gold, editors. Symmetry in the solid state, 30. New York: W.A. INC, 1964 (1929). p. 467167–172.

Google Scholar

48. Gutierrez L, Díaz-de-Anda A, Flores J, Méndez-Sánchez RA, Monsivais G, Morales A, et al. Wannier-Stark ladders in one-dimensional elastic systems. Phys Rev Lett (2006) 97:114301. doi:10.1103/physrevlett.97.114301

PubMed Abstract | CrossRef Full Text | Google Scholar