Exchange bias toggling in amine-ended single-molecule magnetic junctions by contact geometry

The molecular scale magnetic proximity effect is proposed in single-molecule magnetic junctions (SMMJs) consisting of a dissociated amine-ended 1,4-benzenediamine (BDA) molecule coupled to two ferromagnetic Co electrodes. Our self-developed JunPy + Landau-Lifshitz-Gilbert simulation combined with first-principles calculation is employed to investigate the role of contact geometry in the magnetotransport properties of SMMJs with the choice of top, bridge, and hollow contact sites. The strong spinterface effect gives rise to distinct angular dependence of equilibrium field-like spin torque (FLST), asymmetric magnetic hysteresis loop and tunable exchange bias. From the analytical derivation of nonequilibrium Keldysh formalism, we believe that a promising way forward is to activate the multi-reflection process via the so-called molecular spinterface that will allow us to conquer as-yet unexplored magnetotransport properties of organic-based spintronics.

1 Introduction

Multi-toggling of magnetism in nanoscale magnetic heterostructures is significant for both fundamental and application in energy-efficient magnetic data storage, such as computer hard disks and magnetic random access memories (MRAMs). Among the hottest topics in contemporary spintronics, the spinterface [1–6] effect plays a crucial role to modulate the magnetic proximity effects via magnetic field, electric field, mechanical strain, and so on. Much effort has been devoted to solid-state magnetic devices, since the spin polarization and spin-orbit coupling (SOC) are decisive factors in spin transport and magnetic proximity [7–11], such as magnetic anisotropy, exchange bias (EB), and magnetic coercivity.

Electrical and spin switches across a single organic molecule connecting ferromagnetic electrodes are also burgeoning fields for possible applications in nano-spintronics devices [12–14], since chemical design offers various ways to incorporate spin degrees of freedom into a molecule to form the so-called molecular spintronics. Currently, most theoretical works [15–19] focus on the magnetoresistance and the spin-polarized transport in collinear magnetic configurations. The ability to calculate the noncollinear spin torque effect and spin dynamics of magnetic heterostructures remains difficult but important to include the complex structural, electronic, and magnetic properties at spinterfaces for nanoscale spintronics devices.

We introduce in Figure 1 the four steps of DFT + JunPy + LLG calculation procedure, including the density functional theory (DFT) calculation with our self-developed JunPy + LLG simulation, to investigate the magnetoelectric and magnetotransport properties of complex magnetic heterostructures, such as magnetic tunnel junctions (MTJs) [20] and single-molecule magnetic junctions (SMMJs) [21,22]. In this study, we propose the prototypical Co/1,4-benzenediamine (BDA)/Co SMMJs with three kinds of contact geometries for top (BDA-T), bridge (BDA-B), and hollow (BDA-H) contact sites of the N ion bonding to one, two, and three Co apex atoms, respectively. Since the hybridization between Co-d, N-p_y, and π-orbital of the phenyl ring preserve the spin-up pronounced resonance channel [23], the DFT + JunPy + LLG calculation reveals exchange bias toggling via the interplay between spinterface enhanced equilibrium field-like spin torque (FLST) and coercive field of Co electrode. We further use the nonequilibrium Keldysh formalism to clarify the crucial role of multi-reflection processes at interfaces in the non-sinusoidal angular dependence of equilibrium FLST, which may pave the way for unexplored magnetotransport properties of organic-based spintronics.

FIGURE 1

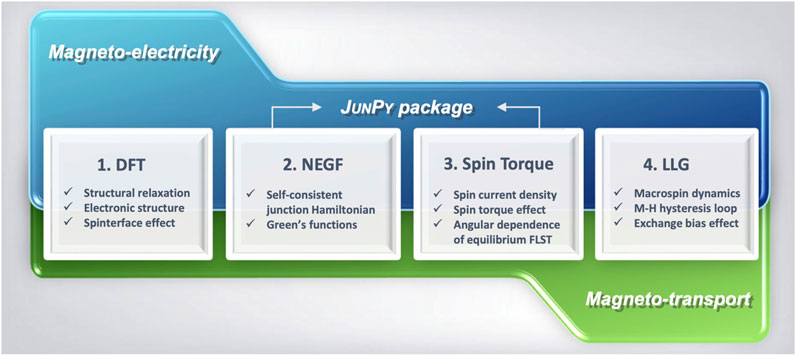
FIGURE 1. DFT + JunPy + LLG calculation procedure to investigate the magnetoelectric and magnetotransport properties of complex magnetic heterostructures, such as magnetic tunnel junctions (MTJs) [20] and single-molecule magnetic junctions (SMMJs) [21, 22].

2 Calculation methods

The first step of DFT + JunPy + LLG calculation is to carry out the first-principles calculation including the complex charge transfer and spinterfacial effect via self-consistent process. In the top of Figures 2A–C, these amine-ended SMMJs are composed of a dissociated 1,4-benzenediamine (BDA) sandwiched by two Co hcp [0001] oriented semi-infinite nanowires. To prevent coupling between SMMJs, we set the lateral separation between two neighboring junctions as 7 Å in both x- and y-directions. The junction geometry is optimized by the Vienna Ab initio simulation package (VASP) [24–27] with DFT based generalized gradient approximation (GGA) in the Perdew, Burke, and Ernzerhof (PBE) [28] form. The lattice constant of Co nanowire is fixed at 2.5 Å, and the Co apex atoms and the central BDA molecule are fully relaxed by using the force criteria of 0.02 eV/Å, the cut-off energy of plane wave basis set as 700 eV, a force criterion of 0.02 eV/Å, the total energy difference for electronic steps as 10^–5 eV, and the k-point sampling of Γ-point. Based on the Pearson’s principle of hard and soft acids and bases (HSAB) [29], the strong coupling between hard metal (Co) and hard base (N) in amine-ended SMMJs favors the covalent bonding between H-dissociated amine linker and Co adatom. This may provide variability in linker–electrode contact geometry, which is crucial but usually not easily controlled during the fabrication of real SMMJs especially for breaking junction techniques [13]. Here we adopt three possible contact geometries, i.e., top (T-III′), bridge (B-II), and hollow (H-III) contact sites proposed in Figure 1 of Ref. [23], as long as the hydrogen ion is dissociated to form a covalent bond between Co-d and N-p_x,y orbitals. On the one hand the N ion bonds to the central phenyl ring, and on the other hand the amine linker tends to dissociate one (two) H ion to form one (two/three) bonding with Co adatom in T (B/H) case to fulfill the octet rule. This thus gives rise to the shorter optimized Co-N bond length of 1.84 Å in both BDA-T and BDA-B cases but the longer one of 1.95 Å in BDA-H case. By using the optimized junction geometries, we next use the two-probe structure with DFT and non-equilibrium Green’s function (NEGF) formalism implemented in Nanodcal transport package [30–32] to investigate the spin-polarized transmission spectum and spinterface effect of SMMJs [23]. The double-ζ double-polarized basis set of local numerical orbitals are applied to all ions, the cut-off energy of real space grid density is 150 Hartree, and the k-point samplings are 1 × 1 × 100 and Γ point for semi-infinite Co electrode and central device, respectively.

FIGURE 2

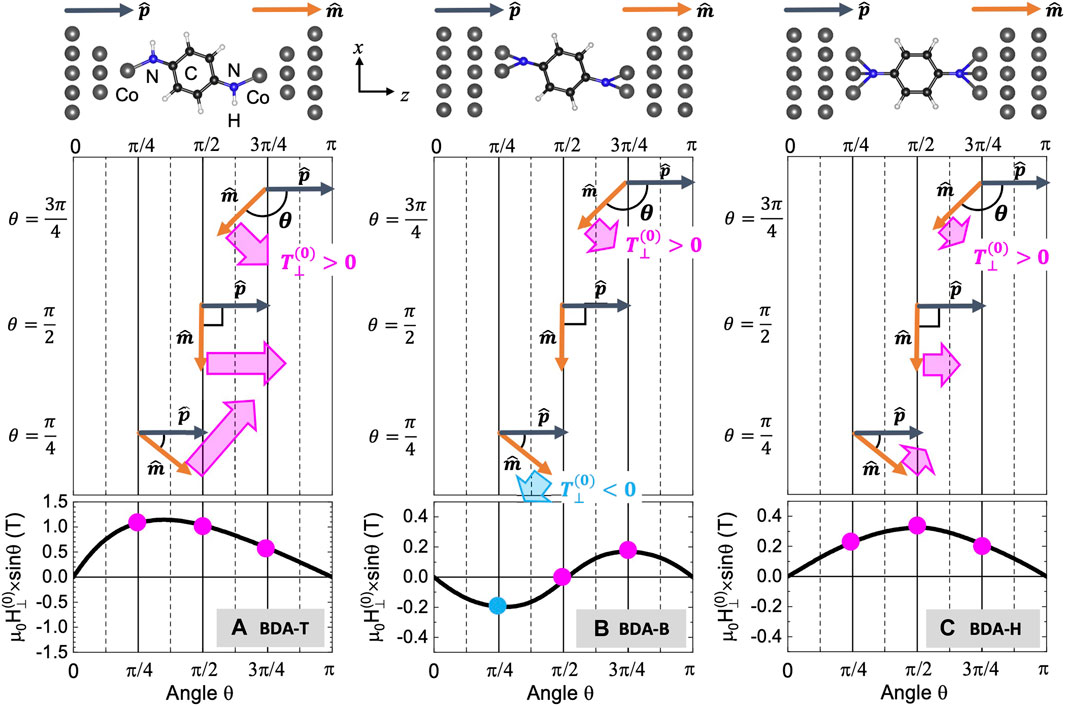
FIGURE 2. [Top] Junction geometries [Middle] the DFT + JunPy calculated equilibrium FLST, $T_{\perp }^{(0)}$, for angle θ = π/4, π/2, and 3π/4, and [Bottom] angular dependence of equilibrium FLST field, ${\mu }_0{H}_{\perp }^{(0)}\times \sin \theta$, for (A) BDA-T (top-site), (B) BDA-B (bridge-site), and (C) BDA-H (hollow-site) cases of amine-ended Co/BDA/Co SMMJs. $\widehat{\mathbf{p}}$ of left (fix) Co electrode is fixed along the z direction, and $\widehat{\mathbf{m}}$ of right (free) electrode is freely rotated by an angle θ around the y axis with respect to the z axis to form a noncollinear magnetic configuration. Here $\widehat{\mathbf{p}}$ and $\widehat{\mathbf{m}}$ are the unit vectors of magnetization of the left (fixed) and right (free) Co nanowires, respectively.

In the second and third steps, our self-developed JunPy package [20, 21, 33] has successfully combined the NEGF and spin torque theory to calculate the angular dependence of equilibrium FLST, $T_{\perp }^{(0)}(\theta )$, in the noncollinear magnetic configurations, which can be formed by fixing $\widehat{\mathbf{p}}$ along the z direction but rotating $\widehat{\mathbf{m}}$ around the y axis with respect to the z axis by an angle θ. Since the weak spin-orbit coupling can be ignored in SMMJs, there are two components of noncollinear spin torque, i.e., the spin-transfer torque (STT, T_‖) and the field-like spin torque (FLST, T_⊥), originated from the spin accumulation of spin current density [34], and only the non-zero equilibrium $T_{\perp }^{(0)}(\theta )$ exists in the absence of an external current. For each angle θ, we repeat Nanodcal + JunPy + NEGF calculation to acquire the self-consistent junction Hamiltonian matrix $\widehat{H}$, the overlap integral $\widehat{S}$, and the reduced Hamiltonian matrix $\widehat{\mathcal{H}}\equiv (\widehat{H}-E\widehat{S})$ to resolve the lesser Green’s function matrix ${\widehat{G}}^{<}$ in the central device region. Here ${\mathrm{Q}}_n^y={\sum }_{i<n}{\sum }_{j>n}{\mathrm{Q}}_{i,j}^y$ with the subscript n = 0 denotes the spin current passing through the interface between the right NH-linker and the right Co apex atoms, where the spin current density between the two atomic sites i and j can be calculated by

${\mathrm{Q}}_{i,j}^y=\frac{1}{4\pi }\int \text{Tr}\left[{\widehat{\mathcal{H}}}_{i,j}{\widehat{G}}_{j,i}^{<}-{\widehat{G}}_{i,j}^{<}{\widehat{\mathcal{H}}}_{j,i}\right]{\mathit{\sigma }}_{\mathit{y}}dE(1)$

and σ_y is the y-component of Pauli matrices. Thus, the net FLST acting on the right (free) Co electrode is defined as $T_{\perp }=Q_0^y$ in the directions of $-\widehat{\mathbf{m}}\times \widehat{\mathbf{p}}$.

The last step of macrospin dynamics simulation is to apply the generalized Landau-Lifshitz-Gilbert (LLG) equation with equilibrium FLST component of spin torque [22, 35] as expressed in the form of

$\frac{1+{\alpha }^2}{\gamma }\frac{d\widehat{\mathbf{m}}}{dt}=-\widehat{\mathbf{m}}\times \left({\mathbf{H}}_{\mathrm{eff}}+{\mathbf{H}}_{\mathrm{pre}}\right)-\widehat{\mathbf{m}}\times \left[\widehat{\mathbf{m}}\times \alpha \left({\mathbf{H}}_{\mathrm{eff}}+{\mathbf{H}}_{\mathrm{damp}}\right)\right],(2)$

where γ is the gyromagnetic ratio, α is the Gilbert damping constant, ${\mathbf{H}}_{\mathrm{damp}}^{(\mathbf{0})}$ and ${\mathbf{H}}_{\mathrm{pre}}^{(\mathbf{0})}$ are the effective fields along damping and precession directions of right Co electrode, respectively. At equilibrium, ${\mathbf{H}}_{\mathrm{damp}}^{(\mathbf{0})}={\mathbf{H}}_{\mathrm{pre}}^{(\mathbf{0})}=H_{\perp }^{(0)}\widehat{\mathbf{p}}$ and $H_{\perp }^{(0)}\sin \theta =T_{\perp }^{(0)}/({\mu }_0{M}_s{t}_{F}A)$ represents the effective field induced by the equilibrium FLST, where M_s, t_F and A are the volume magnetization saturation parameter, the thickness and the lateral area of right Co electrode, respectively. For Co electrode [36], α = 0.01, μ₀H_k = 76 mT, M_s = 1.27 × 10⁶ A/m, the thickness t_F = 100 nm, and the lateral area A = 1.63 × 10^–19 m² are chosen in this work.

3 Results and discussion

3.1 Effect of contact geometry on EB effect: DFT + JunPy + LLG

In the bottom of Figures 2A–C, we demonstrate the angular dependence of DFT + JunPy calculated equilibrium FLST fields, ${\mu }_0{H}_{\perp }^{(0)}$, for top (BDA-T), bridge (BDA-B), and hollow (BDA-H) contact geometries. Because of the covalent bonding between H-dissociated amine linker and Co apex atoms as shown in Figure 2 of Ref. [23], all three cases exhibit pronounced π-resonant spin-up transmission near Fermi energy. Such spinterface effect assists strong enhancement of ${\mu }_0{H}_{\perp }^{(0)}$ which is about one to two orders of magnitude larger than μ₀H_k of Co electrode. To further investigate the effect of equilibrium FLST fields on the magnetization switching, our self-developed JunPy + LLG package is employed to solve the generalized LLG equation in Eq. 2. The DFT + JunPy + LLG calculated magnetic hysteresis curves (m_z-H) for BDA-T, BDA-B, and BDA-H cases at zero temperature are presented in Figures 3A–C, respectively.

FIGURE 3

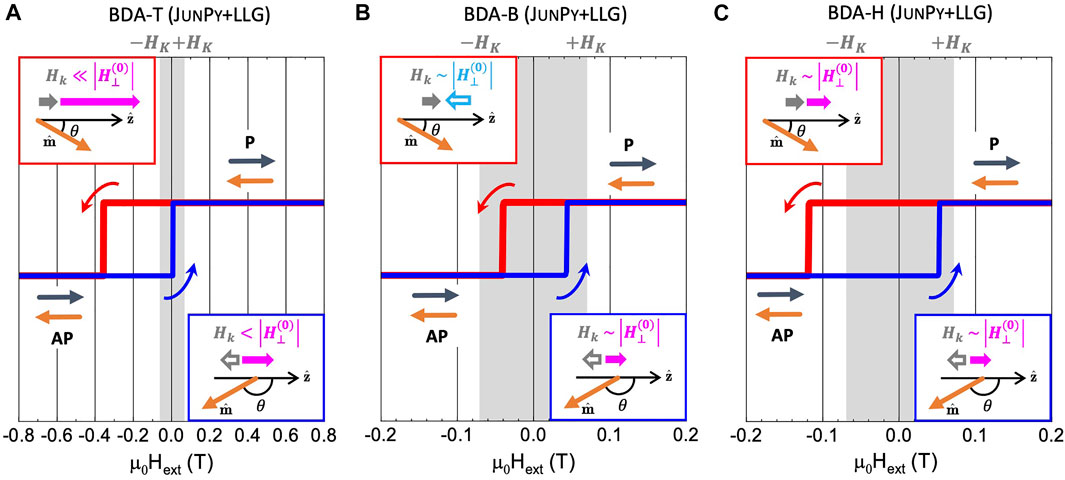
FIGURE 3. The JunPy + LLG calculated magnetic hysteresis curves (m_z-H) for (A) BDA-T (top-site), (B) BDA-B (bridge-site), and (C) BDA-H (hollow-site) cases of amine-ended Co/BDA/Co SMMJs at zero temperature. The insets are the schematics of $H_{\perp }^{(0)}$ and H_k when θ is below and above 90°, where H_k is the cohesive field of the right Co electrode. The gray shaded area represents the field region between ± μ₀H_k. The red (blue) curved arrow is the threshold fields required for P-to-AP (AP-to-P) magnetization switching, where P and AP denote the parallel (θ = 0) and antiparallel (θ = π) magnetic configurations, respectively.

For the BDA-T case in Figure 2A, its ${\mu }_0{H}_{\perp }^{(0)}\times \sin \theta$ exhibits the non-sinusoidal angular dependence with a positive value and a maximum below π/2. Note that the positive and negative magnitudes refer to the field-like and anti-field-like equilibrium fields, respectively. When θ⩽π/2, the large and positive magnitude implies that the free $\widehat{\mathbf{m}}$ tends to move toward the parallel (P) magnetic configuration with θ = 0. In other words, such strong and positive equilibrium FLST field, i.e., $H_{\perp }^{(0)}\gg H_K$ where H_K is cohesive field of right Co electrode, significantly postpones the P-to-AP magnetic switching (red line) at a much more negative external magnetic field (μ₀H_ext) and hence in turn causes large EB effect as shown in Figure 3A. Instead, for θ > π/2 the positive but smaller magnitude pushes the free $\widehat{\mathbf{m}}$ away from the anti-parallel (AP) magnetic configuration with θ = π, that is to say, $|H_{\perp }^{(0)}|>H_K$ assists the AP-to-P magnetic switching (blue line) at less positive field and thus in turn leads to a highly asymmetric magnetic hysteresis loop as shown in Figure 3A.

Unlike BDA-T case, the smaller magnitude with nearly sin 2θ angular dependence of ${\mu }_0{H}_{\perp }^{(0)}\times \sin \theta$ for BDA-B case is presented in Figure 2B. Its negative value for θ < π/2 and positive value for θ > π/2 both result in the fact of $H_{\perp }^{(0)}\sim -H_K$. Interestingly, their comparable magnitudes but opposite signs assist both P-to-AP (red line) and AP-to-P (blue-line) magnetic switching to form a symmetric but narrower magnetic hysteresis loop as shown in Figure 3B. On the other hand, the BDA-H case retains the sinusoidal angular dependence of $T_{\perp }^{(0)}$ similar to conventional MTJs [37], due to its relatively larger Co-N bond length (1.95 Å) compared to those of BDA-T (1.84 Å) and BDA-B (1.84 Å) cases. However, the existence of spinterface effect of BDA-H case still gives notable and positive value of |H⁽⁰⁾|∼ H_K for both θ < π/2 and θ > π/2 and an asymmetric and slightly shifted magnetic hysteresis loop as shown in Figure 3C.

To further demonstrate the validity of our self-developed LLG simulation, we carry out the well-known OOMMF software [38] with the extension of SpinXferEvolve, but this extension simply uses default sinusoidal angular dependence of FLST in MTJs. Therefore, we revise it to include the user-defined angular dependence of FLST by fitting to our DFT + JunPy calculation in Co/BDA/Co SMMJs with three kinds of contact geometries as presented in Figures 2A–C. It is clear to find the excellent agreement between OOMMF simulation in Figures 4A–C and our own LLG calculation in Figures 4A–C.

FIGURE 4

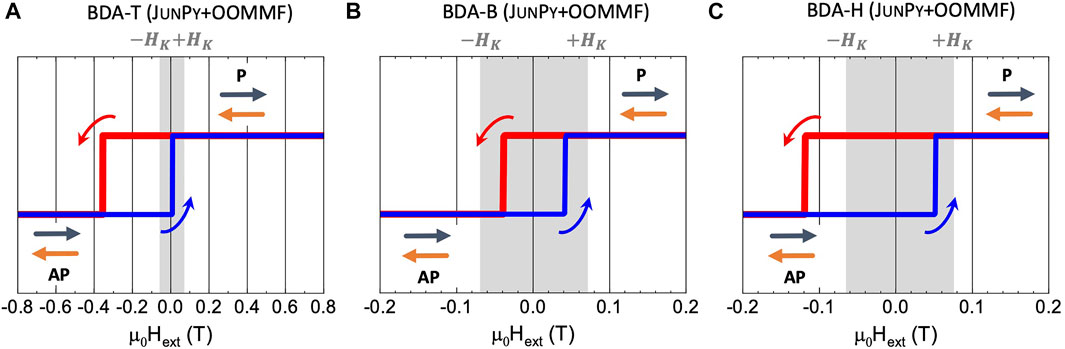
FIGURE 4. The JunPy + OOMMF calculated magnetic hysteresis curves (mz‐H) for (A) BDA‐T (top‐site), (B) BDA‐B (bridge‐site), and (C) BDA‐H (hollow‐site) cases of amine‐ended Co/BDA/Co SMMJs at zero temperature.

3.2 Angular dependence of equilibrium FLST $T_{\perp }^{(0)}$: Analytical derivation

Finally, we turn to investigate the underlying mechanism of non-sinusoidal angular dependence of equilibrium FLST field by using the NEGF method to derive analytical formalism of equilibrium FLST $T_{\perp }^{(0)}$ in Co/Barrier/Co MTJ with noncollinear magnetic configuration. In Figures 5A,B, the central barrier is considered as 1) the resonant tunneling barrier for BDA-based MTJs with strong spinterface effect and 2) the direct tunneling barrier for Co/BDMA/Co SMMJs where additional methylene (CH₂) units are inserted between N-atom and the phenyl ring to form the 1,4-benzenedimethanamine (BDMA) molecule and then eventually destroy the spinterface effect. This is because CH₂ unit well separates N-p_x,y orbital and π orbital of central phenyl ring near Fermi energy as shown in Figure 3 of Ref. [23].

FIGURE 5

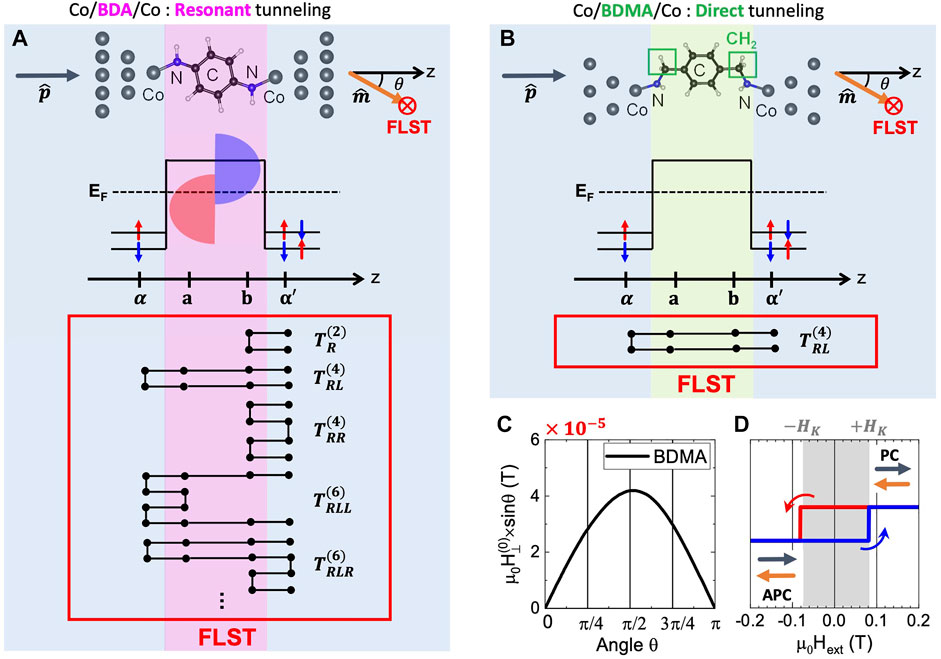
FIGURE 5. [Top] Junction geometries, [Middle] schematic of energy profile, and [Bottom] schematic of multi-reflection paths of $T_{\perp }=Q_0^y$ for (A) resonant tunneling via spinterface effect of Co/BDA/Co SMMJs and (B) direct tunneling for Co/BDMA/Co SMMJs. The red and blue shaded areas represent the pronounced π-resonant spin-polarized density of states of central barrier for BDA-case. Here α (α′) is the last (first) site of left (right) Co lead, and a and b are the first and last sites of the central barrier, respectively. (C) Angular dependence of equilibrium FLST field, ${\mu }_0{H}_{\perp }^{(0)}\times \sin \theta$ and (D) the JunPy + LLG calculated magnetic hysteresis curves (m_z-H) for Co/BDMA/Co SMMJ.

The net equilibrium FLST acting on the right (free) Co electrode can be defined by the one-dimensional tight-binding model with non-equilibrium Keldysh formalism [39],

$\begin{array}{ccc}\hfill T_{\perp }^{\left(0\right)}=Q_0^y& =\hfill & \frac{1}{4\pi }\int \mathit{Tr}\left[t\left({\widehat{G}}_{{\alpha }^{\prime }b}^{<}-{\widehat{G}}_{b{\alpha }^{\prime }}^{<}\right){\sigma }_y\right]dE\hfill \\ \hfill & =\hfill & T_R^{\left(2\right)}+\left[T_{RL}^{\left(4\right)}+T_{RR}^{\left(4\right)}\right]+\left[T_{\mathit{RLL}}^{\left(6\right)}+T_{\mathit{RLR}}^{\left(6\right)}+T_{\mathit{RRL}}^{\left(6\right)}+T_{\mathit{RRR}}^{\left(6\right)}\right]+O\left(t^8\right),\hfill \end{array}(3)$

where b and α′ denote the last site of barrier and first site of right Co electrode, respectively, and t is the coupling between barrier and the two Co electrodes. In consideration of multi-reflection process between two Co leads, the $T_R^{(2)}$, $T_{RL,RR}^{(4)}$, and $T_{\mathit{RLL,RLR,RRL,RRR}}^{(6)}$ presented in the bottom of Figure 5A denote the equilibrium FLST contributed by multi-reflection at one, two, and three left (L) or right (R) interfaces, respectively. The details of analytical derivation are arranged in the following. For Co/Barrier/Co MTJ, ${\widehat{g}}_{L,B,R}^{r,a,<}$ are the retarded, advanced, and lesser Green’s functions for the isolated left (L) Co, central barrier (B), and right (R) Co; t is the coupling between the two neighboring regions; and the coupled Green’s function matrix of the MTJ can be written as

${\widehat{G}}^{r,a}=\left[\begin{array}{ccc}\hfill {\left({\widehat{g}}_L^{r,a}\right)}^{-1}\hfill & \hfill t\hfill & \hfill 0\hfill \\ \hfill t\hfill & \hfill {\left({\widehat{g}}_B^{r,a}\right)}^{-1}\hfill & \hfill t\hfill \\ \hfill 0\hfill & \hfill t\hfill & \hfill {\left({\widehat{g}}_R^{r,a}\right)}^{-1}\hfill \end{array}\right]\text{with}{\widehat{g}}_B^{r,a}=\left[\begin{array}{cc}\hfill {\widehat{g}}_{aa}^{r,a}\hfill & \hfill {\widehat{g}}_{ab}^{r,a}\hfill \\ \hfill {\widehat{g}}_{ba}^{r,a}\hfill & \hfill {\widehat{g}}_{bb}^{r,a}\hfill \end{array}\right].(4)$

Note that ${\widehat{G}}^{r,a}$ is a 4 × 4 matrix with matrix elements of ${\widehat{G}}^{r,a}[\mathrm{2,2}]={\widehat{g}}_{aa}^{r,a}$, ${\widehat{G}}^{r,a}[\mathrm{2,3}]={\widehat{g}}_{ab}^{r,a}$, ${\widehat{G}}^{r,a}[\mathrm{3,2}]={\widehat{g}}_{ba}^{r,a}$, and ${\widehat{G}}^{r,a}[\mathrm{3,3}]={\widehat{g}}_{bb}^{r,a}$, and all Green’s functions are expanded as 2 × 2 matrices in spin space. Following by the Dyson equation, we can use the equations of ${\widehat{G}}_{{\alpha }^{\prime }b}^{<}={\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{r}t{\widehat{G}}_{bb}^{<}+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}t{\widehat{G}}_{bb}^a$, ${\widehat{G}}_{b{\alpha }^{\prime }}^{<}={\widehat{G}}_{bb}^{r}t{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}+{\widehat{G}}_{bb}^{<}t{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a$, and ${\widehat{G}}_{bb}^{<}={\widehat{G}}_{ba}^{r}t{\widehat{g}}_{\alpha \alpha }^{<}t{\widehat{G}}_{ab}^a+{\widehat{G}}_{bb}^{r}t{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}t{\widehat{G}}_{bb}^a$ to recast

$t\left({\widehat{G}}_{{\alpha }^{\prime }b}^{<}-{\widehat{G}}_{b{\alpha }^{\prime }}^{<}\right)=t^2{\widehat{G}}_R^{\left(2\right)}+t^4\left[{\widehat{G}}_{RL}^{\left(4\right)}+{\widehat{G}}_{RR}^{\left(4\right)}\right]+t^6\left[{\widehat{G}}_{\mathit{RLL}}^{\left(6\right)}+{\widehat{G}}_{\mathit{RLR}}^{\left(6\right)}+{\widehat{G}}_{\mathit{RRL}}^{\left(6\right)}+{\widehat{G}}_{\mathit{RRR}}^{\left(6\right)}\right]+O\left(t^8\right)(5)$

where

$\begin{array}{ccc}\hfill {\widehat{G}}_R^{\left(2\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}\hfill \\ \hfill {\widehat{G}}_{RL}^{\left(4\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill {\widehat{G}}_{RR}^{\left(4\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill {\widehat{G}}_{\mathit{RLL}}^{\left(6\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{aa}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{aa}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{aa}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a\hfill \\ \hfill & \hfill & -{\widehat{\hspace{0.17em}g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{aa}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{aa}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{aa}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill {\widehat{G}}_{\mathit{RLR}}^{\left(6\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a\hfill \\ \hfill & \hfill & -{\widehat{\hspace{0.17em}g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill {\widehat{G}}_{\mathit{RRL}}^{\left(6\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{ba}^a{\widehat{g}}_{\alpha \alpha }^a{\widehat{g}}_{ab}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a\hfill \\ \hfill & \hfill & -{\widehat{\hspace{0.17em}g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^r{\widehat{g}}_{ab}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a-{\widehat{g}}_{ba}^r{\widehat{g}}_{\alpha \alpha }^{<}{\widehat{g}}_{ab}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill {\widehat{G}}_{\mathit{RRR}}^{\left(6\right)}& =\hfill & {\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a+{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a\hfill \\ \hfill & \hfill & -{\widehat{\hspace{0.17em}g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^r{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a-{\widehat{g}}_{bb}^r{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^{<}{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a{\widehat{g}}_{bb}^a{\widehat{g}}_{{\alpha }^{\prime }{\alpha }^{\prime }}^a\hfill \\ \hfill \cdots & \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}(6)$

By substituting Eqs 5, 6 into Eq. 3, we can derive the corresponding $T_R^{(2)}$, $T_{RL,RR}^{(4)}$, and $T_{\mathit{RLL,RLR,RRL,RRR}}^{(6)}$ contributions of net $T_{\perp }^{(0)}$ in consideration of multi-reflection processes. It is worth to mention that Eq. 6 is similar to Eqs 7–9 of Xiao et al. [36] for metallic spin valves due to its diffusive component to the spin-dependent reflection at interfaces.

We finally discuss the angular dependence of equilibrium FLST for noncollinear Co/BDA/Co(θ) SMMJ in Figure 5A. To simulate its strong spin-up dominated π-resonant tunneling, both $g_{i,j}^{\uparrow }$ and $g_{i,j}^{\downarrow }$ are complex numbers for (i,j)=(a,b) inside the resonant barrier, namely, the equilibrium FLST must consider all multi-reflection processes. We then summarize a general expression as

$T_{L^M{R}^{N-M}}^{\left(2N\right)}=\sin \theta \times \left[a_0+\sum _{n=1}^{N-M-1}{a}_n{\cos }^n\theta \right](7)$

to represent the t^2N-th order of equilibrium FLST including the Nth multi-reflection processes of M and (N − M) times at left Co/N and right N/Co interfaces, respectively, and a₀ and a_n’s are real numbers. Notably, this allows us to modulate the spinterface induced non-sinusoidal angular dependence of equilibrium FLST fields via the contact geometry in BDA-based SMMJs as shown in Figures 2A–C.

It is interesting to recall that BDA-H case exhibits pronounced π-resonant spin-up transmission near Fermi energy even though its Co-N bond length (1.95 Å) is relatively larger than those of BDA-T (1.84 Å) and BDA-B (1.84 Å) cases. This gives rise to a weaker spinterface effect of BDA-H case that still can assist the enhancement of equilibrium FLST, i.e., |H⁽⁰⁾|∼ H_K, but the larger Co-N bond length significantly weakens those contributions from multi-reflection process and hence in turn preserves the sinusoidal angular dependence of $T_{\perp }^{(0)}$ as shown in Figure 2C. In sharp contrast, the central BDMA molecule of noncollinear Co/BDMA/Co(θ) SMMJ can be simplified as the direct tunneling barrier, due to the elimination of spinterface effect by inserting additional CH₂ units as shown in Figure 5B. Similar to the insulating barrier in MTJs [37], it has been known that $T_{\perp }\sim T_{RL}^{(4)}$ exhibits sinusoidal angular dependence and a much smaller magnitude which is about two orders of magnitude smaller than that of BDA-H case. Therefore, the fact of $|H_{\perp }^{(0)}|\ll H_K$ does not cause EB effect and then remains symmetric P-to-AP and AP-to-P magnetic switching at ∓ H_K as presented in Figures 5C,D.

4 Conclusion

We summarize the four steps of DFT + JunPy + LLG calculation, which successfully resolve computational difficulties in spin torque, magnetotransport and magnetic proximity for complex magnetic heterojunctions with noncollinear magnetic configurations. Here we propose three types of dissociated amine-ended Co/BDA/Co SMMJs with top, bridge, and hollow contact sites together with strong equilibrium FLST fields, i.e., $|H_{\perp }^{(0)}|⩾H_K$. Our calculation results illustrate the underlying mechanism in an important aspect, namely, molecular scale exchange bias effect, via the modulation of angular dependence of equilibrium FLST. In consideration of spinterface induced resonant tunneling via central BDA molecule, the nonequilibrium Keldysh formalism is applied to derive the non-sinusoidal angular dependence of equilibrium FLST resulting from the multi-reflection processes at interfaces.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

Y-HT conceived the study and carried out the DFT + JunPy + LLG calculation. Y-HT and Y-CC carry out the analytical derivation and the macrospin dynamics simulation. B-HH developed JunPy + LLG code. All authors discussed the results and wrote the manuscript.

Funding

This work is supported by the Ministry of Science and Technology (MOST 107-2633-M-008-004- and 108-2628-M-008-004-MY3) and the National Center for Theoretical Sciences (NCTS).

Acknowledgments

We thank Yu-Sheng Lin to support the analytical derivation of spin torque effect via resonant tunneling. We thank to National Center for High-performance Computing (NCHC) of National Applied Research Laboratories (NARLabs) in Taiwan for providing computational and storage resources.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sanvito S. The rise of spinterface science. Nat Phys (2010) 6:562–4. doi:10.1038/nphys1714

CrossRef Full Text | Google Scholar

2. Ruden P. Interfaces are critical. Nat Mater (2011) 10:8–9. doi:10.1038/nmat2933

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Tsymbal EY. Electric toggling of magnets. Nat Mater (2012) 11:12–3. doi:10.1038/nmat3205

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dieny B, Chshiev M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev Mod Phys (2017) 89:025008. doi:10.1103/RevModPhys.89.025008

CrossRef Full Text | Google Scholar

5. Cinchetti M, Dediu VA, Hueso LE. Activating the molecular spinterface. Nat Mater (2017) 16:507–15. doi:10.1038/nmat4902

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Go D, Freimuth F, Hanke J-P, Xue F, Gomonay O, Lee K-J, et al. Theory of current-induced angular momentum transfer dynamics in spin-orbit coupled systems. Phys Rev Res (2020) 2:033401. doi:10.1103/PhysRevResearch.2.033401

CrossRef Full Text | Google Scholar

7. Fan Y, Smith KJ, Lüpke G, Hanbicki AT, Goswami R, Li CH, et al. Exchange bias of the interface spin system at the Fe/MgO interface. Nat Nanotechnol (2013) 8:438–44. doi:10.1038/nnano.2013.94

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Manna PK, Yusuf SM. Two interface effects: Exchange bias and magnetic proximity. Phys Rep (2014) 535:61–99. doi:10.1016/j.physrep.2013.10.002

CrossRef Full Text | Google Scholar

9. Liang X, Deng L, Huang F, Tang T, Wang C, Zhu Y, et al. The magnetic proximity effect and electrical field tunable valley degeneracy in MoS2/EuS van der waals heterojunctions. NANOSCALE (2017) 9:9502–9. doi:10.1039/c7nr03317f

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lin P-H, Yang B-Y, Tsai M-H, Chen P-C, Huang K-F, Lin H-H, et al. Manipulating exchange bias by spin–orbit torque. Nat Mater (2019) 18:335–41. doi:10.1038/s41563-019-0289-4

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Srivastava PK, Hassan Y, Ahn H, Kang B, Jung S-G, Gebredingle Y, et al. Exchange bias effect in ferro-/antiferromagnetic van der waals heterostructures. Nano Lett (2020) 20:3978–85. doi:10.1021/acs.nanolett.0c01176

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Aragonès AC, Medina E, Ferrer-Huerta M, Gimeno N, Teixidó M, Palma JL, et al. Measuring the spin-polarization power of a single chiral molecule. Small (2017) 13:1602519. doi:10.1002/smll.201602519

CrossRef Full Text | Google Scholar

13. Gehring P, Thijssen JM, van der Zant HSJ. Single-molecule quantum-transport phenomena in break junctions. Nat Rev Phys (2019) 1:381–96. doi:10.1038/s42254-019-0055-1

CrossRef Full Text | Google Scholar

14. Ke G, Duan C, Huang F, Guo X. Electrical and spin switches in single-molecule junctions. InfoMat (2020) 2:92–112. doi:10.1002/inf2.12068

CrossRef Full Text | Google Scholar

15. Liu D, Hu Y, Guo H, Han XF. Magnetic proximity effect at the molecular scale: First-principles calculations. Phys Rev B (2008) 78:193307. doi:10.1103/PhysRevB.78.193307

CrossRef Full Text | Google Scholar

16. Mandal S, Pati R. What determines the sign reversal of magnetoresistance in a molecular tunnel junction? ACS Nano (2012) 6:3580–8. doi:10.1021/nn3006569

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Smogunov A, Dappe YJ. Symmetry-derived half-metallicity in atomic and molecular junctions. Nano Lett (2015) 15:3552–6. doi:10.1021/acs.nanolett.5b01004

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Li D, Banerjee R, Mondal S, Maliyov I, Romanova M, Dappe YJ, et al. Symmetry aspects of spin filtering in molecular junctions: Hybridization and quantum interference effects. Phys Rev B (2019) 99:115403. doi:10.1103/PhysRevB.99.115403

CrossRef Full Text | Google Scholar

19. Zhang L-M, Miao Y-Y, Cao Z-P, Qiu S, Zhang G-P, Ren J-F, et al. Bias-induced reconstruction of hybrid interface states in magnetic molecular junctions. Chin Phys B (2022) 31:057303. doi:10.1088/1674-1056/ac3caf

CrossRef Full Text | Google Scholar

20. Huang B-H, Chao C-C, Tang Y-H. Thickness dependence of spin torque effect in Fe/MgO/Fe magnetic tunnel junction: Implementation of divide-and-conquer with first-principles calculation. AIP Adv (2021) 11:015036. doi:10.1063/9.0000117

CrossRef Full Text | Google Scholar

21. Tang Y-H, Huang B-H. Manipulation of giant field-like spin torque in amine-ended single-molecule magnetic junctions. J Phys Chem C (2018) 122:20500–5. doi:10.1021/acs.jpcc.8b03772

CrossRef Full Text | Google Scholar

22. Tang Y-H, Huang B-H. Underlying mechanism for exchange bias in single-molecule magnetic junctions. Phys Rev Res (2021) 3:033264. doi:10.1103/PhysRevResearch.3.033264

CrossRef Full Text | Google Scholar

23. Chiang K-R, Tang Y-H. Effect of contact geometry on spin transport in amine-ended single-molecule magnetic junctions. ACS Omega (2021) 6:19386–91. doi:10.1021/acsomega.1c00930

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B (1993) 47:558–61. doi:10.1103/PhysRevB.47.558

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kresse G, Hafner J. Ab initio molecular dynamics for open-shell transition metals. Phys Rev B (1993) 48:13115–8. doi:10.1103/PhysRevB.48.13115

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kresse G, Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys Rev B (1994) 49:14251–69. doi:10.1103/PhysRevB.49.14251

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kresse G, Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci (1996) 6:15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

28. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Pearson RG. Hard and soft acids and bases. J Am Chem Soc (1963) 85:3533–9. doi:10.1021/ja00905a001

CrossRef Full Text | Google Scholar

30. Waldron D, Liu L, Guo H. Ab initio simulation of magnetic tunnel junctions. Nanotechnology (2007) 18:424026. doi:10.1088/0957-4484/18/42/424026

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Taylor J, Guo H, Wang J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys Rev B (2001) 63:245407. doi:10.1103/PhysRevB.63.245407

CrossRef Full Text | Google Scholar

32. Ke Y, Xia K, Guo H. Disorder scattering in magnetic tunnel junctions: Theory of nonequilibrium vertex correction. Phys Rev Lett (2008) 100:166805. doi:10.1103/PhysRevLett.100.166805

PubMed Abstract | CrossRef Full Text | Google Scholar

33.[Dataset] Huang B-H, Tang Y-H. The detailed information of our newly developed JunPy package can be found at (2018). Available at: https://labstt.phy.ncu.edu.tw/junpy.

Google Scholar

34. Stiles MD, Zangwill A. Anatomy of spin-transfer torque. Phys Rev B (2002) 66:014407. doi:10.1103/PhysRevB.66.014407

CrossRef Full Text | Google Scholar

35. de Sousa DJP, Haney PM, Zhang DL, Wang JP, Low T. Bidirectional switching assisted by interlayer exchange coupling in asymmetric magnetic tunnel junctions. Phys Rev B (2020) 101:081404. doi:10.1103/PhysRevB.101.081404

CrossRef Full Text | Google Scholar

36. Xiao J, Zangwill A, Stiles MD. Macrospin models of spin transfer dynamics. Phys Rev B (2005) 72:014446. doi:10.1103/PhysRevB.72.014446

CrossRef Full Text | Google Scholar

37. Tang Y-H, Kioussis N, Kalitsov A, Butler WH, Car R. Controlling the nonequilibrium interlayer exchange coupling in asymmetric magnetic tunnel junctions. Phys Rev Lett (2009) 103:057206. doi:10.1103/PhysRevLett.103.057206

PubMed Abstract | CrossRef Full Text | Google Scholar

38.[Dataset] Donahue J, Porter DG. OOMMF user’s guide version 1.0. Gaithersburg, MD: National Institute of Standards and Technology (1999).

Google Scholar

39. Tang Y-H, Huang Z-W, Huang B-H. Analytic expression for the giant fieldlike spin torque in spin-filter magnetic tunnel junctions. Phys Rev B (2017) 96:064429. doi:10.1103/PhysRevB.96.064429

CrossRef Full Text | Google Scholar