New fermions in the light of the (g − 2)μ

The very precise measurement of the anomalous magnetic moment of the muon, recently released by the Muon g-2 experiment at Fermilab, can serve to set stringent constraints on new particles. If the observed 4σ discrepancy from the Standard Model value is indeed real, it will set a tight margin on the scale of the masses and couplings of these particles. Instead, if the discrepancy is simply a result of additional theoretical and experimental uncertainties to be included, strong constraints can be put on their parameters. In this mini-review, we summarize the impact of the latest muon g-2 measurement on new fermions that are predicted by a wide range of new physics models and with exotic quantum numbers and interactions. We will particularly discuss the case of vector-like leptons, excited leptons, and supersymmetric fermions, as well as spin-3/2 isosinglet fermions, which have been advocated recently.

1 Introduction

The Fermilab Muon g − 2 collaboration has recently released [1] a new measurement of the anomalous magnetic moment, $a_{\mu }=\frac{1}{2}{(g-2)}_{\mu }$, of the muon, $a_{\mu }^{\text{Fermilab}}=(116592040\pm 54)\times 10^{-11}$, representing a 3.3σ deviation from the Standard Model (SM) value, for which a wide consensus among theorists gave the prediction [2].

$a_{\mu }^{\text{SM}}=\left(116591810\pm 43\right)\times 10^{-11},(1)$

before a new lattice QCD analysis [3] predicted a value that is more agreeing with the SM expectation. When combined with the result of the previous Brookhaven muon experiment [4] which had a deviation of about 3.7σ from the SM expectation, one obtains a final result

$a_{\mu }^{\text{EXP}}=\left(116592061\pm 41\right)\times 10^{-11},(2)$

which implies a 4.2σ deviation from the SM prediction (if the new lattice result is ignored) [1].

$\mathrm{\Delta }{a}_{\mu }=a_{\mu }^{\text{EXP}}-a_{\mu }^{\text{SM}}=\left(251\pm 59\right)\times 10^{-11}.(3)$

It is extremely tempting to attribute the discrepancy Δa_μ to additional contributions from models of new physics beyond the SM and, before the issue of the theoretical uncertainties is resolved, this is the attitude that we choose to take. In any case, if the discrepancy is alleviated or eliminated by a more refined theoretical description, the new measurement would allow to strongly constrain the basic parameters of this new physics and in a way that should be complementary to the direct searches that are performed in the high-energy frontier experiments at the Large Hadron Collider (LHC).

In this review note, we will confront this new and precise (g − 2)_μ result with the predictions coming from a variety of models beyond the SM, which contain additional heavy fermions. These particles can have the usual lepton and baryon quantum numbers but come with exotic SU(2)_L × U (1)_Y assignments.

A well-known example of such a possibility is given by vector-like fermions, when both the left- and right-handed components appear in the same electroweak doublet, allowing for a consistent generation of their masses without the need of the Higgs mechanism. These fermions often occur in grand unified theories [5] and have been advocated e.g. to explain the hierarchies in the SM flavour sector [6–8]. One can also have sequential fermions, such as a fourth generation, or mirror fermions which have chiral properties that are opposite to those of the SM fermions. However, it is necessary to modify the SM Higgs sector in order to evade the strong constraints from the precise determination of the Higgs boson properties at the LHC [9–12]. The mixing of the heavy and light fermions that have the same U (1)_Q and SU(3)_C quantum numbers gives rise to new interactions [5, 13] which allow for the decays of the heavy states into the lighter ones and to generate contributions which could be observed in highly precise experiments.

Another type of new fermions which have been discussed in the past are excited fermions. They are a characteristic signature of compositeness in the matter sector which was and is still advocated to explain some pattern in the mass spectrum. The SM fermions would then correspond to the ground states of the spectrum and the excited states would decay to the former ones through a magnetic type de-excitation. In the simplest case, the excited fermions have spin and isospin $\frac{1}{2}$, and the transition between excited and fundamental fermions is described by an SU(3)_C × SU(2)_L × U (1)_Y invariant effective interaction of the magnetic type [5, 14]. Hence, besides the full-strength couplings to gauge bosons, excited states have couplings to SM fermions and gauge bosons that are inversely proportional to the compositeness scale Λ. These couplings determine the decay and production properties of the excited states and, e.g. induce anomalous contributions to the dipole moments.

We will also discuss the case of supersymmetric theories in their minimal version, the so-called minimal supersymmetric extension of the SM or MSSM. In this scenario, the Higgs sector is enlarged to contain two doublet fields and each SM particle or additional Higgs boson has a supersymmetric partner with a spin that differs by $\frac{1}{2}$. The superpartners of the gauge and Higgs bosons will mix to give the physical states, the spin-$\frac{1}{2}$ charginos and neutralinos, with the lightest neutralino being the lightest SUSY particle which is stable and forms the dark matter. The charginos and neutralinos would contribute to the (g − 2)_μ along with the scalar partners of the muon, the smuons and their associated sneutrinos. These particles have been, for a long time, considered as the best candidates to explain the previous discrepancy in the measurement.

Finally, we will also discuss new particles with a spin higher than unity and, in particular, we will consider the case of a massive electrically neutral and colourless spin-$\frac{3}{2}$ fermion, which was recently discussed in dark matter [15], collider [16] and nuclear physics [17] phenomenology but also in the context of the new g − 2 value [18]. Massive spin-$\frac{3}{2}$ particles are present in supersymmetric extensions of gravity and string-theoretical models. The phenomenological studies of generic higher-spin particles had severe problems in the past, related to the non-physical degrees of freedom in their representations that need to be eliminated as they lead to pathologies like the violation of causality and perturbative unitarity. These problems are avoided in a recently proposed Effective Field Theory (EFT) approach to generic higher-spin particles [15–17] which considers only the physical degrees of freedom. Spin-$\frac{3}{2}$ fermions have interactions with leptons and hence generate a contribution to the muon (g − 2). We will summarize it here and compare it with the corresponding results for the spin-$\frac{1}{2}$ fermions.

2 New fermion contributions to the g–2

2.1 Vector-like leptons

For charged heavy leptons with exotic SU(2)_L × U (1)_Y quantum numbers, except for singlet heavy neutrinos without electromagnetic or weak charges, the couplings to the photon, the W and the Z bosons are unsuppressed. The heavy states mix with the SM leptons in a model-dependent and a possibly rather complicated manner, especially if different fermion generations can mix.

In the following, we will consider as an example the case of vector-like leptons that have been introduced in order to explain flavour hierarchies in the SM; see Refs. [6–8] for detailed studies. Two doublets L_L and L_R and two singlets E_L and E_R are introduced with a Lagrangian given by [6].

$L\propto M_E{\bar{E}}_L{E}_R+M_L{\bar{L}}_R{L}_L+m_E{\bar{E}}_L{e}_R+m_L{\bar{L}}_R{\ell }_L+{\lambda }_{LE}{\bar{L}}_L{E}_R\mathrm{\Phi }+{\bar{\lambda }}_{LE}{\bar{L}}_R{E}_L{\mathrm{\Phi }}^{†}+\mathrm{h}.\mathrm{c}.,(4)$

with the L_L, E_R and L_R, E_L fields having, respectively, the same and opposite quantum numbers as the SM leptons ℓ_L, e_R; Φ is the SM Higgs doublet. The mass eigenstates are obtained by diagonalizing the mass mixing in L through 2 × 2 unitary matrices, where the mixing angles read tan θ_L = m_L/M_L and tan θ_R = m_E/M_E. After rotating the fields, the previous Lagrangian becomes

$\begin{array}{cc}\hfill L& \propto \sqrt{M_E^2+m_E^2}{\bar{E}}_L{E}_R+\sqrt{M_L^2+m_L^2}{\bar{L}}_R{L}_L+{\bar{\lambda }}_{LE}{\bar{L}}_R{E}_L{\mathrm{\Phi }}^{†}\hfill \\ \hfill & +{\lambda }_{LE}\left(\sin {\theta }_L\sin {\theta }_R{\bar{\ell }}_L{e}_R+\cos {\theta }_L\sin {\theta }_R{\bar{L}}_L{e}_R+\sin {\theta }_L\cos {\theta }_R{\bar{\ell }}_L{E}_R+\cos {\theta }_L\cos {\theta }_R{\bar{L}}_L{E}_R\right)\mathrm{\Phi }+\mathrm{h}.\mathrm{c}.,\hfill \end{array}(5)$

After symmetry breaking, the spectrum will consist of two heavy leptons with masses $\sqrt{M_L^2+m_L^2}$ and $\sqrt{M_E^2+m_E^2}$ and the light leptons with masses given approximately by $m_{{\ell }_i}\simeq {\lambda }_{LE}{\sin }_{{\theta }_L}^i{\sin }_{{\theta }_R}^{i}v+\mathcal{O}(v^2/M_{L,E}^2)$, where i is the generation index and v ≃ 246 GeV the Higgs vev. Notice that the Yukawa couplings have been assumed to be zero and are generated after electroweak symmetry breaking through the mixing between heavy and light fermions, once the former have been integrated out.

The heavy charged and neutral leptons contribute to the anomalous magnetic moment through Feynman diagrams that involve the exchange of 2 W bosons with the neutral lepton and the exchange of two charged states with a Z or Higgs boson. Heavy exotic fermion contributions to leptonic (g − 2) have been also discussed and evaluated in Refs. [6–8, 19–26]. Here, we simply display the contributions to a_μ in the limit of small mixing angles, retaining only terms of order $v^2/M_{L,E}^2$

$\mathrm{\Delta }{a}_{\mu }\simeq \frac{1}{16{\pi }^2}\frac{m_{\mu }^2}{M_L{M}_E}\mathrm{R}\mathrm{e}\left({\lambda }_{LE}{\bar{\lambda }}_{LE}\right)\approx 10^{-9}\mathrm{R}\mathrm{e}\left({\lambda }_{LE}{\bar{\lambda }}_{LE}\right){\left(\frac{300\mathrm{G}\mathrm{e}\mathrm{V}}{\sqrt{M_L{M}_E}}\right)}^2.(6)$

Thus, for M_L, M_E values of the order of the electroweak symmetry breaking scale v and for large Yukawa couplings to the muon ${\lambda }_{LE},{\bar{\lambda }}_{LE}$, the contributions to a_μ can be significant.

2.2 Excited leptons

In the case of the charged excited leptons that we will denote by ℓ^*, we assume for simplicity that they have spin and isospin $\frac{1}{2}$. Besides the ℓ^*ℓ^*V interaction with the V = γ, W, Z, gauge bosons, there is a magnetic-type coupling between the excited leptons, the ordinary ones and the gauge bosons ℓ^*ℓV which allows for the decays of the heavy states, ℓ^* → Vℓ [14]. This coupling induces a contribution to the anomalous magnetic moment of the lepton via diagrams in which there is a transition of the magnetic type with a μ^*μ^* loop along with the Z boson and the photon, as well as diagrams in which the magnetic transition occurs at the γμ^*μ vertex. The Lagrangian describing this transition should respect a chiral symmetry in order to induce not excessively large contributions to the anomalous moment. As a consequence, only the left- or the right-handed component of the excited lepton takes part in the generalized magnetic d -excitation. The corresponding Lagrangian then reads

$L_{\ell {\ell }^{*}\gamma }=\frac{e{\kappa }_{L/R}}{\sqrt{2}\mathrm{\Lambda }}\overline{{\ell }^{*}}{\sigma }^{\mu \nu }{\ell }_{L/R}{F}_{\mu \nu }+\mathrm{h}.\mathrm{c}..(7)$

In the equation given above, Λ is the compositeness scale that we will set to the excited lepton mass. This interaction should be generalized to the SU(2)_L × U_Y(1) case where the photon field strength is extended to the W_μν and B_μν ones. In such an extension, that will be used in our analysis below, we will set all the weight factors for the photon and W, Z field strengths to κ_L/R to simplify the discussion. This also ensure that the excited neutrino has no tree-level electromagnetic couplings [14]. Thus, apart from the masses of the excited leptons that we will also equate, $m_{{\ell }^{*}}=m_{{\nu }_{\ell }^{*}}$, the only free parameter will be the strength κ_L,R/Λ of the de-excitation which involves either a left-handed or a right-handed fermion.

The contribution Δa_μ of the μ^* and its partner ${\nu }_{\mu }^{*}$ to the muon magnetic moment has been calculated long ago [27–31] and the result in the case where the simplifications above are performed, assuming $m_{{\ell }^{*}}=m_{{\nu }_{\ell }^{*}}=\mathrm{\Lambda }\gg M_W$, which we believe to be a good approximation, is simply given by [30].

$\mathrm{\Delta }{a}_{\mu }=\frac{\alpha }{\pi }\frac{{\kappa }_{L,R}^2}{{\mathrm{\Lambda }}^2}{m}_{\mu }^2{c}_{L/R},(8)$

where the numerical values of the c_L, c_R coefficients in these limits are c_L ≃ 10 and c_R ≃ 5.3, respectively for left-handed Vμ^*μ_L and right-handed Vμ^*μ_R transitions. Note that, according to Ref. [30] on which our analysis is based, in the equation above the approximation $m_{{\ell }^{*}}=m_{{\nu }_{\ell }^{*}}=\mathrm{\Lambda }\gg M_W$ is already valid for Λ ≈ 200 GeV (see Fig. 15 of that paper) and we will extend it down to 100 GeV. In addition, the excited lepton contribution to the g − 2 will decrease with increasing $m_{{\ell }^{*}}$ and will decouple at very large masses.

2.3 Supersymmetric particles

In this subsection, we will briefly discuss the contributions to a_μ of the superparticles in the minimal supersymmetric extension of the SM (MSSM) [32], namely the one with the chargino-sneutrino and neutralino-smuon loops. These have also been calculated long ago [33–41] and the approximate result, taking into account only the chargino-sneutrino contribution which is an order of magnitude larger than the one of the neutralino-smuon loop, is rather simple and accurate [41].

$\mathrm{\Delta }{a}_{\mu }\simeq \frac{\alpha }{8\pi s_W^2}\tan \beta \times \frac{m_{\mu }^2}{{\tilde{m}}^2}\approx 1.5\times 10^{-11}\tan \beta {\left[\frac{\tilde{m}}{\mathrm{T}\mathrm{e}\mathrm{V}}\right]}^{-2},(9)$

where tan β is the ratio of vacuum expectation values of the two doublet Higgs fields that break the electroweak symmetry, 1 ≲ tan β ≲ 60 and $\tilde{m}$ is a SUSY scale given by the largest mass between the chargino and the sneutrino states, $\tilde{m}=\mathrm{m}\mathrm{a}\mathrm{x}(m_{\tilde{\nu }},m_{{\chi }_1^{+}})$. Hence, a large SUSY contribution to a_μ can be generated for large enough tan β values and superparticle masses of order a few hundred GeV.

We note that the sign of the SUSY contribution is equal to the sign of the higgsino mass parameter μ, $\mathrm{\Delta }{a}_{\mu }\propto (\alpha /\pi )\times \tan \beta (\mu M_2)/{\tilde{m}}^4$ with M₂ the gaugino (wino) mass parameter. On should note too that the extended two-Higgs doublet Higgs sector of the MSSM will in principle also contribute to the g − 2, but as the Higgs particles are heavy or do not have strong couplings to muons, the impact is expected to be very small. This might not be the case in extensions of the MSSM, such as the next-to-minimal supersymmetric SM or NMSSM, in which one could have a light pseudoscalar Higgs boson with enhanced couplings to muons [42] that could significantly contribute to the g − 2 [43].

2.4 Spin-3/2 fermions

Among the dimension-7 operators which describe the interactions with the SM fields of a charge and colour neutral SM isosinglet spin-$\frac{3}{2}$ field denoted by ψ_3/2 [16], the following ones will contribute to the g − 2, keeping only couplings to (second generation) leptons

$-\mathcal{H}=\frac{1}{{\mathrm{\Lambda }}^3}{\psi }_{3/2}^{\mathit{abc}}\left[c_B{\tilde{\varphi }}^{†}{\sigma }_{ab}^{\mu \nu }{B}_{\mu \nu }{L}_{Lc}^2+c_W{\tilde{\varphi }}^{†}{\sigma }_{ab}^{\mu \nu }{\sigma }_n{W}_{\mu \nu }^n{L}_{Lc}^2\right]+\text{h.c.},(10)$

where a, b, c are two-spinor indices; $L_a^i$ are the left-handed lepton doublets $L_{La}^i=({\nu }_{La}^i,e_{La}^i)$; B_μν and W_μν denote the U (1)_Y and SU(2)_L field strengths; and ϕ is the SM Higgs doublet given in the unitary gauge by $\varphi =(0,H+v)/\sqrt{2}$ (with v = 246 GeV and H the SM Higgs boson). The constant tensors ${\sigma }_{a\dot{a}}^{\mu }$ are given in terms of the identity matrix σ⁰ and Pauli σ^1,2,3 matrices; while ${{({\sigma }^{\mu \nu })}_a}^b\equiv i({\sigma }_{a\dot{b}}^{\mu }{\bar{\sigma }}^{\nu \dot{b}b}-{\sigma }_{a\dot{b}}^{\nu }{\bar{\sigma }}^{\mu \dot{b}b})/4$. Finally, c_γ ≡ − c_B cos θ_W + c_W sin θ_W is the γνψ_3/2 coupling.

The contribution of the spin-$\frac{3}{2}$ singlet fermion to the anomalous magnetic moment is given by [18].

$\mathrm{\Delta }{a}_{\mu }^{\psi }=\frac{m_{\mu }^2{v}^2{m}_{3/2}^2}{8{\pi }^2{\mathrm{\Lambda }}^6}\left[|c_W{|}^2{f}_1\left(m_{3/2}\right)+\frac{\mathbf{R}\mathbf{e}\left(c_W^{*}{c}_{\gamma }\right)}{\sin \left({\theta }_W\right)}{f}_2\left(m_{3/2}\right)\right],(11)$

where the functions f₁ and f₂ are given by

$f_1=-\frac{13}{27}+\frac{7}{18}\log \left(\frac{{\mu }^2}{m_{3/2}^2}\right),f_2=\frac{2}{3}\log \left(\frac{{\mu }^2}{m_{3/2}^2}\right).(12)$

when m_3/2 ≫ M_W, in the $\overline{\mathrm{M}\mathrm{S}}$-renormalization scheme with a scale μ. The contribution is, thus, of order Λ⁻⁶ with the scale Λ may be associated with the compositeness scale.

Eq. 11 gives the contribution from ψ to the magnetic moment at a high-energy scale, and its value has to be run down to the scale of the muon mass. Following Ref. [44] in which the running and matching from several scales to low energies in the case of the muon dipole moments has been derived, and assuming that m_3/2 is sufficiently close to the reference value of 250 GeV so that one can fix the renormalization scale μ to this value, one finds a corrected value given by Eq. (11) should be corrected by a factor 0.89.

3 Numerical results

3.1 Spin–1/2 fermions

Our numerical results for the three cases of exotic spin-$\frac{1}{2}$ fermions discussed in the previous subsections are collected in Figure 1 where we present the typical predictions for their contributions to the (g − 2)_μ as a function of their corresponding mass scale. In the case of vector-like fermions, the M scale is defined as $M=\sqrt{M_L{M}_E}$ which, together with the assumption that the Yukawa couplings are simply given by ${\lambda }_{LE}={\bar{\lambda }}_{LE}=2$ (to avoid too light vector-leptons which should be excluded by present data [5]), leads to the curve displayed in purple in Figure 1. For excited leptons, the scale M is defined in the simplest way as $M=\mathrm{\Lambda }=m_{{\mu }^{*}}=m_{{\nu }_{\mu }^{*}}$, and we have considered two extreme situations, κ_L = 1 and κ_R = 1, which lead to the coefficient values c_L = 10 and c_R = 5.3 respectively. The resulting contributions to a_μ are presented in the figure in red colors. Finally, in the supersymmetric case, the scale is simply the common mass of the scalar leptons $M=\tilde{m}$, and we have chosen the values tan β = 3 and tan β = 30 to illustrate our results. The resulting typical contributions to a_μ are shown by the green curves in Figure 1. The results of the new Fermilab (g − 2)_μ measurement, including the ± 1σ band, are displayed by the grey band.

FIGURE 1

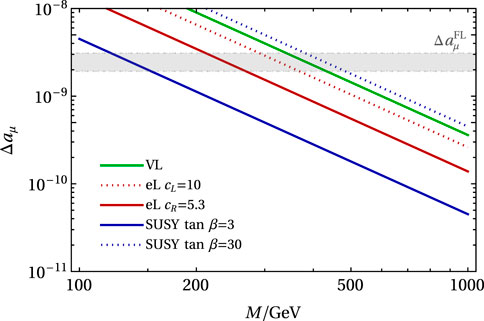
FIGURE 1. Contributions to the (g −2)_μ from various spin-$\frac{1}{2}$ fermions as functions of the corresponding mass scale M: vector-like leptons for ${\lambda }_{LE}={\bar{\lambda }}_{LE}=2$ and $M=\sqrt{M_L{M}_E}$ (purple line), excited leptons with κ_L,R =1 and M = Λ for the two cases c_L ≈10 (dotted red line) and c_R ≈5.3 (solid red line) and supersymmetric particles for $M=\tilde{m}$ for the two cases of tan β =3 (solid green line) and tan β =30 (dotted green line). The light grey band shows the 1σ region of the Fermilab measurement.

A comparison of the predicted results with the new (g − 2)_μ Fermilab measurement indicates that all the considered spin-$\frac{1}{2}$ new fermions could explain the discrepancy with respect to the SM prediction for new particle masses in the vicinity of a few hundred GeV. In turn, if the latter discrepancy has to be attributed to additional theoretical errors, for instance, the models would be severely constrained by the experiment and, typically, the scale of new physics would be constrained to be above several hundred GeV.

3.2 Spin–3/2 leptons

The contribution to (g − 2)_μ from the higher-spin field as a function of its mass m_3/2 and for different values of the parameter c_γ is shown in Figure 2 for a new physics scale Λ = 500 TeV. The results can be roughly summarized in terms of the two mass parameters as

$|a_{\mu }^{\psi }|\lesssim 2\times 10^{-11}{\left[\frac{\mathrm{\Lambda }}{\mathrm{T}\mathrm{e}\mathrm{V}}\right]}^{-6}{\left[\frac{m_{3/2}}{\mathrm{T}\mathrm{e}\mathrm{V}}\right]}^2,(13)$

when c_W, c_γ < 1 as expected in the EFT approach. This contribution to (g − 2)_μ is consistent with the SM unless the EFT scale is close to the electroweak scale, Λ < 250 GeV, in which case the validity of the EFT approach starts to be questionable. Also, note that Figure 2 slightly violates the bound Eq. 13 for masses close to the EFT scale. This behaviour is simply an artefact of the large logarithm log (m_3/2/μ) that is present. In addition, the contribution $a_{\mu }^{\psi }$ is negative when c_γ = 0. A positive $a_{\mu }^{\psi }$ value can be obtained for specific values of the model parameters, namely, for sufficiently low m_3/2 values when c_γ > 0, or for high enough m_3/2 values when c_γ < 0.

FIGURE 2

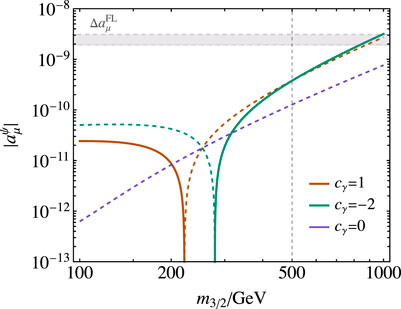
FIGURE 2. $a_{\mu }^{\psi }$ for different m_3/2 and c_γ values while the other parameters are fixed as Λ =500 GeV, μ =250 GeV and c_W =1. The solid and dashed lines correspond to $a_{\mu }^{\psi }>0$ and $a_{\mu }^{\psi }<0$, respectively. The light grey region represents the 1σ band of the Fermilab measurement. On the right of the vertical thin dashed line where m_3/2> Λ, the EFT approach starts to be unreliable.

As can be seen, for m_3/2 ≲Λ = 500 GeV, the spin-3/2 contribution to (g − 2)_μ is typically of order 10^–10–10⁻¹¹, more than an order of magnitude below the experimental sensitivity in the most favourable case. For a particle with such mass and couplings, the production cross section at the LHC in the process $pp\to q{\bar{q}}^{\prime }\to W^{*}\to {\psi }_{3/2}\mu +X$, as calculated in Ref. [16], was found to be rather significant, reaching a level of 10 fb at very high masses, a rate that should be sufficient to observe the particle (which could mainly decay into a clear signature consisting, e.g., of a W boson and a muon) at the next LHC runs with expected integrated luminosities of several 100 fb⁻¹ to several ab⁻¹.

Nevertheless, one can obtain an anomalous ψ_3/2 contribution close to the measured (g − 2)_μ value if both the effective scale Λ and the mass m_3/2 of the new particle are close to the weak scale, O (300 GeV). Even for a scale Λ = 500 GeV, the spin-$\frac{3}{2}$ contribution can still reach the measured value as seen in the figure, if its mass is close to 1 TeV. These values are at the boundary of validity of the EFT. In addition, they should lead to a challenging ψ_3/2 production cross section at the LHC.

4 Conclusion

The new measurement of the anomalous magnetic moment of the muon recently performed at Fermilab has a significant deviation from the prediction in the SM, 4.2σ, which is slightly less than the 5σ value traditionally set as the threshold to claim the observation of a new phenomenon. This gives hope that, at last, new physics beyond the SM has been found. This hope is nevertheless tempered by possible additional theoretical uncertainties that have been overlooked and an intense effort would be required in order to settle this crucial issue, hopefully before a new and more precise measurement is released by the experiment. In the meantime, one cannot refrain from interpreting this discrepancy, confront it with various models of new physics beyond the SM and draw the resulting conclusions.

This is what we have done in this mini-review. We have discussed the contributions of various hypothetical new fermions to the (g − 2)_μ and delineated the scale of their masses and couplings that allows to explain the possible excess compared to the SM expectation. We have considered spin-$\frac{1}{2}$ new leptons with exotic SU(2)_L × U (1)_Y quantum numbers such as vector-like leptons, excited leptons that are present in composite models and supersymmetric particles, namely the combined contributions of neutralinos/charginos with smuons and their associated sneutrinos. All these scenarios have been widely studied in the past and we simply update the results in the light of the new measurement. However, we have also included a new scenario that has been addressed only recently in Ref. [18]. This is the case of a generic massive isosinglet spin-$\frac{3}{2}$ fermion in which an EFT approach is used to describe the higher-spin fermion interactions involving only the physical degrees of freedom, thus allowing to calculate in a consistent way the physical observables such as the contributions to the (g − 2).

All these new fermions can give significant contributions to the muon (g − 2) which, when confronted with the latest experimental measurement, imply that their masses should be below the TeV scale, if they have to explain the discrepancy from the SM expectation (if this discrepancy with the SM result is indeed real). As shown in the two figures that summarize our results, this implies particles with masses in the few hundred GeV range, which could be observed at the next high-luminosity run of the CERN Large Hadron Collider. If the discrepancy is instead due to additional or overlooked theoretical uncertainties, the new result will impose strong constraints on the masses and couplings of the new spin-$\frac{1}{2}$ and $\frac{3}{2}$ particles.

Author contributions

All authors contributed to the analysis and the writing of the paper.

Funding

This work is supported by the Estonian Research Council grants MOBTTP135, PRG803, MOBTT5, MOBJD323 and MOBTT86, and by the European Union through the European Regional Development Fund CoE program TK133 “The Dark Side of the Universe.” J.C.C. is supported by the STFC under grant ST/P001246/1. A.D. is supported by the Junta de Andalucia through the Talentia Senior program and by the grants A-FQM-211-UGR18, P18-FR-4314 with ERDF.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Abi B, Albahri T, Al-Kilani S, Allspach D, Alonzi L, Anastasi A, et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys Rev Lett (2021) 126:141801. doi:10.1103/PhysRevLett.126.141801

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Aoyama T, Asmussen N, Benayoun M, Bijnens J, Blum T, Bruno M, et al. The anomalous magnetic moment of the muon in the Standard Model. Phys Rep (2020) 887:1–166. doi:10.1016/j.physrep.2020.07.006

CrossRef Full Text | Google Scholar

3. Borsanyi S, Fodor Z, Guenther J, Hoelbling C, Katz S, Lellouch L, et al. Leading hadronic contribution to the muon magnetic moment from lattice qcd. Nature (2021) 593:51–5. doi:10.1038/s41586-021-03418-1

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. Final report of the E821 muon anomalous magnetic moment measurement at BNL. Phys Rev D (2006) 73:072003. doi:10.1103/PhysRevD.73.072003

CrossRef Full Text | Google Scholar

5. Djouadi A, Ng J, Rizzo TG. New particles and interactions (1995). doi:10.1142/9789812830265_0008

CrossRef Full Text | Google Scholar

6. Giudice GF, Paradisi P, Passera M. Testing new physics with the electron g-2. J High Energ Phys (2012) 11:113. doi:10.1007/JHEP11(2012)113

CrossRef Full Text | Google Scholar

7. Kannike K, Raidal M, Straub D, Strumia A. Anthropic solution to the magnetic muon anomaly: The charged see-saw. J High Energ Phys (2012) 02:106. [Err: JHEP 10, 136 (2012)]. doi:10.1007/JHEP02(2012)106

CrossRef Full Text | Google Scholar

8. Dermisek R, Raval A. Explanation of the muong−2anomaly with vectorlike leptons and its implications for Higgs decays. Phys Rev D (2013) 88:013017. doi:10.1103/PhysRevD.88.013017

CrossRef Full Text | Google Scholar

9. Djouadi A, Gambino P, Kniehl BA. Two loop electroweak heavy fermion corrections to Higgs boson production and decay. Nucl Phys B (1998) 523:17–39. doi:10.1016/S0550-3213(98)00147-3

CrossRef Full Text | Google Scholar

10. Denner A, Dittmaier S, Muck A, Passarino G, Spira M, Sturm C, et al. Higgs production and decay with a fourth standard-model-like fermion generation. Eur Phys J C (2012) 72:1992. doi:10.1140/epjc/s10052-012-1992-3

CrossRef Full Text | Google Scholar

11. Djouadi A, Lenz A. Sealing the fate of a fourth generation of fermions. Phys Lett B (2012) 715:310–4. doi:10.1016/j.physletb.2012.07.060

CrossRef Full Text | Google Scholar

12. Kuflik E, Nir Y, Volansky T. Implications of Higgs searches on the four generation standard model. Phys Rev Lett (2013) 110:091801. doi:10.1103/PhysRevLett.110.091801

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Djouadi A. New fermions at e+ e- colliders. 1. Production and decay. Z Phys C - Particles Fields (1994) 63:317–26. doi:10.1007/BF01411024

CrossRef Full Text | Google Scholar

14. Boudjema F, Djouadi A, Kneur JL. Excited fermions at e+ e- and e P colliders. Z Phys C - Particles Fields (1993) 57:425–49. doi:10.1007/BF01474339

CrossRef Full Text | Google Scholar

15. Criado JC, Koivunen N, Raidal M, Veermäe H. Dark matter of any spin – An effective field theory and applications. Phys Rev D (2020) 102:125031. doi:10.1103/PhysRevD.102.125031

CrossRef Full Text | Google Scholar

16. Criado JC, Djouadi A, Koivunen N, Raidal M, Veermäe H. Higher-spin particles at high-energy colliders. J High Energ Phys (2021) 254. doi:10.1007/JHEP05(2021)254

CrossRef Full Text | Google Scholar

17. Criado JC, Djouadi A, Koivunen N, Müürsepp K, Raidal M, Veermäe H. An effective field theory of the Delta-resonance. arXiv:2106.09031v1 (2021).

Google Scholar

18. Criado JC, Djouadi A, Koivunen N, Müürsepp K, Raidal M, Veermäe H. Confronting spin-3/2 and other new fermions with the muon g-2 measurement. Phys Lett B (2021) 820:136491. doi:10.1016/j.physletb.2021.136491

CrossRef Full Text | Google Scholar

19. Rizzo TG. Exotic fermions inE6and the anomalous magnetic moments of leptons. Phys Rev D (1986) 33:3329–33. doi:10.1103/PhysRevD.33.3329

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Nardi E, Roulet E, Tommasini D. Global analysis of fermion mixing with exotics. Nucl Phys B (1992) 386:239–66. doi:10.1016/0550-3213(92)90566-T

CrossRef Full Text | Google Scholar

21. Vendramin IE. E 6-lepton mixing and lepton magnetic moment. Nuov Cim A (1988) 100:757–62. doi:10.1007/BF02813322

CrossRef Full Text | Google Scholar

22. Kephart TW, Pas H. Muon anomalous magnetic moment in string inspired extended family models. Phys Rev D (2002) 65:093014. doi:10.1103/PhysRevD.65.093014

CrossRef Full Text | Google Scholar

23. Csikor F, Fodor Z. Constraints on mirror fermion mixing angles from anomalous magnetic moment data. Phys Lett B (1992) 287:358–62. doi:10.1016/0370-2693(92)90996-H

CrossRef Full Text | Google Scholar

24. Chavez H, Martins Simoes JA. The muon in an left–right symmetric model with mirror fermions. Nucl Phys B (2007) 783:76–89. doi:10.1016/j.nuclphysb.2007.05.026

CrossRef Full Text | Google Scholar

25. Aboubrahim A, Ibrahim T, Nath P. Leptonic g − 2 moments, CP phases and the Higgs boson mass constraint. Phys Rev D (2016) 94:015032. doi:10.1103/PhysRevD.94.015032

CrossRef Full Text | Google Scholar

26. Crivellin A, Hoferichter M, Schmidt-Wellenburg P. Combined explanations of (g − 2)_{μ, e} and implications for muon EDM. Phys Rev D (2018) 98:113002. doi:10.1103/PhysRevD.98.113002

CrossRef Full Text | Google Scholar

27. Renard FM. Limits on masses and couplings of excited electrons and muons. Phys Lett B (1982) 116:264–8. doi:10.1016/0370-2693(82)90339-2

CrossRef Full Text | Google Scholar

28. del Aguila F, Mendez A, Pascual R. On the g − 2 and the pp → Z → eeγ Events. Phys Lett B (1984) 140:431–4. doi:10.1016/0370-2693(84)90786-X

CrossRef Full Text | Google Scholar

29. Choudhury SR, Ellis RG, Joshi GC. Limits on excited spin-3/2 leptons. Phys Rev D (1985) 31:2390–2. doi:10.1103/PhysRevD.31.2390

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Mery P, Moubarik SE, Perrottet M, Renard FM. Constraints on nonstandard effects from present and future muon g − 2 measurements. Z Phys C - Particles Fields (1990) 46:229–52. doi:10.1007/BF01555999

CrossRef Full Text | Google Scholar

31. Rakshit S. Muon anomalous magnetic moment constrains models with excited leptons. arXiv:hep-ph/0111083 (2001).

Google Scholar

32. Drees M, Godbole R, Roy P. Theory and phenomenology of sparticles: An account of four-dimensional N=1 supersymmetry in high energy physics. Singapore: World Scientific (2004).

Google Scholar

33. Ellis JR, Hagelin JS, Nanopoulos DV. Spin-zero leptons and the anomalous magnetic moment of the muon. Phys Lett B (1982) 116:283–6. doi:10.1016/0370-2693(82)90343-4

CrossRef Full Text | Google Scholar

34. Grifols JA, Mendez A. Constraints on supersymmetric particle masses from (g − 2) μ. Phys Rev D (1982) 26:1809–11. doi:10.1103/PhysRevD.26.1809

CrossRef Full Text | Google Scholar

35. Barbieri R, Maiani L. The muon anomalous magnetic moment in broken supersymmetric theories. Phys Lett B (1982) 117:203–7. doi:10.1016/0370-2693(82)90547-0

CrossRef Full Text | Google Scholar

36. Kosower DA, Krauss LM, Sakai N. Low-energy supergravity and the anomalous magnetic moment of the muon. Phys Lett B (1983) 133:305–10. doi:10.1016/0370-2693(83)90152-1

CrossRef Full Text | Google Scholar

37. Chattopadhyay U, Nath P. Upper limits on sparticle masses fromg−2and the possibility for discovery of supersymmetry at colliders and in dark matter searches. Phys Rev Lett (2001) 86:5854–7. doi:10.1103/PhysRevLett.86.5854

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Carena M, Giudice G, Wagner C. Constraints on supersymmetric models from the muon anomalous magnetic moment. Phys Lett B (1997) 390:234–42. doi:10.1016/S0370-2693(96)01396-2

CrossRef Full Text | Google Scholar

39. Martin SP, Wells JD. Muon anomalous magnetic dipole moment in supersymmetric theories. Phys Rev D (2001) 64:035003. doi:10.1103/PhysRevD.64.035003

CrossRef Full Text | Google Scholar

40. Chakraborti M, Heinemeyer S, Saha I. Improved (g − 2)_μ measurements and wino/higgsino dark matter. arXiv:2103.13403 (2021).

Google Scholar

41. Moroi T. Muon anomalous magnetic dipole moment in the minimal supersymmetric standard model. Phys Rev D (1996) 53:6565–75. [Erratum: Phys.Rev.D 56, 4424 (1997)]. doi:10.1103/PhysRevD.53.6565

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Djouadi A, Drees M, Ellwanger U, Godbole R, Hugonie C, King S, et al. Benchmark scenarios for the NMSSM. J High Energ Phys (2008) 07:002. doi:10.1088/1126-6708/2008/07/002

CrossRef Full Text | Google Scholar

43. Arcadi G, Djouadi A, Queiroz F. Models with two Higgs doublets and a light pseudoscalar:a portal to dark matter and the possible (g − 2)_μ excess. Phys Lett B (2021) 834:137436. doi:10.1016/j.physletb.2022.137436

CrossRef Full Text | Google Scholar

44. Aebischer J, Dekens W, Jenkins EE, Manohar AV, Sengupta D, Stoffer P. Effective field theory interpretation of lepton magnetic and electric dipole moments. arXiv:2102.08954 (2021).

CrossRef Full Text | Google Scholar