- 1Key Laboratory of Hunan Province on Information Photonics and Freespace Optical Communications, Hunan Institute of Science and Technology, Yueyang, China
- 2College of Physics and Electronics, Hunan Institute of Science and Technology, Yueyang, China
- 3School of Mathematics and Computer Science, Panzhihua University, Panzhihua, China
In recent years, many researchers have leveraged various memristors to design many novel memristive chaotic systems with complex dynamics. Compared with other chaotic systems, applying these memristive chaotic systems to image encryption is expected to solve some key problems in this field. Therefore, exploiting a recently reported memristive chaotic system, this paper proposes a novel image encryption scheme based on the memristive chaotic system and combining bidirectional bit-level cyclic shift and dynamic DNA-level diffusion (IES-M-BD). First, a discrete memristive chaotic map is employed to generate chaotic sequences. Then, the plaintext image is shifted circularly on bit-level according to chaotic sequences and the hash value of the plaintext image. After that, the shifted matrix is recombined on the bit plane and encoded dynamically by DNA encoding rules. Next, dynamic DNA-level diffusion and DNA-level permutation are carried out in two rounds. Finally, the encrypted image is obtained after dynamic DNA decoding. Simulation tests and performance analyses are also carried out in this paper. The simulation results and the security analyses demonstrate that this encryption scheme has a high security level and can resist various attacks.
1 Introduction
In 1971, Professor Chua first hypothesized the memristor concept [1]. A memristor is a passive two-terminal electronic element that describes the relationship between charge and flux. Due to the nonlinearity of the memristor, it is easy to cause the chaotic phenomenon in the circuit and enhance the complexity of the chaotic system [2]. It was not until 2008 that HP Labs reported the first physical implementation of a memristor [3]. The invention of the memristor has further stimulated researchers’ interest in the application of chaotic systems. Numerous memristive chaotic systems have so far been introduced [4–6]. The most notable distinction between memristive chaotic systems and conventional dynamical systems is that the former’s long-term dynamical behavior heavily depends on the memristor’s initial state, which results in the dynamic phenomenon of coexisting attractors [7–9]. As a result, this feature will offer sufficient pattern selectivity in encrypted secret communication.
As one of the important carriers of information, images are widely transmitted and stored over the Internet. Thus, the privacy and security of image information are receiving more and more attention [10–16]. Different from text, an image has bulk data capacity, and the adjacent pixels have a strong correlation. When an image is encrypted with the traditional encryption methods, the encryption performance is not ideal. In recent years, various encryption schemes for image information have been proposed, and the image encryption scheme based on chaos has been widely discussed due to the pseudo-randomness, highly sensitive to initial conditions, and ergodicity of chaotic systems [17–24]. A chaos-based image cryptosystem generally adopts the structure of permutation and diffusion. Recently, bit-level permutation has gradually replaced pixel-level permutation [25–29], owing to the latter disturbs the pixel position of an image, but does not change the statistical characteristics. Zhu et al. [27] proposed chaos-based image encryption using a bit-level permutation. In 2017, Li et al. [28] proposed a hyper-chaos-based image encryption algorithm, the pixel-level permutation and bit-level permutation are utilized to strengthen the security of the cryptosystem. In 2018, Teng et al. [29] employed bit-level permutation in a chaotic color image encryption. The bit-level permutation can not only change the position of the pixels but also change their value. Therefore, image encryption algorithms that adopt bit-level permutations may possess a high security level. Meanwhile, image encryption schemes based on DNA complementary rules have been proposed continuously [30–34]. Zhang et al. [30] proposed an image fusion encryption algorithm based on DNA sequence operations and combined hyper-chaotic maps. In [31], Chai et al. presented an image encryption algorithm using DNA sequence operations and a 2D Logistic chaotic system. Moreover, a new color image encryption scheme based on a four-wing hyperchaotic system and dynamic DNA encoding was proposed in [33]. In these studies, image encryption schemes based on DNA technology showed high security, and DNA technology possesses other advantages such as working in parallel and having ultra-low power consumption.
While the research on image encryption continues to advance, there are also many researchers engaged in cryptanalysis work that is connected to image encryption [26, 35–42]. After their analysis and evaluation, some image encryption schemes are confirmed to be not as secure as they claim and have some rationality and practicality problems. Specifically, the representative problems with the current image encryption schemes are as follows:
• 1. The employed chaotic systems have distinguishing characteristics, such as limited chaotic range and uneven trajectory distribution.
• 2. Some schemes’ secret key designs are irrational, necessitating the replacement of the secret key each time a new image is encrypted. When there are a lot of images to be encrypted, such designs are impractical.
• 3. The hash value of the plaintext image is utilized inappropriately. When encrypting different images, such designs necessitate the generation of chaotic sequences on a constant basis, thus resulting in low encryption efficiency.
• 4. The entire encryption process of some schemes is independent of the plaintext image, making them difficult to effectively resist plaintext attacks.
In this paper, to address the problems of existing image encryption schemes, a novel image encryption scheme based on a memristive chaotic system and combining bidirectional bit-level cyclic shift and dynamic DNA-level diffusion (IES-M-BD) is proposed. The following is a summary of the novelties and contributions of our proposed scheme.
• 1. A memristive chaotic system with excellent chaotic performance and uniform trajectory distribution is adopted to generate chaotic sequences.
• 2. Our proposed IES-M-BD is designed to exploit a more reasonable binary sequence as the secret key, and does not need to change the secret key when encrypting different images.
• 3. A bidirectional bit-level cyclic shift operation is designed, which can realize permutation and confusion at the same time.
• 4. In IES-M-BD, the hash value of the plaintext image is utilized to affect the cyclic shift and DNA-level diffusion operations. Thus, the plaintext sensitivity of IES-M-BD is ensured.
• 5. A novel DNA sequence operation design, including dynamic column-level DNA encoding, dynamic DNA-level diffusion, DNA-level permutation, and dynamic column-level DNA decoding, not only improves the encryption efficiency, but also ensures the security of IES-M-BD.
The rest of this paper is organized as follows. In Section 2, the preliminaries are introduced. In Section 3, we describe IES-M-BD in detail. In Section 4, the simulation tests and security analyses are presented. Finally, the conclusions are drawn in Section 5.
2 Preliminaries
In this section, we briefly introduce the adopted discrete memristive chaotic system, the SHA-256 hash value of the plaintext image, and the DNA Sequence operation.
2.1 Memristive chaotic system
A 3D chaotic map with discrete memristor is adopted to generate pseudo random sequences for bit-level cyclic shift and dynamic DNA-level diffusion. Based on the discrete HP memristor model, this chaotic map is derived from the sine map and an iterative chaotic map with infinite collapse [5], which is defined as:
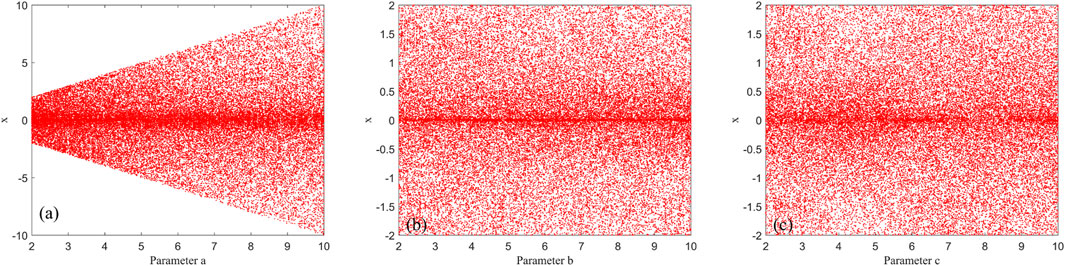
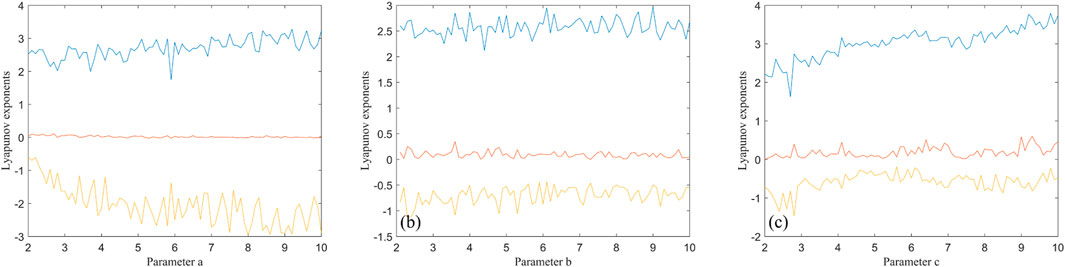
where x, y, and z represent the system states variables, α, γ, ω are amplitude, internal perturbation, and angular frequency, β is a system parameter evolved from HP memristor model. Here ω is set to π. Set α = 2, β = 3, γ = 3, and the initial state values (x0, y0, z0) = (0.3, 0.5, 1), one can get the attractors presented in Figure 1. Addtionally, the bifurcation diagrams and Lyapunov exponential spectrums are shown in Figure 2 and Figure 3, respectively.
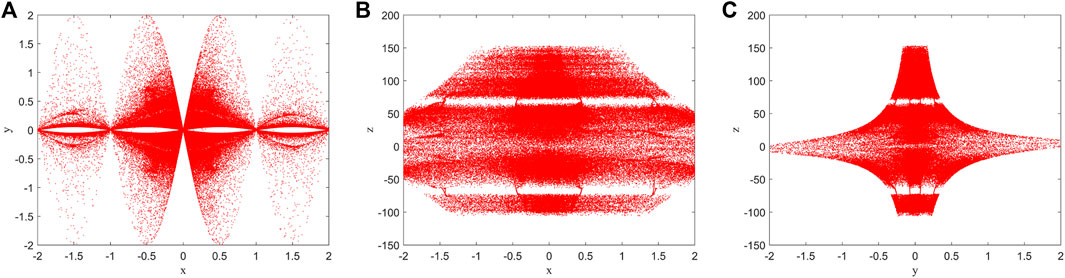
FIGURE 1. The phase diagrams with parameters a = 2, b = 3 and c = 3: (A) x-y plane; (B) x-z plane; (C) y-z plane.
When
2.2 SHA-256 hash value
SHA-256 is one of the most widely used hash algorithms in the world, it can convert image data into a 256-bit hash value. The hash value will change dramatically if one make any minor change to the image. SHA-256 is often used in encryption schemes to enhance their sensitivity to the plaintext image. In IES-M-BD, the hash value of the plaintext image is adopted to affect the cyclic shift and DNA-level diffusion operations. Thus, the plaintext sensitivity of IES-M-BD is enhanced. Even if the plaintext image only changes by one pixel bit, the encrypted image will be completely different. In this paper, we denote the hash value of the plaintext image as H(1) = b1b2 … b32, and let
where bi (i = 1, 2, … , 32) represents the ith byte consisting of eight consecutive bits in H(1), and ⊕ represents the bitwise XOR operation.
2.3 DNA sequence operation
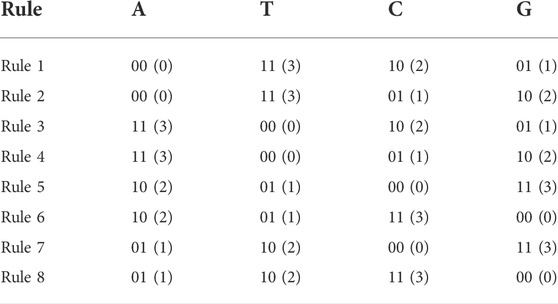
Each DNA sequence has four types of nucleic acid bases, which are Adenine (A), Thymine (T), Cytosine (C), and Guanine (G). These four nucleic acid bases follow the principle of complementary, where A and T, C and G are complementary pairs. Each nucleic acid base is encoded by a 2-bit binary code. So, there are types of encoding rules, but only eight of them can satisfy the complementary rule, which are shown in Table 1.
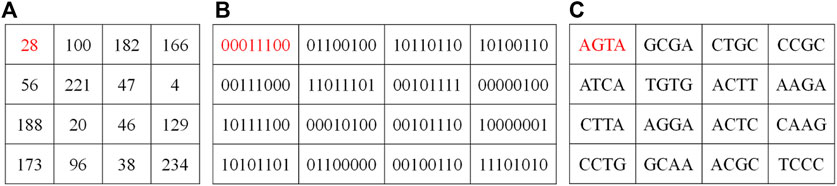
For an 8-bit gray image, each pixel can be encoded as a DNA sequence, whose length is 4. For example, a pixel value of 28 in a gray image, as shown in Figure 4, expressed as a binary number of 00011100, which can be encoded to a DNA sequence AGTA by DNA encoding Rule 1. Moreover, the addition, subtraction, and XOR operations of DNA sequences are similar to traditional binary addition, subtraction, and XOR operations. Corresponding to the eight types of DNA encoding rules, there are eight types of addition, subtraction, and XOR operations for DNA sequences.
3 Proposed encryption scheme
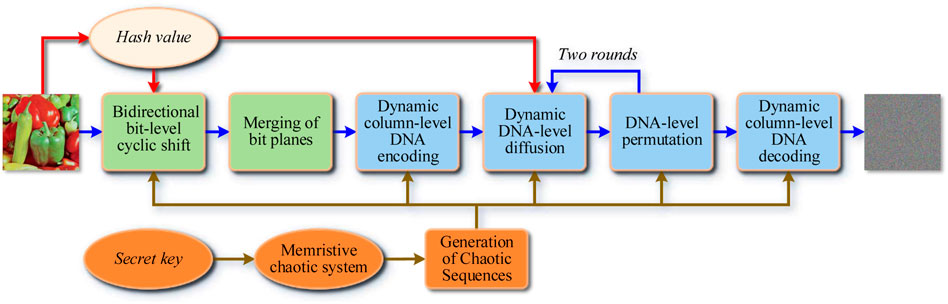
As a symmetrical image encryption scheme, IES-M-BD mainly consists of seven encryption steps. These encryption steps are Generation of Chaotic Sequences, Bidirectional Bit-level Cyclic Shift, Merging of Bit Planes, Dynamic Column-level DNA Encoding, Dynamic DNA-level Diffusion, DNA-level Permutation, and Dynamic Column-level DNA Decoding, respectively, as shown in Figure 5. In this section, we will describe each encryption step one by one.
3.1 Generation of chaotic sequences
In this section, we will describe in detail the process of generating chaotic sequences using the secret key and memristive chaotic system. The process mainly consists of three steps as shown below. In this paper, unless otherwise specified, we all assume that the size of the plaintext image that needs to be encrypted is M × N.
• Step 1: Convert the secret key K into the control parameters (α, β, γ) and initial state values (x0, y0, z0) of the memristive chaotic system. In IES-M-BD, K is a binary sequence with a length of 312 bits, that is, K = a1a2 … a312. The specific conversion method is as follows.
• Step 2: Iterate the memristive chaotic system M × N + H(2) times with the chaotic system parameters obtained in the previous step. Discard the system state values obtained in the previous H(2) iterations, and save the remaining system state values as chaotic sequences X = {x1, x2, … xM×N}, Y = {y1, y2, … yM×N}, and Z = {z1, z2, … zM×N}.
• Step 3: Further process X, Y, Z to obtain six chaotic sequences S(1), S(2), S(3), S(4), S(5), S(6)that needs to be used in the subsequent encryption steps. The specific processing method is as follows.
where i = H(2) + 1, H(2) + 2, … , H(2) + M,
where i = H(3) + 1, H(3) + 2, … , H(3) + N × 8.
where i = 1, 2, … , M × N.
where i = 1, 2, … , M × N.
where i = 1, 2, … , M × N.
3.2 Bidirectional bit-level cyclic shift
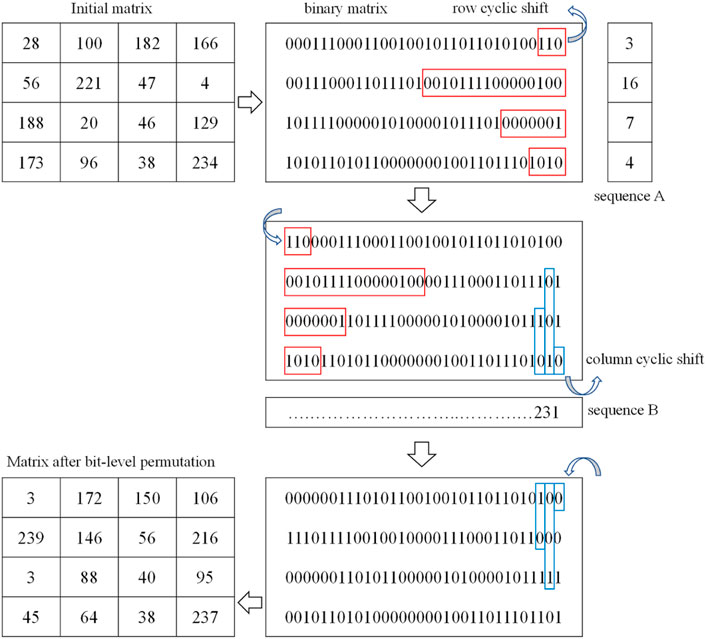
For a gray image, the brightness of each pixel is an integer number ranging from 0 to 255, where 0 means completely black. Thus, the brightness could be transformed into an 8-bit binary value. So, an image of size M × N can be converted to a M × (N × 8) binary matrix. In IES-M-BD, we adopt the bit-level permutation to scramble the positions of these binary values. The bit-level permutation uses row cyclic shift and column cyclic shift, so we call it Bidirectional Bit-level Cyclic Shift (BBCS). For example, as shown in Figure 6, an initial matrix of size 4 × 4 was transformed into a 4 × 32 binary matrix, then each row of the binary matrix was operated by row cyclic shift in turn. The value of row cyclic shift was obtained by the chaotic sequence S(1) and the hash value H(1). The next step was to perform a similar column cyclic shift. Finally, a matrix after BBCS was obtained. Specifically, the BBCS of IES-M-BD can be subdivided into the following steps.
• Step 1: Convert the plaintext image P into the binary matrix B of size M × (N × 8).
• Step 2: Initialize a column vector μ of length M, and let
where mean (•) returns the average value of the elements in an operand, min (•) returns the minimum value of the elements in an operand, and max (•) returns the maximum value of the elements in an operand. Then, use μ(1) to perform a cyclic shift operation on the first row of B.
• Step 3: Perform a cyclic shift operation on the remaining rows of B row by row. That is, for the ith row of B, let
where i = 2, 3, … , M, and t(r) = (S(1) (i) mod 32) + 1. Then, use μ(i) to perform a cyclic shift operation on the ith row of B.
• Step 4: Initialize a row vector υ of length N × 8, and let
Then, use υ(1) to perform a cyclic shift operation on the first column of B.
• Step 5: Perform a cyclic shift operation on the remaining columns of B column by column. That is, for the ith column of B, let
where i = 2, 3, … , N × 8, and t(c) = (S(2) (i) mod 32) + 1. Then, use υ(i) to perform a cyclic shift operation on the ith column of B.
As can be seen from Figure 6, BBCS not only disorganizes the position of pixels in one image, but also changes the value of each pixel. As a result, this bit-level permutation has the function of both permutation and confusion.
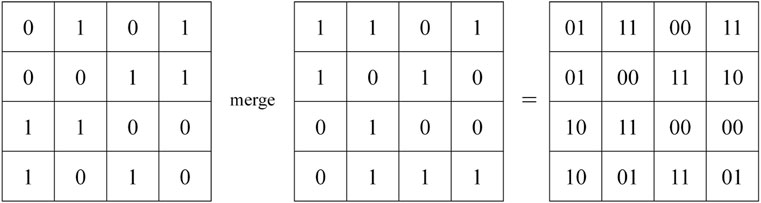
3.3 Merging of bit planes
As mentioned in Section 3.2, after the processing of BBCS, the plaintext image P will become the binary matrix B of size M × (N × 8). Logically, B consists of 8 bit planes B(1), B(2), B(3), B(4), B(5), B(6), B(7), and B(8). Next, merge the 8 bit planes in pairs to obtain the four quaternary matrices Q(1), Q(2), Q(3), and Q(4), as shown in Figure 7.
Specifically, Q(1) is obtained by merging B(1) and B(2), Q(2) is obtained by merging B(3) and B(4), Q(3) is obtained by merging B(5) and B(6), and Q(4) is obtained by merging B(7) and B(8). In this way, after the above processing, a quaternary matrix Q with the size of M × (N × 4) can actually be obtained.
3.4 Dynamic column-level DNA encoding
Compared with the DNA encoding method in which the encoding rule remains unchanged, the dynamic DNA encoding that constantly changes the encoding rule during the encoding process can achieve better encryption effects [32, 34]. In addition, different from the previous element-by-element encoding method, in order to improve the encryption efficiency, IES-M-BD adopts the column-level dynamic encoding method. Specifically, this encryption step can be further subdivided into the following steps.
• Step 1: Reshape the chaotic sequences S(3) and S(4) obtained in Section 3.1 into the matrices of size M × N. Then, the DNA encoding rules are generated in groups of four columns, as shown below.
where R(E) is the obtained DNA encoding rule matrix whose size is M × (N × 4), and j = 1, 2, … , N.
• Step 2: According to R(E) obtained in the previous step, the dynamic DNA encoding of Q is performed in column units, so as to get the DNA base matrix D(C) of size M × (N × 4).
• Step 3: Reshape the chaotic sequence S(5) obtained in Section 3.1 into the matrix of size M × N, and then utilize R(E) to encode it into the chaotic DNA base matrix D(S) of size M × (N × 4) in the same way as in Step 2.
• Step 4: Using the Nth column of the DNA base matrix D(C), the first column of the chaotic matrices S(3), S(4), S(5), and the hash value parameters H(2) and H(3), generate a column vector
of size M × 1. Then, encode V as a column vector D(V)of DNA bases with the first column of R(E).
3.5 Dynamic DNA-level diffusion
According to Shannon’s suggestion, a secure cryptosystem should not only meet confusion requirements, but also diffusion requirements. Therefore, IES-M-BD further performs DNA-level diffusion operations on DC to ensure that the diffusion requirements can be met. Likewise, in order to improve encryption efficiency, the diffusion operation here is performed in units of columns. Besides, to ensure extremely high plaintext sensitivity, we introduce H(1), H(2) and an iterative structure during the encryption process. Specifically, the dynamic DNA-level diffusion of IES-M-BD can be further subdivided into two steps.
• Step 1: Diffuse the first four columns of D(C), so as to get the first four columns of the diffusion result matrix C(1), as shown below.
where ⊕, ⊙, and ⊗ represent DNA addtion, DNA substraction and DNA XOR operations, respectively.
• Step 2: Sequentially diffuse the fifth to Nth column of D(C) in order to get the entire C(1). The specific diffusion method is as follows.
where j = 2, 3, … , 4 × M × N.
3.6 DNA-level permutation
As mentioned in Section 3.5, in order to improve encryption efficiency, the dynamic DNA-level diffusion of IES-M-BD is a one-way diffusion operation in column units. Obviously, this diffusion method cannot ensure the sufficiency of diffusion. Therefore, IES-M-BD further introduces a DNA-level permutation operation, which together with the dynamic DNA-level diffusion forms a two-round iterative structure, thus ensuring the sufficiency of diffusion. Specifically, the DNA-level permutation of IES-M-BD includes the following steps.
• Step 1: Sort the chaotic sequence S(6) obtained in Section 3.1, and save the index obtained by sorting as a 1D index row vector I of length 4 × M × N.
• Step 2: Stretching C(1) from a DNA matrix into a DNA sequence of length 4 × M × N.
• Step 3: Initialize a DNA sequence C(2) of length 4 × M × N, and let C(2) (i) = C(1) (I(i)), where i = 1, 2, … , 4 × M × N.
• Step 4: Reshape the DNA sequence C(2) obtained in the previous step into a matrix of size M × (N × 4).
As shown in Figure 5, after the first round of DNA-level diffusion and permutation operations, IES-M-BD performs another round of such operations. That is, C(2) is diffused again to get C(3), and then C(3) is permutated again to obtain fully diffused C(4).
3.7 Dynamic column-level DNA decoding
Similar to Section 3.4, the DNA decoding operation of IES-M-BD is also dynamic and column-wise, as shown below.
• Step 1: Taking the matrices S(3) and S(4) obtained in Section 3.4, generate the DNA decoding rules in groups of four columns, as shown below.
where R(D) is the obtained DNA encoding rule matrix whose size is M × (N × 4), j = 1, 2, … , N,
• Step 2: According to R(D) obtained in the previous step, the dynamic DNA decoding of C(4) is performed in column units, so as to obtain the quaternary matrix Q(D) of size M × (N × 4).
• Step 3: Merge the four 2-bit planes of Q(D) to obtain the final ciphertext image C(F) of size M × N.
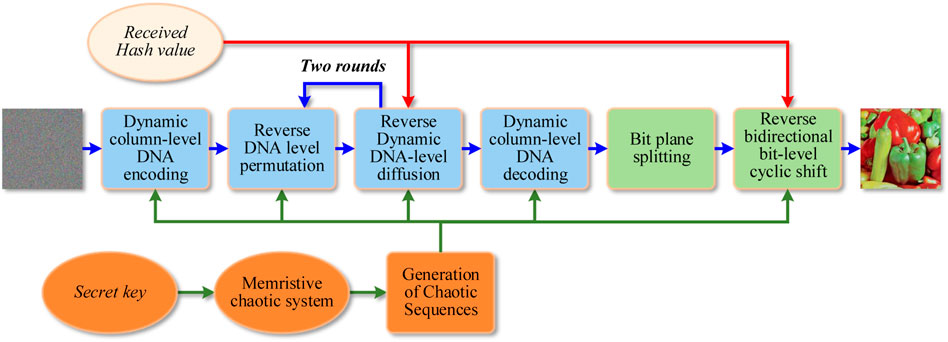
Since IES-M-BD is an image encryption scheme with a symmetric structure, its decryption process is the reverse process of the encryption process, as shown in Figure 8.
4 Simulation tests and performance analysis
In this section, we will perform simulation tests and performance analysis on IES-M-BD. These tests and analyses include encryption and decryption effect test, key space analysis, key sensitivity analysis, differential attack analysis, pixel value distribution test, correlation analysis, information entropy analysis, noise and data loss attack tests, and time analysis. Without loss of generality, when testing and analyzing IES-M-BD, we all use randomly generated secret keys. And the images used in this section are from The USC-SIPI Image Database (http://sipi.usc.edu/database/). In addition, the hardware and software configurations used in this paper is shown in Table 2.
4.1 Effect of encryption and decryption
In order to verify the effect of encryption and decryption, we encrypted some common test images with IES-M-BD, and then decrypted the generated ciphertext images. The relevant test results are shown in Figure 9. It can be seen that the ciphertext images generated by IES-M-BD are very similar to the noise image, and the encryption effect is excellent. In addition, the decrypted image are exactly the same as the original plaintext images without any loss of information, so the decryption effect is also excellent.

FIGURE 9. Encryption and decryption results of IES-M-BD (A1) 7.1.03; (A2) ciphertext of (A1); (A3) decrypted image of (A2); (B1) 5.2.09; (B2) ciphertext of (B1); (B3) decrypted image of (B2); (C1) 5.2.10; (C2) ciphertext of (C1); (C3) decrypted image of (C2); (D1) house; (D2) ciphertext of (D1); (D3) decrypted image of (D2); (E1) 4.2.05; (E2) ciphertext of (E1); (E3) decrypted image of (E2); (F1) 4.2.07; (F2) ciphertext of (F1); (F3) decrypted image of (F2).
4.2 Key space analysis
As we know, an encryption scheme must have a large enough key space to effectively resist brute force attacks. In general, it is believed that the key space of an encryption scheme should be at least greater than 2128 [34]. Considering the problems pointed out by some researchers in their cryptanalytic studies [39, 41–43], we define the secret key of IES-M-BD as a binary sequence of 312 bits, that is, K = a1a2 … a312. Specifically, IES-M-BD uses six sets of bit sequences (52 × 6) in K to generate the control parameters (α, β, γ) and initial state values (x0, y0, z0) of the memristive chaotic system. In this way, the key space of IES-M-BD is 2312. Undoubtedly, this size is much larger than the normally required 2128. Therefore, IES-M-BD can effectively resist brute force attacks.
4.3 Key sensitivity analysis
A secure image encryption scheme should not only have a large enough key space, but also be extremely sensitive to small changes in the secret key, so as to mask the statistical relationship between the secret key and the ciphertext image [44–47]. In order to test the sensitivity of IES-M-BD to the secret key, we first randomly generated a secret key KR. The control parameters and initial state values of the memristive chaotic system generated by KR are shown below.
Next, we sequentially made minimal changes to each set of 52-bit binary sequences in KR, changing only one binary bit in one set of binary sequences at a time. In this way, we obtained six secret keys with the smallest difference from KR, namely

FIGURE 10. Key sensitivity test results of IES-M-BD (A1) 5.2.09; (A2) ciphertext image
As one can see from Figure 10, the ciphertext image will change dramatically even with only minimal changes to the secret key. Consequently, IES-M-BD has extremely high key sensitivity.
4.4 Differential attack analysis
As one know, various differential attacks including chosen-plaintext attack and known-plaintext attack are the most common attack methods for attackers. In order to effectively resist differential attacks, an encryption scheme must have extremely high sensitivity to the plaintext image. This means that even if only a very small change occurs in the plaintext image, the ciphertext image generated by this encryption scheme should change extremely significantly. In this paper, many differential attack tests are performed on IES-M-BD using randomly generated secret keys, and the relevant test results are shown in Figure 11.

FIGURE 11. Differential attack test results of IES-M-BD (A1) 7.1.03; (A2) ciphertext of (A1); (A3) 1 bit of the pixel at (256,256) in (A1) is changed; (A4) ciphertext of (A3); (A5) difference image between (A2) and (A4); (B1) boat.512; (B2) ciphertext of (B1); (B3) 1 bit of the pixel at (512,512) in (B1) is changed; (B4) ciphertext of (B3); (B5) difference image between (B2) and (B4).
According to the test results, even if the plaintext image has only a small change of 1 bit, the ciphertext image generated by IES-M-BD has changed completely. The difference image between the ciphertext images before and after the change is similar to the ordinary ciphertext image and the noise image. Besides, this significant change is independent of the location of changed pixel bits. Consequently, IES-M-BD has excellent ability to resist differential attacks.
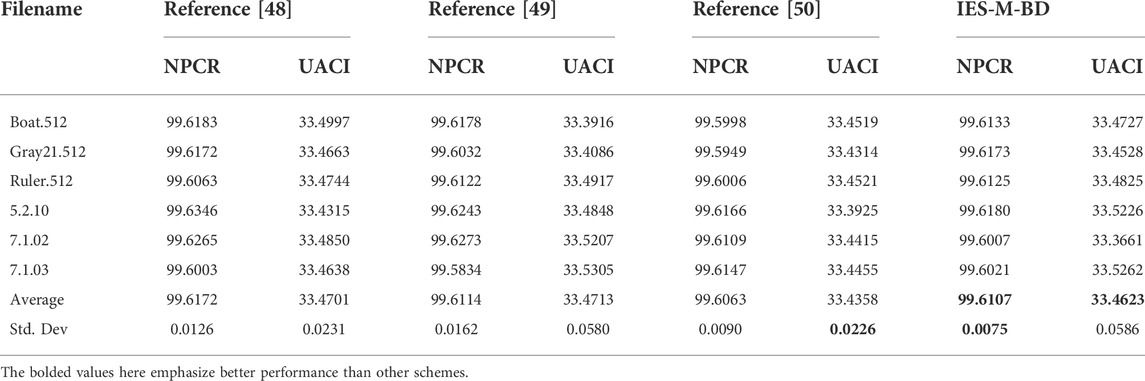
In addition, we also utilize the number of pixel change ratio (NPCR) and unified average change in intensity (UACI) to further evaluate the ability of IES-M-BD to resist differential attacks, as shown in Table 3. Mathematically, these two metrics can be defined as follows.
where I1, I2 are two images, each of them has the size of M × N. According to the test results in Table 3 and the comparison with the other three encryption schemes, one can know that the test results of IES-M-BD are the closest to the ideal value and have very high stability. Therefore, IES-M-BD does have excellent resistance to differential attacks.
4.5 Pixel value distribution
The uniformity of the pixel value distribution of the ciphertext image is also an important aspect to measure the security of an encryption scheme, because it is related to whether it can effectively resist statistical attacks. In order to verify the ability of IES-M-BD to resist statistical attacks, we have drawn some histograms of the plaintext images and the ciphertext images generated by IES-M-BD respectively, as shown in Figure 12. It can be seen that in these ciphertext images, the pixel distribution features in the plaintext images have been completely eliminated, and one cannot perceive any relevant features.
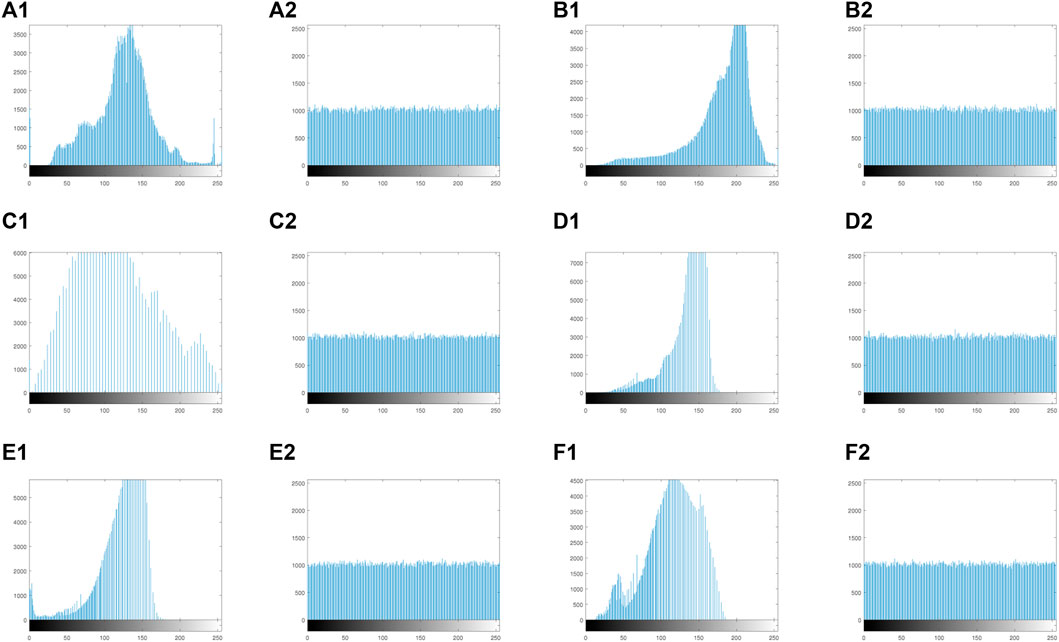
FIGURE 12. Histograms of plaintext images and corresponding ciphertext images (A1) 5.2.08; (A2) ciphertext of 5.2.08; (B1) 5.2.09; (B2) ciphertext of 5.2.09; (C1) 5.2.10; (C2) ciphertext of 5.2.08; (D1) 7.1.03; (D2) ciphertext of 7.1.03; (E1) 7.1.04; (E2) ciphertext of 7.1.04; (F1) 7.1.05; (F2) ciphertext of 7.1.05.
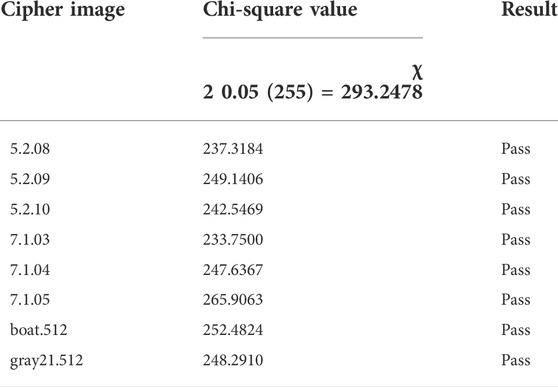
In addition to drawing histograms, one can also quantitatively analyze the pixel distribution uniformity of ciphertext images through the chi-square test [50]. The chi-square test can be defined as follows.
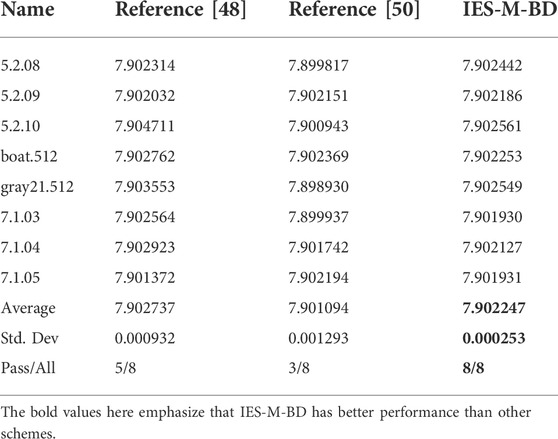
where ni is the number of pixels whose value is i − 1, M × N is the size of the cipher image, k is the number of all possible pixel values (k = 256 for grayscale images), and p = 1/k. Next, one can calculate the critical value of the chi-square test at the significant level α = 0.05. When the chi-square value of a cipher image is less than the critical value, it is considered to have passed the chi-square test. From the test results shown in Table 4, all ciphertext images generated by IES-M-BD have passed the chi-square test. This means that IES-M-BD does have excellent resistance to statistical attacks.
4.6 Correlation analysis
There is a high correlation between adjacent pixels of the plaintext images in each direction, as shown in the first row of Figure 13. Therefore, a secure image encryption scheme should be able to effectively remove such correlations. Since pixel-level cyclic shift and DNA-level permutation are introduced in the encryption process of IES-M-BD, IES-M-BD can completely eliminate the correlation between adjacent pixels, as shown in the second row of Figure 13.
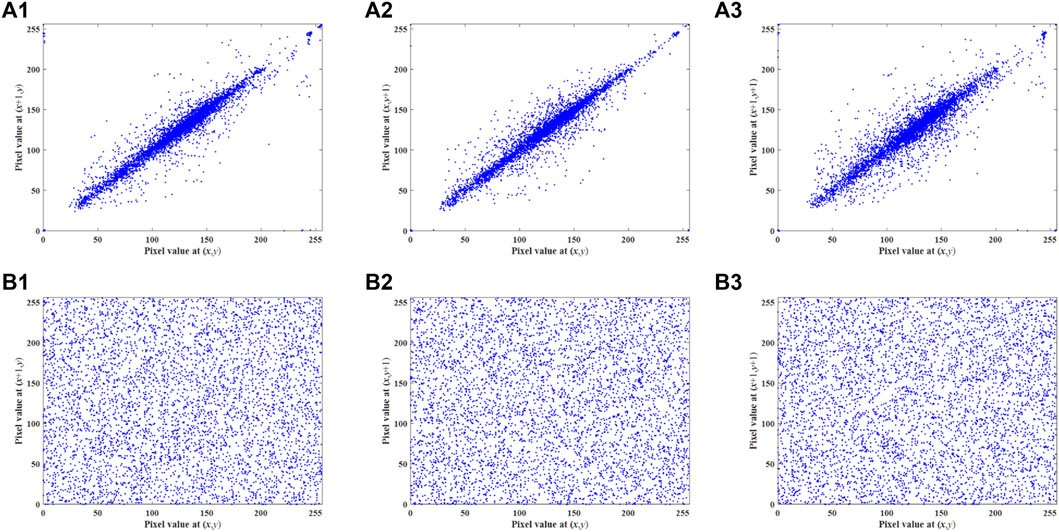
FIGURE 13. Pixel correlations of 5.2.08 and its ciphertext image generated by IES-M-BD (A1) horizontal direction of 5.2.08; (A2) vertical direction of 5.2.08; (A3) diagonal direction of 5.2.08; (B1) horizontal direction of 5.2.08 ciphertext; (B2) vertical direction of 5.2.08 ciphertext; (B3) diagonal direction of 5.2.08 ciphertext.
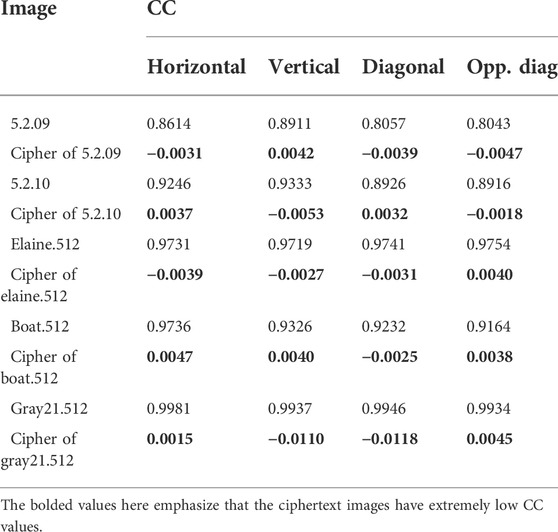
In addition, in order to more accurately verify the correlation between adjacent pixels, many researchers use the correlation coefficient (CC) to perform quantitative analysis. Mathematically, we can define CC as follows.
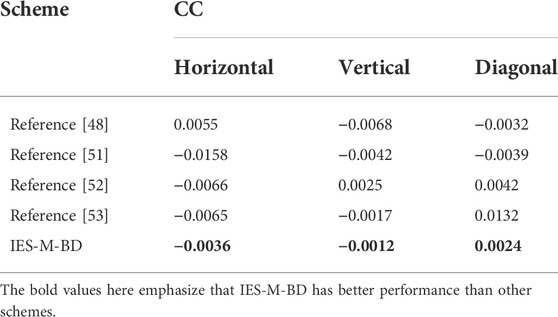
where E(v) and D(v) are the expectation and variance of the grayscale value v, vx and vy are the gray values of two adjacent pixels in a certain direction. After calculating the CC values of a large number of plaintext images and some ciphertext images, we found that the CC values of the plaintext images are high, while the CC values of the ciphertext images generated by IES-M-BD are very low, as shown in Table 5. This means that IES-M-BD can indeed significantly eliminate the correlations between adjacent pixels. As shown in Table 6, compared with some recent encryption schemes, the Lena cipher image generated by IES-M-BD demonstrates certain superiority in the correlation of adjacent pixels. It can be seen that the ciphertext image generated by IES-M-BD has the lowest correlations between adjacent pixels in all directions.
4.7 Information entropy analysis
In order to measure the randomness of images generated by encryption schemes, researchers often use information entropy as an evaluation metric. Specifically, we can define information entropy as follows.
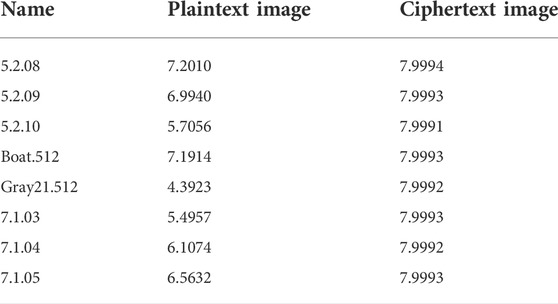
where ux is one of the symbols with a total number of N, and p (ux) represents the occurrence probability of ux. If the number of gray levels is 256, then the ideal value of image information entropy is 8. Therefore, the information entropy of an image generated by an encryption scheme is closer to 8, which means less information leakage. Table 7 compares the information entropy values of some plaintext images and the corresponding ciphertext images. After the encryption of IES-M-BD, the information entropy of the image becomes very close to the ideal value, that is, the obtained ciphertext image has excellent randomness. Not only that, IES-M-BD also shows significant advantages compared with other image encryption schemes, as shown in Table 8.
Considering the limitation of information entropy, another improved metric, local Shannon entropy (LSE), is proposed to better measure the randomness of ciphertext images [57]. Mathematically, LSE can be defined as follows.
where N represents the number of image blocks, S represents the number of pixels each image block has, oi represents each image block randomly selected from the measured image, and H (oi) represents the information entropy of each image block.
According to [57], if the LSE test value of the tested image is between 7.901901305 and 7.903037329, it can be confirmed that the image is random in the sense of LSE. Consequently, we have tested the ciphertext images generated by IES-M-BD, and the specific test results are included in Table 9. According to Table 9, it can be concluded that the test values of IES-M-BD are more stable than that of other schemes, and the pass rate of the LSE test is also higher.
4.8 Resistance to noise and data loss
There are two situations that often occur during the transmission of ciphertext images, that is, the transmitted image is contaminated by noise or part of the data is lost. In fact, malicious attackers may also cause these situations to occur. Therefore, an image encryption scheme must be able to resist these attacks in order to be practical. To simulate these noise attacks, we deliberately add salt and pepper noise (SPN) to the ciphertext images generated by IES-M-BD. Figure 14 shows the relevant test results.

FIGURE 14. Noise attack test results of IES-M-BD (A1) ciphertext image of 7.1.02 (A2) contaminated by SPN with density = 0.05; (A3) contaminated by SPN with density = 0.10; (A4) contaminated by SPN with density = 0.15; (B1) decrypted image of (A1); (B2) decrypted image of (A2); (B3) decrypted image of (A3); (B4) decrypted image of (A4); (C1) ciphertext image of 4.2.07 (C2) contaminated by SPN with density = 0.05; (C3) contaminated by SPN with density = 0.10; (C4) contaminated by SPN with density = 0.15; (D1) decrypted image of (C1); (D2) decrypted image of (C2); (D3) decrypted image of (C3); (D4) decrypted image of (C4).
From the test results shown in Figure 14, although these ciphertext images are contaminated by noise, IES-M-BD can still decrypt the images normally. Although the quality of the decrypted image will decrease with the increase of the noise intensity, this does not hinder the transmission of the visual information of the plaintext image.
Similarly, to evaluate the reliability of IES-M-BD under data loss conditions, we intentionally removed some pixels from the ciphertext images. The relevant test results are shown in Figure 15. As one can see, despite the loss of data, IES-M-BD can still decrypt the images normally. That is, the transmission of the visual information of the plaintext image is not significantly affected. Specifically, the more data is lost, the lower the quality of the decrypted image, while IES-M-BD can still maintain high image quality when some pixels are missing.

FIGURE 15. Occlusion attack test results of IES-M-BD (A1) ciphertext of house; (A2) 1/16 data loss at top-left corner; (A3) 1/16 data loss at top-right corner; (A4) 1/16 data loss at bottom-left corner; (A5) 1/16 data loss at bottom-right corner; (B1) decrypted ciphertext of (A1); (B2) decrypted ciphertext of (A2); (B3) decrypted ciphertext of (A3); (B4) decrypted ciphertext of (A4); (B5) decrypted ciphertext of (A5).
4.9 Time analysis
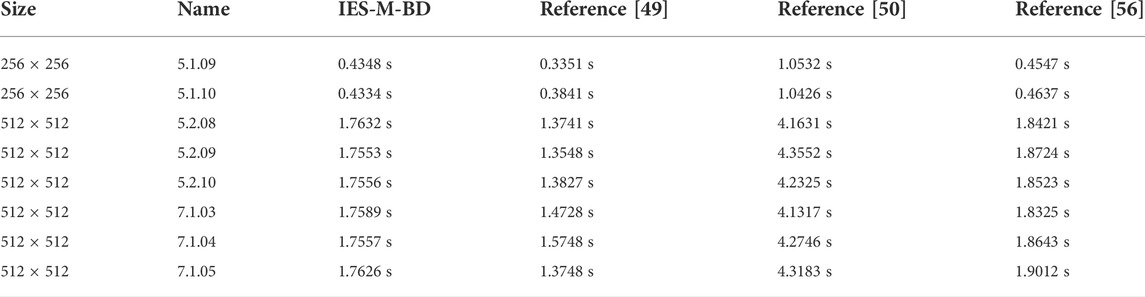
Undoubtedly, in many scenarios of information security application, the encryption efficiency of the cryptographic system is a key factor. Therefore, when designing an image encryption scheme, we should not only consider the security, but also consider the efficiency of the encryption scheme. To this end, we tested IES-M-BD and compared the test results with other encryption schemes, as shown in Table 10. It can be seen that IES-M-BD has higher or comparable encryption efficiency compared with other image encryption schemes. Notably, according to the various analyses above, IES-M-BD is better than the remaining encryption schemes in terms of security. Definitely, in the future, we will also consider further optimization of IES-M-BD to make it more efficient.
5 Conclusion
Aiming at the key problems existing in image encryption, this paper proposes a novel encryption scheme that embraces several innovative designs. Firstly, a discrete memristive chaotic system is exploited to enhance the ergodicity of the generated chaotic sequences. Secondly, the proposed encryption scheme leverages the hash value in a more reasonable way. That is, the proposed image encryption scheme utilizes the hash value to influence the cyclic shift and DNA diffusion operations instead of using it directly as the secret key. Such ingenious design can not only solve the practicability problem brought by the one-time pad secret key design, but also significantly improve the sensitivity of the encryption scheme to the plaintext image. Thirdly, a bidirectional bit-level cyclic shift operation is designed, which can realize permutation and confusion at the same time, thereby further improving the security of the encryption scheme. Finally, the novel DNA sequence operation design, including dynamic column-level DNA encoding, dynamic DNA-level diffusion, DNA-level permutation, and dynamic column-level DNA decoding, not only improves encryption efficiency, but also ensures the security of the proposed encryption scheme once again. In the future, we will continuously optimize this encryption scheme, and extend it to the field of video encryption.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
JZ and XL provided the idea of algorithm, KQ and ZZ carried out the simulations, arranged the architecture and drafted the manuscript. WF and ZQ supervised the work and revised the manuscript. Both authors read and approved the final manuscript.
Funding
This research was funded by the Research Foundation of Education Bureau of Hunan Province of China (No. 19C0864), the Science and Technology Development Center Project of Chinese Ministry of Education (No. 2021KSA01008), the Project of the Sichuan Higher Education Society of China (No. GJXHXXH21-YB-27), the Guiding Science and Technology Plan Project of Panzhihua City (No. 2020ZD-S-40), and the Doctoral Research Startup Foundation of Panzhihua University (No. 2020DOC019).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chua L. Memristor-the missing circuit element. IEEE Trans Circuit Theor (1971) 18:507–19. doi:10.1109/TCT.1971.1083337
2. Buscarino A, Fortuna L, Frasca M, Gambuzza LV. A chaotic circuit based on hewlett-packard memristor. Chaos (2012) 22:023136. Art. No. doi:10.1063/1.4729135
3. Strukov DB, Snider GS, Stewart DR, Williams RS. The missing memristor found. nature (2008) 453:80–3. doi:10.1038/nature06932
4. Peng Y, He S, Sun K. Parameter identification for discrete memristive chaotic map using adaptive differential evolution algorithm. Nonlinear Dyn (2022) 107:1263–75. doi:10.1007/s11071-021-06993-0
5. Peng Y, He S, Sun K. A higher dimensional chaotic map with discrete memristor. AEU - Int J Electronics Commun (2021) 129:153539. Art. No. 153539. doi:10.1016/j.aeue.2020.153539
6. Li CL, Li ZY, Feng W, Tong YN, Du JR, Wei DQ, et al. Dynamical behavior and image encryption application of a memristor-based circuit system. AEU - Int J Electronics Commun (2019) 110:152861. Art. No. 152861. doi:10.1016/j.aeue.2019.152861
7. Bao H, Wang N, Bao B, Chen M, Jin P, Wang G, et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun Nonlinear Sci Numer Simulation (2018) 57:264–75. doi:10.1016/j.cnsns.2017.10.001
8. Sabarathinam S, Volos CK, Thamilmaran K. Implementation and study of the nonlinear dynamics of a memristor-based duffing oscillator. Nonlinear Dyn (2017) 87:37–49. doi:10.1007/s11071-016-3022-8
9. Rajagopal K, Jafari S, Karthikeyan A, Srinivasan A, Ayele B. Hyperchaotic memcapacitor oscillator with infinite equilibria and coexisting attractors. Circuits Syst Signal Process (2018) 37:3702–24. doi:10.1007/s00034-018-0750-7
10. Zhao R, Zhang Y, Xiao X, Ye X, Lan R. Tpe2: Three-pixel exact thumbnail-preserving image encryption. Signal Process. (2021) 183:108019. Art. No. 108019. doi:10.1016/j.sigpro.2021.108019
11. Hua Z, Zhou Y, Huang H. Cosine-transform-based chaotic system for image encryption. Inf Sci (2019) 480:403–19. doi:10.1016/j.ins.2018.12.048
12. Zhou S, He Y, Liu Y, Li C, Zhang J. Multi-channel deep networks for block-based image compressive sensing. IEEE Trans Multimedia (2021) 23:2627–40. doi:10.1109/TMM.2020.3014561
13. Zhou S, Deng X, Li C, Liu Y, Jiang H. Recognition-oriented image compressive sensing with deep learning. IEEE Trans Multimedia (2022) 1. doi:10.1109/TMM.2022.3142952
14. Zhao R, Zhang Y, Xiao X, Ye X, Lan R. TPE2: Three-pixel exact thumbnail-preserving image encryption. Signal Process. (2021) 183. 108019. Art. No. doi:10.1016/j.sigpro.2021.108019
15. Zhang Y, Wang P, Fang L, He X, Chen B. Secure transmission of compressed sampling data using edge clouds. IEEE Trans Industr Inform (2020) 16:6641–51. doi:10.1109/TII.2020.2966511
16. Feng W, Zhang J, Qin Z. A secure and efficient image transmission scheme based on two chaotic maps. Complexity (2021) 2021:1–19. art. no.898998. doi:10.1155/2021/1898998
17. Liu H, Kadir A, Xu C. Color image encryption with cipher feedback and coupling chaotic map. Int J Bifurcation Chaos (2020) 30:2050173. doi:10.1142/S0218127420501734
18. Pourasad Y, Ranjbarzadeh R, Mardani A. A new algorithm for digital image encryption based on chaos theory. Entropy (2021) 23:341. Art. No. 341. doi:10.3390/e23030341
19. Wang S, Wang C, Xu C. An image encryption algorithm based on a hidden attractor chaos system and the knuth–durstenfeld algorithm. Opt Lasers Eng (2020) 128:105995. Art. No. doi:10.1016/j.optlaseng.2019.105995
20. Si Y, Liu H, Chen Y. Constructing keyed strong s-box using an enhanced quadratic map. Int J Bifurcation Chaos (2021) 31:2150146. doi:10.1142/S0218127421501467
21. Li C, Tan K, Feng B, Lü J. The graph structure of the generalized discrete arnold’s cat map. IEEE Trans Comput (2022) 71:364–77. doi:10.1109/TC.2021.3051387
22. Li C, Feng B, Li S, Kurths J, Chen G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans Circuits Syst (2019) 66:2322–35. doi:10.1109/TCSI.2018.2888688
23. Zhang Y, Wang P, Huang H, Zhu Y, Xiao D, Xiang Y, et al. Privacy-assured fogcs: Chaotic compressive sensing for secure industrial big image data processing in fog computing. IEEE Trans Industr Inform (2020) 17:3401–11. doi:10.1109/TII.2020.3008914
24. Zhang Y, Zhao R, Xiao X, Lan R, Liu Z, Zhang X, et al. Hf-tpe: High-fidelity thumbnail- preserving encryption. IEEE Trans Circuits Syst Video Technol (2022) 32:947–61. doi:10.1109/TCSVT.2021.3070348
25. Cao C, Sun K, Liu W. A novel bit-level image encryption algorithm based on 2d-licm hyperchaotic map. Signal Process. (2018) 143:122–33. doi:10.1016/j.sigpro.2017.08.020
26. Özkaynak F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn (2018) 92:305–13. doi:10.1007/s11071-018-4056-x
27. Zhu Z, Zhang W, Wong K, Yu H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf Sci (2011) 181:1171–86. doi:10.1016/j.ins.2010.11.009
28. Li Y, Wang C, Chen H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt Lasers Eng (2017) 90:238–46. doi:10.1016/j.optlaseng.2016.10.020
29. Teng L, Wang X, Meng J. A chaotic color image encryption using integrated bit-level permutation. Multimed Tools Appl (2018) 77:6883–96. doi:10.1007/s11042-017-4605-1
30. Zhang Q, Guo L, Wei X. A novel image fusion encryption algorithm based on dna sequence operation and hyper-chaotic system. Optik - Int J Light Electron Opt (2013) 124:3596–600. doi:10.1016/j.ijleo.2012.11.018
31. Chai X, Chen Y, Broyde L. A novel chaos-based image encryption algorithm using dna sequence operations. Opt Lasers Eng (2017) 88:197–213. doi:10.1016/j.optlaseng.2016.08.009
32. Feng W, He Y, Li H, Li C. A plain-image-related chaotic image encryption algorithm based on DNA sequence operation and discrete logarithm. IEEE Access (2019) 7:181589–609. doi:10.1109/ACCESS.2019.2959137
33. Chai X, Fu X, Gan Z, Lu Y, Chen Y. A color image cryptosystem based on dynamic dna encryption and chaos. Signal Process. (2019) 155:44–62. doi:10.1016/j.sigpro.2018.09.029
34. Li H, Li T, Feng W, Zhang J, Zhang J, Gan L, et al. A novel image encryption scheme based on non-adjacent parallelable permutation and dynamic dna-level two-way diffusion. J Inf Security Appl (2021) 61:102844. Art. No. 102844. doi:10.1016/j.jisa.2021.102844
35. Feng W, He Y. Cryptanalysis and improvement of the hyper-chaotic image encryption scheme based on DNA encoding and scrambling. IEEE Photon J (2018) 10:1–15. Art. No. 7909215. doi:10.1109/JPHOT.2018.2880590
36. Feng W, He Y, Li H, Li C. Cryptanalysis and improvement of the image encryption scheme based on 2D logistic-adjusted-sine map. IEEE Access (2019) 7:12584–97. doi:10.1109/ACCESS.2019.2893760
37. Liu H, Kadir A, Xu C. Cryptanalysis and constructing s-box based on chaotic map and backtracking. Appl Mathematics Comput (2020) 376:125153. doi:10.1016/j.amc.2020.125153
38. Feng W, Zhang J. Cryptanalzing a novel hyper-chaotic image encryption scheme based on pixel-level filtering and DNA-level diffusion. IEEE Access (2020) 8:209471–82. doi:10.1109/ACCESS.2020.3038006
39. Ma Y, Li C, Ou B. Cryptanalysis of an image block encryption algorithm based on chaotic maps. J Inf Security Appl (2020) 54:102566. Art. No. 102566. doi:10.1016/j.jisa.2020.102566
40. Feng W, Qin Z, Zhang J, Ahmad M. Cryptanalysis and improvement of the image encryption scheme based on feistel network and dynamic dna encoding. IEEE Access (2021) 9:145459–70. doi:10.1109/ACCESS.2021.3123571
41. Chen L, Li C, Li C. Security measurement of a medical communication scheme based on chaos and DNA coding. J Vis Commun Image Representation (2022) 83:103424. Art. No. 103424. doi:10.1016/j.jvcir.2021.103424
42. Liu S, Li C, Hu Q. Cryptanalyzing two image encryption algorithms based on a first-order time-delay system. IEEE MultiMedia (2022) 29:74–84. doi:10.1109/MMUL.2021.3114589
43. Li C, Zhang Y, Xie EY. When an attacker meets a cipher-image in 2018: A year in review. J Inf Security Appl (2019) 48:102361. Art. No. 102361. doi:10.1016/j.jisa.2019.102361
44. Li C, Lin D, Lü J, Hao F. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE MultiMedia (2018) 25:46–56. doi:10.1109/MMUL.2018.2873472
45. Li C, Lin D, Lü J. Cryptanalyzing an image-scrambling encryption algorithm of pixel bits. IEEE MultiMedia (2017) 24:64–71. doi:10.1109/MMUL.2017.3051512
46. Zhang Y, He Q, Xiang Y, Zhang LY, Liu B, Chen J, et al. Low-cost and confidentiality-preserving data acquisition for internet of multimedia things. IEEE Internet Things J (2018) 5:3442–51. doi:10.1109/JIOT.2017.2781737
47. Zhang Y, He Q, Chen G, Zhang X, Xiang Y. A low-overhead, confidentiality-assured, and authenticated data acquisition framework for iot. IEEE Trans Industr Inform (2020) 16:7566–78. doi:10.1109/TII.2019.2957404
48. Xu M, Tian Z. A novel image cipher based on 3d bit matrix and Latin cubes. Inf Sci (2019) 478:1–14. doi:10.1016/j.ins.2018.11.010
49. Zhu H, Zhang X, Yu H, Zhao C, Zhu Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dyn (2017) 89:61–79. doi:10.1007/s11071-017-3436-y
50. Zhu H, Zhao Y, Song Y. 2d logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access (2019) 7:14081–98. doi:10.1109/ACCESS.2019.2893538
51. Yin Q, Wang C. A new chaotic image encryption scheme using breadth-first search and dynamic diffusion. Int J Bifurcation Chaos (2018) 28:1850047. Art. No. 1850047. doi:10.1142/S0218127418500475
52. Zahmoul R, Ejbali R, Zaied M. Image encryption based on new beta chaotic maps. Opt Lasers Eng (2017) 96:39–49. doi:10.1016/j.optlaseng.2017.04.009
53. Zefreh EZ. An image encryption scheme based on a hybrid model of dna computing, chaotic systems and hash functions. Multimed Tools Appl (2020) 79:24993–5022. doi:10.1007/s11042-020-09111-1
54. Wang X, Liu L, Zhang Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt Lasers Eng (2015) 66:10–8. doi:10.1016/j.optlaseng.2014.08.005
55. Diaconu AV. Circular inter-intra pixels bit-level permutation and chaos-based image encryption. Inf Sci (2016) 355:356314–27. doi:10.1016/j.ins.2015.10.027
56. Wu X, Wang D, Kurths J, Kan H. A novel lossless color image encryption scheme using 2d dwt and 6d hyperchaotic system. Inf Sci (2016) 349:350137–53. doi:10.1016/j.ins.2016.02.041
Keywords: image encryption, memristor, memristive chaotic system, cyclic shift, DNA sequence operation, permutation, diffusion
Citation: Qian K, Feng W, Qin Z, Zhang J, Luo X and Zhu Z (2022) A novel image encryption scheme based on memristive chaotic system and combining bidirectional bit-level cyclic shift and dynamic DNA-level diffusion. Front. Phys. 10:963795. doi: 10.3389/fphy.2022.963795
Received: 07 June 2022; Accepted: 11 July 2022;
Published: 10 August 2022.
Edited by:
Shaobo He, Central South University, ChinaCopyright © 2022 Qian, Feng, Qin, Zhang, Luo and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Feng, ZmVuZ3cxOTgxQDEyNi5jb20=
 Kun Qian
Kun Qian Wei Feng
Wei Feng Zhentao Qin
Zhentao Qin Jing Zhang
Jing Zhang Xuegang Luo
Xuegang Luo Zhengguo Zhu
Zhengguo Zhu