High-order vortex harmonics generation by bi-circular Laguerre-Gaussian laser fields with relativistic plasmas

Vortex beams with ultra-high brilliance can greatly enrich the light and matter interaction process and even shed light on the unexpected information in relativistic nonlinear optics. Thus, we propose a scheme for relativistic intense vortex harmonic radiation by use of bi-circular Laguerre–Gaussian lasers irradiating relativistic plasmas. Three-dimensional particle-in-cell simulation results show that the emitted harmonics own controllable spin and orbital angular momentum simultaneously, which can be attributed to the vortex mirror model and the related conservation laws. Meanwhile, the conversion efficiency of harmonic generation can be tuned through adjusting the intensity ratio of the two driving field components.

Introduction

Light waves can carry two distinct forms of angular momenta in the direction of propagation: spin and orbital angular momentum (SAM and OAM). The SAM is manifest as right or left circular polarization of light ($\pm \mathrm{\hslash }$ per photon), whereas the OAM is associated with its characteristic helical phase profile which can be described by an angular-dependent phase $\exp \left(il\varphi \right)$, where $\varphi$is the azimuthal coordinate and $l$is the topological charge (known as vortex beams). Different values of $l$ represent different vortex modes, indicating that the OAM carried by each photon is equal to $l\mathrm{\hslash }$. In addition, vortex beams do not have a well-defined phase at the center, resulting in the typical zero intensity center (donut-shaped intensity profile) [1, 2]. These remarkable properties have led to a wide range of applications going from optical communications, bio-photonics, optical micromanipulations to ion acceleration [3], etc. In recent years, high-order vortex beams in the extreme-ultraviolet (XUV) spectral range have attracted more and more attention for their novel potential applications. However, the traditional techniques using spiral phase plates or forked diffraction gratings are not effective due to the limitation of etching resolution. Thus, many novel schemes have been attempted: the free-electron lasers (FELs) can be used to generate such vortex beams, but the huge size and high cost greatly limit the scope of their application. As a table-top and alternative to large-scale instruments, high-harmonic generation (HHG) based on the frequency up-conversion has attracted an increasing attention. This nonlinear process includes laser-gas HHG [4, 5] and laser-plasma HHG [6–22]. These two HHG mechanisms are fundamentally different, and the intensity of emitted harmonics in the latter case can be increased by several orders of magnitude compared with that of the former, in which the limitations of the driving laser intensity (often below ${10}^{15-16}W/c{m}^2$) exist to avoid strong ionization. Among the existing researches of HHG, two-color laser scheme has been extensively investigated in both gas and plasma for its many favorable properties of the harmonic radiation, including high efficiency, spectra tunability and so on [4, 15, 17]. Initially, this scheme was to use the circularly polarized (CP) fundamental driving laser with a Gaussian spatial profile mixed with its counter-rotating second harmonic in collinear illumination, in which the spin angular momentum (SAM) carried by the driving lasers can be successfully transferred to the harmonics. Comparing with the non-collinear one, higher HHG efficiency can be acquired via collinear scheme, which has been proved in Ref. [16]. Based on this, if the driving fields are replaced by two-color twisted CP driving pulses, the OAM of the helical pulses can also be transferred to the harmonics. This point has already been proved in laser-gas HHG process, in which high harmonics with both SAM and OAM were generated and a form of simultaneous SAM and OAM conservation laws were uncovered through theoretical analysis and experimental investigation [23]. However, with the urgent requirement for intense vortex beams up to the relativistic regime, whether this scheme should work in relativistic plasma HHG process needs to be validated.

In this paper, we use full three-dimensional particle-in-cell (PIC) simulations to verify the effectiveness of two-color twisted CP laser scheme in the relativistic plasma HHG regime and find that the similar SAM and OAM conservation laws uncovered in laser-gas HHG are applicable to laser-plasma HHG. As a result, intense harmonic radiation with controllable SAM and OAM can be acquired by use of two-color Laguerre–Gaussian (LG) driving pulses irradiating relativistic plasmas. Its underlying mechanism can be attributed to the “vortex oscillating mirror” (VOM) model [2] and the conservation laws of photon’s energy, SAM and OAM. Meanwhile, the vortex mode and conversion efficiency of radiated harmonics can be flexibly tuned. Therefore, this work provides an efficient and practical approach to produce bright, spectral tunable harmonic radiation with designable SAM and OAM, which may own the potential of extending the existing application areas of vortex beams to ultra-high intensity regime and nanometer spatial, sub-femtosecond temporal scales.

Particle-in-cell simulation results

We perform full three-dimensional PIC simulations to investigate the two-color counter-rotating twisted laser scheme with the open-source EPOCH code [24]. The total electric field of the dichromatic twisted pulses can be expressed as:

$a\left(LG\right)=a_{{\omega }_1}+a_{{\omega }_2}(1)$

Where $a_{{\omega }_1}=a_1\exp \left(-\frac{r^2}{w_1^2}\right)\left(\frac{\sqrt{2}r}{w_1}\right)\exp \left(i{l}_1\varphi \right)\exp \left(i{\omega }_{1}t\right)L_0^{l_1}\left(\frac{2r^2}{w_1^2}\right){\sin }^2\left(\frac{\pi t}{{\tau }_1}\right)\left({\mathbf{e}}_y+i{\mathbf{e}}_{\mathbf{z}}\right)$, $a_{{\omega }_2}=a_2\exp \left(-\frac{r^2}{w_2^2}\right)\left(\frac{\sqrt{2}r}{w_2}\right)\exp \left(i{l}_2\varphi \right)\exp \left(i{\omega }_{2}t\right)L_0^{l_2}\left(\frac{2r^2}{w_2^2}\right){\sin }^2\left(\frac{\pi t}{{\tau }_2}\right)\left({\mathbf{e}}_y-i{\mathbf{e}}_{\mathbf{z}}\right)$. The fundamental laser has a frequency of ${\omega }_1$ corresponding to the wavelength of ${\lambda }_1={\lambda }_0=1\mu m$and the topological charge of $l_1=1$, the second one owns frequency of ${\omega }_2=2{\omega }_1$corresponding to the wavelength of ${\lambda }_2={\lambda }_0/2=0.5\mu m$and the topological charge of $l_2=2$. For the fundamental pulse, the normalized peak amplitude is $a_1=e\left|E_1\right|/m_e{\omega }_{1}c=10$, where$E_1$is the electric field amplitude, $e,m_e,c$are the unit electron charge, the electron mass and the light speed in vacuum, respectively. This corresponds to a laser peak intensity of about$I_1=2.74\times {10}^{20}\left(W/c{m}^2\right)$. The temporal intensity profile owns the full-width at half-maximum pulse duration of ${\tau }_1=50fs$. The laser spot radius is$w_1=5\mu m$. The intensity$I_2$, pulse duration${\tau }_2$ and spot radius$w_2$of the second driving laser component are kept the same with those of the fundamental one. The two driving pulses are spatiotemporally overlapped and normally irradiate the solid target along the X direction to drive the laser-plasma HHG process. The target is fully ionized with a peak electron density of $n_e=100n_c$, where$n_c=\left(m_e{\epsilon }_0{\omega }_0^2\right)/e^2$is the plasma critical density with respect to the fundamental laser frequency and${\epsilon }_0$represents the vacuum dielectric constant. The target thickness is$5\mu m$and has pre-plasma with an exponential density distribution of $n_e\left(x\right)=n_e\exp \left(x/L_s\right)$at the front surface of the plasma target. The pre-plasma scale length is set as$L_s=0.01{\lambda }_1$. The ions are assumed to be immobile. The grid size of the simulation box is$30{\lambda }_0\left(x\right)\times 20{\lambda }_0\left(y\right)\times 20{\lambda }_0\left(z\right)$. The grid cell size is $1500\left(x\right)\times 200\left(y\right)\times 200\left(z\right)$ and each cell is filled with 8 macro-particles. Absorption boundary conditions are used for both fields and particles in the whole simulation process. The sketch of our scheme is shown in Figure 1 (the inset displays the enlarged view of the vortex modes of the fundamental and second-harmonic driving pulses):

FIGURE 1

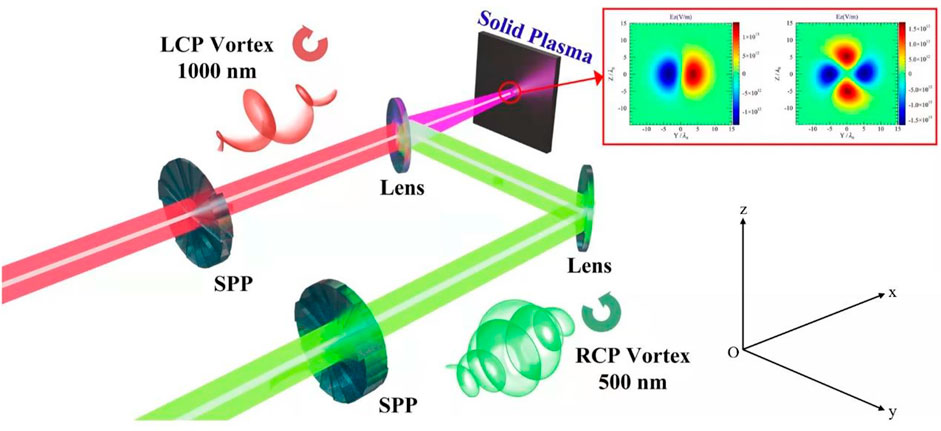
FIGURE 1. The sketch of the two-color counter-rotating LG laser scheme: dichromatic counter-rotating CP twisted laser pulses are spatiotemporally overlapped and normally irradiate the solid target to drive the laser-plasma HHG process (The SPP represent spatial phase plate, the LCP and RCP represent left- and right- CP laser respectively and the inset shows the enlarged view of the vortex modes of the fundamental and second-harmonic driving pulses).

First of all, the spectra feature of produced harmonics including their intensity and ellipticity distribution versus$k_x/k_0$and$k_y/k_0$($k_x/k_0,k_y/k_0$are the spatial frequencies along X and Y directions normalized by the fundamental laser wave number $k_0=2\pi /{\lambda }_0$, respectively) are shown in Figure 2. Here, the ellipticity of emitted harmonics$\epsilon$can be acquired as follows [19]: First, we perform Fourier transform of the two electric filed components of generated harmonics: $E_y\left(f\right)=FFT\left(E_y\right)$, $E_z\left(f\right)=FFT\left(E_z\right)$, where$f$is the frequency of harmonics, $E_y,E_z$are the strength of the harmonic field along the direction$y,z$, respectively. Then, the ellipticity of generated harmonics can be calculated by$\epsilon \left(f\right)=\frac{\left|E_R\left(f\right)\right|-\left|E_L\left(f\right)\right|}{\left|E_R\left(f\right)\right|+\left|E_L\left(f\right)\right|}$. In this equation,$E_R\left(f\right)=\frac{1}{\sqrt{2}}\left[E_y\left(f\right)-i{E}_z\left(f\right)\right]$,$E_L\left(f\right)=\frac{1}{\sqrt{2}}\left[E_y\left(f\right)+i{E}_z\left(f\right)\right]$. From Figure 2A, one can see only the harmonics with orders of $n=3m\pm 1\left(m=\mathrm{1,2,3}\cdot \cdot \cdot \right)$are produced, while every third one is missing. On the other hand, Figure 2B shows that all of the radiated harmonics are quasi-CP (the SAM per photon of harmonics are close to$\pm \mathrm{\hslash }$). In addition, the SAM carried by photons of $3m+1$harmonics ($4{\omega }_0,7{\omega }_0,10{\omega }_0...$) are the same with the fundamental driving pulse ($+\mathrm{\hslash }$), while those carried by photons of $3m-1$harmonics ($5{\omega }_0,8{\omega }_0,11{\omega }_0...$) are consistent with the double-frequency one ($-\mathrm{\hslash }$). These conclusions in frequency domain can be verified by the two panels of the inset, which display the reconstructed three-dimensional image of the electric field vectors of 4th and 5th harmonics (red) and the waveforms of the two orthogonal electric field components$E_y,E_z$ (black), as well as the projection of $E_y,E_z$ (blue). From the inset, one can observe that the amplitude ratios between the two electric components ($E_y,E_z$) are both close to unity, while the phase shift of the 4th harmonic and that of the 5th are$\frac{\pi }{2}$and$-\frac{\pi }{2}$respectively. These results indicate that the selection rules for the allowed orders and SAM of generated harmonics in traditional bi-circular HHG are still upheld in the twisted laser scheme [15].

FIGURE 2

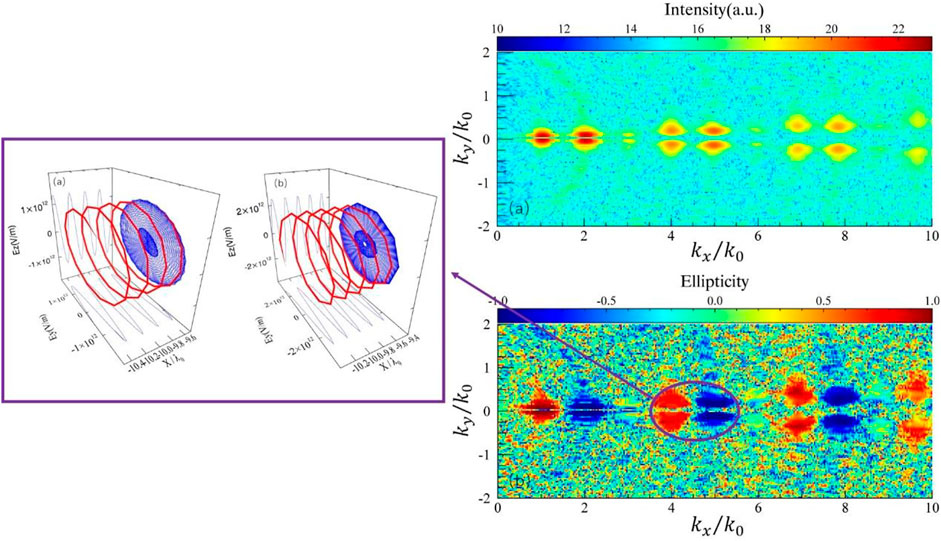
FIGURE 2. (A) The intensity of generated harmonics versus$k_x/k_0$and$k_y/k_0$in frequency domain, (B) The corresponding ellipticity distribution versus$k_x/k_0$and$k_y/k_0$in frequency domain (the spatial frequencies along X and Y directions$k_x,k_y$are normalized by the fundamental laser wave number$k_0=2\pi /{\lambda }_0$). The inset displays the three-dimensional waveforms of the electric fields of a group of neighboring harmonics ($n=\mathrm{4,5}$).

Moreover, it can be noticed here that only low order harmonics ($n\le 10$) are displayed in Figure 2, which can be explained as follows: according to the Shannon criterion and the resolution of the full three-dimensional PIC simulation, the highest resolvable harmonic order can be estimated as around 10. Thus, we only choose the harmonic with ($n\le 10$) for display with sufficiently high resolution. If the resolution is enhanced, much higher order harmonics can certainly be discernible.

In the following, the vortex characteristics of generated harmonics are investigated, which are displayed in Figures 3–5. The six panels of Figure 3 and Figure 4 show the electric field distributions in Z-Y plane at$x=-11\mu m$and the corresponding electric field isosurface of the fourth, fifth, seventh, eighth, tenth and eleventh harmonics at$t=36T_0$respectively. According to the number of intertwined helices, one can see that the corresponding topological charges of the harmonics emitted are also four, five, seven, eight, ten and eleven, which are consistent with the harmonic orders ($l_H=n$). These results indicate that the SAM and OAM conservation rules ($l_H=\frac{n+2{\sigma }_H{\sigma }_1}{3}\left(l_1+l_2\right)-{\sigma }_H{\sigma }_1{l}_2$) which was analytically derived in Ref. [23] are also valid in our scheme (if we substitute our simulation parameters ($l_1=1,l_2=2$) into the SAM and OAM conservation rules, the topological charges of high harmonics can be easily acquired as$l_H=n$). Moreover, the transverse intensity distribution (normalized to${\epsilon }_{0}c{\left(m_e{\omega }_{0}c/e\right)}^2/2$) and its corresponding profile with Y of the fourth harmonic (at the same time with Figures 3, 4) are shown in Figures 5A,B, from which the typical donut-shaped intensity distribution of optical vortices can be clearly observed. These results demonstrate that the radiated field by two-color LG laser scheme owns a complicated structure which contains both quasi-circular polarization and high-order LG modes scaling with the harmonic orders (the n-order harmonic exhibits$L{G}_{n0}$mode) [2]. In other word, besides the SAM, the OAM of driving lasers can also be transferred to the high-harmonics in this HHG scheme.

FIGURE 3

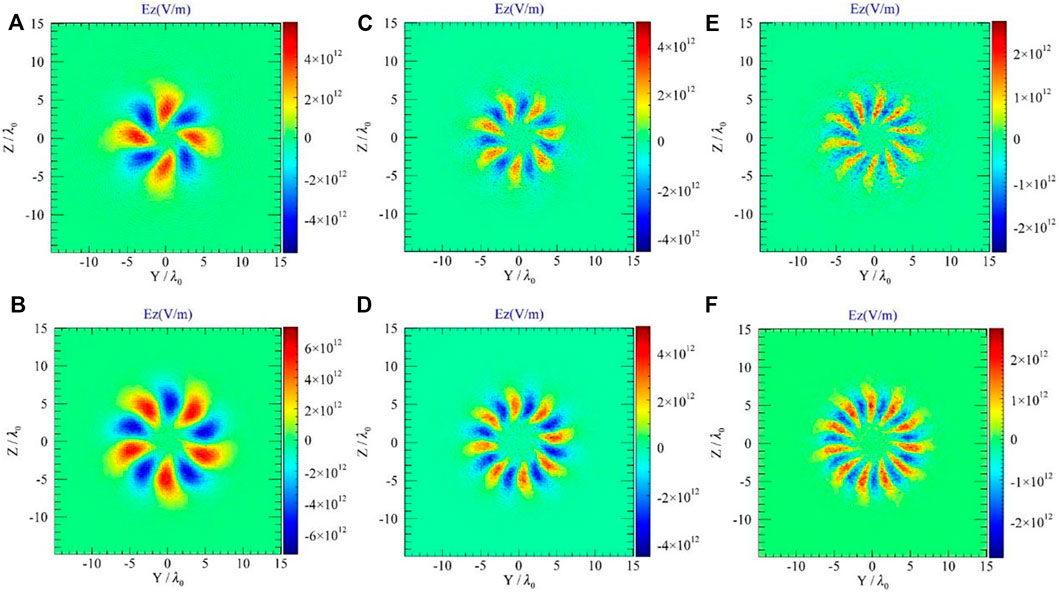
FIGURE 3. The electric field distribution of the (A) fourth, (B) fifth, (C) seventh, (D) eighth, (E) tenth and (F) eleventh harmonics in the Z-Y plane at$x=-11\mu m$and$t=36T_0$.

FIGURE 4

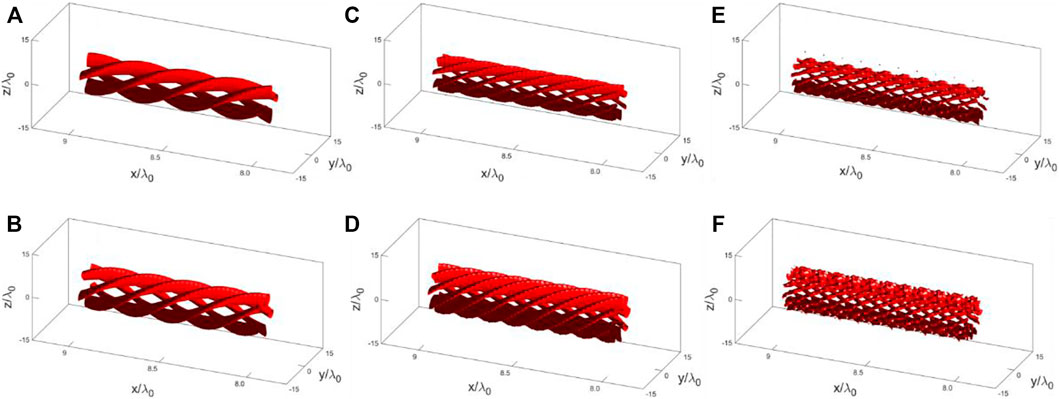
FIGURE 4. The electric field isosurface of the (A) fourth, (B) fifth, (C) seventh, (D) eighth, (E) tenth and (F) eleventh harmonics within a distance of $1{\lambda }_0$in the propagation direction at$t=36T_0$.

FIGURE 5

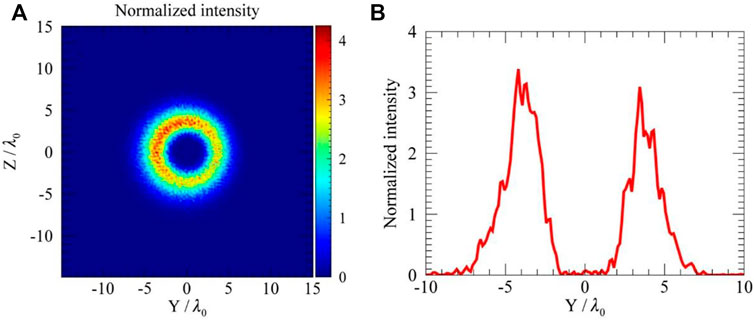
FIGURE 5. (A) The normalized transverse intensity distribution of the fourth harmonic with$L{G}_{40}$mode, (B) The corresponding transverse intensity profile with Y of panel (A).

Up to now, it has been confirmed that the two-color LG laser-gas HHG scheme is also applicable in relativistic plasma HHG process, and the intensity of produced harmonics can be obviously enhanced.

Theoretical analysis

In this part, the physical mechanism of vortex harmonic radiation will be discussed. For the convenience of theoretical derivation, the expression of two-color counter-rotating twisted laser pulses can be simplified as follows [18]:

$a_{{\omega }_1}=a_1{\sin }^2\left(\pi \xi /\tau \right)\left[\cos \left({\omega }_1\xi +l_1\varphi \right){\mathbf{e}}_{\mathbf{y}}+\sin \left({\omega }_1\xi +l_1\varphi \right){\mathbf{e}}_{\mathbf{z}}\right](2)$

$a_{{\omega }_2}=a_2{\sin }^2\left(\pi \xi /\tau \right)\left[\cos \left({\omega }_2\xi +l_2\varphi \right){\mathbf{e}}_{\mathbf{y}}-\sin \left({\omega }_2\xi +l_2\varphi \right){\mathbf{e}}_{\mathbf{z}}\right](3)$

where$\xi =t-x/c$is the propagating factor, $\tau$is the duration of laser pulse, $a_1,a_2$are the amplitudes of the normalized electric fields of laser pulses with the frequency of ${\omega }_1,{\omega }_2$and$l_1,l_2$are their corresponding topological charges.

By squaring the superposed laser electric field$a_{{\omega }_1}+a_{{\omega }_2}$, the normalized laser intensity can be derived:

$I_{total}=a_0^2{\sin }^4\left(\pi \xi /\tau \right)+2a_1{a}_2\cos \left[\left({\omega }_1+{\omega }_2\right)\xi +\left(l_1+l_2\right)\varphi \right]{\sin }^4\left(\pi \xi /\tau \right)(4)$

where $a_0^2=a_1^2+a_2^2$. From Eq. 4, we can see that the plasma electrons driven by dichromatic LG lasers can be described as a “vortex oscillating mirror” (VOM) [2]. On one side, it oscillates at the frequency of ${\omega }_1+{\omega }_2$in the longitudinal direction, on the other side, it is helical in the azimuthal direction. As a result, structured high-harmonics will be efficiently produced due to the VOM effect.

The analysis above preliminarily explains the underlying mechanism of HHG through two-color LG laser scheme. However, they are not able to accurately predict the spectra features of produced harmonics (including the allowed harmonic orders, the polarization features and the vortex modes). To predict these, its characteristic selection rules can be acquired based on the conservation laws for energy, parity, SAM and OAM of photos. Considering the HHG process of our scheme in a simple photon-exchange picture, the conservation of energy, SAM and OAM can be expressed as [2, 15]:

${\omega }_H=n_1{\omega }_1+n_2{\omega }_2(5)$

${\sigma }_H=n_1{\sigma }_1+n_2{\sigma }_2(6)$

$l_H=n_1{l}_1+n_2{l}_2(7)$

In Eqs 5–7, $n_1$and$n_2$are integers associated with the number of driving photos annihilated in the HHG process of the driving pulses at angular frequencies${\omega }_1$and${\omega }_2$. The parity constraints require that$n_2+n_1$must be odd ($n_2=n_1\pm 1$). In addition, ${\sigma }_H,{\sigma }_1,{\sigma }_2$represent the SAM values (in units of $\mathrm{\hslash }$) of the emitted harmonic photon and the two driving lasers with${\omega }_1$and${\omega }_2$, and $l_H,l_1,l_2$are the OAM values(also in units of $\mathrm{\hslash }$) of the radiated harmonics, the fundamental laser driver and the second one. According to our simulation parameters, we can set${\omega }_1={\omega }_0,{\omega }_2=2{\omega }_0$, ${\sigma }_1=1,{\sigma }_2=-1$and$l_1=1,l_2=2$. Thus, Eqs 5–7 can be expressed as${\omega }_H=\left(n_1+2n_2\right){\omega }_0$,${\sigma }_H=n_1-n_2$and$l_H=n_1+2n_2$, respectively. Here, only two cases are allowed: 1) $n_1=m+1,n_2=m$, resulting in${\omega }_H=\left(3m+1\right){\omega }_0,{\sigma }_H=1,l_H=3m+1$, 2) $n_1=m,n_2=m+1$, leading to${\omega }_H=\left(3m-1\right){\omega }_0,{\sigma }_H=-1,l_H=3m-1$($3m+2$is equivalent to$3m-1$). These analytical results are consistent with the SAM and OAM of emitted harmonic radiation which are numerically shown in Figures 2–4.

Discussions

According to the conservation laws for energy, parity, SAM and OAM of photos, it can be easily seen that the vortex modes of emitted harmonics can be tuned just through changing the topological charges of driving pulses. For example, if we set $l_1=l_2=1$(with other parameter unchanged), Eqs 5–7 can be expressed as${\omega }_H=\left(n_1+2n_2\right){\omega }_0$,${\sigma }_H=n_1-n_2$and $l_H=n_1+n_2$. Similarly, if$n_1=m+1,n_2=m$, we can get${\omega }_H=\left(3m+1\right){\omega }_0,{\sigma }_H=1,l_H=2m+1$. While${\omega }_H=\left(3m-1\right){\omega }_0,{\sigma }_H=-1,l_H=2m-1$can be acquired when$n_1=m,n_2=m+1$. Thus, some new vortex modes which are forbidden with$l_1=1,l_2=2$may be acquired. Specifically, the vortex modes of the fourth and thirteenth harmonics will be$l_4=3,l_{13}=9$respectively, as shown in Figure 6. This demonstrates that the OAM of generated harmonics can be flexibly designed through the bi-circular twisted laser scheme.

FIGURE 6

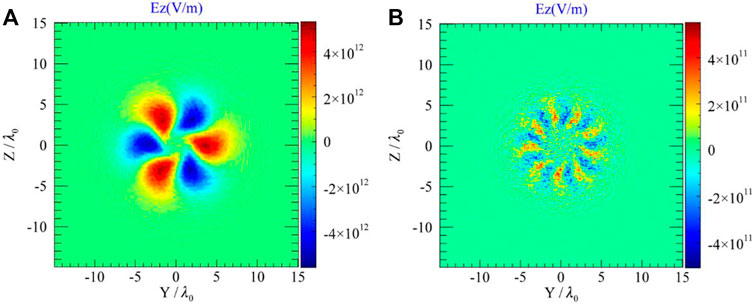
FIGURE 6. The electric field distribution of the (A) fourth, (B) thirteenth harmonics in the Z-Y plane if $l_1=l_2=1$(the other parameters are kept constant).

Finally, the tunability of HHG efficiency (which acts as the key parameter of HHG process) through adjusting the intensity ratio of the two driving field components are also discussed, as displayed in Figure 7. Here the total intensity of the two driving pulses is kept constant ($I_{2\omega }+I_{\omega }=5.48\times {10}^{20}W/c{m}^2$, where$I_{\omega },{I_2}_{\omega }$are the intensity of the driving pulses with frequency of ${\omega }_1,{\omega }_2$(${\omega }_2=2{\omega }_1$) respectively, as introduced in the part of particle-in-cell simulation results) while the intensity ratio$I_{2\omega }/I_{\omega }$is varying from 0 to 0.1, 0.33 and 1. The remaining parameters are kept the same as those in Figures 2–5. The Lissajous figures of the superposed electric fields are shown in Figures 7A–D, and the corresponding harmonic spectra are displayed in Figures 7E–H. When$I_{2\omega }/I_{\omega }=0$, almost no high harmonics appear (as shown in Figure 7E) due to the quasi-CP driving field (as shown in Figure 7A). As the intensity ratio is increased, the superposed driving fields exhibit three-fold symmetry and gradually show linearly-polarized (LP) patterns (as Figures 7B–D display), leading to gradually enhanced HHG efficiencies (as Figures 7F–H display). For the case of $I_{2\omega }/I_{\omega }=1$, the efficiency is close to the$I\left(n\right)\propto n^{-8/3}$scaling, as the typical value of HHG efficiency via relativistically oscillating mirror (ROM) effect [10]. This demonstrates that the HHG efficiency of our bi-circular twisted laser scheme can also be sufficiently high. In addition, the tunability of HHG efficiency can be attributed to the different driving field vector pattern induced by different laser intensity ratio$I_{2\omega }/I_{\omega }$ [15].

FIGURE 7

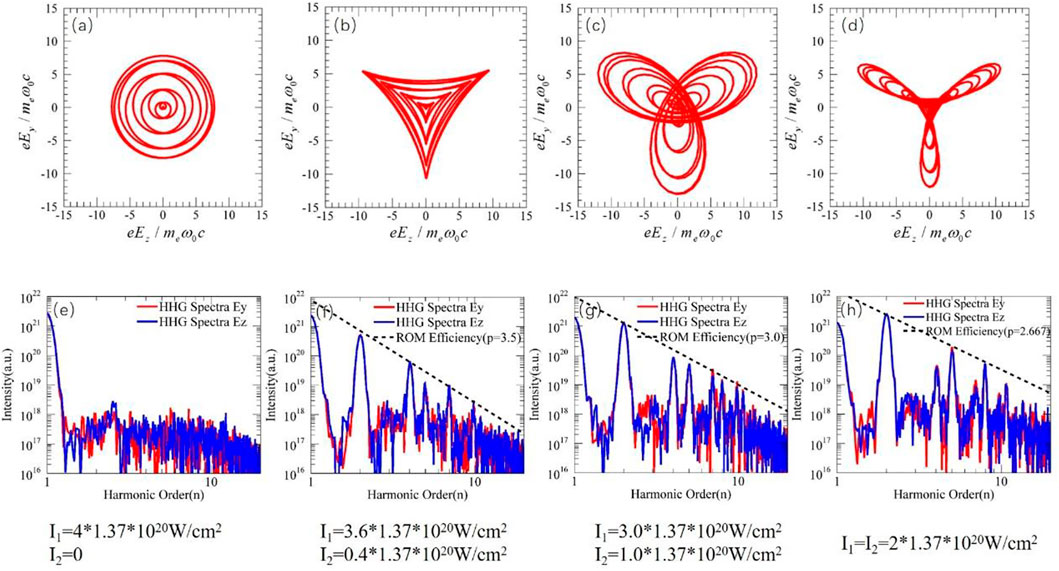
FIGURE 7. Polarization plane projections of the laser electric fields generated with intensity ratios (A)$I_{2\omega }/I_{\omega }=0$, (B)$I_{2\omega }/I_{\omega }=0.1$, (C)$I_{2\omega }/I_{\omega }=0.33$, and (D)$I_{2\omega }/I_{\omega }=1$. The total intensity is kept constant ($I_{2\omega }+I_{\omega }=5.48\times {10}^{20}W/c{m}^2$). (E–H) The produced harmonic spectra corresponding to the driving fields shown in panels (A–D).

Conclusion

With three-dimensional PIC simulations, we have demonstrated a tunable, table-top, intense harmonic radiation source with designable SAM and OAM driven by bi-circular LG lasers. The HHG efficiency can be adjusted through changing the intensity ratio of the two driving laser components, which is easy to implement in experiments. The underlying mechanism can be understood by the VOM model and related conservation laws. Such bright, circularly polarized vortex beams in XUV or soft X-ray region may open a wide range of applications including spatially resolved circular dichroism spectroscopies and the SAM and OAM dichroism X-ray absorption measurements, etc.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DX and HZ conducted the simulations and drafted the manuscript. YY and TY supervised the work. All authors discussed the results and reviewed the manuscript.

Funding

This work was supported by the National Key R&D Program of China (Grant No. 2018YFA0404802), Scientific Research Foundation of Hunan Provincial Education Department (No. 20A042), National Natural Science Foundation of China (Grant Nos.. 12135009, 11774430 and 11875319) and Science and Technology Innovation Program of Hunan Province (Grant No. 2020RC4020).

Acknowledgments

We would like to thank the National Supercomputing Center in Guangzhou (NSCC-GZ) for providing their computing facilities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (Coll Park) (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zhang X-M, Shen B-F, Shi Y, Wang X-F, Zhang L-G, Wang W-P, et al. Generation of intense high-order vortex harmonics. Phys Rev Lett (2015) 114:173901. doi:10.1103/physrevlett.114.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ju LB, Huang TW, Li R, Jiang K, Wu CN, Zhang H, et al. Topological control of laser-driven acceleration structure for producing extremely bright ion beams. Nucl Fusion (2021) 61:066006. doi:10.1088/1741-4326/abeed6

CrossRef Full Text | Google Scholar

4. Gauthier D, Rebernik P, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable orbital angular momentum in high-harmonic generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hernandez-Garcia C, Picon A, San Roman J, Plaja L. Attosecond extreme ultraviolet vortices from high-order harmonic generation. Phys Rev Lett (2013) 111:083602. doi:10.1103/physrevlett.111.083602

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Quere F, Thaury C, Monot P, Dobosz S, Marin P, Geindre JP, et al. Coherent wake emission of high-order harmonics from overdense plasmas. Phys Rev Lett (2006) 96:125004. doi:10.1103/physrevlett.96.125004

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Nomura Y, Horlein R, Tzallas P, Dromey B, Rykovanov S, Major Z, et al. Attosecond phase locking of harmonics emitted from laser-produced plasmas. Nat Phys (2009) 5:124–8. doi:10.1038/nphys1155

CrossRef Full Text | Google Scholar

8. Bulanov SV, Naumova NM, Pegoraro F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma. Phys Plasmas (1994) 1:745–57. doi:10.1063/1.870766

CrossRef Full Text | Google Scholar

9. Lichters R, Meyer-ter-Vehn J, Pukhov A. Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Phys Plasmas (1996) 3:3425–37. doi:10.1063/1.871619

CrossRef Full Text | Google Scholar

10. von der Linde D, Rzazewski K. High-order optical harmonic generation from solid surfaces. Appl Phys B (1996) 63:499–506. doi:10.1007/bf01828947

CrossRef Full Text | Google Scholar

11. Baeva T, Gordienko S, Pukhov A. Theory of high-order harmonic generation in relativistic laser interaction with overdense plasma. Phys Rev E (2006) 74:046404. doi:10.1103/physreve.74.046404

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Thaury C, Quéré F, Geindre J-P, Levy A, Ceccotti T, Monot P, et al. Plasma mirrors for ultrahigh-intensity optics. Nat Phys (2007) 3:424–9. doi:10.1038/nphys595

CrossRef Full Text | Google Scholar

13. Dromey B, Kar S, Bellei C, Carroll DC, Clarke RJ, Green JS, et al. Bright multi-kev harmonic generation from relativistically oscillating plasma surfaces. Phys Rev Lett (2007) 99:085001. doi:10.1103/physrevlett.99.085001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen Z-Y, Pukhov A. Bright high-order harmonic generation with controllable polarization from a relativistic plasma mirror. Nat Commun (2016) 7:12515. doi:10.1038/ncomms12515

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Chen Z-Y. Spectral control of high harmonics from relativistic plasmas using bicircular fields. Phys Rev E (2018) 97:043202. doi:10.1103/physreve.97.043202

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xie D, Zhuo* H-B, Jiao J-L, Zhang S-J, Zhao N, Zhou H-Y. 3D particle simulation of harmonic radiation excited by double circularly-polarized laser pulses irradiating over-dense plasma surface. Appl Phys B (2019) 7:148. doi:10.1007/s00340-019-7263-3

CrossRef Full Text | Google Scholar

17. Xie D, Yin Y, Yu T-P, Zhou H-Y, Chen Z-Y, Zhuo H-B. High-harmonic generation driven by two-color relativistic circularly polarized laser pulses at various frequency ratios. Plasma Sci Technol (2021) 23:045502. doi:10.1088/2058-6272/abe848

CrossRef Full Text | Google Scholar

18. Li Q-N, Xu X-R, Wu Y-B, Yin Y, Zou D-B, Yu T-P. Efficient high-order harmonics generation from overdense plasma irradiated by a two-color co-rotating circularly polarized laser pulse. Opt Express (2022) 30:15470–81. doi:10.1364/oe.459866

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen Z-Y, Li X-Y, Li B-Y, Chen M, Liu F. Isolated elliptically polarized attosecond soft X-ray with high-brilliance using polarization gating of harmonics from relativistic plasmas at oblique incidence. Opt Express (2018) 26:4572–80. doi:10.1364/oe.26.004572

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Pukhov A, an der Brugge D, Kostyukov I. Relativistic laser plasmas for electron acceleration and short wavelength radiation generation. Plasma Phys Control Fusion (2010) 52:124039–10. doi:10.1088/0741-3335/52/12/124039

CrossRef Full Text | Google Scholar

21. an der Brugge D, Pukhov A. Enhanced relativistic harmonics by electron nanobunching. Phys Plasmas (2010) 17:033110. doi:10.1063/1.3353050

CrossRef Full Text | Google Scholar

22. Dromey B, Rykovanov S, Yeung M, Horlein R, Jung D, Gautier DC, et al. Coherent synchrotron emission from electron nanobunches formed in relativistic laser-plasma interactions. Nat Phys (2012) 8:804–8. doi:10.1038/nphys2439

CrossRef Full Text | Google Scholar

23. Dorney K-M, Rego L, Brooks N-J, Roman J-S, Liao C-T, Ellis J-L, et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin-orbit momentum conservation. Nat Photon (2019) 13:123–30. doi:10.1038/s41566-018-0304-3

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Arber TD, Bennett K, Brady CS, Lawrence-Douglas A, Ramsay MG, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Control Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar