High-Fidelity Photonic Three-Degree-of-Freedom Hyperparallel Controlled-Phase-Flip Gate

Encoding computing qubits in multiple degrees of freedom (DOFs) of a photonic system allows hyperparallel quantum computation to enlarge channel capacity with less quantum resource, and constructing high-fidelity hyperparallel quantum gates is always recognized as a fundamental prerequisite for hyperparallel quantum computation. Herein, we propose an approach for implementing a high-fidelity photonic hyperparallel controlled-phase-flip (CPF) gate working with polarization, spatial-mode, and frequency DOFs, through utilizing the practical interaction between the single photon and the diamond nitrogen vacancy (NV) center embedded in the cavity. Particularly, the desired output state of the gate without computation errors coming from the practical interaction is obtained, and the robust fidelity is guaranteed in the nearly realistic condition. Meanwhile, the requirement for the experimental realization of the gate is relaxed. In addition, this approach can be generalized to complete the high-fidelity photonic three-DOF hyperparallel CPF^N gate and parity-check gate. These interesting features may make the present scheme have potential for applications in the hyperparallel quantum computation.

1 Introduction

Quantum information processing (QIP) which is accomplished based on quantum mechanics [1] surpasses classical information processing in terms of communication [2–14], computation [15–18], precision metrology [19], and machine learning [20–22]. Due to the capability of parallel computing, quantum computation exhibits a fascinating performance compared with the conventional computation which works with a serial pattern. For example, it has been suggested that quantum algorithms can largely speed up factorizing a large number [15] and searching data [16, 17], and greatly reduce the computational complexity of simulation [23, 24]. Quantum computation can be referred to as a succession of nontrivial critical single-qubit gates and two-qubit gates, such as controlled-NOT (CNOT) gate or the identical controlled-phase-flip (CPF) gate [25]. Nowadays, numerous works have been made on CNOT gates or CPF gates [26, 27]. Hyperparallel quantum computation, acting on more than one qubit-like degree of freedom (DOF) simultaneously, can achieve full potential of the parallel computation [28]. In 2013, Ren et al. [29] proposed the first scheme for the hyperparallel CNOT gate acting on the polarization and spatial DOFs simultaneously, and later in 2015 a polarization-spatial hyperparallel Toffoli gate was proposed [30]. Hyperparallel quantum gates have attracted much attention in recent years due to their excellent properties. Up to now, some interesting protocols for implementing hyperparallel quantum gates have been proposed via photon-matter platforms [31–36], and the inevitable incomplete and imperfect photon-matter interactions are usually not taken into account.

Photon has been widely recognized as an especially promising physical architecture for implementing hyperparallel quantum gates due to its high transmitting speed, weak interaction with its environment, low cost for preparation, easy and accurate manipulation, and multiple qubit-like DOFs such as polarization, spatial mode, orbital angular momentum, time bin, and frequency [37–41]. It has been demonstrated that by encoding computing qubits in multiple DOFs of a photonic system, hyperparallel quantum gates can be achieved. The polarization and spatial-mode DOFs are particularly appealing for constructing photonic hyperparallel quantum gates [29–35]. For example, In 2014, Wang et al. [33] proposed an interesting scheme for implementing the hybrid hyperparallel CNOT gate, where the spatial-mode and polarization states of a photon control the two stationary electron spins in quantum dots simultaneously. In 2016, Wei et al. [34] constructed a hyperparallel Toffoli gate on a three-photon system in both the polarization and spatial-mode DOFs. Recently, frequency encoded photonic qubit has garnered much interest for its compatibility, stable in any transmission surroundings, and high-dimensional characters. In 2019, Lu et al. [42] demonstrated a frequency-bin based CNOT gate. And in 2020, Wei et al. [36] presented a hyperparallel CPF gate utilizing the frequency DOF together with the spatial-mode and time-bin DOFs of a two-photon system. Frequency-based entanglements were employed by Zeng and Zhu [43] to complete hyper-Bell analysis.

To achieve a deterministic (hyperparallel) quantum photonic gate, an essential prerequisite is obtaining the strong interactions between individual photons, which can be completed by employing cross-Kerr medium or cavity quantum electrodynamics (QED) with trapped atoms or artificial atoms (such as quantum dot, superconductor, diamond nitrogen vacancy (NV) center, Josephson junction). A diamond NV center is a promising candidate owing to its long-lived coherence time even at room temperature [44–48] and optical controllability including fast microwave manipulation, optical preparation, and read out [49–52]. Meanwhile, it has been experimentally realized the strong coupling between the NV center and the whispering-gallery mode (WGM) resonator [53–55], which can enhance the NV-photon interaction and the photon-photon interaction. In 2011, Chen et al. [56] introduced the interaction between the polarized single photon and the NV center confined in the WGM microtoroidal resonator (MTR). Utilizing the photon-NV interactions, where the realistic NV-cavity parameters are not taken into consideration, some interesting works on (hyperparallel) quantum gate have been presented [30, 35, 36, 57–59]. It is worthy to relax the necessary for high-Q cavity system, and to further improve the fidelity of the schemes in realistic environment by preventing the imperfect and incomplete photon-NV interactions. In 2012, by utilizing the practical interaction between the single photon and the atom-cavity system, Li et al. [60] proposed the robust-fidelity entangling gate in which the computation errors coming from the realistic atom-cavity parameters were wiped out. In recent years, much attention has been attracted to the research in high-fidelity (hyperparallel) quantum gates via different methods [32, 61–71].

In this paper, through utilizing the practical interaction between a NV-cavity system and a single photon, we put forward a method for implementing a high-fidelity hyperparallel CPF gate working with three DOFs of a two-photon system. Here, the polarization-polarization-based, the spatial-spatial-based, and the frequency-frequency-based CPF gates are completed simultaneously, which is equal to three CPF gates operating simultaneously on the systems in one DOF, and the potential of parallel computation is further achieved. Particularly, the fidelity of this hyperparallel CPF gate is robust against the realistic NV-cavity parameters, since the computation errors coming from the practical interaction are wiped out by the single-photon detectors. This self-error-detected working pattern also relaxes the requirement for the experimental realization of the gate. In addition, the method can be generalized to achieve the high-fidelity photonic hyperparallel CPF^N gate and parity-check gate working on three DOFs. We use the frequency, spatial-mode, and polarization DOFs to complete our schemes, where a frequency encoded photonic qubit is naturally stable in the transmission surroundings as its alteration requires a nonlinear interaction between photon and an optical fiber, which takes place with a negligible probability, a spatial-mode encoded photonic qubit is robust against the bit-flip channel noise, and a polarization encoded photonic qubit can be skillfully manipulated. These interesting features may make our scheme more useful in the practical quantum computation tasks.

2 Nonlinear Interaction Between a Single Photon and a Diamond NV Center Inside a Microtoroidal Resonator

The nonlinear interaction between a single photon and a diamond NV center inside a microtoroidal resonator (MTR) which is employed as the platform for implementing our hyperparallel CPF gate is illustrated in Figure 1. The ground state of a negatively charged diamond NV center is a spin triplet, and there exists 2.88 GHz zero-field splitting between levels |0⟩ with m_s = 0 and |± 1⟩ with m_s = ±1 owing to spin-spin interactions. There exist six excited states defined by the group theory as |A₁⟩ = |E₋⟩| + 1⟩ − |E₊⟩| − 1⟩, |A₂⟩ = |E₋⟩| + 1⟩ + |E₊⟩| − 1⟩, |E_x⟩ = |X⟩|0⟩, |E_y⟩ = |Y⟩|0⟩, |E₁⟩ = |E₋⟩| − 1⟩ − |E₊⟩| + 1⟩, and |E₂⟩ = |E₋⟩| − 1⟩ + |E₊⟩| + 1⟩, which are eigenstates of the full Hamiltonian including spin-orbit and spin-spin interactions in the absence of any perturbation [72]. Here, |E₋⟩, |E₊⟩, |X⟩, and |Y⟩ are orbital states. |A₁⟩ and |A₂⟩ are split from the other excited states by at least 5.5 GHz due to the spin-orbit interaction, and the energy gap between these two states is increased to 3.3 GHz due to spin-spin interaction [56, 72]. Thus, in the limit of low strain and magnetic field, the excited state |A₂⟩ is robust against the stable symmetric properties and preserves the polarization properties of its optical transitions to states |± 1⟩ through polarized radiations |σ_∓⟩ due to total angular momentum conservations. That is to say, as shown in Figure 1, the two transitions |A₂⟩ ↔|± 1⟩ are resonantly coupled to the right- and the left-circularly polarized photons with the identical transition frequency ω₀, respectively.

FIGURE 1

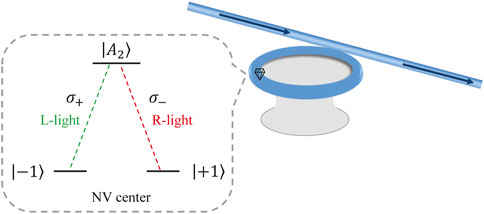
FIGURE 1. Schematic diagram for a diamond NV center confined in a MTR and energy-level diagram of a diamond NV center. The transitions |∓ 1⟩ ↔|A₂⟩ are resonantly coupled to the left-circularly and the right-circularly polarized photons, respectively.

After a circularly polarized single photon with frequency ω_p interacting with a NV-cavity system with mode frequency ω_c, it will be scattered with a reflection coefficient. In the weak excitation limit with the NV center predominantly in the ground state, through solving the Heisenberg equations of motion and the input-output relations, we can obtain the reflection coefficient as [73, 74]

$r\left({\omega }_p\right)=\frac{\left[i\left({\omega }_0-{\omega }_p\right)+\frac{\gamma }{2}\right]\left[i\left({\omega }_c-{\omega }_p\right)-\frac{\kappa }{2}+\frac{{\kappa }_s}{2}\right]+{\mathrm{g}}^2}{\left[i\left({\omega }_0-{\omega }_p\right)+\frac{\gamma }{2}\right]\left[i\left({\omega }_c-{\omega }_p\right)+\frac{\kappa }{2}+\frac{{\kappa }_s}{2}\right]+{\mathrm{g}}^2},(1)$

where κ and κ_s are the cavity damping rate and the side-leakage rate, respectively. γ is the NV center dipolar decay rate, and g is the coupling strength between the cavity and the NV center. By taking g = 0, the reflection coefficient for a cold cavity (i.e., the NV center is uncoupled to the cavity) is obtained as

$r^{\prime }\left({\omega }_p\right)=\frac{i\left({\omega }_c-{\omega }_p\right)-\frac{\kappa }{2}+\frac{{\kappa }_s}{2}}{i\left({\omega }_c-{\omega }_p\right)+\frac{\kappa }{2}+\frac{{\kappa }_s}{2}}.(2)$

Considering the single photon with frequency ω_p = ω₁ ≠ ω₀ being injected into the NV-cavity system with ω_c = ω₀, no matter what the polarization of the photon is or what the spin of the NV center is, the single photon always senses a cold cavity due to a large detuning and then it will be scattered with a reflection coefficient of $r_1^{\prime }=r^{\prime }({\omega }_1)=[2i({\omega }_c-{\omega }_1)-\kappa +{\kappa }_s]/[2i({\omega }_c-{\omega }_1)+\kappa +{\kappa }_s]$. However, when the single photon with frequency ω_p = ω₂ = ω₀ is injected into the NV-cavity system with ω_c = ω₀, if the NV center is initially prepared in the state | − 1⟩, the single photon in the left-polarization state |L⟩ feels a hot cavity and then obtains a reflection coefficient of r₂ = r(ω₂) = [γ(κ_s − κ) + 4g²]/[γ(κ_s + κ) + 4g²] after being scattered, whereas the single photon in the right-polarization state |R⟩ experiences a cold cavity due to a polarization mismatch and then introduces a reflection coefficient of $r_2^{\prime }=r^{\prime }({\omega }_2)=({\kappa }_s-\kappa )/({\kappa }_s+\kappa )$ after being scattered. Conversely, if the NV center is initially prepared in the state | + 1⟩, the |R⟩-polarized photon suffers a hot cavity and gets a reflection coefficient of r₂ after being scattered, whereas |L⟩-polarized photon experiences a cold cavity and gets a reflection coefficient of $r_2^{\prime }$ after being scattered. Here, the reflection coefficients $r_1^{\prime }$, $r_2^{\prime }$, and r₂ are the functions of the realistic NV-cavity parameters. Therefore, the practical interaction rules, dependent on the polarization and frequency of the incident single photon and the spin of the NV center, can be summarized as

$\begin{array}{c}|L\rangle |{\omega }_1\rangle |+1\rangle \to r_1^{\prime }|L\rangle |{\omega }_1\rangle |+1\rangle ,|L\rangle |{\omega }_1\rangle |-1\rangle \to r_1^{\prime }|L\rangle |{\omega }_1\rangle |-1\rangle ,\hfill \\ |R\rangle |{\omega }_1\rangle |+1\rangle \to r_1^{\prime }|R\rangle |{\omega }_1\rangle |+1\rangle ,|R\rangle |{\omega }_1\rangle |-1\rangle \to r_1^{\prime }|R\rangle |{\omega }_1\rangle |-1\rangle ,\hfill \\ |L\rangle |{\omega }_2\rangle |+1\rangle \to r_2^{\prime }|L\rangle |{\omega }_2\rangle |+1\rangle ,|L\rangle |{\omega }_2\rangle |-1\rangle \to r_2|L\rangle |{\omega }_2\rangle |-1\rangle ,\hfill \\ |R\rangle |{\omega }_2\rangle |+1\rangle \to r_2|R\rangle |{\omega }_2\rangle |+1\rangle ,|R\rangle |{\omega }_2\rangle |-1\rangle \to r_2^{\prime }|R\rangle |{\omega }_2\rangle |-1\rangle .\hfill \end{array}(3)$

3 High-Fidelity Photonic Three-DOF Hyperparallel CPF Gate

Based on the practical interaction between the single photon and the NV-cavity system as described in Eq. 3, we propose a scheme for implementing a high-fidelity photonic three-DOF hyperparallel CPF gate, in which the qubits are independently encoded in the frequency, polarization, and spatial-mode DOFs of the single photons. Suppose the control photon a, the target photon b, and the three NV centers are initially prepared in the normalized states

$\begin{array}{cc}\hfill & |\varphi {\rangle }_a=\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)\otimes \left({\beta }_1|{\omega }_1\rangle +{\beta }_2|{\omega }_2\rangle \right)\otimes \left({\gamma }_1|a_1\rangle +{\gamma }_2|a_2\rangle \right),\hfill \\ \hfill & |\varphi {\rangle }_b=\left({\delta }_1|F\rangle +{\delta }_2|S\rangle \right)\otimes \left({\eta }_1|{\omega }_1\rangle +{\eta }_2|{\omega }_2\rangle \right)\otimes \left({\xi }_1|b_1\rangle +{\xi }_2|b_2\rangle \right),\hfill \\ \hfill & |\varphi {\rangle }_1=|+{\rangle }_1,|\varphi {\rangle }_2=|+{\rangle }_2,|\varphi {\rangle }_3=|+{\rangle }_3.\hfill \end{array}(4)$

Here and afterwards, $|\pm \rangle =\frac{1}{\sqrt{2}}(|+1\rangle \pm |-1\rangle )$ are the states of the NV centers; $|F\rangle =\frac{1}{\sqrt{2}}(|R\rangle +|L\rangle )$ and $|S\rangle =\frac{1}{\sqrt{2}}(|R\rangle -|L\rangle )$ are the polarization states of the single photons; |ω₁⟩ and |ω₂⟩ are the frequency states of the single photons; |a₁⟩, |a₂⟩, |b₁⟩, and |b₂⟩ are the spatial-mode states of the single photons.

The photonic hyperparallel CPF gate in three DOFs completes the task that when the polarization state of photon a is |S⟩, a phase flip takes place on the polarization state |S⟩ of photon b, when the spatial-mode state of photon a is |a₂⟩, a phase flip takes place on the spatial-mode state |b₂⟩ of photon b, and when the frequency state of photon a is |ω₂⟩, a phase flip takes place on the frequency state |ω₂⟩ of photon b, simultaneously. The quantum circuit for implementing the three-DOF hyperparallel CPF gate is shown in Figure 2, and the principle is described in detail as follows in step by step.

FIGURE 2

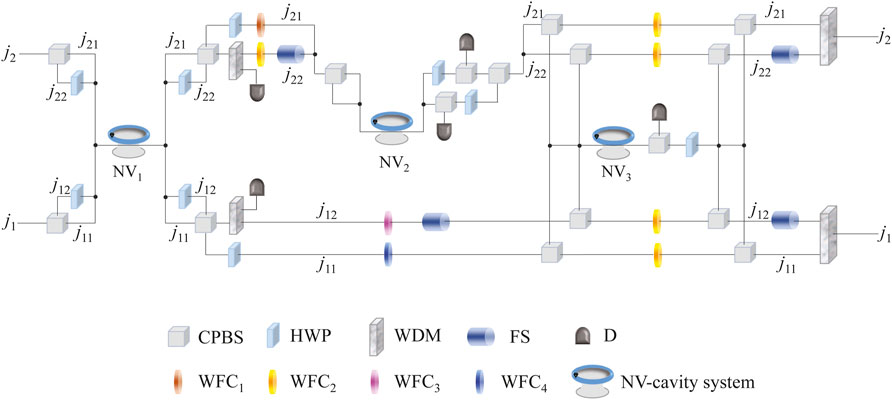
FIGURE 2. Schematic diagram for implementing the high-fidelity photonic three-DOF hyperparallel CPF gate. j₁ and j₂, where j = a, b, are the input ports for the control photon a and the target photon b being injected to the circuit in sequence. CPBS represents a circularly polarizing beam splitter in the basis {|F⟩, |S⟩} transmitting the |F⟩-polarized photon and reflecting the |S⟩-polarized photon. HWP is a half-wave plate set at 0° performing operation |F⟩ ↔|S⟩. WFC_i (i = 1, 2, 3, 4) represent wave-form corrector introducing coefficients $r_1^{\prime }$, $(r_2-r_2^{\prime })/2$, ${(r_2-r_2^{\prime })}^2/4$, and $r_1^{\prime }(r_2-r_2^{\prime })/2$ on the incident photons, respectively. WDM represents a polarization-independent wavelength division multiplexer, which divides photon with different frequencies from one path to different paths or completes the reverse conversion. FS is a frequency shifter which can shift the frequency ω₁ to ω₂. D is a single-photon detector.

Firstly, the control photon a is injected into the circuit from the input ports a₁ and a₂. Through the circularly polarizing beam splitters (CPBSs), the wave packets in |F⟩ are transmitted to the paths a₁₁ and a₂₁ for interacting with the NV₁-cavity system directly. Whereas the wave packets in |S⟩ are reflected to the paths a₁₂ and a₂₂, pass through the half plate waves (HWPs) resulting in |F⟩ ↔|S⟩, and interact with the NV₁-cavity system. In this process, the wave packets in the four paths are respectively routed to interact with the NV₁-cavity system. Then after the wave packets in the paths a₁₂ and a₂₂ pass through the HWPs, they reunite with the wave packets in the paths a₁₁ and a₂₁ at the CPBSs, and the state of the system is changed from

$|\mathrm{\Phi }{\rangle }_0=|\varphi {\rangle }_a\otimes |\varphi {\rangle }_b\otimes |\varphi {\rangle }_1\otimes |\varphi {\rangle }_2\otimes |\varphi {\rangle }_3(5)$

to

$\begin{array}{ll}\hfill |\mathrm{\Phi }{\rangle }_1=& \left[\frac{r_2-r_2^{\prime }}{2}\left({\alpha }_1{\beta }_2|S\rangle |{\omega }_2\rangle +{\alpha }_2{\beta }_2|F\rangle |{\omega }_2\rangle \right){|-\rangle }_1\left({\gamma }_1|a_{11}\rangle +{\gamma }_2|a_{21}\rangle \right)\right.+\frac{r_2+r_2^{\prime }}{2}\left({\alpha }_1{\beta }_2|F\rangle |{\omega }_2\rangle +{\alpha }_2{\beta }_2|S\rangle |{\omega }_2\rangle \right)|+{\rangle }_1\hfill \\ \hfill & \left({\gamma }_1|a_{12}\rangle +{\gamma }_2|a_{22}\rangle \right)+{r_1^{\prime }\left({\alpha }_1{\beta }_1|F\rangle |{\omega }_1\rangle +{\alpha }_2{\beta }_1|S\rangle |{\omega }_1\rangle \right)|+{\rangle }_1\left({\gamma }_1|a_{12}\rangle +{\gamma }_2|a_{22}\rangle \right)]}_a\otimes |\varphi {\rangle }_b\otimes |\varphi {\rangle }_2\otimes |\varphi {\rangle }_3.\hfill \end{array}(6)$

The wave packets in the path a₂₁ pass through the HWP and the wave-form corrector₁ (WFC₁); the wave packets in the path a₂₂ first pass through the wavelength division multiplexer (WDM), which divides photon with different frequencies to the different paths. If the wave packets in the path a₂₂ are in the frequency states |ω₂⟩, they will trigger the single-photon detector which represents the process of the photonic hyperparallel CPF gate is terminated. Otherwise, the wave packets in the path a₂₂ with frequency states |ω₁⟩ will pass through the WFC₂ and the frequency shifter (FS) which shifts the frequency ω₁ to ω₂; Similarly, the wave packets in the path a₁₂ pass through the WDM. If the wave packets in the path a₁₂ are in the frequency states |ω₂⟩, they will trigger the single-photon detector which means the process of the hyperparallel CPF gate is terminated. Otherwise, the wave packets in the path a₁₂ with frequency states |ω₁⟩ pass through the WFC₃ and the FS which shifts the frequency ω₁ to ω₂; the wave packets in the path a₁₁ pass through the HWP and the WFC₄. Before the wave packets in the paths a₂₁ and a₂₂ passing through the CPBSs, the state of the system becomes

$\begin{array}{ll}\hfill |\mathrm{\Phi }{\rangle }_2=& \left[\frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^2}{4}{\beta }_2{\gamma }_1\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)|{\omega }_2\rangle |-{\rangle }_1|a_{11}\rangle \right.+\frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^2}{4}{\beta }_1{\gamma }_1\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)|{\omega }_2\rangle |+{\rangle }_1|a_{12}\rangle \hfill \\ \hfill & +\frac{r_1^{\prime }\left(r_2-r_2^{\prime }\right)}{2}{\beta }_2{\gamma }_2\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)|{\omega }_2\rangle |-{\rangle }_1|a_{21}\rangle {\left.+\frac{r_1^{\prime }\left(r_2-r_2^{\prime }\right)}{2}{\beta }_1{\gamma }_2\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)|{\omega }_2\rangle |+{\rangle }_1|a_{22}\rangle \right]}_a\otimes |\varphi {\rangle }_b\otimes |\varphi {\rangle }_2\otimes |\varphi {\rangle }_3.\hfill \end{array}(7)$

Then, for the wave packets of photon a in the spatial-mode states |a₂⟩, after they passing through the CPBS, the wave packets in the polarization states |F⟩ interact with NV₂-cavity system, pass through the HWP and the CPBS in sequence, and the wave packets in the polarization states |S⟩ interact with NV₂-cavity system, pass through the CPBS and the HWP in sequence. If either of the two single-photon detectors is clicked, the process of the hyperparallel photonic CPF gate is terminated. If there is no click of the two single-photon detectors, the process continues, that is, the two wave packets of different polarizations in the spatial-mode states |a₂⟩ reunite at the CPBS and the state of the system is changed into

$\begin{array}{ll}\hfill |\mathrm{\Phi }{\rangle }_3=& \frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^2}{4}\left[\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)\left({\beta }_2{\gamma }_1|{\omega }_2\rangle |-{\rangle }_1|a_{11}\rangle |+{\rangle }_2+{\beta }_1{\gamma }_1|{\omega }_2\rangle |+{\rangle }_1|a_{12}\rangle |+{\rangle }_2\right.\right.\hfill \\ \hfill & +{\left.{\beta }_2{\gamma }_2|{\omega }_2\rangle |-{\rangle }_1|a_{21}\rangle |-{\rangle }_2+{\beta }_1{\gamma }_2|{\omega }_2\rangle |+{\rangle }_1|a_{22}\rangle |-{\rangle }_2\right]}_a\otimes |\varphi {\rangle }_b\otimes |\varphi {\rangle }_3.\hfill \end{array}(8)$

Next, after photon a passing through the CPBSs, in the path a₁₁(a₁₂, a₂₁, a₂₂), the wave packets in the polarization states |F⟩ pass through the WFC₂, and the wave packets in the polarization states |S⟩ interact with NV₃-cavity system and pass through the CPBS. Similarly, if there is a click of the single-photon detector, the process of the high-fidelity hyperparallel photonic CPF gate is terminated. Otherwise, the process continues, that is, the polarization states of wave packets will be changed into |S⟩ with the operation performed by HWP, which will unite with wave packets in the polarization states |F⟩ at the CPBS. At this time, the state of the system becomes

$\begin{array}{ll}\hfill |\mathrm{\Phi }{\rangle }_4=& \frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^3}{8}\left[\left({\alpha }_1|F\rangle |+{\rangle }_3+{\alpha }_2|S\rangle |-{\rangle }_3\right)\left({\beta }_2{\gamma }_1|{\omega }_2\rangle |-{\rangle }_1|a_{11}\rangle |+{\rangle }_2\right.\right.\hfill \\ \hfill & +{\left.{\beta }_1{\gamma }_1|{\omega }_2\rangle |+{\rangle }_1|a_{12}\rangle |+{\rangle }_2+{\beta }_2{\gamma }_2|{\omega }_2\rangle |-{\rangle }_1|a_{21}\rangle |-{\rangle }_2+{\beta }_1{\gamma }_2|{\omega }_2\rangle |+{\rangle }_1|a_{22}\rangle |-{\rangle }_2\right]}_a\otimes |\varphi {\rangle }_b.\hfill \end{array}(9)$

Subsequently, the wave packets in the paths a₁₂ and a₂₂ pass through the FSs which shift frequency ω₂ to ω₁, and the wave packets in the paths a₁₁ and a₂₁ respectively unite with the wave packets in the paths a₁₂ and a₂₂ to the spatial modes |a₁⟩ and |a₂⟩ by the WDMs. At this time, the system composed of two photons and the three NV centers is changed into

$\begin{array}{cc}\hfill |\mathrm{\Phi }{\rangle }_5=& \frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^3}{8}\left[\left({\alpha }_1|F\rangle |+{\rangle }_3+{\alpha }_2|S\rangle |-{\rangle }_3\right)\left({\beta }_1|{\omega }_1\rangle |+{\rangle }_1+{\beta }_2|{\omega }_2\rangle |-{\rangle }_1\right)\right.{\left.\left({\gamma }_1|a_1\rangle |+{\rangle }_2+{\gamma }_2|a_2\rangle |-{\rangle }_2\right)\right]}_a\otimes |\varphi {\rangle }_b.\hfill \end{array}(10)$

Secondly, Hadamard operations [| + 1⟩ ↔| + ⟩, | − 1⟩ ↔| − ⟩] are performed on the three NV centers, where the Hadamard operation can be implemented with a π/2 microwave pulse, and the state |Φ⟩₅ is changed into

$\begin{array}{cc}\hfill |\mathrm{\Phi }{\rangle }_6=& \frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^3}{8}\left[\left({\alpha }_1|F\rangle |+1{\rangle }_3+{\alpha }_2|S\rangle |-1{\rangle }_3\right)\left({\beta }_1|{\omega }_1\rangle |+1{\rangle }_1\right.\right.+{\left.\left.{\beta }_2|{\omega }_2\rangle |-1{\rangle }_1\right)\left({\gamma }_1|a_1\rangle |+1{\rangle }_2+{\gamma }_2|a_2\rangle |-1{\rangle }_2\right)\right]}_a\otimes |\varphi {\rangle }_b.\hfill \end{array}(11)$

Thirdly, the target photon b is injected into the circuit from the input ports b₁ and b₂. After the same operations as those performed on the control photon a are applied on the target photon b, if none of the five single-photon detectors is clicked, the system will collapse into the state

$\begin{array}{ll}\hfill |\mathrm{\Phi }{\rangle }_7=& \frac{{\mathrm{r\prime }}_1^2{\left(r_2-r_2^{\prime }\right)}^6}{64}\left[{\beta }_1|{\omega }_1{\rangle }_a|+1{\rangle }_1{\left({\eta }_1|{\omega }_1\rangle +{\eta }_2|{\omega }_2\rangle \right)}_b+{\beta }_2|{\omega }_2{\rangle }_a|-1{\rangle }_1{\left({\eta }_1|{\omega }_1\rangle -{\eta }_2|{\omega }_2\rangle \right)}_b\right]\hfill \\ \hfill & \otimes \left[{\gamma }_1|a_1\rangle |+1{\rangle }_2\left({\xi }_1|b_1\rangle +{\xi }_2|b_2\rangle \right)+{\gamma }_2|a_2\rangle |-1{\rangle }_2\left({\xi }_1|b_1\rangle -{\xi }_2|b_2\rangle \right)\right]\hfill \\ \hfill & \otimes \left[{\alpha }_1|F{\rangle }_a|+1{\rangle }_3{\left({\delta }_1|F\rangle +{\delta }_2|S\rangle \right)}_b+{\alpha }_2|S{\rangle }_a|-1{\rangle }_3{\left({\delta }_1|F\rangle -{\delta }_2|S\rangle \right)}_b\right].\hfill \end{array}(12)$

Finally, the three NV centers are measured in the orthogonal basis {|±⟩}. According to Table 1, some feed-forward operations are performed on the control photon a. In detail, if NV₁ center is in the state | − ⟩₁, a frequency-based operation σ_zf = |ω₁⟩⟨ω₁| − |ω₂⟩⟨ω₂| is performed on the control photon a; if NV₂ center is in the state | − ⟩₂, a spatial-based operation σ_zs = |a₁⟩⟨a₁| − |a₂⟩⟨a₂| is performed on the control photon a; if NV₃ center is in the state | − ⟩₃, a polarization-based operation σ_zp = |F⟩⟨F| − |S⟩⟨S| is performed on the control photon a. Conditioned on the results of the measurement on the three NV centers, the two-photon system collapses into the state

$\begin{array}{ll}\hfill \mathrm{|\Phi }{\rangle }_8=& \frac{{r\prime }_1^2{\left(r_2-r_2^{\prime }\right)}^6}{64}[{\alpha }_1|F{\rangle }_a{\left({\delta }_1|F\rangle +{\delta }_2|S\rangle \right)}_b+{\alpha }_2|S{\rangle }_a{\left({\delta }_1|F\rangle -{\delta }_2|S\rangle \right)}_b]\hfill \\ \hfill & \otimes [{\beta }_1|{\omega }_1{\rangle }_a{\left({\eta }_1|{\omega }_1\rangle +{\eta }_2|{\omega }_2\rangle \right)}_b+{\beta }_2|{\omega }_2{\rangle }_a{\left({\eta }_1|{\omega }_1\rangle -{\eta }_2|{\omega }_2\rangle \right)}_b]\hfill \\ \hfill & \otimes [{\gamma }_1|a_1\rangle \left({\xi }_1|b_1\rangle +{\xi }_2|b_2\rangle \right)+{\gamma }_2|a_2\rangle \left({\xi }_1|b_1\rangle -{\xi }_2|b_2\rangle \right)].\hfill \end{array}(13)$

TABLE 1

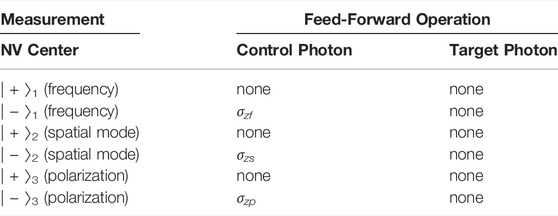
TABLE 1. The relations between the measurement results on the NV centers and the feed-forward operations for completing a deterministic hyperparallel CPF gate working with the three DOFs of a two-photon system.

From Eq. 13, one can see that a photonic three-DOF hyperparallel CPF gate is completed, in which the conditional phase flips take place on the states |S⟩_a|S⟩_b, |ω₂⟩_a|ω₂⟩_b, and |a₂⟩|b₂⟩, simultaneously. Notably, this hyperparallel CPF gate is locally equivalent to the hyperparallel quantum CNOT gate up to Hadamard operations performed on the target photon b.

Fidelity, which can characterize the performance of a quantum gate, is described by F = |⟨Ψ_r|Ψ_i⟩|², where |Ψ_i⟩ and |Ψ_r⟩ are the ideal desired output state and realistic output state, respectively. From Eq. 13, one can see that there are no error items and the only difference between the ideal desired output state and the realistic output state is the global coefficient ${\mathrm{r\prime }}_1^2{(r_2-r_2^{\prime })}^6/64$, which would not affect the fidelity. That is to say, the fidelity of the hyperparallel CPF gate is robust, which is immune to the realistic NV-cavity parameters including the damping rate κ, the side-leakage rate κ_s, the dipolar decay rate γ, and the coupling strength g. Overall, the quantum circuit shown in Figure 2 implements a high-fidelity hyperparallel CPF gate in the frequency, spatial-mode, and polarization DOFs, simultaneously.

4 High-Fidelity Photonic Three-DOF Hyperparallel CPF^N Gate and Parity Check Gate

The quantum circuit shown in Figure 2 can be generalized to implement a high-fidelity hyperparallel CPF^N gate working with a multiple-photon system in the frequency, spatial-mode, and polarization DOFs. Initially, the three NV centers are also prepared in the states |ϕ⟩₁ = | + ⟩₁, |ϕ⟩₂ = | + ⟩₂, and |ϕ⟩₃ = | + ⟩₃. The control photon a is also initially prepared in the normalized arbitrary state

$|\varphi {\rangle }_a={\left({\alpha }_1|F\rangle +{\alpha }_2|S\rangle \right)}_a{\left({\beta }_1|{\omega }_1\rangle +{\beta }_2|{\omega }_2\rangle \right)}_a{\left({\gamma }_1|a_1\rangle +{\gamma }_2|a_2\rangle \right)}_a.(14)$

The N target photons bⁿ(n = 1, 2, … , N) are initially prepared in the normalized arbitrary state

$|\varphi {\rangle }_{b^n}={\left({\delta }_1^n|F\rangle +{\delta }_2^n|S\rangle \right)}_{b^n}{\left({\eta }_1^n|{\omega }_1\rangle +{\eta }_2^n|{\omega }_2\rangle \right)}_{b^n}{\left({\xi }_1^n|b_1\rangle +{\xi }_2^n|b_2\rangle \right)}_{b^n}.(15)$

The procedure of the hyperparallel CPF^N gate completed with the quantum circuit shown in Figure 2 is similar with that of the hyperparallel CPF gate described above but the target photon b is substituted with the target photon string b¹, b², … , b^N, which are injected into the quantum circuit in sequence.

Firstly, the control photon a is injected into the quantum circuit. While the photon a passes through the circuit, if any of the single-photon detectors is clicked, the construction process of the hyperparallel CPF^N gate is terminated. If there is no click of any single-photon detectors, the process goes on and with Hadamard operations respectively performed on the three NV centers, the state of the whole system is changed from |Φ^N⟩₀ to |Φ^N⟩₁, where

$\begin{array}{cc}\hfill |{\mathrm{\Phi }}^N{\rangle }_0=& |\varphi {\rangle }_a\otimes |\varphi {\rangle }_{b^1}\otimes \cdots \otimes |\varphi {\rangle }_{b^N}\otimes |\varphi {\rangle }_1\otimes |\varphi {\rangle }_2\otimes |\varphi {\rangle }_3,\hfill \\ \hfill |{\mathrm{\Phi }}^N{\rangle }_1=& \frac{r_1^{\prime }{\left(r_2-r_2^{\prime }\right)}^3}{8}\left[\left({\alpha }_1|F\rangle |+1{\rangle }_3+{\alpha }_2|S\rangle |-1{\rangle }_3\right)\left({\beta }_1|{\omega }_1\rangle |+1{\rangle }_1+{\beta }_2|{\omega }_2\rangle |-1{\rangle }_1\right)\right.\otimes {\left.\left({\gamma }_1|a_1\rangle |+1{\rangle }_2+{\gamma }_2|a_2\rangle |-1{\rangle }_2\right)\right]}_a\otimes |\varphi {\rangle }_{b^1}\otimes \cdots \otimes |\varphi {\rangle }_{b^N}.\hfill \end{array}(16)$

Secondly, the first target photon b¹ is injected into the circuit. Similarly, while the photon b¹ passes through the circuit, if any of the single-photon detectors is clicked, the construction process of the hyperparallel CPF^N gate is terminated. If none of any single-photon detector is clicked, the process of the hyperparallel CPF^N goes on and the state of the whole system becomes

$\begin{array}{ll}\hfill |{\mathrm{\Phi }}^N{\rangle }_2=& \frac{{\mathrm{r\prime }}_1^2{\left(r_2-r_2^{\prime }\right)}^6}{64}\left[{\beta }_1|+1{\rangle }_1|{\omega }_1{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle +{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}+{\beta }_2|-1{\rangle }_1|{\omega }_2{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle -{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}\right]\hfill \\ \hfill & \otimes \left[{\gamma }_1|+1{\rangle }_2|a_1{\rangle }_a{\left({\xi }_1^1|b_1\rangle +{\xi }_2^1|b_2\rangle \right)}_{b^1}+{\gamma }_2|-1{\rangle }_2|a_2{\rangle }_a{\left({\xi }_1^1|b_1\rangle -{\xi }_2^1|b_2\rangle \right)}_{b^1}\right]\hfill \\ \hfill & \otimes \left[{\alpha }_1|+1{\rangle }_3|F{\rangle }_a{\left({\delta }_1^1|F\rangle +{\delta }_2^1|S\rangle \right)}_{b^1}+{\alpha }_2|-1{\rangle }_3|S{\rangle }_a{\left({\delta }_1^1|F\rangle -{\delta }_2^1|S\rangle \right)}_{b^1}\right].\hfill \end{array}(17)$

Subsequently, the target photons b², … , b^N are injected into the quantum circuit in sequence. Similarly, if any of the single-photon detector is clicked, the process is terminated. Otherwise, the process goes on. Then the state of the whole system is expressed as

$\begin{array}{ll}\hfill |{\mathrm{\Phi }}^N{\rangle }_3& =P^{1+N}\left[|+1{\rangle }_1{\beta }_1|{\omega }_1{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle +{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}{\left({\eta }_1^2|{\omega }_1\rangle +{\eta }_2^2|{\omega }_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\eta }_1^N|{\omega }_1\rangle +{\eta }_2^2|{\omega }_2\rangle \right)}_{b^N}\right.\hfill \\ \hfill & +\left.|-1{\rangle }_1{\beta }_2|{\omega }_2{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle -{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}{\left({\eta }_2^N|{\omega }_1\rangle -{\eta }_2^{\mathrm{N}}|{\omega }_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\eta }_1^N|{\omega }_1\rangle -{\eta }_2^N|{\omega }_2\rangle \right)}_{b^N}\right]\hfill \\ \hfill & \otimes [|+1{\rangle }_2{\gamma }_1|a_1{\rangle }_a{\left({\xi }_1^1|b_1\rangle +{\xi }_2^1|b_2\rangle \right)}_{b^1}{\left({\xi }_1^2|b_1\rangle +{\xi }_2^2|b_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\xi }_1^N|b_1\rangle +{\xi }_2^N|b_2\rangle \right)}_{b^N}\hfill \\ \hfill & +|-1{\rangle }_2{\gamma }_2|a_2{\rangle }_a{\left({\xi }_1^1|b_1\rangle -{\xi }_2^1|b_2\rangle \right)}_{b^1}{\left({\xi }_1^2|b_1\rangle -{\xi }_2^2|b_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\xi }_1^N|b_1\rangle -{\xi }_2^N|b_2\rangle \right)}_{b^N}]\hfill \\ \hfill & \otimes [|+1{\rangle }_3{\alpha }_1|F{\rangle }_a{\left({\delta }_1^1|F\rangle +{\delta }_2^1|S\rangle \right)}_{b^1}{\left({\delta }_1^2|F\rangle +{\delta }_2^2|S\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\delta }_1^N|F\rangle +{\delta }_2^N|S\rangle \right)}_{b^N}\hfill \\ \hfill & +|+1{\rangle }_3{\alpha }_2|S{\rangle }_a{\left({\delta }_1^1|F\rangle -{\delta }_2^1|S\rangle \right)}_{b^1}{\left({\delta }_1^2|F\rangle -{\delta }_2^2|S\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\delta }_1^N|F\rangle -{\delta }_2^N|S\rangle \right)}_{b^N}],\hfill \end{array}(18)$

where $P=r_1^{\prime }{(r_2-r_2^{\prime })}^3/8$.

Finally, after some classical feed-forward operations based on the measurements on the three NV centers in the orthogonal basis {|±⟩} according to Table 1, the system consisting of the control photon and target photons is projected into the state

$\begin{array}{ll}\hfill |{\mathrm{\Phi }}^N{\rangle }_4=& P^{1+N}\times [{\beta }_1|{\omega }_1{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle +{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}{\left({\eta }_1^2|{\omega }_1\rangle +{\eta }_2^2|{\omega }_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\eta }_1^N|{\omega }_1\rangle +{\eta }_2^N|{\omega }_2\rangle \right)}_{b^N}\hfill \\ \hfill & +{\beta }_2|{\omega }_2{\rangle }_a{\left({\eta }_1^1|{\omega }_1\rangle -{\eta }_2^1|{\omega }_2\rangle \right)}_{b^1}{\left({\eta }_1^2|{\omega }_1\rangle -{\eta }_2^2|{\omega }_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\eta }_1^N|{\omega }_1\rangle -{\eta }_2^N|{\omega }_2\rangle \right)}_{b^N}]\hfill \\ \hfill & \otimes [{\gamma }_1|a_1{\rangle }_a{\left({\xi }_1^1|b_1\rangle +{\xi }_2^1|b_2\rangle \right)}_{b^1}{\left({\xi }_1^2|b_1\rangle +{\xi }_2^2|b_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\xi }_1^N|b_1\rangle +{\xi }_2^N|b_2\rangle \right)}_{b^N}\hfill \\ \hfill & +{\gamma }_2|a_2{\rangle }_a{\left({\xi }_1^1|b_1\rangle -{\xi }_2^1|b_2\rangle \right)}_{b^1}{\left({\xi }_1^2|b_1\rangle -{\xi }_2^2|b_2\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\xi }_1^N|b_1\rangle -{\xi }_2^N|b_2\rangle \right)}_{b^N}]\hfill \\ \hfill & \otimes [{\alpha }_1|F{\rangle }_a{\left({\delta }_1^1|F\rangle +{\delta }_2^1|S\rangle \right)}_{b^1}{\left({\delta }_1^2|F\rangle +{\delta }_2^2|S\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\delta }_1^N|F\rangle +{\delta }_2^N|S\rangle \right)}_{b^N}\hfill \\ \hfill & -{\alpha }_2|S{\rangle }_a{\left({\delta }_1^1|F\rangle -{\delta }_2^1|S\rangle \right)}_{b^1}{\left({\delta }_1^2|F\rangle -{\delta }_2^2|S\rangle \right)}_{b^2}\cdot \cdot \cdot {\left({\delta }_1^N|F\rangle -{\delta }_2^N|S\rangle \right)}_{b^N}].\hfill \end{array}(19)$

From Eq. 19, one can see that for each target photon bⁿ, phase flips take place on the frequency state $|{\omega }_2{\rangle }_{b^n}$, the spatial-mode state $|b_2{\rangle }_{b^n}$, and the polarization state $|S{\rangle }_{b^n}$ respectively when the frequency, the spatial-mode, and the polarization state of the control photon a is |ω₂⟩_a, |a₂⟩_a, and |S⟩_a. Meanwhile, from Eq. 19, one can see that there is only a global coefficient between the ideal desired output state and the realistic output state, which means the hyperparallel CPF^N is implemented with a robust fidelity to the realistic NV-cavity parameters. Overall, the quantum circuit is generalized to complete the high-fidelity photonic three-DOF hyperparallel CPF^N gate working on a multiple-photon system.

The quantum circuit shown in Figure 2 can be additionally generalized to implement a high-fidelity hyperparallel quantum parity-check gate in the polarization, frequency, and spatial-mode DOFs. Suppose photon a and photon b are initially prepared in the states |ϕ⟩_a and |ϕ⟩_b respectively. To check the parities of the two-photon states in three DOFs, the three NV centers are all initially prepared in the states | + ⟩, and the two photons are injected into the quantum circuit as shown in Figure 2 in sequence. If there is a click of the single-photon detectors while either of the photons passes through the quantum circuit, the process of the parity check is terminated. Otherwise, the state of the whole system consisting of two photons and three NV centers is transformed into the state

$\begin{array}{ll}\hfill |{\mathrm{\Phi }}^P\rangle =& \frac{{\mathrm{r\prime }}_1^2{\left(r_2-r_2^{\prime }\right)}^6}{64}\left[|+{\rangle }_1\left({\beta }_1{\eta }_1|{\omega }_1{\rangle }_a|{\omega }_1{\rangle }_b+{\beta }_2{\eta }_2|{\omega }_2{\rangle }_a|{\omega }_2{\rangle }_b\right)+|-{\rangle }_1\left({\beta }_1{\eta }_2|{\omega }_1{\rangle }_a|{\omega }_2{\rangle }_b\right)\right.+\left.\left.{\beta }_2{\eta }_1|{\omega }_2{\rangle }_a|{\omega }_1{\rangle }_b\right)\right]\otimes \left[|+{\rangle }_2\left({\gamma }_1{\xi }_1|a_1{\rangle }_a|b_1{\rangle }_b+{\gamma }_2{\xi }_1|a_2{\rangle }_a|b_2{\rangle }_b\right)\right.\hfill \\ \hfill & +\left.|-{\rangle }_2\left({\gamma }_1{\xi }_2|a_1{\rangle }_a|b_2{\rangle }_b\right)+{\gamma }_2{\xi }_1|a_2{\rangle }_a|b_1{\rangle }_b\right)]\otimes \left[|+{\rangle }_3\left({\alpha }_1{\delta }_1|F{\rangle }_a|F{\rangle }_b\right.\right.\hfill \\ \hfill & +\left.\left.\left.{\alpha }_2{\delta }_2|S{\rangle }_a|S{\rangle }_b\right)+|-{\rangle }_3\left({\alpha }_1{\delta }_2|F{\rangle }_a|S{\rangle }_b\right)+{\alpha }_2{\delta }_1|S{\rangle }_a|F{\rangle }_b\right)\right].\hfill \end{array}(20)$

Therefore, after the three NV centers are measured in basis {|±⟩}, the parities of the two-photon states in three DOFs can be obtained as shown in Table 2.

TABLE 2

TABLE 2. The relations between the measurement results on the three NV centers and the parity of the quantum state in the frequency, spatial-mode, and polarization DOFs, respectively.

5 Discussion and Summary

We have detailed the construction process of the photonic three-DOF hyperparallel CPF gate as shown in Figure 2, which can also be generalized to implement the photonic three-DOF hyperparallel CPF^N gate and parity-check gate. Meanwhile, we have shown that in the nearly realistic condition, the error items do not appear in the final output states and the difference between the ideal desired output states and the practical ones is only a global coefficient, as shown in Eqs 13, 19, 20. That is to say, these gates work with fidelities robust to the realistic NV-cavity parameters including g, γ, κ, and κ_s. In what follows, we quantitatively characterize the efficiency of the high-fidelity photonic three-DOF hyperparallel CPF gate, which is obtained as

$\eta =|\frac{{\mathrm{r\prime }}_1^2{\left(r_2-r_2^{\prime }\right)}^6}{64}{|}^2.(21)$

Based on Eq. 21, the numerical simulation results are shown in Figure 3A and Figure 3B, where the efficiency is respectively treated as the function of $\mathrm{g}/\sqrt{\kappa \gamma }$ and (ω₀ − ω₁)/κ with κ_s/κ = 0.05 and ω₂ = ω₀ = ω_c, and the function of $\mathrm{g}/\sqrt{\kappa \gamma }$ and κ_s/κ with (ω₀ − ω₁)/κ = 5 and ω₂ = ω₀ = ω_c. From Figure 3, one can see that the efficiency is much more sensitive to the variations of $\mathrm{g}/\sqrt{\kappa \gamma }$ and κ_s/κ compared with the variation of (ω₀ − ω₁)/κ. An optical coupling of a NV center to an on-chip microcavity with the parameters [g, κ, γ_total, γ_ZPL]/2π = [0.3, 26, 0.013, 0.0004]GHz has been demonstrated in the experiment [55]. Based on these experimental parameters, the efficiency η = 38.51% can be obtained provided κ_s/κ = 0.05 and (ω₀ − ω₁)/κ = 5. The efficiency is sacrificed for the high fidelity. That is to say, the computation errors are turned into detectable photon losses, which is advantageous for quantum computation.

FIGURE 3

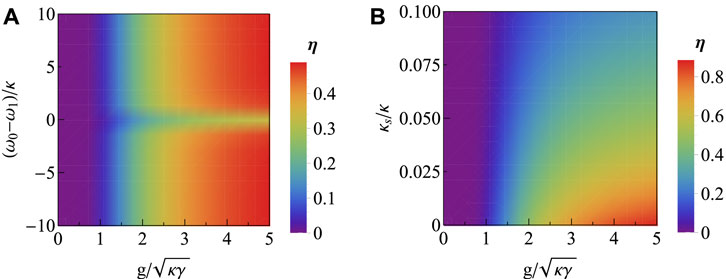
FIGURE 3. (A) The efficiency of high-fidelity hyperparallel CPF gate vs. $\mathrm{g}/\sqrt{\kappa \gamma }$ and (ω₀ − ω₁)/κ with ω₀ = ω_c and κ_s/κ = 0.05. (B) The efficiency of high-fidelity hyperparallel CPF gate vs. $\mathrm{g}/\sqrt{\kappa \gamma }$ and κ_s/κ with ω₀ = ω_c and (ω₀ − ω₁)/κ = 5.

The fidelities of the present photonic three-DOF hyperparallel gates are robust to the realistic NV-cavity parameters. In a more generally realistic condition, some other factors effecting the fidelities should be evaluated, one of which is the mixture of the excited states of NV centers. A degree of mixing among the excited states of NV centers comes from a relatively low strain which is induced by the fabrication of optical resonators, and it would lead to an imperfect dipolar transition between the excited state and the ground state which is the interaction unit in our protocol. Fortunately, the excited state |A₂⟩ is robust to the low strain and magnetic fields owing to the stable symmetric properties, and the mixing between the state |A₂⟩ and the other excited states is very tiny in the low-strain regime, as demonstrated in the experiment implemented by Togan et al. [72], where small number ɛ is used to describe the imperfect dipolar transition between the excited state and the ground state | + 1⟩ induced by the low strain. It has been figured out that in the case ɛ = 0.12 (0.08), the fidelity of the interaction between the NV center in the state | + 1⟩ and the polarized photon in the state $|F\rangle =(|R\rangle +|L\rangle )/\sqrt{2}$ reaches 0.9928 (0.9968), which shows that the effect of the low strain on the fidelity of the interaction can be ignored [58]. Another factor of degrading the fidelity is the finite zero phonon line (ZPL) emission, which is relevant to the emitted photons from NV centers. In 2009, Barclay et al. [55] showed that it is possible to enhance the ZPL emission rate γ_ZPL/γ_total by 47% if the Q value of the microdisk can be increased to 2.5 × 10⁴. In recent years, several techniques have been proposed which can enhance the ZPL emission rate γ_ZPL/γ_total from 3% to 70% [75–79]. In addition, the fidelity is slightly lowered by errors in readout, spin preparation, spin decoherence, spin operation, spin flips during the process [80]. And the impact from the intracavity loss and linear optical elements loss [26, 34] should be considered. However, these limitations caused by the technical imperfections are not fundamental and can be largely improved with the further technical advances. For example, the spin-coherence time can achieve millisecond level in isotopically purified diamond [46] or by utilizing dynamical decoupling techniques [47, 48]. Moreover, Dolde et al. [50] realized the single electron spin operation with the fidelity F ≈ 0.99 by utilizing engineered microwae pulses, and Fuchs et al. [49] reduced the manipulation time to the order of nanosecond.

We encode qubits in three DOFs including the polarization and spatial-mode and frequency DOFs of a two-photon system to complete our high-fidelity hyperparallel CPF gate, which further expands the capability of parallel computation compared with the ones working with one or two DOFs. The polarization and spatial-mode DOFs can be skillfully manipulated in experiment where arbitrary single-qubit operations on them are completed with linear optical elements, such as beam splitters, (circular) polarization beam splitters, phase shifter, and half-wave or quarter-wave plates. Frequency DOF has the advantages of large information capacity, highly nonlocal properties, and compatibility with current fiber optic technology infrastructure [81]. Extraordinary experimental and theoretical progress has been made on the frequency-encoded photonic qubits, such as the designation of the optical devices used to perform operations on the frequency-encoded photons [82, 83], the demonstration on coherent interference of frequency-encoded photons [84–88], the schemes of quantum gate for frequency qubits [42, 89], and the realization of discrete-frequency-entangled states [90]. In our protocol, the optical devices, including WDM for dividing photon with different frequencies from one path to different pathes or completing the reverse conversion and FS for shifting the frequency, are utilized to manipulate frequencies and they are experimentally available. The WDM can be realized with Fiber Bragg Grating [91, 92], optical cavity [93, 94], or asymmetric Mach-Zehnder on the frequency encoding [95, 96]. The FS can be obtained by means of frequency up-conversion or down-conversion process [97–101].

In summary, we have proposed the approach for implementing the high-fidelity hyperparallel CPF gate working with the polarization, spatial-mode, and frequency DOFs of the two-photon system. The hyperparallel CPF gate works in the self-error-corrected pattern where the clicks of the single photon detectors remind the errors induced by the practical interaction and terminate the construction of the gate. Accordingly, the self-error-corrected pattern guarantees the realistic output state against the computation errors coming from practical interaction, enables the gate to work with high fidelity, and relaxes the current experimental requirement. In addition, the method can be generalized to implement high-fidelity photonic three-DOF hyperparallel CPF^N gate and parity-check gate. Maybe these features make this work useful in the hyperparallel quantum computation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

G-YW: Conceptualization, Methodology, Validation, Writing-Original Draft, Writing-Review and Editing. H-RW: Conceptualization, Methodology, Validation, Writing-Review and Editing.

Funding

This work is supported by the National Natural Science Foundation of China under Grant No. 12004029 and the Fundamental Research Funds for the Central Universities under Grant No. FRF-TP-19-011A3.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press (2000).

Google Scholar

2. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/physrevlett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bennett CH, Wiesner SJ. Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Phys Rev Lett (1992) 69:2881–4. doi:10.1103/physrevlett.69.2881

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Liu XS, Long GL, Tong DM, Li F. General Scheme for Superdense Coding between Multiparties. Phys Rev A (2002) 65:022304. doi:10.1103/physreva.65.022304

CrossRef Full Text | Google Scholar

5. Ekert AK. Quantum Cryptography Based on Bell's Theorem. Phys Rev Lett (1991) 67:661–3. doi:10.1103/physrevlett.67.661

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bennett CH, Brassard G, Mermin ND. Quantum Cryptography without Bell's Theorem. Phys Rev Lett (1992) 68:557–9. doi:10.1103/physrevlett.68.557

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Hillery M, Bužek V, Berthiaume A. Quantum Secret Sharing. Phys Rev A (1999) 59:1829–34. doi:10.1103/physreva.59.1829

CrossRef Full Text | Google Scholar

8. Long GL, Liu XS. Theoretically Efficient High-Capacity Quantum-Key-Distribution Scheme. Phys Rev A (2002) 65:032302. doi:10.1103/physreva.65.032302

CrossRef Full Text | Google Scholar

9. Deng FG, Long GL, Liu XS. Two-step Quantum Direct Communication Protocol Using the Einstein-Podolsky-Rosen Pair Block. Phys Rev A (2003) 68:042317. doi:10.1103/physreva.68.042317

CrossRef Full Text | Google Scholar

10. Zhang W, Ding DS, Sheng YB, Zhou L, Shi BS, Guo GC. Quantum Secure Direct Communication with Quantum Memory. Phys Rev Lett (2007) 118:220501. doi:10.1103/PhysRevLett.118.220501

CrossRef Full Text | Google Scholar

11. Liu B, Xia S, Xiao D, Huang W, Xu B, Li Y. Decoy-state Method for Quantum-Key-Distribution-Based Quantum Private Query. Sci China Phys Mech Astron (2022) 65:240312. doi:10.1007/s11433-021-1843-7

CrossRef Full Text | Google Scholar

12. Lv S-X, Jiao X-F, Zhou P. Multiparty Quantum Computation for Summation and Multiplication with Mutually Unbiased Bases. Int J Theor Phys (2019) 58:2872–82. doi:10.1007/s10773-019-04170-z

CrossRef Full Text | Google Scholar

13. Zhou L, Sheng Y-B. One-step Device-independent Quantum Secure Direct Communication. Sci China Phys Mech Astron (2022) 65:250311. doi:10.1007/s11433-021-1863-9

CrossRef Full Text | Google Scholar

14. Li Z, Wei K. Improving Parameter Optimization in Decoy-State Quantum Key Distribution. Quan Eng (2022) 2022:9717591. doi:10.1155/2022/9717591

CrossRef Full Text | Google Scholar

15. Shor PW. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In: Goldwasser S, editor. Proceedings 35th annual Symposium on Foundations Of Computer Science; 1994 Nov 20–22; Santa Fe, NM. IEEE (1994). p. 124–34.

Google Scholar

16. Grover LK. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys Rev Lett (1997) 79:325–8. doi:10.1103/physrevlett.79.325

CrossRef Full Text | Google Scholar

17. Long GL. Grover Algorithm with Zero Theoretical Failure Rate. Phys Rev A (2001) 64:022307. doi:10.1103/physreva.64.022307

CrossRef Full Text | Google Scholar

18. Xu GF, Tong DM. Realizing Multi-Qubit Controlled Nonadiabatic Holonomic gates with Connecting Systems. AAPPS Bull (2022) 32:13. doi:10.1007/s43673-022-00043-6

CrossRef Full Text | Google Scholar

19. Giovannetti V, Lloyd S, Maccone L. Quantum-enhanced Measurements: Beating the Standard Quantum Limit. Science (2004) 306:1330–6. doi:10.1126/science.1104149

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cai X-D, Wu D, Su Z-E, Chen M-C, Wang X-L, Li L, et al. Entanglement-based Machine Learning on a Quantum Computer. Phys Rev Lett (2015) 114:110504. doi:10.1103/physrevlett.114.110504

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Allcock J, Zhang S. Quantum Machine Learning. Natl Sci Rev (2019) 6:26–8. doi:10.1093/nsr/nwy149

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ouyang XL, Huang XZ, Wu YK, Zhang WG, Wang X, Zhang HL, et al. Experimental Demonstration of Quantum-Enhanced Machine Learning in a Nitrogen-Vacancy-center System. Phys Rev A (2020) 101:012307. doi:10.1103/physreva.101.012307

CrossRef Full Text | Google Scholar

23. Zhang N-N, Tao M-J, He W-T, Chen X-Y, Kong X-Y, Deng F-G, et al. Efficient Quantum Simulation of Open Quantum Dynamics at Various Hamiltonians and Spectral Densities. Front Phys (2021) 16:51501. doi:10.1007/s11467-021-1064-y

CrossRef Full Text | Google Scholar

24. Wang B-X, Tao M-J, Ai Q, Xin T, Lambert N, Ruan D, et al. Efficient Quantum Simulation of Photosynthetic Light Harvesting. Npj Quan Inf (2018) 4:52. doi:10.1038/s41534-018-0102-2

CrossRef Full Text | Google Scholar

25. Barenco A, Bennett CH, Cleve R, DiVincenzo DP, Margolus N, Shor P, et al. Elementary gates for Quantum Computation. Phys Rev A (1995) 52:3457–67. doi:10.1103/physreva.52.3457

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Reiserer A, Kalb N, Rempe G, Ritter S. A Quantum Gate between a Flying Optical Photon and a Single Trapped Atom. Nature (2014) 508:237–40. doi:10.1038/nature13177

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Tiecke TG, Thompson JD, de Leon NP, Liu LR, Vuletić V, Lukin MD. Nanophotonic Quantum Phase Switch with a Single Atom. Nature (2014) 508:241–4. doi:10.1038/nature13188

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ren Bao-Cang BC, Deng Fu-Guo FG. Hyper-parallel Photonic Quantum Computation and Manipulation on Hyperentangled States. Acta Phys Sin (2015) 64:160303. doi:10.7498/aps.64.160303

CrossRef Full Text | Google Scholar

29. Ren B-C, Wei H-R, Deng F-G. Deterministic Photonic Spatial-Polarization Hyper-Controlled-Not Gate Assisted by a Quantum Dot inside a One-Side Optical Microcavity. Laser Phys Lett (2013) 10:095202. doi:10.1088/1612-2011/10/9/095202

CrossRef Full Text | Google Scholar

30. Ren BC, Wang GY, Deng FG. Universal Hyperparallel Hybrid Photonic Quantum gates with Dipole-Induced Transparency in the Weak-Coupling Regime. Phys Rev A (2015) 91:032328. doi:10.1103/physreva.91.032328

CrossRef Full Text | Google Scholar

31. Ren B-C, Deng F-G. Hyper-parallel Photonic Quantum Computation with Coupled Quantum Dots. Sci Rep (2014) 4:4623. doi:10.1038/srep04623

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Li T, Long GL. Hyperparallel Optical Quantum Computation Assisted by Atomic Ensembles Embedded in Double-Sided Optical Cavities. Phys Rev A (2016) 94:022343. doi:10.1103/physreva.94.022343

CrossRef Full Text | Google Scholar

33. Wang T-J, Zhang Y, Wang C. Universal Hybrid Hyper-Controlled Quantum gates Assisted by Quantum Dots in Optical Double-Sided Microcavities. Laser Phys Lett (2014) 11:025203. doi:10.1088/1612-2011/11/2/025203

CrossRef Full Text | Google Scholar

34. Wei H-R, Deng F-G, Long GL. Hyper-parallel Toffoli Gate on Three-Photon System with Two Degrees of freedom Assisted by Single-Sided Optical Microcavities. Opt Express (2016) 24:18619–30. doi:10.1364/oe.24.018619

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ren B-C, Wang AH, Alsaedi A, Hayat T, Deng F-G. Three-photon Polarization-Spatial Hyperparallel Quantum Fredkin Gate Assisted by diamond Nitrogen Vacancy center in Optical Cavity. Annalen Der Physik (2018) 530:1800043. doi:10.1002/andp.201800043

CrossRef Full Text | Google Scholar

36. Wei HR, Liu WQ, Chen NY. Implementing a Two‐Photon Three‐Degrees‐of‐Freedom Hyper‐Parallel Controlled Phase Flip Gate through Cavity‐Assisted Interactions. Annalen Der Physik (2020) 532:1900578. doi:10.1002/andp.201900578

CrossRef Full Text | Google Scholar

37. Marrucci L, Manzo C, Paparo D. Optical Spin-To-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/physrevlett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Nagali E, Sciarrino F, De Martini F, Marrucci L, Piccirillo B, Karimi E, et al. Quantum Information Transfer from Spin to Orbital Angular Momentum of Photons. Phys Rev Lett (2009) 103:013601. doi:10.1103/PhysRevLett.103.013601

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Pinheiro ARC, Souza CER, Caetano DP, Huguenin JAO, Schmidt AGM, Khoury AZ. Vector Vortex Implementation of a Quantum Game. J Opt Soc Am B (2013) 30:3210–4. doi:10.1364/josab.30.003210

CrossRef Full Text | Google Scholar

40. Milione G, Nguyen TA, Leach J, Nolan DA, Alfano RR. Using the Nonseparability of Vector Beams to Encode Information for Optical Communication. Opt Lett (2015) 40:4887–90. doi:10.1364/ol.40.004887

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Balthazar WF, Souza CER, Caetano DP, Galvão EF, Huguenin JAO, Khoury AZ. Tripartite Nonseparability in Classical Optics. Opt Lett (2016) 41:5797–800. doi:10.1364/ol.41.005797

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Lu HH, Lukens JM, Williams BP, Imany P, Peters NA, Weiner AM, et al. A Controlled-NOT Gate for Frequency-Bin Qubits. Npj Quan Inf (2019) 5:5797–800. doi:10.1038/s41534-019-0137-z

CrossRef Full Text | Google Scholar

43. Zeng Z, Zhu K-D. Complete Hyperentangled Bell State Analysis Assisted by Hyperentanglement. Laser Phys Lett (2020) 17:075203. doi:10.1088/1612-202x/ab9117

CrossRef Full Text | Google Scholar

44. Jelezko F, Gaebel T, Popa I, Gruber A, Wrachtrup J. Observation of Coherent Oscillations in a Single Electron Spin. Phys Rev Lett (2004) 92:076401. doi:10.1103/PhysRevLett.92.076401

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Childress L, Gurudev Dutt MV, Taylor JM, Zibrov AS, Jelezko F, Wrachtrup J, et al. Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in diamond. Science (2006) 314:281–5. doi:10.1126/science.1131871

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Balasubramanian G, Neumann P, Twitchen D, Markham M, Kolesov R, Mizuochi N, et al. Ultralong Spin Coherence Time in Isotopically Engineered diamond. Nat Mater (2009) 8:383–7. doi:10.1038/nmat2420

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Naydenov B, Dolde F, Hall LT, Shin C, Fedder H, Hollenberg LCL, et al. Dynamical Decoupling of a Single-Electron Spin at Room Temperature. Phys Rev B (2011) 83:081201. doi:10.1103/physrevb.83.081201

CrossRef Full Text | Google Scholar

48. de Lange G, Wang ZH, Ristè D, Dobrovitski VV, Hanson R. Universal Dynamical Decoupling of a Single Solid-State Spin from a Spin bath. Science (2010) 330:60–3. doi:10.1126/science.1192739

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Fuchs GD, Dobrovitski VV, Toyli DM, Heremans FJ, Awschalom DD. Gigahertz Dynamics of a Strongly Driven Single Quantum Spin. Science (2009) 326:1520–2. doi:10.1126/science.1181193

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Dolde F, Bergholm V, Wang Y, Jakobi I, Naydenov B, Pezzagna S, et al. High-fidelity Spin Entanglement Using Optimal Control. Nat Commun (2014) 5:3371. doi:10.1038/ncomms4371

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Robledo L, Childress L, Bernien H, Hensen B, Alkemade PFA, Hanson R. High-fidelity Projective Read-Out of a Solid-State Spin Quantum Register. Nature (2011) 477:574–8. doi:10.1038/nature10401

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Holzgrafe J, Beitner J, Kara D, Knowles HS, Atatüre M. Error Corrected Spin-State Readout in a Nanodiamond. Npj Quan Inf (2019) 5:13. doi:10.1038/s41534-019-0126-2

CrossRef Full Text | Google Scholar

53. Park Y-S, Cook AK, Wang H. Cavity QED with diamond Nanocrystals and Silica Microspheres. Nano Lett (2006) 6:2075–9. doi:10.1021/nl061342r

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Barbour RJ, Dinyari KN, Wang H. A Composite Microcavity of diamond Nanopillar and Deformed Silica Microsphere with Enhanced Evanescent Decay Length. Opt Express (2010) 18:18968–74. doi:10.1364/oe.18.018968

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Barclay PE, Fu K-MC, Santori C, Beausoleil RG. Chip-based Microcavities Coupled to Nitrogen-Vacancy Centers in Single crystal diamond. Appl Phys Lett (2009) 95:191115. doi:10.1063/1.3262948

CrossRef Full Text | Google Scholar

56. Chen Q, Yang WL, Feng M, Du JF. Entangling Separate Nitrogen-Vacancy Centers in a Scalable Fashion via Coupling to Microtoroidal Resonators. Phys Rev A (2011) 83:054305. doi:10.1103/physreva.83.054305

CrossRef Full Text | Google Scholar

57. Wei HR, Deng FG. Compact Quantum gates on Electron-Spin Qubits Assisted by diamond Nitrogen-Vacancy Centers inside Cavities. Phys Rev A (2013) 88:042323. doi:10.1103/physreva.88.042323

CrossRef Full Text | Google Scholar

58. Wang TJ, Wang C. Universal Hybrid Three-Qubit Quantum gates Assisted by a Nitrogen-Vacancy center Coupled with a Whispering-Gallery-Mode Microresonator. Phys Rev A (2014) 90:052310. doi:10.1103/physreva.90.052310

CrossRef Full Text | Google Scholar

59. Wei H-R, Lu Long G. Hybrid Quantum gates between Flying Photon and diamond Nitrogen-Vacancy Centers Assisted by Optical Microcavities. Sci Rep (2015) 5:12918. doi:10.1038/srep12918

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Li Y, Aolita L, Chang DE, Kwek LC. Robust-fidelity Atom-Photon Entangling gates in the Weak-Coupling Regime. Phys Rev Lett (2012) 109:160504. doi:10.1103/physrevlett.109.160504

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Borregaard J, Kómár P, Kessler EM, Sørensen AS, Lukin MD. Heralded Quantum gates with Integrated Error Detection in Optical Cavities. Phys Rev Lett (2015) 114:110502. doi:10.1103/physrevlett.114.110502

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Li T, Deng FG. Error-rejecting Quantum Computing with Solid-State Spins Assisted by Low-Q Optical Microcavities. Phys Rev A (2016) 94:062310. doi:10.1103/physreva.94.062310

CrossRef Full Text | Google Scholar

63. Qin W, Wang X, Miranowicz A, Zhong Z, Nori F. Heralded Quantum Controlled-phase gates with Dissipative Dynamics in Macroscopically Distant Resonators. Phys Rev A (2017) 96:012315. doi:10.1103/physreva.96.012315

CrossRef Full Text | Google Scholar

64. Ren B-C, Deng F-G. Robust Hyperparallel Photonic Quantum Entangling Gate with Cavity QED. Opt Express (2017) 25:10863–73. doi:10.1364/oe.25.010863

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Shapira Y, Shaniv R, Manovitz T, Akerman N, Ozeri R. Robust Entanglement gates for Trapped-Ion Qubits. Phys Rev Lett (2018) 121:180502. doi:10.1103/physrevlett.121.180502

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Wang G-Y, Li T, Ai Q, Deng F-G. Self-error-corrected Hyperparallel Photonic Quantum Computation Working with Both the Polarization and the Spatial-Mode Degrees of freedom. Opt Express (2018) 26:23333–46. doi:10.1364/oe.26.023333

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Li M, Zhang M. Robust Universal Photonic Quantum gates Operable with Imperfect Processes Involved in diamond Nitrogen-Vacancy Centers inside Low-Q Single-Sided Cavities. Opt Express (2018) 26:33129–41. doi:10.1364/oe.26.033129

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Li M, Lin J-Y, Zhang M. High-fidelity Hybrid Quantum gates between a Flying Photon and diamond Nitrogen-Vacancy Centers Assisted by Low-Q Single-Sided Cavities. Annalen Der Physik (2019) 531:1800312. doi:10.1002/andp.201800312

CrossRef Full Text | Google Scholar

69. Wei H-R, Zheng Y-B, Hua M, Xu G-F. Robust-fidelity Hyperparallel Controlled-Phase-Flip Gate through Microcavities. Appl Phys Express (2020) 13:082007. doi:10.35848/1882-0786/aba64a

CrossRef Full Text | Google Scholar

70. Xu Y, Chu J, Yuan J, Qiu J, Zhou Y, Zhang L, et al. High-fidelity, High-Scalability Two-Qubit Gate Scheme for Superconducting Qubits. Phys Rev Lett (2020) 125:240503. doi:10.1103/physrevlett.125.240503

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Han Y-H, Cao C, Fan L, Zhang R. Heralded High-Fidelity Quantum Hyper-CNOT gates Assisted by Charged Quantum Dots inside Single-Sided Optical Microcavities. Opt Express (2021) 29:20045–62. doi:10.1364/oe.426325

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Togan E, Chu Y, Trifonov AS, Jiang L, Maze J, Childress L, et al. Quantum Entanglement between an Optical Photon and a Solid-State Spin Qubit. Nature (2010) 466:730–4. doi:10.1038/nature09256

PubMed Abstract | CrossRef Full Text | Google Scholar

73. An JH, Feng M, Oh CH. Quantum-information Processing with a Single Photon by an Input-Output Process with Respect to Low-Q Cavities. Phys Rev A (2009) 79:032303. doi:10.1103/physreva.79.032303

CrossRef Full Text | Google Scholar

74. Hu CY, Young A, O’Brien JL, Munro WJ, Rarity JG. Giant Optical Faraday Rotation Induced by a Single-Electron Spin in a Quantum Dot: Applications to Entangling Remote Spins via a Single Photon. Phys Rev B (2008) 78:085307. doi:10.1103/physrevb.78.085307

CrossRef Full Text | Google Scholar

75. Kolesov R, Grotz B, Balasubramanian G, Stöhr RJ, Nicolet AAL, Hemmer PR, et al. Wave-particle Duality of Single Surface Plasmon Polaritons. Nat Phys (2009) 5:470–4. doi:10.1038/nphys1278

CrossRef Full Text | Google Scholar

76. Schietinger S, Barth M, Aichele T, Benson O. Plasmon-Enhanced Single Photon Emission from a Nanoassembled Metal-Diamond Hybrid Structure at Room Temperature. Nano Lett (2009) 9:1694–8. doi:10.1021/nl900384c

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Barclay PE, Fu KMC, Santori C, Faraon A, Beausoleil RG. Hybrid Nanocavity Resonant Enhancement of Color Center Emission in Diamond. Phys Rev X (2011) 1:011007. doi:10.1103/physrevx.1.011007

CrossRef Full Text | Google Scholar

78. Faraon A, Barclay PE, Santori C, Fu K-MC, Beausoleil RG. Resonant Enhancement of the Zero-Phonon Emission from a Colour Centre in a Diamond Cavity. Nat Photon (2011) 5:301–5. doi:10.1038/nphoton.2011.52

CrossRef Full Text | Google Scholar

79. Faraon A, Santori C, Huang Z, Acosta VM, Beausoleil RG. Coupling of Nitrogen-Vacancy Centers to Photonic Crystal Cavities in Monocrystalline Diamond. Phys Rev Lett (2012) 109:033604. doi:10.1103/PhysRevLett.109.033604

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Bernien H, Hensen B, Pfaff W, Koolstra G, Blok MS, Robledo L, et al. Heralded Entanglement between Solid-State Qubits Separated by Three Metres. Nature (2013) 497:86–90. doi:10.1038/nature12016

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Ou BQ, Liu C, Sun Y, Chen PX. Deterministically Swapping Frequency-Bin Entanglement from Photon-Photon to Atom-Photon Hybrid Systems. Phys Rev A (2018) 97:023839. doi:10.1103/physreva.97.023839

CrossRef Full Text | Google Scholar

82. Lu HH, Lukens JM, Peters NA, Odele OD, Leaird DE, Weiner AM, et al. Electro-optic Frequency Beam Splitters and Tritters for High-Fidelity Photonic Quantum Information Processing. Phys Rev Lett (2018) 120:030502. doi:10.1103/PhysRevLett.120.030502

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Hu YW, Yu MJ, Zhu D, Sinclair N, Shams-Ansari A, Shao LB, et al. On-chip Electro-Optic Frequency Shifters and Beam Splitters. Nature (2021) 599:7886. doi:10.1038/s41586-021-03999-x

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Clemmen S, Farsi A, Ramelow S, Gaeta AL. Ramsey Interference with Single Photons. Phys Rev Lett (2016) 117:223601. doi:10.1103/physrevlett.117.223601

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Kobayashi T, Ikuta R, Yasui S, Miki S, Yamashita T, Terai H, et al. Frequency-domain Hong-Ou-Mandel Interference. Nat Photon (2011) 10:441–4. doi:10.1038/nphoton.2016.74

CrossRef Full Text | Google Scholar

86. Kobayashi T, Yamazaki D, Matsuki K, Ikuta R, Miki S, Yamashita T, et al. Mach-Zehnder Interferometer Using Frequency-Domain Beamsplitter. Opt Express (2017) 25:12052–60. doi:10.1364/oe.25.012052

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Lu H-H, Lukens JM, Peters NA, Williams BP, Weiner AM, Lougovski P. Quantum Interference and Correlation Control of Frequency-Bin Qubits. Optica (2018) 5:1455–60. doi:10.1364/optica.5.001455

CrossRef Full Text | Google Scholar

88. Imany P, Odele OD, Alshaykh MS, Lu H-H, Leaird DE, Weiner AM. Frequency-domain Hong-Ou-Mandel Interference with Linear Optics. Opt Lett (2018) 43:2760–3. doi:10.1364/ol.43.002760

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Lukens JM, Lougovski P. Frequency-encoded Photonic Qubits for Scalable Quantum Information Processing. Optica (2017) 4:8–16. doi:10.1364/optica.4.000008

CrossRef Full Text | Google Scholar

90. Ramelow S, Ratschbacher L, Fedrizzi A, Langford NK, Zeilinger A. Discrete Tunable Color Entanglement. Phys Rev Lett (2009) 103:253601. doi:10.1103/physrevlett.103.253601

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Bloch M, McLaughlin SW, Merolla J-M, Patois F. Frequency-coded Quantum Key Distribution. Opt Lett (2007) 32:301–3. doi:10.1364/ol.32.000301

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Zhang T, Yin Z-Q, Han Z-F, Guo G-C. A Frequency-Coded Quantum Key Distribution Scheme. Opt Commun (2008) 281:4800–2. doi:10.1016/j.optcom.2008.06.009

CrossRef Full Text | Google Scholar

93. Huntington EH, Ralph TC. Separating the Quantum Sidebands of an Optical Field. J Opt B Quan Semiclass. Opt. (2002) 4:123–8. doi:10.1088/1464-4266/4/2/307

CrossRef Full Text | Google Scholar

94. Zhang J. Einstein-Podolsky-Rosen Sideband Entanglement in Broadband Squeezed Light. Phys Rev A (2003) 67:054302. doi:10.1103/physreva.67.054302

CrossRef Full Text | Google Scholar

95. Huntington EH, Ralph TC. Components for Optical Qubits Encoded in Sideband Modes. Phys Rev A (2004) 69:042318. doi:10.1103/physreva.69.042318

CrossRef Full Text | Google Scholar

96. Huntington EH, Milford GN, Robilliard C, Ralph TC. Coherent Analysis of Quantum Optical Sideband Modes. Opt Lett (2005) 30:2481–3. doi:10.1364/ol.30.002481

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Langrock C, Diamanti E, Roussev RV, Yamamoto Y, Fejer MM, Takesue H. Highly Efficient Single-Photon Detection at Communication Wavelengths by Use of Upconversion in Reverse-Proton-Exchanged Periodically Poled LiNbO₃ Waveguides. Opt Lett (2005) 30:1725–7. doi:10.1364/ol.30.001725

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Takesue H, Diamanti E, Honjo T, Langrock C, Fejer MM, Inoue K, et al. Differential Phase Shift Quantum Key Distribution experiment over 105 Km Fibre New J Phys (2005) 7:232. doi:10.1088/1367-2630/7/1/232

CrossRef Full Text | Google Scholar

99. Takesue H. Erasing Distinguishability Using Quantum Frequency Up-Conversion. Phys Rev Lett (2008) 101:173901. doi:10.1103/physrevlett.101.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Zhou Z-Y, Liu S-L, Li Y, Ding D-S, Zhang W, Shi S, et al. Orbital Angular Momentum-Entanglement Frequency Transducer. Phys Rev Lett (2016) 117:103601. doi:10.1103/physrevlett.117.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Ikuta R, Kusaka Y, Kitano T, Kato H, Yamamoto T, Koashi M, et al. Wide-band Quantum Interface for Visible-To-Telecommunication Wavelength Conversion. Nat Commun (2011) 2:537. doi:10.1038/ncomms1544

CrossRef Full Text | Google Scholar