- State Key Laboratory of Advanced Optical Communication System and Network, School of Electronics, Peking University, Beijing, China
Ultracold atoms in optical lattices are a powerful tool for quantum simulation, precise measurement, and quantum computation. A fundamental problem in applying this quantum system is how to manipulate the higher bands or orbitals in Bloch states effectively. Here we mainly review our methods for manipulating high orbital ultracold atoms in optical lattices with different configurations. Based on these methods, we construct the atom-orbital qubit under nonadiabatic holonomic quantum control and Ramsey interferometry with trapped motional quantum states. Then we review the observation of the novel quantum states and the study of the dynamical evolution of the high orbital atoms in optical lattices. The effective manipulation of the high orbitals provides strong support for applying ultracold atoms in the optical lattice in many fields.
1 Introduction
Ultracold atoms confined in optical lattices are a powerful tool for quantum simulation [1–3, 3–6], precision measurement [7], and quantum computation [8]. An optical lattice is formed by the interference of laser beams, creating a spatially periodic potential for ultracold atoms. The periodic potential generates the Bloch bands and Bloch states corresponding to different orbitals. Different to the study of ground band of optical lattice, by effectively manipulating the orbital degrees of freedom of ultracold atoms in the optical lattice, novel quantum states are found [9–12], and new qubits [8] and interferometers [13] based on the atomic orbitals are realized. In applying these high orbital ultracold atoms in optical lattices, a fundamental problem is how to manipulate the orbitals. Unlike internal states of atoms, the effective manipulation of Bloch states in optical lattices is complex because of the lack of selection rules [14]. Recently, methods to effectively manipulate Bloch states and high orbitals of optical lattices have been proposed, such as stimulated Raman transitions [15], shortcut method [14, 16–21], phase imprint [22], moving lattices [23], and band swapping technique [9, 11, 12, 24].
In this paper, we review our practical methods for manipulating high orbital atoms in optical lattices. These methods contain the shortcut method [14], band swapping technique [9, 11, 12, 24], and the amplitude modulation method to manipulate atoms in optical lattices [25]. The shortcut is a nonadiabatic coherent control composed of lattice pulse sequences [14]. The band swapping technique refers to quickly switching the structure of deep and shallow composite lattice, realizing the inversion of Bloch bands, and pumping atoms to the target band [9]. The manipulation of atoms in an optical lattice by amplitude modulation is another flexible way to control Bloch states coherently. In this method, the modulation with more than one frequency is applied to the lattice, couples the different orbitals, and realizes a large-momentum-transfer beam splitter [25]. We can manipulate any Bloch state of optical lattices with different configurations based on these methods. All the experiments in this paper are based on a Bose-Einstein-Condensate (BEC) of 87Rb prepared in a hybrid trap with the harmonic trap frequencies (ωx, ωy, ωz) = 2π × (28, 55, 60) Hz [21]. The experiments are mainly carried out in one dimensional (1D) and two dimensional (2D) triangular optical lattices. For 1D lattice, atoms are confined in more than 50 discrete pancakes with each pancakes containing 2000 atoms on average [10]. For triangular lattice, there are around 800 tubes with each tube containing 60 atoms on average [12].
The structure of this review is organized as follows. In section 2, we introduce the Bloch bands of atoms in optical lattices and review three methods for manipulating high orbital atoms in optical lattices. Then, we review the related applications based on these methods in section 3, including the atom-orbital qubit under nonadiabatic holonomic quantum control, Ramsey interferometry with trapped motional quantum states of the optical lattice. In section 4, we review the observations of exotic quantum states of p-orbital ultracold atoms. In section 5, we analyze the dynamical character of high orbital atoms in optical lattices. Finally, section 6 is the summary of this paper.
2 Manipulation of high orbital atoms in optical lattices
2.1 Bloch bands of atoms in optical lattice
An optical lattice is formed by the interference of a set of laser beams with electric field amplitude
where ki is the wave number and βi is the initial phase of laser beams i, and α is the coefficient related to detuning, atomic energy level, etc. For red detuned beams, α is negative. After neglecting the interactions between atoms, the Hamiltonian for single atom in optical lattice is
where n = 1, 2, 3 … is the index of the Bloch bands, q is the quasi-momentum, and un,q is a periodic function. The bloch states Ψn,q, or the eigenstates of
where bi is the reciprocal lattice vector.
Figure 1 shows two different configurations of optical lattices, 1D lattice and triangular lattice. As for the 1D lattice in Figure 1A, the lattice constant is d = λ/2 and the band spectrum is shown in Figure 1B (when lattice depth V = 5Er, where Er = ℏ2k2/2m is the recoil energy and k = 2π/λ). From the bottom to the top of the spectrum, the Bloch bands are S-, P-, D-, F-, and G-band, corresponding to n = 1, 2, 3, 4, 5, respectively. In Figure 1C, the triangular lattice with lattice constant 2/3λ, is constructed by three laser beams. The spectrum of this triangular lattice is different from that of the 1D lattice, where Bloch bands split into some different bands, as shown in Figure 1D (when the lattice depth is 3Er).
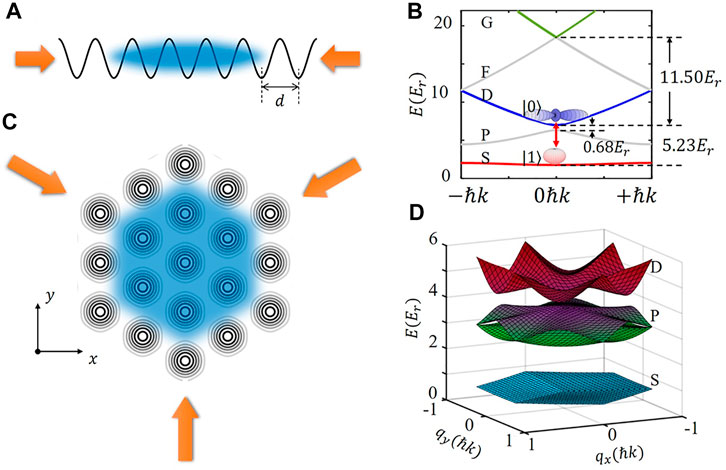
FIGURE 1. Schematic diagram and band structure of optical lattices. (A) is a 1D optical lattice with the lattice constant d. (B) The band-gap structures of 1D optical lattice for lattice depth V = 5Er with laser wavelength 1,064 nm. (C) is a triangular optical lattice, with the corresponding band structure (D) for lattice depth V = 3Er.
Before introducing the manipulation of the atoms in Bloch bands, we review the methods used in our experiments to probe the Bloch states. The first method is the band mapping technique [14, 15, 26–28]. In the experiment, if we switch off the lattice adiabatically within around 1 ms, the atoms in different bands can be mapped to different momentum components, measured after the time of flight (TOF). In addition, the value of quasi-momentum can be obtained from the position of atoms in corresponding Brillouin zones after the band mapping process and TOF. Figure 2A shows the band mapping result of atoms in a triangular lattice. Atoms are mainly distributed in the fourth Brillouin zone, corresponding to the D-band.
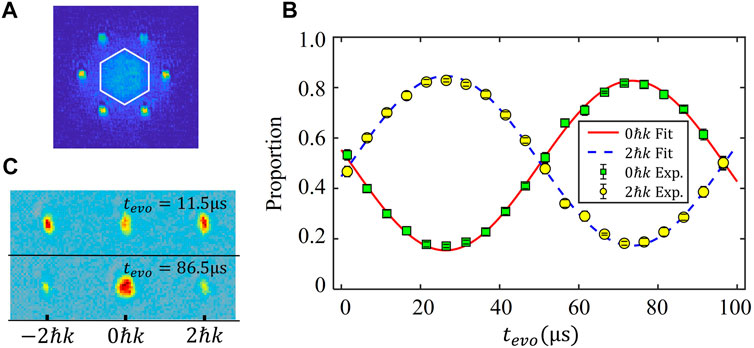
FIGURE 2. (A) Experimental result of atoms in D-band after band mapping process. The white hexagon is the boundary of the first Brillouin zone of the triangular lattice. The atoms are mainly distributed in the fourth Brillouin zone. (B) TOF quantum state tomography process. The initial state is a superposition Bloch state of the 1D optical lattice. After different evolution time tevo, the atom number proportion at 0ℏk and ± 2ℏk are shown by the green and yellow points. (C) The momentum distribution of atoms at tevo = 11.5μs and 86.5μs. The lattice depth is V = 5Er.
The band mapping method is easy to implement in the experiment, and the atomic population of different Bloch bands can be obtained. However, in this mapping process, the phase information of the Bloch state is lost. Then we use a TOF quantum state tomography (TOFQST) method to extract full information about the Bloch states [8]. For example, we use the TOFQST to detect the superposition of Bloch states in a 1D optical lattice with depth V = 5Er. In the experiment, we let the state evolve in the static lattice for a certain time tevo. Then we turn off the lattice diabatically and measure the momentum distribution after 31 ms TOF, which is shown in figure 2BC. By fitting the experimental data, we can obtain the full information of the states
2.2 Shortcut to manipulating atoms in optical lattice
2.2.1 Introduction of the shortcut method
This section demonstrates a shortcut method for manipulating atoms in different Bloch bands [14, 16–21]. This method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. The shortcut is composed of a series of optical lattice pulse sequences, which is shown in 3A. Each pulse pulse-i consists of two parts. First, the lattice is turned on for
We consider a general situation for transferring an arbitrary initial state |ψi⟩ to a target state |ψt⟩, where the states |ψi⟩ and |ψt⟩ can be the Bloch eigenstates or the superposition states. This shortcut applied to the initial state can be expressed as an evolution operator
By optimizing the pulse sequences
To verify the effectiveness of the shortcut, we demonstrate some experimental results in Figures 2, 3. In Figure 3C, we list some pulse sequences for manipulating Bloch states, where the initial states are all the ground states of the harmonic trap, |p = 0⟩ zero momentum state. For 1D optical lattice, we achieve to transfer atoms from zero momentum state to D-band, G-band, and the superposition states of S and D band with zero quasi-momentum, which corresponds to Figure 3B1B2, and Figure 2BC, and this theory fidelity is more than 99% [14]. For the D-band of the triangular optical lattice with depth V = 3Er, we give the shortcut sequence with 99.95% fidelity in Figure 3C, and the experimental band mapping results is shown in Figure 2A [21].
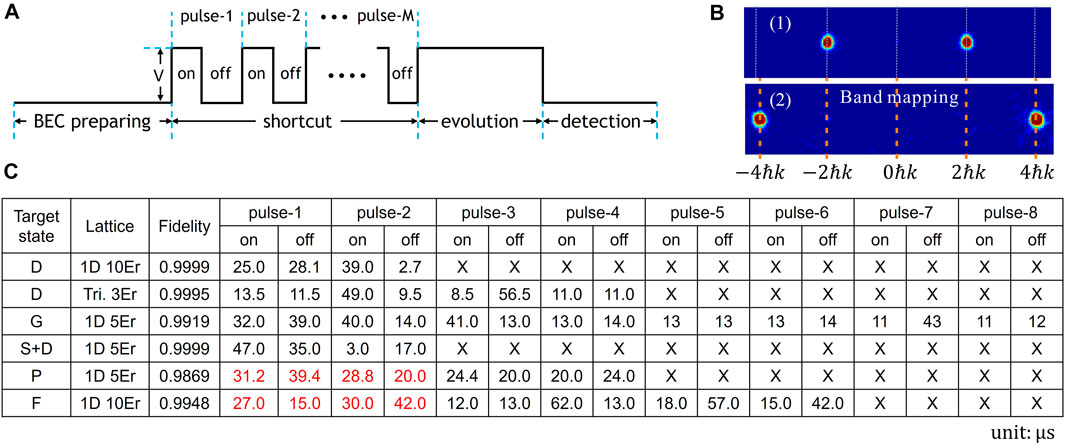
FIGURE 3. (A) The timing diagram of the shortcut. (B) The band mapping result of D-band (top) and G-band (bottom) with zero quasi-momentum for 1D optical lattice. (C) The parameters of shortcut for different target states and optical lattice. The red time parameter is for the sequence of misplacement lattice for the P-band and F-band sequences. The quasi-momentum of all target states in this figure is zero. This symbol X indicates that there is no pulse.
2.2.2 Manipulating bloch states with different symmetries
The symmetry of Bloch states with different energy bands and quasi momentum is different. For example, in the 1D optical lattice, Eq. 3 is rewritten as
The parity of Bloch states on S-, D-, and G-bands with zero quasi-momentum is even, which is shown in Figure 4A. On the contrary, the P- and F-bands with zero quasi-momentum are odd parity. Moreover, the symmetries of Bloch states with non-zero quasi-momentum are also different from that of zero quasi-momentum states. On the other hand, the symmetries of the 1D optical lattice and the initial states |p = 0⟩ are even. Hence, we can easily prepare and manipulate even parity Bloch states, such as S-, D-, and G-bands with zero quasi-momentum. However, it is challenging to prepare states with different parity or change the symmetry. In order to expand the application scope of the shortcut, we propose two methods.
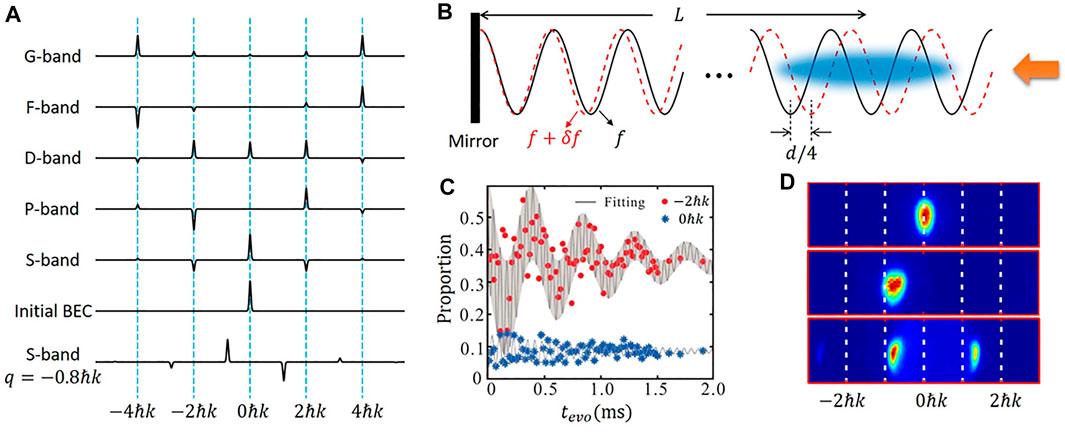
FIGURE 4. (A) From the bottom to the top, the solid lines represent the momentum distributions of different states (S-band with q = −0.8ℏk, initial BEC with p = 0, S-, P-, D-, F-, and G-band with zero quasi-momentum). (B) Two 1D lattices with a d/4 position shift. (C) Population oscillations around momenta − 2ℏk (red points) and 0ℏk (blue stars). The solid lines are the fitting curves. (D) The experimental images: from top to bottom, the images are for the initial BEC with p = 0, the BECs with p0 = −0.8ℏk after acceleration, and the final states Ψ1,−0.8ℏk.
The first method is to use two misplacement lattices [10, 14, 18]. In experiments, we realize this configuration through a reflective optical path and two laser beams with frequency difference δf, as shown in Figure 4B. When the distance L between BECs and mirror and laser frequency f are fixed, we can realize the misplacement of d/4 of the two sets of standing wave optical lattices by adjusting the frequency difference δf. Because δf ≪ f, the lattice constants of the two lattices can be regarded as the same. As an example, we transfer atoms from |p = 0⟩ to P-band with zero quasi-momentum Ψ2,0. We apply two sets of shortcut sequences in turn. The first one is of the lattice with frequency f + δf, and the second is of f. When the first sequence is switched to the second, each momentum state component cℓ|ℓ ⋅ 2ℏk⟩ will be attached with a phase and becomes
The second method is to change the symmetry of the initial state. For example, we demonstrate how to transfer atoms from initial BEC to non-zero quasi-momentum Bloch state in S-band. As shown in Figure 4D, the atoms with p = 0 is accelerated to obtain a momentum p0 = −0.8ℏk. Immediately afterward, the designed shortcut sequence is used to transfer atoms into the S-band at − 0.8ℏk quasi-momentum. The bottom figure of 4D is the momentum distribution of the final state in the experiment [14].
Hence, our shortcut method can be applied to manipulate arbitrary Bloch states in any Bloch band within a very short time and with high fidelity. Moreover, This shortcut can be applied to optical lattices with different configurations.
2.2.3 Atomic momentum patterns with narrower intervals
The previous method is mainly for the Bloch state with a certain single quasi-momentum, and the intervals of the momentum peaks are 2ℏk (for 1D optical lattice). The manipulation of the entire Bloch band and the preparation of narrow momentum peak distribution will also appear in many applications, such as the atom interferometer [29–31]. However, the manipulation of this superposition state with different quasimomenta is seldom studied [19]. In this section, we expand the shortcut to manipulating the superposed Bloch states with different quasi-momenta. Figure 5A shows the time sequence for the manipulating process of the superposed states. The first challenge is to prepare the superposition states |ψ(0)⟩ with different quasi-momentum that spread the whole S-band, as shown in Figure 5B. In the experiment, we first prepare a superposed state
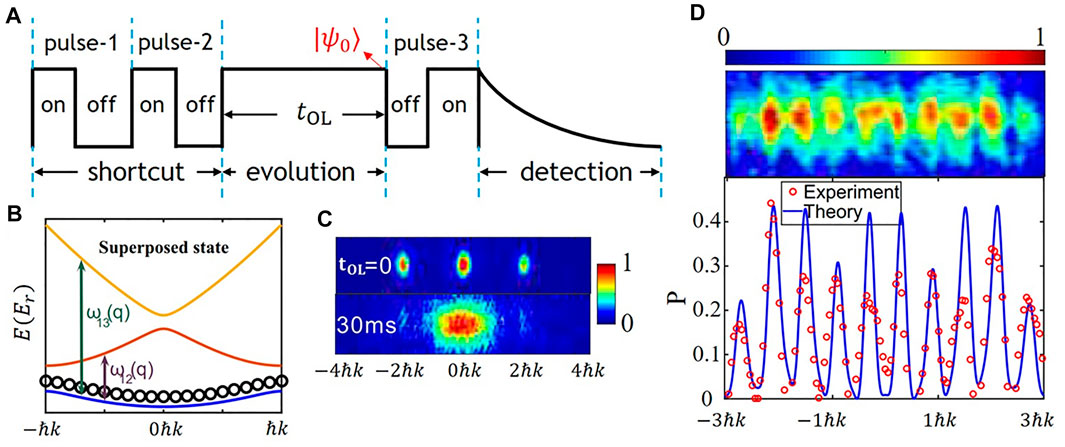
FIGURE 5. (A) Time sequence: after the first two pulses and the 30 ms holding time in the optical lattice, the state becomes the superposition of the Bloch states in S-band with quasi-momentum taking the values throughout the first Brillouin zone, denoted as |ψ(0)⟩. (B) The superposition of Bloch states of S-band spreading the whole S-band. (C) The comparison of the experimental results between tOL = 0 ms and tOL = 30 ms. These results are obtained after the sequence in (A) but without pulse-3. (D) Patterns with ten main peaks for the experimental measurements (the red circles) and the theoretical curves (the solid blue line).
The next challenge is how to design the pulse-3 in Figure 5A for atomic momentum patterns with narrower intervals. First, we analyze the action of the pulse on |ψ(0)⟩. The initial state can be expressed as
After the pulse-3 (with interal
where Ci is the corrresponding amplitudes from the numerical calculations, Wℓ,ℓ′ = ℏ2 [(2ℓk + q)2 − (2ℓ′k + q)2]/2m and ωn,n′ = En,q − En′,q (the band gap between n and n′ band at quasi-momentum q) corresponds to the energy difference between different momentum states and Bloch states, respectively. By designing the
2.3 Band swapping tecnique for loading atoms into high bands
The band swapping technique is another method for loading atoms into high Bloch bands, which can be used to study the characteristics of Bloch bands and orbits. This technique is first proposed in [9] to load atoms into the P-band of a checkerboard square lattice and is also applicable to other configurations of optical lattices. The key to realizing this technology is constructing a controllable composite optical lattice, including deep and shallow wells. Compared with the shortcut method, the band swapping technique is more suitable for the study of ground state or metastable state.
Here, we take a hexagonal lattice as an example to show the process of band swapping [12]. We choose triangle lattice because it is more complex than square lattice, and it is impossible to separate variables in two directions directly. Three intersecting far-red-detuned laser beams form the hexagonal lattice in the x − y plane with an enclosing angle of 120o. Each beam is formed by combining two linearly polarized lights with polarization directions oriented in the x − y plane (denoted as ϵ light) and along the z axis (denoted as ϵ′ light), respectively. The ϵ light form a honeycomb lattice as shown in Figure 6A. The ϵ′ light form a triangular lattice as shown in Figure 6B. The superposition of the two groups of optical lattices is the configuration shown in Figure 6C, which consists of two wells with different depths (denoted as
where
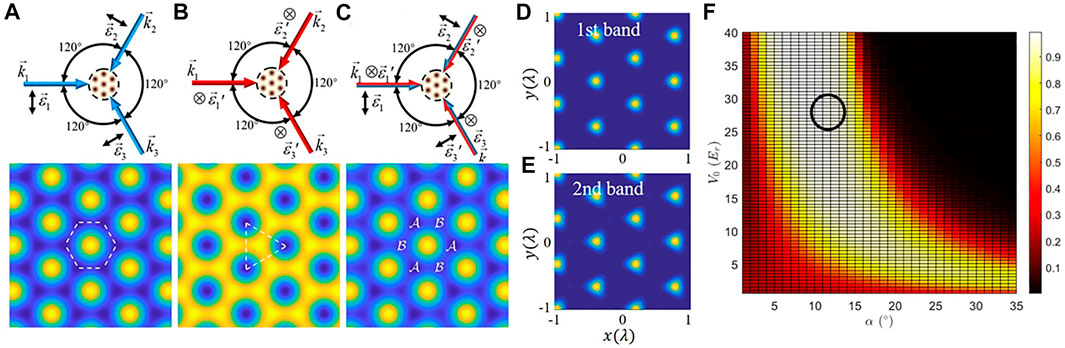
FIGURE 6. The arrangement of the laser beams forms the honeycomb (A) and triangular (B) lattice. The two groups of sublattices form a composite hexagonal lattice (C), which consists
2.4 Manipulation of atoms in optical lattice by amplitude modulation
The modulation with more than one frequency component to optical lattices provides a flexible way to control quantum states coherently [25]. In this section, we demonstrate bi-frequency modulations, which can be used to couple the S- and G-band of 1D optical lattice and realize a large-momentum-transfer beam splitter.
For atoms in an amplitude modulated lattice system along the x axis, as schematically shown in Figure 7A, the time-dependent Hamiltonian can be written as
The second term on the right hand represents optical lattice potential without modulation. The last term is the amplitude modulation with modulation amplitude Vi, the frequency ωi, and the phase ϕi of each frequency component [25].
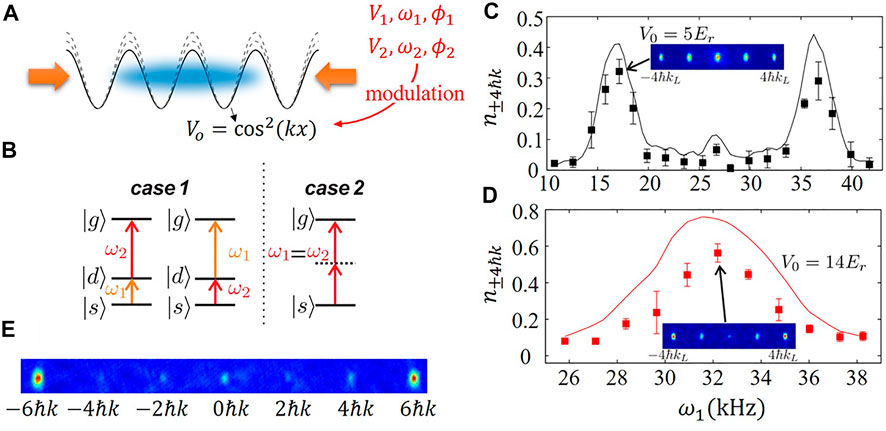
FIGURE 7. (A) Schematic diagram of the polychromatic amplitude modulation lattice. (B) Two special cases in detecting the transfer population spectrum. In case 1, absorption of photons with ω1 or ω2 is resonant with D-band. In case 2, two frequencies are equal. Spectrum for the population on ± 4ℏk states with increasing of modulation frequency ω1 for (C) V0 = 5Er with V1 = 1.4Er, V2 = 1.6Er, modulation time t = 300μs, and for (D) V0 = 14Er with V1 = V2 = 2.5Er, and t = 150μs. (E) A large-momentum-transfer beam splitter with a separation of 12ℏk.
According to the Floquet’s theorem, a bi-frequency modulation induced two-photon process between S- and D-band is described by an effective Hamiltonian HSG as
where Ωnn′ = ⟨Ψn,0| cos2 (kx)|Ψn′,0⟩ with Ψn,0 the Bloch states on n band at zero quasi-momentum. We include six nearly degenerate states considering four main process in the excitation, which are |ES⟩, |ED − ℏω1⟩, |ED − ℏω2⟩, |EG − ℏ(ω1 + ω2)⟩, |EG − 2ℏω1⟩, and |EG − 2ℏω2⟩. Using this basis a general state
In the experiment, we keep the frequences ω1 and ω2 satisfying ω1 + ω2 = ωSG. According to Eq. 10, there are two cases which would benefit the excitation process (shown in Figure 7B).
Case 1: Resonant two-photon process. When ω1 = ωSD or ω2 = ωSD, atoms are transferred from Ψ1,0 to Ψ5,0 with the assistance of D band as an intermediate band.
Case 2: Equal frequency two-photon process. When ω1 = ω2 = ωSG/2, two modulations with the same frequency can be added together, and the coupling strength of the process is doubled.
In the experiments, we sweep the frequency ω1 for different lattice depth V = 5Er and 14Er, and measure the population on momentum states ± 4ℏk that relect the transfer rate to G-band. For V = 5Er, in Figure 7C, two peaks appear at ω1 = ωSD and ω2 = ωSD follows Case 1. And the central peak at frequency ω1 = ω2 = ωSG/2 following Case 2 is much lower than Case 1. For V = 14Er, only one peak is measured in Figure 7D, which means Case 1 and Case 2 are fulfilled simultaneously. Under this condition, the coupling is greatly enhanced. This bi-frequency modulation can also be applied to realize a large-momentum-transfer beam splitter, such as a distribution at ± 6ℏk. We choose the frequency ω1 = ωSD = ωDG and ω2 = ωGI (with I the seventh Bloch band). The experimental result is shown in Figure 7E [25].
This polychromatic amplitude modulation can be further improved to achieve more complex manipulation. We can control each period of the modulation waveform separately. Each period can be regarded as a pulse, which is shown in Figure 8A. The modulation amplitude Ai, phase ϕi, and frequency ωi are optimized to achieve more accurate Bloch states manipulation, such as holonomic quantum control [8], which will be discussed in detail next section.
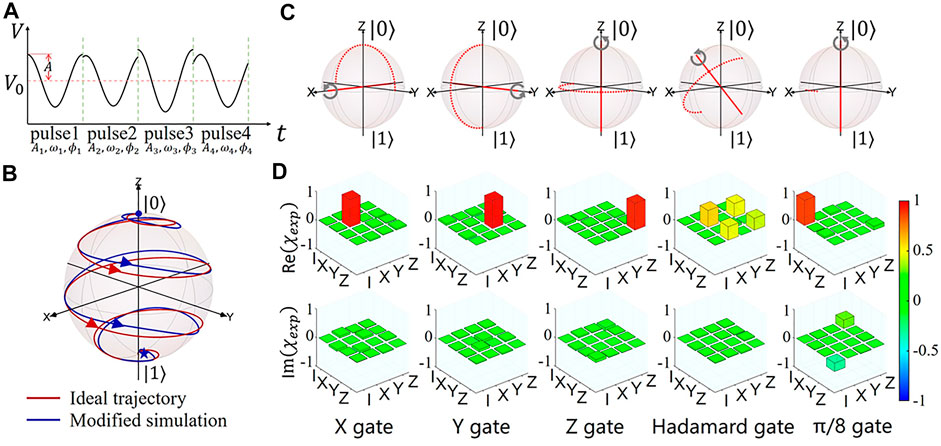
FIGURE 8. (A) The pulse sequence of the holonomic gate. (B) Simulated time evolution of the |0⟩ on the Bloch sphere under the holonomic X gate. (C) The schematic illustration of the quantum process. (D) Process matrices of the implemented holonomic X, Y, Z, Hadamard, and π/8 gates by quantum process tomography measurements.
In this section, we list three methods for manipulating ultracold atoms of high orbitals in optical lattices. The shortcut method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. This method can be used to construct atomic orbital interferometers and qubits and to study the dynamic properties of high orbital atoms in optical lattices. The band swapping technique considers the interaction between atoms and the additional potential trap (such as harmonic trap) besides the optical lattice, which is more suitable for studying the ground and metastable states of the system. The amplitude modulation focuses on coupling different Bloch bands and can be used to realize quantum gates and the large-momentum-transfer beam splitter.
3 Application of manipulating high orbital atoms in optical lattices
3.1 Atom-orbital qubit under nonadiabatic holonomic quantum control
In section 2.4, we mentioned that the amplitude modulation pulses could realize the holonomic quantum control. This section demonstrates an atom-orbital qubit by manipulating the s and d orbitals of BECs in the 1D optical lattice. Moreover, we achieve noise-resilient single-qubit gates by performing holonomic quantum control, allowing geometrical protection. The atom-orbital qubit and quantum control are based on the shortcut and amplitude modulation methods [8].
As shown in Figure 1A, the band gap between S and D band (5.23Er) is much smaller than that between D and G band (11.50Er) for optical lattice depth V = 5Er. With leakage to other bands neglected, the system corresponds to a two-level system, defining our atom-orbital qubit, Ψ3,0 and Ψ1,0 being orbital states identified as the qubit basis states |0⟩ and |1⟩. The 1D optical lattice potential is Vp(x) = V0 cos2 (kx), which is formed by 1,064 nm laser beams. We use shortcut method to initialize the qubit to an arbitrary state, |ψ⟩ = cos θ|0⟩ + sin θeiφ|1⟩. By TOFQST, we extract the fidelities of initial states
The modulation pulses on potential takes form
where amplitude A, phase ϕ and frequency ω programmable in our experiment. After a rotating wave approximation, we have a qubit control Hamiltonian H(t)
with Δ the gap between the S and D bands at zero quasi-momentum, and the induced coupling by the lattice modulation
We implement nonadiabatic holonomic orbital control base on dynamical invariant of the Hamiltonian in Equation (12). To exploit the geometrical protection, the dynamical phase has to be canceled, which corresponds to
Then, we calculate a control sequence of lattice modulation frequency, amplitude, and phase, denoted by Θ ≡ (ωi, Ai, ϕi). After orbital leakage elimination, the gate fidelity is improved to above 98% in the multiorbital numerical simulation. The simulated time evolution of the |0⟩ on the Bloch sphere under the holonomic X gate is shown in Figure 8B. Besides, we also design the holonomic X, Y, Z, Hadamard, and π/8 gates. We further perform quantum process tomography to characterize the holonomic quantum gates, which is shown in Figure 8D. The measured quantum process fidelities are 98.47(9)%, 98.35(11)%, 97.81(13)%, 98.53(8)%, 98.63(15)%, and 98.63 (15)%, for the X, Y, Z, Hadamard, and π/8 gates, respectively [8]. There are four main factors limiting fidelities: a) orbital leakage: although we have greatly eliminated the band leakage, there are still a small number of atoms in high bands that affect the current fidelities. b) De-phasing mechanism: the quasi-momentum broadening of BEC and the non-uniformity of light intensity of optical lattice will lead to the de-phasing effect, which causes the decrease of fidelity. c) Atom interaction: As discussed in section 5.1, atoms in the D band will be scattered to the ground band due to collision, which will affect the fidelities. d) Error caused by measurement: It is mainly caused by the vibration of the imaging system during the absorption imaging process. For a) and b), we can overcome them through super lattice or more complex lattice. We can construct a more perfect two-level so that the G-band is far away from the D-band. Further, by constructing flat bands, the dephasing effect brought by momentum broadening and non-uniformity of the light can be suppressed, so as to greatly improve the fidelity. If we want to further improve the fidelity, we need to consider the factors of c) and d). We can use Feshbach resonance technology to reduce the atomic interaction, and reduce the imaging error through the improvement of the mechanical structure of the imaging system.
3.2 Ramsey interferometry with trapped motional quantum states of the optical lattice
Ramsey interferometry (RI) using internal electronic or nuclear states find wide applications in science and engineering [32]. In this section, we review a new RI with the S- and D-bands in an optical lattice [13], similar to Figure 1B (in this section, the laser wavelength of the optical lattice is 852 nm, and the lattice depth is 10Er). A key challenge for constructing this RI is to realize π-pulse and π/2-pulse analogous to those in conventional RIs. In section 3.1, we have achieved the arbitrary holonomic quantum control, which ensures the noise-resilient but increases the control time. However, we want to study the quantum many-body lattice dynamics by this RI, which requires the time duration of the π-pulse and π/2-pulse to be as short as possible. Hence, we use the shortcut method to design these pulse sequences.
The full time sequence for RI with two shortcut π/2-pulses
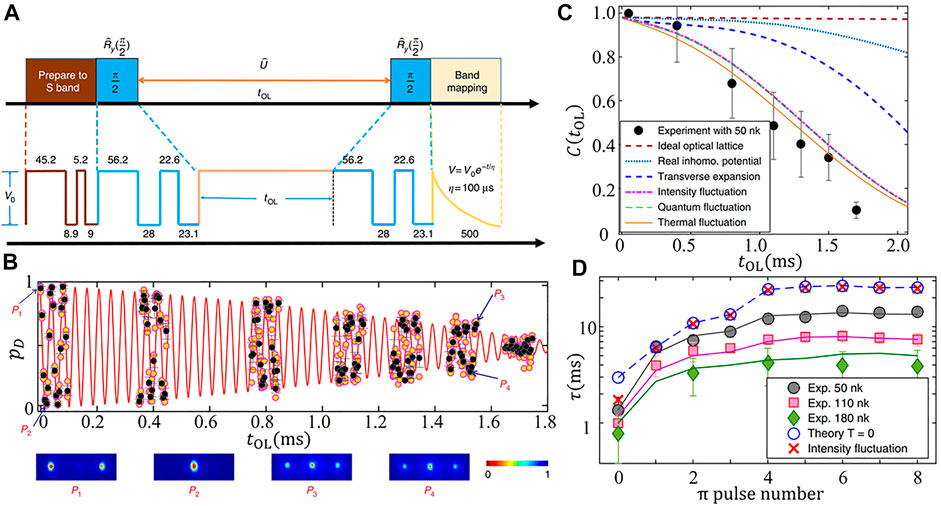
FIGURE 9. (A) Time sequences for the Ramsey interferometry. The atoms are first loaded into the S-band, followed by the RI sequence π/2-pulse, holding time tOL, and the second π/2-pulse. Finally, band mapping is used to detect the number of atoms in the different bands. The used sequences designed by the shortcut method are shown in the figures (unit: μs). (B) The oscillation of the population of atoms in the D-band pD. The images below show typical time of flight pictures after band mapping. (C) The experimental contrast (black points) and the theoretical calculation for V0 = 10Er. In theory, we begin with an ideal optical lattice and gradually add the effect of lattice inhomogeneity, transverse expansion of atom cloud, intensity fluctuation of laser amplitude, quantum fluctuation, and thermal fluctuation. (D) Coherence time τ vs the number of applied π-pulse n with different temperatures.
In order to improve the performance of the RI, we now investigate the mechanisms that lead to RI signal attenuation. The decay of the contrast, shown by the black points in Figure 9C, mainly comes from de-phasing and de-coherence mechanisms. These mechanisms are caused by the imperfect design of the π/2 pulse, non-uniform potential distribution of the Gaussian beam in the radial direction, atom-atom interaction leading to transverse expansion, intensity fluctuation of the lattice, and thermal fluctuations of the system. The theoretical calculation with different mechanisms is shown in Figure 9C, which is consistent with the experimental results. The expansion leads to a significant reduction in contrast (blue dashed line in Figure 9C). In our experiment, the influence of the quantum fluctuation is not significant.
To further improve the contrast of the RI, we develop a matter-wave band echo technique. A π-pulse is designed, which swaps the atom population in the S- and D-band. The π-pulse is inserted into the center of the evolution process. After implementing one π-pulse, the intensity fluctuation can be well suppressed. After applying six echo pulses, the effects of non-uniform lattice potential and transverse expansion are eliminated. The coherence times τ (defined as the time when the contrast C (tOL) drops to 1/e) with different echo pulses are shown in Figure 9D. The coherent time is increased from 1.3 to 14.5 ms by the echo pulses [13].
4 Exotic quantum states of p-orbital ultracold atoms in optical lattices
4.1 Observation of a dynamical sliding phase superfluid with P-Band bosons
The Sliding phase [33], which is introduced to characterize intricate phase transitions in a wide range of the many-body system, appears under extreme conditions for thermal equilibrium systems or quantum ground states, causing a grievous challenge in experimental implementation [34–40]. Here, we review the observation of a sliding phase superfluid in a dynamical system of ultracold atoms in the P-band [10]. We load the atoms into P-band with zero quasi-momentum by the shortcut as shown in Figure 4. The quantum system is driven to a far-out-of-equilibrium but a phase-coherent state. We hold the condensate in the P-band for a certain time tevo. Then the TOF images are taken in two probe directions with probe light along the z-axis (denoted as probe-1) and along the x-axis (denoted as probe-2). The distribution in different probe directions is analyzed via a bimodal fitting, as shown in Figure 10A. We extract the coherent fraction from the bimodal fitting so that the phase coherence of the dynamical many-body state can be inferred [10].
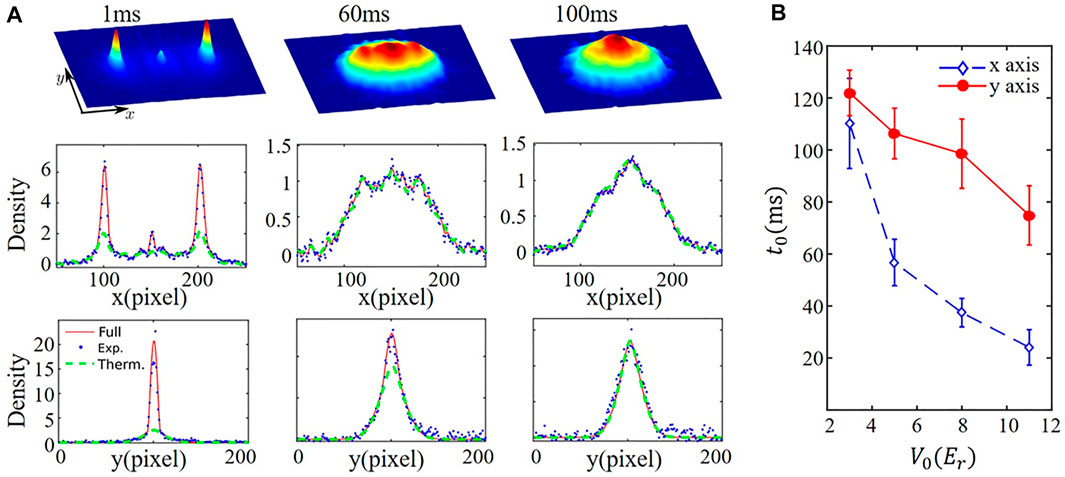
FIGURE 10. (A) Momentum distributions measured at three different holding times tevo = 1, 60, 100 ms, along different directions (with V0 = 5Er). The corresponding distribution along the x-direction is given in the second row with blue dots. The solid red line gives a full fitting line, while the green dashed line gives the distribution of the thermal component. The third row shows the atomic distribution in the y-direction for images measured by probe 2. (B) The time t0 for the atoms to lose coherence in lattice and pancake directions with different optical-lattice depths. The blue diamonds are for the x-direction (lattice) by probe one and the dotted points are for the y-direction (pancake). The optical lattice is the 1D lattice.
From the time evolution, we identify three distinct dynamical regions. At an early time, the system has superfluid phase in all directions, as shown in Figure 10A at tevo = 1 ms. In the second state, the phase coherence of the quantum gas survives partially. The bimodal fitting in Figure 10A at tevo = 60 ms shows that there is a finite condensed component in the pancake directions, but no such component in the lattice direction, which is called the sliding phase. At the last state, the quantum gas has rethermalized with a complete loss of phase coherence. The bimodal fitting shows that all atoms are thermal in the complete absence of any condensed component. We define the lifetime t0 for the atoms to lose coherence in lattice and pancake directions, which is shown in Figure 10B for different lattice depth. We find that with the total atom number fixed in the experiment, a critical lattice depth appears beyond which the sliding phase superfluid starts to emerge. Moreover, we also verify that P-band is necessary to realize the dynamical sliding phase in our experiment, and the sliding phase is absent for cold atoms in the S-band at equilibrium [10].
4.2 Observation of a potts-nematic superfluidity in a hexagonal sp2 optical lattice
In this section, we review the observation of a Potts-nematic quantum state in a system of cold atoms loaded into the second band of a hexagonal optical lattice [12]. We use the band swapping method to load the atoms into the second band, as shown in section 2.3. After the atoms are transferred into the band maximum of the second band, the phase coherence in the state will immediately disappear. After a few milliseconds, the phase coherence reemerges, and the quantum state spontaneously chooses one orientation, giving rise to a three-state Potts nematicity. We divide the experimental TOF images into three classes and take the average within each class [12]. The post-classification averaged results are shown in Figure 11B.
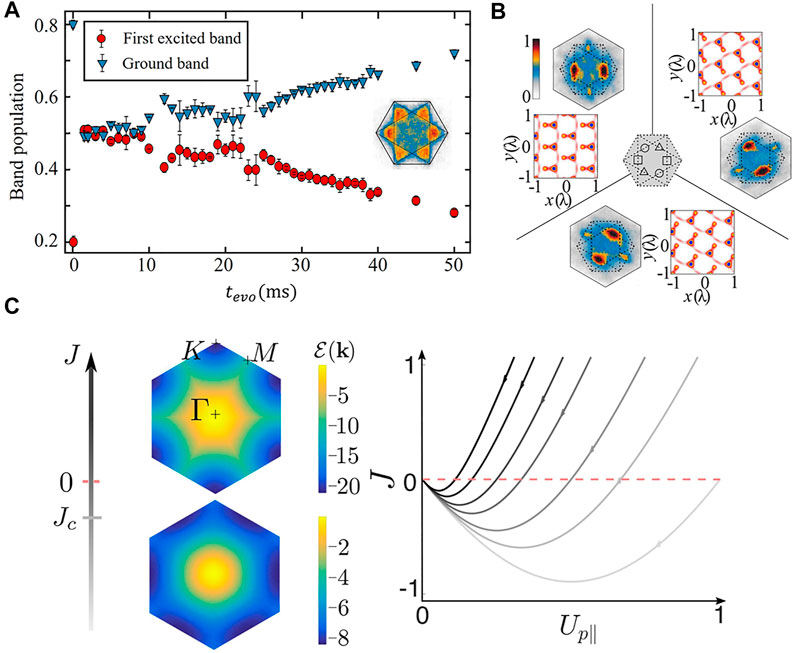
FIGURE 11. (A) The measured time evolution of the atomic population in the ground and the second bands of the hexagonal optical lattice. (B) The averaged momentum distribution for three symmetries. (C) Theoretical quantum phase transitions varying the orbital Josephson coupling. The energy ɛ(k) for a plane-wave condensate at a lattice momentum k. The energy ɛ(k) has minima at K (M) points for J > Jc (J < Jc). The right figure is the sketch of the renormalization of the p-orbital couplings to low energy.
To gain insight into the mechanism supporting the Potts-nematic order in the sp2-orbital hybridized band, we provide a mean-field theory analysis assuming a plane-wave condensate. The interaction can be expressed as
where
5 Dynamical evolution for atoms in high bands of optical lattices
5.1 The scattering channels induced by two-body collision of D-band atoms in optical lattices
The mechanism of atomic collisions in excited bands plays an essential role in the atomic dynamics in high bands of optical lattices and the simulation of condensed matter physics [21]. Atoms distributed in an excited band of an optical lattice can collide and decay to other bands through different scattering channels [17, 21]. The decay rate and scattering channels of optical lattices with different configurations are different. Here, we first compare the lifetime of atoms in the D-band for one-dimensional lattice and triangular lattice. In experiments, we utilize the shortcut method to load BECs to the D (D1) band of the 1D optical lattice (triangular optical lattice). Then the BECs in the optical lattice evolve for a certain time tevo. Finally, we apply band mapping to measure the proportion pD (tOL) of atoms in the D-band, which is shown in Figure 12A for 1D lattice and 12B for triangular lattice. We define the lifetime τ of atoms in the D-band as the proportion pD reduces to 1/e. The lifetime for the triangular lattice is 5.0 ms, which is much longer than that of the 1D lattice, 2.1 ms. The difference in collisional scattering cross-section leads to the difference of a lifetime. Next, we will carefully analyze the scattering cross-section and the scattering channels [21].
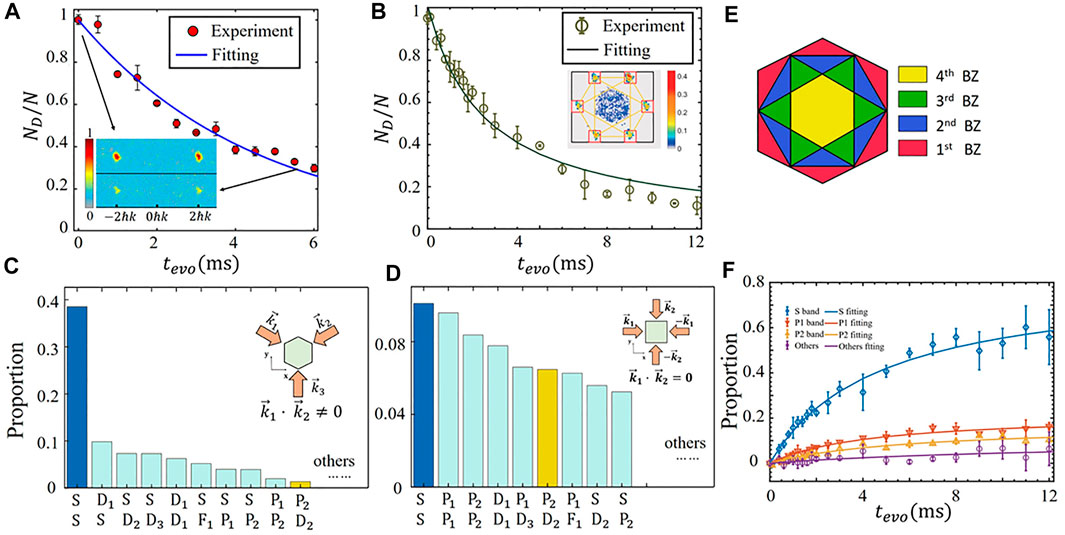
FIGURE 12. (A) The proportion of D-band over the evolution time in 1D lattice. (B) The proportion of the first D-band (D1-band) in the triangular lattice. The proportions of several main scattering channels are shown in (C) (triangular lattice) and (D) (square lattice). The inserts show the diagram of a square optical lattice and triangular optical lattice. (E) Schematic diagram of the first four Brillouin zones of a triangular optical lattice. Yellow, green, blue, and red areas represent 1st, 2nd, 3rd, 4th BZ, respectively. (F) The atomic proportion in S (P1, P2 band, and others), of which the solid lines with the same color fit lines.
We take triangular and square lattices as examples to study the difference in the scattering process. We use the scattering theory to calculate the cross-section of each scattering channel in those two types of lattices. Two-body collisional scattering cross section for two atoms initially at the Γ point ((qx, qy)=(0,0)) of D1 band jumping to band n1 and n2 can be written as:
where va is the atomic velocity and as is atomic s-wave scattering length. And the overlapping integral of eigenstates
where Ψn,q(r) is Bloch function of the eigenstate at quasi-momentum q in the n band. In the calculation, we assume the periodic boundary conditions, and consider that
5.2 Quantum dynamical oscillations of ultracold atoms in the F and D bands
Here we review the observation of quantum dynamical oscillations of ultracold atoms in the F and D bands of the 1D optical lattice [20]. We can control the Bragg reflections at the Brillouin-zone edge up to the third order and observe three different types of quantum oscillations [20].
The BECs is initially loaded in the G band, where the atoms mostly populate at momenta 4ℏk, as shown in Figure 3B(2). Then the atoms fall into the F-band due to the small gap between G- and F-bands. The following trace of the atoms is shown in the extended band structures as shown in Figure 13D. Once the BECs are in the F-band, it loses momentum while gaining potential energy from the harmonic confinement (A1 → A2). Once arriving A2, the atoms face different dynamics depending on the lattice depth. When the depth is small
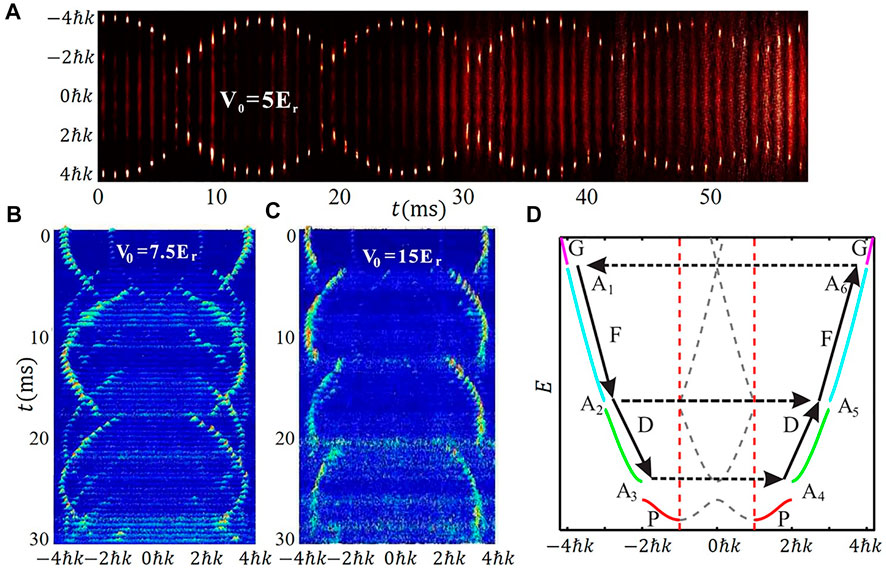
FIGURE 13. Quantum oscillations of the BECs in higher bands of the 1D optical lattice. Experimental results in momentum space with lattice depth (A) 5Er, (B) 7.5Er, and (C) 15Er. (D) Schematic of extended Bloch bands of the 1D optical lattice.
5.3 Nonlinear dynamical evolution for P-band ultracold atoms in 1D optical lattice
The dynamical evolution for atoms in P-band is different from that of F- and D-bands [18]. After loading the BECs into the P-band with zero quasi-momentum for the lattice depth 5Er, we hold the BECs for time tevo and then measure the momentum distribution. The momentum distributions at different holding time tevo are shown in Figure 14A. We use the normalized populations Wℓ(tevo) of momentum states |ℓ ⋅ 2ℏk + q⟩ to better quantify the dynamical evolution of atoms. At the beginning of the evolution process tevo < 1.5 ms, we find Wℓ(tevo) oscillating rapidly, as shown in Figure 4C and Figure 14A(1) [2]. Then, after a short transition time, a different type of oscillation begins to emerge around tevo = 2 ms. The period of this oscillation is 14.9 ms, which is shown in Figures 14A,B [3-5].
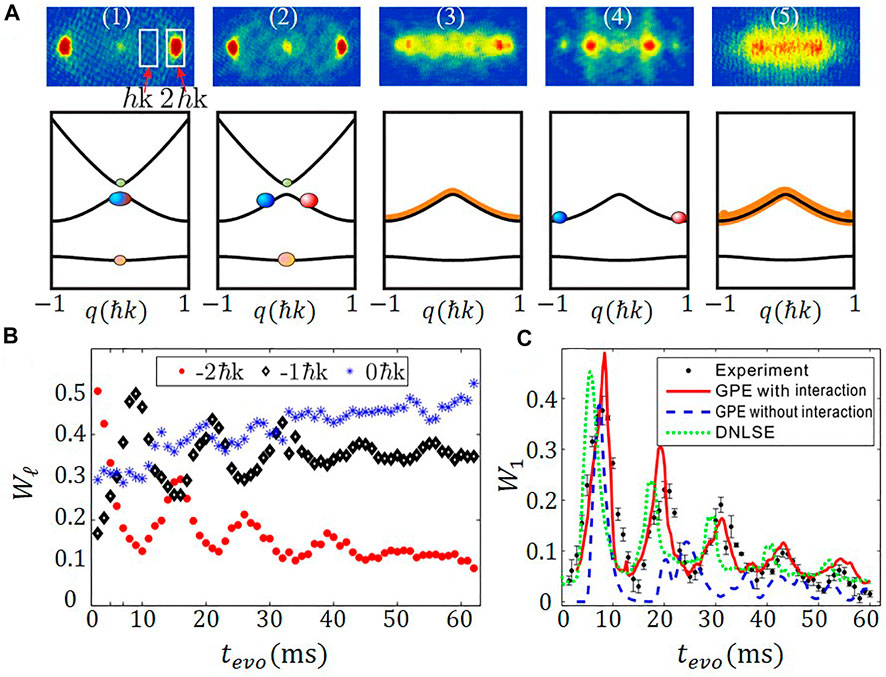
FIGURE 14. (A) First row: the measured momentum distributions of the BEC in the P-band of the 1D lattice at different holding times (0 ms, 2 ms, 5 ms, 7 ms, and 30 ms), and the white rectangles are the region for us to calculate the proportion of different momentum states; the second row: schematic illustration of the corresponding population distributions in the Bloch band. (B) Population oscillations around momenta 0ℏk (blue stars), − ℏk (black diamonds), and − 2ℏk (red dots) with t > 2 ms. The oscillation period is about 14.9 ms with V = 5Er. (C) Population for ℏk vs. time tevo. The experimental results and theoretical simulations with and without the interaction correspond to the black dots with an error bar, red solid curves, and blue dashed curves, respectively.
The short-period oscillations shown in Figure 4C are beating signals due to the coherent superposition of different bands. From the numerical analysis, the superposed state is close to
6 Discussion and conclusion
In this review, we concentrate on the methods to prepare and control the BEC in optical lattices linked to one-body physics. The many-body interactions also play an important role in the system of ultracold atoms in the optical lattices. For the control methods mentioned in this review, such as the shortcut method, amplitude modulation, and nonadiabatic holonomic control, the operation time (
In summary, we review our practical methods for manipulating the high orbitals of ultracold atoms in optical lattices. The shortcut method is characterized by short time and high fidelity, which can directly transfer ultracold atoms from the ground state in the harmonic trap to any Bloch state, and accurately manipulate atoms of different orbitals in optical lattices. This method can be used to construct atomic orbital interferometers and qubits and to study the dynamic properties of high orbital atoms in optical lattices. The band swapping technique considers the interaction between atoms and the additional potential trap (such as harmonic trap) besides the optical lattice, which is more suitable for studying the ground and metastable states of the system. The amplitude modulation focuses on coupling different Bloch bands and can be used to realize quantum gates and the large-momentum-transfer beam splitter. Based on these methods, the atom-orbital qubit under nonadiabatic holonomic quantum control and Ramsey interferometry with trapped motional quantum states of the optical lattice can be constructed. Many exotic quantum states of the high orbital atoms have been observed. Then we study the quantum dynamical evolution of atoms in high bands. The effective manipulation of the high orbitals provides strong support for applying the ultracold atoms in the optical lattice in quantum simulation, quantum computing, and quantum precision measurement.
Author contributions
SJ: Drafting the manuscript XC: Revising the manuscript XZ: Revising the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grants No. 12104020, No. 61727819, and No. 11334001), the National Basic Research Program of China (Grants No. 2021YFA0718300 and No. 2021YFA1400901), the Project funded by China Postdoctoral Science Foundation (Grant No. 2020TQ0017), the Science and Technology Major Project of Shanxi (No. 202101030201022), and the Space Application System of China Manned Space Program.
Acknowledgments
Thank Yiqiu Wang for establishing this experimental group of ultra-cold atoms in China. In completing the above work, thank Xiaopeng Li, Jörg Schmiedmayer, Biao Wu, Hongwei Xiong, Guangjiong Dong, Peng Zhang, and Lan Yin.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Greiner M, Mandel O, Esslinger T, Hänsch TW, Bloch I. Quantum phase transition from a superfluid to a mott insulator in a gas of ultracold atoms. Nature (2002) 415:39–44. doi:10.1038/415039a
2. Bloch I, Dalibard J, Nascimbène S. Quantum simulations with ultracold quantum gases. Nat Phys (2012) 8:267–76. doi:10.1038/nphys2259
3. Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev Mod Phys (2008) 80:885–964. doi:10.1103/RevModPhys.80.885
4. Goldman N, Budich JC, Zoller P. Topological quantum matter with ultracold gases in optical lattices. Nat Phys (2016) 12:639–45. doi:10.1038/nphys3803
5. Georgescu IM, Ashhab S, Nori F. Quantum simulation. Rev Mod Phys (2014) 86:153–85. doi:10.1103/RevModPhys.86.153
6. Gross C, Bloch I. Quantum simulations with ultracold atoms in optical lattices. Science (2017) 357:995–1001. doi:10.1126/science.aal3837
7. Moan ER, Horne RA, Arpornthip T, Luo Z, Fallon AJ, Berl SJ, et al. Quantum rotation sensing with dual sagnac interferometers in an atom-optical waveguide. Phys Rev Lett (2020) 124:120403. doi:10.1103/PhysRevLett.124.120403
8. Shui H, Jin S, Li Z, Wei F, Chen X, Li X, et al. Atom-orbital qubit under nonadiabatic holonomic quantum control. Phys Rev A (Coll Park) (2021) 104:L060601. doi:10.1103/PhysRevA.104.L060601
9. Wirth G, Ölschläger M, Hemmerich A. Evidence for orbital superfluidity in the p-band of a bipartite optical square lattice. Nat Phys (2011) 7:147–53. doi:10.1038/nphys1857
10. Niu L, Jin S, Chen X, Li X, Zhou X. Observation of a dynamical sliding phase superfluid with p-band bosons. Phys Rev Lett (2018) 121:265301. doi:10.1103/PhysRevLett.121.265301
11. Wang XQ, Luo GQ, Liu JY, Liu WV, Hemmerich A, Xu ZF. Evidence for an atomic chiral superfluid with topological excitations. Nature (2021) 596:227–31. doi:10.1038/s41586-021-03702-0
12. Jin S, Zhang W, Guo X, Chen X, Zhou X, Li X. Evidence of potts-nematic superfluidity in a hexagonal sp2 optical lattice. Phys Rev Lett (2021) 126:035301. doi:10.1103/PhysRevLett.126.035301
13. Hu D, Niu L, Jin S, Chen X, Dong G, Schmiedmayer J, et al. Ramsey interferometry with trapped motional quantum states. Commun Phys (2018) 1:29. doi:10.1038/s42005-018-0030-7
14. Zhou X, Jin S, Schmiedmayer J. Shortcut loading a Bose-Einstein condensate into an optical lattice. New J Phys (2018) 20:055005. doi:10.1088/1367-2630/aac11b
15. Müller T, Fölling S, Widera A, Bloch I. State preparation and dynamics of ultracold atoms in higher lattice orbitals. Phys Rev Lett (2007) 99:200405. doi:10.1103/PhysRevLett.99.200405
16. Liu X, Zhou X, Xiong W, Vogt T, Chen X. Rapid nonadiabatic loading in an optical lattice. Phys Rev A (Coll Park) (2011) 83:063402. doi:10.1103/PhysRevA.83.063402
17. Zhai Y, Yue X, Wu Y, Chen X, Zhang P, Zhou X. Effective preparation and collisional decay of atomic condensates in excited bands of an optical lattice. Phys Rev A (Coll Park) (2013) 87:063638. doi:10.1103/PhysRevA.87.063638
18. Hu D, Niu L, Yang B, Chen X, Wu B, Xiong H, et al. Long-time nonlinear dynamical evolution for p-band ultracold atoms in an optical lattice. Phys Rev A (Coll Park) (2015) 92:043614. doi:10.1103/PhysRevA.92.043614
19. Yang B, Jin S, Dong X, Liu Z, Yin L, Zhou X. Atomic momentum patterns with narrower intervals. Phys Rev A (Coll Park) (2016) 94:043607. doi:10.1103/PhysRevA.94.043607
20. Wang Z, Yang B, Hu D, Chen X, Xiong H, Wu B, et al. Observation of quantum dynamical oscillations of ultracold atoms in the f and d bands of an optical lattice. Phys Rev A (Coll Park) (2016) 94:033624. doi:10.1103/PhysRevA.94.033624
21. Guo X, Yu Z, Peng P, Yin G, Jin S, Chen X, et al. Dominant scattering channel induced by two-body collision of d-band atoms in a triangular optical lattice. Phys Rev A (Coll Park) (2021) 104:033326. doi:10.1103/PhysRevA.104.033326
22. Taie S, Ozawa H, Ichinose T, Nishio T, Nakajima S, Takahashi Y. Coherent driving and freezing of bosonic matter wave in an optical lieb lattice. Sci Adv (2015) 1:e1500854. doi:10.1126/sciadv.1500854
23. Browaeys A, Häffner H, McKenzie C, Rolston SL, Helmerson K, Phillips WD. Transport of atoms in a quantum conveyor belt. Phys Rev A (Coll Park) (2005) 72:053605. doi:10.1103/PhysRevA.72.053605
24. Ölschläger M, Wirth G, Hemmerich A. Unconventional superfluid order in the f band of a bipartite optical square lattice. Phys Rev Lett (2011) 106:015302. doi:10.1103/PhysRevLett.106.015302
25. Niu L, Hu D, Jin S, Dong X, Chen X, Zhou X. Excitation of atoms in an optical lattice driven by polychromatic amplitude modulation. Opt Express (2015) 23:10064–74. doi:10.1364/OE.23.010064
26. Köhl M, Moritz H, Stöferle T, Günter K, Esslinger T. Fermionic atoms in a three dimensional optical lattice: Observing fermi surfaces, dynamics, and interactions. Phys Rev Lett (2005) 94:080403. doi:10.1103/PhysRevLett.94.080403
27. Kastberg A, Phillips WD, Rolston SL, Spreeuw RJC, Jessen PS. Adiabatic cooling of cesium to 700 nk in an optical lattice. Phys Rev Lett (1995) 74:1542–5. doi:10.1103/PhysRevLett.74.1542
28. Greiner M, Bloch I, Mandel O, Hänsch TW, Esslinger T. Exploring phase coherence in a 2d lattice of bose-einstein condensates. Phys Rev Lett (2001) 87:160405. doi:10.1103/PhysRevLett.87.160405
29. de Saint-Vincent MR, Brantut JP, Bordé CJ, Aspect A, Bourdel T, Bouyer P. A quantum trampoline for ultra-cold atoms. Europhys Lett (2010) 89:10002. doi:10.1209/0295-5075/89/10002
30. Impens F, Santos FPD, Bordé CJ. The theory of quantum levitators. New J Phys (2011) 13:065024. doi:10.1088/1367-2630/13/6/065024
31. Cronin AD, Schmiedmayer J, Pritchard DE. Optics and interferometry with atoms and molecules. Rev Mod Phys (2009) 81:1051–129. doi:10.1103/RevModPhys.81.1051
32. Riehle F, Kisters T, Witte A, Helmcke J, Bordé CJ. Optical ramsey spectroscopy in a rotating frame: Sagnac effect in a matter-wave interferometer. Phys Rev Lett (1991) 67:177–80. doi:10.1103/PhysRevLett.67.177
33. O’Hern CS, Lubensky TC, Toner J. Sliding phases in XY models, crystals, and cationic lipid-dna complexes. Phys Rev Lett (1999) 83:2745–8. doi:10.1103/PhysRevLett.83.2745
34. Granato E, Kosterlitz JM. Critical behavior of coupled xy models. Phys Rev B (1986) 33:4767–76. doi:10.1103/PhysRevB.33.4767
35. Choi MY, Doniach S. Phase transitions in uniformly frustrated xy models. Phys Rev B (1985) 31:4516–26. doi:10.1103/PhysRevB.31.4516
36. Feigel’man M, Geshkenbein V, Larkin A. Pinning and creep in layered superconductors. Physica C: Supercond (1990) 167:177–87. doi:10.1016/0921-4534(90)90502-6
37. Klemm RA, Luther A, Beasley MR. Theory of the upper critical field in layered superconductors. Phys Rev B (1975) 12:877–91. doi:10.1103/PhysRevB.12.877
38. Stoebe T, Mach P, Huang CC. Unusual layer-thinning transition observed near the smectic-a-isotropic transition in free-standing liquid-crystal films. Phys Rev Lett (1994) 73:1384–7. doi:10.1103/PhysRevLett.73.1384
39. Cheng M, Ho JT, Hui SW, Pindak R. Electron-diffraction study of free-standing liquid-crystal films. Phys Rev Lett (1987) 59:1112–5. doi:10.1103/PhysRevLett.59.1112
Keywords: high orbitals, optical lattice, ultracold atoms, quantum manipulation, quantum simulation
Citation: Jin S, Chen X and Zhou X (2022) The manipulation of ultracold atoms of high orbitals in optical lattices. Front. Phys. 10:957151. doi: 10.3389/fphy.2022.957151
Received: 30 May 2022; Accepted: 09 August 2022;
Published: 06 September 2022.
Edited by:
Andrea Bertoldi, ParisTech Institut d’Optique Graduate School, FranceReviewed by:
Santiago F. Caballero-Benitez, Instituto de Física, Universidad Nacional Autónoma de México, MexicoXin Zheng, University of Wisconsin-Madison, United States
Copyright © 2022 Jin, Chen and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoji Zhou, eGp6aG91QHBrdS5lZHUuY24=
 Shengjie Jin
Shengjie Jin Xuzong Chen
Xuzong Chen Xiaoji Zhou
Xiaoji Zhou