- 1Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics, Zhejiang University, Hangzhou, China
- 2School of Photoelectric Engineering, Guangdong Polytechnic Normal University, Guangzhou, China
- 3Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, South China Normal University, Guangzhou, China
In the ABCD optical system, the propagation properties and the radiation forces are obtained by studying the cross spectral density of partially coherent self-shifting cosine-Gaussian beams. A self-shifting phenomenon occurs when the beams propagate in the strongly nonlocal nonlinear medium. The shifting parameters could influence the bend characteristics of the propagation trajectory and the beam center, while the power ratio affects the periods of the parabolic trajectory. Furthermore, the radiation forces on a Rayleigh particle in the focusing optical system are studied, and the obtained force distributions depend on the refractive index, the shifting parameters, and the coherence widths. What we report here has potential applications in optical communication and optical tweezing.
1 Introduction
The study of novel partially coherent related structured light fields and their generation, transmission, and regulation is a hot research topic in the international optical field [1, 2]. Partially coherent sources are common in practice. Compared with completely coherent beams, partially coherent beams are less affected by disturbance [3]. The cross spectral density (CSD) is a significant physical quantity in partially coherent beams. It should satisfy the quasi-Hermiticity and the non-negative definiteness [4–6]. The experimentally produced partially coherent beams with various complex degrees of coherence was obtained by Wang et al. [7]. Due to the wide applications in ghost imaging, free space optical communications, particle trapping, and optical scattering [6–10], partially coherent beams have attracted intensive attention.
In nonlocal nonlinear media, various beams of different degrees have been reported in many aspects [11–18]. In the case of nonlocal nonlinearity, the nonlinear responses of the medium under the optical field are related to both the point and optical fields around it. Among which, the phenomenological model under strong nonlocal conditions is Snyder-Mitchell model [11]. The lead glass and nematic liquid crystals are strongly nonlocal nonlinear media (SNNM), which have been demonstrated by some experimental results [19, 20]. Deng et al. reported the stable propagation of different types of soliton and beams in SNNM [11, 12]. Analytical expressions of the corresponding characteristic parameters for example the beam size, the center of gravity, the curvature radius, and linear momentum of Airy beams propagating in SNNM have been studied [21]. Under the framework of fractional nonlinear Schrödinger equation, Zhang et al. analyzed the attractive and repulsion forces between abnormal Airy beams [22], revealing a new situation of the interaction of Airy beams and providing an alternative mechanism to control the generation of breathing solitons. Different types of spatiotemporal self-accelerating wave packets in SNNM are also studied. The numerical simulation findings consistent with their theoretical findings in the strongly nonlocal requirement, and the numerical simulation under different perturbation conditions is discussed [23, 24].
With the development of science and technology, people are no longer satisfied with the observation of microscopic particles, how to manipulate and control the studied particles put forward more profound questions, and are committed to exploring new research methods [25–28]. Piconewton-level forces optical trapping and manipulating particles with micrometer-size, while simultaneously measuring displacement with nanometer-level precision have been extensively studied [27, 29]. Trapping particles by radiation pressures in a succession of groundbreaking papers were reported by Ashkin et al. [25–27]. Without losing of generality, the optical force is decomposed into the scattering force and the gradient force. Gradually, optical trapping techniques continued to improve, then become better established, and finally have emerged as a formidable tool with extensive and far-reaching applications. Nowadays, optical trapping produced by various beams [30–33] such as Laguerre–Gaussian beams, twist beams, and rotating beams are reported by many researchers. Guo et al. investigated the radiation forces on a Rayleigh dielectric particle induced by a highly focused parabolic scaling Bessel beam [34], the findings indicate that this beam can trap high-index particles at the focus and near the focus. Combined with the new light field, the realization of specific manipulation of nonabsorbing nanoparticles is a significant development trend of optical tweezers.
Therefore, we concentrate on the propagation properties and radiation forces of the partially coherent self-shifting cosine-Gaussian beams (PCSCBs) in the ABCD optical system. The power factors, the shifting parameters, and the beam order that influence the propagation characteristics in SNNM are discussed in detail. PCSCBs with a self-shifting effect are beneficial for trapping particles. Therefore, we analyze the radiation forces of such focused beams with different refractive indexes, shifting parameters, and coherence widths.
2 Theoretical model of PCSCBs in ABCD matrix
Here, we choose the PCSCBs [2, 6, 35], which meet the requirements of Fourier transformability, even magnitude, and odd phase. In the initial plane (z = 0), its CSD function can be written as
where σx and σy are the transverse intensity widths along the x and y directions, δx and δy are the coherent length, a and b are the shifting parameters,
where Hz is based on the ABCD matrix,
When r1 = r2 = r, the spectral density and the CSD of the PCSCBs at the output plane are associated by the formula as
After substituting Eqs 1–3 into Eq. 4, we can express the spectral density as
where
In Eq. 5, the exact analytical solution is based on the ABCD matrix. Now we can analyze the propagation properties in SNNM and the radiation forces in the focusing system, respectively.
3 Propagation properties of PCSCBs in SNNM
In the nonlinear media, the propagation of PCSCBs obeys the nonlinear Schrödinger equation [12,32]
where Δn = n1 ∫N (r − r′)|I (r′, z)|2d2r′ is the nonlinear perturbation of the refraction index, n1 is the nonlinear index coefficient, n0 is the linear refractive index of the medium, and N is the symmetrical real spatial response function of the medium [24]. In addition, the Gaussian function
where
After substituting Eq. 8 into Eq. 5, we can obtain the spectral density of PCSCBs. We set the parameters in SNNM as σx = 1mm, σy = 0.3mm, δx = 1mm, δy = 0.3mm, and a = b.
In SNNM, Figure 1 displays the change of the spectral density for PCSCBs with the propagation distance in different shifting parameters and beam orders. The transverse distributions of the PCSCBs change from unimodal distribution to bimodal distribution, and with the increase of propagation distance z, the center peak decreases. We notice that positive shifting parameters in Figures 1B,D bring negative linear shifting along the x direction, while the negative one in Figures 1A,C behaves in the opposite direction. It is found that the larger the beam order is, the faster the spectral density decays.
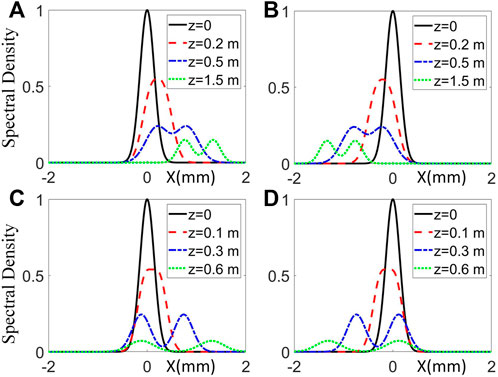
FIGURE 1. The distributions of the spectral density at the selected propagation distances in SNNM with β = 1. (A) n = 1, a = −10mm−1, (B) n = 1, a = 10mm−1, (C) n = 2, a = −10mm−1, and (D) n = 2, a = 10mm−1.
Figure 2 illustrates that the trajectory evolution of the PCSCBs changes periodically in SNNM, and the period is L = 2π. Different shifting parameters change the structure of the trajectory bending trend. The evolution initially broadens because beam diffraction initially overcomes beam-induced refraction. Different beam orders do not affect the trajectory evolution period, but the trajectory profiles behave differently.
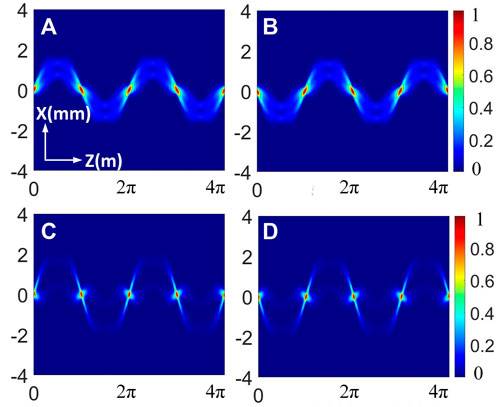
FIGURE 2. Propagation trajectory of the PCSCBs in SNNM with β = 1. (A) n = 1, a = −10 mm−1, (B) n = 1, a = 10 mm−1, (C) n = 2, a = −10 mm−1, and (D) n = 2, a = 10 mm−1.
To further discover the effect of the shifting parameters, we discuss the beam center [29], which can be given as
In Figure 3, the beam center distributions undergo a parabolic trajectory. The beam center changes vividly with different β, the period is L = 2π with β = 1, and L = π with β = 0.5. Though the beam center undergoes a parabolic profile, the shifting parameters change their bends characteristics. As the PCSCBs behave with interesting features, it is meaningful to explore the potential applications in optical trapping. Thus, we discuss the radiation forces generated by the focused PCSCBs next.
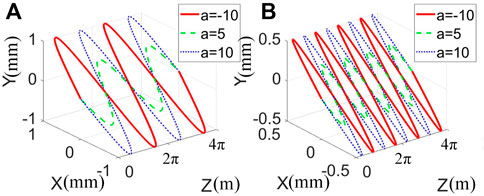
FIGURE 3. The numerical demonstrations of the beam center in SNNM with different shifting parameters. (A) β = 1, (B) β = 0.5.
4 Radiation forces produced by the focused PCSCBs
The research of the optical radiation force has a profound impact on many micro manipulation technologies [25, 28]. In the following, the radiation forces of the PCSCBs acting on a nonabsorbent Rayleigh dielectric particle are studied. When the particle radius r0 is sufficiently small compared with the wavelength (i.e., r0 ≤ λ/20), it can be seen as a point dipole in the light field. Considering the propagation of the PCSCBs through a lens system, where z is the distance from the input plane to the output plane, f is the focal length, and z1 is the axial distance from the focal plane to the output plane, the ABCD matrix for this focusing system [30] is
After substituting Eq. 11 into Eq. 5, we can got the intensity of the PCSCBs in the focusing system. Light forces depend not only on the physical properties of the particle but also on the properties of the light field (e.g., amplitude, phase, polarization, etc.) are closely related. In this paper, the scattering force component is proportional to the distribution of the intensity, while the gradient force distribution is given on the basis of its electric field amplitude. Assuming that the particle is under a steady state, the scattering force and the gradient force [28, 32] can be expressed as
where
Figure 4 gives information on the radiation forces produced by the focused PCSCBs on the high-index particle (η > 1) and the low-index particle (η < 1) on the trapped plane. To achieve stable trapping, the gradient forces need to be larger than scattering forces. Because the scattering forces push the Rayleigh particles along the propagation direction, while the gradient forces pull the Rayleigh particles toward the maximum of the transverse optical field. That is to say, R = Fgrad,z/Fscat ≥ 1, where the ratio R represents the stability standard. One can find stable equilibrium points in Figures 4A,B,D, where the refractive index the Rayleigh particle is smaller than the refractive index of the ambient, the particle can be trapped at the focus point by the partially coherent PCSCBs. Near the focal plane, the scattering force is smaller than the longitudinal gradient force. However, in Figure 4C, the high-index particle can be trapped at the focus (z1 = 0) when x = ±0.3 μm. These two kind of particles can be trapped in the mean time at different x positions of the trapped plane.
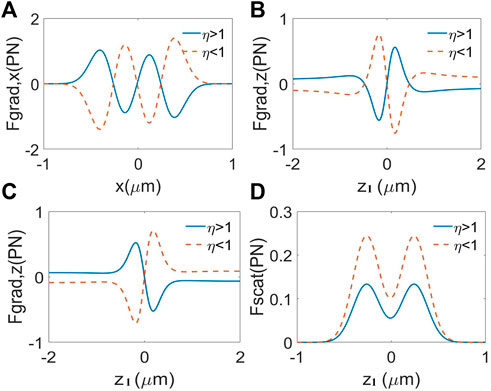
FIGURE 4. Effects of the refraction index on the radiation forces. The high-index particle (η > 1) in solid lines, the low-index particle (η < 1) in dashed lines. (A), (B) and (D) at the focus, x = 0 μm, (C) at the points of x = ±0.3 μm.
Furthermore, we investigate the effect of the shifting parameter a and the coherent length δ on radiation forces acting on the low-index particle η < 1 (see Figure 5), respectively. It is shown in Figures 5A1,A3 that the bigger shifting parameters bring the stronger scattering forces and gradient forces along x direction. However, in Figure 5A2, the gradient forces along the z direction become weaker as a increases. Nevertheless, it needs to be noted that the gradient force along the z direction is still bigger than the scatting force with the same a. In Figures 5B1–B3, one could see that the gradient force and the scattering force grow up with the increase of the coherence width, meaning that the trapping stiffness becomes higher. Moreover, the peak position moves far away from the focus point as δ increases. We also note that the shifting parameter and the coherent length do not have an influence on the position where the PCSCBs capture the particles.
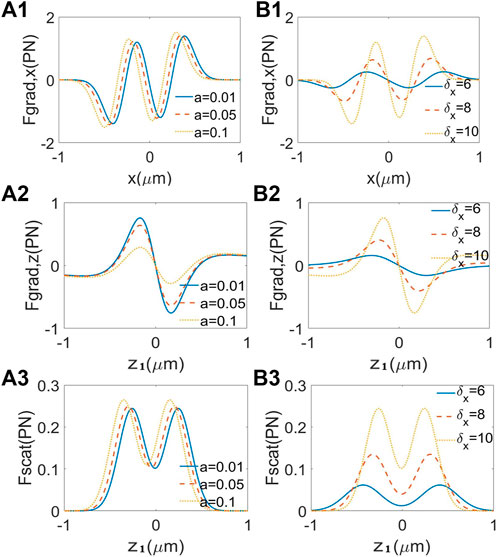
FIGURE 5. Effects of the shifting parameter a and the coherent length δ on the radiation forces for the low-index particle at the focal plane. (A1–A3) σx = 10 mm, σy = 4 mm, δx = 10 mm, δy = 4 mm. (B1–B3) a = 0:01 mm−1.
5 Conclusion
To summarize, we have investigated the CSD of the partially coherent PCSCBs, studied propagation properties through the SNNM, and researched the radiation forces on a nonabsorbing nanoparticle in the focusing optical system. In SNNM, the PCSCBs is transverse self-shifting in different directions as various shifting parameters. While propagating, we observed that the spectral density decreases faster as the beam order increases. The propagation trajectory and the beam center change periodically. The power factors affect the periods, and the shifting parameters influence the bend characteristics.
In the focusing optical system, the optical force on a nonabsorbent Rayleigh dielectric particle has been decomposed into the scattering force and the gradient force. The radiation forces generated by the focused PCSCBs on the high-index particle (η > 1) and the low-index particle (η < 1) are discussed. These two kinds of particles can be trapped in the mean time at different x positions on the trapped plane. Specifically, the low-index particle is trapped at the focus point, while the high-index particle is trapped at the focus at x = ±0.3 μm. It is worthy to note that variation of the shifting parameter and the coherent length will cause the radiation force distributions to change but not affect the position where the PCSCBs capture the particles.
With all of these magnificent properties, the theoretical and numerical outcomes delivered in this paper could help understand the behavior of PCSCBs in the SNNM and the focusing optical system. The results indicate their potential applications in optical communication and optical trapping nonabsorbent nanoparticles.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
XP and DZ proposed the idea. XP wrote the original manuscript. SH and DD gave suggestions in numerical simulation. YH, DD, and DZ supervised the project. All authors contributed to the revision of the manuscript and approved the final version.
Funding
Postdoctoral Research Program of Zhejiang Province (ZJ2021034); National Natural Science Foundation of China (12004081, 12174122, 12174338, 62175042); Talent Introduction Project Foundation of Guangdong Polytechnic Normal University (2021SDKYA142).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wolf E. Introduction to the theory of coherence and polarization of light. Cambridge: Cambridge University Press (2007).
2. Mei Z, Korotkova O, Zhao D, Mao Y. Self-focusing vortex beams. Opt Lett (2021) 46:2384. doi:10.1364/ol.423220
3. Collett E, Wolf E. Partially coherent sources which produce the same far-field intensity distribution as a laser. Opt Commun (1978) 25:293–6. doi:10.1016/0030-4018(78)90131-1
4. Cai Y, Chen Y, Yu J, Liu X, Liu L. Generation of partially coherent beams. Prog Opt (2017) 62:157–223.
5. Cai Y, Chen Y, Wang F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [invited]. J Opt Soc Am A (2014) 31:2083. doi:10.1364/josaa.31.002083
6. Korotkova O, Chen X. Phase structuring of the complex degree of coherence. Opt Lett (2018) 43:4727. doi:10.1364/ol.43.004727
7. Wang F, Liang C, Yuan Y, Cai Y. Generalized multi-Gaussian correlated Schell-model beam: From theory to experiment. Opt Express (2014) 22:23456. doi:10.1364/oe.22.023456
8. Zhao C, Cai Y. Trapping two types of particles using a focused partially coherent elegant Laguerre-Gaussian beam. Opt Lett (2011) 36:2251. doi:10.1364/ol.36.002251
9. Korotkova O, Andrews L, Phillips R. Model for a partially coherent Gaussian beam in atmospheric turbulence with application in Lasercom. Opt Eng (2004) 43:330. doi:10.1117/1.1636185
10. Liu L, Wang H, Liu L, Dong Y, Wang F, Hoenders B, et al. Propagation properties of a twisted Hermite-Gaussian correlated schell-model beam in free Space. Front Phys (2022) 10:847649. doi:10.3389/fphy.2022.847649
11. Snyder A, Mitchell D. Accessible solitons. Science (1997) 276:1538–41. doi:10.1126/science.276.5318.1538
12. Deng D, Guo Q, Hu W. Complex-variable-function Gaussian beam in strongly nonlocal nonlinear media. Phys Rev A (2009) 79:023803. doi:10.1103/physreva.79.023803
13. Deng D, Guo Q. Ince-Gaussian solitons in strongly nonlocal nonlinear media. Opt Lett (2007) 32:3206. doi:10.1364/ol.32.003206
14. Bekenstein R, Segev M. Self-accelerating optical beams in highly nonlocal nonlinear media. Opt Express (2011) 19:23706. doi:10.1364/oe.19.023706
15. Mihalache D, Mazilu D, Crasovan L, Towers I, Buryak A, Malomed B, et al. Stable spinning optical solitons in three dimensions. Phys Rev Lett (2002) 88:073902. doi:10.1103/physrevlett.88.073902
16. Ou J, Plum E, Zhang J, Zheludev N. Giant nonlinearity of an optically reconfigurable plasmonic metamaterial. Adv Mater (2015) 28:729–33. doi:10.1002/adma.201504467
17. Xu J, Plum E. Defect-induced nonlinearity in 2D nanoparticles. Opt Express (2022) 30:7162. doi:10.1364/oe.443977
18. Xu J, Plum E, Savinov V, Zheludev N. Second harmonic generation in amorphous silicon-on-silica metamaterial. APL Photon (2021) 6:036110. doi:10.1063/5.0037428
19. Conti C, Peccianti M, Assanto G. Observation of optical spatial solitons in a highly nonlocal medium. Phys Rev Lett (2004) 92:113902. doi:10.1103/physrevlett.92.113902
20. Rotschild C, Cohen O, Manela O, Segev M, Carmon T. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys Rev Lett (2005) 95:213904. doi:10.1103/physrevlett.95.213904
21. Zhou G, Chen R, Ru G. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys Lett (2014) 11:105001. doi:10.1088/1612-2011/11/10/105001
22. Zhang L, Zhang X, Wu H, Li C, Pierangeli D, Gao Y, et al. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt Express (2019) 27:27936. doi:10.1364/oe.27.027936
23. Peng X, He S, He Y, Deng D. Propagation of self-accelerating Hermite complex-variable-function Gaussian wave packets in highly nonlocal nonlinear media. Nonlinear Dyn (2020) 102:1753–60. doi:10.1007/s11071-020-06003-9
24. Peng X, He Y, Deng D. Three-dimensional chirped Airy Complex-variable-function Gaussian vortex wave packets in a strongly nonlocal nonlinear medium. Opt Express (2020) 28:1690. doi:10.1364/oe.384852
25. Ashkin A. Acceleration and trapping of particles by radiation pressure. Phys Rev Lett (1970) 24:156–9. doi:10.1103/physrevlett.24.156
26. Ashkin A, Dziedzic J, Bjorkholm J, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett (1986) 11:288. doi:10.1364/ol.11.000288
27. Ashkin A, Dziedzic J. Optical trapping and manipulation of viruses and bacteria. Science (1987) 235:1517–20. doi:10.1126/science.3547653
28. Harada Y, Asakura T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt Commun (1996) 124:529–41. doi:10.1016/0030-4018(95)00753-9
29. Wang H, Sun C, Tu J, Zhen W, Deng D. Propagation dynamics and radiation forces of autofocusing circle Bessel Gaussian vortex beams in a harmonic potential. Opt Express (2021) 29:28110. doi:10.1364/oe.435588
30. Peng X, Chen C, Chen B, Peng Y, Zhou M, Yang X, et al. Optical trapping Rayleigh particles by using focused partially coherent multi-rotating elliptical Gaussian beams. Chin Opt Lett (2016) 14:011405.
31. Zhang Y, Yan H, Zhao D. Optical trapping Rayleigh particles with a twist effect. Opt Lasers Eng (2020) 130:106101. doi:10.1016/j.optlaseng.2020.106101
32. Zhou Y, Zhao D. Research on statistical properties and application of Off-Axis Gaussian Schell-Model beams. Ann Phys (2021) 533:2100017. doi:10.1002/andp.202100017
33. Guo M, Zhao D. Radiation forces on a Rayleigh dielectric sphere produced by highly focused parabolic scaling Bessel beams. Appl Opt (2017) 56:1763. doi:10.1364/ao.56.001763
34. Guo M, Zhao D. Changes in radiation forces acting on a Rayleigh dielectric sphere by use of a wavefront-folding interferometer. Opt Express (2016) 24:6115. doi:10.1364/oe.24.006115
Keywords: partially coherent, cross spectral density, strongly nonlocal nonlinear media, radiation force, propagation
Citation: Peng X, He S, He Y, Deng D and Zhao D (2022) Propagation properties and radiation forces of partially coherent self-shifting cosine-Gaussian beams. Front. Phys. 10:955711. doi: 10.3389/fphy.2022.955711
Received: 29 May 2022; Accepted: 28 June 2022;
Published: 15 July 2022.
Edited by:
Liangliang Lu, Nanjing Normal University, ChinaReviewed by:
Jie Xu, University of Southampton, United KingdomLu Lu, Nanjing Normal University, China
Copyright © 2022 Peng, He, He, Deng and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yingji He, aGV5aW5namk4QDEyNi5jb20=; Dongmei Deng, ZG1kZW5nQDI2My5uZXQ=; Daomu Zhao, emhhb2Rhb211QHlhaG9vLmNvbQ==
 Xi Peng
Xi Peng Shangling He3
Shangling He3 Dongmei Deng
Dongmei Deng