- Department of Physics and Biophysics, University of San Diego, San Diego, CA, United States
Shear driven patterning is seen in many soft matter systems. We use rheology and optical microscopy to probe the structures formed when we shear a colloid-polymer mixture containing temperature-sensitive microgel particles. By increasing the temperature, we can increase the particle attraction and transition from liquid-like to gel-like behavior. And by applying shear flow to the sample as the temperature and, hence, state of the system changes, we can affect the morphology of mesoscopic colloidal clusters. We can produce gels comprised of fibrous, elongated colloid-dense clusters, or we can form more isotropic clusters. The rheology is measured and shear-induced flocculation observed for colloid-polymer systems with different cluster morphologies. At shear rates high enough to produce elongated clusters but low enough to not break clusters apart, we observe log-like flocs that are aligned with the vorticity direction and roll between the parallel plates of our rheometer.
Introduction
Colloidal suspensions find wide use for their rheological properties and their ability to assemble into complex structures [1]. With a multitude of routes for colloidal synthesis, particle sizes large enough for detection with optical methods, and tunable interparticle interactions, the structure and mechanical properties of colloidal assemblies can be readily observed, measured, and modified. Therefore, the assembly of colloidal particles has been probed to, e.g., understand the kinetics of crystal nucleation and growth [2], the mechanisms of gelation [3], and the fabrication of capsules [4]. Likewise, the rheology of colloidal suspensions has been used to, e.g., develop theoretical models for non-linear flow responses [5] and tailor the properties of 3D printer ink [6]. Whether to test fundamental models of matter or to drive applied research towards product development, these two aspects of colloids—elementary building blocks of complex assemblies and rheological modifiers—are often quite entangled [7]. Flow can assist in the assembly of higher order structures, such as colloidal crystals [8, 9], and the details of a sample’s microstructure can assist in explaining rheological properties, like shear thinning or thickening in dense suspensions [10] or how a gel yields and flows [11, 12].
In many colloidal systems, researchers have observed anisotropic shear-induced structures which align along the vorticity direction. These structures are of great interest due to their implications in determining the (potentially directional dependent) rheology of complex fluids and in revealing routes to fabricate anisotropic materials. Such anisotropic shear-induced structures have been studied experimentally through orthogonal superposition rheology [13, 14], rheo-scattering experiments [15, 16], and real space rheo-optical methods [17, 18]. Of the plethora of anisotropic shear-induced structures observed, a subset feature log-rolling flocs, whose formation strongly depends on the degree of confinement. These vorticity-aligned log-rolling flocculated structures have been observed in emulsions [19]; particle-loaded polymer blends [20]; carbon nanotube suspensions [21, 22]; carbon black suspensions [23–25]; mud samples [26]; and other suspensions of attractive particles [27, 28]. A complete understanding of such log-rolling floc formation is crucial for applications where complex fluids might flow through confined geometries (e.g., 3D printing) and for scalable methods of producing anisotropic materials (e.g., films with anisotropic conductivity [29, 30]).
A large advance in the understanding of this type of shear-induced patterning came from the experiments and simulations performed by Varga et al. in 2019 [27]. The authors demonstrated that density fluctuations within a sheared and confined suspension of attractive particles can set up eddies which, due to hydrodynamic coupling between the particle aggregates and the boundaries, promote the stable formation of log-rolling flocs. Further, the authors showed that if the shear forces are sufficiently large, flocs will break apart and stable vorticity-aligned log-rolling structures will not form. Whether the shear force is too large or not depends on the interparticle attraction, a fact which motivates the use of the Mason number, Mn, the ratio of the shear force on a particle to the interparticle force at contact. Stable logs were only observed below a critical Mason number, Mnc, with Mnc decreasing with increasing distance between the confining boundaries.
In this work, we explore the log-rolling floc formation in a colloid-polymer system containing thermoresponsive microgel colloidal particles using an optical microscope attachment on a rheometer with a parallel-plate geometry. Using poly(N-isopropylacrylamide) (pNIPAM) microgel particles allows us to vary the interparticle attraction in situ by changing the temperature, a property used in many prior investigations of colloidal phase behavior and rheology [31–36].
We find that, for our system, the morphology of colloidal clusters—assemblies of particles on a mesoscopic scale between that of the particle size (∼1 μm) and system size (>150 μm)—is an important factor influencing log formation. With our thermoresponsive colloid-polymer system, we can create colloidal gels comprised of elongated, highly anisotropic clusters or more isotropic clusters. Gels consisting of more elongated clusters tend to more readily form log-rolling flocs. Our work highlights the importance of investigating the impact of this mesoscopic cluster scale on shear-induced pattern formation. In many previous studies of colloidal gels, a cluster-centric view has proven fruitful. For example, past work has shown that colloidal clusters may determine the length scale for mechanical energy storage in colloidal gels [37] with inter-cluster bonds or cluster-cluster connections governing the elasticity [38–40]. Here, we show that a perspective which focuses on the mesoscopic cluster scale may also help elucidate macroscopic pattern formation in attractive colloidal suspensions.
Materials and methods
Materials
We synthesized pNIPAM microgel particles in a manner similar to previous syntheses by our group [41, 42] and following the guidance of previously published protocols [43]. We use ammonium persulfate (APS, purity 98%), N-isopropylacrylamide (NIPAM, 97%), and N,N′- methylenebisacrylamide (BIS, 99%), all used as received from Sigma Aldrich without purification. We synthesize particles in a 250 mL three necked round bottom flask heated to 80°C and under nitrogen atmosphere. In 200 mL of deionised water, we add 3.38 g of NIPAM and 0.15 g of BIS. Once dissolved, this solution is transferred to the three necked flask. We then add 0.11 g of APS dissolved in 3 ml of deionised water. We let the reaction run for 4 h with constant stirring with a magnetic stir bar and continuous bubbling of nitrogen through the solution. We concentrate the pNIPAM particle solution through centrifugation. We centrifuge the suspension at 30,000 g for 90 min. The supernatant is removed and fresh deionized water is added.
We estimate the pNIPAM particle volume fraction by measuring the viscosity of different particle dilutions using a Cannon-Ubbelohde dilution viscometer. According to the Einstein-Bachelor relation, the viscosity of a suspension of spherical particles relative to that of the suspending medium is
We determine the size of our pNIPAM particles around the lower critical solution temperature (LCST) using dynamic light scattering (DLS) measurements taken with a Malvern Zetasizer NanoZS using a 632.8 nm laser with a detection angle of 173°. Above the LCST at 34°C, the diameter is 480 ± 30 nm (mean and standard deviation of four runs on the Zetasizer) and we used a particle concentration of
We use xanthan polymer, Ticaxan® Xanthan VI from TIC Gums, to act as a depletant. Xanthan has been used in previous colloid-polymer samples to generate fluid-fluid phase separation or gelation [41, 42, 45]. As reported by the manufacturer, the molecular weight is in the range of 4–12 × 106 g mol−1. We prepare a stock solution of xanthan with a concentration of 0.2% by weight with 0.1 M NaCl (Sigma Aldrich, >99%) and 2 mM NaN3 (Sigma Aldrich, >99.5%).
We made samples to investigate shear-induced pattern formation by combining in equal parts our concentrated pNIPAM stock solution and the 0.2% xanthan solution. This results in a sample with a pNIPAM microgel particle volume fraction of 0.3.
Rheology
Rheological measurements are performed on a Discovery Hybrid Rheometer (DHR-3) from TA Instruments. For all data included here, we use a parallel plate geometry with a 40-mm-diameter upper plate and a bottom 1-mm-thick glass plate. The upper plate is made of stainless steel with a mirror finish to allow for better image quality when using the attached microscope. We use TA Instruments’ Upper Heated Plate accessory to vary the sample temperature between 23°C and 34°C.
We load ∼210 μL of our colloid-polymer mixture onto the rheometer by pipetting the solution onto the center of the bottom glass plate. The upper plate is slowly lowered while rotating at 0.2 rad/s. The upper plate is lowered until the sample completely fills the gap which usually results in a gap height of between 150 and 160 μm. To prevent sample evaporation, we seal the edge of the sample with mineral oil.
Before experimental runs, we try to erase the sample’s shear and loading history by performing a conditioning step where the sample is sheared at 1,000 s−1 for 120 s, sheared at −1,000 s−1 for 120 s, and then allowed to equilibrate at rest for 180 s. This preshearing procedure is similar to ones used in other studies of shear-induced structuring [24, 25, 27, 28]. For the majority of experiments we discuss here, we then proceed to heat the sample from room temperature to 34°C at a rate of 0.5°C/min while steadily shearing the sample at a rate,
Our rheometer is equipped to counter-rotate the bottom glass plate which results in a stagnation plane between the parallel plates. For most of our experimental runs, we do not enable this counterrotation. However, we occasionally use this feature to observe the formation of vorticity-aligned flocs without having such flocs leave the imaging field of view. When this counterrotation is used, we indicate so in the caption.
Microscopy
We use the modular microscopy accessory from TA Instruments to image the shear-induced flocculation. For images included here, we use Nikon objectives with either 2×, 10×, or 40× magnification (2× 0.1 NA Plan Apo; 10× 0.3 NA Plan Fluor; 40× 0.45 NA ELWD SPlan Fluor). Epi-illumination is provided by a 470-nm LED (M470L3, Thorlabs). Images are recorded on an Allied Vision Manta G-033 CCD camera with a resolution of 656 × 492 pixels at a maximum frame rate of 88 frames per second. We use the software Micro-Manager to record image sequences [46].
For macroscopic imaging where we can capture one-quarter of the 40-mm-diameter geometry, we use a macro lens attached to a 1,920 × 1,200 pixel CCD camera (Imaging Source, DMK 33UX174). Images are typically recorded at five frames per second. We illuminate the sample with a dual gooseneck LED light (AmScope, LED-14M).
Results and discussion
We prepare aqueous solutions of pNIPAM microgel particles and xanthan which exhibit temperature-dependent structural and mechanical properties. This colloid-polymer mixture shows gel-like behavior at room temperature as observed with optical microscopy (Figure 1A) and rheology (Figure 1B; Supplementary Figure S1). This behavior is due to the depletion attraction between the pNIPAM particles mediated by the xanthan polymers.
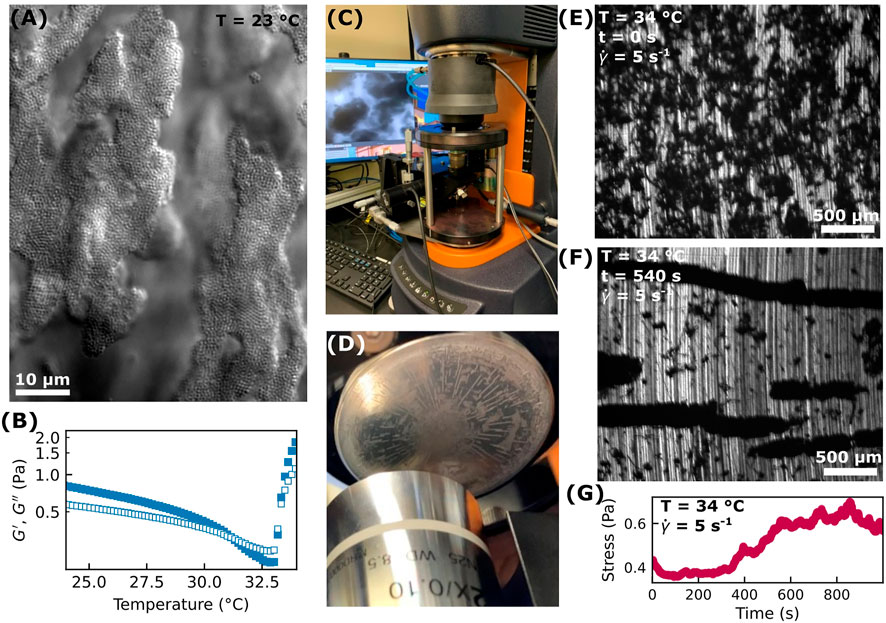
FIGURE 1. (A) At room temperature, the colloid-polymer mixture forms a weak gel as observed with a brightfield microscope using a 60× objective lens. (B) As measured with a DHR-3 instrument using a parallel-plate geometry, the storage (
When sheared at room temperature (23°C) between parallel plates (40 mm diameter, ∼150 μm gap size), we observe colloid-rich domains aligning along the flow direction. At room temperature, we never observe vorticity-aligned flocs for any of the shear rates we used, 0.5 s−1–15 s−1. This may be due to the fact that even at the lowest shear rate in this range, the shear forces acting on a particle are too large compared to the interparticle depletion attraction for stable vorticity-aligned logs to form.
We next explore if shear-induced patterning is seen at temperatures above pNIPAM’s lower critical solution temperature (LCST) of about 32°C–33°C. Above this temperature, pNIPAM particles become more hydrophobic with an increased interparticle attraction. As the temperature of our sample increases from room temperature to 34°C, the interparticle attraction varies in a non-trivial way. As the temperature increases while remaining below the LCST, the pNIPAM particles decrease in size. This reduces the volume fraction of pNIPAM particles and reduces the strength of the depletion attraction. A quantitative picture of how the pNIPAM interparticle attraction varies as a function of temperature in the presence of a depletant is beyond the scope of this work (though the rich phenomena that similar pNIPAM-containing systems exhibit have been investigated previously by our lab [41] and by others [47]). However, we do see the effect of this change in interparticle attraction in Figure 1B. The storage and loss moduli,
At this higher temperature of 34°C, we do observe, with our rheo-optical setup (Figures 1C–F) the formation of vorticity-aligned flocs similar to what has been observed previously in other attractive suspensions or soft matter systems (see also Supplementary Videos S1–S3). The formation of such flocs coincides with an increase in the shear stress along with more variability in the stress as seen in Figure 1G. This increase in stress or viscosity associated with log-rolling floc formation is consistent with previous work on systems of colloidal rods [28], carbon black dispersions [24], and nanotube suspensions [21]. If, after the log-rolling flocs form, we leave the sample undisturbed at 34°C, then the logs seem to remain intact for at least several minutes but we have not investigated this thoroughly. However, if we bring the temperature back down to 23 C, then the pNIPAM particles will disperse away from the flocs.
Interestingly, we only observe the formation of the kind of vorticity-aligned flocs seen in Figures 1D,F in certain circumstances. If, after following the sample conditioning steps described in the Methods section (i.e., applying a shear of 1,000 s−1 for 120 s, −1,000 s−1 for 120 s, and allowing the sample to equilibrate at rest for 180 s), we increase the temperature to 34°C while the sample is at rest (i.e., no applied shear) and then, with the sample temperature held at 34°C, apply a steady shear of anywhere between 0.5 and 15 s−1 we do not observe the formation of flocs. That is, if
Instead of heating the sample to 34°C while the sample is quiescent, we also try applying a steady shear to the sample as we heat it from 23°C to 34°C at 0.5°C/min. That is, we set

FIGURE 2. Shearing the sample as the temperature increases produces distinctly different cluster morphologies. (A) Samples are sheared at a constant rate of
We believe that the shear-rate-dependent shape of clusters can be understood considering the large body of work on how fluid droplets deform in shear flow. Though our colloid-polymer system exhibits gel-like behavior for most of the temperature range, our rheological (Figure 1B) and imaging (Supplementary Video S4) data shows liquid-like behavior at temperatures just below the LCST where colloid-dense and colloid-poor fluids likely coexist. Studies of flow-induced deformation of droplets and soft materials date back at least a century with the seminal work of G. I. Taylor [48, 49]. More recent experimental work on systems more resembling our own demonstrate that droplets sheared in confined geometries take on string-like elongated shapes with aspect ratios that increase with the shear rate [50] and that fluid-fluid phase separated colloid-polymer systems exhibit flow-elongated domains with aspect ratios dependent on the shear rate [51]. In our system, the low contrast between the colloid-dense regions and the continuous phase at temperatures below the LCST (given that the swollen pNIPAM particles are mostly water) make precise measurements of the shape of colloid-dense regions as a function of shear rate difficult. Nevertheless, we can use image autocorrelations to measure the approximate size of colloid-dense domains in the shear and vorticity directions as a function of shear rate at a constant temperature of 31°C. As seen in Supplementary Figure S3, the aspect ratio of these colloid-dense domains increases with increasing shear rate.
We believe that it is the morphology of the colloid-dense regions—a property dependent on the shear rate used as the sample is heated—that largely influences whether vorticity-aligned flocs form. Of course, as previous work has found, other factors like gap height, particle volume fraction, and interparticle attraction also matter, but those factors are not systematically varied in our present work. We contend that a consideration of the mesoscale colloidal-cluster morphology explains why we see the formation of vorticity-aligned flocs for an intermediate range of shear rates.
For
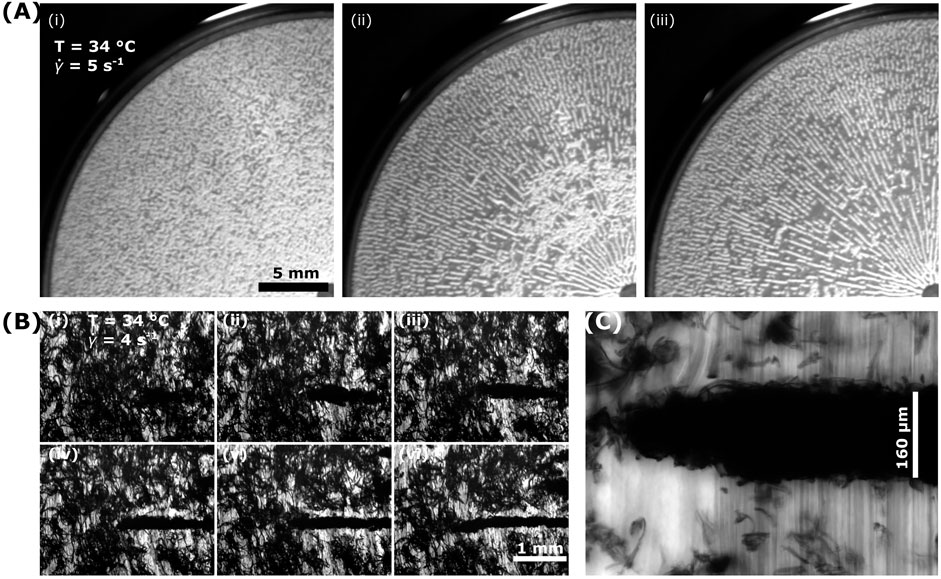
FIGURE 3. Shear-induced vorticity-aligned floc formation across scales. (A) Using a macro lens to capture a quarter of the parallel-plate geometry (diameter of 40 mm), we observe samples having undergone a temperature ramp to 34°C with a constant shear rate of
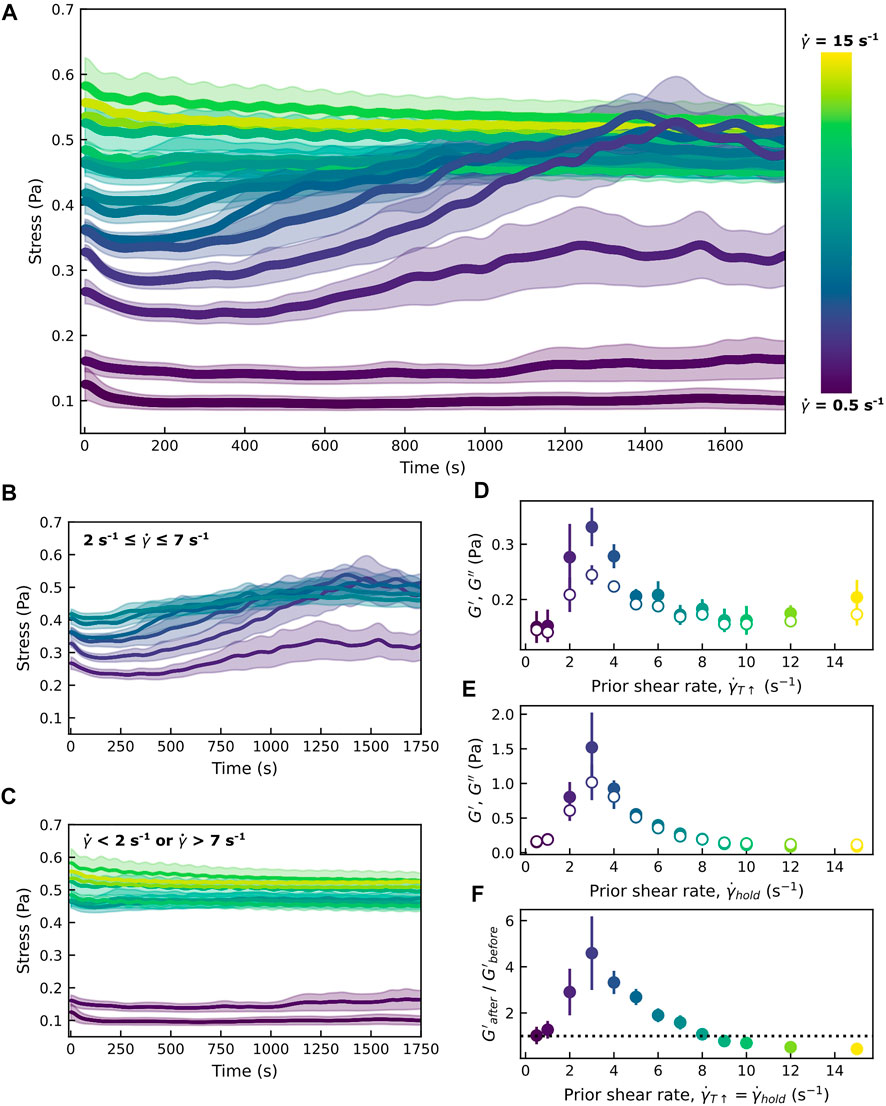
FIGURE 4. Shear-induced floc formation coincides with increases in the measured stress. (A) The colloid-polymer sample in a parallel-plate geometry is first heated to 34°C as described while subjected to shear at a rate
Previous studies investigating the formation of vorticity-aligned flocs have noted an upper bound on the shear rate (a critical shear rate,
However, our work also shows that there is a minimum shear rate below which vorticity-aligned flocs are not seen. We believe that this is due to how shear is deforming the colloid-dense mesoscale domains as the temperature increases and the interparticle interaction goes from a relatively weak depletion-induced attraction to a stronger hydrophobic attraction. At low shear rates, mesoscale colloidal clusters deform little due to the shear forces. At higher shear rates, colloidal clusters stretch out into high-aspect ratio structures. In comparison to more isotropic colloidal clusters, elongated clusters will form a larger number of connections with neighboring clusters. The fact that anisotropic particles can form a percolating network at a lower concentration than spherical particles has been shown in many studies of rod-shaped particles [28, 52]. In the experiments shown here, the concentration and aspect ratio of our pNIPAM colloidal particles are constants. But, the aspect ratios of the shear-deformed clusters do change. And just as rod-like particles will form space-spanning networks at a lower volume fraction than isotropic particles [52], elongated clusters will form more connections with neighboring clusters than isotropic clusters.
Moreover, the cluster morphology also affects the mechanical properties. After increasing the temperature from 23 to 34 °C during which we apply steady shear at a rate of
Conclusion
Our data suggests that an important factor influencing the propensity for shear-induced macroscopic patterning in our samples is the mesoscopic cluster morphology. Prior studies have shown how the degree of confinement (i.e., gap height), interparticle attraction, and volume fraction dictate whether vorticity-aligned log-rolling flocs will form. Our results show that for systems like ours the structure of the sample on the cluster scale also matters. A sample comprised of elongated, fiber-like colloidal clusters seems more likely to form shear-induced vorticity-aligned flocs than a sample containing isotropic colloidal clusters. This finding dovetails with recent work looking at the shear driven patterns of colloidal rod suspensions [28]. They found that vorticity-aligned flocs formed for rods at lower volume fractions than for spheres, due to the lower volume fraction of rods needed to form a percolating structure. From past work on colloidal rods [52], one can appreciate how shaping the colloidal clusters into elongated structures will more readily lead to a well-connected network if one considers the colloidal clusters as renormalized particles. In our work, we show how the colloidal clusters can be shaped using shear flow applied to the sample when the colloidal particle’s attraction is weak enough to allow colloid-rich domains to stretch out in the direction of flow. However, for other systems, control over the cluster morphology could be achieved by using different external fields or the interparticle potential [53].
More generally, this work highlights the importance of the experimental history of a sample. How a colloidal gel’s rheological properties depend on its shear history (i.e., rheological hysteresis) has been the subject of much research [54, 55]. For our thermoresponsive system, both the shear history and the temperature history are factors in the rheology and structure. This thermokinematic memory has been explored in other industrially relevant materials [56] and relates to recent work probing how temperature changes and the rate of temperature changes can (potentially in combination with shear) structure colloidal materials [47, 57–59].
Pattern formation due to flow in colloidal and complex fluids can be used to manufacture small-scale structures. It can also be a hinderance when material needs to flow through confined spaces, such as in 3D printing. Therefore, a complete understanding of shear driven structuration will help streamline current processing and potentially lead to new strategies for tuning soft materials.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
RM conceived and designed the study. RR and DT performed experiments. RM, RR, and DT analysed data. RM and RR wrote the manuscript. All authors helped revise and approve the submitted manuscript.
Funding
Support for this research came from a National Science Foundation Major Research Instrumentation award (CBET 1919429). Support also came from a Cottrell Scholars Award from the Research Corporation for Science Advancement to RM.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.955006/full#supplementary-material
References
1. Fernandez-Nieves A, Puertas AM. Fluids, colloids and soft materials: An introduction to soft matter physics. John Wiley & Sons (2016).
2. Hensley A, Jacobs WM, Rogers WB. Self-assembly of photonic crystals by controlling the nucleation and growth of DNA-coated colloids. Proc Natl Acad Sci U S A (2022) 119(1):e2114050118. doi:10.1073/pnas.2114050118
3. Royall CP, Faers M, Fussell S, Hallett J. Real space analysis of colloidal gels: Triumphs, challenges and future directions. J Phys : Condens Matter (2021) 33:453002. doi:10.1088/1361-648x/ac04cb
4. Rodriguez AMB, Binks BP. Capsules from Pickering emulsion templates. Curr Opin Colloid Interf Sci (2019) 44:107–29. doi:10.1016/j.cocis.2019.09.006
5. Brader JM. Nonlinear rheology of colloidal dispersions. J Phys : Condens Matter (2010) 22(36):363101. doi:10.1088/0953-8984/22/36/363101
6. Zhu C, Pascall AJ, Dudukovic N, Worsley MA, Kuntz JD, Duoss EB, et al. Colloidal materials for 3D printing. Annu Rev Chem Biomol Eng (2019) 10(1):17–42. doi:10.1146/annurev-chembioeng-060718-030133
7. Vermant J, Solomon MJ. Flow-induced structure in colloidal suspensions. J Phys : Condens Matter (2005) 17(4):R187–216. doi:10.1088/0953-8984/17/4/r02
8. Joy M, Muangnapoh T, Snyder MA, Gilchrist JF. Flow-induced alignment of (100) fcc thin film colloidal crystals. Soft Matter (2015) 11(36):7092–100. doi:10.1039/c5sm01076d
9. Ackerson BJ, Pusey PN. Shear-induced order in suspensions of hard spheres. Phys Rev Lett (1988) 61(8):1033–6. doi:10.1103/physrevlett.61.1033
10. Cheng X, McCoy JH, Israelachvili JN, Cohen I. Imaging the microscopic structure of shear thinning and thickening colloidal suspensions. Science (2011) 333(6047):1276–9. doi:10.1126/science.1207032
11. Min Kim J, Eberle APR, Kate Gurnon A, Porcar L, Wagner NJ. The microstructure and rheology of a model, thixotropic nanoparticle gel under steady shear and large amplitude oscillatory shear (Laos). J Rheology (2014) 58(5):1301–28. doi:10.1122/1.4878378
12. Boromand A, Jamali S, Maia JM. Structural fingerprints of yielding mechanisms in attractive colloidal gels. Soft Matter (2017) 13(2):458–73. doi:10.1039/c6sm00750c
13. Colombo G, Kim S, Schweizer T, Schroyen B, Clasen C, Mewis J, et al. Superposition rheology and anisotropy in rheological properties of sheared colloidal gels. J Rheology (2017) 61(5):1035–48. doi:10.1122/1.4998176
14. Wang Y, Ewoldt RH. New insights on carbon black suspension rheology -- anisotropic thixotropy and anti-thixotropy (2022). arXiv:220205772 [cond-mat].
15. DeGroot JV, Macosko CW, Kume T, Hashimoto T. Flow-induced anisotropic SALS in silica-filled PDMS liquids. J Colloid Interf Sci (1994) 166(2):404–13. doi:10.1006/jcis.1994.1311
16. Pignon F, Magnin A, Piau J-M. Butterfly light scattering pattern and rheology of a sheared thixotropic clay gel. Phys Rev Lett (1997) 79(23):4689–92. doi:10.1103/physrevlett.79.4689
17. Cheng X, Xu X, Rice SA, Dinner AR, Cohen I. Assembly of vorticity-aligned hard-sphere colloidal strings in a simple shear flow. Proc Natl Acad Sci U S A (2012) 109(1):63–7. doi:10.1073/pnas.1118197108
18. Lin NYC, Cheng X, Cohen I. Biaxial shear of confined colloidal hard spheres: The structure and rheology of the vorticity-aligned string phase. Soft Matter (2014) 10(12):1969–76. doi:10.1039/c3sm52880d
19. Montesi A, Peña AA, Pasquali M. Vorticity alignment and negative normal stresses in sheared attractive emulsions. Phys Rev Lett (2004) 92(5):058303. doi:10.1103/physrevlett.92.058303
20. Mao C, Huang Y, Qiao Y, Zhang J, Kong M, Yang Q, et al. Vorticity-aligned droplet bands in sheared immiscible polymer blends induced by solid particles. Langmuir (2020) 36(16):4383–95. doi:10.1021/acs.langmuir.0c00511
21. Lin-Gibson S, Pathak JA, Grulke EA, Wang H, Hobbie EK. Elastic flow instability in nanotube suspensions. Phys Rev Lett (2004) 92(4):048302. doi:10.1103/physrevlett.92.048302
22. Ma AWK, Mackley MR, Rahatekar SS. Experimental observation on the flow-induced assembly of Carbon nanotube suspensions to form helical bands. Rheol Acta (2007) 46(7):979–87. doi:10.1007/s00397-007-0183-x
23. Osuji CO, Weitz DA. Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system. Soft Matter (2008) 4(7):1388–92. doi:10.1039/b716324j
24. Negi AS, Osuji CO. New insights on fumed colloidal rheology—Shear thickening and vorticity-aligned structures in flocculating dispersions. Rheol Acta (2009) 48(8):871–81. doi:10.1007/s00397-008-0341-9
25. Grenard V, Taberlet N, Manneville S. Shear-induced structuration of confined carbon black gels: Steady-state features of vorticity-aligned flocs. Soft Matter (2011) 7(8):3920–8. doi:10.1039/c0sm01515f
26. Shakeel A, MacIver MR, van Kan PJM, Kirichek A, Chassagne C. A rheological and microstructural study of two-step yielding in mud samples from a port area. Colloids Surf A: Physicochemical Eng Aspects (2021) 624:126827. doi:10.1016/j.colsurfa.2021.126827
27. Varga Z, Grenard V, Pecorario S, Taberlet N, Dolique V, Manneville S, et al. Hydrodynamics control shear-induced pattern formation in attractive suspensions. Proc Natl Acad Sci U S A (2019) 116:12193–8. doi:10.1073/pnas.1901370116
28. Das M, Chambon L, Varga Z, Vamvakaki M, Swan JW, Petekidis G. Shear driven vorticity aligned flocs in a suspension of attractive rigid rods. Soft Matter (2021) 17(5):1232–45. doi:10.1039/d0sm01576h
29. Huang J, Xu J, Sheng Y, Zhu Y, Jiang W, Xu D, et al. Fabrication of polymer film with extraordinary conductive anisotropy by forming parallel conductive vorticity-aligned stripes and its formation mechanism. Macromol Mater Eng (2016) 301(6):743–9. doi:10.1002/mame.201600026
30. Mao C, Huang J, Zhu Y, Jiang W, Tang Q, Ma X. Tailored parallel graphene stripes in plastic film with conductive anisotropy by shear-induced self-assembly. J Phys Chem Lett (2013) 4(1):43–7. doi:10.1021/jz301811b
31. Romeo G, Fernandez‐Nieves A, Wyss HM, Acierno D, Weitz DA. Temperature-controlled transitions between glass, liquid, and gel states in dense p-NIPA suspensions. Adv Mater (2010) 22(31):3441–5. doi:10.1002/adma.200904189
32. Yunker PJ, Chen K, Gratale MD, Lohr MA, Still T, Yodh AG. Physics in ordered and disordered colloidal matter composed of poly( N -isopropylacrylamide) microgel particles. Rep Prog Phys (2014) 77(5):056601. doi:10.1088/0034-4885/77/5/056601
33. Minami S, Watanabe T, Suzuki D, Urayama K. Rheological properties of suspensions of thermo-responsive poly( N -isopropylacrylamide) microgels undergoing volume phase transition. Polym J (2016) 48(11):1079–86. doi:10.1038/pj.2016.79
34. Appel J, Fölker B, Sprakel J. Mechanics at the glass-to-gel transition of thermoresponsive microgel suspensions. Soft Matter (2016) 12(9):2515–22. doi:10.1039/c5sm02940f
35. Karg M, Pich A, Hellweg T, Hoare T, Lyon LA, Crassous JJ, et al. Nanogels and microgels: From model colloids to applications, recent developments, and future trends. Langmuir (2019) 35(19):6231–55. doi:10.1021/acs.langmuir.8b04304
36. Chaudhary G, Ghosh A, Kang JG, Braun PV, Ewoldt RH, Schweizer KS. Linear and nonlinear viscoelasticity of concentrated thermoresponsive microgel suspensions. J Colloid Interf Sci (2021) 601:886–98. doi:10.1016/j.jcis.2021.05.111
37. Ramakrishnan S, Chen Y-L, Schweizer KS, Zukoski CF. Elasticity and clustering in concentrated depletion gels. Phys Rev E (2004) 70(4):040401. doi:10.1103/physreve.70.040401
38. Laurati M, Petekidis G, Koumakis N, Cardinaux F, Schofield AB, Brader JM, et al. Structure, dynamics, and rheology of colloid-polymer mixtures: From liquids to gels. J Chem Phys (2009) 130(13):134907. doi:10.1063/1.3103889
39. Zaccone A, Wu H, Del Gado E. Elasticity of arrested short-ranged attractive colloids: Homogeneous and heterogeneous glasses. Phys Rev Lett (2009) 103(20):208301. doi:10.1103/physrevlett.103.208301
40. Whitaker KA, Varga Z, Hsiao LC, Solomon MJ, Swan JW, Furst EM. Colloidal gel elasticity arises from the packing of locally glassy clusters. Nat Commun (2019) 10(1):2237. doi:10.1038/s41467-019-10039-w
41. Dang S, Brady J, Rel R, Surineni S, O’Shaughnessy C, McGorty R. Core–shell droplets and microcapsules formed through liquid–liquid phase separation of a colloid–polymer mixture. Soft Matter (2021) 17:8300–7. doi:10.1039/d1sm01091c
42. Wang J, McGorty R. Measuring capillary wave dynamics using differential dynamic microscopy. Soft Matter (2019) 15(37):7412–9. doi:10.1039/c9sm01508f
43. Still T, Chen K, Alsayed AM, Aptowicz KB, Yodh AG. Synthesis of micrometer-size poly(N-isopropylacrylamide) microgel particles with homogeneous crosslinker density and diameter control. J Colloid Interf Sci (2013) 405:96–102. doi:10.1016/j.jcis.2013.05.042
44. Borrega R, Cloitre M, Betremieux I, Ernst B, Leibler L. Concentration dependence of the low-shear viscosity of polyelectrolyte micro-networks: From hard spheres to soft microgels. Europhys Lett (1999) 47(6):729–35. doi:10.1209/epl/i1999-00451-1
45. Jamie EAG, Davies GJ, Howe MD, Dullens RPA, Aarts DGAL. Thermal capillary waves in colloid–polymer mixtures in water. J Phys : Condens Matter (2008) 20(49):494231. doi:10.1088/0953-8984/20/49/494231
46. Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, Stuurman N. Advanced methods of microscope control using μManager software. J Biol Methods (2014) 1(2):10. doi:10.14440/jbm.2014.36
47. Fussell SL, Royall CP, van Duijneveldt JS. Controlling phase separation in microgel-polymeric micelle mixtures using variable quench rates (2021). arXiv:210404022 [cond-mat].
48. Taylor GI. The viscosity of a fluid containing small drops of another fluid. Proc R Soc Lond Ser A, Containing Pap a Math Phys Character (1932) 138(834):41–8.
49. Taylor GI. the formation of emulsions in definable fields of flow. Proc R Soc Lond A: Math Phys Eng Sci (1934) 146(858):501–23.
50. Pathak JA, Migler KB. Droplet−String deformation and stability during microconfined shear flow. Langmuir (2003) 19(21):8667–74. doi:10.1021/la0346907
51. Derks D, Aarts DGAL, Bonn D, Imhof A. Phase separating colloid polymer mixtures in shear flow. J Phys : Condens Matter (2008) 20(40):404208. doi:10.1088/0953-8984/20/40/404208
52. Solomon MJ, Spicer PT. Microstructural regimes of colloidal rod suspensions, gels, and glasses. Soft Matter (2010) 6(7):1391–400. doi:10.1039/b918281k
53. Soto-Bustamante F, Valadez-Pérez NE, Liu Y, Castañeda-Priego R, Laurati M. Clusters in colloidal dispersions with a short-range depletion attraction: Thermodynamic identification and morphology. J Colloid Interf Sci (2022) 618:442–50. doi:10.1016/j.jcis.2022.03.061
54. Divoux T, Grenard V, Manneville S. Rheological hysteresis in soft glassy materials. Phys Rev Lett (2013) 110(1):018304. doi:10.1103/physrevlett.110.018304
55. Jamali S, Armstrong RC, McKinley GH. Multiscale nature of thixotropy and rheological hysteresis in attractive colloidal suspensions under shear. Phys Rev Lett (2019) 123(24):248003. doi:10.1103/physrevlett.123.248003
56. Geri M, Venkatesan R, Sambath K, McKinley GH. Thermokinematic memory and the thixotropic elasto-viscoplasticity of waxy crude oils. J Rheology (2017) 61(3):427–54. doi:10.1122/1.4978259
57. Smith KM, Hsiao LC. Migration and morphology of colloidal gel clusters in cylindrical channel flow. Langmuir (2021) 37(34):10308–18. doi:10.1021/acs.langmuir.1c01287
58. Cardenas-Vasquez ED, Smith KM, Doolan TJ, Hsiao LC. Shear-induced microstructural variations in nanoemulsion-laden organohydrogel fibers. ACS Appl Polym Mater (2020) 2(2):594–603. doi:10.1021/acsapm.9b00979
Keywords: colloids, rheology, microgel particles, rheo-optics, shear-induced aggregation
Citation: Rel R, Terwilliger D and McGorty R (2022) Shear-induced vorticity aligned flocs in a temperature responsive colloid-polymer mixture. Front. Phys. 10:955006. doi: 10.3389/fphy.2022.955006
Received: 27 May 2022; Accepted: 22 August 2022;
Published: 15 September 2022.
Edited by:
Emanuela Del Gado, Georgetown University, United StatesReviewed by:
Orhan Özdemir, Istanbul University-Cerrahpasa, TurkeyRyan Poling-Skutvik, University of Rhode Island, United States
Ali Mohraz, University of California, Irvine, United States
Copyright © 2022 Rel, Terwilliger and McGorty. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan McGorty, cm1jZ29ydHlAc2FuZGllZ28uZWR1
 Ryle Rel
Ryle Rel Dennis Terwilliger
Dennis Terwilliger Ryan McGorty
Ryan McGorty