Baryon breakdown in black hole

According to relativity theory, a black hole is a distinct region in spacetime; according to astronomical observations, it is a celestial body transforming matter into high-energy jets. We propose that a black hole is, indeed, a star, where particles transform into photons through a specific nuclear reaction, besides radiative accretion disk processes. Our reasoning draws from statistical physics of open quantized systems. The many-body theory describes elementary particles comprising quanta of actions and their reactions as conversions of matter-bound quanta into vacuum quanta. The proposed transformation details the annihilation of neutrons into gamma rays. This reaction, characteristic of a black hole, begins when the strength of gravitation exceeds the strength of the strong force. Then gluons detach from quarks and attach to surrounding high-energy quanta of the gravitational field. Without gluons, the tightly packed neutrons cannot hold up their SU(3) symmetry. The tetrahedral structures flatten out so that quarks of opposite charges end up pairwise on top of each other and annihilate into rays of light quanta as electrons and positrons do. Finally, the quanta jet out along the black hole spinning axis, where the gravitation due to the collapsing core gives in most. Over the eons, these episodic effluxes from a precessing supermassive black hole amass into Fermi bubbles.

1 Introduction

The renowned Hertzsprung-Russell (HR) diagram displays stars’ luminosity versus color [1]. The mass-to-light ratio for the main-sequence stars is nearly constant over seven magnitudes in luminosity [2]. Its characteristic bands, essentially straight lines on a log-log plot, correspond by color and temperature [3] to distinct nuclear reactions [4] where quanta bound in matter transform into freely propagating quanta, i.e., radiation. While all of this is well established, we draw attention to the fact that the HR diagram lacks a class of stars, the most brilliant ones, namely black holes.

At first, it might seem strange to consider a black hole as a shining star. Per definition, black hole gravity is too strong for photons to escape [5]. Then again, supermassive black holes at galaxy centers emit bipolar beams of gamma and X-rays that appear to form Fermi bubbles over the eons of emission [6,7]. These highly collimated jets with characteristic spectral evolution emanate right from the hole. Since they cannot be unambiguously ascribed and correlated to processes in accretion disks [8–13], we propose that they stem from a reaction distinct to the black hole yet akin to a nuclear reaction of an ordinary star.

We note that while each evolutionary phase of an aging star is powered by a distinct nuclear reaction [14], the black hole is not associated with such a process. Instead, the black hole is mathematized as a region of spacetime enclosed by an event horizon [15]. While the curved spacetime is a superb continuum model of gravitation, it is not the theory of particles and their dissipative reactions.

As long as without direct observations and detailed knowledge about elementary particle structures and their transformations, it is difficult to deduce what happens to matter in a black hole since spiraling through the event horizon. In any case, black holes devour matter and discharge bright beams just as stars consume matter for intense radiation. So, it seems pertinent to propose elementary particle reactions underlying black hole emissions.

In line with the hypothesis that the black hole is a star among stars, gamma-ray bursts, coinciding with mergers of stellar black holes [16,17], suggest a reaction that goes off only when a critical density is exceeded. Also, fast radio bursts originating from collisions of black holes and neutron stars [18] imply a reaction having a threshold in density. Although the origin of the hard X-ray emission is poorly understood [19], the highly collimated and intermittent bipolar jets point at a compact source in the core rather than the accretion disk processes [20]. Illuminatingly, neutron stars without accretion disk jet X-rays [21].

After all, black holes are not that exceptional celestial bodies. Their masses overlap with massive stars. Moreover, the black hole mass versus stellar velocity dispersion in a galaxy bulge follows a power law [22] similar to Faber–Jackson relation for luminosity versus central stellar velocity dispersion of elliptical galaxies [23,24], Tully-Fisher relation for mass versus intrinsic luminosity of a spiral galaxy [25,26], the initial mass function for a star population [27], and the relation between the surface gas density and star formation rate [28]. Like the HR diagram’s bands, these relationships are straight lines on log-log plots.

Since power laws are ubiquitous [29–31], not only at cosmic [32,33] but all scales [34,35], we employ the general theory of statistical mechanics for open quantized systems [36] and infer that the black hole operational principle is the same as that of other dissipative systems, i.e., the second law of thermodynamics. The black hole packed with energy evolves in the least time toward balance with its energy-sparse surroundings by converting matter into light quanta. The black hole entropy [37] is consistent with this thermodynamic tenet.

Furthermore, the black hole gravity, albeit massive, is no different from other bodies. Only the intermittent jets instead of continuous radiation distinguish black holes from ordinary stars. Conversely, singularity, wormhole, event horizon, and information loss paradox are assigned to black holes by theory, not astronomical observations [38]. For instance, in Feynman’s field theory, the singularity has been interpreted as a relativistic compact object [39]. Such a relativistic star supposedly becomes an eternally collapsing object dominated by radiation pressure [40]. Theorizing, however fascinating, leaves the basic empirical question open: What are black holes made of?

Be that as it may with speculations, there is consensus that a neutron star phase precedes the terminal black hole state in evolutionary scenarios of a massive star. Thus, we consider a process where neutrons break down and convert into jets of light quanta. Besides the brilliant jets, we reason by the conservation of quanta [41] that most photons jet out in pairs with opposite phases [42–45]. The paired quanta without net electromagnetic field are thus not readily detectable, as they do not couple to charges. Nevertheless, the intense flux may manifest itself in pair production, most notably electrons and positrons [46]. Moreover, the massive outflow of energy density causes an increase in the refractive index, i.e., optical length [47], that can be picked up by interferometers, especially when arriving as waves [17]. The voluminous jets of paired quanta, the substance of space [42,45], could account for the emergence of vast voids along the galaxy spin axes [48] and associate with massive outflows of matter stretching out far from galaxies into cosmic expanses [49,50].

Furthermore, we find the conclusion that the black hole is a star consistent with the ancient atomistic axiom. Reworded in the modern form by Isaac Newton [51] and rephrased by Gilbert N. Lewis in 1926 [41], it says that everything, i.e., particles and the vacuum, comprises quanta of light. Likewise, Ludwig Boltzmann assumed an indestructible element when deriving statistical mechanics. Accordingly, the quantum of action as the fundamental elemental constituent is also the basis of the statistical physics of open systems that underlies non-equilibrium thermodynamics for dissipative processes, such as nuclear reactions [36,52–55].

In essence, the many-body theory describes any system, e.g., a star, with an equation of the state that houses all its quanta. Its time derivate, i.e., the equation of motion, is the familiar 2nd law of thermodynamics. Its integral form, in turn, is the principle of least action in its original, open dissipative form [56–58].

The least-action principle lays out paths of light. According to the axiom of everything comprising light quanta [41], consistent with empirical evidence so far, the geodesic concept applies not only to light quanta constituting the vacuum but also to the light quanta constituting particles [42,59,60]. Particles as one-dimensional objects comprising strings of photons parallels the foundational idea of string theory [61,62]. Specifically, we show how the structures of baryons comprising strings of light quanta suggest how nucleons pack, break down, and how their quarks annihilate into rays of light quanta.

Although the adopted approach is unconventional among effective theories of the day, the atomistic axiom is not questioning modern physics. On the contrary, everything comprising quanta renders mathematical models with tangible substance amenable to empirical falsification. For example, quantum electrodynamics (QED) ascribes the anomalous magnetic moment of the electron to vacuum fluctuations and polarizations, but these transients within Heisenberg uncertainty limit are beyond experimental examination. In contrast, we argue that the electron magnetic moment is a property of the electron structure. Accordingly, a change in the structure, for example, from the muon to the electron, causes a change in the magnetic moment.

In any case, the axiomatic tenet is worth examining because it meets the criteria of a scientific theory. Namely, the photon being the indestructible, elemental constituent of everything is a concise, coherent, and broadly applicable axiom. It could be falsified in a straightforward manner. But so far, no photon, as a massless particle, has been found to split, decay, appear out of nothing, or disappear into nothingness. Thus, the photon conservation [41] has withstood the test of time. It has not been negated empirically. However, this state of affairs should not be confused with creating and annihilating photons in quantum field theory using mathematical operators. So, we are not questioning mathematical formalism of modern physics but rather specifying the physical substance that is subject to the theorizing and modeling.

Finally, we acknowledge that our proposal of the black hole having an active core, similar to an ordinary star, at the place of a mathematical singularity is not exactly original [63]. And our proposal of nucleons transforming into photon gas is not new either [64].

2 Baryon structure

Considering that all known constituents of matter transform by either emitting or absorbing quanta [65], and that annihilation produces photons, and that pair production converts photons to particles, the quantum of light could be the fundamental elemental constituent. The axiom is justified as the quantum of action, having energy, E, on its period, t, measures an invariant, Planck’s constant, h = Et.

This postulate of everything, i.e., particles and the vacuum, comprising light quanta [41] is also motivated theoretically [42,43,45,58–60,66]. For example, arguments that the electron spin and magnetic moment are generated by a circulatory motion of quanta along a helical coil, known as Zitterbewegung, follow from geometric analyses of solutions to the Dirac equation [59,67,68]. However, the analyses do not determine how many light quanta make up the spin-½ particle. Likewise, string theory, while associating the vibrational state of a string to the properties of a particle, does not explicitly define the string’s resonant shape [69]. In contrast, we detail the particle as a string of photons whose form determines the particle properties.

Theoretically speaking, a particle is the excited state of a quantum field. Accordingly, we associate the field of quanta with a particle in the same way as the electric field made of photons is associated with the charge of a particle. In other words, the field is the particle’s effect on the surrounding vacuum quanta. The thermodynamic balance between the particle and its field ensures that the particle view and the field view are equivalent in accordance with wave-particle duality. Expressly, the gravitational field mirrors the particle’s geodesic curvature, i.e., mass, the electric field corresponds to the particle’s chirality, i.e., charge, and the magnetic field to the particle’s helicity, i.e., spin [59,70]. This view of a particle as a geodesic comprising light quanta is in line with theory [66] and measurements [71]. Thus, the elementary particles can be understood as Ampèrian current loops of photons.

We first work out the structure of the electron as a string of photons and then the down quark having ¹/₃ fraction of the electron charge and the up quark having ²/₃ fraction of the positron charge.

The key to the electron structure is the fine structure constant, α = e²Z_o/4πℏ. It is the ratio between two actions: the electron action, e²Z_o/4π, where e is the electron charge and Z_o = 1/ϵ_oc is the impedance of free space of permittivity, ϵ_o, and the neutrino action, ℏ = h/2π, which is the quantum of action in the form of a simple loop. As implied by its unit Js, the action is a geometric concept defining a path, x, with momentum, p, that relate to a period, t, with energy, E. So, we proceed to deduce from α what the electron looks like as a path comprising quanta of actions, i.e., a string of photons.

According to the principle of least action [72,73], the electron (e⁻) is a stationary action. Its quanta of actions form an optimal path, a geodesic of constant angular momentum, d_tL = 0. When on a chiral path, the circulating density, ρ gives rise to the charge, e = ρx, and magnetic moment, μ_e. Conversely, when on the path of opposite handedness, the circulating density gives rise to the opposite charge and magnetic moment corresponding to the positron (e⁺).

The vacuum quanta surrounding the particle adapt to the Noetherian current density, ρd_tx, on its chiral path, x, by taking the form of an electric field, E. According to Gauss’ law, the field density integrates to a constant L = ∫2Kdt = ∫∫ρE ⋅dxdt = e²/4πϵ_oc = e²Z_o/4π = αℏ. In this way, the fine structure constant is understood geometrically as the ratio between the geodesic that forms the electron and the single quantum of action, ℏ, in the form of a loop (Figure 1).

FIGURE 1

FIGURE 1. Torus model of the electron comprising 138 quanta. The tiny arrow of each quantum indicates the sense of circulation (Illustration by Mathematica).

As outlined by André-Marie Ampère [74] and reverberated by Alfred Parson [75] and Arthur Compton [76,77], the electron comprises loops in the form of a helical torus (Figure 1) that accounts for its charge, magnetic moment and mass [42,60].

The toroidal path can be parameterized in terms of the major radius, R, and the minor radius, r,

$\begin{array}{cc}\hfill x\left(t\right)& =\cos \left(t\right)\left[R+r\cos \left(nt\right)\right]\hfill \\ \hfill y\left(t\right)& =\sin \left(t\right)\left[R+r\cos \left(nt\right)\right]\hfill \\ \hfill z\left(t\right)& =r\sin \left(nt\right).\hfill \end{array}(1)$

The torus of n loops is of the length $2\pi rn\sqrt{1+{[(R/r)/n]}^2}$. The excellent approximation, $1/\alpha \approx 137\sqrt{1+{(\pi /137)}^2}\approx 137.036$, where 1/α is the hypotenuse of a right triangle with catheti π and 137, suggests, by having the same form, that the electron torus has 137 loops comprising 138 quanta. There is one quantum over the number of loops because each loop with pitch is slightly longer than the planar loop quantum, ℏ. In other words, the helical torus is slightly longer than an equivalent ring array of stacked loop quanta. Also, by the Taniyama-Shimura conjecture, every elliptic curve is modular with an integral number of constituents [78,79]. We emphasize that we did not derive α from numerological arguments [80] but only expressed the torus in mathematical terms.

It is worth recalling that the point-like electron postulate is subject to a caveat. As researchers concluded from their measurements: “If the electron is a composite particle, its constituents are strongly bound, giving the electron the observed point-like quality at experimentally accessible energies.” [81] Thus, there is no compelling experimental evidence that the electron would be a point-like particle without internal structure. The electron’s physical properties and transformations in reactions suggest the contrary. The electron constituents, the quanta in their tight helical coil, are strongly bound to one another like the strongly bound quarks. Still, the electron is not an unbreakable elemental constituent as its annihilation with the positron and its transformations in nuclear reactions prove.

The particle properties, most notably charge (1), magnetic moment (2), and mass (3), are not independent but related, reflecting different characteristics of the same geodesic.

(1) The magnitude and sign of the charge, e⁻, stem from the torus winding number and handedness. The torus of a fixed number of quanta is a closed curve, γ, with a characteristic topological quantum number, ∮_γdθ, that integrates the polar coordinate, θ, over γ.

(2) The electron magnetic moment, μ_e = ∫r × ρvdr = er × p/2m_e = eL/2m_e, integrates the torus action [43]. Customarily, its magnitude, μ_e ≈ μ_B(1 + α/2π), is mathematically decomposed into the Bohr magneton, μ_B = eℏ/2m_e, due to the primary circulation at the major radius, R, and the anomalous moment, μ_Bα/2π, due to the secondary circulation at the minor radius, r. While the anomalous part can be computed very precisely through a QED series expansion of the fine structure constant, here we make sense the electron magnetic moment in terms of the electron structure as a curve comprising photons.

(3) The mass is proportional to the Euler characteristic of the particle’s geodesic, 2πχ = ∫k_gdx, similarly to the Gauss-Bonnet theorem, where the geodesic curvature, k_g = n ⋅ (x′ × x′′)/|x′|³, is the projection of the action’s path, x, onto the vacuum, i.e., the universal surroundings defined by the normal, n, [82]. Thus, the mass depends on both the particle structure and the vacuum structure. In the flat free space, the electron mass is small because integrating k_g over x, the curvatures on the opposite sides of the torus cancel out each other, apart from the helical pitch. Likewise, in graphene, for example, having a band structure with vanishing densities, the electron effective mass is extraordinarily low, and conversely, high in heavy fermion materials.

As the charges of quarks are fractions of the electron and positron charges, we reason that the quarks are arcs of the electron and positron tori because charge is an additive physical quantity. The down quark comprises 46 quanta to generate ¹/₃ of the electron charge. Likewise, the up quark comprises 92 quanta to generate ²/₃ of the positron charge. This stoichiometry is in agreement, for instance, with the Feynman diagram of electron capture.

The gluon, the gauge boson of the strong force, is similar to the photon, the gauge boson of the electromagnetic force. As a single, indivisible quantum of action, also the gluon measures h. However, the Standard Model of particle physics assigns color charge to the gluon thereby differentiating it from a short wavelength photon. This 3-valued hidden quantum number distinguishes the quark and gluon states in hadrons. But knowing the particle structures as signed geodesics of quanta, the undetectable color-labeling is redundant. The geodesic’s sense of circulation defines the order of gluons and quarks in a particle and distinguishes similar constituents from each other. For example, in the neutron, one down quark is before the up quark and the other after (Figure 2).

FIGURE 2

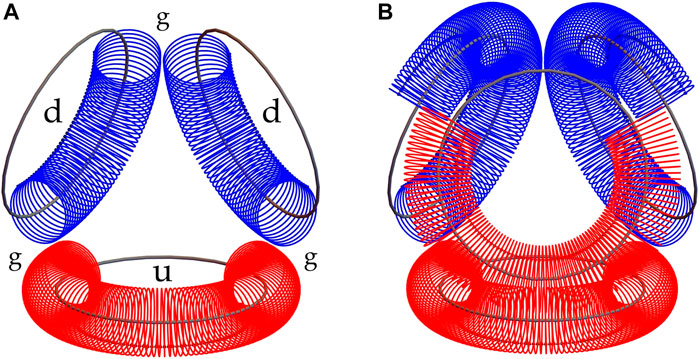
FIGURE 2. (A) Model of the neutron. The up quark (u) comprising 92 quanta is a²/₃ arc of the full torus (the positron) comprising 138 quanta. Accordingly, each of the two down quarks (D) comprising 46 quanta is a¹/₃ arc of the full torus of opposite handedness (the electron). The quarks cannot but coordinate in tetrahedral symmetry when connected via gluons (g), i.e., short-wavelength photons. The neutron is a closed, signed geodesic, i.e., a least-action path with a sense of circulation. (B) Model of two neutrons in the doubly compact configuration of a dibaryon. Under high pressure, the consecutive down quarks may bud out the gluon and fuse into up antiquark (Illustrations by Mathematica).

Most importantly, charges, magnetic moments, and masses as line integrals computed from the quantized geodesics, most notably those of proton, neutron, and electron, comply with measurements [42–44,58,60]. For example, these Ampèrian loops explain why the moments, calculated as sums of the constituent quarks, agree so well with measurements [83].

Three quarks as arcs of tori, when linked via gluons, i.e., short-wavelength photons, cannot but coordinate at three tetrahedron faces to form a closed, stable structure. The symmetry of the closed geodesic complies with SU(3) of baryons (Figure 2).

Moreover, we expect that under extreme pressure, two neutron structures pack interlaced and form a dibaryon [84,85]. The formation of neutron dimers would fuse two down quarks together to from an up antiquark (Figure 2).

These preliminaries provide us with premises, i.e., particle structures and the conservation law of quanta, to examine neutron packing, breakdown, and transformation into radiation in the black hole.

3 Baryon breakdown

Theoretically speaking, when the mass of a star exceeds the Tolman–Oppenheimer–Volkoff limit, the quantum degeneracy pressure of neutrons is insufficient to prevent the star from collapsing because particles break down [86,87]. Contrariwise, a star that is not quite massive enough to collapse into a black hole will end up being a neutron star [88].

Thus, we argue that 1) all matter spiraling into a black hole first transforms into neutrons, e.g., through electron capture, 2) then the black hole gravity is strong enough to break neutrons, 3) so that quarks of opposite charge annihilate into quanta of light 4) and finally jet out along the black hole spinning axis where the gravity of the collapsing core gives in most.

The truncated tetrahedron structure (Figure 2) suggests that in a compact star neutrons pack tightly into a truncated-tetrahedron lattice (Figure 3) [89,90]. The packing, minimizing the net dipole moment, clues us in to the core collapse and transformation of neutrons into rays of photons (Figure 4).

FIGURE 3

FIGURE 3. Tightly packed truncated tetrahedrons fill space almost completely (Illustration: Ferkel-commons.wikimedia.org/w/index.php?curid=21480183).

FIGURE 4

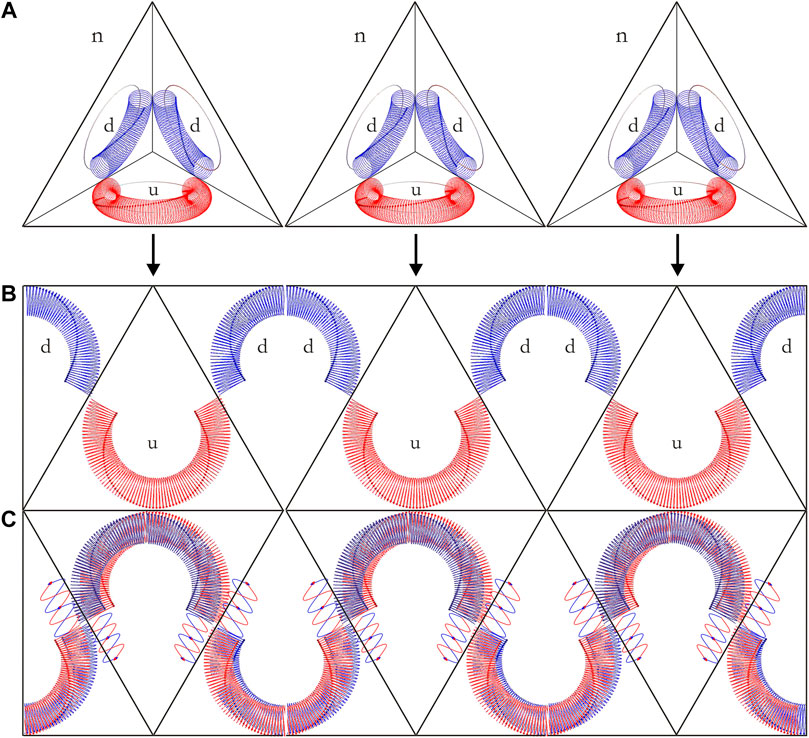
FIGURE 4. (A) When gravity outstrips the strong force in the black hole core, the tightly packed truncated-pyramid structures of neutrons (n) open and (B) flatten into the layers of quarks. Since the up quarks (u, red) and the down quarks (d, blue) of the adjacent layers align on top of each other (C), the arcs of the tori with opposite handedness discharge, i.e., annihilate, into waves of paired quanta that jet out from above and below the planes where curvature, i.e., gravitation, is least (Illustrations by Mathematica).

The neutron neutrality suggests that two neutrons decompose each other into rays of quanta when each up quark coordinates face-to-face with two down quarks, similarly to the tori of the electron and the positron aligning face-to-face in annihilation. Indeed, when the tightly packed neutrons in the truncated tetrahedral lattice flatten to planes, the quarks of adjacent layers cannot but juxtapose.

It is worth emphasizing that while the electron as a particle and the positron as an antiparticle annihilate each other, any structure and its mirror-image structure likewise decompose each other into rays of light quanta, i.e., annihilate. Specifically, along this line of reasoning, two down quarks when merged together is equivalent to the up antiquark.

The baryon breakdown, i.e., the collapse from the tetrahedral to planar quark coordination, occurs first when the enormous black hole gravity becomes comparable in strength to the strong interaction, i.e., the gluon energy. Then there is no energy difference preventing the gluons from disconnecting from quarks and connecting to the surrounding high-energy quanta embodying the immense gravitation.

The ratio of the electrostatic and gravitational fields,

$\frac{\alpha }{{\alpha }_G}=\frac{e^2}{4\pi {ϵ}_{o}r}/\frac{G{m}_e^2}{r},(2)$

given in terms of the electron mass, m_e, yields through α ≈ 1/137.036 the ratio of the strong force to gravity, 1/α_G ≈ 5.71 ⋅ 10⁴⁴. Thus, the critical mass density, ρ_c, for the neutron to break down must be 1/α_G times higher than the average mass density, ρ_M, of the universe [3].

The energy balance, Mc² = GM²/R, between all mass, M, and its gravitational potential [91,92],

$M={\int }_0^R{\rho }_{M}4\pi R^{2}dR={\int }_0^R\frac{1}{4\pi G{t}^2}4\pi R^{2}dR=\frac{c^{2}R}{G},(3)$

gives an estimate for the mass density, ρ_M = 1/4πGt² ≈ 0.6 ⋅ 10⁻²⁶ kg/m³, of the universe of radius, R = ct, and age of, t = 1/H ≈ 13.8 billion years, from the inverse of the Hubble parameter, H, inferred from the speeds of receding galaxies [3]. Thus, the critical mass density for the neutron breakdown is ρ_c = ρ_M/α_G ≈ 3.3 ⋅ 10¹⁸ kg/m³.

Assuming that in a neutron star, the neutrons are packed as tightly as in the atomic nucleus, that pressure, equivalent to the mass density 10¹⁷ kg/m³, is thus not enough to break the neutron’s tetrahedral structure (Figure 2). The critical mass density, ρ_c, is exceeded first in a big enough black hole.

When the gluon is excised from a quark, the baryon geodesic opens up, becoming a reactive boson that cannot hold up against the huge gravity but flattens down to planar three-quark coordination (Figure 4). We expect the collapse from the tetrahedral to planar coordination to propagate rapidly over the lattice because the annihilation of quarks increases the surrounding high-energy photon density, catalyzing the gluon detachment. In other words, the proposed mechanism entails a chain reaction analogous to fission.

Annihilation of a particle with its antiparticle, e.g., the electron with the positron, unwinds matter-bound quanta to the quanta of the void. When matter, like anti-matter, is understood to comprise quanta of actions, it is apparent from the chiral symmetry of right- and left-handed toroidal coils that the quanta emerge from the annihilation in pairs where the two photons have opposite phases (Figure 5). These compound quanta without a net electromagnetic field easily escape detection [42,43,45,58,60].

FIGURE 5

FIGURE 5. Close-up of quark segments of opposite chirality (blue and red coils) unwinding, i.e., annihilating into a ray of co-propagating photons with opposite phases (blue and red waves). As the emitted pairs of photons are without net electromagnetic fields, they are detectable only through their energy density relative to the surrounding vacuum density, e.g., through interference effects.

Reactions, where the up quark and two down quarks stack face-to-face (Figure 4) and annihilate (Figure 5), output paired photons along the black hole spinning axis because, after the core collapse, there the curvature, i.e., gravitation, is least [93,94] (Figure 6). The bipolar rays of paired photons with energy density but without electromagnetic fields are part of space. Theoretically speaking, they are perturbations of spacetime and could be detected accordingly. For example, the black hole jets, dense in paired photons, ought to act as gravitational lenses. Likewise, our reasoning implying that voids emerge mostly along the spin axes of galaxies housing supermassive black holes could be tested through statistical analyses.

FIGURE 6

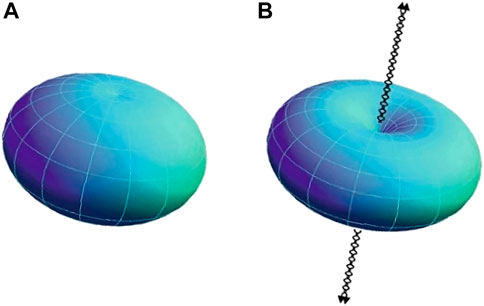
FIGURE 6. (A) A spinning black hole, an oblate body, deforms into (B) a doughnut shape with polar dimplings when neutrons collapse at its core. Decreasing gravity, equivalent to decreasing curvature, opens up paths along the spinning axis for photons to jet out (black paired waves) (Illustrations by Mathematica).

Our conclusion about annihilation as a transformation from bound to free quanta is consistent with the reverse reaction, the pair production, where a particle and its antiparticle materialize from the vacuum. When quanta embody both the particles and the vacuum, we predict that the vacuum energy density, ρ = c²/4πGt² ≈ 0.6 nJ/m³, cannot but be in thermodynamic balance with the gravity of all matter in the universe of age, t [91,92]. By the same token, the vacuum permittivity, ϵ_o, and permeability, μ_o, as well as impedance, Z_o, set the speed of light, c² = 1/ϵ_oμ_o. As envisioned long ago, the vacuum as a physical substance, embodying the photons paired and unpaired in agreement with Bose-Einstein statistics [45], mediates both gravitation and electromagnetism [95].

Along with the paired rays of uncoiled quanta, the readily detectable unpaired photons jet out as well. These high-energy photons are, for example, detached gluons, however redshifted due to the enormous gravity. After the abrupt outburst, we expect the jet to shift down in frequency and dwindle down in volume as the black hole regains a spheroidal shape and gravitation restrengthens along the spinning axis. Our reasoning about the jet spectral evolution could also be judged against observations.

As we understand, emissions over the eons from a precessing black hole give rise to the Fermi bubbles, the huge bulbs above and below the galactic plane filled with gamma rays. Moreover, we expect the high-energy jets, akin to high-energy cosmic rays, to produce pairs of particles and antiparticles from the quanta embodying the vacuum.

Since the spectrum of the Fermi bubbles is very high in energy, the radiation could stem from hadrons [96,97]. Specifically, it could originate from the flattened, dis-integrating neutrons because, in the bubbles, the number of photons decreases inversely proportional to the energy squared, characteristic of a planar source. By contrast, the number of photons around spherical sources, such as ordinary stars, decreases in inverse proportion to the cube of the energy.

4 Baryon conversion

To substantiate the proposed black hole reaction (Figure 4), we also describe the transformation, p⁺ + e⁻ → n + ν_e, from protons (p⁺) and electrons (e⁻) into neutrons (n) (Figure 7). This details how matter converts into neutrons in the first place.

FIGURE 7

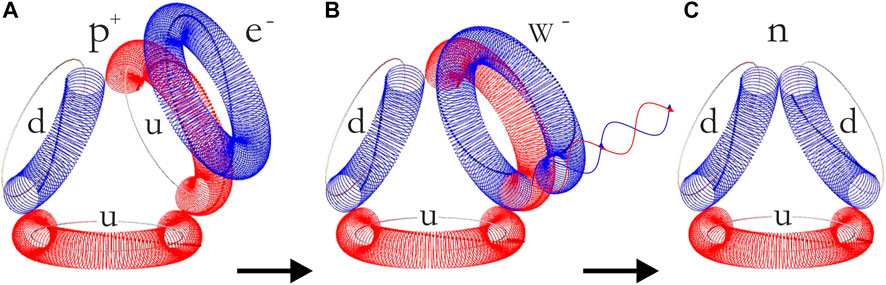
FIGURE 7. (A) An electron (e⁻) next to a proton (p⁺), loses a single quantum, a neutrino, and opens up becoming a highly reactive W⁻ boson, (B) that annihilates with the up quark (u). The bound quanta discharge into the vacuum as pairs of photons of opposite phases (red and blue wavy arrows). (C) The up quark dissolves totally. The remainder of the W⁻ boson, the ¹/₃-arc, is a down quark (D) that closes via gluon to form a neutron (n) (Illustrations by Mathematica).

The electron capture reaction begins when a neutrino (ν_e) is excised from an electron, i.e., e⁻ → W⁻ + ν_e, near a proton. The resulting W⁻ boson and one of the proton up quarks annihilate into a train of paired quanta (Figure 7). The reaction consumes the up quark entirely and terminates with the remainder of W⁻, a ¹/₃-arc, i.e., a down quark. The down quark closes via a gluon the rest of the geodesic comprising the intact up and down quarks to the neutron structure.

The elementary particle structures comprising quantized geodesics render their reactions resembling chemical reactions. Stoichiometry stems from the conservation of quanta. Analogously, the stoichiometry of chemical reactions follows from the conservation of atoms that holds under those conditions.

5 The vacuum structure

The proposed reaction, 2×n → 2×(up quark + 2×down quark + 3g) → 2 × (184γ + 3g), transforms neutrons (n) to huge amounts of photons (γ) including gluons (g) (Figure 4). Thus, not only the photon density but also its structure is of interest.

While general relativity is an excellent mathematical model of the quanta confined in the black hole gravity, the geometrization is tacit about the physical structure of the vacuum that embodies gravitation.

First of all, the vacuum has a structure because its spectrum, the black body radiation, is not arbitrary or formless but has the characteristic shape of Planck’s radiation law. When deriving it, S. N. Bose considered the combinations of a large number of photons, n_i, over all photons, n, occupying an energy level, ɛ_i, relative to the average energy, k_BT. The number of ways, in-phase and antiphase, the photons distribute among numerous rays (Figure 8), degenerate in energy, g_i, is the product of n_i combinations of n_i + 2g_i − 1 elements

$W=\prod _i\frac{\left(n_i+2g_i-1\right)!}{n_i!\left(2g_i-1\right)!}\exp \left(\frac{-n_i{\epsilon }_i}{k_{B}T}\right)\approx \prod _i\frac{\left(n_i+2g_i\right)!}{n_i!2g_i!}\exp \left(\frac{-n_i{\epsilon }_i}{k_{B}T}\right).(4)$

After applying Stirling’s approximation, the logarithm

$\ln W=\sum _i\left(n_i+2g_i\right)\ln \left(n_i+2g_i\right)-n_i\ln n_i-2g_i\ln 2g_i\frac{-n_i{\epsilon }_i}{k_{B}T}(5)$

can be differentiated to obtain the most probable, i.e., stationary-state partition,

$\frac{d\ln W}{dt}=\sum _i\frac{d\ln W}{d{n}_i}\frac{d{n}_i}{dt}=\sum _i\frac{d{n}_i}{dt}\left(\ln \frac{n_i+2g_i}{n_i}-\frac{{\epsilon }_i}{k_{B}T}\right)=0,(6)$

to see that the quanta distribute according to the Bose-Einstein statistics,

$n_i=\frac{2g_i}{e^{{\epsilon }_i/k_{B}T}-1}.(7)$

Thus, the paired-photon vacuum reproduces Planck’s law of radiation. However, the optimal occupancy (Eq. 7) derives from the physical principle of increasing entropy instead of imposing constraints, N = ∑_in_i and E = ∑_iɛ_in_i, as Lagrange multipliers.

FIGURE 8

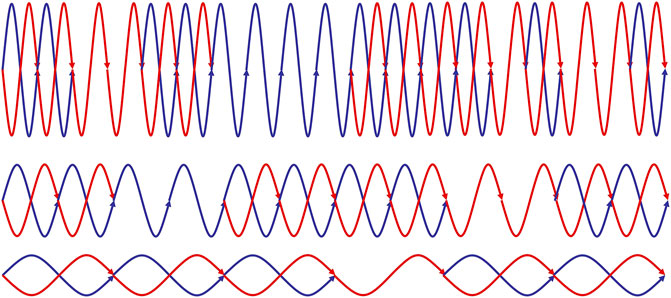
FIGURE 8. The vacuum comprises numerous rays of photons (blue-red waves) with energies, i.e., frequencies or wavelengths that distribute according to the Bose-Einstein statistics. The paired photons cannot be seen as light, but their coupling to the matter, known as mass, is sensed as inertia and gravitation. The unpaired, odd quanta in the rays (blue or red) are visible. Their coupling to matter manifests itself as electromagnetism.

As Bose wrote to Einstein [98], it is enough to assume that the ultimate elementary region in the phase-space has the content h³, the volume by the photon measure, h, to deduce from the Bose-Einstein statistics that the vacuum comprises rays of paired photons (Figure 8).

In line with Planck’s law, the pairs open up with increasing temperature, and conversely, the photons pair up with decreasing temperature. And in line with vacuum polarization, the photon pairs open up to counteract imposed electric field. Likewise, as Maxwell realized, displacement current demonstrates that the vacuum has physical substance. Moreover, the paired-photon vacuum responds to an accelerating charge by unpairing and radiating photons.

Moreover, we note that the vacuum comprising quanta of light can be modeled with the mean-energy density photon wave function,

$\psi \left(\mathbf{r},t\right)=\int \frac{\sqrt{E}d\mathbf{p}}{h^{3/2}}\gamma \left(\mathbf{p},t\right)e^{i\mathbf{p}\cdot \mathbf{r}/h},(8)$

where the integral is over the photon probability amplitudes, γ, of momentum, p, and energy, E, in the unit volume, h³. Since the massless photon does not localize, the dependence on the position, r, is formal [99,100].

A wave packet of the vacuum wave functions represents perturbations that a particle imposes on the vacuum. The wave packet obeys the Schrödinger equation and disperses because the particle with mass couples to the vacuum. In contrast, a photon as part of the vacuum (Figure 8) abides by the dispersionless wave equation. In other words, without the physical vacuum particles would not have mass as without the Higgs field. In this sense, the paired-photon boson resembles the Higgs boson. However, the massless photon does not decay, whereas the massive Higgs boson is short-lived.

The vacuum spectrum is the background reference. Additional spectral lines relate to characteristic sources. For example, helium was found in 1868 in the spectrum of the Sun. Likewise, the spectra of jets disclose characteristics of compact sources [101].

Since Planck’s law gives through the Stefan-Boltzmann law, j = σT⁴, the total radiated power per unit surface area of a body at temperature, T, thermodynamics is at hands for a black hole comprising photon gas at gluon wavelength, λ. The total energy, M_oc², of a black hole with mass, M_o, within the radius, r_o, is related to its gravitational potential by

$M_o{c}^2=\frac{G{M}_o^2}{r_o}\iff c^2{r}_o=G{M}_o.(9)$

The surface area, $A=4\pi r_o^2$, is proportional to the black hole entropy, S ∝ A/λ², where the gluon’s physical wavelength, λ, rather than the theoretical Planck length, L_P = Gℏ/c³, prevents the gravitational compression from proceeding to the renowned but aphysical singularity.

6 The substance of gravitation

Thinking that the paired-photon strings form the fabric of space, their density gradients are gravitational fields [47,91,102–104]. This substance of space seeks thermodynamic balance in the least time. From this viewpoint, the Lorenz gauge is not just a gimmick to deal with mathematical redundancy in the field variables, but a continuity condition that equates flows of density with changes in density. Thus, the bodies coupled by their masses to the moving vacuum move along geodesics. Conversely, an orbit is closed at a stationary state, where the influxes and effluxes of gravitons tally.

So, it is not that bodies would attract each other. Instead, they couple to the vacuum in motion toward thermodynamic balance. Nearby bodies move toward each other as the paired photons between them move to the greater, sparser universe. Conversely, distant galaxies move apart because more space comes in between from the greater universe’s numerous nuclear reactions where matter transforms into paired photons.

At a stationary state, influx and efflux of quantized space tally. This zero-velocity radius, r_o = GM_o/c², at a distance of about 4 million light-years, relates to R = GM/c² as M_o of the Local Group relates to M of the universe [105–107]. Likewise, the kinetic energy, mv², of an orbiter of mass, m, and velocity, v, balances gravitational potential energy, GmM_⊙/r, at a distance, r, due to a central mass, M_⊙, as by Kepler’s third law. Accordingly, galaxies rotate and move subject to the local and universal gravitation of all ordinary matter [55].

Transformations of matter-bound quanta into quanta of space inevitably cause expansion at the rate H = 1/t that decreases as d_tH = −1/t² [52] because quanta carry energy on their periods of time [108]. In other words, time is not an abstract concept but as physical of an attribute as energy. In contrast, the metric expansion, ds² = −c²dt² + a²dx², is a parametric model, tunable by the scale factor, a(t), to match the physical process.

Since the photon does not decay, it qualifies as the ground-state substance of space. In line with theory of gravitation, the photon pair, propagating at the speed of light, is its own antiparticle with twofold symmetry. So, as we see it, the paired photon, a massless spin-2 particle, is indistinguishable from the theorized carrier of gravitation [109]. Correspondingly, the photon, a massless spin-1 particle, is the carrier of electromagnetism. Moreover, gravitation and electro-magnetism cannot but share the same 1/r-form when the photon-embodied vacuum as a relativistic substance mediates both forces [45], as was thought already early on [95].

While our portrayal of the vacuum as a paired-quantum substance may not meet expectations of amalgamating quantum theory and general relativity, it complies with observations. The Michelson-Morley experiment [110] rejected a light-carrying medium, not a light-embodying medium. The proposed paired-photon vacuum also makes sense of the classical experiments of Arago [111], Fizeau [112], Trouton and Noble [113], and Sagnac [114], and modern measurements named after Casimir [115], and Aharonov and Bohm [116,117]. Revealingly, the dynamic Casimir effect yields photons out of the vacuum two by two at a time [118].

7 Black hole merger

For the sake of theoretical consistency, we analyze the spiraling of two bodies down to the merger along the least-time path, i.e., geodesic, using the same general, scale-free principle of least action applied above in inferring the particle structures as geodesics and motions of bodies along geodesics.

Along the spiral, the change in kinetic energy, 2K, equals the gradient in the potential energy, U, and dissipation, d_tQ,

$d_{t}2K=-\mathbf{v}\cdot \nabla U+i{d}_{t}Q,(10)$

where the prefactor, i, is used to distinguish the vector potential (radiation) from the scalar potential (gravitation) [52]. When the dissipative part of the total potential is denoted by i, the time-dependent equation can be solved formally, for example, to give the expected lifetime of a decaying particle [119]. Due to the dissipative decay, the system moves from one state to another. Conversely, when the dissipation vanishes, the system arrives at a stationary state, given by the virial theorem, 2K + U = 0, where the total potential has only the real part, U, because energy is conserved.

While gravitational waves are customarily modeled mathematically as ripples in spacetime [120], they can be regarded physically through Eq. 10 as energy density waves embodied by the paired photons, i.e., gravitons [45]. When the density wave strikes an interferometer, variation in the index of refraction is detected. Rather than the arms shrinking and stretching, the optical length varies as it does in ordinary interferometry.

As Einstein thought early on [91,121], the refractive index of free space, the background reference, n = 1, is determined by the total mass, M, of the universe. Thus, when the light quantum of frequency, f, and energy, Q = hf, moves from the universal gravitational potential of free space to the local gravitational potential, U, at a distance, r, from a local mass, M_o, the change in kinetic energy balances the changes in U and Q. At any given moment, the balance (Eq. 10),

$\frac{d}{dt}m{v}^2=-\frac{d}{dt}\frac{Gm{M}_o}{r}+\frac{d}{dt}m{c}^2|:c^2\Rightarrow \frac{c^2}{v^2}={\left(1-\frac{G{M}_o}{c^{2}r}\right)}^{-1}\approx 1+\frac{G{M}_o}{c^{2}r},(11)$

means that the photon velocity, v, near the body is lower than the free space speed, c, where the photon free-space energy, hf = mc², is given in terms of mass, m [52]. Also, temporal variation in the vacuum density, as concomitant variation in the speed of light can be detected, for example, by an interferometer.

The varying efflux of energy density originating from two orbiting bodies spiraling down to the merger is picked up as a chirp signal by a sensitive interferometer. The rate of change, d_tω, of the angular velocity, ω, can be calculated up to high orders by post-Newtonian formalism. Here, only for the sake of consistency, we derive the established mathematical form of the chirp from the same principle of least action that was used above.

To an excellent approximation, the binary’s path of free energy consumption (Eq. 10) in the gravitational potential follows a logarithmic spiral [35]. Along this least-time path, the angle, ϕ, between the tangent and radial line at any point, (r, ωt), is a constant of the orbital evolution at the rate, ω, over the period, t.

For simplicity, we consider an equal-mass binary, i.e., m₁ = m₂ = m, and denote their sum by M = m₁ + m₂ = 2m, and product by m₁m₂ = m². In the familiar case without dissipation, dQ = dmc² = 0, the angle is arctan(dQ/dU) = ϕ = π/2, and the closed, stationary orbit of a semimajor axis, r, is defined by the conserved gravitational potential, U = Gm²/r. Conversely, in the general case with dissipation, the angle of the logarithmic spiral, arctan(dQ/dU) = ϕ, is also a constant but ≠ π/2. Thus, the semimajor axis of a logarithmic spiral dissipating one quantum at a time can be written as

$r\propto \exp \left(-\frac{\omega t}{\varphi }\right)=\exp \left(-\frac{dU}{dQ}\omega t\right)=\exp \left(-\frac{Gm}{r{c}^2}\omega t\right),(12)$

where c² is the squared speed of light. When ϕ is a constant, the time derivate,

$\frac{dr}{dt}=-\frac{Gm}{c^2}\omega ,(13)$

as well as Kepler’s third law for the binary, r³ω² = GM, can be used to express the chirp,

$\frac{d\omega }{dt}=-\frac{GM}{c^{3}t}\frac{d\omega }{dr}\frac{dr}{dt}=\frac{3{\left(GM\right)}^{5/2}}{8\pi c^5{r}^{5/2}}{\omega }^2=\frac{3{\left(GM\right)}^{5/3}}{8\pi c^5}{\omega }^{11/3},(14)$

where the amplitude of the density wave has damped down by the factor, GM/c³t, at a distance, d = ct = 2πc/ω, and also shifted to red as much as the universe has been expanding and diluting in density [52,122]. Thus, the principle of least action reproduces the chirp waveform (Eq. 14) [123].

8 Discussion

The proposed black hole reaction transforming neutrons into high-energy jets raises some obvious questions. First (1), is the black-hole gravitational energy density enough to rival the strong force? Second (2), how can the paired photon efflux escape the immense gravity? Third (3), how can the proposal be falsified? Fourth (4), how does the proposal relate to the Standard Model of particle physics and of cosmology?

(1) First, we conclude that the gravity of a black hole, equivalent to several tens of solar masses, is indeed enough to break baryons. The ratio between the strong force and the gravitational coupling constant, $1/{\alpha }_G=e^2/4\pi {ϵ}_{o}G{m}_e^2=5.71\cdot 10^{44}$ [124], over 44 orders of magnitude, provides an estimate for the critical density, ρ_c, for the baryon breakdown. Since the neutron star mass density, 10¹⁷ kg/m³, is some 43 orders higher than that of the universal mass density, 10⁻²⁶ kg/m³ [3], one or two orders of magnitude more ought to be enough to trigger the proposed process above ρ_c.

This estimate is consistent with the formation of non-hadronic medium [125,126]. It also complies with current comprehension of the density in stellar black holes whose masses range from few to several tens of solar masses [127]. The same estimate for the critical mass for the baryon breakdown follows from assuming that a gamma-ray burst along with gravitational waves came from the merger of two stellar black holes [17]. In general, gravitational waves are expected to coincide with the most luminous rays that could possibly emerge from the most energetic constituents of matter.

(2) Second, we reason that indeed light quanta can escape from a black hole as highly collimated jets because the gravitation decreases substantially and sharply along the spinning axis when the black hole morphs from an oblate spinning spheroid into a doughnut shape [94]. The curvature ends up of being least along the spinning axis because the proposed reaction collapses the core of tetrahedral neutron lattice into planes of quarks (Figure 5).

Moreover, gravity plummets because mass decreases. As Euler understood, mass is a geometric characteristic, the signed geodesic curvature [82, 83]. Thus, the three quarks of the neutron, when forced from the tetrahedral coordination down to the plane, have a mass of only about 4/3m_e, where m_e is the electron mass [42,43,45,58–60]. Since the mass per particle decreases dramatically due to the baryon breakdown, i.e., more than a thousandfold, the photons can beam out along the spinning axis.

We also propose that the spectral evolution of a jet [129-130] reports from changes in the core rather than on the disk. We interpret an outburst followed by a decay in frequency so that first the gravitation plummets along the spinning axis as baryons break down abruptly and photons shoot out as X-rays. But soon, the photon frequencies shift more and more to red because gravity recovers as the black hole regains a spheroidal shape. We expect a power-law slope of the flux versus frequency because the power law is typical of a least-time process. Accordingly, a change in the slope implies a change from one mechanism to another [35].

Furthermore, assuming that the chain reaction consumes matter and light much faster than the accretion disk fuels quanta, the powerful reaction will cease from time to time for refueling. This conclusion about a pulsed activity also seems motivated for the supermassive black hole whose density peaks above the critical value only at its core [127]. However, even in that case, it may still take massively annihilated matter before the gravity along the spinning axis gives in for the photons to jet out. Thus, our proposal is in line with outbursts correlating with stellar black accretion disk dynamics and those of supermassive black holes.

(3) Third, our proposal is falsifiable. It would be false if experiments proved that particles or antiparticles are not made of light quanta or that the photon is not indivisible or indestructible. The tenet would be incorrect quantitatively if the transformation from neutrons to photons differed from the proposed stoichiometry or if the reaction would go off below the estimated critical density of a black hole of several tens of solar masses.

Furthermore, our proposal would be wrong if it were observed that space does not stem from matter transforming into paired rays of light quanta. This would mean, for example, that the cosmological constant would depart from the flatness, Λ ≡ H²/c² = 4πGρc/c⁴ = 1/R², where the energy density of the universe is precisely the critical ρc to cause expansion at the Hubble rate H ≡ 1/t decreasing d_tH = −1/t² with time, t, as the universe of radius, R = ct, ages. Although this statement contradicts the inference about an accelerated expansion powered by dark energy Riess et al., 1998, it complies with empirical evidence [52]. As quanta bound in matter transform into the vacuum quanta, the total energy density, ρ = c²/4πGt², decreases with time, t. So, also the angular size of an object decreases as θ ∝ 1/t [54]. In contrast, the angular size redshift relation is non-monotonous in the ΛCDM cosmology. Objects ever further away than the redshift z > 1.25 appear peculiarly as if ever larger but this is contrary to observations 132.

Thinking that the jets produce particles and antiparticles, and high-energy particles, i.e., cosmic rays, in turn generate secondary particles and photons 133, we find it consistent with our proposal that the black hole in the galactic center has been inferred to power fluxes of the most energetic particles [134]. These observations comply with interpreting the cosmic ray spectrum by the principle of least action [107].

As we are aware, the proposed reaction powering black hole emissions complies with observations so far. For the future, our proposal provides predictions and possibilities for falsification beyond black hole observations as it also outlines elementary particle structures and reactions and correlates the dispersion of galaxies and voids and entails that the universe evolves as flat.

(4) Fourth, our proposal compares to familiar forms of physics by expressing the variational principle of least action, S_o ≡∫p ⋅dq. However, the conjugate momenta p of the generalized coordinates q are understood as properties of the quanta rather than mere parameters of optimization. This tangible stance embodies gravitation with paired photons rather than geometrizes it. Consequently, when density cannot exceed baryon breakdown, black hole singularity is not an issue. Likewise, rather than theorizing radiation, e.g., Hawking radiation, from the geometrized gravitation, we propose physical processes that cause the propagation of light quanta. Also, in line with quantum field theory, the neutron field, for instance, corresponds to the vacuum characteristics around the neutron. So, our proposal embodies theoretical concepts with substance for them to be falsifiable.

All in all, our view of the black hole as a star is not a stray remark. The general least-action principle [35,36] also accounts for galaxy rotation and velocity dispersion and for bending and propagation of light without dark matter and dark energy parameters [52–55]. Thus, the holistic insight placing everything on the same axiomatic footing cannot but recognize the black hole as a star among stars.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LL and AA contributed equally to the key idea and analyzed it against data; AA wrote the paper.

Acknowledgments

We thank Pekka Teerikorpi and Jeroen van Bemmel for comments and corrections.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hertzsprung E. Über die sterne der unterabteilungen c und ac nach der spektralklassifikation von antonia c. maury. Astr Nachr ; AN (1908) 179:373–80. doi:10.1002/asna.19081792402

CrossRef Full Text | Google Scholar

2. Mihalas D, Routly P. Galactic astronomy. San Francisco, CA, USA: Freeman (1968).

Google Scholar

3. Unsöld A, Baschek B. The new cosmos: An introduction to astronomy and astrophysics. New York NY USA: Springer (2001).

Google Scholar

4. Clayton DD. Principles of stellar evolution and nucleosynthesis. New York: McGraw-Hill (1968).

Google Scholar

5. Schutz B. Gravity from the ground up: An introductory guide to gravity and general relativity. Cambridge, UK: Cambridge University Press (2003).

Google Scholar

6. Dogiel V, Chernyshov D, Cheng K, Wang Y, Ko C, Ip W-H (2011). Fermi bubbles as a result of star capture in the galactic center. arXiv:1109.6087 [astro-ph.HE].

Google Scholar

7. Ackermann M, Albert A, Atwood W, Baldini L, Ballet J, Barbiellini G, et al. The spectrum and morphology of the fermi bubbles. Astrophys J (2014) 793:64. doi:10.1088/0004-637X/793/1/64

CrossRef Full Text | Google Scholar

8. Abramowicz MA, Fragile PC. Foundations of black hole accretion disk theory. Living Rev Relativ (2013) 16:1. doi:10.12942/lrr-2013-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Loisel GP, Bailey JE, Liedahl DA, Fontes CJ, Kallman TR, Nagayama T, et al. Benchmark experiment for photoionized plasma emission from accretion-powered x-ray sources. Phys Rev Lett (2017) 119:075001. doi:10.1103/PhysRevLett.119.075001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dallilar Y, Eikenberry SS, Garner A, Stelter RD, Gottlieb A, Gandhi P, et al. A precise measurement of the magnetic field in the corona of the black hole binary v404 cygni. Science (2017) 358:1299–302. doi:10.1126/science.aan0249

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Gandhi P, Bachetti M, Dhillon VS, Fender RP, Hardy LK, Harrison FA, et al. An elevation of 0.1 light-seconds for the optical jet base in an accreting galactic black hole system. Nat Astron (2017) 1:859–64. doi:10.1038/s41550-017-0273-3

CrossRef Full Text | Google Scholar

12. Nixon CJ, Pringle JE. What is wrong with steady accretion discs? A&A (2019) 628:A121. doi:10.1051/0004-6361/201935852

CrossRef Full Text | Google Scholar

13. Blandford R, Meier D, Readhead A. Relativistic jets from active galactic nuclei. Annu Rev Astron Astrophys (2019) 57:467–509. doi:10.1146/annurev-astro-081817-051948

CrossRef Full Text | Google Scholar

14. Ryan SG, Norton AJ. Stellar evolution and nucleosynthesis. Cambridge, UK: Cambridge University Press (2010).

Google Scholar

15. Kruskal MD. Maximal extension of schwarzschild metric. Phys Rev (1960) 119:1743–5. doi:10.1103/PhysRev.119.1743

CrossRef Full Text | Google Scholar

16. Loeb A. Electromagnetic counterparts to black hole mergers detected by ligo. Astrophys J (2016) 819:L21. doi:10.3847/2041-8205/819/2/l21

CrossRef Full Text | Google Scholar

17. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Observation of gravitational waves from a binary black hole merger. Phys Rev Lett (2016) 116:061102. doi:10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lorimer DR, Bailes M, McLaughlin MA, Narkevic DJ, Crawford F. A bright millisecond radio burst of extragalactic origin. Science (2007) 318:777–80. doi:10.1126/science.1147532

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lucchini M, Russell TD, Markoff SB, Vincentelli F, Gardenier D, Ceccobello C, et al. Correlating spectral and timing properties in the evolving jet of the microblazar maxi j1836-194. Mon Not R Astron Soc (2020) 501:5910–26. doi:10.1093/mnras/staa3957

CrossRef Full Text | Google Scholar

20. Neronov A, Vovk I, Malyshev D. Central engine of a gamma-ray blazar resolved through the magnifying glass of gravitational microlensing. Nat Phys (2015) 11:664–7. doi:10.1038/nphys3376

CrossRef Full Text | Google Scholar

21. Pavan L, Pühlhofer G, Bordas P, Audard M, Balbo M, Bozzo E, et al. Closer view of the igr j11014-6103 outflows. A&A (2016) 591:A91. doi:10.1051/0004-6361/201527703

CrossRef Full Text | Google Scholar

22. Haehnelt MG, Kauffmann G. The correlation between black hole mass and bulge velocity dispersion in hierarchical galaxy formation models. Mon Not R Astron Soc (2000) 318:L35–8. doi:10.1046/j.1365-8711.2000.03989.x

CrossRef Full Text | Google Scholar

23. Faber SM, Jackson RE. Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys J (1976) 204:668. doi:10.1086/154215

CrossRef Full Text | Google Scholar

24. Gebhardt K, Bender R, Bower G, Dressler A, Faber SM, Filippenko AV, et al. A relationship between nuclear black hole mass and galaxy velocity dispersion. Astrophys J (2000) 539:L13–6. doi:10.1086/312840

CrossRef Full Text | Google Scholar

25. Tully RB, Fisher JR. A new method of determining distance to galaxies. Astron Astrophysics (1977) 500:105.

Google Scholar

26. McGaugh SS. The baryonic tully-Fisher relation of galaxies with extended rotation curves and the stellar mass of rotating galaxies. Astrophys J (2005) 632:859–71. doi:10.1086/432968

CrossRef Full Text | Google Scholar

27. Salpeter EE. The luminosity function and stellar evolution. Astrophys J (1955) 121:161. doi:10.1086/145971

CrossRef Full Text | Google Scholar

28. Schmidt M. The rate of star formation. Astrophys J (1959) 129:243. doi:10.1086/146614

CrossRef Full Text | Google Scholar

29. Gaddum JH. Lognormal distributions. Nature (1945) 156:463–6. doi:10.1038/156463a0

CrossRef Full Text | Google Scholar

30. Limpert E, Stahel W, Abbt M. Lognormal distributions across the sciences: Keys and clues. BioScience (2001) 51:341–52. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2

CrossRef Full Text | Google Scholar

31. Newman MEJ. Power laws, pareto distributions and zipf’s law. Contemp Phys (2005) 46:323–51. doi:10.1080/00107510500052444

CrossRef Full Text | Google Scholar

32. Baryshev Y, Teerikorpi P. Discovery of cosmic fractals. Singapore: World Scientific Publishing Co. Pte Ltd (2002).

Google Scholar

33. Koen C, Kondlo L. Fitting power-law distributions to data with measurement errors. Monthly Notices R Astronomical Soc (2009) 397:495–505. doi:10.1111/j.1365-2966.2009.14956.x

CrossRef Full Text | Google Scholar

34. Grönholm T, Annila A. Natural distribution. Math Biosciences (2007) 210:659–67. doi:10.1016/j.mbs.2007.07.004

CrossRef Full Text | Google Scholar

35. Mäkelä T, Annila A. Natural patterns of energy dispersal. Phys Life Rev (2010) 7:477–98. doi:10.1016/j.plrev.2010.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tuisku P, Pernu TK, Annila A. In the light of time. Proc R Soc A (2009) 465:1173–98. doi:10.1098/rspa.2008.0494

CrossRef Full Text | Google Scholar

37. Bekenstein JD. Black holes and the second law. Lett Nuovo Cimento (1972) 4:737–40. doi:10.1007/BF02757029

CrossRef Full Text | Google Scholar

38. Thorne KS, Price RH. Black holes: The membrane paradigm. New Haven CT USA: Yale University Press (1986).

Google Scholar

39. Baryshev Y, Teerikorpi P. Fundamental questions of practical cosmology: Exploring the realm of galaxies. Netherlands: Springer (2011).

Google Scholar

40. Mitra A. Radiation pressure supported stars in einstein gravity: Eternally collapsing objects. Mon Not R Astron Soc (2006) 369:492–6. doi:10.1111/j.1365-2966.2006.10332.x

CrossRef Full Text | Google Scholar

41. Lewis GN. The conservation of photons. Nature (1926) 118:874–5. doi:10.1038/118874a0

CrossRef Full Text | Google Scholar

42. Annila A. All in action. Entropy (2010) 12:2333–58. doi:10.3390/e12112333

CrossRef Full Text | Google Scholar

43. Annila A. The meaning of mass. Int J Theor Math Phys (2012) 2:67–78. doi:10.5923/j.ijtmp.20120204.03

CrossRef Full Text | Google Scholar

44. Grahn P, Annila A, Kolehmainen E. On the exhaust of electromagnetic drive. AIP Adv (2016) 6:065205. doi:10.1063/1.4953807

CrossRef Full Text | Google Scholar

45. Grahn P, Annila A, Kolehmainen E. On the carrier of inertia. AIP Adv (2018) 8:035028. doi:10.1063/1.5020240

CrossRef Full Text | Google Scholar

46. Laurent P, Titarchuk L. Electron–positron pair creation close to a black hole horizon: Redshifted annihilation line in the emergent x-ray spectra of a black hole. i. Astrophys J (2018) 859:89. doi:10.3847/1538-4357/aac090

CrossRef Full Text | Google Scholar

47. Einstein A. Relativität und gravitation. erwiderung auf eine bemerkung von m. abraham. Ann Phys (1912) 38:1059–64. doi:10.1002/andp.19123431014

CrossRef Full Text | Google Scholar

48. Varela J, Betancort-Rijo J, Trujillo I, Ricciardelli E. The orientation of disk galaxies around large cosmic voids. Astrophys J (2011) 744:82. doi:10.1088/0004-637x/744/2/82

CrossRef Full Text | Google Scholar

49. Keenan RC, Barger AJ, Cowie LL. Evidence for a ∼ 300 megaparsec scale under-density in the local galaxy distribution. Astrophys J (2013) 775:62. doi:10.1088/0004-637x/775/1/62

CrossRef Full Text | Google Scholar

50. Haider M, Steinhauser D, Vogelsberger M, Genel S, Springel V, Torrey P, et al. .Large-scale mass distribution in the illustris simulation. Mon Not R Astron Soc (2016) 457:3024–35. doi:10.1093/mnras/stw077

CrossRef Full Text | Google Scholar

51. Newton I. Opticks: Or, A treatise of the reflections, refractions, inflections and colours of light. London, UK: William and John Innys (1721).

Google Scholar

52. Annila A. Least-time paths of light. Mon Not R Astron Soc (2011) 416:2944–8. doi:10.1111/j.1365-2966.2011.19242.x

CrossRef Full Text | Google Scholar

53. Annila A. Probing mach’s principle. Mon Not R Astron Soc (2012) 423:1973–7. doi:10.1111/j.1365-2966.2012.21022.x

CrossRef Full Text | Google Scholar

54. Koskela M, Annila A. Least-action perihelion precession. Mon Not R Astron Soc (2011) 417:1742–6. doi:10.1111/j.1365-2966.2011.19364.x

CrossRef Full Text | Google Scholar

55. Annila A. Rotation of galaxies within gravity of the universe. Entropy (2016) 18:191–205. doi:10.3390/e18050191

CrossRef Full Text | Google Scholar

56. Maupertuis P-LMd. Accord de différentes lois de la nature qui avaient jusqu’ici paru incompatibles. Mem Acad R Sci Paris (1744) 417–26.

Google Scholar

57. Maupertuis P-LMd. Les loix du mouvement et du repos déduites d’un principe métaphysique. Histoire de l’Académie Royale des Sci des Belles Lettres (1746) 267–94.

Google Scholar

58. Annila A. Natural thermodynamics. Physica A: Stat Mech its Appl (2016) 444:843–52. doi:10.1016/j.physa.2015.10.105

CrossRef Full Text | Google Scholar

59. Hestenes D. The zitterbewegung interpretation of quantum mechanics. Found Phys (1990) 20:1213–32. doi:10.1007/BF01889466

CrossRef Full Text | Google Scholar

60. Annila A, Kolehmainen E. Atomism revisited. Phys Essays (2016) 29:532–41. doi:10.4006/0836-1398-29.4.532

CrossRef Full Text | Google Scholar

61. Maldacena J, Strominger A, Witten E. Black hole entropy in m-theory. J High Energ Phys (1997) 1997:002. doi:10.1088/1126-6708/1997/12/002

CrossRef Full Text | Google Scholar

62. Lunin O, Mathur SD. Statistical interpretation of the bekenstein entropy for systems with a stretched horizon. Phys Rev Lett (2002) 88:211303. doi:10.1103/PhysRevLett.88.211303

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Chapline G (2004). Dark energy stars. arXiv:astro-ph/0503200.

Google Scholar

64. Chapline G, Barbieri J. Collective baryon decay and gravitational collapse. Int J Mod Phys D (2014) 23:1450025. doi:10.1142/S0218271814500254

CrossRef Full Text | Google Scholar

65. Griffiths D. Introduction to elementary particles. Weinheim, Germany: Wiley (2020).

Google Scholar

66. Fermi E. Über die magnetischen momente der atomkerne. Z Physik (1930) 60:320–33. doi:10.1007/BF01339933

CrossRef Full Text | Google Scholar

67. Huang K. On the zitterbewegung of the Dirac electron. Am J Phys (1952) 20:479–84. doi:10.1119/1.1933296

CrossRef Full Text | Google Scholar

68. Barut AO, Bracken AJ. Zitterbewegung and the internal geometry of the electron. Phys Rev D (1981) 23:2454–63. doi:10.1103/PhysRevD.23.2454

CrossRef Full Text | Google Scholar

69. Yau S, Nadis S. The shape of inner space: String theory and the geometry of the universe’s hidden dimensions. New York, USA: Basic Books (2010).

Google Scholar

70. Povh B, Lavelle M, Rith K, Scholz C, Zetsche F. Particles and nuclei: An introduction to the physical concepts. Berlin Heidelberg: Springer (2008).

Google Scholar

71. Mezei F. La nouvelle vague in polarized neutron scattering. Physica B+C (1986) 137:295–308. doi:10.1016/0378-4363(86)90335-9

CrossRef Full Text | Google Scholar

72. Dirac PAM. The Lagrangian in quantum mechanics. Phys Z Sowjetunion (1933) 3:64–72.

Google Scholar

73. Feynman R. Quantum mechanics and path integrals. New York, United States: McGraw-Hill (1965).

Google Scholar

74. Williams LP. Ampère’s electrodynamic molecular model. Contemp Phys (1962) 4:113–23. doi:10.1080/00107516208201724

CrossRef Full Text | Google Scholar

75. Parson AL. A magneton theory of the structure of the atom. Smithsonian Miscellaneous Collections (1915) 65:1.

Google Scholar

76. Compton AH. Scientific papers of Arthur holly Compton: X-ray and other studies. Chicago: University Press (1973).

Google Scholar

77. Allen HS. The case for a ring electron. Proc Phys Soc Lond (1918) 31:49–68. doi:10.1088/1478-7814/31/1/303

CrossRef Full Text | Google Scholar

78. Wiles A. Modular elliptic curves and fermat’s last theorem. Ann Math (1995) 141:443–551. doi:10.2307/2118559

CrossRef Full Text | Google Scholar

79. Derickx M, Najman F, Siksek S. Elliptic curves over totally real cubic fields are modular. Alg Number Th (2020) 14:1791–800. doi:10.2140/ant.2020.14.1791

CrossRef Full Text | Google Scholar

80. Dattoli G (2010). The fine structure constant and numerical alchemy. arXiv doi:10.48550/ARXIV.1009.1711

CrossRef Full Text | Google Scholar

81. Bender D, Derrick M, Fernandez E, Gieraltowski G, Hyman L, Jaeger K, et al. Tests of qed at 29 gev center-of-mass energy. Phys Rev D (1984) 30:515–27. doi:10.1103/PhysRevD.30.515

CrossRef Full Text | Google Scholar

82. Do Carmo M. Differential geometry of curves and surfaces. Englewood Cliffs, NJ, USA: Prentice-Hall (1976).

Google Scholar

83. Perkins D. Introduction to high energy physics. Cambridge, United Kingdom: Cambridge University Press (2000).

Google Scholar

84. Kagiyama S, Nakamura A, Omodaka T. Compressible bag model and dibaryon stars. Z Phys C - Particles Fields (1992) 56:557–60. doi:10.1007/BF01474728

CrossRef Full Text | Google Scholar

85. Faessler A, Buchmann AJ, Krivoruchenko MI. Constraints on the ω- and σ-meson coupling constants with dibaryons. Phys Rev C (1997) 56:1576–81. doi:10.1103/PhysRevC.56.1576

CrossRef Full Text | Google Scholar

86. Tolman RC. Static solutions of einstein’s field equations for spheres of fluid. Phys Rev (1939) 55:364–73. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

87. Oppenheimer JR, Volkoff GM. On massive neutron cores. Phys Rev (1939) 55:374–81. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

88. Haensel P, Potekhin AY, Yakovlev DG. Neutron stars. New York NY USA: Springer (2007).

Google Scholar

89. Lagarias J, Zong C. Mysteries in packing regular tetrahedra. Not Am Math Soc (2012) 59:1392–549. doi:10.1090/noti918

CrossRef Full Text | Google Scholar

90. Haji-Akbari A, Chen ER, Engel M, Glotzer SC. Packing and self-assembly of truncated triangular bipyramids. Phys Rev E (2013) 88:012127. doi:10.1103/PhysRevE.88.012127

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Dicke RH. Gravitation without a principle of equivalence. Rev Mod Phys (1957) 29:363–76. doi:10.1103/RevModPhys.29.363

CrossRef Full Text | Google Scholar

92. Feynman R, Morínigo F, Wagner W, Hatfield B. Feynman lectures on gravitation. Reading, Massachusetts: Addison-Wesley (1995).

Google Scholar

93. Semenov V, Dyadechkin S, Punsly B. Simulations of jets driven by black hole rotation. Science (2004) 305:978–80. doi:10.1126/science.1100638

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Bannikova EY, Vakulik VG, Shulga VM. Gravitational potential of a homogeneous circular torus: A new approach. Mon Not R Astron Soc (2011) 411:557–64. doi:10.1111/j.1365-2966.2010.17700.x

CrossRef Full Text | Google Scholar

95. Faraday M. On the possible relation of gravity to electricity. Philosophical Trans R Soc A (1851) 1:141.

Google Scholar

96. Su M, Slatyer TR, Finkbeiner DP. Giant gamma-ray bubbles from fermi-lat: Active galactic nucleus activity or bipolar galactic wind? Astrophys J (2010) 724:1044–82. doi:10.1088/0004-637x/724/2/1044

CrossRef Full Text | Google Scholar

97. Ayala Solares H, Hui CM, Hüntemeyer P. Fermi bubbles with HAWC. Proc Sci (2016) ICRC2015:749. doi:10.22323/1.236.0749

CrossRef Full Text | Google Scholar

98. Venkataraman G. Bose and his statistics. Hyderabad, India: Universities Press (1992).

Google Scholar

99. Sipe JE. Photon wave functions. Phys Rev A (Coll Park) (1995) 52:1875–83. doi:10.1103/PhysRevA.52.1875

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Smith BJ, Raymer MG. Photon wave functions, wave-packet quantization of light, and coherence theory. New J Phys (2007) 9:414. doi:10.1088/1367-2630/9/11/414

CrossRef Full Text | Google Scholar

101. Abdalla H, Adam R, Aharonian F, Benkhali FA, Angüner EO, Arakawa M, et al. Resolving acceleration to very high energies along the jet of centaurus a. Nature (2020) 582:356–9. doi:10.1038/s41586-020-2354-1

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Wilson H. An electromagnetic theory of gravitation. Phys Rev (1921) 17:54–9. doi:10.1103/PhysRev.17.54

CrossRef Full Text | Google Scholar

103. Sarazin X, Couchot F, Djannati-Ataï A, Urban M. Can the apparent expansion of the universe be attributed to an increasing vacuum refractive index? Eur Phys J C (2018) 78:444. doi:10.1140/epjc/s10052-018-5932-8

CrossRef Full Text | Google Scholar

104. Edwards MR. Optical gravity in a graviton spacetime. Optik (2022) 260:169059. doi:10.1016/j.ijleo.2022.169059

CrossRef Full Text | Google Scholar

105. Sandage A. The redshift-distance relation. ix. perturbation of the very nearby velocity field by the mass of the local group. Astrophys J (1986) 307:1–19. doi:10.1086/164387

CrossRef Full Text | Google Scholar

106. Karachentsev ID, Kashibadze OG, Makarov DI, Tully RB. The hubble flow around the local group. Mon Not R Astron Soc (2009) 393:1265–74. doi:10.1111/j.1365-2966.2008.14300.x

CrossRef Full Text | Google Scholar

107. Annila A. Cosmic rays report from the structure of space. Adv Astron (2015) 135025:11. doi:10.1155/2015/135025

CrossRef Full Text | Google Scholar

108. Annila A. The matter of time. Entropy (2021) 23:943. doi:10.3390/e23080943

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Misner C, Thorne K, Wheeler J. Gravitation. San Francisco, CA: W. H. Freeman (1973).

Google Scholar

110. Michelson AA, Morley EW. On the relative motion of the Earth and the luminiferous ether. Am J Sci (1887) 34:333–45. doi:10.2475/ajs.s3-34.203.333

CrossRef Full Text | Google Scholar

111. Arago DFJ. M´emoire sur la vitesse de la lumi‘ere, lu ‘a la premi‘ere classe de l’institut, le 10 d´ecembre 1810. Comptes Rendus de l’Acad´emie des Sci (1853) XXXVI:38–49.

Google Scholar

112. Fizeau H. Sur les hypothèses relatives à l’éther lumineux. Comptes Rendus (1851) 33:349–55.

Google Scholar

113. Trouton FT, Noble HR. V. the mechanical forces acting on a charged electric condenser moving through space. Philosophical Trans R Soc Lond Ser A, Containing Pap a Math or Phys Character (1904) 202:165–81. doi:10.1098/rsta.1904.0005

CrossRef Full Text | Google Scholar

114. Sagnac G. L’éther lumineux démontré par l’effet du vent relatif d’éther dans un interféromètre en rotation uniforme. Comptes Rendus (1913) 157:708–10.

Google Scholar

115. Casimir HBG. On the attraction between two perfectly conducting plates. Proc Koninklijke Nederlandse Akademie van Wetenschappen (1948) 51:793–5.

Google Scholar

116. Aharonov Y, Bohm D. Significance of electromagnetic potentials in the quantum theory. Phys Rev (1959) 115:485–91. doi:10.1103/PhysRev.115.485

CrossRef Full Text | Google Scholar

117. Overstreet C, Asenbaum P, Curti J, Kim M, Kasevich MA (2022). Observation of a gravitational aharonov-bohm effect. Science 375, 226–9. doi:10.1126/science.abl7152

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Wilson CM, Johansson G, Pourkabirian A, Simoen M, Johansson JR, Duty T, et al. Observation of the dynamical casimir effect in a superconducting circuit. Nature (2011) 479:376–9. doi:10.1038/nature10561

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Griffiths D. Introduction to quantum mechanics. Upper Saddle River, New Jersey: Prentice-Hall (1995).

Google Scholar

120. Barish BC, Weiss R. Ligo and the detection of gravitational waves. Phys Today (1999) 52:44–50. doi:10.1063/1.882861

CrossRef Full Text | Google Scholar

121. Einstein A. Uber den einfluss der schwerkraft auf die ausbreitung des lichtes. Ann Phys (1911) 35:898–908. doi:10.1002/andp.19113401005

CrossRef Full Text | Google Scholar

122. Schutz B (1997). Low-frequency sources of gravitational waves: A tutorial. arXiv:gr-qc/9710079.

Google Scholar

123. Abbott BP, Abbott R, Abbott TD, Abraham S, Acernese F, Ackley K, et al. Gwtc-1: A gravitational-wave transient catalog of compact binary mergers observed by ligo and virgo during the first and second observing runs. Phys Rev X (2019) 9:031040. doi:10.1103/PhysRevX.9.031040

CrossRef Full Text | Google Scholar

124. Barrow JD. The constants of nature. New York NY USA: Pantheon Books (2002).

Google Scholar

125. Karsch F, Laermann E, Peikert A. Quark mass and flavour dependence of the qcd phase transition. Nucl Phys B (2001) 605:579–99. doi:10.1016/S0550-3213(01)00200-0

CrossRef Full Text | Google Scholar

126. Foka P, Janik MA. An overview of experimental results from ultra-relativistic heavy-ion collisions at the cern lhc: Bulk properties and dynamical evolution. Rev Phys (2016) 1:154–71. doi:10.1016/j.revip.2016.11.002

CrossRef Full Text | Google Scholar

127. Celotti A, Miller JC, Sciama DW. Astrophysical evidence for the existence of black holes. Class Quan Gravity (1999) 16:A3–A21. doi:10.1088/0264-9381/16/12a/301

CrossRef Full Text | Google Scholar

128. Slobodyan Y. Geodesic curvature. Encyclopedia of mathematics. Dordrecht, Netherlands: Springer (2001).

Google Scholar

129. Fender RP, Homan J, Belloni TM. Jets from black hole x–ray binaries: Testing, refining and extending empirical models for the coupling to x–rays. Mon Not R Astron Soc (2009) 396:1370–82. doi:10.1111/j.1365-2966.2009.14841.x

CrossRef Full Text | Google Scholar

130. Kalemci E, Dinçer T, Tomsick JA, Buxton MM, Bailyn CD, Chun YY. Complete multiwavelength evolution of galactic black hole transients during outburst decay. i. conditions for “compact” jet formation. Astrophys J (2013) 779:95. doi:10.1088/0004-637x/779/2/95

CrossRef Full Text | Google Scholar

131. Riess AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A, Garnavich PM, et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J (1998) 116:1009–38. doi:10.1086/300499

CrossRef Full Text | Google Scholar

132. Narlikar J. An introduction to cosmology. Cambridge, UK: Cambridge University Press (2002).

Google Scholar

133. Hubbell JH. Electron positron pair production by photons: A historical overview. Radiat Phys Chem (2006) 75:614–23. doi:10.1016/j.radphyschem.2005.10.008

CrossRef Full Text | Google Scholar

134. Abramowski A, Aharonian F, Benkhali FA, Akhperjanian AG, Angüner EO, Backes M, et al. Acceleration of petaelectronvolt protons in the galactic centre. Nature (2016) 531:476–9. doi:10.1038/nature17147

PubMed Abstract | CrossRef Full Text | Google Scholar