Dark solitons impinging on interfaces in a superfluid Fermi gas

Ultracold quantum gases in the superfluid regime exhibit solitons, localized excitations that require nonlinearity of the underlying field equation in order to preserve their shape as they propagate. Here, we investigate the behavior of solitons at an inhomogeneity: an interface that separates two different interaction regimes of a superfluid Fermi gas. It is known that the soliton properties depend on the interaction regime, but what happens as a soliton impinges on such an interface is not clear. Using an effective field theory to describe the superfluid Fermi gas, we reveal the nontrivial dynamics of such a collision. Whether the original soliton makes it through the interface depends on the amplitude of the soliton. Regardless of whether the original soliton is transmitted or not, there will always be a shock wave with a phonon train created behind the interface and reflected secondary solitons. The details of this dynamics depends strongly on the equation of state corresponding to underlying microscopic theory describing the superfluid Fermi gas, and we argue that these collisions are realistic experimental probes to test microscopic theories of pairing in ultracold Fermi gases.

1 Introduction

Ultracold quantum gases are highly tunable systems that allow to study quantum phenomena on a macroscopic scale. By controlling many parameters, such as the geometry, the interaction strength, the dimensionality, and the number of particles, ultracold atomic gases have been used to quantum simulate condensed matter models under circumstances and in regimes not accessible in solids [1, 2]. With the advent of box potentials for quantum gases [3], uniform systems can be studied experimentally, allowing for a more direct comparison to many theoretical models. Using acousto-optic modulators these potentials can be customized in shape and made time-dependent [4]. This has opened up the path to explore non-equilibrium dynamics of (typically nonlinear) quantum field theories [5]. A recent example is the study of analog Hawking radiation in Bose-Einstein condensates [6, 7]: by creating regions where the background flow velocity is higher than the speed of sound, a sonic black hole can be created and observed to emit phonons analogous to Hawking radiation. In order to create the horizon, a step-like potential is added to the uniform box potential, and this step creates an interface that is moved at speeds intermediate to the speed of sound left and right of the interface [6].

Not only Bose gases but also fermionic quantum gases have been trapped in uniform, tunable box potentials [8]. Atomic Fermi gases can also be brought in the superfluid regime [9]. This requires pairing between fermionic atoms, and the experimental tunability of the interaction strength between the atoms (via a Feshbach resonance) allows to explore the superfluidity from the regime of strongly bound pairs forming a Bose-Einstein condensate (BEC) to the regime of weakly bound pairs forming a Bardeen–Cooper–Schrieffer (BCS) superfluid. Superfluid Fermi gases can be described by an effective field theory, valid for excitations with energy below twice the superfluid gap [10]. These include Anderson-Bogoliubov phonons as well as vortices and solitons. Whereas the phonons are small amplitude oscillations suitably described by a linearization of the field equation, solitons rely intrinsically on the nonlinearity of the full field equation [11].

Dark solitons -dips in the density which preserve their shapes while moving-are the subject of intense investigation, in particular in superfluid atomic gases [12–22]. Dark solitons in fermionic superfluids behave differenty in the BCS regime and in the BEC regime [20]. For strongly bound pairs, the solitons behave as in a regular Bose-Einstein condensate: they collide with each other without losing energy and pass through each other without changing shape. In the BCS regime, the proximity of the pair-breaking continuum changes the dynamics and in a collision energy is lost in the form of a train of Anderson-Bogoliubov phonons [22]. This raises the question of how solitons will behave when impinging on an interface between two Fermi superfluids that are in a different interaction regime. Such systems have now become experimentally realizable as described in the previous paragraph, making the above question of experimental interest. In this contribution, we use the effective field theory for superfluid Fermi gases to describe theoretically the dynamics of a soliton meeting an interface to a region where the pairs are bound at different interaction strength. We will show that this leads to a scattering event with both transmitted and reflected solitons, depending on the parameters left and right of the interface. In Section 2, we start with reviewing the framework of the effective field theory and the description of solitons in this approach. Section 3 discusses the creation of an the interface between regions with different interaction strength. In Section 4, we discuss how to introduce a dark soliton to the left of the interface, moving towards the interface. In Section 5 the results of our simulation are presented and discussed. Finally, in Section 6 we draw conclusion.

2 Effective field theory for superfluid Fermi gases

We consider a system of fermionic atoms with mass m, interacting through an s-wave contact potential with scattering length a_s. As identical fermions cannot interact in the s-wave channel, two different hyperfine states need to be trapped, and pairs will form between atoms with different spin state. We restrict ourselves to the case where there are an equal number of fermions in both spin states. Below the superfluid critical temperature, these pairs form a pair condensate, that can be described by a macroscopic wave function Ψ(r, t). This “pair wavefunction” has a straightforward hydrodynamic interpretation: its modulus squared represents the density of condensed pairs, and the velocity field is proportional to the gradient of the phase of the pair wave function. It obeys the following field equation [10, 21]:

$i\frac{\partial \left(|\mathrm{\Psi }{|}^{2}D\left(|\mathrm{\Psi }{|}^2\right)\right)}{\partial |\mathrm{\Psi }{|}^2}\frac{\partial \mathrm{\Psi }}{\partial t}=-C{\nabla }_{\mathbf{r}}^2\mathrm{\Psi }+Q\frac{{\partial }^2\mathrm{\Psi }}{\partial t^2}+\left(\mathcal{A}\left(|\mathrm{\Psi }{|}^2\right)+2E{\nabla }_{\mathbf{r}}^2|\mathrm{\Psi }{|}^2-2R\frac{{\partial }^2|\mathrm{\Psi }{|}^2}{\partial t^2}\right)\mathrm{\Psi }.(1)$

The coefficients in this equation are fixed by the chemical potential μ, the global superfluid gap Δ (which we choose real), and the temperature T. The nonlinearity arises to a lesser extent from the dependence of the coefficient D on Ψ. The more important source of nonlinearity stems from

$\mathcal{A}\left(|\mathrm{\Psi }{|}^2\right)=-\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\left(\frac{1}{\beta }\log \left[2\cosh \left(\beta E_{\mathbf{k}}\right)\right]-{\xi }_{\mathbf{k}}-\frac{{\left|\mathrm{\Psi }\right|}^2}{2k^2}\right)-\frac{{\left|\mathrm{\Psi }\right|}^2}{8\pi k_F{a}_s}.(2)$

Here k_F = (3πn)^1/3, with n the density of particles. We will use units such that ℏ = k_F = 2m = 1. In these units ξ_k = k² − μ, and $E_{\mathbf{k}}=\sqrt{{\xi }_{\mathbf{k}}^2+|\mathrm{\Psi }{|}^2}$. The other coefficients in Eq. 1 can be expressed in terms of the thermal function

$f_1\left(\epsilon \right)=\frac{\tanh \left(\beta \epsilon \right)}{2\epsilon }(3)$

with β = 1/(k_BT), and its derivatives

$f_{n+1}\left(\epsilon \right)=-\frac{1}{2n\epsilon }\frac{\partial f_n}{\partial \epsilon }.(4)$

The main dynamics is governed by

$C=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{2k^2}{3}{f}_2\left({\tilde{E}}_{\mathbf{k}}\right),(5)$

$D=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{{\xi }_{\mathbf{k}}}{|\mathrm{\Psi }{|}^2}\left[f_1\left({\xi }_{\mathbf{k}}\right)-f_1\left(E_{\mathbf{k}}\right)\right],(6)$

$E=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{4k^2{\xi }_{\mathbf{k}}}{3}{f}_4\left({\tilde{E}}_{\mathbf{k}}\right),(7)$

and in general smaller corrections to it are provided by the terms with coefficients

$Q=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{1}{2{\mathrm{\Delta }}^2}\left[f_1\left({\tilde{E}}_{\mathbf{k}}\right)-\left({\tilde{E}}_{\mathbf{k}}^2+{\xi }_{\mathbf{k}}^2\right)f_2\left({\tilde{E}}_{\mathbf{k}}\right)\right](8)$

$R=\int \frac{d\mathbf{k}}{{\left(2\pi \right)}^3}\frac{1}{2{\mathrm{\Delta }}^2}\left\{\frac{1}{3{\mathrm{\Delta }}^2}\left[f_1\left({\tilde{E}}_{\mathbf{k}}\right)+\left({\tilde{E}}_{\mathbf{k}}^2-3{\xi }_{\mathbf{k}}^2\right)f_2\left({\tilde{E}}_{\mathbf{k}}\right)\right]+\frac{4\left({\xi }_{\mathbf{k}}^2-2{\tilde{E}}_{\mathbf{k}}^2\right)}{3}{f}_3\left({\tilde{E}}_{\mathbf{k}}\right)+2{\tilde{E}}_{\mathbf{k}}^2{\mathrm{\Delta }}^2{f}_4\left({\tilde{E}}_{\mathbf{k}}\right)\right\}.(9)$

Here ${\tilde{E}}_{\mathbf{k}}=\sqrt{{\xi }_{\mathbf{k}}^2+{\mathrm{\Delta }}^2}$, where Δ is the superfluid gap for a uniform Fermi superfluid at temperature T and density n. That means that in a Fermi superfluid in a box potential, far away from any vortex or soliton, |Ψ| = Δ. Closer to the vortex or the soliton, the pair density varies; a reduced density will locally reduce |Ψ| to values smaller than Δ.

The derivation Eq. 1 and its coefficients has been presented elsewhere [11]. It relies on a gradient expansion of the action for the pair field. At temperatures close to the critical temperature this description is valid, and in the BEC interaction regime it is valid at all temperatures, as has been verified by comparison with Bogoliubov-de Gennes theory [11]. The coefficients C, Q, E, and R are already of second order in the dertivatives of the pair wavefunction, such that no additional dependence on |Ψ| needs to be taken into account, and ${\tilde{E}}_{\mathbf{k}}$ can be used instead of E_k.

3 Interface between interaction regimes

In this paper we consider system with an interface (perpendicular to the x-axis), separating two regions with different scattering lengths. In the left half-space the scattering length is denoted by a_L, whereas in the right half space the scattering length is a_R. This could be created using a position dependent magnetic field and a Feshbach resonance. Alternatively, in a confined, quasi-1D system the effective interaction strength can be tuned by the strength of the confinement. In either case, it is probably not possible to make the interface infinitely sharp and thus we consider a spatially dependent profile for the interaction strength 1/[k_Fa_s(x)]:

$\frac{1}{a_s\left(x\right)}=\frac{1}{2}\left(a_{\text{R}}^{-1}+a_{\text{L}}^{-1}\right)+\frac{1}{2}\left(a_{\text{R}}^{-1}-a_{\text{L}}^{-1}\right)\tanh \left(x/\lambda \right).(10)$

The parameter λ determines the sharpness of the interface. Here we choose $\lambda =0.5k_F^{-1}$. This choice makes the interface sharper than the healing length of the pair condensate, but smooth enough to allow for numerical stability when performing a finite element simulation of Eq. 1. Furthermore, we choose interactions strengths in the crossover regime between BEC and BCS: 1/(k_Fa_L) = 0.4 and 1/(k_Fa_R) = 0.2. In these regimes, the effective field theory is still valid for all temperatures, as the pair correlation length is smaller than the healing length [11].

Some care should be taken, as we work in units $k_F={(3{\pi }^2\bar{n})}^{1/3}$ where $\bar{n}$ is the average density in the system. Introducing regions with different interaction strength will however lead to changes in the density away from this average, as discussed below. Nevertheless, we will keep defining our units, i.e. k_F and E_F, in terms of this average density. Note that in our units (k_F = 1), the average density is $\bar{n}=1/(3{\pi }^2)$.

For a uniform system, the chemical potential depends on the density, the interaction strength, and the temperature. In the BEC limit, the mean-field chemical potential is no longer equal to the Fermi energy at low temperature, as it would be in the BCS limit. It must be calculated from the coupled gap and number equations of the superfluid. The mean-field gap and number equations for 1/(k_Fa_L) = 0.4 lead to μ_L/E_F = 0.420, whereas 1/(k_Fa_R) = 0.2 corresponds to μ_R/E_F = 0.203. If two such uniform systems are brought into contact, such that they can exchange particles, then they will do so until the balance in chemical potentials is restored, at μ/E_F = 0.312. This will lead in turn to a difference in density, $n_L=1.38\bar{n}$ and $n_R=0.7\bar{n}$. Note that to keep the average density at $\bar{n}$, in an experimental realization the left and right containers should have appropriate sizes. Also, as expected, the pair binding energies will also be different in the left and right half-spaces: Δ_L/E_F = 1.1442 and Δ_R/E_F = 0.6568. From the density difference alone one can already conclude that not all dark solitons will retain their shape when propagating through the interface. A dark soliton where the density dip equals $\bar{n}$ can exist in the left-half space, but not in the right one. In the next section, we explore the propagation in more details.

Before introducing the solitons, the system is relaxed using Eq. 1, in order to find the correct profile of Ψ(x) at the interface. Indeed, Ψ(x) will relax back to Δ_L for x → −∞ over a distance given by the healing length ξ_L in the left pair condensate. Similarly, on the right side of the interface the pair condensate heals to its background value over a length scale ξ_R. These length scales depend on temperature and also on the scattering length, so they will be different left from right. They will also be different from λ, the width of the “step” in the scattering length, which is chosen as the shortest length scale.

4 Dark solitons in a uniform pair condensate

The goal of our numerical experiment is to send in a soliton from the left half-space towards the interface, and observe dynamics that follow from Eq. 1. In order to do this, we consider an essentially one-dimensional problem (along the x-direction), with the interface at x = 0. Equation 1 is solved using a fourth-order Runga-Kutta method on a grid with step size about an order of magnitude smaller than the healing length of the pair condensate.

For the initial state Ψ₀ we choose a right-moving dark soliton some distance from the interface, in the left half-space. A soliton in a uniform pair condensate is described by

${\mathrm{\Psi }}_0\left(x,t\right)={\mathrm{\Delta }}_{\text{L}}a\left(x-v_{s}t\right)\exp \left[i\theta \left(x-v_{s}t\right)\right],(11)$

for x < 0. Far away from the soliton, |Ψ(x)| = Δ_L. The factor a is smaller than or equal to unity: it suppresses the pair density divided by the background value Δ_L. Indeed, dark solitons are characterized by a dip in the density, whereas bright solitons (not studied here) would have a bump in the density. The phase θ exhibites a step across the soliton, leading to the velocity field that makes the soliton move. For a uniform condensate, there exist analytical solutions for both a and θ [20, 22]. Note that both the amplitude and the phase are not independent functions of position and time, but only functions of x − v_st where v_s is the soliton velocity. This expresses the fact that as the soliton moves in a uniform condensate, it does not change its shape. The soliton shape and velocity profile are determined [22] in terms of the superfluid density

${\rho }_{\text{sf}}\left(a\right)=2C|a{\mathrm{\Delta }}_{\text{L}}{|}^2-2Q|a{\mathrm{\Delta }}_{\text{L}}{|}^2{v}_s^2,(12)$

the quantum pressure

${\rho }_{\text{qp}}\left(a\right)=2\left(C-4E\right)|a{\mathrm{\Delta }}_{\text{L}}{|}^2-2\left(Q-4R|a{\mathrm{\Delta }}_{\text{L}}{|}^2\right)v_s^2,(13)$

and the phase stiffness

$\kappa \left(a\right)=D\left(|{\mathrm{\Psi }}_0\left(x\right)|\right){\mathrm{\Delta }}_{\text{L}}^2(14)$

These depend only on the amplitude function a, and not on the phase. Note that far away from the solition, the phase stiffness goes to ${\kappa }_{\infty }=D({\mathrm{\Delta }}_{\text{L}}){\mathrm{\Delta }}_{\text{L}}^2$. With these derived quantities, the amplitude a(x) can be computed from inverting the relation

$x=\pm \frac{1}{\sqrt{2}}\underset{a_0}{\overset{a}{\int }}\sqrt{\frac{{\rho }_{\mathit{\text{qp}}}\left(a^{\prime }\right)}{\mathcal{A}\left({a^{\prime }}^2\right)-\mathcal{A}\left({\mathrm{\Delta }}_{\text{L}}^2\right)-v_s^2\left[\kappa \left(a^{\prime }\right){a^{\prime }}^2-{\kappa }_{\infty }\right]/{\rho }_{\text{sf}}\left(a^{\prime }\right)}}d{a}^{\prime }.(15)$

Here a₀ is the amplitude at the center of the soliton. It is found by setting the denominator in (15) equal to zero and solving with respect to the amplitude. The faster the dark soliton, the smaller the dip in the condensate and the closer a₀ equals unity. For a soliton at zero velocity, v_s = 0, a(x) is obtained from this relation, the phase profile is computed from

$\theta \left(x\right)=v_s\underset{-\infty }{\overset{x}{\int }}\frac{\kappa \left[a\left(x^{\prime }\right)\right]a{\left(x^{\prime }\right)}^2-{\kappa }_{\infty }}{{\rho }_{\text{sf}}\left(a\left(x^{\prime }\right)\right)}d{x}^{\prime }.(16)$

This is the exact solution for a soliton in a uniform condensate [11]. Here, we use it as the initial condition, to the left of the interface. The soliton’s core is placed far enough from the interface so that a(x) is exponentially close to unity near the interface, and given an initial velocity. Below, we will investigate different initial velocities. The higher the initial velocity, the shallower the soliton.

5 Solitons colliding on the interface

The result of the simulation for a₀ = 0.5 is shown in Figure 1. This corresponds with a soliton propagating at v_s/v_F ≈ 0.35 The red dotted line shows the initial, unrelaxed, background value of |Ψ(x)| when no solitons are present. The black curve in panel (a) shows the state a small time after the start of the simulation. The order parameter at the interface has relaxed to its equilibrium value, showing a slower healing to the background values Δ_L and Δ_R. To the left of the interface, at k_Fx = −19.0, the soliton is present. The remaining curve show the soliton at slightly later times, expressed in units of $t_F=2m/(\hslash k_F^2)$. In this panel, the soliton is still far enough from the interface so as not to be influenced by it: it moves at a fixed velocity towards the interface, without changing its shape.

FIGURE 1

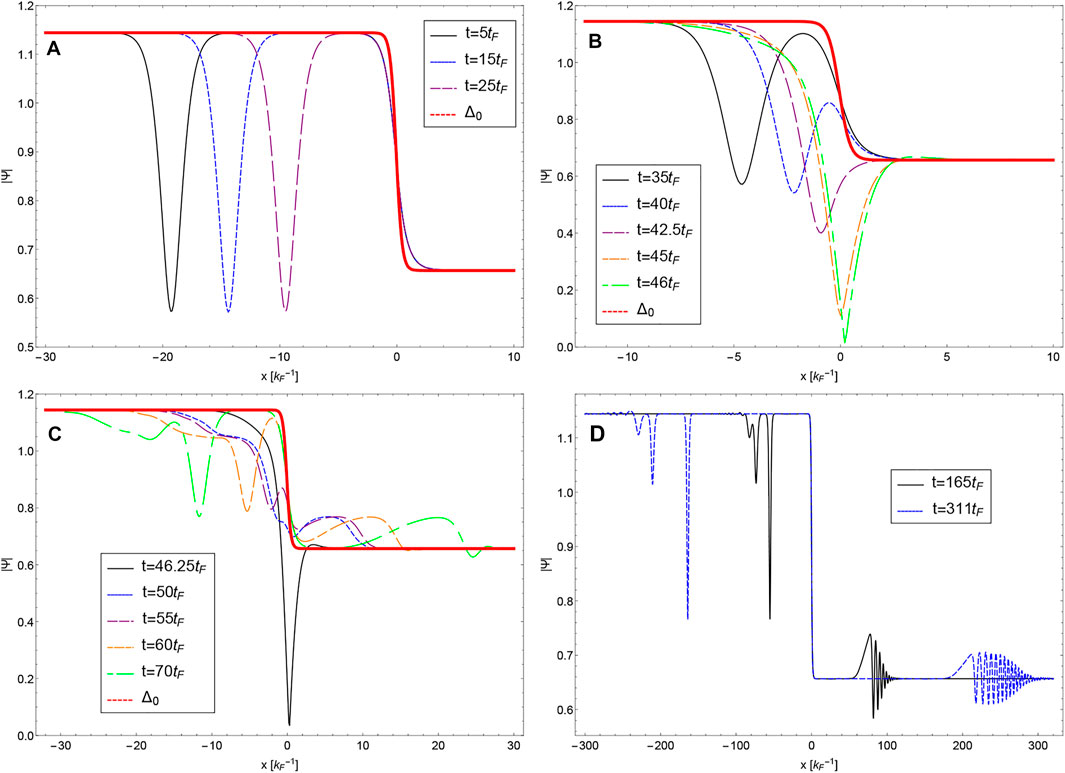
FIGURE 1. The time evolution of a soliton colliding with an interface in the pair condensate is shown. The interface at x =0 separates regions with different interaction strength and hence pair density. The red dotted line shows the background value of the pair condensate order parameter |Ψ(x)| when no soliton is present, before relaxation. The various curves and panels show the profile with a soliton at different times during the evolution. In panel (A) the soliton is still far from the interface, reaching it in panel (B). Panel (C) shows the situation shortly after the collision, whereas panel (D), with a different scale on the x-axis, shows the long-time evolution.

In panel (b) the soliton reaches the interface. The different curves again show |Ψ(x, t)| at different times. The decrease in the background density to the right of the interface causes the soliton to become “darker”, i.e. the central pair density in the soliton core decreases, reaching zero (a “black soliton”) around t = 46t_F. Also the shape of the solitary wave is affected by the interface, it becomes asymmetric and sharpens (even though it still remains wider than the healing lengths).

Panel (c) continues the series of time frames. Density dips are reflected back to the left, and a bump in the density propagates to the left. The soliton was unable to cross into the right region, even though it created a shock wave, taking away some energy from the original soliton. To identify this bump as a shock wave, panel (d) shows the longer time evolution after the collision (note that the scale on the x-axis has changed too). The propagation of the bump, and the presence of a train of phonons in front of it, is characteristic for a shock wave in a Fermi superfluid [23]. Fermi gases with 1/(k_Fa_R) = 0.2 exhibit a supersonic dispersion relation for the Anderson-Bogoliubov mode, so that a dispersive wave pattern will appear in front of the shock wave.

Still in panel (d), the nature of the reflected dips in the density is clear: these represent a sequence (here, three) solitons moving back. We checked that the phase steps also match those of solitons. Their characteristic velocities match the depth of the soliton core, and they preserve their shape as they move farther away from the interface. The soliton was unable to penetrate the interface, but it was clearly not reflected as a whole. Energy was lost in the form of a shock wave, and the reflected soliton fractures in three different solitons. Energy is conserved overall, but it is not clear what constraints lead to the fracturing of the initial soliton into three reflected ones.

In order for a soliton to cross the interface, it should be shallow enough (and hence, fast enough) not to become a black soliton during the crossing of the interface. To investigate this, we raise the central density to a₀ = 0.7 (so a 30% suppression of the background density at the soliton core). The results are shown in Figure 2. Panel (a) shows the initial stage of the time evolution, with the faster soliton in the region to the left of the interface. In panel (b), the |Ψ(x, t)| profiles are shown for times right before reaching the interface (now at t ≈ 36t_F). The soliton shape is less deformed, and seems to simply shift down along with the background density. However, from panel (c) it is clear that there is no simple transmission from one to the other region. Indeed, apart from the transmitted soliton, which becomes darker and hence slower, there is still a partial reflection, and the creation of a shock wave (with a phonon train in front of it) to the right of the transmitted soliton. These different features remain visible at later times in panel (d). Note that there is a second, very shallow reflected soliton: again the reflected wave is fractured into multiple solitons. Varying the depth of the initial soliton, we found that a critical value of a₀ ≈ 0.67 exists such that shallower solitons can pass the interface, whereas deeper solitons cannot. However, there is always a reflected part consisting of several solitons, and a transmitted shock wave.

FIGURE 2

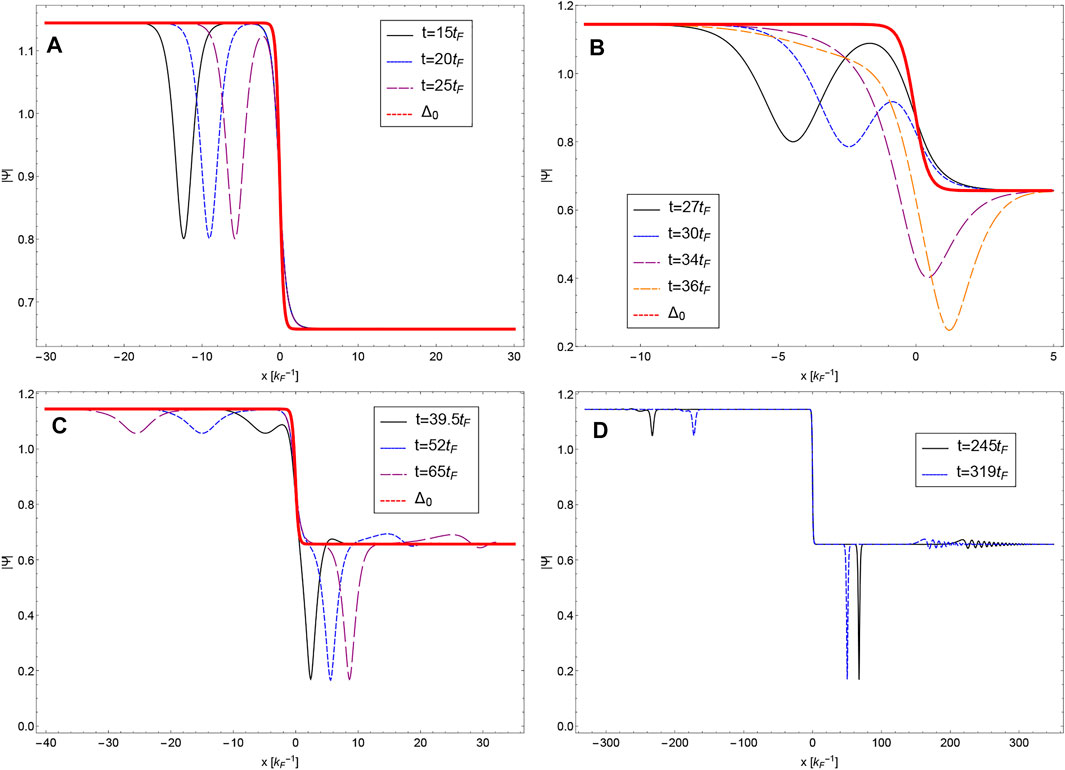
FIGURE 2. The time evolution of a soliton colliding with an interface in the pair condensate is shown, as in the previous figure. The various curves and panels show the profile with a soliton at different times during the evolution. In panel (A) the soliton moves to the interface, colliding with it in panel (B). Panel (C) shows the situation shortly after the collision, whereas panel (D), with a different scale on the x-axis, shows the long-time evolution.

6 Conclusion

We investigated solitons impinging on an interface in a Fermi superfluid, separating regions with different interaction strength and density, in the unitary regime. To do this, we use an effective field theory that describes the superfluid through the order parameter for the pair condensate. This allows for solutions in the form of dark solitons, propagating without changing their shape in a uniform superfluid. When such a soliton reaches the interface, it can only pass the interface to the region with lower density when its velocity is high enough, and the dip in the pair density of the soliton core is shallow enough. However, in all cases we find that the impact of the soliton on the interface leads to the formation of a shock wave on the other side of the interface and to several reflected solitons moving back.

Advances in experimental techniques to taylor the trapping potential for ultracold atomic gases both spatially and temporally allowed to create such interfaces [3, 6]. Solitons have been created in a Bose-Einstein condensed gas [24]. Solitons are more difficult to create in a three-dimensional superfluid Fermi gas [25], as they decay in solitonic vortices. However, confining the system in a cigar-shaped trap allows to stabilize the solitons [21]. The behavior of solitons at an interface, as described above, will constitute a good test for microscopic theories of pairing in superfluid Fermi gases. In particular, at unitarity, different theories will result in different equations of state leading to small changes in the values of the parameters of the effective field theory. The reflected soliton train and the shock wave, as well as the critical value for transmission of the original soliton will depend strongly on these parameters so that a future experimental realization of the soliton-interface collision can be used to shed light on the microscopic description of Fermi superfluids near unitarity.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Fonds voor Wetenschappelijk Onderzoek—funding for a research programme on superfluid Fermi gases, fundamental research in theoretical physics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev Mod Phys (2008) 80:885. doi:10.1103/RevModPhys.80.885

CrossRef Full Text | Google Scholar

2. Dalibard J, Gerbier F, Juzeliunas G, Öhberg P. Colloquium: Artificial gauge potentials for neutral atoms. Rev Mod Phys (2011) 83:1523–43. doi:10.1103/revmodphys.83.1523

CrossRef Full Text | Google Scholar

3. Navon N, Smith RP, Hadzibabic Z. Quantum gases in optical boxes. Nat Phys (2021) 17:1334–41. doi:10.1038/s41567-021-01403-z

CrossRef Full Text | Google Scholar

4. Trypogeorgos D, Harte T, Bonnin A, Foot C. Precise shaping of laser light by an acousto-optic deflector. Opt Express (2013) 21:24837–46. doi:10.1364/oe.21.024837

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Michael MH, Schmiedmayer J, Demler E. From the moving piston to the dynamical Casimir effect: Explorations with shaken condensates. Phys Rev A (2019) 99:053615. doi:10.1103/PhysRevA.99.053615

CrossRef Full Text | Google Scholar

6. Steinhauer J. Observation of self-amplifying Hawking radiation in an analog black hole laser. Nat Phys. (2014) 10:864. doi:10.1038/nphys3104

CrossRef Full Text | Google Scholar

7. Carusotto I, Fagnocchi S, Recati A, Balbinot R, Fabbri A. Numerical observation of Hawking radiation from acoustic black holes in atomic Bose–Einstein condensates. New J Phys (2008) 10:103001. doi:10.1088/1367-2630/10/10/103001

CrossRef Full Text | Google Scholar

8. Mukherjee B, Yan Z, Patel PB, Hadzibabic Z, Yefsah T, Struck J, et al. Homogeneous atomic Fermi gases. Phys Rev Lett (2017) 118:123401 doi:10.1103/physrevlett.118.123401

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Regal CA, Greiner M, Jin DS. Observation of resonance condensation of fermionic atom pairsObservation of resonance condensation of fermionic atom pairs. Phys Rev Lett (2004) 92:040403 doi:10.1103/physrevlett.92.040403

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Klimin SN, Tempere J, Lombardi G, Devreese JT. Finite temperature effective field theory and two-band superfluidity in Fermi gases. Eur Phys J B (2015) 88:122. doi:10.1140/epjb/e2015-60213-4

CrossRef Full Text | Google Scholar

11. Klimin SN, Tempere J, Devreese JT. Finite tempereture effective field theory for dark solitons in superfluid Fermi gases. Phys Rev A (2014) 90:053613. doi:10.1103/PhysRevA.90.053613

CrossRef Full Text | Google Scholar

12. Skulte J, Broers L, Cosme JG, Mathey L Vortex and soliton dynamics in particle-hole-symmetric superfluids, Phys Rev Res 3 (2021). p. 043109. doi:10.1103/PhysRevResearch.3.043109

CrossRef Full Text | Google Scholar

13. Qu R-L, Li K, Bai Y-X, Zhao H-S. The different temperature-dependent behaviors of dark solitons in Fermi superfluid gases along the BCS–BEC crossover. J Low Temp Phys (2021) 205:135–42. doi:10.1007/s10909-021-02622-7

CrossRef Full Text | Google Scholar

14. Ren T, Aleiner I. Solitons in one-dimensional systems at the BCS-BEC crossover. Phys Rev A (2019) 99:013626. doi:10.1103/PhysRevA.99.013626

CrossRef Full Text | Google Scholar

15. Ebling U, Alavi A, Brand J. Signatures of the BCS-BEC crossover in the yrast spectra of Fermi quantum rings. Phys Rev Res (2021) 3:023142. doi:10.1103/PhysRevResearch.3.023142

CrossRef Full Text | Google Scholar

16. Zhao LC, Wang W, Tang Q, Yang ZY, Yang WL, Liu J. Spin soliton with a negative-positive mass transitionSpin soliton with a negative-positive mass transition. Phys Rev A (Coll Park) (2020) 101:043621. doi:10.1103/physreva.101.043621

CrossRef Full Text | Google Scholar

17. Debnath A, Khan A, Basu S. Dropleton-soliton crossover mediated via trap modulation. Phys Lett A (2022) 439:128137. doi:10.1016/j.physleta.2022.128137

CrossRef Full Text | Google Scholar

18. Chen Y, Ren Y, Liu Z, Liu T, Wu H, Xiong Z, et al. Bright soliton dynamics in higher-dimensional system with power-law nonlinearity. Int J Mod Phys B (2021) 35:2150138. doi:10.1142/s0217979221501381

CrossRef Full Text | Google Scholar

19. Andreev PA. Novel soliton in dipolar BEC caused by the quantum fluctuations. Eur Phys J D (2021) 75:60. doi:10.1140/epjd/s10053-021-00071-1

CrossRef Full Text | Google Scholar

20. Lombardi G, Van Alphen W, Klimin SN, Tempere J Soliton-core filling in superfluid Fermi gases with spin imbalance, Phys Rev A 93 (2016). p. 013614. doi:10.1103/PhysRevA.93.013614

CrossRef Full Text | Google Scholar

21. Lombardi G, Van Alphen Wout W, Klimin SN, Tempere J. Snake instability of dark solitons across the BEC-BCS crossover : An effective-field-theory perspective. Phys Rev A (2017) 96:033609. doi:10.1103/PhysRevA.96.033609

CrossRef Full Text | Google Scholar

22. Van Alphen W, Lombardi G, Klimin SN, Tempere J. Dark soliton collisions in superfluid Fermi gases. New J Phys (2018) 20:053052.

CrossRef Full Text | Google Scholar

23. Van Loon S, Van Alphen W, Tempere J, Kurkjian H. Transition from supersonic to subsonic waves in superfluid Fermi gases. Phys Rev A (2018) 98:063627. doi:10.1103/PhysRevA.98.063627

CrossRef Full Text | Google Scholar

24. Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K. Dark solitons in bose-einstein CondensatesMotion of a solitonic vortex in the BEC-BCS crossover. Phys Rev Lett (1999) 83:5198.

CrossRef Full Text | Google Scholar

25. Ku MJH, Ji W, Mukherjee B, Guardado SE, Cheuk LW, Yefsah T, et al. Motion of a solitonic vortex in the BEC-BCS crossover. Phys Rev Lett (2014) 113:065301 doi:10.1103/PhysRevLett.113.065301

PubMed Abstract | CrossRef Full Text | Google Scholar