
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys., 14 July 2022
Sec. Soft Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.953067
This article is part of the Research TopicProbing Out-of-Equilibrium Soft MatterView all 10 articles
A thermophilic suspension of nanoparticles heated from below exhibits a complex stability diagram determined by the competition between the stabilizing flux of nanoparticles induced by thermophoresis and the destabilizing flux determined by thermal convection. We investigate Rayleigh-Bénard convection in a suspension of highly thermophilic nanoparticles with large negative separation ratio ψ = −3.5 heated from below. We show that transient localized states appear in the range of Rayleigh numbers 2200
In the presence of a density stratification, a layer of fluid exhibits a rich phenomenology determined by the action of gravity that can lead to oscillations and wave propagation [1, 2]. A typical case is represented by a single component fluid heated from below, where the stratification is determined by the thermal dilation of the fluid, which can transfer heat either in a conductive or in a convective regime. The stability of the system is parametrized by the dimensionless Rayleigh number Ra
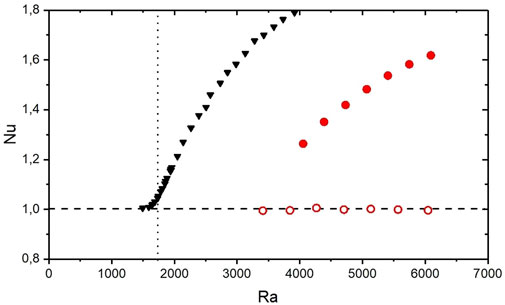
FIGURE 1. Stability diagram. Nusselt number as a function of Rayleigh number for a single component fluid (liquid Helium, triangles) and LUDOXTM colloidal silica nanoparticles in water at a concentration of 4.0% w/w (circles). The colloidal sample exhibits bistability, represented by the co-existence of a stable convective branch (full circles) and a stable conductive branch (open circles). The dashed horizontal line represents the purely conductive regime (Nu = 1), while the vertical dotted line is the threshold Rac = 1708 for Rayleigh-Bénard convection in a single component fluid. Transient rotating structures are observed in the range of Rayleigh numbers 2000 < Ra
In this work we focus on the investigation of transient Rayleigh-Bénard convection in a suspension of highly thermophilic nanoparticles with large negative separation ratio ψ = −3.5 heated from below, under experimental conditions similar to those employed in theoretical studies [20–22]. We show that transient localized states appear in the range of Rayleigh numbers 2200
The study of spatially localized states is of great interest in the field of pattern formation, as they appear in a great variety of physical and biological systems [23, 24]. In the case of localized stationary convective states, they take the name of convectons, and there is a growing number of works studying them from a theoretical, computational and experimental point of view [10, 23, 25–27].
The sample chosen for the experiment is a colloidal suspension made by distilled water and LUDOXTM TMA, a commercial colloid made of silica nanoparticle with an average diameter of 22 nm. In this work we have used concentrations of 4.0% w/w. The thermophysical properties are detailed in Table 1. This sample has been selected as a model system for the investigation of thermophoresis at the mesoscopic scale in the absence of gravity within the framework of the Giant Fluctuations and TechNES space projects of the European Space Agency [28, 29]. Within these projects, a series of experiments will be performed on the International Space Station to investigate the non-equilibrium fluctuations determined by the thermophoretic process. Preliminary studies performed on Earth under isothermal conditions showed the presence of a peculiar relaxation dynamics of non-equilibrium concentration fluctuations, characterized by anomalous diffusion at large wave vectors [30]. For these reasons, it is very important to achieve a full understanding of the stability of this colloidal suspension in the presence of gravity.
The central element of the apparatus is a thermal gradient cell, consisting in a layer of fluid confined by two sapphire plates through which a thermal gradient can be applied. The heating elements are two ring-shaped Thermo Electric Devices (TED) thermally coupled to the sapphire plates. The other side of both the TED elements is in contact with a thermal reservoir, consisting of two annular aluminium chambers, inside which there is a steady flow of water at constant temperature. The purpose of this reservoir is to remove the excess heat. The cell is mounted on an optical bench in the configuration where the sample layer is horizontal, and is illuminated by a superluminous diode (Superlum SLD-261) with central wavelength 670 nm. The limited temporal coherence of the source avoids interference determined by multiple reflections of the beam on the surfaces of the cell windows. The sensor employed is a monochrome CCD Camera (JAI CV-M300) with a resolution of 576 × 768 pixels and a depth of 8 bit, operating at a frame rate of 10 images per second. An achromatic doublet with focal length of 30 cm, placed between the sample cell and the camera images a plane at distance z = −90.6 ± 0.5 cm from the sample in a shadowgraph configuration that allows to visualize the self-organized structures generated by the convective motions. The camera is controlled remotely by a computer through a National Instrument PCI-1407 frame-grabber.
Heat conduction in fluids is greatly affected by the presence of colloidal particles that exhibit a thermophilic behaviour. In particular, the presence of even a small amount of thermophilic particles has a stabilizing effect when the suspension is heated from below and, as a result, the sample can transfer heat either in a conductive or in a convective regime, depending on the initial condition (Figure 1) [15, 16]. The conductive regime can be accessed by imposing slowly a temperature difference to the sample heating from below, so that the thermophilic particles accumulate at the bottom of the cell and stabilize the sample against Rayleigh-Bénard convection. The convective regime can be accessed by first heating the sample from above to determine the accumulation of nanoparticles at the top of the cell, and then suddenly reversing the temperature gradient by heating from below. Under these conditions a Rayleigh-Bénard instability starts and the accumulation of the thermophilic particles at the bottom of the cell is prevented by the convective flow that keeps the particles mixed. Conversely, if the temperature gradient is reversed by slowly heating from below thermophoresis determines the rapid formation of a stable boundary layer at the bottom of the cell and the system ends up in the conductive regime.
The bistable heat transfer is currently a well established feature of strongly thermophilic nanoparticles [15, 16], but bistability is apparent only for Rayleigh numbers Ra
In order to study the transient convective regime in this range of Rayleigh numbers we have performed experiments according to the following procedure: i) The sample is heated from above for 1 h, applying a temperature difference ΔT = 10.5K. This ensures that, because of the strong thermophilic behaviour of LUDOXTM TMA, the colloidal particles diffuse towards the upper plate, and the sample enters a regime of solutal convection [31–33]. The time needed to enter this solutal convective regime has been determined empirically. Physically, it corresponds to the diffusive time τδ = δ2/D needed for the formation of a thin—unstable—boundary layer of thickness δ at the top of the cell, and is affected by the size of the nanoparticles through their diffusion coefficient D. ii) The temperature gradient is abruptly reverted to a negative value. In our tests we used temperature differences of ΔT = −3.00 K, − 3.38 K, − 3.75 K, − 4.13 K. iii) shadowgraph images of the sample are recorded with a frame rate of, approximatively, 10 images/second.
Under these conditions, when the sample is first heated from above at the beginning of the experiment, solutal convection destabilizes the suspension (Figure 2A) so that, when the gradient is inverted, a convective instability develops in the sample, even when the sample is below the threshold needed for the development of stationary Rayleigh-Bénard convection in the nanofluid (Figure 2). At the beginning, the convective patterns are the usual convective rolls that characterize Rayleigh-Bénard convection, spanning all the area of the cell. After some time, the patterns begin to rotate around the vertical axis (clockwise or anticlockwise, indifferently). Subsequently, convection begins to die out starting from the borders of the cell, giving rise to the formation of a single rotating localized pattern. Eventually, the rotating pattern shrinks in size, until it disappears completely and the sample reaches the stationary conductive state. The duration of the entire phenomenon, measured from the inversion of the gradient, is of the order of 1–3 h. The same phenomenology is observed for all temperature differences studied.
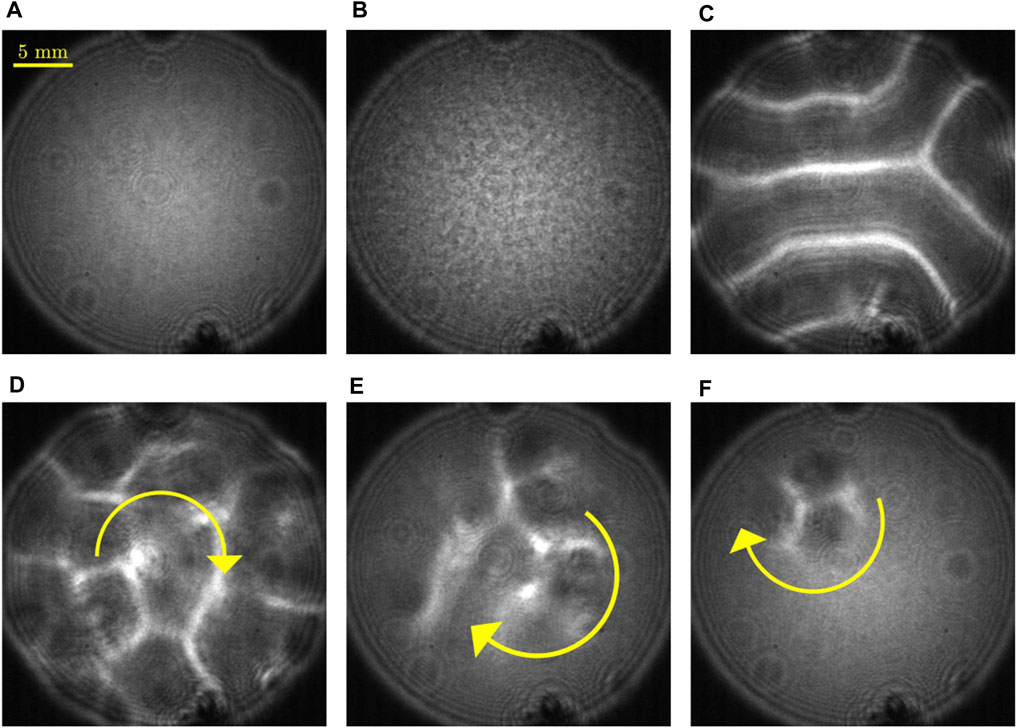
FIGURE 2. Image sequence representing the evolution of the convective instability in a 3.1 mm thick layer of LUDOXTM TMA 4% w/w. (A) at the beginning, heating from above with a temperature difference of 10.5K, no macroscopic motions are present; (B) after a time of the order of tens of minutes solutal convection develops in the cell; (C) after 1 h, the temperature difference is inverted and set to -4.13 K. In, approximatively 3 min thermal convective rolls appear in the sample; (D) the rolls, after a time that depends on the Rayleigh number, start to rotate; (E) they die out starting from the borders; (F) they gradually shrink in size, until they finally disappear.
By looking at sequences of images, we measured some characteristic parameters of the localized states as a function of Rayleigh number. The interesting quantities are the wave vector k of the patterns and their angular velocity ω, and the typical timescales tap needed for the appearance of the convective structure, trot needed for the rotation of the pattern to start, and tex needed for the patterns to disappear. The results are summarized in Figure 3.
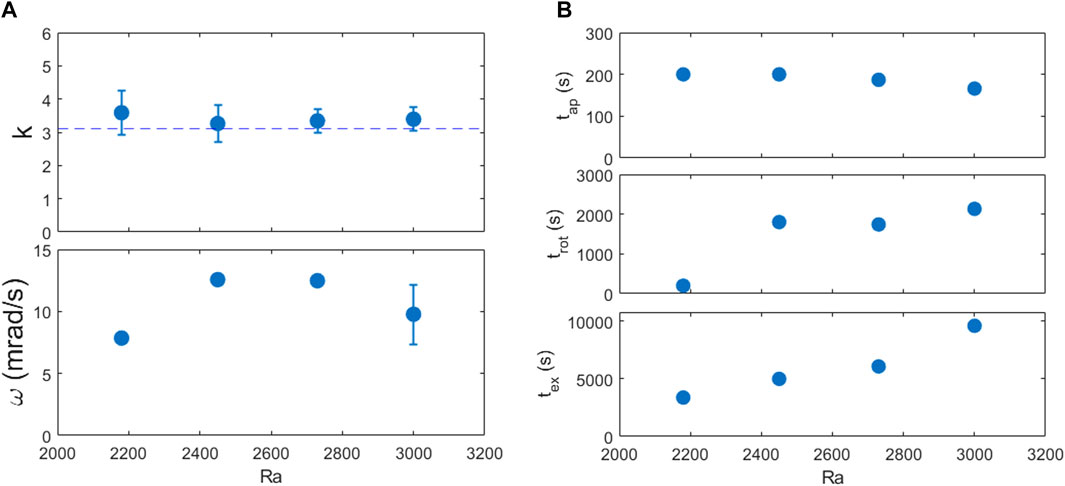
FIGURE 3. (A): dimensionless wave number k (top) and angular velocity ω of the patterns (bottom) as a function of Rayleigh number. The dashed line marks the theoretical wave number kc = 3.117 of Rayleigh-Bénard convection close to the onset. (B): time needed for the appearance of the convective pattern, tap (top), time for the beginning of the rotation of the pattern, trot (middle), and time of extinction of the convective instability, tex (bottom), plotted as a function of the Rayleigh number. Time t = 0 corresponds to the instant when the gradient gets reversed.
The characteristic wave vector k is compatible with the value 3.117 predicted for Rayleigh-Bénard convection close to the threshold. The angular velocity of the patterns has been determined from the visual observation of a large number of complete revolutions of the localized pattern (typically 10–20 revolutions). In selecting the maximum number of revolutions to consider for a reliable determination of the angular velocity we relied on the fact that the structure of the rotating pattern needed to be preserved, so that the motion of the spatial features of the patterns could be followed during their rotation. This method proved to be more effective and immune to errors than the automatic processing of the angular correlations.
The rotation of the patterns is very slow, a complete revolution taking a time in the range 500–800 s. The time tap needed for the appearance of the structures is of the order of 200 s, and slightly decreases as the Rayleigh number increases. The behaviour of the time trot needed for the rotation to start is of major interest, because it exhibits a variation of a factor 10 when the Rayleigh number is increased from 2180 to 3000, indicating that the range explored is extremely important and revealing. Indeed, in this range, as already noted, there is a competition between the Rayleigh-Bénard thermal convection and the stabilizing effect of the colloidal particles. This competition leads to the formation of travelling waves patterns, which, in a circular cell, become rotating patterns, due to the confinement determined by the lateral boundary. However, in the regime of subcritical Rayleigh numbers explored by us Rayleigh-Bénard convection prevails, and the stabilizing effect due to the accumulation of the colloid on the bottom of the cell is hampered by the continuous remixing of the particles. Under these conditions, the sedimentation of the particles is slowed down, and so are the appearance of travelling waves and the beginning of the rotation. The time needed for convection to disappear also exhibits a marked dependence on the Rayleigh number, and is in qualitative agreement with the results of simulations on suspensions of thermophilic nanoparticles with large negative separation ratio heated from below [20].
Our system is different from most of those that, to our knowledge, have been previously characterized experimentally or theoretically and by means of simulations. In fact, a large number of studies has been devoted to the investigation of water-ethanol mixtures heated form below. Depending on the concentration of ethanol, this system can exhibit a negative separation ratio ψ > − 1, leading to the oscillatory onset of a convective instability when the fluid is heated from below. Water-ethanol mixtures exhibit a multistable heat transfer at sufficiently small supercritical Rayleigh numbers [3, 5, 6, 8, 11, 12, 14], where depending on the initial condition and on the history of the system the transfer of heat can either occur by conduction or by steady overturning convection, similarly to the bistable behaviour reported by us. The investigation of transient behaviour during the onset of convection shows the development of localized pulses of travelling-wave convection in 1D [9, 23] and 2D geometries [10]. Under supercritical conditions, localized rotating structures develop, and gradually expand until they reach the boundaries of the cell [10, 27]. Conversely, bringing back the system in a subcritical condition after the onset of convection determines the formation of rotating structures that gradually shrink in time until they disappear [13, 34].
All these works deal with binary fluids with a negative separation ratio −1 < ψ < 0, a condition where the thermal contribution to the density variation is larger than the solutal one. At variance, our system is a colloidal suspension of nanoparticles and has a separation ratio ψ = −3.5, so that the solutal contribution to the density profile largely dominates the thermal one. Indeed, many of the solutions studied in the cited works are travelling waves that don’t die out, whereas the instability that we observed in the end disappears, notwithstanding the fact that the system is under supercritical conditions, due to the stabilization determined by the highly thermophilic particles.
The case of thermal convection in a suspension of thermophilic nanoparticles with a large negative separation ratio ψ = −10 has been investigated theoretically by Ryskin and Pleiner [17]. They studied the linear and nonlinear behaviour starting from a suspension with an initially uniform distribution of nanoparticles. They found that at small supercritical Rayleigh numbers Ra
Cherepanov and Smorodin have performed a detailed theoretical investigation of the stability of a colloidal suspension heated from below and with negative separation ratio ψ = −0.8, taking into account not only the Soret effect but also the effect of sedimentation induced by gravity [21,22]. The sedimentation length lg becomes in this case an important parameter: for lg ≪ h the colloid gets almost entirely accumulated at the bottom boundary, and the system behaves as a single component fluid. When lg ≥ h, the threshold for Rayleigh-Benard convection gradually increases to values of the order of several time the threshold for a single component fluid. While the parameters adopted in these studies partially mirror the ones of our sample, the separation ratio ψ = −0.8 adopted by Cherepanov and Smorodin corresponds to the condition where the Rayleigh-Bénard convection dominates over the solutal stabilization. By contrast, in the case investigated by us the sedimentation length is moderately high, lg/h = 20, but the strong negative separation ratio ψ = −3.5 determines an accumulation of particles at the bottom boundary dominated by the Soret effect and affected only marginally by sedimentation.
Recent experimental studies have outlined the potentiality of the bistability of nanofluids with large negative separation ratio, like the one we studied in this work, to actively control heat transfer by switching between the conductive regime and the convective one (and vice-versa) exploiting the thermophilic behaviour of the nanoparticles [15, 16]. Cherepanov and Smorodin performed 2-dimensional simulations of thermophilic nanofluids with a separation ratio ψ = −7.5 heated from below mirroring the one used in these experiments. This study has been able to reproduce accurately the following quantitative aspects observed in experiments performed on a Hyflon MFA suspension of nanoparticles at a concentration of 4.0% w/w [15]: i) The presence of transient and stationary travelling wave regimes separated by a threshold Rayleigh number Ra* ≈ 3400; ii) the modifications determined by the presence of nanoparticles on the bifurcation diagram of the Nusselt number as a function of Rayleigh Number; iii) the diagram of the lifetime of travelling waves in the transient regime as a function of Rayleigh number.
Simulations along the same lines of the ones performed by Cherepanov and Smorodin on suspensions of Hyflon MFA nanoparticles should be able to describe effectively the experimental results provided by us in this publication, in particular the bifurcation diagram (Figure 1), and the lifetime of transient convection (Figure 3) in a suspension of Ludox nanoparticles.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
AV conceived the study and wrote the paper. AP performed measurements. MC and AV coordinated research. All the authors analysed results and contributed to the manuscript.
Work partially supported by the European Space Agency, CORA-MAP TechNES Contract No. 4000128933/19/NL/PG.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank M. Allevi, M. Bernardin, R. Cerbino, F. Comitani, and G. Donzelli for early discussion.
2. Carpineti M, Croccolo F, Vailati A. Levitation, Oscillations, and Wave Propagation in a Stratified Fluid. Eur J Phys (2021) 42:055011. doi:10.1088/1361-6404/ac0fba
3. Walden R, Kolodner P, Passner A, Surko CM. Traveling Waves and Chaos in Convection in Binary Fluid Mixtures. Phys Rev Lett (1985) 55:496–9. doi:10.1103/physrevlett.55.496
4. Kolodner P, Passner A, Surko CM, Walden RW. Onset of Oscillatory Convection in a Binary Fluid Mixture. Phys Rev Lett (1986) 56:2621–4. doi:10.1103/physrevlett.56.2621
5. Moses E, Fineberg J, Steinberg V. Multistability and Confined Traveling-Wave Patterns in a Convecting Binary Mixture. Phys Rev A (1987) 35:2757–60. doi:10.1103/physreva.35.2757
6. Heinrichs R, Ahlers G, Cannell DS. Traveling Waves and Spatial Variation in the Convection of a Binary Mixture. Phys Rev A (1987) 35:2761–4. doi:10.1103/physreva.35.2761
7. Kolodner P, Bensimon D, Surko CM. Traveling-wave Convection in an Annulus. Phys Rev Lett (1988) 60:1723–6. doi:10.1103/physrevlett.60.1723
8. Niemela JJ, Ahlers G, Cannell DS. Localized Traveling-Wave States in Binary-Fluid Convection. Phys Rev Lett (1990) 64:1365–8. doi:10.1103/physrevlett.64.1365
9. Kolodner P, Glazier JA, Williams H. Dispersive Chaos in One-Dimensional Traveling-Wave Convection. Phys Rev Lett (1990) 65:1579–82. doi:10.1103/PhysRevLett.65.1579
10. Lerman K, Bodenschatz E, Cannell DS, Ahlers G. Transient Localized States in 2d Binary Liquid Convection. Phys Rev Lett (1993) 70:3572–5. doi:10.1103/physrevlett.70.3572
11. Lerman K, Ahlers G, Cannell DS. Different Convection Dynamics in Mixtures with the Same Separation Ratio. Phys Rev E (1996) 53:R2041–R2044. doi:10.1103/physreve.53.r2041
12. Porta AL, Surko CM. Dynamics of Two-Dimensional Traveling-Wave Convection Patterns. Phys Rev E (1996) 53:5916–34.
13. Lerman K, Cannell DS, Ahlers G. Analysis of Transients for Binary Mixture Convection in Cylindrical Geometry. Phys Rev E (1999) 59:2975–85. doi:10.1103/physreve.59.2975
14. Aegertner CM, Surko CM. Effect of Lateral Boundaries on Traveling-Wave Dynamics in Binary Fluid Convection. Phys Rev E (2001) 63:046301.
15. Donzelli G, Cerbino R, Vailati A. Bistable Heat Transfer in a Nanofluid. Phys Rev Lett (2009) 102:104503. doi:10.1103/physrevlett.102.104503
16. Bernardin M, Comitani F, Vailati A. Tunable Heat Transfer with Smart Nanofluids. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:066321. doi:10.1103/PhysRevE.85.066321
17. Ryskin A, Pleiner H. Thermal Convection in Colloidal Suspensions with Negative Separation Ratio. Phys Rev E Stat Nonlin Soft Matter Phys (2005) 71:056303. doi:10.1103/PhysRevE.71.056303
18. Shliomis MI, Smorodin BL. Onset of Convection in Colloids Stratified by Gravity. Phys Rev E Stat Nonlin Soft Matter Phys (2005) 71:036312. doi:10.1103/PhysRevE.71.036312
19. Smorodin BL, Cherepanov IN, Myznikova BI, Shliomis MI. Traveling-wave Convection in Colloids Stratified by Gravity. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84:026305. doi:10.1103/PhysRevE.84.026305
20. Cherepanov I, Smorodin B. Traveling Waves of a Colloidal Suspension in a Closed Cell. Eur Phys J E (2022) 45. doi:10.1140/epje/s10189-022-00192-4
21. Cherepanov IN, Smorodin BL. Influence of Sedimentation Length on the Convective Stability of a Colloidal Suspension. J Exp Theor Phys (2017) 125:1199–207. doi:10.1134/s1063776117120020
22. Cherepanov IN, Smorodin BL. Convection of strong Stratified Colloidal Suspension. Microgravity Sci Technol (2019) 31:517–25. doi:10.1007/s12217-019-09726-6
23. Batiste O, Knobloch E, Alonso A, Mercader I. Spatially Localized Binary-Fluid Convection. J Fluid Mech (2006) 560:149–58. doi:10.1017/s0022112006000759
24. Knobloch E. Spatially Localized Structures in Dissipative Systems: Open Problems. Nonlinearity (2008) 21:T45–T60. doi:10.1088/0951-7715/21/4/t02
25. Batiste O, Knobloch E. Simulations of Localized States of Stationary Convection in 3he-4he Mixtures. Phys Rev E (2005) 95:244501. doi:10.1103/PhysRevLett.95.244501
26. Batiste O, Knobloch E. Simulations of Oscillatory Convection in 3he-4he Mixtures in Moderate Aspect Ratio Containers. Phys Fluids (2005) 17:064102. doi:10.1063/1.1920349
27. Mercader I, Alonso A, Batiste O. Spatiotemporal Dynamics Near the Onset of Convection for Binary Mixtures in Cylindrical Containers. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 77:036313. doi:10.1103/PhysRevE.77.036313
28. Baaske P, Bataller H, Braibanti M, Carpineti M, Cerbino R, Croccolo F, et al. The NEUF-DIX Space Project - Non-EquilibriUm Fluctuations during DIffusion in compleX Liquids. Eur Phys J E (2016) 39. doi:10.1140/epje/i2016-16119-1
29. Vailati A, Baaske P, Bataller H, Bolis S, Braibanti M, Carpineti M, et al. Giant Fluctuations Induced by thermal Diffusion in Complex Liquids. Microgravity Sci Technol (2020) 32:873–87. doi:10.1007/s12217-020-09815-x
30. Giavazzi F, Savorana G, Vailati A, Cerbino R. Structure and Dynamics of Concentration Fluctuations in a Non-equilibrium Dense Colloidal Suspension. Soft Matter (2016) 12:6588–600. doi:10.1039/c6sm00935b
31. Cerbino R, Vailati A, Giglio M. Soret Driven Convection in a Colloidal Solution Heated from above at Very Large Solutal Rayleigh Number. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 66:055301. doi:10.1103/PhysRevE.66.055301
32. Mazzoni S, Giavazzi F, Cerbino R, Giglio M, Vailati A. Mutual Voronoi Tessellation in Spoke Pattern Convection. Phys Rev Lett (2008) 100:188104. doi:10.1103/physrevlett.100.188104
33. Giavazzi F, Vailati A. Scaling of the Spatial Power Spectrum of Excitations at the Onset of Solutal Convection in a Nanofluid Far from Equilibrium. Phys Rev E Stat Nonlin Soft Matter Phys (2009) 80:015303. doi:10.1103/PhysRevE.80.015303
Keywords: thermophilic nanoparticles, Rayleigh-Bénard convection, travelling waves, localized structures, convectons
Citation: Carpineti M, Castellini S, Pogliani A and Vailati A (2022) Transient Localized Rotating Structures in a Suspension of Highly Thermophilic Nanoparticles. Front. Phys. 10:953067. doi: 10.3389/fphy.2022.953067
Received: 25 May 2022; Accepted: 22 June 2022;
Published: 14 July 2022.
Edited by:
Ramon Castañeda-Priego, University of Guanajuato, MexicoReviewed by:
Alokmay Datta, University of Calcutta, IndiaCopyright © 2022 Carpineti, Castellini, Pogliani and Vailati. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Vailati, YWxiZXJ0by52YWlsYXRpQHVuaW1pLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.